A Novel Domination in Vague Influence Graphs with an Application

Abstract

Vague influence graphs (VIGs) are well articulated, useful and practical tools for managing the uncertainty preoccupied in all real-life difficulties where ambiguous facts, figures and explorations are explained. A VIG gives the information about the effect of a vertex on the edge. In this paper, we present the domination concept for VIG. Some issues and results of the domination in vague graphs (VGs) are also developed in VIGs. We defined some basic notions in the VIGs such as the walk, path, strength of $\mathcal{I}n$-pair , strong $\mathcal{I}n$-pair, $\mathcal{I}n$-cut vertex, $\mathcal{I}n$-cut pair (CP), complete VIG and strong pair domination number in VIG. Finally, an application of domination in illegal drug trade was introduced.

1. Introduction

Graphs are a common method to visually illustrate relationships in data. The purpose of a graph is to present data that are too numerous or complicated to be described adequately in the text and in less space. The fuzzy graph (FG) theory is an important area of research that is the backbone of representations of any network with ambiguity. Crisp graphs are not sufficient to capture the uncertainty of parameters in networks, for example, strong relationships and effective, influential or popular persons. Zadeh [1] introduced the subject of a fuzzy set (FS) in 1995. Rosenfeld [2] proposed the subject of FGs. The definitions of FGs from the Zadeh fuzzy relations in 1973 were presented by Kaufmann [3]. Bhutani and Rosenfeld [4] explained the concept of strong edge (SE) in FGs. FGs and their generalizations have played an essential role in dealing with real-life problems involving uncertainties. Gau and Buehrer [5] proposed the concept of a vague set (VS) by replacing the value of an element in a set with a sub interval of [0, 1]. Moreover, a VG can concentrate on determining the uncertainties coupled with the inconsistent and indeterminate information of any real-world problems where FGs may not lead to adequate results. Ramakrishna in [6] proposed a new concept of VGs, belonging to the FGs family, which had good capabilities when faced with problems that could not be expressed by FGs. The notion of a VG is a new mathematical attitude to model the ambiguity and uncertainty in decision-making issues. Study on VG and results from these graphs were introduced by Kosari et al. [7,8,9,10]. Furthermore, a review was carried out on different types of FGs, and the new results were studied [11,12,13]. In graph theory, a dominating set (DS) for a graph G is a subset D of its vertices, such that any vertex of G is either in D or has a neighbor in D. The domination number $\gamma \left(G\right)$ is the number of vertices in a smallest DS for G. DSs are of practical interest in several areas. In wireless networking, DSs are used to find efficient routes within ad hoc mobile networks. They have also been used in document summarization and in designing secure systems for electrical grids. The concept of DS in FGs, both theoretically and practically, is very valuable. A DS in FGs is used for solving problems of different branches in applied sciences such as location problems. In this way, the study of new concepts such as DS is essential in FG. Domination in VGs has applications in several fields. Domination emerges in the facility location problems, where the number of facilities is fixed and one endeavors to minimize the distance that a person needs to travel to get to the closest facility. Selvam et al. [14] proposed the issue of domination in the join of FGs using SE. Domination in the join of incidence FGs using strong pairs was defined by Nazeer et al. [15]. Notes on domination and strong domination and total domination in FGs were introduced by Manjusha and Sunitha [16,17,18].

FGs are unable to give information about the impact of vertices on the edges. This shortage in FGs was the basic problem which is covered by $\mathcal{I}n$-FGs. It was Dinesh who introduced the extension of FGs known as $\mathcal{I}n$-FGs, which give information regarding the effect of vertices on the edges [19].

VIGs can represent natural flow networks with extra illegal flow conditions. They have been used in physical problems related to networking and trafficking. Through this paper, the connectivity thoughts in VIG are extended along with the study of several fundamental properties of such graphs. Special influence vertices are studied and the relationships between several influence parameters have been found.

Mathew et al. [20,21] expressed the notions of fuzzy end vertices for $\mathcal{I}n$-FGs. Natarajan et al. [22] studied strong (weak) domination in FGs. Certain properties of domination in VG products were explained by Shi et al. [23]. New results on VG were reported by Akram et al. [24,25]. Borzooei et al. [26] explained the new definition of domination in VGs. Double domination in VGs was developed by Banitalebi [27]. Some properties of double domination in VGs were defined by [28]. New results of FGs were presented by Rashmanlou et al. [29,30]. The concept of a strong pair domination number in intuitionistic $\mathcal{I}n$-FGs was introduced by Rehman et al. [31]. Poulik et al. [32] presented the Randic index in graphs.

1.1. Methodology and Importance of VIG

The idea of VIG is proposed for three reasons. First, FGs are not able to provide the effect of vertices on the edges, and this flaw is covered by $\mathcal{I}n$-FGs, but they only provide the effect of a vertex on an edge and not on all the edges of the graph. The effect of vertices on any edge of the graph is given in VIGs. However, VIGs are incapable of intimating the degree of non-membership of the vertices, edges and $\mathcal{I}n$-pairs. This is the main reason behind the idea of VIGs.

Second, it broadens the ideas of domination, minimal strong fuzzy in $\mathcal{I}n$-pair DS and minimum strong $\mathcal{I}n$-pair domination number in VIGs.

Third, there is a vertex m along with an edge $nl$, and they are not connected. Then, by using the influence theory, an $\mathcal{I}n$-path can be generated between vertex m to vertices $n,l$ and edge $nl$. Lastly, $\mathcal{I}n$-FG shows the effect of a vertex on which vertices are connected with it only, whereas VIGs are capable of reflecting not only the impact of a vertex on any edge of the graph but also providing the effect of a vertex of a graph on the edge of the other graph. In the FG theory, there was no such concept .

1.2. Research Gaps and Motivation of Study

The following points influenced us to write this article:

• Due to the enormous applications of domination in FGs, including domination for FGs in distinct decision-making problems, it seems advantageous to expand the notion of domination in VIG.
• There are numerous applications of the domination in VIG in chemistry, computer science, psychology, and others.
• Moreover, some basic notions related to domination such as walk, path, strength of $\mathcal{I}n$-pair, strong $\mathcal{I}n$-pair, and $\mathcal{I}n$-cut vertex have not yet been discussed and studied in the literature, and therefore, we expanded the notion of domination of $\mathcal{I}n$-FG to the domination of VIG, and the strong pair domination number is investigated.

1.3. Contribution of This Study

VGs provide tools for modeling different types of real-world networks. However, we should consider more relations, especially the relationship between edges with their corresponding vertices, which usually refer to incidences where external factors influence the real flow in a network. Then, VIGs may sometimes model certain real-world situations better. In this regard, we introduce dominating sets in VIGs by using influence edges due to the importance of the concept of domination and its application in various issues.

Domination in VG theory is one of the most widely used topics in other sciences, including psychology, computer science, nervous systems, artificial intelligence, decision-making theory, and combinations of them. VIGs are highly practical tools for the study of different computational intelligence and computer science domains. Dominations in VIGs have many applications, such as, in wireless networking, dominations are used to find efficient routes within networks. They have also been used in document summarization and in designing secure systems for electrical grids, ect.

Hence, in this study, we extended the $\mathcal{I}n$-FG notion to the VIG and discussed the well-known problems of domination, walk, path, $\mathcal{I}n$-pair, strong $\mathcal{I}n$-pair and $\mathcal{I}n$-cut vertex on VIG. Likewise, we introduced the new concepts of the strong pair domination number in VIGs. Finally, an application of domination in illegal drug trade was introduced.

2. Preliminaries

In this part, we study some essential definitions and notions of graphs. Such as, FGs, VGs and domination sets. Before stating the definitions, we fix some notations for graphs and sets.

Definition 1 

([33]). A graph ${\mathcal{G}}^{*}$ is a pair $(X,E)$, where X is called the vertex set and $E\subseteq X\times X$ is called the edge set.

Definition 2. 

Given a crisp graph ${\mathcal{G}}^{*}=(X,E)$, a subset of vertices $D\subseteq X$ is called a DS, if for every vertex $u\in X-D$, there is a vertex $v\in D$ such that $(u,v)\in E$.

Definition 3 

([34]). In graph theory, a path in a graph is a finite or infinite sequence of edges which joins a sequence of vertices which, by most definitions, are all distinct (and since the vertices are distinct, so are the edges). Paths are fundamental concepts of graph theory, described in the introductory sections of most graph theory texts.

Definition 4 

([33]). An FG $\mathcal{G}=(\varphi ,\psi )$ is a pair of function $\varphi :X\to [0,1]$ and $\psi :X\times X\to [0,1]$ such that, for all $m,m\in X$,

$$\begin{array}{ccc}& & \psi \left(mn\right)\le min\left\{\varphi \right(m),\varphi (n\left)\right\}.\hfill \end{array}$$

Definition 5. 

A path $\mathcal{P}$ of length l in an FG $\mathcal{G}=(\varphi ,\psi )$ is a sequence of distinct vertices $x_0,x_1,x_2,\dots ,x_l$ such that $\psi \left(x_{k-1}{x}_k\right)>0,k=1,2,3,\dots ,l$. The degree of membership value (MV) of a weakest edge is defined as its strength. The strength of connectedness between two vertices m and n is defined as the maximum (MA) of the strength of all paths between m and n and is denoted by ${\psi }^{\infty }(m,n)$ or $CON{N}_{\mathcal{G}}(m,n)$.

An edge $mn$ is called an SE if ${\psi }^{\infty }(m,n)=\psi \left(mn\right)$. If $\psi \left(mn\right)=0$ for each $m\in X$, then n is named an isolated vertex. If $mn$ is an SE, then its weight is at least as great as the strength of the connectedness of its end vertices when it is deleted. Note that, $CON{N}_{\mathcal{G}-mn}\left(mn\right)$ is the strength of the connectedness between m and n in an FG obtained from $\mathcal{G}$ by deleting the edge $mn.$

Definition 6. 

Let $\mathcal{G}=(\varphi ,\psi )$ be an FG. Any edge $mn$ is called effective edge if $\psi \left(mn\right)=min\left\{\varphi \right(m),\varphi (n\left)\right\}$.

Definition 7 

([5]). A vague set (VS) $\mathcal{Q}$ is a pair $({\mathcal{Q}}^t,{\mathcal{Q}}^f)$ on a set X, where ${\mathcal{Q}}^t$ and ${\mathcal{Q}}^f$ are real- valued functions which can be defined from X to $[0,1]$, so that ${\mathcal{Q}}^t\left(m\right)+{\mathcal{Q}}^f\left(m\right)\le 1,\forall m\in X.$

Definition 8 

([6]). A pair $\mathcal{G}=(\mathcal{Q},\mathcal{Z})$ is called a VG on graph ${\mathcal{G}}^{*}=(X,E)$, where $\mathcal{Q}=({\mathcal{Q}}^t,{\mathcal{Q}}^f)$ is a VS on X and $\mathcal{Z}=({\mathcal{Z}}^t,{\mathcal{Z}}^f)$ is a VS on E such that

$$\begin{array}{c}{\mathcal{Z}}^t\left(mn\right)\le min\{{\mathcal{Q}}^t\left(m\right),{\mathcal{Q}}^t\left(n\right)\},\hfill \\ {\mathcal{Z}}^f\left(mn\right)\ge max\{{\mathcal{Q}}^f\left(m\right),{\mathcal{Q}}^f\left(n\right)\}.\hfill \end{array}$$

for all $mn\in E$. Note that $\mathcal{Z}$ is called a vague relation on $\mathcal{Q}$. A VG $\mathcal{G}$ is named strong if

$$\begin{array}{c}{\mathcal{Z}}^t\left(mn\right)=min\{{\mathcal{Q}}^t\left(m\right),{\mathcal{Q}}^t\left(n\right)\},\hfill \\ {\mathcal{Z}}^f\left(mn\right)=max\{{\mathcal{Q}}^f\left(m\right),{\mathcal{Q}}^f\left(n\right)\},\hfill \end{array}$$

for all $mn\in E.$

Definition 9. 

Suppose $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VG. Then,

(i) 

A path $\mathcal{P}:m=m_0,m_1,m_2,\dots ,m_{q-1},m_q=n$ in $\mathcal{G}$ is a sequence of distinct vertices where ${\mathcal{Z}}^t\left(m_{k-1}{m}_k\right)>0$, ${\mathcal{Z}}^f\left(m_{k-1}{m}_k\right)<1$, $k=1,2,3,\dots ,q$. The length of $\mathcal{P}$ is q.

(ii) 

If $\mathcal{P}:m=m_0,m_1,m_2,\dots ,m_{q-1},s_q=n$ is a path between m and n of length q, then ${\left({\mathcal{Z}}^t\left(mn\right)\right)}^q=sup\{{\mathcal{Z}}^t\left(m{m}_1\right)\wedge {\mathcal{Z}}^t\left(m_1{m}_2\right)\wedge \dots \wedge {\mathcal{Z}}^t\left(m_{q-1}n\right)\}$ and ${\left({\mathcal{Z}}^f\left(mn\right)\right)}^q=inf\{{\mathcal{Z}}^f$$\left(m{m}_1\right)\vee {\mathcal{Z}}^f\left(m_1{m}_2\right)\vee \dots \vee {\mathcal{Z}}^f\left(m_{q-1}n\right)\}$.

$CON{N}_{\mathcal{G}}(m,n)=(CON{N}_{\mathcal{G}}^t(m,n),CON{N}_{\mathcal{G}}^f(m,n))=({\mathcal{Z}}^{t^{\infty }}\left(mn\right),{\mathcal{Z}}^{f^{\infty }}\left(mn\right))$ is named the strength of connectedness between any two vertices m and n in $\mathcal{G}$ where $CON{N}_{\mathcal{G}}^t(m,n)=sup\left\{{\left({\mathcal{Z}}^t\left(mn\right)\right)}^q\right\}$ and $CON{N}_{\mathcal{G}}^f(m,n)=inf\left\{{\left(f_{\mathcal{Z}}\left(mn\right)\right)}^q\right\},$$q=1,2,\dots ,\infty$.

Definition 10. 

Let ${\mathcal{G}}^{*}=(X,E)$ be a crisp graph. Then, the triad $\mathcal{G}=(X,E,K)$ in which $K\subseteq X\times E$ is called $\mathcal{I}n$-graph. An element of K is called an $\mathcal{I}n$-pair.

Definition 11. 

Let ${\mathcal{G}}^{*}=(X,E,K)$ be an $\mathcal{I}n$-graph. A triad $\tilde{\mathcal{G}}=(\varphi ,\psi ,\lambda )$, where $\varphi ,\psi$ and λ are fuzzy subsets of $X,E$ and K, respectively, is called an $\mathcal{I}n$-FG of ${\mathcal{G}}^{*}$, if $\lambda (m,mn)\le min\left\{\varphi \right(m),\psi (mn\left)\right\},\forall m\in X,mn\in E$. A vertex m and an edge $mn$ are connected if there exists a path $m,(m,mn),mn$ between them. The vertices $m,n$ are connected if there exists a path $m,(m,mn),mn,(n,mn),n$ between them.

Example 1. 

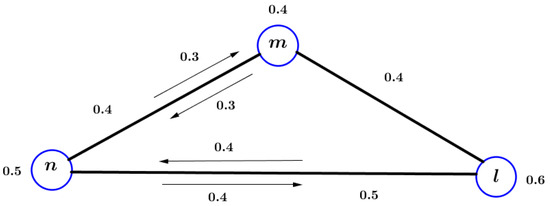
Consider the $\mathcal{I}n$-FG $\tilde{\mathcal{G}}=(\varphi ,\psi ,\lambda )$ presented in Figure 1. In this $\mathcal{I}n$-FG, we have $\varphi \left(m\right)=0.4,\varphi \left(n\right)=0.5,\varphi \left(l\right)=0.6$ and $\psi \left(mn\right)=0.4,\psi \left(ml\right)=0.4,\psi \left(ln\right)=0.5$ and $\lambda (m,nm)=\lambda (n,nm)=0.3,\lambda (n,nl)=\lambda (l,nl)=0.4$. In this $\mathcal{I}n$-FG, the vertices $m,n$ are connected vertices because there exist a path $m,(m,mn),mn,(n,mn),n$ between them.

Figure 1. An $\mathcal{I}n$-FG $\mathcal{G}$.

Definition 12. 

An $\mathcal{I}n$-FG $\tilde{\mathcal{G}}=(\varphi ,\psi ,\lambda )$ of an $\mathcal{I}n$-graph ${\mathcal{G}}^{*}=(X,E,K)$ is complete $\mathcal{I}n$-FG, if $\lambda (m,nl)=min\left\{\varphi \right(m),\psi (nl\left)\right\},\forall (m,nl)\in K$.

Definition 13. 

Let $\mathcal{G}=(\varphi ,\psi )$ be an FG with any two vertices m and n. A vertex m dominates the vertex n if $\psi \left(mn\right)\le min\left\{\varphi \right(m),\varphi (n\left)\right\}$. A subset $\mathcal{S}$ of the set X is called an SE DS if for every $n\in X-\mathcal{S},\exists m\in \mathcal{S}$ such that m dominates n. A DS $\mathcal{S}$ is called MIL DS if there is no proper subset of $\mathcal{S}$ that is DS. The effective edge domination number is the MIL fuzzy cardinality created from all MIL DS and is shown by ${\alpha }_{EE}\left(\mathcal{G}\right)$, and the related set $\mathcal{S}$ is known as MIL effective edge DS.

List of abbreviations used throughout this paper.

• $FS$ stands for “Fuzzy Set”;
• $FG$ stands for “Fuzzy Graph”;
• $VS$ stands for “Vague Set”;
• $VG$ stands for “Vague Graph”;
• $VIG$ stands for “Vague influence Graph”;
• $in$ stands for “Influence”;
• $DS$ stands for “Domination Set”;
• $SE$ stands for “Strong Edge”;
• $CP$ stands for “Cut Pair”;
• $MV$ stands for “Membership Value”;
• $MA$ stands for “Maximum”;
• $MI$ stands for “Minimum”;
• $MIL$ stands for “Minimal”.

3. Vague Influence Graphs

In this section, we study a new notion of the influence graph and influence pair domination set on VGs. Namely, we obtain the domination set on VIGs. Furthermore, some properties of VIGs are established.

Definition 14. 

A triad $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is called a VIG on graph ${\mathcal{G}}^{*}=(X,E,K)$, where $\mathcal{Q}=({\mathcal{Q}}^t,{\mathcal{Q}}^f)$ is a VS on X, and $\mathcal{Z}=({\mathcal{Z}}^t,{\mathcal{Z}}^f)$ is a VS on E, and $\mathcal{R}=({\mathcal{R}}^t,{\mathcal{R}}^f)$ is a VS on K, such that

$$\begin{array}{c}{\mathcal{R}}^t(m,nl)\le min\{{\mathcal{Q}}^t\left(m\right),{\mathcal{Z}}^t\left(nl\right)\},\hfill \\ {\mathcal{R}}^f(m,nl)\ge max\{{\mathcal{Q}}^f\left(m\right),{\mathcal{Z}}^f\left(nl\right)\}\hfill \end{array}$$

for all $m\in X,nl\in E$ .

Definition 15. 

Consider that $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG. The vertex m and an edge $nl$ are shown as connected if there exists a path of $m,(m,nl),nl$ between them.

Example 2. 

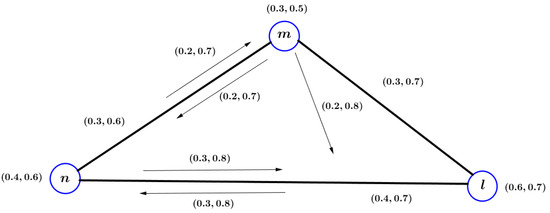
Consider a VIG $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ presented in Figure 2. In this VIG, we have $\mathcal{Q}\left(m\right)=(0.3,0.5),\mathcal{Q}\left(n\right)=(0.4,0.6),\mathcal{Q}\left(l\right)=(0.6,0.7)$ and $\mathcal{Z}\left(mn\right)=(0.3,0.6),\mathcal{Z}\left(ml\right)=(0.3,0.7),\mathcal{Z}\left(ln\right)=(0.4,0.7)$ and $\mathcal{R}(m,nm)=\mathcal{R}(n,nm)=(0.3,0.6),\mathcal{R}(n,nl)=\mathcal{R}(l,nl)=(0.3,0.8),\mathcal{R}(m,nl)=(0.2,0.8)$. In this VIG, vertex m and an edge $nl$ are shown as connected because there exists a path of $m,(m,nl),nl$ between them.

Figure 2. A VIG $\mathcal{G}$.

Definition 16. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. If it involves an $\mathcal{I}n$-pair then $\mathcal{G}$ is VIG. A sequence $\mathcal{P}:m,(m,nl),nl,(n,nl),l$ is a walk in $\mathcal{G}$, and it is an $\mathcal{I}n$($m-l$) path, whereas $\mathcal{P}:m,(m,nl),nl$ is also an $\mathcal{I}n$($m-nl$) path. Every two vertices in VIG are known to be connected if there exists any $\mathcal{I}n$-pair between them. Here, $(m,nl)$ is an $\mathcal{I}n$-pair as $m,n$ and l are distinct. This $\mathcal{I}n$-pair shows the influence of vertex m on the edge $nl$.

Definition 17. 

Suppose $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG. An $\mathcal{I}n$-pair in $\mathcal{G}$ is named effective $\mathcal{IP}$ if

$$\begin{array}{c}{\mathcal{R}}^t(m,nl)=min\{{\mathcal{Q}}^t\left(m\right),{\mathcal{Z}}^t\left(nl\right)\},\hfill \\ {\mathcal{R}}^f(m,nl)=max\{{\mathcal{Q}}^f\left(m\right),{\mathcal{Z}}^f\left(nl\right)\}.\hfill \end{array}$$

Definition 18. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, the influence of path $\mathcal{P}$ indicated by $\mathcal{I}n\left(\mathcal{P}\right)=({\mathcal{I}}^{t}n\left(\mathcal{P}\right),{\mathcal{I}}^{f}n\left(\mathcal{P}\right))$ and is described as, $\mathcal{I}{n}^t\left(\mathcal{P}\right)=min\left\{{\mathcal{R}}^t(m,nl)\right|(m,nl)\in \mathcal{P}\}$, $\mathcal{I}{n}^f\left(\mathcal{P}\right)=max\left\{{\mathcal{R}}^f(m,nl)\right|(m,nl)\in \mathcal{P}\}$, where $\mathcal{I}{n}^t$ and $\mathcal{I}{n}^f$ show the MV and the non-MVs of $\mathcal{I}n$-pair lies in the path exists between m to $nl$.

Definition 19. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. An $\mathcal{I}n$-pair $(m,nl)$ is known as strong $\mathcal{IP}$ if $\mathcal{R}(m,nl)\ge CON{N}_{\mathcal{G}-(m,nl)}(m,nl)$. An $\mathcal{I}n$-pair $(m,nl)$ is known as the strongest In-pair if $\mathcal{R}(m,nl)>CON{N}_{\mathcal{G}-(m,nl)}(m,nl)$. An $\mathcal{I}n$-pair $(m,nl)$ is known as weak $\mathcal{IP}$ if $\mathcal{R}(m,nl)<CON{N}_{\mathcal{G}-(m,nl)}(m,nl)$.

Definition 20. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. The greatest $\mathcal{I}n$-strength between m and $nl$ is the highest MV with lowest non-MV from all the $\mathcal{I}n$-paths between m to $nl$ which is represented by $CON{N}^{\infty }(m,nl)=(CON{N}^{t\infty }(m,nl),CON{N}^{f\infty }(m,nl))$ and is defined $CON{N}^{\infty }(m,nl)=max\left\{CON{N}^{tq}(m,nl)\right|q=1,2,3,\dots ,\infty \}$ and $CON{N}^{\infty }(m,nl)=min\left\{CON{N}^{fq}(m,nl)\right|q=1,2,3,\dots ,\infty \}$.

Theorem 1. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. If $(m,nl)$ is a strong $\mathcal{I}n$-pair, then $\mathcal{G}$ involves a strong $\mathcal{I}n$-path $\mathcal{P}$.

Proof. 

Suppose $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG. Then, a pair $(m,nl)$ is an effective $\mathcal{I}n$-pair if ${\mathcal{R}}^t(m,nl)=min\{{\mathcal{Q}}^t\left(m\right),{\mathcal{Z}}^t\left(nl\right)\}$ and ${\mathcal{R}}^f(m,nl)=max\{{\mathcal{Q}}^f\left(m\right),{\mathcal{Z}}^f\left(nl\right)\}$. Now, consider that $m-nl$ is an $\mathcal{I}n$-path $\mathcal{P}:m,(m,nl),nl$. Any $\mathcal{I}n$-pair incident from m to $nl$ can not have $\mathcal{I}n$-MV more than $nl$. Similarly, any $\mathcal{I}n$-pair $(m,nl)$ which is influenced at $nl$ can not have $\mathcal{I}n$-MV more than $(m,nl)$. It means that the $\mathcal{I}n$-path $\mathcal{P}:m,(m,nl),nl$ has $\mathcal{I}n$-strength from MVs as $min\left\{\mathcal{Q}\right(m),\mathcal{Z}(nl\left)\right\}$ and $\mathcal{I}n$-strength from non-MVs as $max\left\{\mathcal{Q}\right(m),\mathcal{Z}(nl\left)\right\}$. Therefore, $\mathcal{P}$ becomes the strong $\mathcal{I}n$-path with the effective $\mathcal{I}n$-pair. □

Theorem 2. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. If the $\mathcal{I}n$-path $\mathcal{P}$ involves the alone $\mathcal{I}n$-pair, then the $\mathcal{I}n$-pair should be strong.

Proof. 

Suppose $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG with an $\mathcal{I}n$-pair $(m,nl)$ and $\mathcal{R}(m,nl)=min$$\left\{\mathcal{Q}\right(m),\mathcal{Z}(nl\left)\right\}$. Suppose the $\mathcal{I}n$-pair is not a strong $\mathcal{I}n$-pair, then $CON{N}_{\mathcal{G}-(m,nl)}(m,nl)>\mathcal{R}(m,nl)$, which is just possible if there exist any other $\mathcal{I}n$-path that is a contradiction. Thus, if the $\mathcal{I}n$-path $\mathcal{P}$ contains the alone $\mathcal{I}n$-pair, then the $\mathcal{I}n$-pair should be strong. □

Theorem 3. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. If $\mathcal{R}(m_0,m_1{m}_2)=max\{\mathcal{R}(m_0,m_1{m}_2):(m_0,m_1{m}_2)$$\in \mathcal{R}\}$, then $(m_0,m_1{m}_2)$ is known as strong $\mathcal{I}n$-pair.

Proof. 

Suppose $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG. Let the $\mathcal{I}n$-pair $(m_0,m_1{m}_2)$ be not a strong $\mathcal{I}n$-pair. Then, there is any $\mathcal{I}n$-path $\mathcal{P}:m_0,(m_0,m_1{m}_2),m_1{m}_2,\dots ,m_0{m}_n$ so that the highest $\mathcal{I}n$-strength of $\mathcal{P}>\mathcal{R}(m_0,m_1{m}_2)$. Clearly, there is $\mathcal{R}(m_i,m_{i+1}{m}_{i+2})>\mathcal{R}(m_0,m_1{m}_2)$ for every $i=1,2,3,\dots ,n$. This shows that there is any $\mathcal{I}n$-pair that is a strong $\mathcal{I}n$-pair, which is a contradiction. Therefore, if $\mathcal{R}(m_0,m_1{m}_2)=max\{\mathcal{R}(m_0,m_1{m}_2):(m_0,m_1{m}_2)\in \mathcal{R}\}$, then $(m_0,m_1{m}_2)$ is known as a strong $\mathcal{I}n$-pair. □

Theorem 4. 

Suppose $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG having a strong $\mathcal{I}n$-pair$(m,nl)$, then it must be a strong $\mathcal{I}n$-pair.

Proof. 

Suppose $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG having a strong $\mathcal{I}n$-pair $(m,nl)$. Then, by using the definition of a strong $\mathcal{I}n$-pair $(m,nl)$ in $\mathcal{G}$, we have ${\mathcal{R}}^t(m,nl)=min\{{\mathcal{Q}}^t\left(m\right),{\mathcal{Z}}^t\left(nl\right)\}$ and ${\mathcal{R}}^f(m,nl)=max\{{\mathcal{Q}}^f\left(m\right),{\mathcal{Z}}^f\left(nl\right)\}$. Suppose ${\mathcal{Q}}^t\left(m\right)\ge {\mathcal{Z}}^t\left(nl\right)$, then ${\mathcal{R}}^t(m,nl)={\mathcal{Z}}^t\left(nl\right)$. So, for any $\mathcal{I}n$-path $\mathcal{P}:m,(m,nl),nl$, the influence of $\mathcal{P}\le {\mathcal{Z}}^t\left(nl\right)$. By using Theorem 1, the $\mathcal{I}n$-path $\mathcal{P}$ involves the alone $\mathcal{I}n$-pair, then the $\mathcal{IP}$ should be strong, and according to Theorem 2, the $\mathcal{I}n$-pair having MA degree of MV should be a strong $\mathcal{I}n$-pair. As the $\mathcal{I}n$-pair is alone and has MA degree of MV, we have ${\mathcal{R}}^t(m,nl)={\mathcal{Z}}^t\left(nl\right)>CON{N}_{\mathcal{G}-(m,nl)}^t(m,nl)$. Now, suppose ${\mathcal{Q}}^t\left(m\right)\le {\mathcal{Z}}^t\left(nl\right)$, then ${\mathcal{R}}^t(m,nl)={\mathcal{Q}}^t\left(m\right)$. So, for any $\mathcal{I}n$-path $\mathcal{P}:m,(m,nl),nl$, the influence of $\mathcal{P}\le {\mathcal{Q}}^t\left(m_0\right)$. Again by using Theorems 1 and 2, we have ${\mathcal{R}}^t(m,nl)={\mathcal{Q}}^t\left(m\right)>CON{N}_{\mathcal{G}-(m,nl)}^t(m,nl)$. For non-MVs, consider ${\mathcal{Q}}^f\left(m\right)\le {\mathcal{Z}}^f\left(nl\right)$, then ${\mathcal{R}}^f(m,nl)={\mathcal{Z}}^f\left(nl\right)$. So, for any $\mathcal{I}n$-path $\mathcal{P}:m,(m,nl),nl$, the influence of $\mathcal{P}\ge {\mathcal{Z}}^t\left(nl\right)$. By using Theorems 1 and 2, we have ${\mathcal{R}}^f(m,nl)={\mathcal{Q}}^f\left(m\right)>CON{N}_{\mathcal{G}-(m,nl)}^t(m,nl)$. Now, suppose ${\mathcal{Q}}^f\left(m\right)\le {\mathcal{Z}}^f\left(nl\right)$, then ${\mathcal{R}}^f(m,nl)={\mathcal{Q}}^f\left(m\right)$. So, for any $\mathcal{I}n$-path $\mathcal{P}:m,(m,nl),nl$, the influence of $\mathcal{P}\ge {\mathcal{Q}}^f\left(m\right)$. Again, by using Theorems 1 and 2, we have ${\mathcal{R}}^f(m,nl)={\mathcal{Q}}^f\left(m\right)>CON{N}_{\mathcal{G}-(m,nl)}^f(m,nl)$. Therefore, $(m,nl)$ is a strong $\mathcal{I}n$-pair. □

Theorem 5. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, a vertex $x\in \mathcal{Q}$ is called an $\mathcal{I}n$-cut vertex of $\mathcal{G}$ if $CON{N}_{\mathcal{G}-x}(m,nl)<\mathcal{R}(m,nl)$ for some $m,nl\in \mathcal{Q}\cup \mathcal{Z}$.

Example 3. 

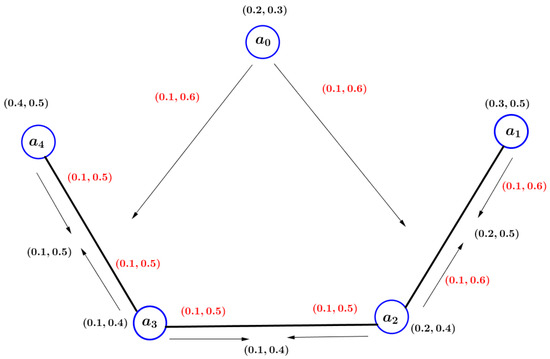
Consider that $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG as shown in Figure 3. In this VIG, there are two $\mathcal{I}n$-paths from $a_0$ to $a_3$ namely: ${\mathcal{P}}_1:a_0,(a_0,a_3{a}_4),a_3{a}_4,(a_3,a_3{a}_4),a_3$ and ${\mathcal{P}}_2:a_0,(a_0,a_1{a}_2),a_1{a}_2,$$(a_2,a_1{a}_2),a_2,(a_2,a_2{a}_3),a_2{a}_3,(a_3,a_2{a}_3),a_3$. For ${\mathcal{P}}_1$, $CON{N}_{\mathcal{G}-a_0}(a_0,a_3{a}_4)=(0,0)<(0.1,0.6)$$=\mathcal{R}(a_0,a_3{a}_4)$, and for ${\mathcal{P}}_2$, $CON{N}_{\mathcal{G}-a_0}(a_0,a_1{a}_2)=(0,0)<(0.2,0.6)=\mathcal{R}(a_0,a_1{a}_2).$

Figure 3. A VIG $\mathcal{G}$ with cut vertex $a_0$.

Definition 21. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, $\mathcal{G}$ is described as VIG block if $\mathcal{G}$ does not involve any cut vertex.

Theorem 6. 

Suppose $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG with an $\mathcal{I}n$-pair $(m,nl)$. Then, the vertex deleted from the $\mathcal{I}n$-pair is a cut vertex of $\mathcal{G}$.

Proof. 

Suppose $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG with an $\mathcal{I}n$-pair $(m,nl)$. There is only one $\mathcal{I}n$-path from m to $nl$ namely $m,(m,nl),nl$ having $CON{N}_{\mathcal{G}-m}(m,nl)<CON{N}_{\mathcal{G}}(m,nl)$. Therefore, m is a $\mathcal{I}n$-cut vertex. □

Definition 22. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, an edge $m_j{m}_{j+1}\in \mathcal{Z}$ for each $j=1,2,3,\dots ,q$ is called a bridge of $\mathcal{G}$ if $CON{N}_{\mathcal{G}-m_j{m}_{j+1}}(m_0,m_1{m}_2)<CON{N}_{\mathcal{G}}(m_0,m_1{m}_2)$ for some $m_0,m_1{m}_2\in \mathcal{Q}\cup \mathcal{Z}$.

Definition 23. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, $\mathcal{G}$ is bridgeless if it involves no bridge.

Definition 24. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, an $\mathcal{I}n$-pair $(m,nl)\in \mathcal{R}$ is defined to be an $\mathcal{I}n$-CP of $\mathcal{G}$ if $CON{N}_{\mathcal{G}-m}(m,nl)<CON{N}_{\mathcal{G}}(m,nl)$ for some $m,nl\in \mathcal{Q}\cup \mathcal{Z}$.

Example 4. 

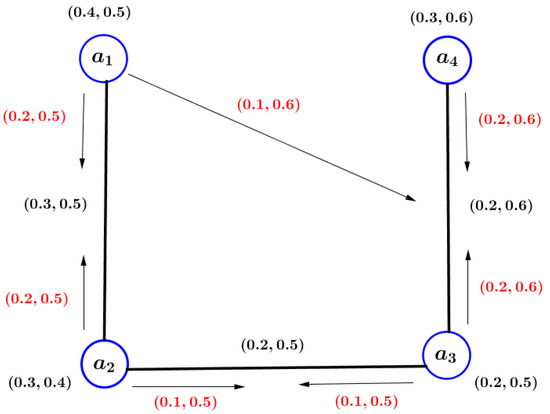
Consider that $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG as shown in Figure 4. The MV and non-MV of pairs of VIG are shown in Table 1.

Figure 4. VIG $\mathcal{G}$.

Table 1. VIG $\mathcal{R}$.

$\mathcal{R}$	MV and Non-MV of Pairs
$(m_1,m_1{m}_2)$	(0.2, 0.6)
$(m_3,m_1{m}_3)$	(0.3, 0.6)
$(m_2,m_1{m}_2)$	(0.2, 0.6)
$(m_1,m_1{m}_3)$	(0.3, 0.6)
$(m_2,m_2{m}_3)$	(0.2, 0.5)
$(m_1,m_2{m}_3)$	(0.2, 0.6)
$(m_3,m_2{m}_2)$	(0.2, 0.5)
$(m_1,m_3{m}_4)$	(0.2, 0.6)
$(m_3,m_3{m}_4)$	(0.2, 0.4)
$(m_2,m_1{m}_4)$	(0.2, 0.6)
$(m_4,m_3{m}_4)$	(0.2, 0.4)
$(m_2,m_3{m}_4)$	(0.2, 0.5)
$(m_1,m_1{m}_4)$	(0.2, 0.6)
$(m_4,m_1{m}_2)$	(0.2, 0.6)
$(m_4,m_1{m}_4)$	(0.2, 0.6)
$(m_4,m_2{m}_3)$	(0.2, 0.5)
$(m_2,m_2{m}_4)$	(0.2, 0.5)
$(m_3,m_1{m}_2)$	(0.2, 0.6)
$(m_4,m_2{m}_4)$	(0.2, 0.5)
$(m_3,m_1{m}_4)$	(0.2, 0.6)

In this VIG, there is only one $\mathcal{I}n$-path from $a_1$ to $a_3{a}_4$, namely $a_1,(a_1,a_3{a}_4),a_3{a}_4$. If we delete the edge $a_3{a}_4$, we obtain $(0,0)=CON{N}_{\mathcal{G}-a_3{a}_4}(a_1,a_3{a}_4)<CON{N}_{\mathcal{G}}(a_1,a_3{a}_4)=(0.1,0.6)$. Hence, $a_3{a}_4$ is an influence bridge. If we delete the $\mathcal{I}n$-pair $(a_1,a_3{a}_4)$, we have $(0,0)=CON{N}_{\mathcal{G}-(a_1,a_3{a}_4)}(a_1,a_3{a}_4)<CON{N}_{\mathcal{G}}(a_1,a_3{a}_4)=(0.1,0.6)$. Hence, $(a_1,a_3{a}_4)$ is an $\mathcal{I}n$-CP.

Definition 25. 

A VIG $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is known as a complete VIG, if every vertex m has the influence on every edge $nl$ with ${\mathcal{R}}^t(m,nl)=min({\mathcal{Q}}^t\left(m\right),{\mathcal{Z}}^t\left(nl\right))$ and ${\mathcal{R}}^f(m,nl)=max({\mathcal{Q}}^f\left(m\right),$${\mathcal{Z}}^f\left(nl\right))$.

Example 5. 

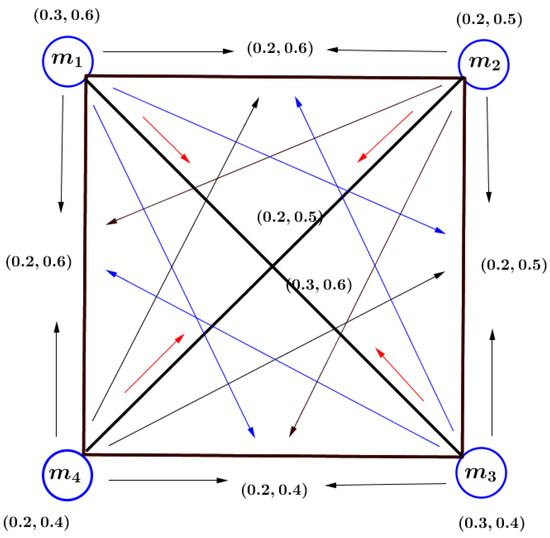
Consider that $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a complete VIG as shown in Figure 5. The MV and non-MV of pairs of VIG are shown in Table 1.

Figure 5. A complete VIG $\mathcal{G}$.

This is a complete VIG because $m_1$ has an influence on $m_1{m}_2,m_1{m}_3,m_2{m}_3,m_3{m}_4$ and $m_1{m}_4$. Similarly, $m_2$ has an influence on $m_1{m}_2,m_1{m}_4,m_2{m}_4,m_3{m}_4$ and $m_2{m}_3$. Furthermore, also, $m_3$ has an influence on $m_3{m}_2,m_3{m}_4,m_3{m}_1,m_1{m}_2$ and $m_1{m}_4$. Lastly, $m_4$ has an influence on $m_4{m}_3,m_4{m}_1,m_4{m}_2,m_2{m}_3$ and $m_1{m}_2$. This graph $\mathcal{G}$ also has a vague fuzzy influence cycle.

Definition 26. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, $\mathcal{G}$ is a cycle if $\mathcal{G}=({\mathcal{Q}}^{*},{\mathcal{Z}}^{*},{\mathcal{R}}^{*})$ is a cycle, while $\mathcal{G}$ is shown as a fuzzy cycle if $\mathcal{G}$ is a cycle and it does not contains a unique $m_1{m}_2\in \mathcal{Z}$ such that $\mathcal{Z}(m_1,m_2)=min\mathcal{Z}\left(m_i{m}_j\right)|m_i{m}_j\in \mathcal{Z}$. The VIG $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is known as a VIG cycle if it does not contains a unique $\mathcal{I}n$-pair so that ${\mathcal{R}}^t(m_0,m_1{m}_2)=min\{{\mathcal{Q}}^t\left(m_0\right),{\mathcal{Z}}^t\left(m_1{m}_2\right)\}$ and ${\mathcal{R}}^f(m_0,m_1{m}_2)=max\{{\mathcal{Q}}^f\left(m_0\right),{\mathcal{Z}}^f\left(m_1{m}_2\right)\}$.

Theorem 7. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. If $\mathcal{G}$ is complete, then each $\mathcal{I}n$-pair of $\mathcal{G}$ is a CP.

Proof. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a complete VIG. If we remove any vertex from $\mathcal{G}$, then it must reduce the $\mathcal{I}n$-connectivity between two vertices or between the vertex and edge. Assume any three vertices $m,n$ and l makes a complete VIG. If we remove a vertex m from $\mathcal{G}$, we obtain $CON{N}_{\mathcal{G}-m}(m,nl)<CON{N}_{\mathcal{G}}(m,nl)$. Therefore, if $\mathcal{G}$ is complete, then each pair of $\mathcal{G}$ is a CP. □

Theorem 8. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, a pair $(m,nl)$ is an $\mathcal{I}n$-pair CP if and only if the removal of the pair $(m,nl)$ reduces the $\mathcal{I}n$-connectivity between m and $nl$.

Proof. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Suppose $(m,nl)$ is the $\mathcal{I}n$-CP in $\mathcal{G}$. Now, by using the definition, we have $CON{N}_{\mathcal{G}-(m,nl)}(m,nl)<\mathcal{R}(m,nl)$. From all the $\mathcal{I}n$-paths $m-nl$, the path $\mathcal{P}:m,(m,nl),nl$ will have the MA-influenced strength, namely $\mathcal{R}(m,nl)$. So, it is clear that by removing the $\mathcal{I}n$-pair $,(m,nl)$ the $\mathcal{I}n$-connectivity between m and $nl$ will be reduced.

Conversely, if we have $CON{N}_{\mathcal{G}-(m,nl)}(m,nl)<\mathcal{R}(m,nl)$, then by the definition, it shows that the pair $(m,nl)$ is an $\mathcal{I}n$-CP of $\mathcal{G}$. □

Definition 27. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG with any three vertices $m,n$ and l. A vertex m dominates the vertex l if $\mathcal{R}(m,nl)\ge CONN(m,nl)$. A subset $\mathcal{S}$ of the set X is called a strong $\mathcal{I}n$-pair DS, if for each $l\in X-\mathcal{S},\exists m\in \mathcal{S}$ such that m dominates l.

Definition 28. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, the degree of vertex m in $\mathcal{G}$ is represented by $deg\left(m\right)=(de{g}^t\left(m\right),de{g}^f\left(m\right))$ and is described as $de{g}^t\left(m\right)=\sum (m,nl),(m,nl)\in {\mathcal{R}}^t$, where $m\ne n\ne l$ and $de{g}^f\left(m\right)={\sum }_{m,n\ne l}(m,nl),(m,nl)\in {\mathcal{R}}^f$, where $m\ne n\ne l$.

Definition 29. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, the minimum(MI) degree of $\mathcal{G}$ is represented by $\omega \left(\mathcal{G}\right)=({\omega }^t\left(\mathcal{G}\right),{\omega }^f\left(\mathcal{G}\right))$ and is described as ${\omega }^t\left(\mathcal{G}\right)=min\left\{de{g}^t\left(m\right)\right|m\in \mathcal{Q}\}$, ${\omega }^f\left(\mathcal{G}\right)=max\left\{de{g}^f\left(m\right)\right|m\in \mathcal{Q}\}$.

Definition 30. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, the MA degree of $\mathcal{G}$ is represented by $\gamma \left(\mathcal{G}\right)=({\gamma }^t\left(\mathcal{G}\right),{\gamma }^f\left(\mathcal{G}\right))$ and is described as ${\gamma }^t\left(\mathcal{G}\right)=max\left\{de{g}^t\left(m\right)\right|m\in \mathcal{Q}\}$, ${\gamma }^f\left(\mathcal{G}\right)=min\left\{de{g}^f\left(m\right)\right|m\in \mathcal{Q}\}$.

Definition 31. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, the order of $\mathcal{G}$ is shown by $\mathcal{O}\left(\mathcal{G}\right)=({\mathcal{O}}^t\left(\mathcal{G}\right),{\mathcal{O}}^f\left(\mathcal{G}\right))$ and is described as

$$\begin{array}{c}{\mathcal{O}}^t\left(\mathcal{G}\right)=\sum _{m\in \mathcal{Q}}\mathcal{Q}\left(m\right),\forall m\in {\mathcal{O}}^t,\hfill \\ {\mathcal{O}}^f\left(\mathcal{G}\right)=\sum _{m\in \mathcal{Q}}\mathcal{Q}\left(m\right),\forall m\in {\mathcal{O}}^f.\hfill \end{array}$$

Definition 32. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, the size of $\mathcal{G}$ is shown by $\mathcal{S}\left(\mathcal{G}\right)=({\mathcal{S}}^t\left(\mathcal{G}\right),$${\mathcal{S}}^f\left(\mathcal{G}\right))$ and is defined as ${\mathcal{S}}^t\left(\mathcal{G}\right)=\sum (m,nl),(m,nl)\in {\mathcal{R}}^t$, where $m\ne n\ne l$ and ${\mathcal{S}}^f\left(\mathcal{G}\right)={\sum }_{m,n\ne l}(m,nl),(m,nl)\in {\mathcal{R}}^f$, where $m\ne n\ne l$.

Definition 33. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. A strong $\mathcal{I}n$-pair DS $\mathcal{S}$ is known as a MIL strong $\mathcal{I}n$-pair DS if no proper subset of $\mathcal{S}$ is a strong $\mathcal{I}n$-pair DS.

Definition 34. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. The MI strong $\mathcal{I}n$-pair domination number obtained from all MIL strong $\mathcal{I}n$-pair SDs and is represented by $\beta \left(\mathcal{G}\right)$.

Definition 35. 

Let $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ be a VIG. Then, the MI number of elements in the MIL strong $\mathcal{I}n$-pair DS is shown by $\mathcal{M}\left(\beta \right(\mathcal{G}\left)\right)$, where $\mathcal{M}\left(\beta \left(\mathcal{G}\right)\right)=min\left\{\right|{\mathcal{S}}_j\left|\right\}$, ${\mathcal{S}}_j$ is a MIL strong $\mathcal{I}n$-pair DS.

Theorem 9. 

Suppose that $\mathcal{G}=(\mathcal{Q},\mathcal{Z},\mathcal{R})$ is a VIG. If $\mathcal{G}$ is complete, then $\beta \left(\mathcal{G}\right)=min\left\{\mathcal{Q}\right(m\left)\right|m\in X\}$.

Proof. 

Suppose that $\mathcal{S}$ is a DS. Let $m_0\in \mathcal{S}$ and $m_1\in X-\mathcal{S}$. As $\mathcal{G}$ is a complete VIG, so each $\mathcal{I}n$-pair is an effective $\mathcal{I}n$-pair, then by using the Theorem 7, every $\mathcal{I}n$-pair is a CP. Now, by using Theorem 8, every CP is a strong $\mathcal{I}n$-pair as it decreases the $\mathcal{I}n$-connectivity between $m_0$ and $m_1{m}_2$. It implies that $m_0$ dominates each $m_1\in X-\mathcal{S}$. It shows that $\mathcal{S}=\left\{m_0\right\}$ is a MIL strong $\mathcal{I}n$-pair DS. Therefore, $\beta \left(\mathcal{G}\right)=min\left\{\mathcal{Q}\right(m\left)\right|m\in X\}.$ □

4. Application: Recognition of Companies Participating in Illegal Drug Trade

Graph theory has expanded greatly as a result of a wide variety of applications in optimization combinatorial issues, chemistry, physics and other fields. In this section, we describe a real-world application of VIGs.

Currently, the illegal drug trade is seen as a high-risk, high-reward dirty industry. It is estimated that arms, medicine, drugs, alcohol and tobacco are the five largest illegal businesses in the world. The drug trade is a big business that generates billions of dollars in illegal income. Criminals mostly design many creative methods of illegal drug transportation, focusing on buying and selling. It is hard to find hidden ways to enforce the law, so the police must be aware of the latest illegal trends. For the drug trading market, we can use VIG to highlight the safest path chosen by the dangerous international networks of illegal drug trade between two companies and can also announce its removal, which reduces the safety of that route.

Consider how many companies in the world take part illegal drug trade, which is a major threat to humans, in the following series: $X=\{C_1,C_2,C_3,C_4,C_5,C_6\}$ (see in Figure 6). VIG $\mathcal{Q}$ defined on set X is presented in Table 2.

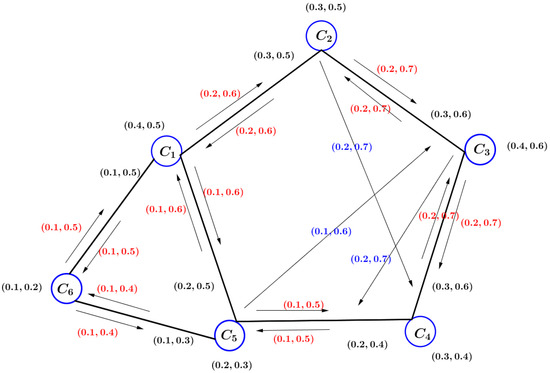
Figure 6. A VIG $\mathcal{G}$.

Table 2. VIG $\mathcal{Q}$ on set X.

Company	Law Enforcement Efforts of the Country for Illegal Drug Trade	Involvement of the Country in Organized Illegal Drug Trade
$C_1$	0.4	0.5
$C_2$	0.3	0.5
$C_3$	0.4	0.6
$C_4$	0.3	0.4
$C_5$	0.2	0.3
$C_6$	0.1	0.2

In Table 2, ${\mathcal{Q}}^t$ shows law enforcement efforts of the company for illegal drug trade,${\mathcal{Q}}^f$ indicates the involvement of the company in organized illegal drug trade, and the neutral approach of the company to illegal drug trade can be considered as a degree of indeterminacy. We define VIG $\mathcal{Z}$ in Table 3. An element of VIG $\mathcal{Z}$ represents illegal drug trade between those two companies.

Table 3. VIG $\mathcal{Z}$ on set E.

$\mathcal{Z}$	Rate of Illegal Drug Trade	Negative Effect
$C_1{C}_2$	0.3	0.5
$C_2{C}_3$	0.3	0.6
$C_3{C}_4$	0.3	0.6
$C_4{C}_5$	0.2	0.4
$C_5{C}_1$	0.2	0.5
$C_1{C}_6$	0.1	0.5
$C_5{C}_6$	0.1	0.3

In Table 3, ${\mathcal{Z}}^t$ shows the rate of illegal drug trade between companies, and ${\mathcal{Z}}^f$ shows the rate of the world’s negative effect for that illegal drug trade.

Consider that ${\mathcal{R}}^t(C_1,C_1{C}_5)$ and ${\mathcal{R}}^f(C_1,C_1{C}_5)$ represent the degree of safety and degree of risk for illegal drug trade, respectively, to use $C_1$ as a source company, relationship on $C_1{C}_5$ and arrive at destination company $C_5$. Similarly, the MV and non-MV of the other pairs of VIG are shown in Table 4.

Table 4. VIG $\mathcal{R}$ on set K.

$\mathcal{R}$	Degree of Safety	Degree of Risk
$(C_1,C_1{C}_2)$	0.2	0.6
$(C_2,C_1{C}_2)$	0.2	0.6
$(C_2,C_2{C}_3)$	0.2	0.7
$(C_3,C_2{C}_3)$	0.2	0.7
$(C_3,C_3{C}_4)$	0.2	0.7
$(C_4,C_3{C}_4)$	0.2	0.7
$(C_4,C_4{C}_5)$	0.1	0.5
$(C_5,C_4{C}_5)$	0.1	0.5
$(C_5,C_5{C}_1)$	0.1	0.6
$(C_1,C_1{C}_5)$	0.1	0.6
$(C_2,C_3{C}_4)$	0.2	0.7
$(C_3,C_4{C}_5)$	0.2	0.7
$(C_5,C_2{C}_3)$	0.1	0.6
$(C_1,C_1{C}_6)$	0.1	0.5
$(C_6,C_1{C}_6)$	0.1	0.5
$(C_5,C_5{C}_6)$	0.1	0.4
$(C_6,C_5{C}_6)$	0.1	0.4

The interesting thing is that there are multiple $\mathcal{I}n$-paths between every two vertices. Consider, we are finding the $\mathcal{I}n$-paths from $C_1$ to $C_3$, thus all possible $C_1-C_3{C}_4$ are as follows:

• $P_1:C_1,(C_1,C_1{C}_5),C_1{C}_5,(C_5,C_1{C}_5),C_5,(C_5,C_2{C}_3),C_2{C}_3,(C_3,C_2{C}_3),C_3,(C_3,C_3{C}_4),$$C_3{C}_4.$
• $P_2:C_1,(C_1,C_1{C}_2),C_1{C}_2,(C_2,C_1{C}_2),C_2,(C_2,C_3{C}_4),C_3{C}_4.$
• $P_3:C_1,(C_1,C_1{C}_2),C_1{C}_2,(C_2,C_1{C}_2),C_2,(C_2,C_2{C}_3),C_2{C}_3,(C_3,C_2{C}_3),C_3,(C_3,C_3{C}_4),$$C_3{C}_4.$
• $P_4:C_1,(C_1,C_1{C}_5),C_1{C}_5,(C_5,C_1{C}_5),C_5,(C_5,C_4{C}_5),C_4{C}_5,(C_4,C_4{C}_5),C_4,(C_4,C_3{C}_4),$$C_3{C}_4,.$
• $P_5:C_1,(C_1,C_1{C}_6),C_1{C}_6,(C_6,C_1{C}_6),C_6,(C_6,C_5{C}_6),C_5{C}_6,(C_5,C_5{C}_6),C_5,(C_5,C_2{C}_3),$$C_2{C}_3,(C_3,C_2{C}_3),C_3,(C_3,C_3{C}_4),C_3{C}_4.$
• $P_6:C_1,(C_1,C_1{C}_6),C_1{C}_6,(C_6,C_1{C}_6),C_6,(C_6,C_5{C}_6),C_5{C}_6,(C_5,C_5{C}_6),C_5,(C_5,C_4{C}_5),$$C_4{C}_5,(C_4,C_4{C}_5),C_4,(C_4,C_3{C}_4),C_3{C}_4.$

The $\mathcal{I}n$ strengths of these $\mathcal{I}n$-pairs are given by

$\mathcal{IP}\left(P_1\right)=(0.1,0.7)$, $\mathcal{IP}\left(P_2\right)=(0.2,0.7)$, $\mathcal{IP}\left(P_3\right)=(0.2,0.7)$,

$\mathcal{IP}\left(P_4\right)=(0.1,0.7)$, $\mathcal{IP}\left(P_5\right)=(0.1,0.7)$, $\mathcal{IP}\left(P_6\right)=(0.1,0.7)$.

The t-$\mathcal{I}n$ strength and f-$\mathcal{I}n$ strength of connectedness are given by

$CON{N}_{\mathcal{G}}^t(C_1,C_3{C}_4)=max\left\{{\mathcal{IP}}^t(P_1,P_2,P_3,P_4,P_5,P_6)\right\}=0.2$

$CON{N}_{\mathcal{G}}^f(C_1,C_3{C}_4)=min\left\{{\mathcal{IP}}^f(P_1,P_2,P_3,P_4,P_5,P_6)\right\}=0.7$

$CON{N}_{\mathcal{G}}(C_1,C_3{C}_4)=(CON{N}_{\mathcal{G}}^t(C_1,C_3{C}_4),CON{N}_{\mathcal{G}}^f(C_1,C_3{C}_4))=(0.2,0.7)$

Here, we consider that if the connection between companies is reduced, the amount of illegal drug trade will decrease. Let us remove $(C_3,C_2{C}_3)$ and $(C_1,C_1{C}_2)$ of VIG $\mathcal{G}$, as shown in Figure 7. Then, $CON{N}_{\mathcal{G}-(C_3,C_2{C}_3)}(C_1,C_3{C}_4)=(0.1,0.7).$ Therefore, the removal of $(C_3,C_2{C}_3)$ and $(C_1,C_1{C}_2)$ decreases the safety of the path.

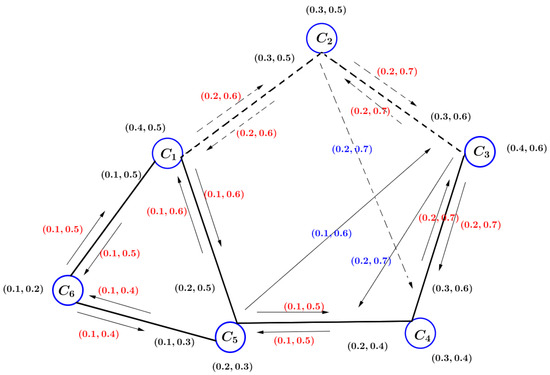
Figure 7. A VIG $\mathcal{G}$.

Comparative Analysis

We want to eliminate the safest route through which the dangerous international drug trade networks between two companies conduct their interactions. Therefore, we need to check this application with the VIG graph. In this section, we considered six companies $(C_1,C_2,C_3,C_4,C_5,C_6)$ that have the most illegal interactions with each other and that these companies have caused an increase in illegal drug trade due to their interactions with each other. Each of the paths shows the rate of illegal drug trade between companies and rate of the world’s negative effect for that illegal drug trade. Here, we consider that if the connection between companies is reduced, the amount of illegal drug trade will be reduced. First, we chose two companies $C_1$ and $C_3$. There are several routes between these two companies that we are finding in the $\mathcal{I}n$-paths from $C_1$ to $C_3$. Then, we obtained the $\mathcal{I}n$ strength and strength of connectedness. By removing the route that had the most power of penetration and connection between the two companies, the safety of the route decreased, so by reducing the interactions between the companies, the amount of illegal drug trade can be prevented.

5. Conclusions

A VG, an extension of the basic notion of an FG, can be employed to deal with deeper aspects of uncertainty and imprecision for which the use of FGs would not fully succeed. VIGs are efficient tools for studying different computational intelligence and computer science domains. In this paper, we introduced the notion of domination in VIGs using a strong $\mathcal{I}n$-pair. The concepts of the MI strong $\mathcal{I}n$-pair DS and MI strong fuzzy $\mathcal{I}n$-pair domination number are described for a VIG. The attributes of several specific values are given, including the $\mathcal{I}n$-cut vertex, $\mathcal{I}n$-bridges, $\mathcal{I}n$-CPs, strong $\mathcal{I}n$-pair with their mutual relationship in the VIGs, and some results are presented. Due to unforeseen circumstances, there is an area for broad theoretical and practical level interpretations of these subjects. In the future, we intend to broaden the scope of our research to include topological indices and the notion of energy in VIGs. There is a scope for extensive theoretical and practical-level analysis of these topics.