Bayesian Inference for a Hidden Truncated Bivariate Exponential Distribution with Applications

Abstract

In many real-life scenarios, one variable is observed only if the other concomitant variable or the set of concomitant variables (in the multivariate scenario) is truncated from below, above, or from a two-sided approach. Hidden truncation models have been applied to analyze data when bivariate or multivariate observations are subject to some form of truncation. While the statistical inference for hidden truncation models (truncation from above) under the frequentist and the Bayesian paradigms has been adequately discussed in the literature, the estimation of a two-sided hidden truncation model under the Bayesian framework has not yet been discussed. In this paper, we consider the Bayesian inference for a general two-sided hidden truncation model based on the Arnold–Strauss bivariate exponential distribution. In addition, a Bayesian model selection approach based on the Bayes factor to select between models without truncation, with truncation from below, from above, and two-sided truncation is also explored. An extensive simulation study is carried out for varying parameter choices under the conjugate prior set-up. For illustrative purposes, a real-life dataset is re-analyzed to demonstrate the applicability of the proposed methodology.

1. Introduction

A hidden truncation model, also known as a selective reporting model or latent variable model, is a mathematical model that describes observed variables truncated with respect to some hidden covariable(s). An example of hidden truncation provided by Arnold and Beaver [1] is that the observed variable is the waist size for uniforms of elite troops, and the hidden covariable is the height of the troops. The elite troops are selected only if they meet a specific minimum height requirement. Therefore, the variable waist size will not be observed unless the troop meets the minimum height requirement. Hidden truncation models have been used in studying personal income data when an individual’s income is either not always correctly specified or may be unreported. Different hidden truncation models and their inference are developed mostly using the classical approach. If the data are subject to hidden truncation, then it is natural to expect that the behavior of the random phenomenon differs from a non-truncated model. Note that the notion of the mixture model is related to the hidden truncated model. Arnold and Gomez [2] showed that the two-parameter skew–normal distribution can be viewed as having arisen from a standard normal density by hidden truncation or an additive component construction, and they conjectured that this apparent relation between hidden truncation and mixture models only occurs in the normal case. However, the hidden truncation and mixture models are slightly different, as in a mixture model, there is no such hidden covariable subject to truncation. Sometimes, through a natural mechanism or otherwise, a dataset has already been subject to one of the types of hidden truncation, such as the Quasar data as originally and independently studied in Efron and Petrosian [3].

A non-exhaustive list of the references on hidden truncation models is as follows. One may cite the seminal paper by Azzalini [4] to propel research endeavors in this area. It is conjectured and supported by appropriate real-life scenarios, including but not limited to income modeling, astronomical data, survival analysis, etc., such that hidden truncation models provide flexible alternatives to the somewhat constrained and elliptically contoured distributions for modeling bivariate/multivariate or matrix-variate data in higher dimensions. Arnold [5] developed and studied several univariate, bivariate, and multivariate parametric families of distributions based on hidden truncation. Arnold and Beaver [1] suggested that a hidden truncation model involves a plethora of model parameters. Subsequently, it almost always involves a ubiquitous normalizing constant, making inferences under a frequentist framework virtually impossible. This is mainly because parameter estimates in conjunction with such models will not be available in closed forms or at least analytically intractable, and quite often, they have constraints. Furthermore, using a frequentist approach, non-normal models involving a two-sided truncation would require special attention when exploring inferential aspects. However, efforts have been made to estimate the model parameters for hidden truncation models under the frequentist approach with some limitations. For example, Ghosh and Nadarajah [6] discussed the inference under the classical approach of a hidden truncated Pareto (type-II) model starting from a bivariate Pareto (type-II) model. Hidden truncation in bivariate and multivariate Pareto data has been developed and applied to income modeling (see the references in [7]). Zaninetti [8] found that a left-truncated beta distribution better fits the initial mass function for stars compared to the lognormal distribution, which has commonly been used in astrophysics. Kotz et al. [9] (Chapter 44) also discussed the details of the formation of distributions through truncation.

Under the Bayesian paradigm, one-sided hidden truncated Pareto (type-II and type-IV) has been discussed by Ghosh [10,11], but not much discussion has been made on the applicability as well as the efficacy of the proposed Bayesian methodology in terms of prior choices, including the choice of hyperparameters, among others. Noticeably, nonparametric methods for estimation corresponding to two-sided truncated data have been developed by Efron and Petrosian [3]. This serves as a major motivation for the current research work.

In this paper, we explore the estimation of model parameters for a two-sided hidden truncated model, assuming that the data come from a bivariate exponential distribution defined by Arnold and Strauss [12]. Since the exponential distribution is an important probability model for studies involving non-negative random variables, such as the frailty models, this probability model is selected to utilize the proposed Bayesian estimation strategy with the hope that the proposed technique can be well adopted for several other non-normal models. For a detailed study on the genesis of the construction of hidden truncated non-normal models, readers may refer to [7] and the references therein. Next, we delve into the hidden truncation models and discuss the reason to start with a bivariate exponential-type model. Hidden truncation involves ubiquitous normalizing constants followed by the truncation parameter(s) masking within other parameters embedded in such a way that there is an estimate for the composite function, say $\psi \left(\theta \right)$, in which $\theta$ involves not only the truncation parameter but also location and scale parameters of the conditioning variable. Moving away from the normal distribution under the hidden truncation model will increase the difficulty in model fitting and related statistical inference. In search for a simpler non-normal model involving a two-sided hidden truncation, the bivariate exponential distribution proposed by Arnold and Strauss [12] is selected for illustrative purposes. As the statistical parameter estimation of a hidden truncation model is challenging, especially when there is a lack of information on the truncation limits in the model, we aim to provide a feasible approach based on the Bayesian paradigm that can be used in practical situations.

The rest of the paper is organized as follows. In Section 2, the mathematical derivation for a basic two-component model of hidden truncated distributions and the mathematical derivation of a two-sided hidden truncated bivariate exponential (HTBEXP, in short) model are provided. Section 3 provides the details of the Bayesian inference adopted in this paper for the HTBEXP model developed in Section 2 under both an informative and non-informative and improper priors set-up. Section 4 explores the Bayes factor to deal with model selection procedures out of all possible candidate models. In Section 5, a Monte Carlo simulation study under the Bayesian paradigm is used to evaluate the performance of the proposed Bayesian estimation method. For illustrative purposes, a real-life dataset is re-analyzed in Section 6 to exhibit the efficacy of the proposed estimation strategy. Finally, some concluding remarks are presented in Section 7.

2. Hidden Truncation in Arnold–Strauss Bivariate Exponential Model

Let $(X,Y)$ be a two-dimensional absolutely continuous random vector. Consider the conditional distribution of X given $Y\in M$, where M is a Borel set in $\mathbb{R}$. In a hidden truncation model, variable X is the variable of interest, and variable Y is a related unobservable variable that may be related to X. Let $f_{X,Y}(x,y)$ be the joint probability density function (PDF) of the random vector $(X,Y)$, and let $f_X\left(x\right)$ and $f_Y\left(y\right)$ be the marginal PDFs of random variables X and Y, respectively. The conditional PDF of X given $Y\in M$ can be expressed as

$$\begin{array}{c}\hfill f_{X|Y\in M}\left(x\right)=f_X\left(x\right)\left[\frac{Pr(Y\in M|X=x)}{Pr(Y\in M)}\right].\end{array}$$

(1)

The following three forms of hidden truncation models can be considered:

(i)

Truncation from below (also known as lower truncation): $M=(d_1,\infty )$, where $-\infty <d_1<\infty$ is the lower truncation point;

(ii)

Truncation from above (also known as upper truncation): $M=(-\infty ,d_2)$, where $-\infty <d_2<\infty$ is the upper truncation point;

(iii)

Two-sided truncation: $M=(d_1,d_2]$, where $d_1$ and $d_2$ are the lower and upper truncation points, respectively, with $-\infty <d_1<d_2<\infty$.

For a two-sided hidden truncation, observations are only available for X’s whose corresponding concomitant variable Y is in $(d_1,d_2]$, for $-\infty <d_1<d_2<\infty$. Hence, Equation (1) reduces to

$$\begin{array}{c}\hfill f_{X|Y\in (d_1,d_2]}\left(x\right|d_1<Y\le d_2)=f_X\left(x\right)\left[\frac{Pr\left(d_1<Y\le d_2|X=x\right)}{Pr\left(d_1<Y\le d_2\right)}\right].\end{array}$$

(2)

This type of hidden truncation model is characterized as follows:

• The underlying marginal distribution of X can be specified by the PDF $f_X\left(x\right)$;
• The conditional distribution of Y given $X=x$ can be specified by the conditional PDF $f_{Y|X}\left(y|x\right)$;
• The specified values of truncation points are denoted by $d_1$ and $d_2$;
• There could be some other model parameters in addition to $d_1$ and $d_2$.

For the conditional PDF in Equation (2), if we consider $d_1\to -\infty$ and $d_2\to +\infty$, the PDF reduces to the unconditional marginal PDF of X. The shape of the conditional PDF will be more sensitive for smaller values of the lower truncation point $d_1$ compared to small or large values of the upper truncation point $d_2$. From the outset, the hidden truncation from below will not augment the original model since the resulting density will again be a member of the same family of distributions with only a reparametrization of the parent model. Consequently, we focus primarily on the hidden truncation from both sides in the more general framework, as the hidden truncation from below and/or from above will be a particular case of two-sided hidden truncation.

In this paper, for the applications in situations with random variables having non-negative supports (e.g., the survival and reliability analyses), a two-dimensional random vector $(X,Y)$ with non-negative coordinates that follows the Arnold–Strauss bivariate exponential (ASBE) distribution is considered. The joint PDF of the random vector $(X,Y)$ of ASBE distribution is

$$\begin{array}{c}\hfill f_{X,Y}(x,y)=Kexp\left[-\left(ax+by+cxy\right)\right],\mathrm{for}x>0,y>0,a>0,b>0,c>0,\end{array}$$

(3)

where K is the normalizing constant defined as

$$\begin{array}{c}\hfill K={\left[-cexp\left(\frac{ab}{c}\right)Ei\left(-\frac{ab}{c}\right)\right]}^{-1}.\end{array}$$

(4)

Here, $Ei\left(x\right)$ is the exponential integral function defined by $Ei\left(x\right)={\int }_{-\infty }^x{t}^{-1}exp\left(t\right)dt$. The associated marginal PDF of X will be

$$f_X\left(x\right)=\frac{Kexp\left(-ax\right)}{b+cx},x>0,$$

(5)

and the marginal density of Y will be

$$f_Y\left(y\right)=\frac{Kexp\left(-by\right)}{a+cy},y>0.$$

Therefore, the normalizing constant K can also be defined as

$$K={\left[{\int }_0^{\infty }\frac{exp(-ax)}{b+cx}dx\right]}^{-1}={\left[{\int }_0^{\infty }\frac{exp(-by)}{a+cy}dy\right]}^{-1}.$$

Since $\mathrm{P}\mathrm{r}\left(Y>y|X=x\right)$ for each fixed $X=x$ is monotonically decreasing in x for all possible values of y, the joint density in Equation (3) is negative quadrant dependent, and hence it has a negative correlation coefficient. In the context of hidden truncation, we assume that the random variable of interest X and the hidden covariable Y are dependent non-negative random variables that follow the ASBE distribution.

Note that the conditional PDF of Y given $X=x$ is

$$f_{Y|X=x}\left(y|X=x\right)=\left(b+cx\right)exp\left[-(b+cx)y\right],y>0.$$

Next, a two-sided hidden truncation for the random variable Y, say $d_1<Y\le d_2$, where $0\le d_1<d_2<\infty$ is considered. We can obtain

$$\begin{array}{ccc}\hfill Pr\left(d_1<Y\le d_2|X=x\right)& =& {\int }_{d_1}^{d_2}(b+cx)exp\left[-(b+cx)y\right]dy\hfill \\ & =& exp\left[-(b+cx)d_1\right]-exp\left[-(b+cx)d_2\right],\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill Pr\left(d_1<Y\le d_2\right)& =& {\int }_{d_1}^{d_2}\frac{Kexp\left(-by\right)}{a+cy}dy.\hfill \end{array}$$

(6)

Therefore, the conditional PDF of X given $d_1<Y\le d_2$, can be expressed as

$$\begin{array}{ccc}\hfill f\left(x|d_1<Y\le d_2\right)& =& f_X\left(x\right)\left[\frac{f_{Y|X=x}\left(y|X=x\right)}{Pr\left(d_1<Y\le d_2\right)}\right]\hfill \\ & =& \frac{exp\left(-ax\right)\left\{exp\left[-(b+cx)d_1\right]-exp\left[-(b+cx)d_2\right]\right\}}{\left(b+cx\right){\int }_{d_1}^{d_2}\frac{exp\left(-by\right)}{a+cy}dy}\hfill \\ & =& \frac{exp\left(-ax\right)\left\{exp\left[-(b+cx)d_1\right]-exp\left[-(b+cx)d_2\right]\right\}}{\left(b+cx\right)M(a,b,c,d_1,d_2)},x>0,\hfill \end{array}$$

(7)

where

$$\begin{array}{c}\hfill M(a,b,c,d_1,d_2)={\int }_{d_1}^{d_2}\frac{exp\left(-by\right)}{a+cy}dy\end{array}$$

(8)

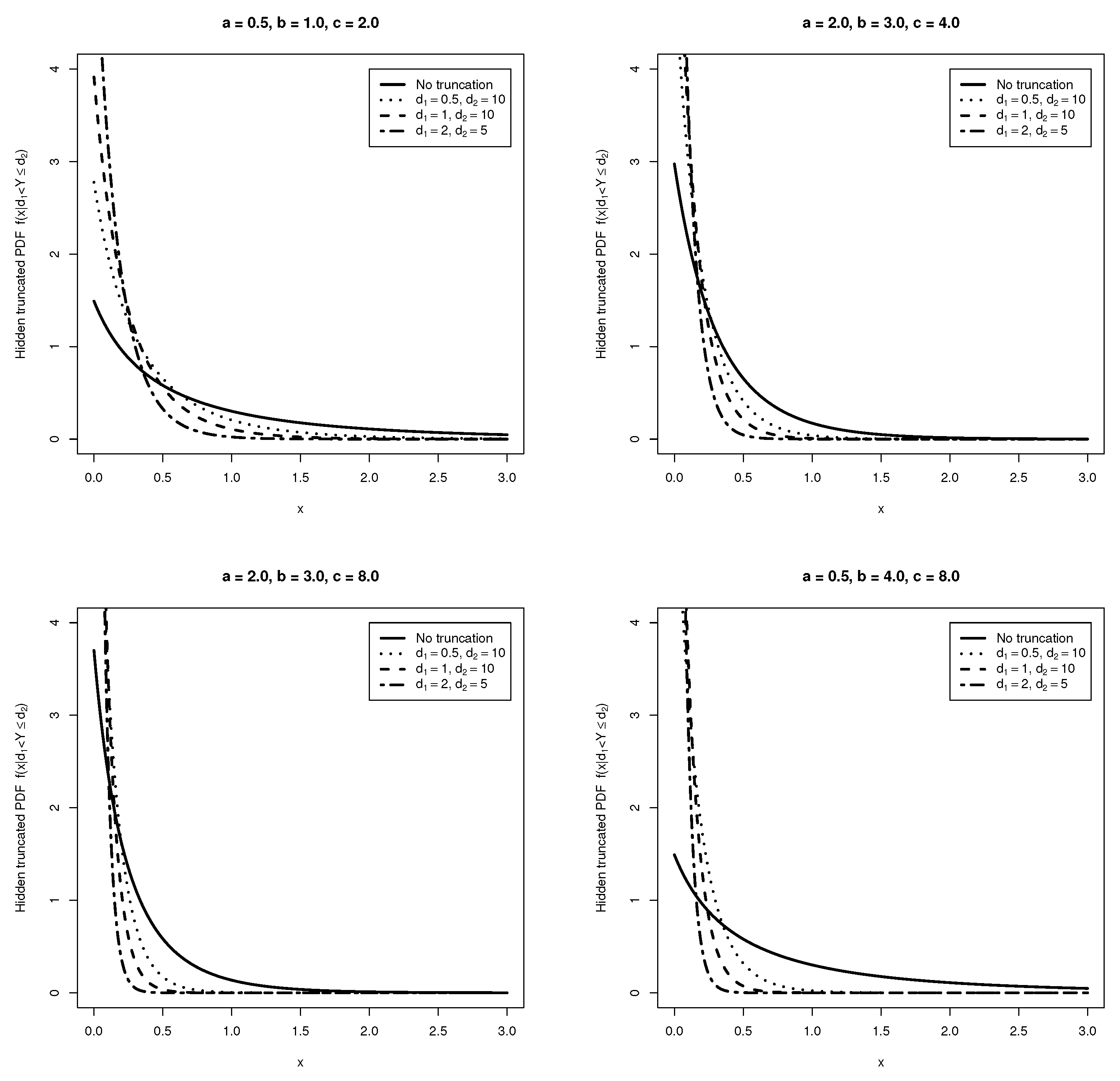
is a constant depending only on the parameters and not the random variable X. Figure 1 presents the hidden truncated PDFs of X given $d_1<Y\le d_2$ for different values of the parameters a, b, c, $d_1$, and $d_2$ based on the ASBE distribution along with the non-truncated exponential distribution.

From Figure 1, the hidden truncated PDFs are always right-skewed with different intensities for given choices of a, b, and c along with the truncated parameters $0\le d_1<d_2<\infty$. In Section 3, we discuss in detail the Bayesian inference of the density given in Equation (7).

3. Bayesian Inference

Let $X=(X_1,X_2,\dots ,X_n)$ be a random sample from the hidden-truncated distribution with the PDF in Equation (7), and $\mathit{x}=(x_1,x_2,\dots ,x_n)$ be the observed values of X. Based on $\mathit{x}=(x_1,x_2,\dots ,x_n)$, the associated likelihood function can be expressed as

$$\begin{array}{ccc}& & L(a,b,c,d_1,d_2|\mathit{x})\hfill \\ & =& \frac{1}{{\left[M(a,b,c,d_1,d_2)\right]}^n}\prod _{i=1}^n\frac{exp\left(-a{x}_i\right)\left\{exp\left[-(b+c{x}_i)d_1\right]-exp\left[-(b+c{x}_i)d_2\right]\right\}}{b+c{x}_i}.\hfill \end{array}$$

(9)

This section discusses the choices for the priors of the model parameters. Due to the condition that $d_1<d_2$, we consider dependent priors for parameters $d_1$ and $d_2$. For parameters $a,b$, and c, the following two scenarios are considered:

• Independent priors for parameters $a, b$, and c;
• Dependent priors for parameters $a, b$, and c.

3.1. Prior Specifications

3.1.1. Independent Priors for the Parameters a, b, and c

When the underlying distribution follows an exponential distribution, it is common that a gamma-type distribution is used as a prior distribution in a subjective Bayesian framework. Since the ASBE distribution is a member of the exponential family, the conjugacy of priors is expected. Consider a random variable that follows a gamma distribution with shape parameter $\alpha$ and rate parameter $\beta$, denoted as $Gamma(\alpha ,\beta )$, with the following PDF

$$\begin{array}{c}\hfill g(w;\alpha ,\beta )=\frac{{\beta }^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}{w}^{\alpha -1}exp(-\beta w),w>0,\alpha >0,\beta >0.\end{array}$$

The following independent priors for parameters a, b, c, and dependent priors for $d_1$, and $d_2$ are considered:

• The prior for parameter a

  $$\begin{array}{c}\hfill {\pi }_1\left(a\right)\sim Gamma({\alpha }_1,{\beta }_1).\end{array}$$
• The prior for parameter b

  $$\begin{array}{c}\hfill {\pi }_2\left(b\right)\sim Gamma({\alpha }_2,{\beta }_2).\end{array}$$
• The prior for parameter c

  $$\begin{array}{c}\hfill {\pi }_3\left(c\right)\sim Gamma({\alpha }_3,{\beta }_3).\end{array}$$
• For the upper and lower truncation points $d_1$ and $d_2$, since $d_1<d_2$, the following dependent priors are considered:

  $$\begin{array}{ccc}\hfill {\pi }_4\left(d_1\right)& \propto & \frac{1}{{(1+d_1)}^2}I(0<d_1<d_2),\hfill \\ \hfill {\pi }_5\left(d_2\right|d_1)& =& \frac{1}{\delta -d_1}I(d_1<d_2<\delta ).\hfill \end{array}$$

Remark 1.

Regarding the prior specifications on $d_1$ and $d_2$, the marginal prior distribution for $d_1$ is assumed to be a truncated distribution with support $(0,d_2]$. A uniform distribution for $d_2|d_1$ on the interval $[d_1,\delta ]$ is used, where δ is a hyperparameter that should be chosen properly for the underlying Bayesian analysis. For instance, the informed expert can provide a judicious choice of hyperparameters. These conditional priors for the two truncation points may not be the optimal choice of priors, but among all the other different priors that we have considered, this one seems to perform satisfactorily.

Based on the likelihood function in Equation (9), along with the joint prior distribution under independent a priori, and with the dependent prior choices for $d_1$ and $d_2,$ the joint posterior distribution of the five model parameters can be expressed as

$$\begin{array}{ccc}\hfill & & h(a,b,c,d_1,d_2|\mathit{x})\hfill \\ & \propto & L(a,b,c,d_1,d_2|\mathit{x})\times {\pi }_1\left(a\right)\times {\pi }_2\left(b\right)\times {\pi }_4\left(c\right)\times {\pi }_4\left(d_1\right)\times {\pi }_5\left(d_2\right|d_1)\hfill \\ & & \frac{1}{{\left[M(a,b,c,d_1,d_2)\right]}^n}\prod _{i=1}^n\frac{exp\left(-a{x}_i\right)\left\{exp\left[-(b+c{x}_i)d_1\right]-exp\left[-(b+c{x}_i)d_2\right]\right\}}{b+c{x}_i}\hfill \\ & \times & g(a;{\alpha }_1,{\beta }_1)g(b;{\alpha }_2,{\beta }_2)g(c;{\alpha }_3,{\beta }_3)\left[\frac{1}{{(1+d_1)}^2}\right]\left[\frac{1}{\delta -d_1}\right].\hfill \end{array}$$

(10)

Note that the marginal posterior distribution of each of the model parameters can be derived from the joint posterior in Equation (10). For instance, the posterior distribution of a can be obtained as

$$\begin{array}{c}\hfill p_1\left(a\right|x)=\frac{1}{D}{\int }_0^{d_2}{\int }_{d_1}^{\delta }{\int }_0^{\infty }{\int }_0^{\infty }h(a,b,c,d_1,d_2|\mathit{x})dbdcd{d}_{2}d{d}_1,\end{array}$$

where D is the normalizing constant defined as

$$\begin{array}{c}\hfill D={\int }_0^{d_2}{\int }_{d_1}^{\delta }{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }h(a,b,c,d_1,d_2|\mathit{x})dadbdcd{d}_{2}d{d}_1.\end{array}$$

Similarly, the posterior distributions for the remaining other parameters can be obtained. It is worth pointing out that each of the marginal distributions involves the quantity $M(a,b,c,d_1,d_2)$ defined in Equation (8), which is a constant. Due to the presence of the term D, an accurate approximation of the expectation in calculating the posterior mean is needed, and a five-dimensional numerical integration will be involved here. In this work, Gibbs sampling is used to find the Bayes estimates (posterior means) of the model parameters. Detailed procedures associated with the Metropolis–Hastings (MH) algorithms will be presented in Section 3.2.

3.1.2. Dependent Priors for Parameters a, b and c

In reality, the model parameters may be dependent. Hence, it is more reasonable to consider dependent priors. Here, some general prior choices for the model parameters are considered. Suppose we have specific information (in the form of a prior belief) about any of the parameters. Then, one can build informative priors for the rest of the parameter(s). For instance, if we know that parameter a can take values between 2 and 4, then a reasonable prior distribution for the parameter a would be any priors with support on $(2,4)$, e.g., a uniform distribution on the interval $(2,4)$. Although the use of dependent priors will increase the complexity of our analysis, one may still want to consider such priors. For analytically intractable models as given in Equation (7), the corresponding posterior analysis can be efficiently performed by Markov Chain Monte Carlo (MCMC) algorithms. However, in a real-life scenario, it is common that one might not have explicit knowledge of the priors for each parameter and the dependency between these parameters. Specifically, this occurs when we consider a situation in which the prior belief on either of the parameters a, b, or c, or some of the parameters a, b, and c depend on the two unknown truncation parameters $d_1$ and $d_2$.

Instead of independent priors, dependent priors for parameters a, b, and c can be considered. In this scenario, we assume that the prior distributions of a, b, and c follow conditional gamma distributions. For example,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\pi }_1^{*}\left(a\right|b,c)\sim Gamma({\xi }_1(b,c),{\lambda }_1(b,c)),\hfill \\ {\pi }_2^{*}\left(b\right|a,c)\sim Gamma({\xi }_2(a,c),{\lambda }_2(a,c)),\hfill \\ {\pi }_3^{*}\left(c\right|a,b)\sim Gamma({\xi }_3(a,b),{\lambda }_3(a,b)).\hfill \end{array}\right.\end{array}$$

On the other hand, the same prior distributions for $d_1$ and $d_2$ that were defined in Section 3.1.1 are used.

Next, the joint prior PDF of parameters a, b, and c can be expressed as (see [13] for details)

$$\begin{array}{ccc}\hfill f\left(a,b,c\right)& =& exp\{m_{000}-m_{100}a+m_{200}lna-m_{010}b+m_{110}ab-m_{210}blna\hfill \\ & & +m_{020}lnb-m_{120}alnb+m_{220}lnalnb-m_{001}c+m_{101}ca-m_{201}clna\hfill \\ & & +m_{011}cb-m_{111}abc-m_{021}clnb+m_{121}calnb+m_{211}cblna\hfill \\ & & -m_{221}lnb+m_{002}lnc-m_{102}alnc+m_{202}lnalnc-m_{012}blnc\hfill \\ & & +m_{112}ablnc-m_{212}blnalnc-m_{022}lnblnc-m_{122}alnblnc\hfill \\ & & +m_{222}lnalnblnc\}I(a>0)I(b>0)I(c>0).\hfill \end{array}$$

(11)

The family of PDFs in Equation (11) involves 27 hyperparametrs. A simplified sub-model, which still retains considerable flexibility, can be obtained by setting $m_{ijk}=0$, whenever $i+j+k>2$. Then, Equation (11) reduces to

$$\begin{array}{ccc}{f}^{*}(a,b,c)\hfill & =& exp\left(m_{000}-m_{100}a+m_{200}lna-m_{010}b+m_{110}ab+m_{020}lnb-m_{001}c\right.\hfill \\ & & \left. +m_{101}ca+m_{011}cb+m_{002}lnc\right)I(a>0)I(b>0)I(c>0).\hfill \end{array}$$

(12)

When the simplified 10-parameter model in Equation (12) is used, the joint posterior distribution from Equation (9) reduces to

$$\begin{array}{c}\hfill h^{*}(a,b,c,d_1,d_2|x)\propto L(a,b,c,d_1,d_2|x)\times f^{*}(a,b,c)\times {\pi }_4\left(d_1\right)\times {\pi }_5\left(d_2\right|d_1).\end{array}$$

(13)

3.2. Computation Algorithms

In this subsection, we present the detailed procedures for the MCMC algorithms in which the MH algorithms within Gibbs chains are utilized. Furthermore, different types of MH algorithms are adopted depending on the types of full conditional distributions. Since the procedures regarding the joint posterior distribution for dependent priors are similar, we present the posterior analysis based on only independent priors for brevity. From the joint posterior distribution in Equation (10), we can construct the full conditional distributions to proceed with utilizing the Gibbs sampling. The full conditional distributions are given as follows:

$$\begin{array}{ccc}\hfill p\left(a\right|b,c,d_1,d_2,\mathit{x})& \propto & \frac{1}{{\left[M(a,b,c,d_1,d_2)\right]}^n}{a}^{{\alpha }_1-1}exp\left\{-\left[\sum _{i=1}^n{x}_i+{\beta }_1\right]a\right\}I(a>0);\hfill \\ \hfill p\left(b\right|a,c,d_1,d_2,\mathit{x})& \propto & \frac{1}{{\left[M(a,b,c,d_1,d_2)\right]}^n}\prod _{i=1}^n\left[\frac{exp\{-(b+c{x}_i)d_1\}-exp\{-(b+c{x}_i)d_2\}}{b+c{x}_i}\right]\hfill \\ & & \times b^{{\alpha }_2-1}exp\{-{\beta }_{2}b\}I(b>0);\hfill \\ \hfill p\left(c\right|a,b,d_1,d_2,\mathit{x})& \propto & \frac{1}{{\left[M(a,b,c,d_1,d_2)\right]}^n}\prod _{i=1}^n\left[\frac{exp\{-(b+c{x}_i)d_1\}-exp\{-(b+c{x}_i)d_2\}}{b+c{x}_i}\right]\hfill \\ & & \times c^{{\alpha }_3-1}exp\{-{\beta }_{3}c\}I(c>0);\hfill \\ \hfill p\left(d_1\right|a,b,c,d_2,\mathit{x})& \propto & \frac{1}{{\left[M(a,b,c,d_1,d_2)\right]}^n}\prod _{i=1}^n\left[\frac{exp\{-(b+c{x}_i)d_1\}-exp\{-(b+c{x}_i)d_2\}}{b+c{x}_i}\right]\hfill \\ & & \times \frac{1}{{(1+d_1)}^2}I(0<d_1<d_2);\hfill \\ \hfill p\left(d_2\right|a,b,c,d_1,\mathit{x})& \propto & \frac{1}{{\left[M(a,b,c,d_1,d_2)\right]}^n}\prod _{i=1}^n\left[\frac{exp\{-(b+c{x}_i)d_1\}-exp\{-(b+c{x}_i)d_2\}}{b+c{x}_i}\right]\hfill \\ & & \times \frac{1}{\delta -d_1}I(d_1<d_2<\delta ).\hfill \end{array}$$

(14)

Note that none of the full conditional distributions has a closed-form expression. Hence, we propose using MH algorithms within each Gibbs chain. For parameters a, b, and c, a truncated normal distribution is used as a proposal density with a left-truncation point of zero. In particular, an adaptive MH algorithm that updates the variance of proposal distributions throughout the entire sampling process is used. In general, the proposal density of parameter $\theta$ ($\theta =a,b,c,d_1$, or $d_2$) is used as a (truncated) normal distribution, with the current value being its mean and the variance depending on forthcoming iterations. More specifically, suppose we want to update parameter $\theta$ in the ${(h+1)}^{th}$ step based on an initial value of ${\theta }^{\left(0\right)}$ and observed values of the first h iterations are denoted by ${\theta }^{\left(1\right)},{\theta }^{\left(2\right)},\cdots ,{\theta }^{\left(h\right)}$. The candidate value ${\theta }^{*}$ can be generated from a normal distribution with mean ${\theta }^{\left(h\right)}$ and variance $V^{\left(h\right)}$, where

$$\begin{array}{c}\hfill V^{\left(h\right)}=\left\{\begin{array}{cc}{V}^{\left(0\right)},\hfill & ifh=0,\hfill \\ \gamma [\mathrm{Var}\left({\theta }^{\left(0\right)},\cdots ,{\theta }^{(h-1)}\right)+\zeta ],\hfill & ifh>0.\hfill \end{array}\right.\end{array}$$

(15)

Here, $V^{\left(0\right)}$ is an initial (could be arbitrary) variance of the proposal distribution of parameter $\theta$, $\gamma$ is the adjusting coefficient, and $\zeta$ is a small constant to prevent the variance in Equation (15) from shrinking to zero. One of the important aspects of the adaptive MH algorithm is that it updates its variance so that the parameter being sampled reaches a desired acceptance rate. It is known that the optimal acceptance rate for one parameter is 0.44, so we set $\gamma =2.4/\sqrt{k}$, where k is the dimension of the parameter space. This ensures that the desired acceptance rate stays around 0.44; see [14] for pertinent details.

On the other hand, an independent MH algorithm is used to generate random variates from the full conditional distribution of $d_1$. The algorithm for generating a random variate from $p\left(d_1\right|\mathrm{others})$ is described below. When $d_1^{\left(j\right)}$ is the current value of the Markov chain, updating $d_1^{(j+1)}$ is required. The steps of the algorithm are described as follows.

A1.

Let q be the candidate density with a form:

$$\begin{array}{c}\hfill q\left(d_1\right)=\frac{1+d_2}{d_2}\frac{1}{{(1+d_1)}^2}\mathrm{for}0<d_1<d_2,\end{array}$$

(16)

where $d_2\equiv d_2^{\left(j\right)}$ is the value of the current state.

A2.

Generate $d_1^{*}$ from the PDF in Equation (16). Following Devroye [15], and the inverse cumulative distribution function (CDF) technique, $d_1^{*}$ can be generated from the following equation:

$$\begin{array}{c}\hfill d_1^{*}=\frac{1+d_2}{1+d_2(1-u)}-1,\end{array}$$

(17)

where u is a random variate from $Unif(0,1)$.

A3.

Next, the acceptance probability $\omega$ is calculated:

$$\begin{array}{c}\hfill \omega (d_1^{\left(j\right)},d_1^{*})=\frac{p\left(d_1^{*}\right)q\left(d_1^{\left(j\right)}\right)}{p\left(d_1^{\left(j\right)}\right)q\left(d_1^{*}\right)},\end{array}$$

where $p(·)$ is the full conditional distribution of $d_1$ in Equation (14). Now, set $d_1^{(j+1)}=d_1^{*}$ if $u\le \omega (d_1^{\left(j\right)},d_1^{*})$, and $d_1^{(j+1)}=d_1^{\left(j\right)}$ otherwise.

Finally, we employ the random-walk MH for updating $d_2$. When $d_2^{\left(j\right)}$ is given, we wish to update $d_2^{(j+1)}$. Generate $d_2^{*}$ from $\mathrm{Unif}(d_2^{\left(j\right)}-ϵ,d_2^{\left(j\right)}+ϵ)$ for $ϵ>0$. Next, we calculate the acceptance probability:

$$\begin{array}{c}\hfill \omega (d_2^{\left(j\right)},d_2^{*})=\frac{p\left(d_2^{*}\right)I(d_1<d_2^{*}<\delta )}{p\left(d_2^{\left(j\right)}\right)I(d_1<d_2^{\left(j\right)}<\delta )},\end{array}$$

where $d_1\equiv d_1^{\left(j\right)}$ is the value of the current state. If $u\le \omega (d_2^{\left(j\right)},d_2^{*})$ and $I(d_1<d_2^{*}<\delta )$, then set $d_2^{(j+1)}=d_2^{*}$. Otherwise, $d_2^{(j+1)}=d_2^{\left(j\right)}$, and $u\sim \mathrm{Unif}(0,1)$.

Remark 2.

The efficacy of the MCMC algorithm involving analytically intractable models, such as the case here with the constant $M(a,b,c,d_1,d_2)$, can be a concern. For instance, the constant $M(a,b,c,d_1,d_2)$ is in an integral form, and the exact value may not be able to be obtained analytically. However, we can approximate $M(a,b,c,d_1,d_2)$ accurately for given values of a, b, c, $d_1$, and $d_2$ and perform the Bayesian computation with the MCMC strategy without any difficulty. Noticeably, the results based on the simulation study are supportive of this assertion. One may need to consider non-standard MCMC techniques for doubly intractable posteriors; see, for example, [16]. In the Section 4, we discuss the selection strategy to select among all possible candidate hidden truncation models using the Bayes factor, the most appropriate and plausible model.

4. Selection between Different Hidden Truncation Models

In this section, we consider the following four models for the hidden truncated bivariate exponential distribution:

• $M_1$: No hidden truncated model, i.e., $d_1=0$ and $d_2=\infty$.
• $M_2$: A truncated from below model, i.e., $0<d_1<d_2=\infty$.
• $M_3$: A truncate from above model, i.e., $0=d_1<d_2<\infty$.
• $M_4$: A truncate from both sides model, i.e., $d_1>0$ and $d_2<\infty$.

Let ${\mathsf{\Theta }}_j$ denote the parameter space for model $M_j$ ($j=1,2,3,4$). Hence, we have ${\mathsf{\Theta }}_1=(a,b,c)$, ${\mathsf{\Theta }}_2=(a,b,c,d_1)$, ${\mathsf{\Theta }}_3=(a,b,c,d_2)$, and ${\mathsf{\Theta }}_4=(a,b,c,d_1,d_2)$. Based on the observed values $\mathit{x}=(x_1,x_2,\cdots x_n)$ from each of models $M_1$, $M_2$, and $M_3$, the likelihood functions under these three models are given respectively by

$$\begin{array}{ccc}\hfill L_1(a,b,c|\mathit{x})& =& \frac{1}{{\left[I_1(a,b,c)\right]}^n}\prod _{i=1}^n\frac{exp\{-a{x}_i\}}{b+c{x}_i},\hfill \\ \hfill L_2(a,b,c,d_1|\mathit{x})& =& \frac{1}{{\left[I_2(a,b,c,d_1)\right]}^n}\prod _{i=1}^n\frac{exp\{-a{x}_i\}exp\{-(b+c{x}_i)d_1\}}{b+c{x}_i},\hfill \\ \hfill L_3(a,b,c,d_2|\mathit{x})& =& \frac{1}{{\left[I_3(a,b,c,d_2)\right]}^n}\prod _{i=1}^n\frac{exp\{-a{x}_i\}[1-exp\{-(b+c{x}_i)d_2\}]}{b+c{x}_i},\hfill \end{array}$$

(18)

where $I_1(a,b,c)$ is the same as $1/K$ in Equation (4) of the current text, and

$$\begin{array}{c}\hfill I_2(a,b,c,d_1)={\int }_{d_1}^{\infty }\frac{exp\{-by\}}{a+cy}dy\mathrm{and}{I}_3(a,b,c,d_2)={\int }_0^{d_2}\frac{exp\{-by\}}{a+cy}dy.\end{array}$$

For model $M_4$, the likelihood function $L(a,b,c,d_1,d_2|\mathit{x})$ is presented in Equation (9).

Remark 3.

Regarding prior specifications for models $M_1$, $M_2$, and $M_3$, we use the same prior distributions utilized in the full model $M_4$ by deleting irrelevant parameters to estimate the corresponding parameters. Subsequently, we could obtain MCMC outputs in the three models that can also approximate marginal distributions.

To choose the most plausible model based on the observed data, we consider using the Bayesian approach based on the Bayes factor. Suppose that there are q different models, namely, $M_1,\dots ,M_q$, any of which could be meaningful, and they contend with each other for model selection. If model $M_i$ holds true, the data $\mathit{x}=(x_1,\cdots ,x_n)$ follow a parametric distribution with PDF $f_i\left(x\right|{\mathsf{\theta }}_i)$, where ${\mathsf{\theta }}_i$ is an unknown parameter vector for $M_i$. Let ${\mathsf{\Theta }}_i$ be the parameter space for the parameter vector ${\mathsf{\theta }}_i$, where ${\mathsf{\Theta }}_i$ may or may not be nested. Bayesian model selection proceeds by choosing a prior PDF ${\pi }_i\left({\mathsf{\theta }}_i\right)$ for ${\mathsf{\theta }}_i$ under $M_i$, and a prior model probability $p\left(M_i\right)$ of $M_i$ being true for $i=1,\cdots ,q$. The posterior model of the probability that $M_i$ is true can be obtained as (for pertinent details, see, [17])

$$\begin{array}{c}\hfill P\left(M_i\right|\mathit{x})=[\sum _{j=1}^q\frac{p\left(M_j\right)}{p\left(M_i\right)}{B}_{ji}\left(\mathit{x}\right){]}^{-1},\end{array}$$

(19)

where the Bayes factor $B_{ji}\left(\mathit{x}\right)$ of model $M_j$ to $M_i$ is defined by

$$\begin{array}{c}\hfill B_{ji}\left(\mathit{x}\right)=\frac{m_j\left(\mathit{x}\right)}{m_i\left(\mathit{x}\right)}=\frac{{\int }_{{\mathsf{\Theta }}_j}{f}_j\left(\mathit{x}\right|{\theta }_j){\pi }_j\left({\theta }_j\right)d{\theta }_j}{{\int }_{{\mathsf{\Theta }}_i}{f}_i\left(\mathit{x}\right|{\theta }_i){\pi }_i\left({\theta }_i\right)d{\theta }_i},\end{array}$$

(20)

where $m_i\left(\mathit{x}\right)$ is called the marginal or predictive density of x under $M_i$. Subsequently, the model with the largest posterior probability in Equation (19) becomes the most plausible model. It is customary to use vague model probabilities, i.e., $p\left(M_i\right)=1/q$ for $i=1,\cdots ,q$. Then, Equation (19) becomes $P\left(M_i\right|\mathit{x})={\left[{\sum }_{j=1}^q{B}_{ji}\right]}^{-1}$. Clearly,

$$\begin{array}{c}\hfill B_{ii}=1\mathrm{and}{B}_{ij}=B_{ji}^{-1},\mathrm{for}i,j=1,\cdots ,q.\end{array}$$

(21)

Meanwhile, we use the method proposed by Newton and Raftery [18] to evaluate the marginals of the four models. The procedure is described as follows. Observe that the posterior distribution can be represented as $p\left(\mathsf{\theta }\right|\mathit{x})\propto L_j\left(\mathsf{\theta }\right|\mathit{x})\times {\pi }_j\left(\mathsf{\theta }\right)$ under model $M_j$ for $j=1,2,3,4$. For notational simplicity, let $\mathsf{\theta }=(a,b,c,d_1,d_2)$ under the full model $M_4$. Now, let $\left\{{\mathsf{\theta }}^{\left(g\right)}\right\}\equiv \{{\mathsf{\theta }}^{\left(1\right)},\cdots ,{\mathsf{\theta }}^{\left(G\right)}\}$ be G, drawing from the posterior density obtained by conventional MCMC methods such as the Gibbs sampler. Newton and Raftery [18] suggested that the marginal can be estimated as

$$\begin{array}{c}\hfill {\widehat{m}}_4\left(\mathit{x}\right)=\left\{\frac{1}{G}\sum _{g=1}^G\right(\frac{1}{L_4\left(\mathit{x}\right|{\mathsf{\theta }}^{\left(g\right)})}){\}}^{-1}.\end{array}$$

(22)

Note that the estimate in Equation (22) is the harmonic mean of the likelihood evaluated at MCMC samples.

5. Monte Carlo Simulation Studies

In this section, Monte Carlo simulation studies are used to evaluate the Bayesian parameter estimation and model selection procedures proposed in this paper for the hidden truncation models. First, a Monte Carlo simulation study is used to evaluate the performance of Bayes estimates for the model parameters of the probability distribution given in Equation (7). For illustrative purposes, we consider the true values of the model parameters to be $(a,b,c,d_1,d_2)=(2,3,4,1,10),$ and three different sample sizes n = 100, 200, and 300. For each simulated dataset, the posterior means, posterior medians, and the associated 95% highest posterior density (HPD) credible intervals of the model parameters are computed. After collecting the posterior estimates based on a total of 200 replications, the performance of the point estimates is evaluated based on the average posterior mean, coverage probability (CP), and average width (AW) of the 95%. The total and burn-in MCMC iterations of the Bayesian estimation procedure are set to be 20,000 and 5000, respectively. Regarding the hyperparameters of the prior distributions on a, b, and c, we set $\left({\alpha }_1,{\beta }_1\right)=(4,2)$, $\left({\alpha }_2,{\beta }_2\right)=\left(9,3\right)$, and $\left({\alpha }_3,{\beta }_3\right)=\left(16,4\right)$, in order to obtain the mean of each prior distribution to be the same as the true value and the variances as one for the three prior gamma distributions. For the hyperparameter(s) of the distribution on $d_2|d_1$, we set $\delta =20$. Moreover, regarding the initial variances in Equation (15) of the zero-truncated normal distributions, we set a standard deviation of two for each of a, b, and c.

Table 1. Simulation results when the data are generated from $M_4$ with parameter values $(a,b,c,d_1,d_2)=(2,3,4,1,10)$.

Sample Size	Posterior Estimate	Parameters
		$\mathit{a}$	$\mathit{b}$	$\mathit{c}$	${\mathit{d}}_{\mathbf{1}}$	${\mathit{d}}_{\mathbf{2}}$
100	Average posterior mean	$2.443$	$2.952$	$4.102$	0.903	10.504
	MSE of posterior mean	$0.203$	$0.011$	$0.017$	$0.054$	$0.279$
	Average posterior variance	$1.411$	$0.974$	$0.938$	$0.192$	$30.125$
	Coverage probability (CP)	100%	100%	100%	100%	100%
	Average width (AW)	$4.348$	$3.715$	$3.695$	$1.621$	$17.968$
200	Average posterior mean	$2.458$	$2.951$	$4.092$	$0.898$	$10.495$
	MSE of posterior mean	$0.217$	$0.021$	$0.023$	$0.031$	$0.264$
	Average posterior variance	$1.442$	$0.962$	$0.921$	$0.175$	$30.159$
	Coverage probability	100%	100%	100%	100%	100%
	Average width	$4.411$	$3.682$	$3.665$	$1.585$	$19.955$
300	Average posterior mean	$2.433$	$2.960$	$4.098$	$0.901$	$10.495$
	MSE of posterior mean	$0.210$	$0.028$	$0.031$	$0.027$	$0.269$
	Average posterior variance	$1.407$	$0.957$	$0.901$	$0.164$	$30.125$
	Coverage probability (CP)	100%	100%	100%	100%	100%
	Average width (AW)	$4.371$	$3.674$	$3.610$	$1.552$	$17.944$

provides the average posterior means, the mean square errors (MSEs) of the posterior means, the average posterior variances, the CPs, and AWs for the model parameters based on 200 simulations.

From Table 1, we observe that all the CPs are 100%, which indicates that the standard errors of the estimates are relatively large. The posterior means of b, c, $d_1$, and $d_2$ are close to the true values for decently large sample sizes. However, the posterior means for a are overestimated with large average widths for the HPD intervals. We also observe that there are no dramatic improvements in parameter estimation accuracy when the sample size increases. Since we are dealing with subjective prior choices, there are infinitely many combinations on the hyperparameters, and the performance of the Bayesian estimation procedure depends on the choice of the hyperparameters. For instance, based on our preliminary study (results are not shown here), the performance can be poor when prior distributions with large prior variances are used. Although the choices of hyperparameter values used in this simulation study may not be optimal, these choices of hyperparameter values provide satisfactory results among the choices we examined.

In the second Monte Carlo simulation study, the performance of the model selection procedure is evaluated when the four models $M_1$–$M_4$ are considered candidate models. In this simulation study, data are generated from the four models $M_1$–$M_4$, and the model selection method based on Bayes factors presented in Section 4 is applied to each simulated dataset. Then, we obtain the proportions to determine which model has the largest posterior model probability. Recall that the posterior probabilities can be computed by Equation (19) in conjunction with Equation (22). For comparative purposes, we compute the average posterior probabilities in two ways by assuming the equal prior model probability of $1/4$ for each model $M_1$–$M_4$:

I.

The average of posterior probabilities, no matter which model is selected out of 500 replications (denoted as Post. Prob. I in

Table 2. Posterior probabilities and Bayes estimates for different models.

True Model	Posterior Probability & Parameter Estimate	Contending Models
		${\mathit{M}}_{\mathbf{1}}$	${\mathit{M}}_{\mathbf{2}}$	${\mathit{M}}_{\mathbf{3}}$	${\mathit{M}}_{\mathbf{4}}$
$M_1$	Post. Prob. I	0.251	0.249	0.251	0.249
	Freq. (Prop.) of selection	125 (0.250)	142 (0.284)	96 (0.192)	137 (0.274)
	Post. Prob. II	0.265	0.261	0.265	0.261
	Post. mean (median) for a	1.912 (1.910)	1.339 (1.350)	1.971 (1.964)	1.372 (1.379)
	Post. mean (median) for b	2.777 (2.660)	3.320 (3.210)	2.771 (2.657)	3.344 (3.227)
	Post. mean (median) for c	4.158 (4.088)	3.471 (3.392)	4.179 (4.101)	3.480 (3.408)
	Post. mean (median) for $d_1$	$d_1=0$	0.250 (0.224)	$d_1=0$	0.251 (0.220)
	Post. mean (median) for $d_2$	$d_2=\infty$	$d_2=\infty$	10.000 (10.000)	10.000 (10.000)
$M_2$	Post. Prob. I	0.239	0.261	0.239	0.261
	Freq. (Prop.) of selection	46 (0.092)	186 (0.372)	44 (0.088)	224 (0.448)
	Post. Prob. II	0.271	0.270	0.278	0.270
	Post. mean (median) for a	5.301 (5.315)	2.033 (1.889)	5.299 (5.308)	2.043 (1.899)
	Post. mean (median) for b	2.377 (2.250)	3.060 (2.951)	2.338 (2.207)	3.062 (2.939)
	Post. mean (median) for c	4.460 (4.376)	3.789 (3.691)	4.483 (4.402)	3.786 (3.716)
	Post. mean (median) for $d_1$	$d_1=0$	1.127 (1.113)	$d_1=0$	1.131 (1.103)
	Post. mean (median) for $d_2$	$d_2=\infty$	$d_2=\infty$	10.000 (9.999)	10.000 (10.000)
$M_3$	Post. Prob. I	0.251	0.250	0.250	0.249
	Freq. (Prop.) of selection	105 (0.210)	140 (0.280)	109 (0.218)	146 (0.292)
	Post. Prob. II	0.264	0.260	0.265	0.261
	Post. mean (median) for a	1.941 (1.934)	1.358 (1.368)	1.934 (1.922)	1.360 (1.368)
	Post. mean (median) for b	2.759 (2.645)	3.321 (3.206)	2.763 (2.643)	3.339 (3.227)
	Post. mean (median) for c	4.161 (4.087)	3.488 (3.416)	4.186 (4.109)	3.482 (3.406)
	Post. mean (median) for $d_1$	$d_1=0$	0.250 (0.222)	$d_1=0$	0.247 (0.217)
	Post. mean (median) for $d_2$	$d_2=\infty$	$d_2=\infty$	10.000 (9.999)	10.000 (10.000)
$M_4$	Post. Prob. I	0.239	0.261	0.239	0.261
	Freq. (Prop.) of selection	45 (0.090)	205 (0.410)	42 (0.084)	208 (0.416)
	Post. Prob. II	0.274	0.270	0.276	0.270
	Post. mean (median) for a	5.224 (5.230)	2.033 (1.889)	5.287 (5.229)	2.042 (1.897)
	Post. mean (median) for b	2.348 (2.220)	3.055 (2.945)	2.342 (2.207)	3.059 (2.949)
	Post. mean (median) for c	4.482 (4.393)	3.787 (3.692)	4.481 (4.399)	3.790 (3.695)
	Post. mean (median) for $d_1$	$d_1=0$	1.139 (1.127)	$d_1=0$	1.122 (1.101)
	Post. mean (median) for $d_2$	$d_2=\infty$	$d_2=\infty$	10.000 (10.001)	10.000 (10.000)

);

II.

The average of posterior probabilities is based only on the samples possessing the highest posterior probability in each replication (denoted as Post. Prob. I in Table 2). For example, the “Post. Prob. II” when the true model is $M_1$ in Table 2, 0.265 for contending model $M_1$ is computed based on 125 samples that model $M_1$ is selected.

Based on 500 simulated samples from each model, the above two types of posterior probabilities, the frequency and proportion of selecting a particular model, and the average posterior means (medians) based only on selected models for each model parameter are presented in Table 2. The numerical summaries in Table 2 with the same prior specifications and iterations are in accordance with the adopted MCMC procedures described in Section 3.2.

From Table 2, we observe that the parameter estimates based on either the posterior mean or the posterior median of the four models yield decently reasonable results for all cases considered. To select the most plausible model, although the procedure based on the Bayes factor (posterior probability) does not capture the true model in all the cases, the procedure based on the Bayes factor tends to select model $M_4$, which is the most general hidden truncation model among the four models with the largest number of parameters.

Since the number of parameters models $M_1$–$M_4$ are different, instead of evaluating the performance based on the parameter estimates, we consider the estimation of the conditional mean $E\left(X|w_1<Y<w_2\right)$, where $w_1$ and $w_2$ are pre-specified values based on the model and the values of $d_1$ and $d_2$ (e.g., for model $M_1$, $w_1=0$ and $w_2=\infty$), which is a function of the model parameters. Specifically, for given values of $w_1$ and $w_2$, the conditional expectation is

$$\begin{array}{ccc}\hfill \tau (a,b,c)& =& {\int }_0^{\infty }x{f}_{X|y}\left(x\right|w_1<Y<w_2)dx\hfill \\ & =& {\int }_0^{\infty }\frac{x{e}^{-ax}[exp\{-(b+cx)w_1\}-exp\{-(b+cx)w_2\}]}{(b+cx)M^{*}(a,b,c,w_1,w_2)},\hfill \end{array}$$

where

$$\begin{array}{c}\hfill M^{*}(a,b,c,w_1,w_2)={\int }_{w_1}^{w_2}\frac{e^{-by}}{a+cy}dy.\end{array}$$

Let R be the total number of simulations (i.e., $R=500$ in this study) and $r_i$ be the number of samples that model $M_i$ is selected with the largest posterior model probability ($i=1,2,3,4$), where $R=r_1+r_2+r_3+r_4$. Suppose ${\widehat{\tau }}_{ij}(a,b,c)$ is the estimate of $\tau (a,b,c)$ based on the j-th sample, where model $M_i$ is selected as the most plausible model for $i=1,2,3,4$, $j=1,2,\dots ,r_i.$ The MSEs based on the simulated data corresponding to selected model $M_i$, denoted as $MS{E}_i$, can be calculated as

$$\begin{array}{c}\hfill MS{E}_i=\frac{1}{r_i}\sum _{j=1}^{r_i}{[{\widehat{\tau }}_{ij}(a,b,c)-\tau (a,b,c)]}^2.\end{array}$$

(23)

To illustrate the effect on the performance of estimating the conditional expectation with the model selection procedure, the MSE with the model selection procedure is calculated as

$$\begin{array}{c}\hfill MS{E}_{MS}=\frac{1}{R}\sum _{i=1}^4\sum _{j=1}^{r_1}{[{\widehat{\tau }}_{ij}(a,b,c)-\tau (a,b,c)]}^2.\end{array}$$

(24)

The simulated values of $MS{E}_i$ ($i=1,2,3,4$) and $MS{E}_{MS}$ for estimating the conditional expectation associated with the model selection perspectives are presented in

Table 3. Mean square errors for estimating the conditional expectation.

	Contending Models
True Model	${\mathit{M}}_{\mathbf{1}}$	${\mathit{M}}_{\mathbf{2}}$	${\mathit{M}}_{\mathbf{3}}$	${\mathit{M}}_{\mathbf{4}}$	Model Selection ${\mathit{MSE}}_{\mathit{MS}}$
	${\mathit{MSE}}_{\mathbf{1}}$	${\mathit{MSE}}_{\mathbf{2}}$	${\mathit{MSE}}_{\mathbf{3}}$	${\mathit{MSE}}_{\mathbf{4}}$
$M_1$	0.00069	0.00085	0.00068	0.00086	0.00081
$M_2$	0.00016	0.00010	0.00016	0.00011	0.00012
$M_3$	0.00069	0.00085	0.00068	0.00085	0.00081
$M_4$	0.00016	0.00011	0.00015	0.00010	0.00012

. Note that the proportions of selecting the correct models with the highest posterior probability are all the same as in Table 2. As expected, the value of ${MSE}_i$ is the smallest if $M_i$ is the true model in most cases. The simulation results in Table 3 show that the model selection procedure can reduce the risk of mis-specifying the underlying model. On the other hand, we observe that the values of $MS{E}_1$ and $MS{E}_3$ are similar, while the values of $MS{E}_2$ and $MS{E}_4$ are similar. Note that models $M_1$ and $M_3$ assume $d_1=0$, while $M_2$ and $M_4$ assume $d_1>0$ with an unknown value. This observation suggests that determining whether $d=0$ may provide further information to improve the estimation of the conditional expectation.

6. Illustrative Example

In this section, the proposed methodologies in this paper are illustrated using a real dataset comprised of independently collected quadruplets of the redshift and the apparent magnitude of a quasar object previously analyzed by Efron and Petrosian [3]. The dataset is available in the R package DTDA version 3.0.1 [19] named Quasars. The original data consist of $n=210$ observations with the following variables $(z_i,m_i,{d_1}_i,{d_2}_i)$ for $i=1,\cdots ,n$, where $z_i$ denotes the redshift of the i-th quasar, $m_i$ denotes its apparent magnitude, and the two values ${d_1}_i$ and ${d_2}_i$ indicate lower and upper truncation bounds corresponding to the apparent magnitude, respectively. The variable of interest is the transformed logarithm of luminosity values provided in the first column of the dataset Quasars, i.e., $V_i=t(z_i,m_i)$, where t is a transformation that depends on the cosmological model assumed (see [20,21] for a detailed description). The anti-logarithm transformation $X_i=exp\left(V_i\right)$ is considered such that the support of the random variable $X_i$ is $[0,\infty )$. We conjecture that the dataset has been subjected to a two-sided truncation and the PDF in Equation (7) would be appropriate to model this dataset, where the observation $X_i$ is subjected to a two-sided truncation by other covariates, and the same truncation points apply for $X_i$, $i=1,2,\cdots ,n$, i.e., $d_{1i}\equiv d_1$ and $d_{2i}\equiv d_2$.

Based on the model in Equation (7), and using the Bayesian methodologies proposed in this paper, the results presented in

Table 4. Posterior probabilities, posterior means (medians), and 95% HPD intervals for quasar data.

Model	Posterior Probability	Parameters
		$\mathit{a}$	$\mathit{b}$	$\mathit{c}$	${\mathit{d}}_{\mathbf{1}}$	${\mathit{d}}_{\mathbf{2}}$
$M_1$	$0.203$	0.535 (0.536)	7.044 (6.741)	0.994 (0.893)	$d_1=0$	$d_2=\infty$
		$(0.433, 0.644)$	$(2.645, 11.889)$	$(0.166, 2.067)$	$d_1=0$	$d_2=\infty$
$M_2$	0.305	0.435 (0.450)	6.261 (6.000)	0.666 (0.588)	0.238 (0.170)	$d_2=\infty$
		$(0.195, 0.614)$	$(1.969, 10.649)$	$(0.060, 1.388)$	$(0, 0.686)$	$d_2=\infty$
$M_3$	$0.209$	0.537 (0.536)	7.073 (6.741)	0.992 (0.889)	$d_1=0$	$9.499 \left(9.499\right)$
		$(0.436, 0.646)$	$(2.588, 11.989)$	$(0.158, 2.100)$	$d_1=0$	$(9.020, 9.971)$
$M_4$	$0.283$	0.439 (0.452)	6.500 (6.232)	0.722 (0.634)	0.210 (0.148)	9.500 (9.501)
		$(0.226, 0.628)$	$(2.392, 11.198)$	$(0.117, 1.527)$	$(0, 0.661)$	$(9.006, 9.956)$

are obtained. Regarding the hyperparameters of the prior distributions on a, b, and c, we set $\left({\alpha }_j,{\beta }_j\right)=(4,1)$ for $j=1,2,3$ because we have no information on these parameters. The same value of $\delta =20$ as in the Monte Carlo simulation studies is used. In Table 4, we report the posterior probabilities for each of the four models $M_1$–$M_4$, and the posterior means and medians (presented in the parenthesis) along with the corresponding 95% HPD intervals. From a model selection perspective, model $M_2$ is selected with the largest posterior probability of $0.305$, assuming equal prior model probability for all four models. We notice that $M_4$ has the second largest posterior probability of $0.283$, which agrees with our observation of the similarity of models $M_2$ and $M_4$ in the simulation results. Regarding the posterior inference, we observe that the estimates of a, b, and c have some patterns. The estimates under models $M_1$ and $M_3$ are close to each other, while those values are close to each other when models $M_2$ and $M_4$ are applied. Thus, the HPD intervals are changed accordingly. Figure 2 shows the trace plots for all parameters when the four models are adapted, respectively. Overall, the plots for a, b, and c are decently well behaved, while there are some fluctuations in the plots of $d_1$ and $d_2$.

We want to highlight the fact that the parameter estimates/values of parameter $d_1$ and $d_2$ (i.e., the last two columns) in Table 4 and for the Model $M_2$ having the maximum posterior probability confirm the fact that the data (alias the main study variable, $X_i$) have been subject to a one-sided upper truncation, as the value of $d_1\ne 0.$ In this data application, we have explored all possible scenarios of hidden truncation (including zero truncation) and then adopted strategy searches for the best-case scenario under the Bayesian paradigm.

7. Concluding Remarks

In this article, we explore the features of a two-sided hidden truncated model in terms of estimation under the Bayesian paradigm and, most importantly, detecting with a desired level of accuracy whether or not the data have been subject to hidden truncation starting with a simple model in two dimensions, namely, the bivariate exponential distribution proposed by Arnold and Strauss [12]. Indeed, there are several other versions of the classical bivariate exponential distribution, but they may have a singular part (i.e., if two random variables $Y_1$ and $Y_2$ follow a bivariate distribution, there is a positive probability that $Y_1=Y_2$) [22] (see, for example, [23]), which makes it more difficult to consider from real-world and mathematical perspectives. For this reason, we resort to a simple model that is an absolutely continuous statistical distribution, develop the corresponding hidden-truncation model, and provide some feasible model-fitting methodologies that can be used in practice. Consequently, inferential aspects under the Bayesian paradigm for the parameters of a doubly (two-sided) hidden truncation model are still in their infancy stage and have not been explored in detail to the best of our knowledge. Statistical inference of the hidden truncation models with unknown truncation point(s) is a challenging problem, especially when there is very little information about the truncation point(s) in the observed sample. One can expect to mimic the inferential results obtained in this paper to other types of hidden truncated bivariate exponential models, albeit with computational complexity and possibly with a different set of informative and non-informative priors that might be challenging. Needless to say, the associated computational complexity and judicious selection of prior choices, especially for the truncation points, are the natural hindrance to developing the methodology and theory. Inference under the Bayesian framework, as discussed in the simulation study as well as in the real-data application, is encouraging in the sense that the Bayesian estimates of the parameters are reasonably good under both settings. Efficient estimation for multiple constraints models, i.e., the estimation of model parameters for a hidden truncated model under a multi-component set-up, where, for example, the main study variable Y is observed only when the associated concomitant variables, say, $X_j$ are truncated from below, such as $X_j<c_j$ (or ${\ell }_j<X_j<d_j$), will be of great interest in the context of several real-life applications. However, the real-life applicability of such models and their analytical traceability are the two key factors that should be addressed first. Research in this direction is in progress, and we hope to report the results in a future paper.