Statistical Inferences about Parameters of the Pseudo Lindley Distribution with Acceptance Sampling Plans

Abstract

Different non-Bayesian and Bayesian techniques were used to estimate the pseudo-Lindley (PsL) distribution’s parameters in this study. To derive Bayesian estimators, one must assume appropriate priors on the parameters and use loss functions such as squared error (SE), general entropy (GE), and linear-exponential (LINEX). Since no closed-form solutions are accessible for Bayes estimates under these loss functions, the Markov Chain Monte Carlo (MCMC) approach was used. Simulation studies were conducted to evaluate the estimators’ performance under the given loss functions. Furthermore, we exhibited the adaptability and practicality of the PsL distribution through real-world data applications, which is essential for evaluating the various estimation techniques. Also, the acceptance sampling plans were developed in this work for items whose lifespans approximate the PsL distribution.

1. Introduction

Quality control and parameter estimation are pivotal for ensuring product reliability and accuracy in various industries. In this paper, we explored two interconnected concepts to enhance quality assurance and statistical inference: the construction of an acceptance sampling plan tailored to the pseudo-Lindley distribution, and the estimation of pseudo-Lindley distribution parameters using Bayesian and non-Bayesian methods.

The pseudo-Lindley (PsL) distribution, known for its flexibility in modeling lifetime data and reliability analysis, provides a robust framework for statistical analysis in diverse fields [1,2,3]. Our study delved into the intricate interplay between acceptance sampling strategies and parameter estimation techniques within this distribution context.

Firstly, we addressed constructing an acceptance sampling plan that is customized for the PsL distribution. Acceptance sampling plans are fundamental tools in quality control, allowing for efficient batch assessment while reducing inspection costs. By developing a tailored sampling plan for the PsL distribution, we aimed to optimize decision-making processes regarding batch acceptance or rejection based on statistical analysis. In the literature, some relevant works have provided insights into the construction, optimization, and application of acceptance sampling plans. For example, Refs. [4,5,6,7,8,9].

The Lindley (Li) distribution and its various extensions have been extensively studied and analyzed in the context of acceptance sampling plans. Ref. [10] created both single and double acceptance sampling plans for products with lifespans following the power Lindley distribution. These plans were developed considering both infinite and finite lot sizes. Operating characteristic curves for these sampling plans were derived, and they were generated for different parameter values. Ref. [11] developed an acceptance sampling plan (ASP) tailored for scenarios where the life test is truncated at a predetermined time. Specifically, they focused on situations where a product’s lifetime follows a two-parameter quasi-Lindley distribution. Their work contributes to the understanding and application of acceptance sampling plans in settings with specific lifetime distribution characteristics. Ref. [12] examined continuous acceptance sampling plans for truncated Lindley distribution and optimized CUSUM schemes using the Gauss–Chebyshev integration method. Ref. [13] introduced an acceptance sampling inspection plan designed for cases where the quality characteristic follows either the Lindley or power Lindley distributions. Ref. [14] created an acceptance sampling plan for a truncated life test with products following a two-parameter Lindley distribution. They determined the necessary minimum sample size and failure threshold for lot acceptance across various combinations of Lindley-distributed parameters, the termination time of the test, and the quality-and-risk standards agreed upon by suppliers and buyers. Ref. [15] studied the single acceptance sampling plan for the odd Lindley Pareto distribution. Finally, [16] employed the modified Lindley distribution for analyzing product lifetimes and deciding on batch acceptance or rejection when a life test concludes at a predetermined time. This study introduces single, double, and multiple acceptance sampling strategies, and optimal sample sizes for each were calculated to ensure that the actual mean lifespan exceeds the specified mean lifespan at the consumer’s risk level. Additionally, this research examined operating characteristic functions across different quality levels and determined the minimum ratios of an actual mean lifespan to prescribe the mean lifespan at specified levels of producer’s risk for each acceptance sampling plan.

Secondly, we delved into estimating PsL distribution parameters using both Bayesian and non-Bayesian methodologies. Parameter estimation is critical for accurately modeling data and making informed decisions in statistical inference. By incorporating prior knowledge into parameter estimation, Bayesian methods offer robustness and flexibility in uncertain environments. In contrast, non-Bayesian methods provide straightforward and computationally efficient alternatives. In this context, various authors have examined and investigated parameter estimation methods for the Lindley distribution and its extensions (which have two parameters), such as Ref. [17]—where the simulation and estimation issues of the Lindley distribution were studied using a maximum likelihood (ML) estimator. Refs. [18,19] suggested two-parameter weighted Lindley (WL) and power Lindley (PL) distribution using the mixture and power transformed methods, respectively. In a simulation study, they discussed the coverage probability (CP), the width of the confidence interval (CI), the bias, and the mean square error (MSE) of the ML estimates of the parameters. Ref. [20] estimated the parameters of the PL distribution using Bayesian estimation (BE) under a hybrid censored sample of lifetime data. Ref. [21] used three non-Bayesian estimator methods, i.e., ML, least squares (LS), and maximum product spacings (MPS) estimators, to estimate the PL parameters, and the BEs were built under the assumption of a quadratic loss function. Pak et al. [22] investigated the BEs of the PL distribution using the squared error (SE), general entropy (GE), and linear-exponential (LINEX) loss functions, among others. Every one of the BEs was calculated with gamma priors that were assumed for the various parameters. On the other hand, Ghitany et al. [23] studied the estimating problem $\varrho =P(Z>K)$ under complete samples using the ML estimation and bootstrap methods, where $Z\sim PL(\alpha ,{\theta }_1)$ and $K\sim PL(\alpha ,{\theta }_2)$ were two independent random variables. Joukar et al. [24] investigated and studied using MLE and BE to estimate problem $\varrho =P(X>Y)$ under progressively type-II censored samples. Ref. [25] suggested a new extension of the Li distribution as an alternative to the Weibull (W), Li, exponentiated exponential (EE), and Gamma (Ga) distributions, which are called generalized Lindley (GL) distribution. Two classical estimation methods were used including the method of moments (MOM) and ML estimators. Singh et al. [26,27] investigated the BE of GL parameters under progressive and completely censored samples. Asgharzadeh et al. (2016) [28] suggested a new WL distribution. This distribution consists of the WL distribution [18] and the well-known Li distribution as special cases. Finally, Shanker et al. [29,30] introduced quasi-Lindley (QL) and Janardan (J) distributions using the mixture method; the probability density functions (PDF) of QL and J were gound to be more flexible than the Li and Exp distributions, and the MOM and the MLE were used to estimate the different parameters. Several researchers have investigated and evaluated the performance of BEs under different assumptions for prior beliefs and various types of loss functions, including both symmetric and asymmetric ones. As previously discussed in studies on the Li distribution and its two-parameter extensions, there is also a wealth of literature exploring BEs. For example, see [15,31,32,33,34,35,36]; for more details, see [37].

In this study, acceptance sampling plans (ASP) were developed for the PsL model, assuming that the life test will end at a specified time. Additionally, both Bayesian and non-Bayesian methods for estimating PsL parameters were explored.

The remainder of this paper is organized as follows: The definition of the PsL distribution is provided in Section 2. Section 3 describes developing the proposed ASP’s structure. Classical inference methods are covered in Section 4. In Section 5, BE methods are explored when assuming independent priors, employing various loss functions, including SE, LINEX, and GE loss functions. To demonstrate the distribution’s flexibility, a simulated exercise is presented in Section 6. We compared different estimation methods applied to real-life data, as detailed in Section 7, and Section 8 provides the summary.

2. Pseudo Lindley Distribution

Zeghdoudi et al. [38,39] proposed the pseudo-Lindley (PsL) distribution as a new extension of the Li distribution, which is a mixture of Exp($\theta$) and Ga($2,\theta$) distributions with the mixing probability $p=\frac{\delta -1}{\delta }$. They found that the hazard rate function (HRF) of the PsL distribution was increasing, discussed some mathematical properties, and used MLE to estimate the parameters of the PsL distribution. Gane et al. [40] explored the estimators of the parameters using the MOM, and they constructed statistical tests based on the asymptotic laws derived from these estimators. The efficiency of these tests for different data sizes was used in verifying the reliability and was demonstrated through simulation studies.

The probability density function (PDF) and cumulative distribution function (CDF) of the PsL distribution are defined as follows:

$$\begin{array}{c}\hfill f(x,\nu ,\delta )=\left\{\begin{array}{cc}\frac{\nu (\delta -1+\nu x)e^{-\nu x}}{\delta },\hfill & x,\nu >0,\delta \ge 1,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(1)

and

$$\begin{array}{c}\hfill F(x,\nu ,\delta )=1-\frac{(\delta +\nu x)e^{-\nu x}}{\delta },x,\nu >0,\delta \ge 1,\end{array}$$

(2)

where the corresponding reliability and HRF are given by

$$\begin{array}{c}\hfill R(x,\nu ,\delta )=\frac{(\delta +\nu x)e^{-\nu x}}{\delta },x,\nu >0,\delta \ge 1,\end{array}$$

(3)

and

$$\begin{array}{c}\hfill h(x,\nu ,\delta )=\frac{\nu (\delta +\nu x-1)}{\delta +\nu x},x,\nu >0,\delta \ge 1.\end{array}$$

(4)

The quantile function is given as follows:

$$\begin{array}{c}\hfill Q_x\left(p\right)=-\frac{\delta }{\nu }-\frac{1}{\nu }{W}_{(-1)}\left[\delta e^{-\delta }(p-1)\right],\end{array}$$

(5)

where $W_{(-1)}(.)$ is the negative Lambert-W function and $0<p<1.$

The mean, variance, median, and mode of the PsL distribution are given, respectively, as follows: $\mathrm{mean}=\frac{\delta +1}{\nu \delta },\mathrm{variance}=\frac{{\delta }^2+2\delta -1}{{\nu }^2{\delta }^2},\mathrm{median}=-\frac{\delta }{\nu }-\frac{1}{\nu }{W}_{(-1)}\left[\delta e^{-\delta }(\frac{1}{2}-1)\right]$, and $\mathrm{mode}\left(X\right)=\left\{\begin{array}{cc}\frac{2-\delta }{\nu }\hfill & \mathrm{if}1\le \delta <2,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

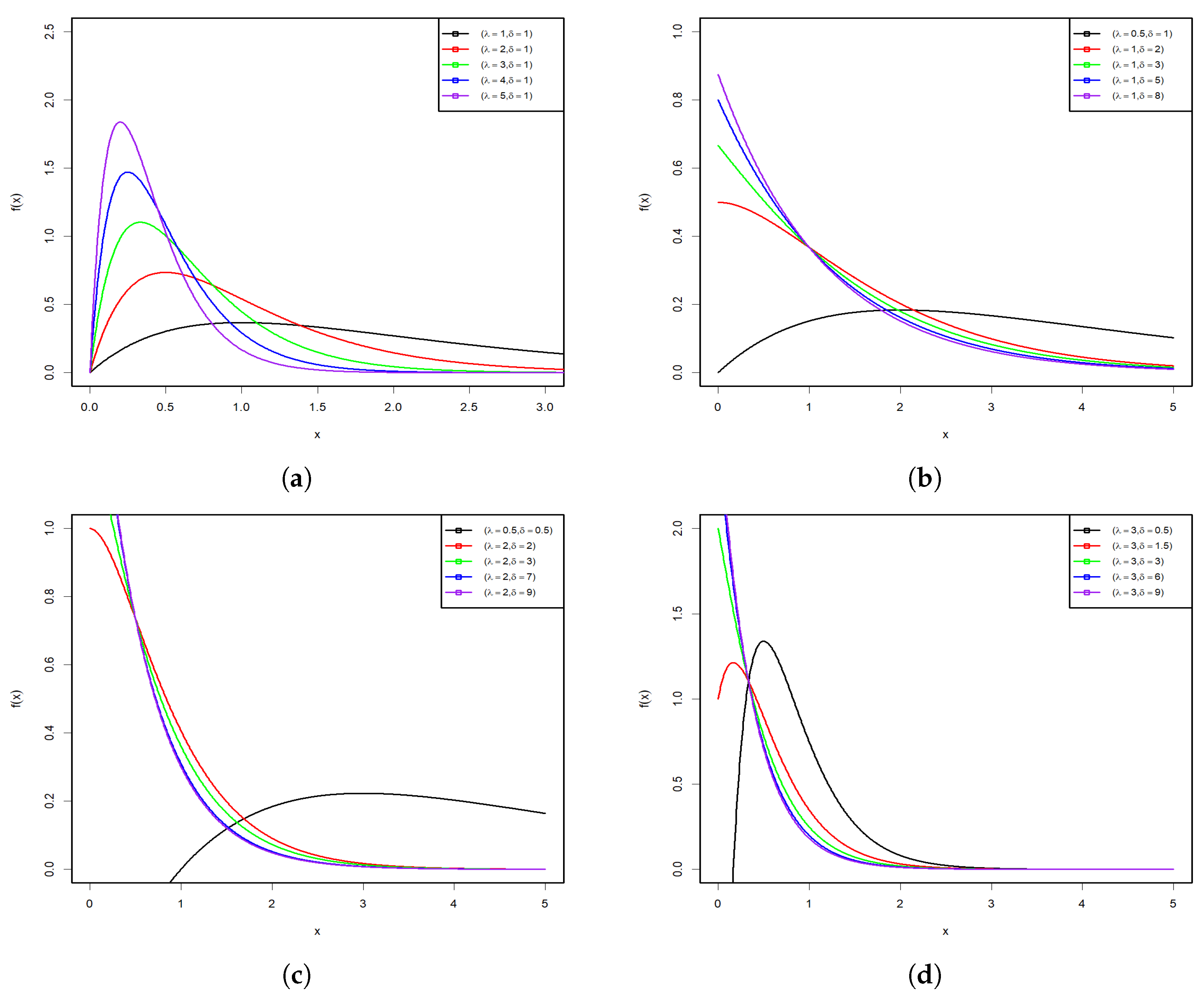
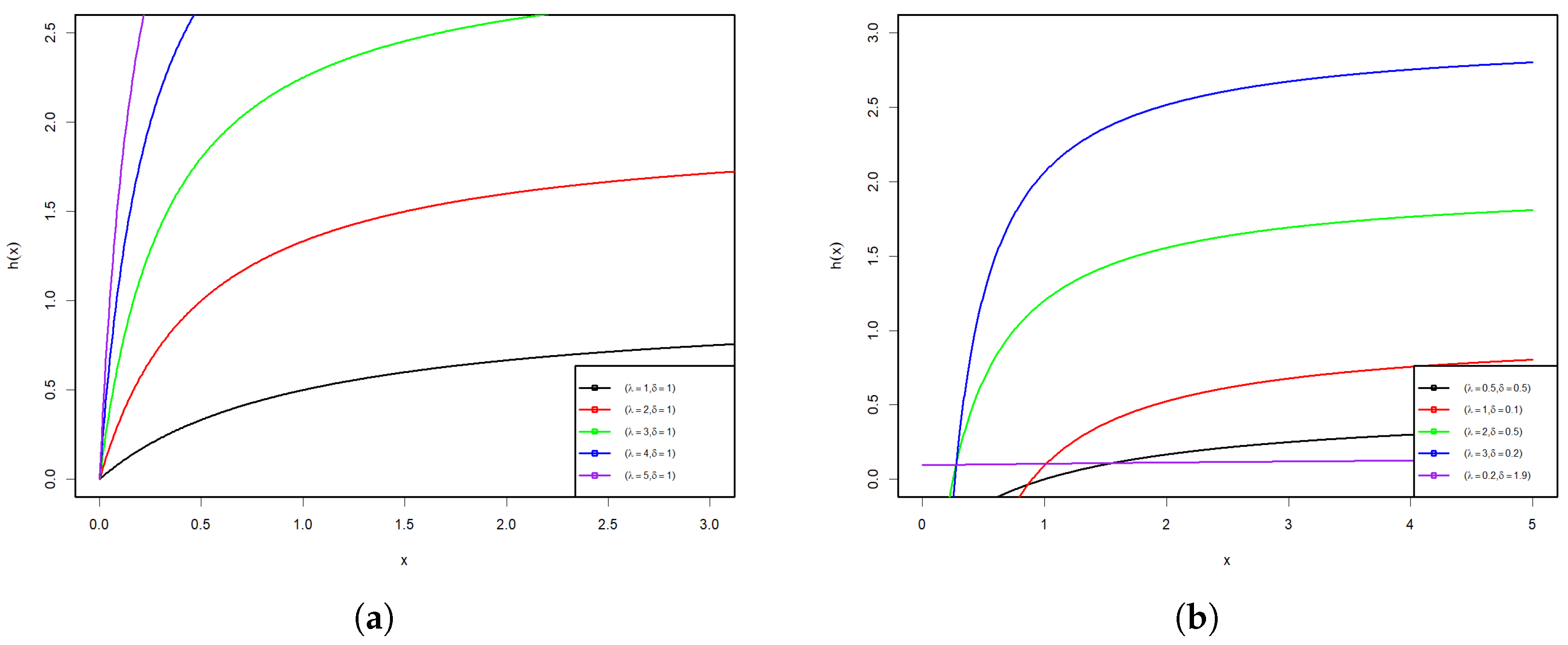
Figure 1 and Figure 2 display some graphs of the PDF and HRF of the PsL distribution for various parameter values. Figure 1a–d shows that the PDF of the PsL distribution has many shapes, such as right-skew, inverted bathtub, and inverse-J shaped, along with different Kurtosis. Conversely, Figure 2a,b reveals that the HRF of PsL distribution is increasing and constant.

3. Acceptance Sampling Plans

Assuming that the lifespan of the product conforms to the PsL distribution characterized by two parameters—which are denoted as $\nu$ and $\delta$, as described in Equation (2)—and that the declared median, denoted as M, of the units asserted by a manufacturer is $M_0$, then our objective is to conclude whether the proposed batch should be accepted or rejected based on the condition that the actual median lifespan of the units exceeds the predetermined threshold $M_0$. A common procedure in life testing involves concluding the test at a predefined time t and recording the count of failures. To determine the median lifetimes, the experiment is carried out throughout $t=a{M}_0$ units. The ASP has been extensively investigated in various studies like [8,9,15,41,42,43,44]. Ref. [43] describes the concept of accepting the offered batch based on evidence that $M\ge M_0$, with a probability of at least $u^{*}$ (consumer’s risk), by taking into account the ASP. The process to determine this is as follows: Obtain a random sample comprising n units from the proposed batch and perform an experiment throughout t units of time. If, through the experiment, fewer units (referred to as the acceptance number)—denoted by c—fail, then the entire lot is accepted; otherwise, the lot is rejected. As per the suggested ASP, the accepting probability of a batch is determined by considering batches of sufficient size to facilitate the application of the binomial distribution. This probability is expressed as

$$\begin{array}{c}\hfill L\left(u\right)=\sum _{j=0}^c\left(\genfrac{}{}{0pt}{}{n}{j}\right)u^j{(1-u)}^{n-j},j=1,2,\dots ,n,\end{array}$$

where $u=F(t_0,\nu ,\delta )$, which is defined by (2). The function $L\left(u\right)$ denotes the operational characteristic of the sampling plan, which represents the acceptance probability of the lot relative to the failure probability. Moreover, utilizing the formula $t=a{M}_0$, $u_0$ can be expressed accordingly:

$$\begin{array}{c}\hfill u_0=F(a{M}_0,\nu ,\delta )=1-\frac{(\delta +\nu a{M}_0)e^{-\nu a{M}_0}}{\delta }.\end{array}$$

(6)

The challenge is identifying the lowest positive integer n given specific values of $u^{*},c,$ and $a{M}_0$. Consequently, the function of operating characteristics can be reformulated as follows:

$$\begin{array}{c}\hfill L\left(u_0\right)=\sum _{j=0}^c\left(\genfrac{}{}{0pt}{}{n}{j}\right)u_0^j{(1-u_0)}^{n-j}\le 1-u^{*},\end{array}$$

(7)

where the $u_0$ is given by (6). The n smallest values that meet the inequality (7) and their corresponding operational characteristic probabilities are determined and presented in

Table 1. Sampling plan for the PsL distribution with $\nu =0.25$ and $\delta =1.20$.

${\mathit{u}}^{*}$	c	$\mathit{a}=0.25$		$\mathit{a}=0.45$		$\mathit{a}=0.60$		$\mathit{a}=0.80$		$\mathit{a}=1.00$
		$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{u}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{u}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{u}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{u}}_{\mathbf{0}}\mathbf{\right)}$	$\mathit{n}$	$\mathit{L}\mathbf{\left(}{\mathit{u}}_{\mathbf{0}}\mathbf{\right)}$
0.25	0	3	0.8128	2	0.7945	1	1.0000	1	1.0000	1	1.0000
	2	18	0.7689	9	0.7846	7	0.7627	5	0.8215	4	0.8750
	8	71	0.7507	34	0.7762	25	0.7609	18	0.8024	15	0.7880
	10	89	0.7500	43	0.7678	31	0.7607	23	0.7736	19	0.7597
0.5	0	7	0.5369	4	0.5415	3	0.5842	2	0.6006	2	0.6410
	2	27	0.5212	13	0.5388	9	0.5774	7	0.5455	6	0.6350
	8	88	0.5100	42	0.5267	30	0.5265	22	0.5259	18	0.5860
	10	109	0.5002	52	0.5163	37	0.5194	27	0.5237	22	0.5760
0.95	0	29	0.0549	14	0.0502	9	0.0646	6	0.0781	5	0.0665
	2	62	0.0529	29	0.0534	20	0.0557	14	0.0584	11	0.0657
	8	144	0.0508	67	0.0553	47	0.0531	33	0.0582	26	0.0599
	10	169	0.0508	79	0.0550	55	0.0526	39	0.0580	30	0.0580

,

Table 2. Sampling plan for the PsL distribution with $\nu =0.30$ and $\delta =2.20$.

${\mathit{u}}^{*}$	c	$\mathit{a}=0.25$		$\mathit{a}=0.45$		$\mathit{a}=0.60$		$\mathit{a}=0.80$		$\mathit{a}=1.00$
		$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$
0.25	0	2	0.8548	1	1.0000	1	1.0000	1	1.0000	1	1.0000
	2	13	0.7521	8	0.7805	6	0.7986	5	0.7986	4	0.8750
	8	48	0.7639	28	0.7785	22	0.7777	18	0.7534	15	0.7880
	10	61	0.7515	35	0.7778	28	0.7552	22	0.7762	19	0.7597
0.5	0	5	0.5338	3	0.5582	2	0.6724	2	0.5813	2	0.6874
	2	19	0.5029	11	0.5170	8	0.5839	7	0.5056	6	0.6876
	8	60	0.5076	34	0.5381	27	0.5070	21	0.5277	18	0.5880
	10	74	0.5024	42	0.5309	33	0.5114	26	0.5098	22	0.5870
0.95	0	20	0.0507	11	0.0542	8	0.0622	6	0.0664	5	0.0645
	2	42	0.0508	23	0.0572	17	0.0651	13	0.0653	11	0.0647
	8	97	0.0503	54	0.0553	41	0.0563	31	0.0640	26	0.0589
	10	114	0.0502	64	0.0528	49	0.0502	37	0.0590	30	0.0580

,

Table 3. Sampling plan for the PsL distribution with $\nu =0.35$ and $\delta =1.30$.

${\mathit{u}}^{*}$	c	$\mathit{a}=0.25$		$\mathit{a}=0.45$		$\mathit{a}=0.60$		$\mathit{a}=0.80$		$\mathit{a}=1.00$
		$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$
0.25	0	3	0.7940	2	0.7842	1	1.0000	1	1.0000	1	1.0000
	2	17	0.7502	9	0.7611	6	0.8396	5	0.8169	4	0.8750
	8	64	0.7554	33	0.7600	24	0.7775	18	0.7928	15	0.7880
	10	80	0.7609	41	0.7589	30	0.7782	23	0.7618	19	0.7597
0.5	0	7	0.5065	3	0.6149	2	0.7020	2	0.5966	2	0.6865
	2	25	0.5059	13	0.5330	9	0.5570	7	0.5373	6	0.6865
	8	80	0.5037	40	0.5277	29	0.5370	22	0.5109	18	0.5981
	10	98	0.5024	50	0.5029	36	0.5206	27	0.5070	22	0.5880
0.95	0	26	0.0559	13	0.0591	9	0.0590	6	0.0756	5	0.0655
	2	56	0.0526	27	0.0589	19	0.0521	14	0.0551	11	0.0647
	8	130	0.0506	64	0.0532	46	0.0500	33	0.0532	26	0.0589
	10	153	0.0504	75	0.0526	54	0.0517	39	0.0525	30	0.0680

,

Table 4. Sampling plan for the PsL distribution with $\nu =0.40$ and $\delta =2.30$.

${\mathit{u}}^{*}$	c	$\mathit{a}=0.25$		$\mathit{a}=0.45$		$\mathit{a}=0.60$		$\mathit{a}=0.80$		$\mathit{a}=1.00$
		$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$
0.25	0	2	0.8533	1	1.0000	1	1.0000	1	1.0000	1	1.0000
	2	12	0.7889	7	0.8236	6	0.7968	5	0.7978	4	0.8750
	8	48	0.7549	28	0.7698	22	0.7740	18	0.7516	15	0.7880
	10	60	0.7531	35	0.7715	28	0.7507	22	0.7743	19	0.7597
0.5	0	5	0.5363	3	0.5560	2	0.6712	2	0.5807	2	0.6750
	2	18	0.5356	11	0.5425	8	0.6885	7	0.5042	6	0.6875
	8	59	0.5168	34	0.5300	27	0.5015	21	0.5253	18	0.5980
	10	73	0.5080	42	0.5219	33	0.5054	26	0.5070	22	0.5880
0.95	0	19	0.0576	11	0.0531	8	0.0614	6	0.0660	5	0.0655
	2	41	0.0543	23	0.0555	17	0.0638	13	0.0648	11	0.0647
	8	96	0.0504	54	0.0526	41	0.0545	31	0.0631	26	0.0599
	10	113	0.0502	63	0.0573	48	0.0582	37	0.0580	30	0.0580

,

Table 5. Sampling plan for the PsL distribution with $\nu =0.15$ and $\delta =1.40$.

${\mathit{u}}^{*}$	c	$\mathit{a}=0.25$		$\mathit{a}=0.45$		$\mathit{a}=0.60$		$\mathit{a}=0.80$		$\mathit{a}=1.00$
		$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$
0.25	0	3	0.7795	2	0.7760	1	1.0000	1	1.0000	1	1.0000
	2	15	0.7795	8	0.8084	6	0.8311	5	0.8131	4	0.8750
	8	59	0.7655	32	0.7556	24	0.7564	18	0.7848	15	0.7880
	10	75	0.7545	40	0.7570	30	0.7546	23	0.7520	19	0.7597
0.5	0	6	0.5364	3	0.6022	2	0.6956	2	0.5934	1	1.0000
	2	23	0.5152	12	0.5382	9	0.5407	7	0.5306	5	0.6875
	8	74	0.5115	39	0.5128	29	0.5073	21	0.5717	17	0.5982
	10	91	0.5115	48	0.5093	35	0.5323	26	0.5590	21	0.5881
0.95	0	25	0.0533	12	0.0615	9	0.0598	6	0.0736	5	0.0655
	2	52	0.0526	26	0.0586	19	0.0597	14	0.0726	11	0.0647
	8	120	0.0510	62	0.0504	44	0.0597	32	0.0640	26	0.0589
	10	142	0.0507	73	0.0504	52	0.0591	38	0.0617	30	0.0580

and

Table 6. Sampling plan for the PsL distribution with $\nu =0.20$ and $\delta =2.40$.

${\mathit{u}}^{*}$	c	$\mathit{a}=0.25$		$\mathit{a}=0.45$		$\mathit{a}=0.60$		$\mathit{a}=0.80$		$\mathit{a}=1.00$
		$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$
0.25	0	2	0.8521	1	1.0000	1	1.0000	1	1.0000	1	1.0000
	2	12	0.7852	7	0.8215	6	0.7952	5	0.7971	4	0.8750
	8	47	0.7673	28	0.7649	22	0.7707	17	0.8170	15	0.7980
	10	60	0.7504	35	0.7660	27	0.7910	22	0.7726	19	0.7737
0.5	0	5	0.5272	3	0.5540	2	0.6701	2	0.5801	2	0.6700
	2	18	0.5298	11	0.5086	8	0.5786	7	0.5030	6	0.6875
	8	59	0.5062	34	0.5231	26	0.5522	21	0.5231	18	0.5982
	10	72	0.5159	42	0.5142	33	0.5001	26	0.5047	22	0.5880
0.95	0	19	0.0561	11	0.0522	8	0.0607	6	0.0657	5	0.0655
	2	41	0.0522	23	0.0540	17	0.0627	13	0.0643	11	0.0647
	8	95	0.0512	54	0.0504	41	0.0529	31	0.0623	26	0.0589
	10	112	0.0504	63	0.0547	48	0.0515	37	0.0572	30	0.0580

for the assumed parameters as follows:

• Consumer risk assumptions: $u^{*}$ is taken as 0.25, 0.5, and 0.95.
• Acceptance numbers for each proposed lot: c is set as 0, 2, 8, and 10.
• The factor median lifetime, denoted as a, is assumed as 0.25, 0.45, 0.60, 0.80, and 1. If a = 1, then $t=M_0=0.5$ for all values of $\nu$ and $\delta$.
• Six parameter cases for the PsL distribution were considered $(0.25,1.20)$, $(0.30,2.20)$, $(0.35,1.30)$, $(0.40,2.30)$, $(0.15,1.40),$ and (0.20$,2.40)$.

From the results presented in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, we observed the following findings:

• Concerning the parameters of the ASP, as both $u^{*}$ and c increase, the necessary sample sizes n increases and the corresponding $L\left(p_0\right)$ decreases.
• When the value of a increases, the sample size n decreases and $L\left(u_0\right)$ increases.
• In all tables, for $a=1$, we had $u_0=0.5$ since $t_0=M_0$; thus, all outcomes $(n,L\left(u_0\right))$ for any parameter vector $(\nu ,\delta )$ were identical.

4. Classical Inference Methods

Here, we estimate the PsL distribution parameters using various non-Bayesian methods, including ML, LS, AD, MPS, and CVM estimation methods.

Assuming that $X_j\sim PsL(\nu ,\delta ),j=1,2,\dots ,k$, then the log-likelihood (L) function for the PsL distribution is given by

$$\begin{array}{cc}\hfill L& =\prod _{j=1}^{k}f(x_j,\nu ,\delta )\hfill \\ \hfill & ={\left(\frac{\nu }{\delta }\right)}^k{e}^{-\nu {\sum }_{j=1}^k{x}_j}\prod _{j=1}^k(\delta -1+\nu x_j).\hfill \end{array}$$

(8)

Taking the logarithm of the L function and simplifying gives

$$\begin{array}{c}\hfill \ell =klog\nu -klog\delta -\nu \sum _{j=1}^k{x}_j+\sum _{j=1}^{k}log(\delta -1+\nu x_j).\end{array}$$

(9)

For $\nu$ and $\delta$, the partial derivatives of the ℓ are given as follows

$$\begin{array}{c}\hfill \frac{\partial \ell }{\partial \nu }=\frac{k}{\nu }-\sum _{j=1}^k{x}_j+\sum _{j=1}^k\frac{x_j}{\delta -1+\nu x_j},\end{array}$$

(10)

and

$$\begin{array}{c}\hfill \frac{\partial \ell }{\partial \delta }=-\frac{k}{\delta }+\sum _{j=1}^k\frac{1}{\delta -1+\nu x_j}.\end{array}$$

(11)

To find the MLEs of the PsL distribution, we had to find the values of $\nu$ and $\delta$ that maximize the ℓ function in (9), when (10) and (11) equate to zero. This can be conducted using numerical optimization techniques like the Newton-Raphson method in the R studio programming language.

Subject to certain regularity conditions, the MLEs ($\widehat{\nu },\widehat{\delta }$) exhibited an approximate bi-variate normal distribution with mean ($\nu ,\delta$), which are denoted as $(\widehat{\nu },\widehat{\delta })\sim N_2\left(\left(\nu ,\delta \right),I^{-1}(\nu ,\delta )\right)$, as well as a covariance matrix, which is denoted as $I^{-1}(\nu ,\delta )$, where

$$I(\widehat{\nu },\widehat{\delta })=\left[\begin{array}{cc}\frac{\partial logL}{\partial {\nu }^2}& \frac{\partial logL}{\partial \nu \partial \delta }\\ \frac{\partial logL}{\partial \delta \partial \nu }& \frac{\partial logL}{\partial {\delta }^2}\end{array}\right]$$

The asymptotic variances for the $\nu$ and $\delta$ were determined by the diagonal elements of matrix $I^{-1}(\widehat{\nu },\widehat{\delta })$. Subsequently, the $100(1-\alpha )\%$ confidence interval for both $\nu$ and $\delta$ can be established using a normal approximation in the following equations: $\left\{\widehat{\nu }\pm {\mathbf{Z}}_{\alpha /2}\sqrt{var\left(\widehat{\nu }\right)}\right\}$ and $\left\{\widehat{\delta }\pm {\mathbf{Z}}_{\alpha /2}\sqrt{var\left(\widehat{\delta }\right)}\right\}$.

Assume that the $x_{\left(1\right)}<x_{\left(2\right)}<\dots <x_{\left(k\right)}$ are the order-random observations associated with a random sample of size k drawn from the PsL distribution.

The LS estimation method can be used to estimate the parameters $\nu$ and $\delta$ of the PsL distribution based on a set of observed data by minimizing the LS function for the PsL distribution concerning $\nu$ and $\delta$, which is defined in the following equations:

$$\begin{array}{cc}\hfill LS(\nu ,\delta )& =\sum _{j=1}^k{\left(F\left(x_{\left(j\right)}\right)-\frac{j}{k+1}\right)}^2\hfill \\ \hfill & =\sum _{j=1}^k{\left(1-\frac{(\delta +\nu x_{\left(j\right)})e^{-\nu x_{\left(j\right)}}}{\delta }-\frac{j}{k+1}\right)}^2.\hfill \end{array}$$

(12)

The AD method is a statistical method used for goodness-of-fit testing and the estimation of parameters in probability distributions. The AD method was introduced by [45]. The AD estimators of $\nu$ and $\delta$ for the PsL distribution were calculated by minimizing the AD function, which is given as follows:

$$\begin{array}{c}\hfill AD(\nu ,\delta )=-k-\frac{1}{k}\sum _{j=1}^k(2j-1)(logF\left(x_{\left(j\right)}\right)+log(1-F\left(x_{(k+1-j)}\right))).\end{array}$$

(13)

The MPS estimator is a non-parametric method for estimating the unknown parameters of a probability distribution based on the product of spacings between ordered sample values (Ferguson & Klass, 1972) [46]. The MPS estimators of $\nu$ and $\delta$ for the PsL distribution were determined by minimizing the

$$\begin{array}{c}\hfill MPS(\nu ,\delta )=\frac{1}{k+1}\sum _{j=1}^{k+1}ln{D}_{\left(j\right)},\end{array}$$

where $D_j$ is the uniform spacings from the PsL distribution, $D_{\left(j\right)}=F(x_{\left(j\right)},\nu ,\delta )-F(x_{(j-1)},\nu ,\delta );j=1,2,\dots ,k+1,$$\sum D_{\left(j\right)}=1,$$F\left(x_{\left(0\right)}\right)=0,$ and $F\left(x_{(k+1)}\right)=1$. Then, we have

$$\begin{array}{c}\hfill MPS(\nu ,\delta )=\frac{1}{k+1}\sum _{j=1}^{k+1}ln\left[\frac{(\delta +\nu x_{\left(j\right)})e^{-\nu x_{\left(j\right)}}}{\delta }-\frac{(\delta +\nu x_{(j-1)})e^{-\nu x_{(j-1)}}}{\delta }\right].\end{array}$$

(14)

The CVM method of estimation for the PsL distribution involves finding the parameters $\nu$ and $\delta$ that minimize the CVM function $CVM(\nu ,\delta )$, which measures the discrepancy between the empirical distribution function of a sample and the theoretical function of the PsL distribution. The CVM estimators of $\nu$ and $\delta$ were obtained by minimizing

$$\begin{array}{cc}\hfill CVM(\nu ,\delta )& =\frac{1}{12}+\sum _{j=1}^k{\left[F\left(x_{\left(j\right)}\right)-\frac{2j-1}{2j}\right]}^2\hfill \\ \hfill & =\frac{1}{12}+\sum _{j=1}^k{\left[1-\frac{(\delta +\nu x_{\left(j\right)})e^{-\nu x_{\left(j\right)}}}{\delta }-\frac{2j-1}{2j}\right]}^2.\hfill \end{array}$$

(15)

Due to the analytical difficulty of the aforementioned Equations (12)–(15), Monte Carlo simulation was employed to estimate the $\nu$ and $\delta$ using the R programming language.

5. Bayesian Estimation (BE) Methods

BE is a statistical method that allows for the inference of unknown parameters by combining prior knowledge and observed data. In BE, a prior distribution is specified for the parameter(s) of interest, which represents the beliefs or assumptions about the parameter(s) before observing any data. Then, the observed data are used to update the prior distribution to a posterior distribution using Bayes’ theorem.

Here, we suppose that parameter $\nu$ has a gamma prior distribution and $\delta$ has a shifted gamma prior distribution due to $\delta >1$ [47,48]. Therefore, we have

$$\begin{array}{c}\hfill {\Pi }_1\left(\nu \right)\propto {\nu }^{b_1-1}{e}^{-a_1\nu };\nu >0,a_1,b_1>0,\end{array}$$

(16)

$$\begin{array}{c}\hfill {\Pi }_1\left(\delta \right)\propto {(\delta -1)}^{b_2-1}{e}^{-a_2(\delta -1)};\delta >1,a_2,b_2>0,\end{array}$$

(17)

and the joint prior distribution of the $\xi =(\nu ,\delta )$ is obtained as follows:

$$\begin{array}{c}\hfill \Pi \left(\xi \right)\propto {\nu }^{b_1-1}{(\delta -1)}^{b_2-1}{e}^{-a_1\nu -a_2(\delta -1)}.\end{array}$$

(18)

The corresponding joint posterior of $\xi$ is given as follows:

$$\begin{array}{c}\hfill \Pi (\xi \setminus x̠)=\frac{\mathbf{L}(\xi \setminus x̠)\Pi \left(\xi \right)}{{\int }_0^{\infty }{\int }_0^{\infty }\mathbf{L}(\xi \setminus x̠)\Pi \left(\xi \right)d{\xi }^{\prime }},\end{array}$$

(19)

so

$$\begin{array}{c}\hfill \Pi (\xi \setminus x̠)=K{\nu }^{n+b_1-1}\frac{{(\delta -1)}^{b_2-1}}{{\delta }^n}{e}^{-\nu (a_1+{\sum }_{i=1}^n{x}_i)-a_2(\delta -1)}\prod _{i=1}^n(\delta -1+\nu x_i),\end{array}$$

(20)

where $a_1,a_2,b_1$, and $b_2$ are called hyper-parameters, while K is called the normalizing constant.

In the context of this study, an exploration of three diverse loss functions was carried out, where, among these, the SE loss function was widely utilized, which is given by

$$\begin{array}{c}\hfill {\mathbf{L}}_{SE}(t\left(\xi \right),\widehat{t}\left(\xi \right))={\left(t\left(\xi \right)-\widehat{t}\left(\xi \right)\right)}^2,\end{array}$$

(21)

where the $\widehat{t}\left(\xi \right)$ is an estimator of the $t\left(\xi \right)$. Moreover, employing the SE loss function within the Bayesian framework results in an equal penalty for both overestimation and underestimation. A solution for such challenges is to utilize the LINEX and GE loss functions.

The definition of the LINEX loss function is as follows:

$$\begin{array}{c}\hfill {\mathbf{L}}_{LINEX}(t\left(\xi \right),\widehat{t}\left(\xi \right))=e^{\upsilon \left(t\left(\xi \right)-\widehat{t}\left(\xi \right)\right)}-\upsilon \left(t\left(\xi \right)-\widehat{t}\left(\xi \right)\right)-1,\upsilon \ne 0.\end{array}$$

(22)

The GE loss function is defined as follows:

$$\begin{array}{c}\hfill {\mathbf{L}}_{GE}(t\left(\xi \right),\widehat{t}\left(\xi \right))={\left(\frac{\widehat{t}\left(\xi \right)}{t\left(\xi \right)}\right)}^{\rho }-\rho ln\left(\frac{\widehat{t}\left(\xi \right)}{t\left(\xi \right)}\right)-1,\rho \ne 0.\end{array}$$

(23)

Now, through using the SE loss function, the BEs of the $t\left(\xi \right)$ are given by

$$\begin{array}{c}\hfill {\widehat{t}}_{SEL}\left(\xi \right)=E\left[t\left(\xi \right)\setminus x̠\right]={\int }_{\xi }t\left(\xi \right)\Pi (\xi \setminus x̠)d\xi .\end{array}$$

(24)

In using the LINEX loss function, the BEs of the $t\left(\xi \right)$ are given by

$$\begin{array}{c}\hfill {\widehat{t}}_{LINEX}\left(\xi \right)=-\frac{1}{\upsilon }ln\left(E_t\left[e^{-\upsilon t\left(\xi \right)}\setminus x̠\right]\right),\end{array}$$

(25)

and the BEs of the $t\left(\xi \right)$, through using the GE loss function, are obtained by

$$\begin{array}{c}\hfill {\widehat{t}}_{GE}\left(\xi \right)={\left(E_t\left[t{\left(\xi \right)}^{-\rho }\setminus x̠\right]\right)}^{\frac{-1}{\rho }}.\end{array}$$

(26)

Since the above Equations (24)–(26) are hard to calculate analytically, we used the MCMC to estimate the unknown parameters using the R program. Next, we employed the MCMC method to produce posterior samples and to determine appropriate BEs. The MCMC technique serves as a useful simulation method for calculating quantities of interest in the posterior and sampling from posterior distributions. Utilizing the MCMC method with the aforementioned three functions, one can determine the Bayesian estimates for ${\xi }^{\left(i\right)}=\left({\nu }^{\left(i\right)},{\delta }^{\left(i\right)}\right)$ through the subsequent steps:

$$\begin{array}{c}\hfill {\widehat{\xi }}_{SEL}=\frac{1}{N-t_B}\sum _{i=t_B}^N{\xi }^{\left(i\right)},\end{array}$$

(27)

$$\begin{array}{c}\hfill {\widehat{\xi }}_{LINEX}=-\frac{1}{\upsilon }ln\left(\frac{1}{N-t_B}\sum _{i=t_B}^N{e}^{-\upsilon {\xi }^{\left(i\right)}}\right),\end{array}$$

(28)

and

$$\begin{array}{c}\hfill {\widehat{\xi }}_{GEL}={\left(\frac{1}{N-t_B}\sum _{i=t_B}^N{\left[{\xi }^{\left(i\right)}\right]}^{-\rho }\right)}^{-1/\rho },\end{array}$$

(29)

where $t_B$ represents the burn-in period of the MCMC. The construction of credible intervals (CI) for $\nu$ and $\delta$ can be achieved by following the algorithm detailed in [49]. Therefore, the $100(1-\Phi )\%$ credible interval for $\xi$ is $\left({\xi }^{(\Phi /2)},{\xi }^{(1-\Phi /2)}\right)$.

6. Simulation Study

In this section, we evaluate the performance of non-Bayesian and Bayesian estimators for the parameters of the PsL distribution. The Bayesian estimation was conducted using the SE, GE, and LINEX loss functions, as discussed earlier. The simulation considered various scenarios with different values for $(\nu ,\delta )=(0.50,2.00),(1.00,1.50),(1.25,1.50)$, and $(0.50,1.75)$. In the LINEX loss function, we examine two values of $\upsilon$, which were $-0.5$ and $0.5$. Similarly, under the GE loss function, we considered $\rho =-0.5$ and $0.5$. The random sample of sizes $n=25,50,75,100,$ and 200 were taken. The assessment of the estimator’s effectiveness was based on the mean squared error (MSE), average interval length (AIL), root mean squared error (RMSE), bias, confidence interval (CI), and coverage probability (CP). The results of the non-Bayes estimates are recorded in

Table 7. The MSE, RMSE, bias, CI, AIL, and CP for the PsL parameters when using non-Bayesian methods, with $\nu =0.50$ and $\delta =2.00$.

Methods	N	25		50		75		100		200
	Par.	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$
MLE	MSE	0.2773	1.9557	0.0924	1.0950	0.0642	0.9312	0.0550	0.9201	0.0489	0.9031
	RMSE	0.5266	1.3985	0.3039	1.0464	0.2534	0.9650	0.2346	0.9592	0.2212	0.9503
	RBias	0.3620	0.9479	0.2490	0.9210	0.2294	0.9432	0.2230	0.9461	0.2159	0.9438
	HPD_lower	0.4222	0.0000	0.5225	0.5892	0.5700	0.7130	0.5904	0.7853	0.6282	0.8763
	HPD_upper	1.7980	2.0206	0.9729	1.7155	0.8911	1.4890	0.8635	1.3768	0.8067	1.2788
	AIL	1.3758	2.0206	0.4504	1.1263	0.3211	0.7760	0.2731	0.5915	0.1785	0.4025
	CP	95.2	95.1	95.5	96.9	96.1	96.4	96.3	96.8	97	96.8
MPS	MSE	0.0306	2.4675	0.0329	0.9919	0.0349	0.8965	0.0360	0.8268	0.0405	0.8110
	RMSE	0.1749	1.5708	0.1815	0.8398	0.1869	0.8346	0.1898	0.8526	0.2012	0.8006
	RBias	0.1324	0.9061	0.1615	0.8221	0.1735	0.8118	0.1801	0.8115	0.1963	0.8050
	HPD_lower	0.4272	0.7758	0.5034	0.8477	0.5428	0.9154	0.5685	0.9319	0.6122	0.9523
	HPD_upper	0.8711	2.6667	0.8291	1.8280	0.8115	1.5727	0.7951	1.4786	0.7812	1.2987
	AIL	0.4439	1.8909	0.3257	0.9803	0.2687	0.6573	0.2266	0.5467	0.1690	0.3464
	CP	97	96	96.5	95.2	96.6	96.1	96.6	96	96.4	96
LS	MSE	0.0347	2.5789	0.0243	0.8747	0.0218	0.5384	0.0200	0.4789	0.0186	0.4755
	RMSE	0.1862	1.6059	0.1560	0.9352	0.1476	0.7338	0.1413	0.6920	0.1364	0.6918
	RBias	0.1090	0.8123	0.1145	0.7759	0.1193	0.6869	0.1212	0.6206	0.1266	0.6196
	HPD_lower	0.3329	0.6479	0.3958	0.8229	0.4689	0.8693	0.4757	0.9345	0.5319	1.0350
	HPD_upper	0.9070	3.4961	0.8204	2.7320	0.8047	2.1278	0.7559	1.9700	0.7309	1.7114
	AIL	0.5740	2.8482	0.4246	1.9091	0.3358	1.2585	0.2802	1.0354	0.1990	0.6764
	CP	96.2	95.2	97	95.3	97.3	95.5	96.4	95.9	97	96.2
WLS	MSE	0.0372	0.8507	0.0316	0.9651	0.0310	0.6409	0.0304	0.6552	0.0322	0.7107
	RMSE	0.1928	0.9224	0.1777	0.9824	0.1760	0.8005	0.1743	0.8094	0.1795	0.8430
	RBias	0.1416	0.5975	0.1550	0.6991	0.1611	0.7794	0.1641	0.7964	0.1749	0.8384
	HPD_lower	0.4070	0.7342	0.4937	0.8524	0.5428	0.9032	0.5626	0.9611	0.5952	1.0032
	HPD_upper	0.9041	2.3679	0.8272	1.7946	0.8117	1.5591	0.7876	1.4923	0.7525	1.3296
	AIL	0.4971	1.6337	0.3334	0.9422	0.2688	0.6559	0.2249	0.5312	0.1574	0.3264
	CP	96.1	95.4	96.3	95.3	96.6	95.8	97	96	96.2	96.4
CVM	MSE	0.0483	1.1657	0.0305	0.7473	0.0258	0.7183	0.0229	0.6392	0.0201	0.5117
	RMSE	0.2198	1.0797	0.1746	0.8645	0.1606	0.8509	0.1515	0.7995	0.1418	0.7153
	RBias	0.1578	0.6386	0.1388	0.6023	0.1350	0.6018	0.1328	0.6000	0.1324	0.5913
	HPD_lower	0.3981	0.6681	0.4505	0.7846	0.4850	0.8504	0.4986	0.9169	0.5297	1.0240
	HPD_upper	0.9786	2.5954	0.8678	2.3435	0.8215	1.9704	0.7810	1.8659	0.7282	1.6714
	AIL	0.5805	1.9273	0.4173	1.5589	0.3365	1.1200	0.2824	0.9490	0.1985	0.6474
	CP	96.9	95.6	98.2	95.2	97.1	95.5	97	95.9	96.3	96.2
AD	MSE	0.0405	1.3451	0.0318	0.6281	0.0289	0.6063	0.0271	0.5995	0.0257	0.6111
	RMSE	0.2012	1.1598	0.1783	0.7925	0.1700	0.7786	0.1647	0.7743	0.1602	0.7817
	RBias	0.1558	0.6186	0.1530	0.5977	0.1521	0.5398	0.1516	0.5473	0.1536	0.3703
	HPD_lower	0.4335	0.7195	0.4774	0.8781	0.5138	0.9094	0.5242	0.9562	0.5640	1.0226
	HPD_upper	0.9289	2.2452	0.8360	1.9540	0.8080	1.6947	0.7726	1.6179	0.7419	1.5079
	AIL	0.4954	1.5257	0.3586	1.0759	0.2942	0.7853	0.2485	0.6616	0.1778	0.4852
	CP	97.6	95.3	96.7	95.6	96.7	95.3	96.2	95.7	96.4	97.1
RTAD	MSE	0.0418	1.1089	0.0317	1.4120	0.0285	0.6393	0.0266	0.6071	0.0246	0.6017
	RMSE	0.2045	1.0530	0.1781	1.0031	0.1687	0.7996	0.1631	0.7792	0.1568	0.7757
	RBias	0.1609	0.6411	0.1542	0.6241	0.1518	0.6088	0.1509	0.5410	0.1506	0.3580
	HPD_lower	0.4388	0.5740	0.4841	0.7394	0.5206	0.7940	0.5338	0.9163	0.5621	0.9685
	HPD_upper	0.9189	2.6304	0.8276	2.0965	0.8026	1.8100	0.7709	1.7853	0.7354	1.5639
	AIL	0.4801	2.0564	0.3435	1.3572	0.2821	1.0160	0.2371	0.8691	0.1732	0.5954
	CP	97.2	95.3	97	95.2	96.9	95.6	96.7	97	96.8	96.7

,

Table 8. The MSE, RMSE, bias, CI, AIL, and CP for the PsL parameters when using non-Bayesian methods, with $\nu =1.00$ and $\delta =1.50$.

Methods	N	25		50		75		100		200
	Par.	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$
MLE	MSE	1.3449	0.8372	0.5413	0.5243	0.2846	0.4344	0.2147	0.4112	0.1613	0.3847
	RMSE	1.1597	0.9150	0.7357	0.7241	0.5334	0.6591	0.4634	0.6412	0.4016	0.6202
	RBias	0.8191	0.7855	0.5459	0.6727	0.4483	0.6398	0.4209	0.6304	0.3921	0.6168
	HPD_lower	0.8821	0.0000	1.0015	0.0000	1.1263	0.5740	1.1563	0.6755	1.2286	0.7735
	HPD_upper	3.6656	1.3576	2.7584	1.1805	1.8028	1.1266	1.7034	1.1048	1.5568	1.0247
	AIL	2.7835	1.3576	1.7569	1.1805	0.6765	0.5525	0.5471	0.4293	0.3282	0.2513
	CP	95.3	95.1	95.2	95.1	96.0	97.3	96.4	98.1	96.9	97.8
MPS	MSE	0.0801	0.5541	0.0842	0.5131	0.0906	0.4300	0.0947	0.3529	0.1047	0.2822
	RMSE	0.2831	0.7444	0.2902	0.6616	0.3011	0.5796	0.3077	0.5629	0.3236	0.5312
	RBias	0.1984	0.4592	0.2544	0.4323	0.2805	0.4194	0.2924	0.4078	0.3165	0.3296
	HPD_lower	0.7764	0.6786	1.0037	0.8192	1.0689	0.8658	1.1006	0.8928	1.1955	0.8945
	HPD_upper	1.5594	2.0718	1.5139	1.3717	1.4781	1.2368	1.4701	1.1594	1.4580	1.0528
	AIL	0.7829	1.3932	0.5102	0.5526	0.4092	0.3711	0.3695	0.2666	0.2624	0.1583
	CP	95.6	95.3	96.2	95.7	96.1	96.4	96.7	96.4	97.9	95.8
LS	MSE	0.0864	1.6706	0.0623	0.2955	0.0530	0.1586	0.0494	0.1595	0.0444	0.1534
	RMSE	0.2940	1.2925	0.2495	0.5436	0.2302	0.3983	0.2222	0.3994	0.2107	0.3917
	RBias	0.1436	0.4131	0.1773	0.3851	0.1868	0.3277	0.1903	0.3197	0.1939	0.3055
	HPD_lower	0.5960	0.5662	0.8676	0.7432	0.9593	0.8599	0.9781	0.8360	1.0375	0.9387
	HPD_upper	1.6262	2.3804	1.5246	1.7725	1.4827	1.6578	1.4221	1.4811	1.3637	1.3512
	AIL	1.0302	1.8142	0.6571	1.0294	0.5234	0.7979	0.4440	0.6451	0.3262	0.4126
	CP	96.5	95.1	96.6	95.3	97.7	96.4	97.9	95.4	97.1	96.5
WLS	MSE	0.0890	0.4259	0.0763	0.1949	0.0747	0.1993	0.0736	0.2143	0.0757	0.1252
	RMSE	0.2984	0.6526	0.2763	0.4415	0.2734	0.4404	0.2714	0.4329	0.2751	0.4346
	RBias	0.1997	0.5798	0.2348	0.4693	0.2496	0.4417	0.2546	0.4340	0.2672	0.4313
	HPD_lower	0.7658	0.7002	1.0055	0.8414	1.0473	0.8645	1.0758	0.8774	1.1454	0.9220
	HPD_upper	1.6220	1.9884	1.5433	1.4520	1.4633	1.2967	1.4315	1.2236	1.4000	1.1342
	AIL	0.8562	1.2883	0.5378	0.6106	0.4159	0.4321	0.3556	0.3462	0.2547	0.2122
	CP	96.2	95.6	96.6	96.9	96.1	96.4	96.7	96.2	97.1	96.2
CVM	MSE	0.1166	1.2194	0.0774	0.2308	0.0631	0.1771	0.0568	0.1774	0.0481	0.1633
	RMSE	0.3415	1.1043	0.2783	0.4804	0.2512	0.4208	0.2382	0.4112	0.2192	0.4041
	RBias	0.2208	0.4648	0.2152	0.4577	0.2117	0.4010	0.2086	0.3887	0.2029	0.3855
	HPD_lower	0.7380	0.5496	0.9015	0.7457	0.9881	0.8393	0.9664	0.8242	1.0486	0.9299
	HPD_upper	1.7769	2.0749	1.5679	1.6540	1.5137	1.5651	1.4141	1.4278	1.3765	1.3307
	AIL	1.0389	1.5252	0.6664	0.9083	0.5256	0.7259	0.4477	0.6036	0.3279	0.4008
	CP	97.5	95.2	96.2	95.8	97.8	96.3	96.1	95.6	97.3	96.5
AD	MSE	0.1004	1.7137	0.0778	0.2031	0.0703	0.1899	0.0663	0.1980	0.0613	0.1945
	RMSE	0.3168	1.3091	0.2790	0.4506	0.2652	0.4358	0.2575	0.4449	0.2475	0.4411
	RBias	0.2229	0.4743	0.2324	0.4209	0.2358	0.4106	0.2360	0.4091	0.2359	0.4037
	HPD_lower	0.7670	0.6541	0.9698	0.8128	1.0140	0.8796	1.0189	0.8924	1.0987	0.9273
	HPD_upper	1.6489	1.9951	1.5398	1.4871	1.4674	1.4053	1.4141	1.2919	1.3926	1.2258
	AIL	0.8818	1.3410	0.5700	0.6743	0.4533	0.5257	0.3952	0.3995	0.2938	0.2985
	CP	96.3	95.3	96.4	95.5	96.5	96.9	96.1	95.5	97.4	96.2
RTAD	MSE	0.1117	0.5875	0.0833	0.2569	0.0752	0.2202	0.0718	0.2220	0.0646	0.2099
	RMSE	0.3341	0.7665	0.2886	0.5068	0.2742	0.4693	0.2680	0.4712	0.2542	0.4582
	RBias	0.2456	0.4308	0.2451	0.4271	0.2454	0.4182	0.2469	0.4130	0.2431	0.4061
	HPD_lower	0.8439	0.5557	0.9625	0.6911	1.0282	0.7823	1.0558	0.7899	1.1015	0.8831
	HPD_upper	1.7666	2.1145	1.5331	1.5512	1.5084	1.4878	1.4501	1.3863	1.3967	1.2841
	AIL	0.9227	1.5588	0.5706	0.8600	0.4802	0.7055	0.3943	0.5964	0.2952	0.4010
	CP	97.6	95.6	96.3	95.4	98	96.7	97.5	96.3	97.8	97

,

Table 9. The MSE, RMSE, bias, CI, AIL, and CP for the PsL parameters when using non-Bayesian methods, with $\nu =1.25$ and $\delta =1.50$.

Methods	N	25		50		75		100		200
	Par.	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$
MLE	MSE	2.0955	0.8373	0.8585	0.5243	0.4440	0.4344	0.3371	0.4112	0.2520	0.3847
	RMSE	1.4476	0.9150	0.9265	0.7241	0.6664	0.6591	0.5806	0.6412	0.5020	0.6202
	RBias	1.0246	0.7855	0.6845	0.6727	0.5603	0.6398	0.5264	0.6304	0.4901	0.6168
	HPD_lower	1.0057	0.0000	1.2521	0.0000	1.4077	0.5741	1.4457	0.6757	1.5357	0.7735
	HPD_upper	4.4911	1.3574	3.5028	1.1805	2.2538	1.1267	2.1294	1.1047	1.9457	1.0247
	AIL	3.4854	1.3574	2.2508	1.1805	0.8460	0.5526	0.6837	0.4291	0.4100	0.2511
	CP	95.10	95.10	95.20	95.10	96.00	97.30	96.40	98.10	96.90	97.80
MPS	MSE	0.1237	0.4060	0.1249	0.2095	0.1403	0.2330	0.1538	0.2547	0.1632	0.2822
	RMSE	0.3517	0.6372	0.3534	0.4577	0.3746	0.4827	0.3922	0.5046	0.4040	0.5312
	RBias	0.2514	0.2797	0.3132	0.4331	0.3457	0.4695	0.3727	0.4994	0.3952	0.5295
	HPD_lower	1.0090	0.7591	1.2860	0.8505	1.3427	0.8691	1.4120	0.8841	1.4948	0.9017
	HPD_upper	1.9317	1.9745	1.9167	1.3710	1.8834	1.2628	1.8707	1.1481	1.8188	1.0608
	AIL	0.9227	1.2154	0.6307	0.5205	0.5407	0.3937	0.4587	0.2640	0.3240	0.1591
	CP	95.90	95.90	97.60	96.20	96.60	96.70	97.30	96.10	97.30	96.00
LS	MSE	0.1298	0.7751	0.0872	0.2013	0.0851	0.1714	0.0827	0.1591	0.0689	0.1541
	RMSE	0.3603	0.8804	0.2953	0.4487	0.2917	0.4140	0.2876	0.3989	0.2624	0.3926
	RBias	0.1857	0.1562	0.2128	0.2890	0.2304	0.3277	0.2447	0.3587	0.2422	0.3763
	HPD_lower	0.7692	0.5790	1.0822	0.7261	1.1533	0.8038	1.2225	0.8422	1.2940	0.9392
	HPD_upper	2.0109	2.2967	1.8826	1.7805	1.8300	1.6470	1.7906	1.4856	1.6947	1.3477
	AIL	1.2417	1.7177	0.8004	1.0543	0.6767	0.8432	0.5681	0.6435	0.4008	0.4085
	CP	96.60	95.40	96.90	95.30	96.30	95.50	96.70	96.00	96.80	97.00
WLS	MSE	0.1371	0.4170	0.1109	0.1934	0.1162	0.2027	0.1208	0.2144	0.1177	0.2254
	RMSE	0.3703	0.6457	0.3330	0.4397	0.3409	0.4502	0.3476	0.4630	0.3431	0.4747
	RBias	0.2536	0.2933	0.2864	0.4082	0.3078	0.4329	0.3251	0.4541	0.3336	0.4715
	HPD_lower	1.0222	0.7033	1.2478	0.8356	1.3040	0.8578	1.3416	0.8774	1.4368	0.9324
	HPD_upper	2.0273	1.8865	1.8947	1.4316	1.8580	1.3095	1.7943	1.2154	1.7488	1.1453
	AIL	1.0051	1.1832	0.6469	0.5960	0.5540	0.4516	0.4526	0.3380	0.3120	0.2129
	CP	96.60	95.70	97.20	96.80	96.40	96.40	95.50	96.20	96.80	97.50
CVM	MSE	0.1795	1.1080	0.1095	0.2035	0.1007	0.5292	0.0947	0.1769	0.0745	0.1640
	RMSE	0.4237	1.0526	0.3309	0.4511	0.3173	0.7274	0.3078	0.4206	0.2730	0.4050
	RBias	0.2815	0.2966	0.2590	0.3603	0.2615	0.3519	0.2676	0.3878	0.2536	0.3902
	HPD_lower	0.9424	0.5327	1.1264	0.7053	1.1908	0.8049	1.2441	0.8420	1.3044	0.9305
	HPD_upper	2.1753	1.8656	1.9299	1.6205	1.8677	1.5753	1.8202	1.4444	1.7073	1.3261
	AIL	1.2329	1.3329	0.8035	0.9152	0.6769	0.7704	0.5761	0.6024	0.4029	0.3957
	CP	97.50	95.30	96.80	95.30	96.40	95.80	96.70	96.30	96.80	97.00
AD	MSE	0.1563	0.3737	0.1119	0.1959	0.1099	0.1978	0.1094	0.1982	0.0952	0.1949
	RMSE	0.3954	0.6113	0.3345	0.4426	0.3316	0.4447	0.3307	0.4452	0.3085	0.4415
	RBias	0.2829	0.3356	0.2822	0.4006	0.2911	0.4108	0.3020	0.4292	0.2947	0.4341
	HPD_lower	1.0015	0.7331	1.2176	0.8491	1.2577	0.8636	1.2968	0.8836	1.3497	0.9303
	HPD_upper	2.0843	1.9260	1.9054	1.4859	1.8510	1.4052	1.8061	1.2965	1.7114	1.2268
	AIL	1.0829	1.1929	0.6878	0.6368	0.5933	0.5416	0.5092	0.4130	0.3617	0.2966
	CP	97.10	96.10	97.40	96.10	96.30	96.00	96.20	95.70	96.00	96.40
RTAD	MSE	0.1705	0.4578	0.1248	0.2392	0.1174	0.2309	0.1158	0.2185	0.1008	0.2111
	RMSE	0.4129	0.6766	0.3533	0.4891	0.3427	0.4805	0.3402	0.4675	0.3175	0.4594
	RBias	0.3118	0.3599	0.3035	0.4179	0.3029	0.4168	0.3126	0.4399	0.3040	0.4467
	HPD_lower	1.0717	0.5875	1.2110	0.6719	1.2614	0.7483	1.3260	0.7780	1.3868	0.8589
	HPD_upper	2.1780	1.9837	1.9181	1.5299	1.8727	1.5187	1.8365	1.3642	1.7488	1.2553
	AIL	1.1064	1.3962	0.7071	0.8581	0.6114	0.7705	0.5105	0.5862	0.3619	0.3965
	CP	97.60	95.90	96.90	95.40	96.90	95.80	96.90	95.40	97.70	95.90

,

Table 10. The MSE, RMSE, bias, CI, AIL, and CP for the PsL parameters when using non-Bayesian methods, with $\nu =0.50$ and $\delta =1.75$.

Methods	N	25		50		75		100		200
	Par.	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$
MLE	MSE	0.2960	1.0877	0.1039	0.7006	0.0610	0.6313	0.0520	0.6174	0.0438	0.5980
	RMSE	0.5440	1.0429	0.3224	0.8370	0.2469	0.7946	0.2281	0.7857	0.2092	0.7733
	RBias	0.3760	0.8569	0.2507	0.7821	0.2205	0.7758	0.2131	0.7743	0.2042	0.7684
	HPD_lower	0.4315	0.0000	0.5192	0.5050	0.5673	0.7071	0.5801	0.7338	0.6222	0.8261
	HPD_upper	1.8330	1.6747	0.9880	1.5861	0.8830	1.3625	0.8485	1.2474	0.7912	1.1543
	AIL	1.4015	1.6747	0.4688	1.0811	0.3157	0.6554	0.2683	0.5136	0.1690	0.3281
	CP	95.2	95.1	95.4	97.7	96.2	97.6	96.2	96.8	97.1	96.3
MPS	MSE	0.0230	0.9024	0.0280	0.3958	0.0288	0.4310	0.0293	0.4532	0.0324	0.5044
	RMSE	0.1517	0.9500	0.1674	0.6292	0.1697	0.6565	0.1712	0.6732	0.1800	0.7102
	RBias	0.1108	0.3604	0.1494	0.5859	0.1571	0.6390	0.1629	0.6636	0.1759	0.7062
	HPD_lower	0.4320	0.7078	0.5176	0.8453	0.5365	0.8768	0.5655	0.9321	0.6002	0.9245
	HPD_upper	0.8312	2.4085	0.7975	1.5871	0.7753	1.3925	0.7775	1.3361	0.7459	1.1900
	AIL	0.3991	1.7007	0.2799	0.7418	0.2388	0.5158	0.2120	0.4039	0.1457	0.2655
	CP	97	95.4	96.7	95.3	96.7	95.2	97.2	96.9	96.3	95.6
LS	MSE	0.0252	1.6143	0.0197	0.4510	0.0179	0.3274	0.0155	0.2900	0.0138	0.2839
	RMSE	0.1587	1.2706	0.1403	0.6716	0.1337	0.5722	0.1243	0.5385	0.1174	0.5328
	RBias	0.0840	0.1773	0.1048	0.3861	0.1073	0.4594	0.1065	0.4790	0.1083	0.5079
	HPD_lower	0.3153	0.7016	0.4395	0.8248	0.4675	0.8251	0.4852	0.8982	0.5197	0.9666
	HPD_upper	0.8435	3.1486	0.7990	2.2291	0.7663	1.8067	0.7359	1.7632	0.6955	1.5401
	AIL	0.5282	2.4471	0.3595	1.4044	0.2988	0.9816	0.2507	0.8650	0.1758	0.5735
	CP	95.8	95.2	97.3	95.9	96.9	95.4	96.7	96.1	96.4	95.9
WLS	MSE	0.0270	0.7005	0.0258	0.3734	0.0248	0.3883	0.0237	0.3948	0.0244	0.4231
	RMSE	0.1643	0.8369	0.1607	0.6111	0.1574	0.6231	0.1540	0.6283	0.1563	0.6504
	RBias	0.1153	0.3968	0.1402	0.5627	0.1431	0.6047	0.1449	0.6175	0.1523	0.6461
	HPD_lower	0.3963	0.7384	0.5086	0.8558	0.5299	0.8917	0.5444	0.9408	0.5877	0.9624
	HPD_upper	0.8476	2.2897	0.8015	1.6037	0.7740	1.4320	0.7447	1.3909	0.7219	1.2482
	AIL	0.4513	1.5513	0.2929	0.7479	0.2441	0.5403	0.2003	0.4501	0.1341	0.2858
	CP	96	95.5	96.8	96.2	96.6	96.2	95.9	97.3	96.7	96.4
CVM	MSE	0.0352	1.6502	0.0248	0.3702	0.0211	0.3464	0.0178	0.3182	0.0149	0.3005
	RMSE	0.1877	1.2846	0.1575	0.6084	0.1454	0.5885	0.1335	0.5641	0.1222	0.5482
	RBias	0.1278	0.3932	0.1263	0.4916	0.1213	0.5159	0.1169	0.5181	0.1135	0.5260
	HPD_lower	0.3501	0.6633	0.4530	0.7963	0.4761	0.8134	0.5096	0.8868	0.5240	0.9569
	HPD_upper	0.8963	2.3777	0.8199	1.9633	0.7752	1.7035	0.7611	1.6869	0.7005	1.5094
	AIL	0.5462	1.7144	0.3669	1.1670	0.2991	0.8901	0.2514	0.8001	0.1765	0.5525
	CP	95.7	95.2	96.8	95.9	96.4	95.6	97.8	96.3	96.3	95.9
AD	MSE	0.0302	0.7572	0.0258	0.4068	0.0234	0.3699	0.0210	0.3605	0.0193	0.3611
	RMSE	0.1739	0.8702	0.1608	0.6378	0.1528	0.6082	0.1449	0.6005	0.1390	0.6010
	RBias	0.1291	0.4490	0.1381	0.5449	0.1356	0.5761	0.1333	0.5796	0.1330	0.5904
	HPD_lower	0.4126	0.7090	0.4839	0.8626	0.5101	0.8886	0.5200	0.9101	0.5550	0.9585
	HPD_upper	0.8537	2.1380	0.7985	1.6942	0.7782	1.5276	0.7441	1.4645	0.7117	1.3574
	AIL	0.4410	1.4290	0.3147	0.8317	0.2682	0.6390	0.2241	0.5544	0.1567	0.3989
	CP	96.3	95.2	96.3	95.7	97.2	95.8	96.3	95.6	96.8	95.4
RTAD	MSE	0.0315	2.2088	0.0270	0.4225	0.0239	0.3988	0.0212	0.3777	0.0194	0.3704
	RMSE	0.1774	1.4862	0.1644	0.6500	0.1545	0.6315	0.1455	0.6146	0.1393	0.6086
	RBias	0.1350	0.6044	0.1427	0.5482	0.1389	0.4825	0.1346	0.4798	0.1334	0.3915
	HPD_lower	0.4258	0.5801	0.4887	0.6729	0.5238	0.7998	0.5339	0.8423	0.5535	0.9152
	HPD_upper	0.8665	2.3710	0.7992	1.8006	0.7770	1.6460	0.7478	1.6022	0.7079	1.4498
	AIL	0.4407	1.7909	0.3105	1.1277	0.2533	0.8463	0.2138	0.7599	0.1545	0.5347
	CP	96.6	95.1	96	95.1	97.1	95.9	97.1	96.2	96.2	96.6

, while the Bayes results are shown in

Table 11. The MSE, RMSE, bias, CI, AIL, and CP for the PsL parameters when using Bayesian methods, with $\nu =0.50$ and $\delta =1.75$.

Methods	N	25		50		75		100		200
	Par.	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$
BE_SE	MSE	0.5975	0.9178	0.2851	0.6202	0.0975	0.6088	0.0812	0.6486	0.0823	0.7546
	RMSE	0.7730	0.9580	0.5339	0.7875	0.3122	0.7803	0.2850	0.8054	0.2869	0.8687
	RBias	0.3851	0.6835	0.2476	0.6401	0.2032	0.6966	0.2017	0.7476	0.2126	0.8379
	HPD_lower	0.3859	0.0000	0.3272	0.3351	0.4192	0.3572	0.4053	0.4057	0.4042	0.4388
	HPD_upper	2.3193	2.0798	1.4382	2.1155	1.1804	1.6618	1.1545	1.5300	1.0946	1.2896
	AIL	1.9334	2.0798	1.1110	1.7804	0.7612	1.3045	0.7492	1.1244	0.6905	0.8507
	CP	95.8	95.1	95.4	98.2	96.1	96.4	96.3	96.6	95.9	97.2
BE_LN1	MSE	0.6537	0.9239	0.2996	0.6128	0.1080	0.5965	0.0887	0.6356	0.0918	0.7430
	RMSE	0.8085	0.9612	0.5473	0.7828	0.3286	0.7724	0.2979	0.7972	0.3030	0.8620
	RBias	0.3991	0.6565	0.2524	0.6194	0.2097	0.6815	0.2079	0.7363	0.2190	0.8310
	HPD_lower	0.3483	0.0000	0.2866	0.3373	0.4382	0.3536	0.4093	0.4085	0.4441	0.4445
	HPD_upper	2.3145	2.1848	1.4303	2.2057	1.2135	1.7080	1.1665	1.5627	1.1563	1.2967
	AIL	1.9662	2.1848	1.1436	1.8684	0.7753	1.3544	0.7573	1.1542	0.7122	0.8522
	CP	95.5	95.1	95.3	98.2	96.3	96.3	96.3	96.6	96.5	97.1
BE_LN2	MSE	0.5041	0.9175	0.2144	0.6297	0.0891	0.6218	0.0749	0.6617	0.0755	0.7660
	RMSE	0.7100	0.9579	0.4630	0.7935	0.2985	0.7885	0.2738	0.8135	0.2748	0.8752
	RBias	0.3655	0.7078	0.2349	0.6591	0.1971	0.7107	0.1960	0.7583	0.2067	0.8446
	HPD_lower	0.3729	0.0000	0.3504	0.3329	0.4152	0.3572	0.4014	0.4018	0.4360	0.4604
	HPD_upper	2.2433	1.9866	1.3681	2.0523	1.1577	1.6177	1.1309	1.5009	1.1131	1.3004
	AIL	1.8704	1.9866	1.0177	1.7194	0.7425	1.2605	0.7295	1.0990	0.6771	0.8400
	CP	95.7	95.1	95.7	98.2	96.1	96.5	96.3	96.6	96.4	98
BE_GE1	MSE	0.5655	0.9242	0.2634	0.6327	0.0918	0.6237	0.0761	0.6638	0.0770	0.7693
	RMSE	0.7520	0.9613	0.5132	0.7954	0.3029	0.7897	0.2759	0.8147	0.2775	0.8771
	RBias	0.3734	0.6994	0.2394	0.6546	0.1968	0.7089	0.1954	0.7580	0.2061	0.8460
	HPD_lower	0.3836	0.0000	0.3259	0.3287	0.3943	0.3497	0.3955	0.3964	0.4314	0.4492
	HPD_upper	2.2883	2.0346	1.3701	2.0858	1.1424	1.6366	1.1317	1.5096	1.1152	1.3018
	AIL	1.9048	2.0346	1.0442	1.7571	0.7481	1.2870	0.7363	1.1132	0.6838	0.8526
	CP	95.8	95.1	95.4	98.2	95.9	96.4	96.3	96.6	96.4	98
BE_GE2	MSE	0.5076	0.9396	0.2248	0.6592	0.0817	0.6544	0.0671	0.6946	0.0677	0.7992
	RMSE	0.7125	0.9693	0.4742	0.8119	0.2859	0.8090	0.2590	0.8334	0.2602	0.8940
	RBias	0.3505	0.7300	0.2234	0.6826	0.1844	0.7329	0.1832	0.7784	0.1935	0.8621
	HPD_lower	0.3403	0.0000	0.3403	0.2236	0.4275	0.3265	0.4006	0.3632	0.4121	0.4503
	HPD_upper	2.2141	1.9458	1.3409	1.9139	1.1515	1.5771	1.1098	1.4653	1.0716	1.3175
	AIL	1.8738	1.9458	1.0006	1.6904	0.7240	1.2505	0.7093	1.1022	0.6595	0.8672
	CP	95.6	95.1	95.8	97.7	96.5	96.3	96.6	96.4	96.4	98.7

,

Table 12. The MSE, RMSE, bias, CI, AIL, and CP for the PsL parameters when using Bayesian methods, with $\nu =0.50$ and $\delta =2.00$.

Methods	N	25		50		75		100		200
	Par.	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$
BE_SE	MSE	0.6315	1.1058	0.1985	0.8167	0.0837	0.8405	0.0711	0.8784	0.0741	1.0151
	RMSE	0.7947	1.0516	0.4456	0.9037	0.2892	0.9168	0.2666	0.9372	0.2721	1.0075
	RBias	0.3754	0.8080	0.2338	0.7727	0.2056	0.8364	0.2063	0.8825	0.2195	0.9753
	HPD_lower	0.3741	0.0000	0.4546	0.3523	0.4629	0.3759	0.4898	0.4369	0.4393	0.5280
	HPD_upper	2.3217	2.2244	1.2493	2.1597	1.0934	1.8272	1.0675	1.6968	1.0159	1.4878
	AIL	1.9476	2.2244	0.7947	1.8074	0.6304	1.4514	0.5777	1.2600	0.5765	0.9598
	CP	95.6	95.1	95.9	97.1	96.3	96.1	96.4	96.4	96	98.2
BE_LN1	MSE	0.5911	1.1031	0.1533	0.8019	0.0901	0.8217	0.0770	0.8592	0.0791	1.0002
	RMSE	0.7688	1.0503	0.3916	0.8955	0.3002	0.9065	0.2775	0.9269	0.2812	1.0001
	RBias	0.3779	0.7753	0.2334	0.7473	0.2107	0.8176	0.2113	0.8681	0.2240	0.9674
	HPD_lower	0.2894	0.0000	0.4456	0.3623	0.4649	0.3787	0.4991	0.4406	0.4343	0.5375
	HPD_upper	2.2390	2.3647	1.2595	2.2772	1.1114	1.8862	1.1007	1.7382	1.0196	1.5087
	AIL	1.9496	2.3647	0.8139	1.9148	0.6465	1.5075	0.6016	1.2976	0.5853	0.9711
	CP	95.2	95.1	95.7	97.2	96.3	96.1	96.5	96.4	95.7	98.4
BE_LN2	MSE	0.5193	1.1149	0.1540	0.8340	0.0781	0.8600	0.0662	0.8977	0.0697	1.0299
	RMSE	0.7206	1.0559	0.3925	0.9132	0.2796	0.9274	0.2573	0.9474	0.2640	1.0148
	RBias	0.3561	0.8371	0.2247	0.7958	0.2009	0.8538	0.2017	0.8960	0.2152	0.9830
	HPD_lower	0.3736	0.0000	0.4498	0.3266	0.4130	0.3715	0.4991	0.4332	0.4318	0.5200
	HPD_upper	2.2783	2.1236	1.2216	2.0397	1.0243	1.7748	1.0630	1.6493	0.9990	1.4679
	AIL	1.9047	2.1236	0.7718	1.7131	0.6113	1.4032	0.5640	1.2162	0.5672	0.9479
	CP	95.6	95.1	95.8	97	95.8	96.1	96.9	96.4	95.9	98.1
BE_GE1	MSE	0.5977	1.1190	0.1847	0.8349	0.0794	0.8599	0.0670	0.8978	0.0703	1.0320
	RMSE	0.7731	1.0578	0.4298	0.9137	0.2818	0.9273	0.2588	0.9475	0.2651	1.0159
	RBias	0.3646	0.8261	0.2270	0.7888	0.2004	0.8499	0.2012	0.8941	0.2148	0.9834
	HPD_lower	0.3729	0.0000	0.4470	0.3196	0.4106	0.3642	0.4923	0.4465	0.4291	0.5119
	HPD_upper	2.3027	2.1798	1.2259	2.0863	1.0251	1.8001	1.0622	1.6897	0.9990	1.4745
	AIL	1.9299	2.1798	0.7789	1.7668	0.6145	1.4359	0.5699	1.2432	0.5699	0.9626
	CP	95.6	95.1	95.8	96.9	95.8	96.1	96.8	96.7	95.9	98.1
BE_GE2	MSE	0.5360	1.1480	0.1589	0.8726	0.0718	0.8994	0.0599	0.9372	0.0635	1.0663
	RMSE	0.7321	1.0715	0.3987	0.9341	0.2679	0.9484	0.2446	0.9681	0.2520	1.0326
	RBias	0.3435	0.8608	0.2136	0.8200	0.1903	0.8761	0.1913	0.9166	0.2055	0.9994
	HPD_lower	0.3300	0.0000	0.4323	0.3028	0.3966	0.3411	0.4602	0.4280	0.4180	0.4511
	HPD_upper	2.2246	2.0765	1.1863	1.9884	0.9948	1.7253	1.0220	1.6538	0.9646	1.4210
	AIL	1.8946	2.0765	0.7540	1.6855	0.5982	1.3842	0.5618	1.2258	0.5466	0.9699
	CP	95.4	95.1	95.9	96.9	95.7	96	96.5	96.7	95.8	97.3

,

Table 13. The MSE, RMSE, bias, CI, AIL, and CP for the PsL parameters when using Bayesian methods, with $\nu =1.00$ and $\delta =1.50$.

Methods	N	25		50		75		100		200
	Par.	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$
BE_SE	MSE	2.8088	0.8112	1.4503	0.5118	0.5753	0.4525	0.4295	0.4708	0.4017	0.5431
	RMSE	1.6759	0.9007	1.2043	0.7154	0.7585	0.6727	0.6554	0.6862	0.6338	0.7369
	RBias	0.8666	0.6080	0.5496	0.5536	0.4255	0.5868	0.4142	0.6310	0.4249	0.7109
	HPD_lower	0.5389	0.0000	0.5770	0.0000	0.5740	0.3164	0.5919	0.3452	0.5589	0.4141
	HPD_upper	4.7148	1.9261	3.1722	1.6157	2.5987	1.5212	2.4804	1.3230	2.3959	1.1169
	AIL	4.1758	1.9261	2.5952	1.6157	2.0247	1.2048	1.8885	0.9779	1.8370	0.7028
	CP	95.3	95.1	95.4	95.1	95.4	97.5	95.5	96.8	95.4	98.3
BE_LN1	MSE	3.5284	0.8218	1.6875	0.5088	0.7157	0.4447	0.5454	0.4620	0.5170	0.5345
	RMSE	1.8784	0.9066	1.2990	0.7133	0.8460	0.6669	0.7385	0.6797	0.7190	0.7311
	RBias	0.9492	0.5869	0.5879	0.5382	0.4618	0.5755	0.4499	0.6225	0.4619	0.7049
	HPD_lower	0.5585	0.0000	0.5824	0.0000	0.5642	0.3011	0.6563	0.3458	0.5796	0.4140
	HPD_upper	4.9001	2.0083	3.3237	1.6705	2.7877	1.5366	2.6509	1.3347	2.5261	1.1209
	AIL	4.3416	2.0083	2.7413	1.6705	2.2235	1.2354	1.9946	0.9890	1.9465	0.7069
	CP	95.4	95.1	95.4	95.1	95.3	97.2	95.9	96.8	95.4	98.2
BE_LN2	MSE	2.1768	0.8054	1.0591	0.5163	0.4807	0.4608	0.3563	0.4797	0.3349	0.5516
	RMSE	1.4754	0.8974	1.0291	0.7185	0.6933	0.6788	0.5969	0.6926	0.5787	0.7427
	RBias	0.7850	0.6270	0.5003	0.5678	0.3947	0.5975	0.3839	0.6392	0.3937	0.7168
	HPD_lower	0.5360	0.0000	0.5490	0.0000	0.5710	0.3190	0.5887	0.3779	0.6635	0.4112
	HPD_upper	4.4385	1.8530	3.0274	1.5727	2.5010	1.4859	2.3405	1.3340	2.3564	1.1143
	AIL	3.9025	1.8530	2.4783	1.5727	1.9301	1.1669	1.7518	0.9561	1.6929	0.7030
	CP	95.3	95.1	95.3	95.1	95.4	97.6	95.5	97.7	96.6	98.3
BE_GE1	MSE	2.6681	0.8130	1.3632	0.5202	0.5427	0.4637	0.3992	0.4826	0.3727	0.5554
	RMSE	1.6334	0.9017	1.1675	0.7212	0.7367	0.6809	0.6318	0.6947	0.6105	0.7452
	RBias	0.8396	0.6214	0.5307	0.5658	0.4093	0.5976	0.3975	0.6404	0.4069	0.7190
	HPD_lower	0.4546	0.0000	0.5425	0.0000	0.5558	0.3162	0.5791	0.3650	0.6592	0.4034
	HPD_upper	4.6040	1.8886	3.1324	1.5862	2.5578	1.5028	2.4140	1.3387	2.4523	1.1145
	AIL	4.1495	1.8886	2.5900	1.5862	2.0020	1.1865	1.8350	0.9738	1.7931	0.7111
	CP	95.2	95.1	95.3	95.1	95.4	97.6	95.5	97.7	96.6	98.3
BE_GE2	MSE	2.4105	0.8190	1.2069	0.5382	0.4850	0.4868	0.3461	0.5068	0.3219	0.5804
	RMSE	1.5526	0.9050	1.0986	0.7336	0.6964	0.6977	0.5883	0.7119	0.5674	0.7619
	RBias	0.7873	0.6472	0.4940	0.5896	0.3780	0.6189	0.3653	0.6589	0.3720	0.7351
	HPD_lower	0.5226	0.0000	0.5410	0.0000	0.5753	0.2976	0.5749	0.3488	0.6118	0.3784
	HPD_upper	4.5257	1.8069	3.0946	1.5442	2.5090	1.4620	2.3240	1.3139	2.3103	1.1097
	AIL	4.0031	1.8069	2.5537	1.5442	1.9336	1.1644	1.7491	0.9651	1.6985	0.7313
	CP	95.3	95.1	95.5	95.1	95.7	97.8	95.6	97.7	96.5	98.3

,

Table 14. The MSE, RMSE, bias, CI, AIL, and CP for the PsL parameters when using Bayesian methods, with $\nu =1.25$ and $\delta =1.50$.

Methods	N	25		50		75		100		200
	Par.	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$	$\mathit{\nu }$	$\mathit{\delta }$
BE_SE	MSE	3.9490	0.7251	1.8531	0.4340	0.4964	0.3589	0.3071	0.3585	0.2641	0.3550
	RMSE	1.9872	0.8516	1.3613	0.6588	0.7046	0.5991	0.5541	0.5987	0.5139	0.5042
	RBias	1.0321	0.6345	0.6644	0.5575	0.5001	0.5587	0.4828	0.5748	0.4791	0.5549
	HPD_lower	0.9006	0.0000	1.1361	0.0000	1.3090	0.5800	1.3721	0.6618	1.4875	0.7371
	HPD_upper	5.7101	1.6650	2.9490	1.4263	2.1847	1.3860	2.0927	1.2905	1.9559	1.0950
	AIL	4.8094	1.6650	1.8129	1.4263	0.8756	0.8061	0.7206	0.6287	0.4684	0.3579
	CP	95.10	95.10	95.10	95.10	95.60	97.80	96.10	98.60	96.00	98.30
BE_LN1	MSE	5.0219	0.7292	2.2342	0.4311	0.5781	0.3549	0.3186	0.3551	0.2708	0.3633
	RMSE	2.2410	0.8539	1.4947	0.6566	0.7603	0.5957	0.5645	0.5959	0.5204	0.6028
	RBias	1.1237	0.6176	0.6933	0.5473	0.5139	0.5526	0.4900	0.5710	0.4830	0.5935
	HPD_lower	0.9574	0.0000	1.1418	0.0000	1.3132	0.5926	1.3621	0.6691	1.4902	0.7374
	HPD_upper	6.0797	1.7027	3.0416	1.4770	2.2047	1.4088	2.0940	1.3059	1.9598	1.1030
	AIL	5.1223	1.7027	1.8998	1.4770	0.8915	0.8163	0.7319	0.6369	0.4695	0.3656
	CP	95.30	95.10	95.10	95.10	95.60	97.90	95.60	98.60	96.10	98.30
BE_LN2	MSE	2.9902	0.7241	1.2825	0.4375	0.4386	0.3630	0.2960	0.3618	0.2574	0.3667
	RMSE	1.7292	0.8509	1.1325	0.6614	0.6623	0.6025	0.5441	0.6015	0.5073	0.6055
	RBias	0.9384	0.6498	0.6193	0.5671	0.4877	0.5644	0.4756	0.5785	0.4752	0.5963
	HPD_lower	0.8914	0.0000	1.1304	0.0000	1.3048	0.5697	1.3708	0.6664	1.4847	0.7368
	HPD_upper	5.3206	1.6087	2.7936	1.3882	2.1712	1.3507	2.0870	1.2789	1.9526	1.0916
	AIL	4.4292	1.6087	1.6633	1.3882	0.8664	0.7811	0.7162	0.6125	0.4679	0.3548
	CP	95.10	95.10	95.10	95.10	95.60	97.70	96.20	98.70	96.00	98.30
BE_GE1	MSE	3.7744	0.7278	1.7510	0.4390	0.4838	0.3640	0.3022	0.3625	0.2612	0.3676
	RMSE	1.9428	0.8531	1.3233	0.6625	0.6955	0.6033	0.5497	0.6021	0.5111	0.6063
	RBias	1.0079	0.6456	0.6525	0.5655	0.4946	0.5642	0.4790	0.5786	0.4771	0.5967
	HPD_lower	0.9485	0.0000	1.1310	0.0000	1.3058	0.5549	1.3685	0.6658	1.4856	0.7367
	HPD_upper	5.6979	1.6393	2.8584	1.3994	2.1780	1.3575	2.0892	1.2817	1.9542	1.0919
	AIL	4.7494	1.6393	1.7274	1.3994	0.8723	0.8026	0.7207	0.6159	0.4686	0.3551
	CP	95.30	95.10	95.10	95.10	95.60	97.70	96.10	98.70	96.00	98.30
BE_GE2	MSE	3.4497	0.7347	1.5657	0.4495	0.4598	0.3748	0.2926	0.3704	0.2554	0.3722
	RMSE	1.8573	0.8572	1.2513	0.6704	0.6781	0.6122	0.5409	0.6086	0.5054	0.6101
	RBias	0.9602	0.6669	0.6289	0.5807	0.4837	0.5749	0.4713	0.5857	0.4731	0.6000
	HPD_lower	0.8848	0.0000	1.1181	0.0000	1.2979	0.5963	1.3612	0.6770	1.4820	0.7348
	HPD_upper	5.5138	1.5641	2.8130	1.3557	2.1681	1.3874	2.0804	1.2722	1.9508	1.0823
	AIL	4.6290	1.5641	1.6948	1.3557	0.8702	0.7912	0.7193	0.5952	0.4689	0.3475
	CP	95.30	95.10	95.10	95.10	95.60	98.30	96.10	99.00	96.00	98.30

.

The tabulated values revealed the below observations.

Each of the estimators demonstrated consistent behavior, where the MSE, RMSE, bias, and AIL decreased with an increase in the sample size n, while the CP increased as the sample size n increased.

In all examined scenarios, both classical and Bayesian, as well as the MSE, RMSE, bias, and AIL of the estimator(s) for $\nu$ and $\delta$, the metrics rose with higher values of the $\nu$ and $\delta$ parameters, while keeping n fixed. However, when n is constant, no consistent pattern was evident in the CP.

In classical estimation, ADE demonstrates superior efficiency compared to other estimators, followed by CVME and LSE.

For Bayes estimates, selecting $\upsilon =\rho =0.5$ is a preferable value for determining the BEs for both the GE and LINEX loss functions. The BEs using the LINEX loss function demonstrated greater efficiency compared to those using the SE and GE loss functions. Generally, the MSE follows the order: MSE (LINEX) ≤ MSE (GE) ≤ MSE (SE).

7. Real Data

As shown in this section, eight methods were employed to estimate the PsL parameters. One method utilizes Bayesian estimation (BE) under the square error loss function, whereas the remaining methods are non-Bayesian. Goodness-of-fit statistics, such as the Anderson–Darling (A*), Cramer–Von Mises (W*), and Kolmogorov–Smirnov (K-S) tests, along with the p-value related to the Kolmogorov–Smirnov (K-S) test, were used to compare the performance of the estimation methods.

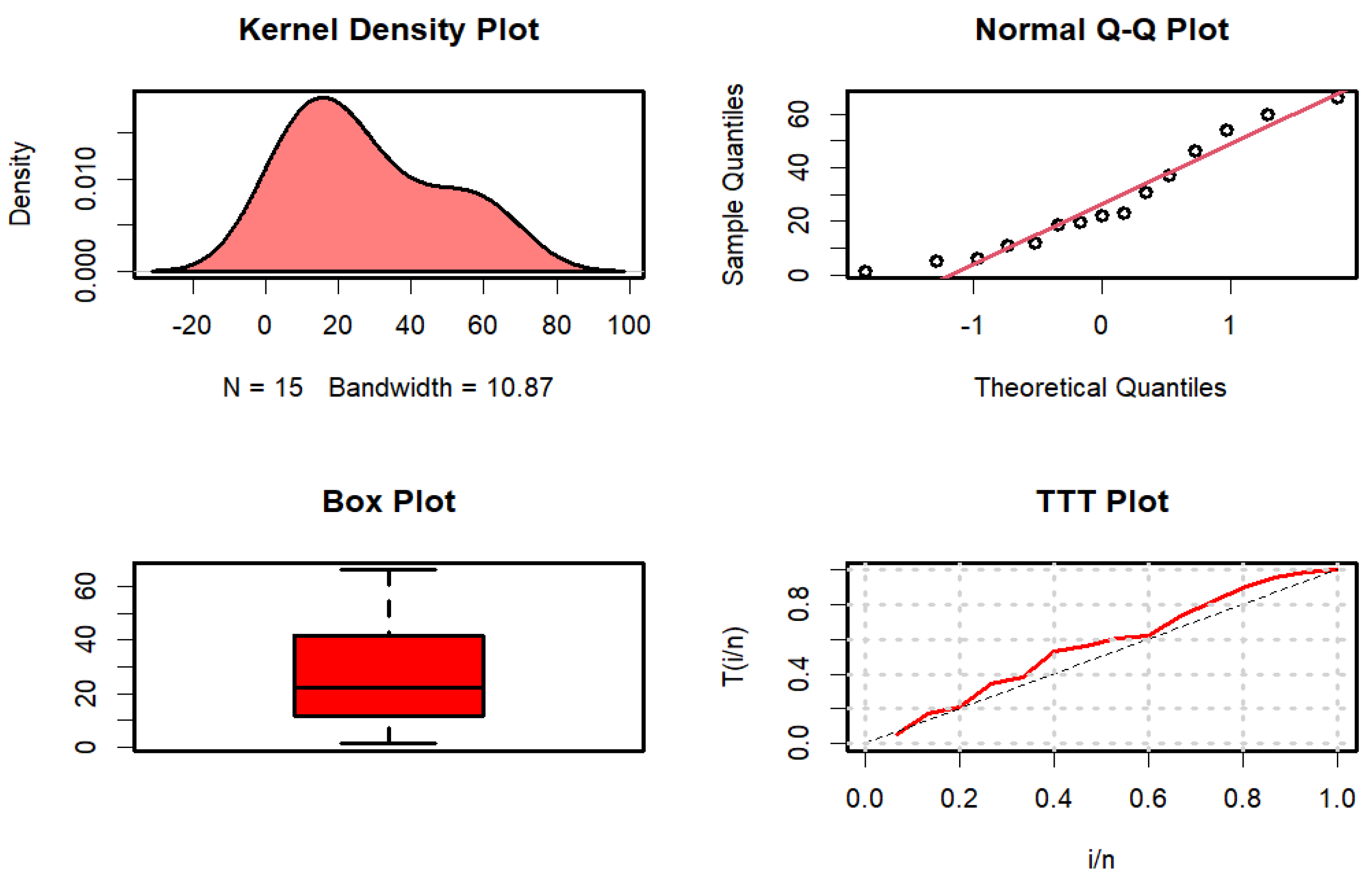
The dataset below presents the failure times (in minutes) for a sample of 15 electronic components subjected to an accelerated life test, as documented in Lawless (2003, p. 204) [50]: (1.4, 5.1, 6.3, 10.8, 12.1, 18.5, 19.7, 22.2, 23.0, 30.6, 37.3, 46.3, 53.9, 59.8, 66.2).

Figure 3 displays the kernel density, quantile-quantile (Q-Q), box, and time-to-target (TTT) plots.

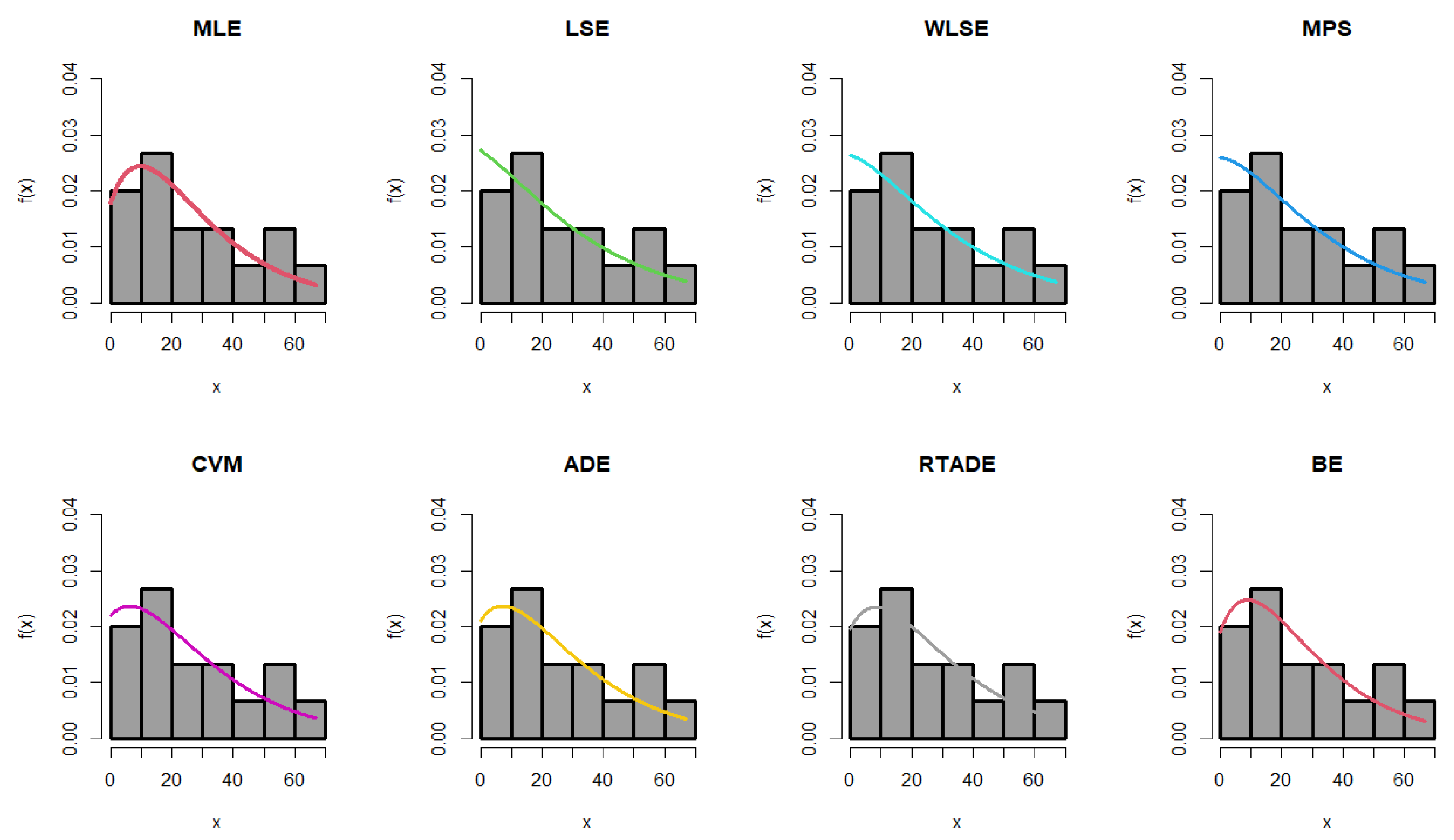
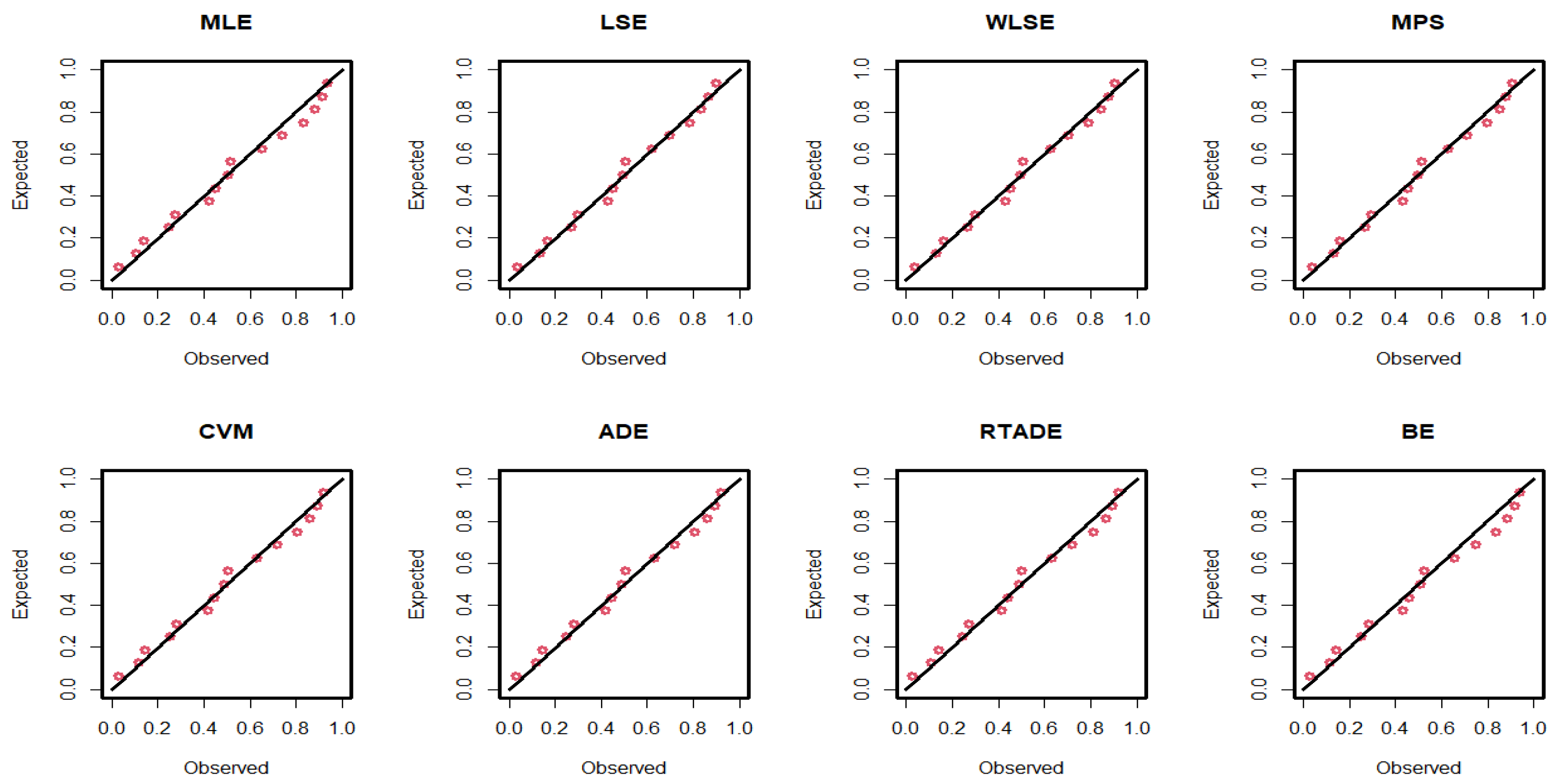
The estimated parameter values, along with the standard errors (SEs) for the MLEs, MPS, LSEs, WLSEs, CVMEs, ADEs, RTADEs, and BEs for the PsL distribution, are presented in

Table 15. Estimated values with corresponding SEs (in brackets) for various estimator methods.

Measures	$\mathit{\nu }$	$\mathit{\delta }$	A*	W*	K-S	p-Value
MLE	0.06223	1.40021	0.1679	0.0223	0.0952	0.9971
	(0.01723)	(0.69229)
MPS	0.050821	2.04649	0.0967	0.0231	0.0967	0.9964
	(0.01915)	(1.93109)
LSE	0.046513	2.41978	0.1892	0.0223	0.1045	0.9908
	(0.10886)	(15.04409)
WLSE	0.0492	2.16097	0.1722	0.0206	0.0966	0.9965
	(0.0086)	(0.96541)
CVM	0.05519	1.65872	0.1488	0.0184	0.0961	0.9967
	(0.089642)	(5.33803)
ADE	0.056626	1.59148	0.1477	0.0186	0.0954	0.9970
	(0.03093)	(1.71603)
RTADE	0.05773	1.51551	0.1489	0.0189	0.0973	0.9961
	(0.04211)	(2.61251)
BE	0.06251	1.43835	0.1785	0.0245	0.0960	0.9945
	(0.00782)	(0.04246)

. It is shown that the K-S statistic value for the MLE was smaller than those for the other methods, and the p-value of the K-S test for the MLE was greater than those for the others. Therefore, the MLE method outperformed the others, as demonstrated in Figure 4 and Figure 5. The following assumptions were used to determine the probability of the operational characteristics and the minimum values of n in the failure time data; for more details, refer to

Table 16. The ASP for the PsL distribution with parameters where $\nu =0.062$ and $\delta =1.40$.

${\mathit{u}}^{*}$	c	$\mathit{a}=0.25$		$\mathit{a}=0.45$		$\mathit{a}=0.60$		$\mathit{a}=0.80$		$\mathit{a}=1.00$
		$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$	$\mathit{n}$	$\mathit{L}\left({\mathit{u}}_{\mathbf{0}}\right)$
0.25	0	2	0.8511	1	1.0000	1	1.0000	1	1.0000	1	1.0000
	2	12	0.7820	7	0.8196	6	0.7938	5	0.7965	4	0.8750
	8	47	0.7628	28	0.7616	22	0.7678	17	0.8158	15	0.7880
	10	59	0.7610	35	0.7612	27	0.7680	22	0.7712	19	0.7597
0.5	0	5	0.5246	3	0.5523	2	0.6692	2	0.5796	2	0.5000
	2	18	0.5240	11	0.5252	8	0.5764	7	0.5220	6	0.5000
	8	58	0.5191	34	0.5171	26	0.5482	21	0.5213	18	0.5000
	10	72	0.5058	42	0.5075	32	0.5456	26	0.5026	22	0.5000
0.95	0	19	0.0549	11	0.0554	8	0.0621	6	0.0654	5	0.0625
	2	41	0.0533	23	0.0528	17	0.0618	13	0.0638	11	0.0547
	8	94	0.0525	53	0.0523	41	0.0516	31	0.0617	26	0.0539
	10	111	0.0511	63	0.0525	48	0.0510	37	0.0565	30	0.0480

.

8. Conclusions

In this study, an ASP was developed using the PsL distribution, where the life test ended at the median lifetime of the PsL distribution. Various truncation periods, along with different characteristics of the PsL distribution and levels of consumer risk, were considered to determine the necessary sample size. Moreover, it was ensured that the acceptance probability at the attained sample sizes remained below or equal to the complement of the consumer’s risk.

The other aspect of this study involves investigating the estimation of parameters for the PsL distribution by employing the two types of estimators, i.e., classical methods and Bayesian methods, with symmetric and asymmetric loss functions. The BEs were derived using the SE, GE, and LINEX loss functions while utilizing appropriate priors on the parameters. Due to the unavailability of closed-form solutions for Bayes estimates under these loss functions, this study employed the MCMC technique. Through extensive simulation studies, we evaluated the performance of the considered methods of estimation under the specified loss functions. Finally, we demonstrated the potential applicability of the PsL distribution by applying it to real-world data, thus providing a practical context for assessing the effectiveness of different estimation methods.