Abstract
A control design for a linear large-scale interconnected system composed of identical subsystems is presented in this paper. The control signal of all subsystems is sampled. For different subsystems, the sampling times are not identical. Nonetheless, it is assumed that a bound exists for the maximal sampling time. The control algorithm is designed using the Wirtinger inequality, and the non-fragile control law is proposed. The size of the linear matrix inequalities to be solved by the proposed control algorithm is independent of the number of subsystems composing the overall system. Hence, the algorithm is computationally effective. The results are illustrated by two examples. The first example graphically illustrates the function of the proposed algorithm while the second one compares with a method for stabilizing a large-scale system obtained earlier, thus illustrating the improved capabilities of the presented algorithm.
Keywords:
large-scale system; Wirtinger inequality; non-fragile control; linear matrix inequality (LMI) MSC:
93A15; 93B17; 93C57
1. Introduction
To design control algorithms for large-scale interconnected systems, one usually divides the overall system into subsystems with not-too-strong interconnections. Then, one designs a control law so that the control input for a particular subsystem depends on the measurements from this subsystem only while, on the other hand, guaranteeing sufficient robustness to mitigate the effects of interconnections with the other subsystems. For more information (see, e.g., [1,2] or [3]). An important subclass of them is symmetrically interconnected systems (every subsystem is connected with every other one); see, e.g., [3], Chapter 12, for a thorough description.
A crucial step in the design of control of linear large-scale interconnected systems composed of identical subsystems is the definition of a certain transformation that converts the large-scale interconnected system into a set of (non-identical) disconnected systems. Stabilization of this set of autonomous systems implies stability of the original large-scale system as well (see, e.g., [4], among others). In [5], this approach to the stabilization of large-scale systems is applied to the control of large-scale nonlinear systems.
Control of large-scale systems is usually implemented via communication networks bringing flexibility and cost-effectiveness, but also introducing some undesired effects, such as sampling and quantization of the signals, the transmission of the measured data as well as the control signals is subject to time delays, packet dropouts are present, etc. (see, e.g., [6,7,8,9,10,11]).
As the state values are not always available for the controller, an observer must be designed. An observer-based decentralized control of large-scale systems was proposed in [12], and for systems with time delays in [13]. Event-triggered controller, allowing for reduction of the communication cost in the control loop, was designed for a nonlinear interconnected system in [14], and the stabilization of a large-scale system with quantized control signals was investigated in [11].
In many practical applications, the properties of the actuators are subject to changes in time due to various causes like material degradation, changing of properties depending on temperature, etc. However, their replacement can often be difficult or costly. Hence, there is a need to propose a control tolerating changes in the properties of the actuators (non-fragile control). This can be modeled as variations in the control gain. Here, additive perturbations of the control gain are considered (see, e.g., [15,16] or, for a related problem of multi-agent system synchronization, in [17] or [18]).
To find a stabilizing control for linear time-delay systems, the Lyapunov–Krasovskii (see, e.g., [5] or, for a multi-agent system, [19]) or Razumikhin functional-based methods (as in [6]) leading to linear matrix inequalities (LMI) are often applied. The Wirtinger inequality can be used in connection with the Lyapunov–Krasovskii-based methods (see, e.g., [20,21]), reducing the conservativeness of the involved estimates. The Lyapunov–Krasovskii functional sometimes requires the derivative of the time delay to be less than one. Hence, these methods are not suitable for systems with sampled controls. The so-called descriptor approach (see [22]) is a remedy [23], which uses this approach in connection with the Wirtinger inequality to stabilize a system with sampled controls. A large-scale system is stabilized by a Wirtinger inequality-based design in [24]. This paper extends these results.
- Purpose of this paper:
- To present an improved algorithm for stabilization of an interconnected large-scale system with sampled controls under less restrictive conditions than required by the algorithm proposed by [6].
- To provide a comparison of both approaches.
- To present an algorithm that enables more general interconnections than the algorithm proposed by [6].
- Based on existing results to propose the non-fragile control law extending the previous results to the case of fluctuating control gain.
The novel method is based on the Wirtinger inequality.
- Notation:
- The LMI means matrix P is a square symmetric positive definite matrix.
- For symmetric matrices, the elements below the diagonal are not written explicitly they are replaced by an asterisk:
- If no confusion can arise, the time argument t is omitted. The time delay is written using subscript: , . However, if the time argument is different from t, it is written in full.
- If A is a square matrix, then denotes the identity matrix with a dimension equal to the dimension of A; 0 denotes a zero block; its dimension will be clear from the context.
- By we denote the block-diagonal matrix .
- The symbol ⊗ denotes the Kronecker product. Its properties are summarized, e.g., in [25].
Outline of the paper: The problem is introduced in Section 2, and the necessary assumptions are presented here. Section 3 contains the design of the control algorithm based on the Wirtinger inequality. This section is divided into two subsections. The Wirtinger inequality-based control design algorithm is derived in the first subsection; however, the dimension of this problem is dependent on the number of subsystems. This issue is remedied in the second subsection, which contains a control algorithm design independent of the number of subsystems. Section 4 contains two illustrative examples; the first one graphically illustrates the capabilities of the algorithm, while the second one provides a comparison with a method derived earlier, thus highlighting the improvements achieved by the algorithm presented here. Then, the conclusions follow.
2. Problem Setting
Consider the following large-scale system, which is composed of N identical subsystems. For every , the ith subsystem is given by
Here, , , are the state, control, and disturbance, respectively. Moreover, , , and . We define also the interconnection matrix as follows: let ; if then if the state of the jth subsystem influences the state of the ith subsystem, otherwise .
Assumption 1.
For every holds (the interconnection of the system has no loops).
Assumption 2.
Matrix E is symmetric.
The second assumption implies that there exists an orthogonal matrix and a real diagonal matrix such that
Without loss of generality, one can assume and .
Remark 1.
Due to the importance of symmetrically interconnected systems (every subsystem is connected to every other subsystem; in this case, whenever , ), special methods for these systems were proposed. Papers [6,15] and Chapter 12 in [3], among others, are focused on the control of this class of interconnected systems. The most distinctive feature is that a different transformation can be defined for these systems: the transformation matrix is not necessarily constructed using eigenvectors; rather,
can be used. This can be beneficial if N is large as construction of this transformation matrix does not require computation of eigenvectors and eigenstructures. Still, the method based on the computation of the eigenvalues is applicable for these systems if the computation of the eigenstructure of matrix E poses no difficulties. Although both methods lead to a stabilizing control, the results can be different in terms of conservativeness. This is why this case is treated separately in this paper.
Denote . As shown in [3] (Chapter 12), for an N-dimensional matrix E, the relation holds.
Let , , , . This allows us to rewrite the N-tuple of subsystems (1) and (2) in the compact form
System (4) is referred to as the overall system.
Assumption 3.
The control is sampled; moreover, it is assumed the time interval of length elapses between the sampling time and the time instant when the measured value is available to the controller. The sequence of sampling times of the ith subsystem is denoted by , .
Assumption 4.
There exists such that for all and all k.
We aim to find a matrix so that the control law
stabilizes the overall system.
In (5), is defined as follows: . This is called the nominal case, as the control gain is not perturbed.
In some cases, the control gain matrix is subject to perturbations. We assume the perturbations are additive as in [15]; the matrix gain is time-dependent. Let there exist measurable functions and matrices , and . Then, we define functions by
Assumption 5.
Functions are measurable, and for all and all , holds.
Then, the control law is given as
The goal is to find matrix K so that stabilization of the overall system is achieved under the control law (7). The delays satisfy the same conditions as in the nominal case. Matrix K is called the nominal control gain matrix.
Remark 2.
Matrices and are supposed to be known and available for the controller synthesis. On the other hand, functions are not known.
3. Control Design
3.1. Wirtinger Inequality and Its Application to the Control of a Large-Scale System
Lemma 1
([26], Lemma 3.1). (Wirtinger inequality) Let be real scalars, be an absolutely continuous function, ; exists and is finite, and exists and is finite. Let there also exist an -dimensional matrix . Then,
This lemma was used to obtain the following result (Theorem 1 in [23]). For the sake of completeness of this paper, we repeat it here without proof.
Theorem 1.
Let . Consider system
where , and the control is sampled, so that Assumptions 3 and 4 hold. Let there exist a scalar and matrices , , , , nonsingular and with compatible dimensions, so that, with matrix Σ defined as
the LMI
holds. Then, system (8) with sampled control is stable.
Remark 3.
Note that matrix inequality (9) is linear either in or in , but not simultaneously in both; hence, it is not applicable to the control synthesis problem. On the other hand, a standard procedure (applied in the subsequent text) yields a related matrix inequality that can be used to the control design.
Remark 4.
Parameter ε is not a decision variable; its value cannot be obtained from the solution of these LMI. Rather, its value must be determined before the above LMIs are solved. The presence of this parameter is characteristic for the control design using the descriptor approach (see [27]).
Remark 5.
Paper [23] presents a slightly more general version, with a general matrix instead of the multiple . However, for the control synthesis problem, this formulation is useful.
Remark 6.
Let (here, is the last sampling time before ). As shown in [23], if the Lyapunov–Krasovskii functional is defined as
then for .
In the following, -dimensional matrices U, X, M, L, and Z, and also matrix and constants and , will be used.
Notation: Let us define the following matrices:
Lemma 2.
Consider System (4), and let Assumptions 3 and 4 hold. Assume there exist -dimensional matrices , , , , Z nonsingular, an -dimensional matrix K, and scalars and , such that, using Notation (10), LMI
holds. Let the control of the ith subsystem be given by (5). Then, if , System (4) is asymptotically stabilized; otherwise, if for all , for every , holds.
Remark 7.
This is a direct counterpart of Theorem 7.1 in [27] for large-scale systems where the sampling times are different for different subsystems. Thus, the proof is sketched here.
Proof.
First, observe that the Schur complement theorem yields , if and only if . Moreover, for any scalar , one has
Now, we are ready to prove that inequality implies the -stability of the overall system. Let us introduce, for the vector,
Observe also that
Define functional by
The procedure described in the following is based on [23], where only one delay is considered. As multiple delays are present in our problem, we sketch a generalization of the results of that paper to systems with multiple delays. Thus, for the case without uncertainties in the control gain matrix, one obtains
Then,
As follows from the first part of the proof, Condition (12) implies . Then, for , the following holds: if , then , which yields asymptotic stability. If and for , then . □
Remark 8.
Finding the minimal γ satisfying assumption of Lemma 2 allows us to find the -optimal control.
Consider now the case when the feedback gain is perturbed. The control gains are given by (6). Denote
In this case, matrix is time dependent; time dependent terms appear in , , and . They are estimated using the following proposition. Before it is formulated, let us choose a matrix , , and also define
With matrix , as well as the matrices defined in (13), we define auxiliary matrices , by
Proposition 1.
With matrices and and with one can see that inequality holds for all .
Proof.
The following holds for :
The Young inequality then yields the result. □
For future purposes, we introduce matrix
as follows:
Moreover, let , be defined as
Lemma 3.
Consider System (4). Let Assumptions 3, 4, and 5 hold. Moreover, assume there exist -dimensional matrices , , , , Z nonsingular and , , such that and scalars and , so that, using notations (10), (11), (13), and (14), the LMI
holds. Assume System (4) with the control input (7). Then, if , System (4) is asymptotically stabilized; otherwise, if for every , then for every , the following holds:
Proof.
Proceeding as in the proof of Lemma 2, one can infer
If one can prove the inequality
for all , one then obtains that (17) implies .
Hence, it remains to prove the validity of (18) for all if . Taking the Schur complement of matrix , one obtains that , if and only if
Proceeding as in the proof of Lemma 4, one has that the above inequality is equivalent to . Taking (1) into account, we arrive at (18).
To sum up, if in . As in the proof of Lemma 2, by integration from 0 to t, we arrive at . On the other hand, if for all , (17) implies if , and one has asymptotic stability of the closed loop. □
3.2. Reduction of the Size of the Problem and Controller Synthesis
The size of the optimization problem (12) is proportional to , hence it is too large for practical implementation. On the other hand, matrices and can be transformed into a block-diagonal matrix, albeit with, in general, not equal terms on the diagonal. This procedure, as well as the subsequent procedure for the controller design, are rather standard; hence, their description is brief.
To proceed, let
Define matrix-valued function as follows:
Lemma 4
(No uncertainties in the control gain). Assume there exist -dimensional matrices , , , , Z nonsingular, and , and scalars and , so that at least one of the following conditions holds:
- 1.
- The eigenvalues of matrix E satisfy
- 2.
- The system is symmetrically connected, andThen, .
Proof.
In the first case, note that the matrix-valued function is convex in d. Hence, conditions (19) imply for all .
With help of relation (3), we introduce matrix , defined by ,
If the first condition in the formulation of this lemma holds, observe that there exists a permutation matrix , such that
hence, .
Define now . Properties of the Kronecker product imply , and one has .
If condition (20) holds, then define
. Then, there is a permutation matrix , such that
which implies . This completes the proof of this case. □
To handle the case with uncertainties in the control gain, let us define matrices
and a matrix-valued function as follows:
Lemma 5
(Case with uncertainties in the control gain). Assume there exist -dimensional matrices , , , , Z nonsingular and , , such that and scalars and , so that at least one of the following conditions holds:
- 1.
- for all .
- 2.
- The system is symmetrically connected andas well as .
Then, .
The proof is analogous to the proof of Lemma 4; hence, it is omitted.
To derive the controller synthesis algorithm, the procedure is similar to that of [23]. Also let , , , , , and . For -dimensional matrices , , , , Q nonsingular, a -dimensional matrix Y, and positive scalars , , define matrices , and a matrix-valued function by
Also define as
Lemma 6.
Consider System (4). Let there exist -dimensional matrices , , , , Q nonsingular, a -dimensional matrix Y, and positive scalars γ, ε. Then, for every matrix , holds if and only if .
Proof.
Let Then, □
The following analogous result holds for the case with uncertainties in the control gain.
Lemma 7.
Let the assumptions of Lemma 6 hold; moreover, let there exist a -dimensional matrix . Then, the condition holds if and only if .
Proof.
The proof is analogous to the proof of Lemma 6. The only difference is that matrix is defined as . □
The following theorem summarizes the results of the above lemmas.
Theorem 2.
1. Consider System (4). Let there exist -dimensional matrices , , , , Q nonsingular, a -dimensional matrix Y, and positive scalars γ, ε. Assume also the validity of at least one of the following conditions:
- (a)
- and .
- (b)
- The overall system is symmetrically connected;and .
Proof of Theorem 2.
The first part is a consequence of Lemmas 6 and 4, the second part is the consequence of Lemmas 6 and 5. □
Remark 9.
Minimization of the parameter γ leads to the -optimal control.
4. Examples
4.1. Example 1
System (4) is composed of 10 subsystems given as follows. The system matrices are given as , , , , elsewhere; its eigenvalues are in the interval . Note that the overall system is unstable. Time delays are defined as , . The sampling occurs at different time instants for different subsystems.
The LMI optimization problem obtained in this example is feasible. Computations from the previous section yield The initial condition was chosen as
Figure 1 illustrates the results. The upper subplot shows the state (solid line), (dotted line), (dashed line) and (dash-dot line). The lower subplot illustrates the norm of the vector . There were no disturbances present in the simulated system. Therefore, the control algorithm achieved a full stabilization of the overall system, in spite of the presence of the interconnections. If some disturbances act upon the system, the state of the system would not, in general, achieve the zero value in the limit. However, the norm of the state would be, for a sufficiently large time, bounded by (16). The simulations were obtained using the Matlab R2021b software.
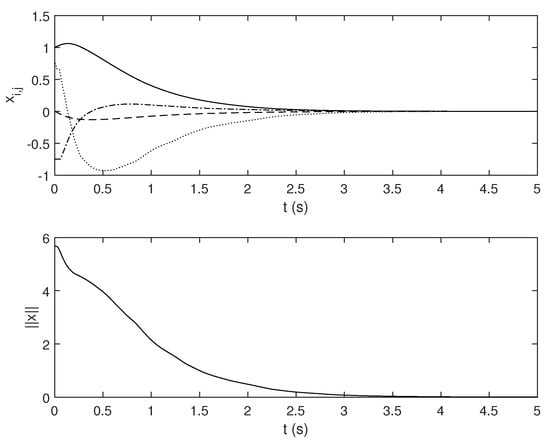
Figure 1.
Simulation results. Upper subplot: (solid line), (dotted line), (dashed line), (dash-dot line). Lower subplot: the norm of .
4.2. Example 2
The purpose of this example is to provide a fair comparison of the algorithm presented here with the algorithm derived in [6]. Both methods are applied to identical systems with equal parameters.
Matrices defining the ith subsystem are given as
, , , .
The system is symmetrically interconnected; matrix , introduced in Remark 1, was applied in both cases.
The results are summarized in Table 1 for various values of and various numbers N of subsystems that were computed using the approach presented in this paper (values and , denoted by K and , respectively, in the above text) and a compared with results obtained by the method based on the Razumikhin functional as described in [6] (values and ; these quantities are denoted by K and , respectively, in [6]).

Table 1.
Comparison of results.
In both cases, the value of the constant computed by the LMIs based on the Wirtinger inequality is considerably smaller. Thus, the presented algorithm exhibits a better capability of disturbance attenuation. Also, it is capable of handling a larger set of parameters of the optimization problem.
5. Conclusions
An algorithm for the stabilization of large-scale interconnected systems with sampled controls was presented. The algorithm is based on the Wirtinger inequality. Results of the presented approach were compared with results previously obtained using an algorithm based on the Razumikhin functional. It is shown that the method presented here is less conservative. On the other hand, it is to point out that the method is applicable to linear systems; nonlinearities must be approximated using the Lipschitz property in combination with methods known from the robust control, hence leading to an overly conservative design.
In future research, we intend to focus on more nonlinear systems, systems with delays, and/or systems with fractional derivatives (see, e.g., [28]); the ultimate goal is to apply the proposed method in a practical setting.
Author Contributions
Conceptualization, V.L. and B.R.; methodology, V.L. and B.R.; software, V.L. and B.R.; validation, B.R.; formal analysis, V.L. and B.R.; writing—original draft preparation, V.L. and B.R.; writing—review and editing, V.L. and B.R.; visualization, B.R.; supervision, V.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to thank the anonymous referees for providing helpful comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bakule, L. Decentralized control: Status and outlook. Annu. Rev. Control 2014, 38, 71–80. [Google Scholar] [CrossRef]
- Liu, K.; Selivanov, A.; Fridman, E. Survey on time-delay approach to networked control. Annu. Rev. Control 2019, 48, 57–79. [Google Scholar] [CrossRef]
- Lunze, J. Feedback Control of Large-Scale Systems; Prentice Hall: Hemel Hempstead, UK, 1992. [Google Scholar]
- Demir, O.; Lunze, J. A decomposition approach to decentralized and distributed control of spatially interconnected systems. IFAC Proc. Vol. 2011, 44, 9109–9114. [Google Scholar] [CrossRef]
- Rehák, B.; Lynnyk, V. Network-based control of nonlinear large-scale systems composed of identical subsystems. J. Frankl. Inst. 2019, 356, 1088–1112. [Google Scholar] [CrossRef]
- Bakule, L.; Papík, M.; Rehák, B. Decentralized H-infinity control of complex systems with delayed feedback. Automatica 2016, 67, 127–131. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Q.; Ge, X.; Ding, D.; Ding, L.; Yue, D.; Peng, C. Networked control systems: A survey of trends and techniques. IEEE/CAA J. Autom. Sin. 2019, 7, 1–17. [Google Scholar] [CrossRef]
- Shanmugam, S.; Vadivel, R.; Gunasekaran, N. Finite-Time Synchronization of Quantized Markovian-Jump Time-Varying Delayed Neural Networks via an Event-Triggered Control Scheme under Actuator Saturation. Mathematics 2023, 11, 2257. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, Y.J.; Lee, S.H.; Kwon, O.M. Enhancing Stability Criteria for Linear Systems with Interval Time-Varying Delays via an Augmented Lyapunov–Krasovskii Functional. Mathematics 2024, 12, 2241. [Google Scholar] [CrossRef]
- Jang, Y.H.; Kim, H.S. Sampled-Data Cooperative Adaptive Cruise Control for String-Stable Vehicle Platooning with Communication Delays: A Linear Matrix Inequality Approach. Machines 2024, 12, 165. [Google Scholar] [CrossRef]
- Rehák, B.; Lynnyk, V. Decentralized networked stabilization of a nonlinear large system under quantization. In Proceedings of the 8th IFAC Workshop on Distributed Estimation and Control in Networked Systems NECSYS 2019, Chicago, IL, USA, 16–17 September 2019; Volume 52, pp. 49–54. [Google Scholar]
- Yu, X.; Liao, F.; Li, L.; Lu, Y. Observer-based decentralized robust H∞ output tracking control with preview action for uncertain and disturbed nonlinear interconnected systems. Asian J. Control 2022, 24, 626–641. [Google Scholar] [CrossRef]
- Tharanidharan, V.; Sakthivel, R.; Shanmugam, H.; Almakhles, D.J. Decentralized observer-based controller design for large-scale systems with quantized measurements and actuator faults. Asian J. Control 2022, 25, 190–200. [Google Scholar] [CrossRef]
- Hu, C.; Zou, Y.; Li, S. Adaptive dynamic programming-based decentralized event-triggered control of large-scale nonlinear systems. Asian J. Control 2021, 24, 1542–1556. [Google Scholar] [CrossRef]
- Bakule, L.; Sen, M. Non-Fragile controllers for a class of time-delay nonlinear systems. Kybernetika 2009, 45, 15–32. [Google Scholar] [CrossRef]
- Chen, J.; Ling, R.; Zhang, D. Distributed non-fragile stabilization of large-scale systems with random controller failure. Neurocomputing 2016, 173, 2033–2038. [Google Scholar] [CrossRef]
- Sakthivel, R.; Kanakalakshmi, S.; Kaviarasan, B.; Ma, Y.K.; Leelamani, A. Finite-time consensus of input delayed multi-agent systems via non-fragile controller subject to switching topology. Neurocomputing 2019, 325, 225–233. [Google Scholar] [CrossRef]
- He, S.; Wu, Y.; Li, Y. Finite-Time Synchronization of Input Delay Complex Networks via Non-fragile Controller. J. Frankl. Inst. 2020, 357, 11645–11667. [Google Scholar] [CrossRef]
- Rehák, B.; Lynnyk, V. Synchronization of nonlinear complex networks with input delays and minimum-phase zero dynamics. In Proceedings of the 19th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 15–18 October 2019; Volume 57, pp. 759–764. [Google Scholar]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef]
- Gyurkovics, E.; Takács, T. Multiple integral inequalities and stability analysis of time delay systems. Syst. Control Lett. 2016, 96, 72–80. [Google Scholar] [CrossRef]
- Fridman, E.; Dambrine, M.; Yeganefar, N. On input-to-state stability of systems with time-delay: A matrix inequalities approach. Automatica 2008, 44, 2364–2369. [Google Scholar] [CrossRef]
- Liu, K.; Fridman, E. Wirtinger’s Inequality and Lyapunov-Based Sampled-Data Stabilization. Automatica 2012, 48, 102–108. [Google Scholar] [CrossRef]
- Rehak, B. Wirtinger inequality-based control design for an interconnected large-scale system with sampled controls. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; Volume 45, pp. 1009–1014. [Google Scholar]
- Chen, N.; Zhai, G.; Gui, W.; Yang, C.; Liu, W. Decentralized H∞ quantisers design for uncertain interconnected networked systems. IET Control Theory Appl. 2008, 4, 177–183. [Google Scholar] [CrossRef]
- Liu, K.; Suplin, V.; Fridman, E. Stability of linear systems with general sawtooth delay. IMA J. Math. Control. Inf. 2010, 27, 419–436. [Google Scholar] [CrossRef]
- Fridman, E. Introduction to Time-Delay Systems; Birkhäuser: Basel, Switzerland, 2015. [Google Scholar]
- Zhang, T.; Li, Y. Global exponential stability of discrete-time almost automorphic Caputo–Fabrizio BAM fuzzy neural networks via exponential Euler technique. Knowl.-Based Syst. 2022, 246, 108675. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).