Consensus Control for Stochastic Multi-Agent Systems with Markovian Switching via Periodic Dynamic Event-Triggered Strategy
Abstract
1. Introduction
- It should be noted that most of the existing consensus control strategies focus on MASs that communicate over a fixed linked graph [4,6,7,9,34]. Therefore, it is essential to address the consensus problem for the MASs with switching topologies. In this study, a continuous-time Markovian process is conducted to represent the system matrices of the stochastic MASs and their communication topologies. Unlike in [13,14,15,16], the DDET strategy as proposed in this study allows the simultaneous switch of system matrices and topologies according to the exact environmental conditions, thus enhancing the adaptivity and flexibility of the system.
- Several DET sampled-data consensus control approaches have been developed for stochastic MASs [33]. In this study, a novel DDET consensus control strategy based on periodic sampling is presented to achieve consensus in stochastic MASs. There are two key challenges to overcome in introducing this DET mechanism. One is to design an appropriate DET scheme to avoid the need for continuously monitoring the triggered condition, and the other is to exclude Zeno behavior. Unlike [19,20,21,27,31,32,35], this approach significantly reduces the communication and computation burden while providing a more flexible and adaptive solution for the consensus control of stochastic MASs.
- The sufficient conditions for achieving consensus in the stochastic MASs with a DET strategy based on periodic sampled-data in a mean-square sense are determined through Lyapunov–Krasovskii functionals and Linear matrix inequalities. The conditions required to ensure the consistent performance of the system under the context of switching system matrices and topologies are proposed, which provides a theoretical basis for the chosen strategy.
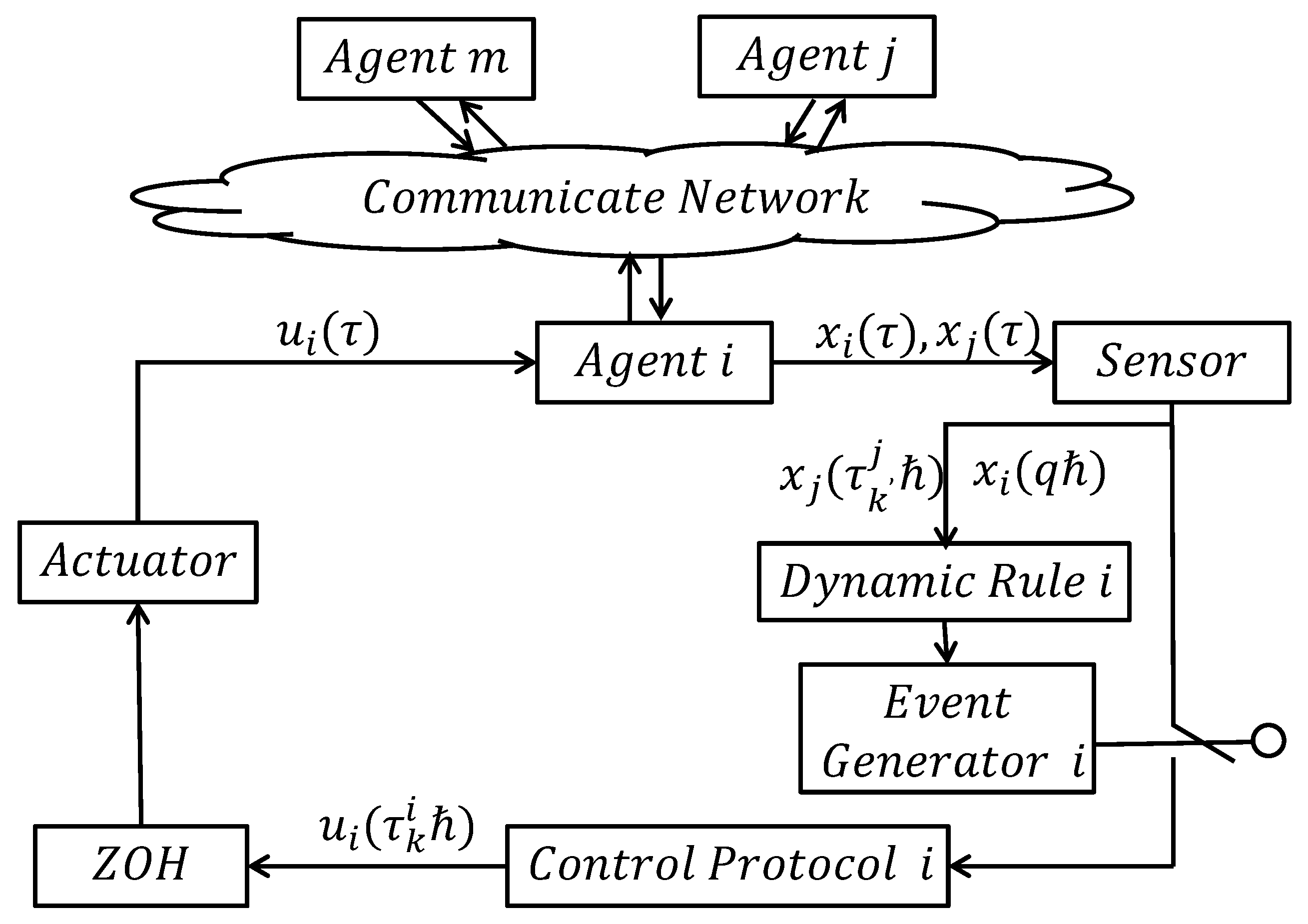
2. Model Description and Preliminaries
- A.
- Markovian process and graph theory
- B.
- Stochastic MASs model
- C.
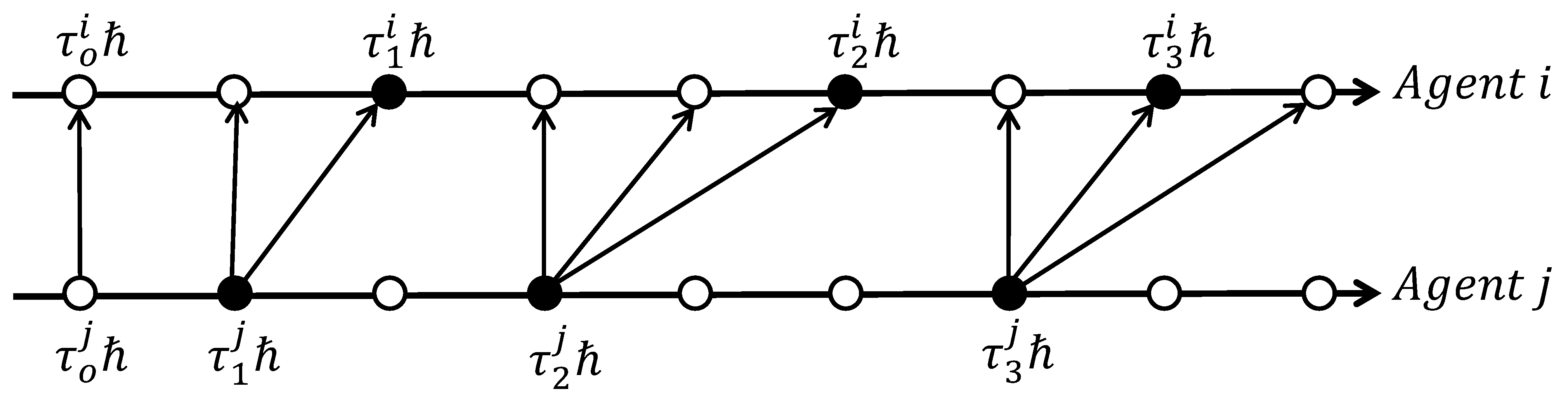
- Dynamic event-triggered consensus protocol
3. Consensus Stability Analysis
| Algorithm 1: Periodic sampling-based DET consensus control operation |
 |
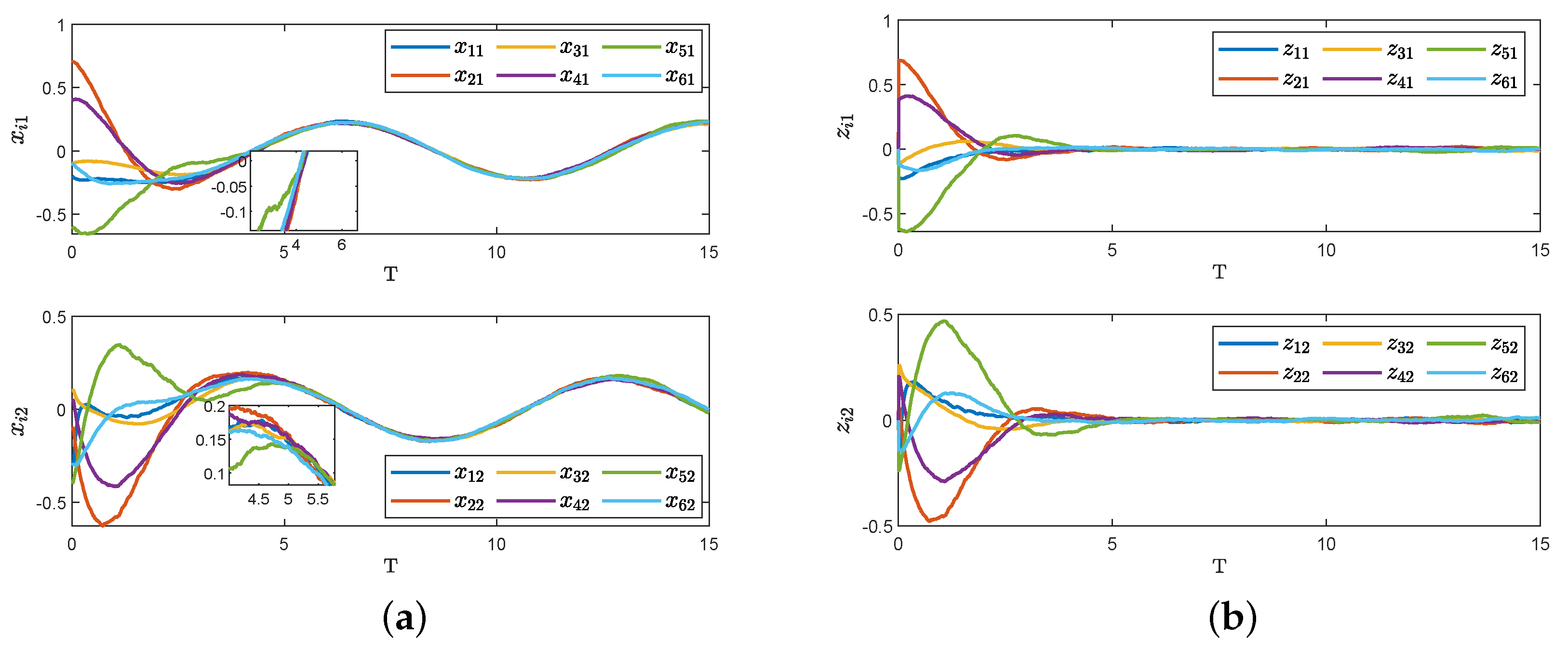
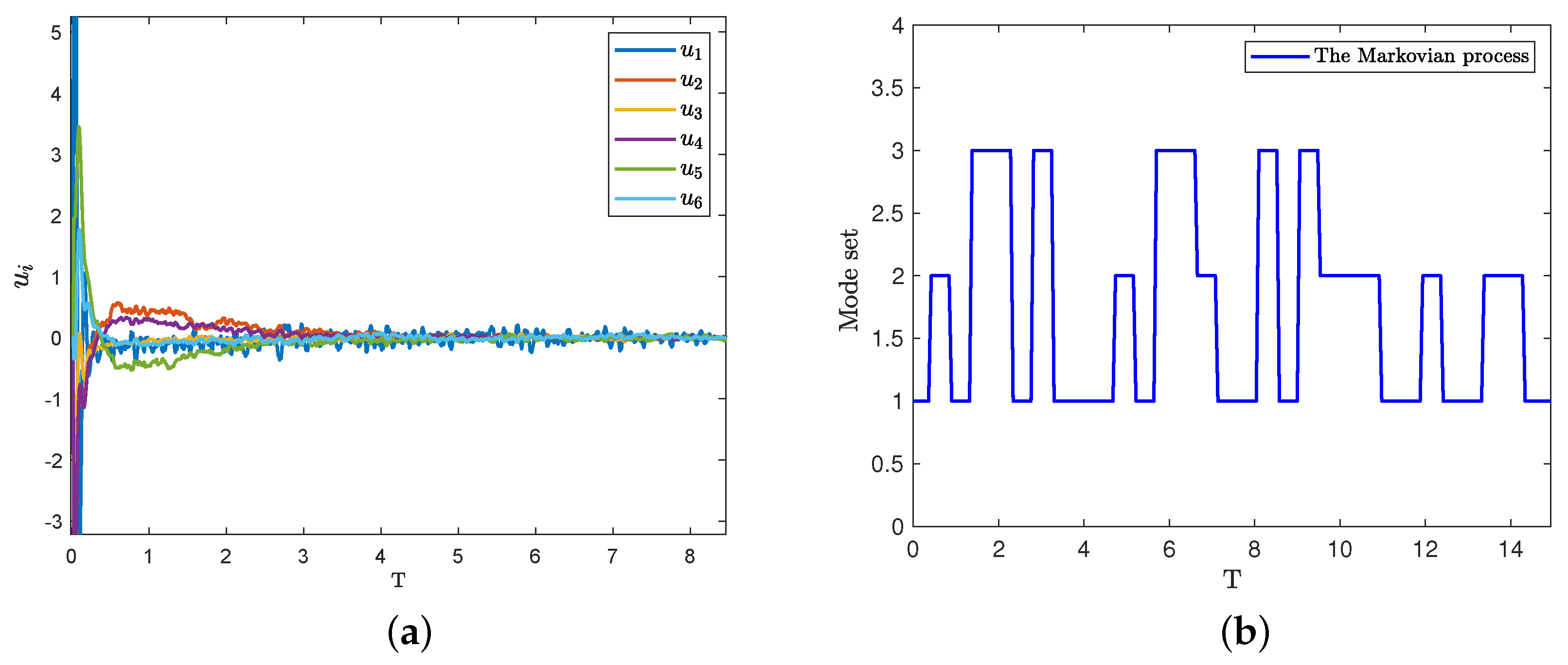
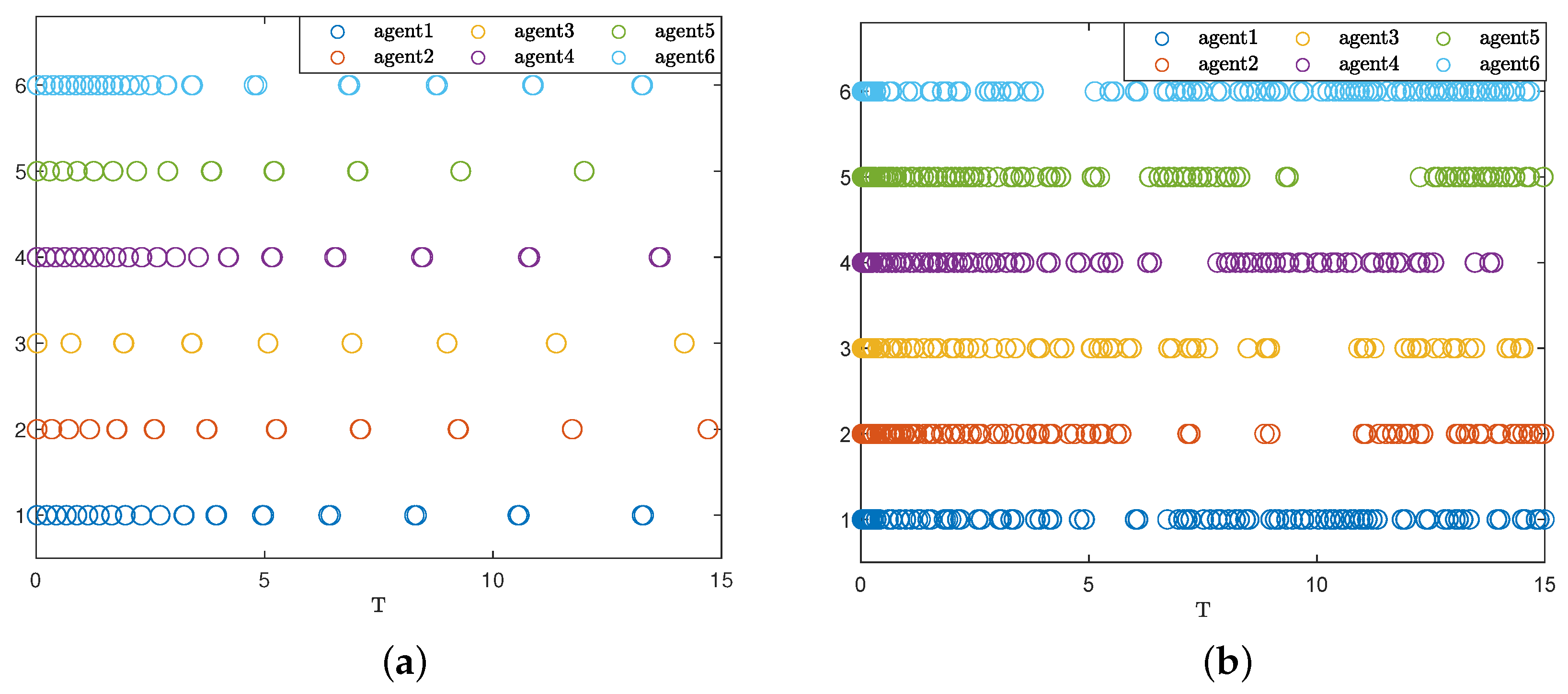
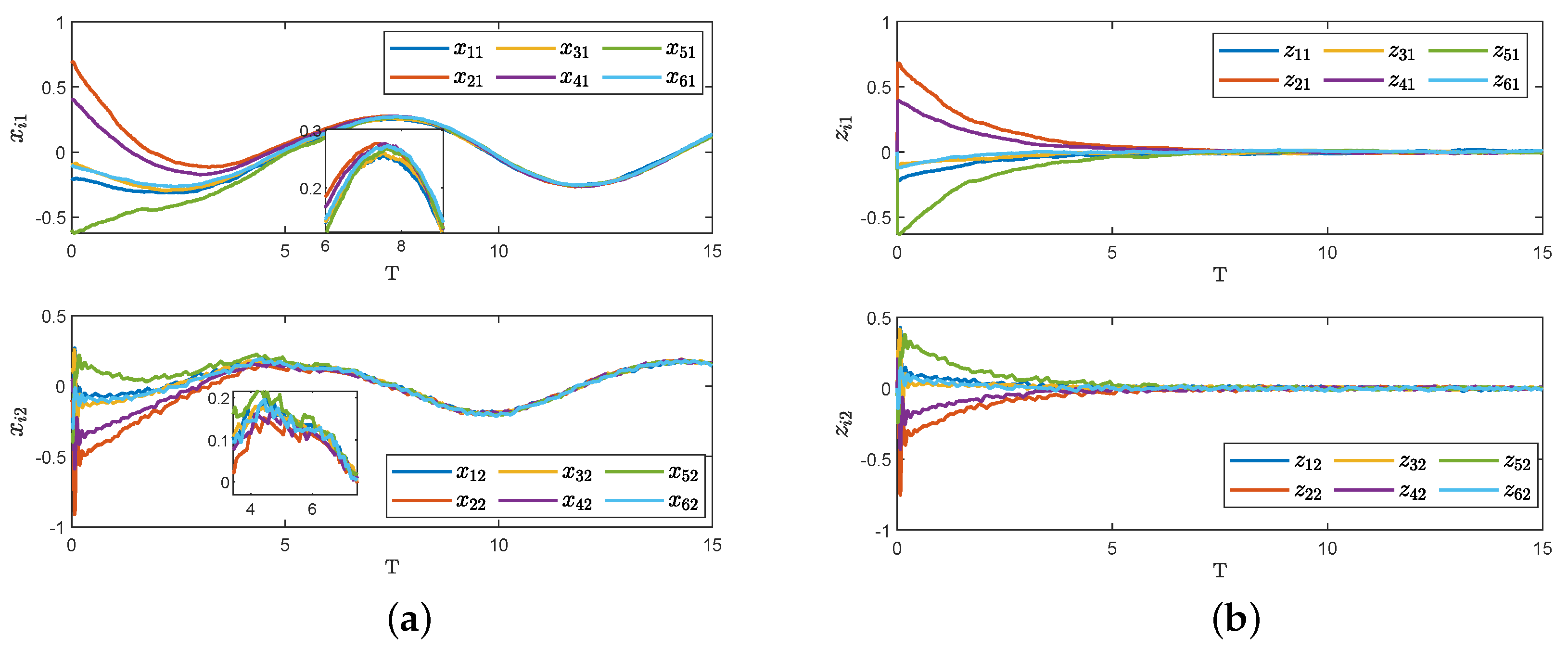
4. Simulation Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, H.; Li, H.; Xiao, R.; Liu, J. Modeling and simulation of dynamic ant colony’s labor division for task allocation of UAV swarm. Phys. A Stat. Mech. Its Appl. 2018, 491, 127–141. [Google Scholar] [CrossRef]
- Ren, W.; Zhao, X.; Li, H.; Fu, Q. Traffic flow impact of mixed heterogeneous platoons on highways: An approach combining driving simulation and microscopic traffic simulation. Phys. A Stat. Mech. Its Appl. 2024, 643, 129803. [Google Scholar] [CrossRef]
- Fan, H.; Chen, X.; Shi, K.; Liang, Y.; Wang, Y.; Wen, H. Mittag-Leffler synchronization in finite time for uncertain fractional-order multi-delayed memristive neural networks with time-varying perturbations via information feedback. Fractal Fract. 2024, 8, 422. [Google Scholar] [CrossRef]
- Sun, H.; Yang, H.; Han, H.; Sun, J.; Qiao, J. Consensus of MASs with input and communication delays by predictor-based protocol. IEEE Trans. Cybern. 2022, 53, 7126–7135. [Google Scholar] [CrossRef]
- Wang, X.; Qian, J.; Su, H.; Lu, X.; Lam, J. Distributed Global Consensus of LTI Mass with Heterogeneous Actuator Saturation and Communication Noises. SIAM J. Control. Optim. 2024, 62, 1690–1716. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Su, H.; Lam, J. Reduced-order interval observer based consensus for MASs with time-varying interval uncertainties. Automatica 2022, 135, 109989. [Google Scholar] [CrossRef]
- Yao, D.; Li, H.; Shi, Y. Event-Based Average Consensus of Disturbed MASs via Fully Distributed Sliding Mode Control. IEEE Trans. Autom. Control. 2024, 69, 2015–2022. [Google Scholar] [CrossRef]
- Liu, P.; Guo, X.; Wang, J.; Coutinho, D.; Wu, Z. Preset-time and preset-accuracy Human-in-the-Loop cluster consensus control for MASs under stochastic actuation attacks. IEEE Trans. Autom. Control. 2024, 69, 1675–1688. [Google Scholar] [CrossRef]
- Ren, C.E.; Zhang, J.; Guan, Y. Prescribed performance bipartite consensus control for stochastic nonlinear multiagent systems under event-triggered strategy. IEEE Trans. Cybern. 2023, 53, 468–482. [Google Scholar] [CrossRef]
- Hu, Z.; Mu, X. Impulsive consensus of stochastic multi-agent systems under semi-Markovian switching topologies and application. Automatica 2023, 150, 110871. [Google Scholar] [CrossRef]
- Zhou, W.; Hu, Y.; Liu, X.; Cao, J. Finite-time adaptive synchronization of coupled uncertain neural networks via intermittent control. Phys. A Stat. Mech. Its Appl. 2022, 596, 127107. [Google Scholar] [CrossRef]
- Cai, J.; Yi, C.; Wu, Y.; Liu, D.; Zhong, D. Leader-following consensus of nonlinear singular switched multi-agent systems via sliding mode control. Asian J. Control. 2024, 26, 1997–2010. [Google Scholar] [CrossRef]
- Yoo, S.J. Distributed consensus tracking of a class of asynchronously switched nonlinear multi-agent systems. Automatica 2018, 87, 421–427. [Google Scholar] [CrossRef]
- Li, X.; Long, L. Distributed event-triggered fuzzy control of heterogeneous switched multiagent systems under switching topologies. IEEE Trans. Fuzzy Syst. 2024, 32, 574–585. [Google Scholar] [CrossRef]
- Xu, B.; Yang, Y. Group consensus of nonlinear multiagent system with switching topology under DoS attacks. Phys. A Stat. Mech. Its Appl. 2022, 605, 127969. [Google Scholar] [CrossRef]
- Parivallal, A.; Sakthivel, R.; Wang, C. Output feedback control for bipartite consensus of nonlinear multi-agent systems with disturbances and switching topologies. Phys. A Stat. Mech. Its Appl. 2022, 589, 126589. [Google Scholar] [CrossRef]
- Cai, J.; Feng, J.; Wang, J.; Zhao, Y. Tracking Consensus of Multi-Agent Systems Under Switching Topologies via Novel SMC: An Event-Triggered Approach. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2150–2163. [Google Scholar] [CrossRef]
- Fan, H.; Chen, X.; Shi, K.; Wen, H. Distributed delayed impulsive control for μ-synchronization of multi-link structure networks with bounded uncertainties and time-varying delays of unmeasured bounds: A novel Halanay impulsive inequality approach. Chaos Solitons Fractals 2024, 186, 115226. [Google Scholar] [CrossRef]
- Wang, X.; Ahn, C.K.; Zhang, J.; Niu, B.; Zhang, G. Initial-value-free nonlinear mapping-based approach to practical finite/fixed-time consensus control for constrained multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3173–3183. [Google Scholar] [CrossRef]
- Chehardoli, H.; Ghasemi, A. Adaptive size-independent control of uncertain leader following systems with only relative displacement information. Phys. A Stat. Mech. Its Appl. 2022, 597, 127289. [Google Scholar] [CrossRef]
- Griffin, C.; Squicciarini, A.; Jia, F. Consensus in complex networks with noisy agents and peer pressure. Phys. A Stat. Mech. Its Appl. 2022, 608, 128263. [Google Scholar] [CrossRef]
- Ren, C.E.; Li, J.; Shi, Z.; Guan, Y.; Chen, C.L.P. Adaptive impulsive consensus of nonlinear multiagent systems with limited bandwidth under uncertain deception attacks. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 4592–4604. [Google Scholar] [CrossRef]
- Chang, J.; Shi, H.; Zhu, S.; Zhao, D.; Sun, Y. Time cost for consensus of stochastic multiagent systems with pinning control. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 94–104. [Google Scholar] [CrossRef]
- Geng, X.; Feng, J.; Wang, J.; Li, N.; Zhao, Y. Prespecified-time bipartite consensus of multi-agent systems via intermittent control. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 2240–2251. [Google Scholar] [CrossRef]
- Ma, L.; Wang, Z.; Lam, H.K. Event-triggered mean-square consensus control for time-varying stochastic multi-agent system with sensor saturations. IEEE Trans. Autom. Control. 2017, 62, 3524–3531. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, C.; Zhao, D.; Sun, B.; Li, Y. Event-triggered consensus control of continuous-time stochastic multi-agent systems. Automatica 2022, 137, 110022. [Google Scholar] [CrossRef]
- Zhu, S.; Bao, H.; Cao, J. Bipartite synchronization of coupled delayed neural networks with cooperative-competitive interaction via event-triggered control. Phys. A Stat. Mech. Its Appl. 2022, 600, 127586. [Google Scholar] [CrossRef]
- He, W.; Mo, Z. Secure event-triggered consensus control of linear multiagent systems subject to sequential scaling attacks. IEEE Trans. Cybern. 2022, 52, 10314–10327. [Google Scholar] [CrossRef]
- Li, M.; Long, Y.; Li, T.; Liang, H.; Chen, C.L.P. Dynamic event-triggered consensus control for input constrained multi-agent systems with a designable minimum inter-event time. IEEE/CAA J. Autom. Sin. 2024, 11, 649–660. [Google Scholar] [CrossRef]
- Yi, C.; Cai, J.; Guo, R. Synchronization of a class of nonlinear multiple neural networks with delays via a dynamic event-triggered impulsive control strategy. Electron. Res. Arch. 2024, 32, 4581–4603. [Google Scholar] [CrossRef]
- Guo, G.; Ding, L.; Han, Q. A distributed event-triggered transmission strategy for sampled-data consensus of multi-agent systems. Automatica 2014, 50, 1489–1496. [Google Scholar] [CrossRef]
- Su, X.; Wang, C.; Chang, H.; Yang, Y.; Assawinchaichote, W. Event-triggered sliding mode control of networked control systems with Markovian jump parameters. Automatica 2021, 125, 109405. [Google Scholar] [CrossRef]
- Qi, W.; Zong, G.; Zheng, W. Adaptive event-triggered SMC for stochastic switching systems with Semi-Markov process and application to boost converter circuit model. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 786–796. [Google Scholar] [CrossRef]
- Matsume, H.; Wang, Y.; Ishii, H. Resilient self/event-triggered consensus based on ternary control. Nonlinear Anal. Hybrid Syst. 2021, 42, 101091. [Google Scholar]
- Fan, H.; Rao, Y.; Shi, K.; Wen, H. Time-varying function matrix projection synchronization of Caputo fractional-order uncertain memristive neural networks with multiple delays via mixed open loop feedback control and impulsive control. Fractal Fract. 2024, 8, 301. [Google Scholar] [CrossRef]
- Cui, M.; Wu, Z.; Xie, X.; Shi, P. Modeling and adaptive tracking for a class of stochastic Lagrangian control systems. Automatica 2013, 49, 770–779. [Google Scholar] [CrossRef]
- Zhu, Y.; Niu, B.; Shang, Z.; Wang, Z.; Wang, H. Distributed adaptive asymptotic consensus tracking control for stochastic nonlinear MASs with unknown control gains and output constraints. IEEE Trans. Autom. Sci. Eng. 2024, 1–11. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, L.; Me, G. Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays. Syst. Control Lett. 2008, 57, 175–183. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, W. Almost sure consensus of stochastic nonlinear multi-agent systems via event-triggered control. Nonlinear Dyn. 2023, 111, 3469–3478. [Google Scholar] [CrossRef]
- Dai, J.; Guo, G. Event-triggered leader-following consensus for multi-agent systems with semi-Markov switching topologies. Inf. Sci. 2018, 459, 290–301. [Google Scholar] [CrossRef]
- Oksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013; pp. 26–30. [Google Scholar]
- Liu, J.; Li, H.; Luo, J. Bipartite consensus control for coupled harmonic oscillators under a coopetitive network topology. IEEE Access 2018, 6, 3706–3714. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, C.; Han, Q.L. The synchronization of networked harmonic oscillators under denial-of-service attacks. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 789–800. [Google Scholar] [CrossRef]
- Yang, Y. Switching cluster synchronization control of networked harmonic oscillators subject to denial-of-service attacks. ISA Trans. 2022, 127, 239–250. [Google Scholar] [CrossRef] [PubMed]

| Symbol | Definition |
|---|---|
| The Markovian switching signal | |
| The state space of the Markovian process | |
| ℏ | The sampling period |
| The k-th event-triggered instant for agent i | |
| The nearest sampling time to the current time , | |
| The consensus error of i-th agent | |
| The consensus error of system (2) | |
| The piecewise function |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Yi, C.; Feng, J.; Wang, J.; Zhao, Y. Consensus Control for Stochastic Multi-Agent Systems with Markovian Switching via Periodic Dynamic Event-Triggered Strategy. Axioms 2024, 13, 694. https://doi.org/10.3390/axioms13100694
Luo X, Yi C, Feng J, Wang J, Zhao Y. Consensus Control for Stochastic Multi-Agent Systems with Markovian Switching via Periodic Dynamic Event-Triggered Strategy. Axioms. 2024; 13(10):694. https://doi.org/10.3390/axioms13100694
Chicago/Turabian StyleLuo, Xue, Chengbo Yi, Jianwen Feng, Jingyi Wang, and Yi Zhao. 2024. "Consensus Control for Stochastic Multi-Agent Systems with Markovian Switching via Periodic Dynamic Event-Triggered Strategy" Axioms 13, no. 10: 694. https://doi.org/10.3390/axioms13100694
APA StyleLuo, X., Yi, C., Feng, J., Wang, J., & Zhao, Y. (2024). Consensus Control for Stochastic Multi-Agent Systems with Markovian Switching via Periodic Dynamic Event-Triggered Strategy. Axioms, 13(10), 694. https://doi.org/10.3390/axioms13100694








