On High-Order Runge–Kutta Pairs for Linear Inhomogeneous Problems
Abstract
1. Introduction
2. RK Methods and Rooted Trees Theory
2.1. Expansions of Taylor Series
2.2. Trees and Rooted Trees
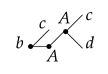 |
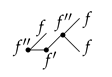 |
3. Derivation of the New Pairs
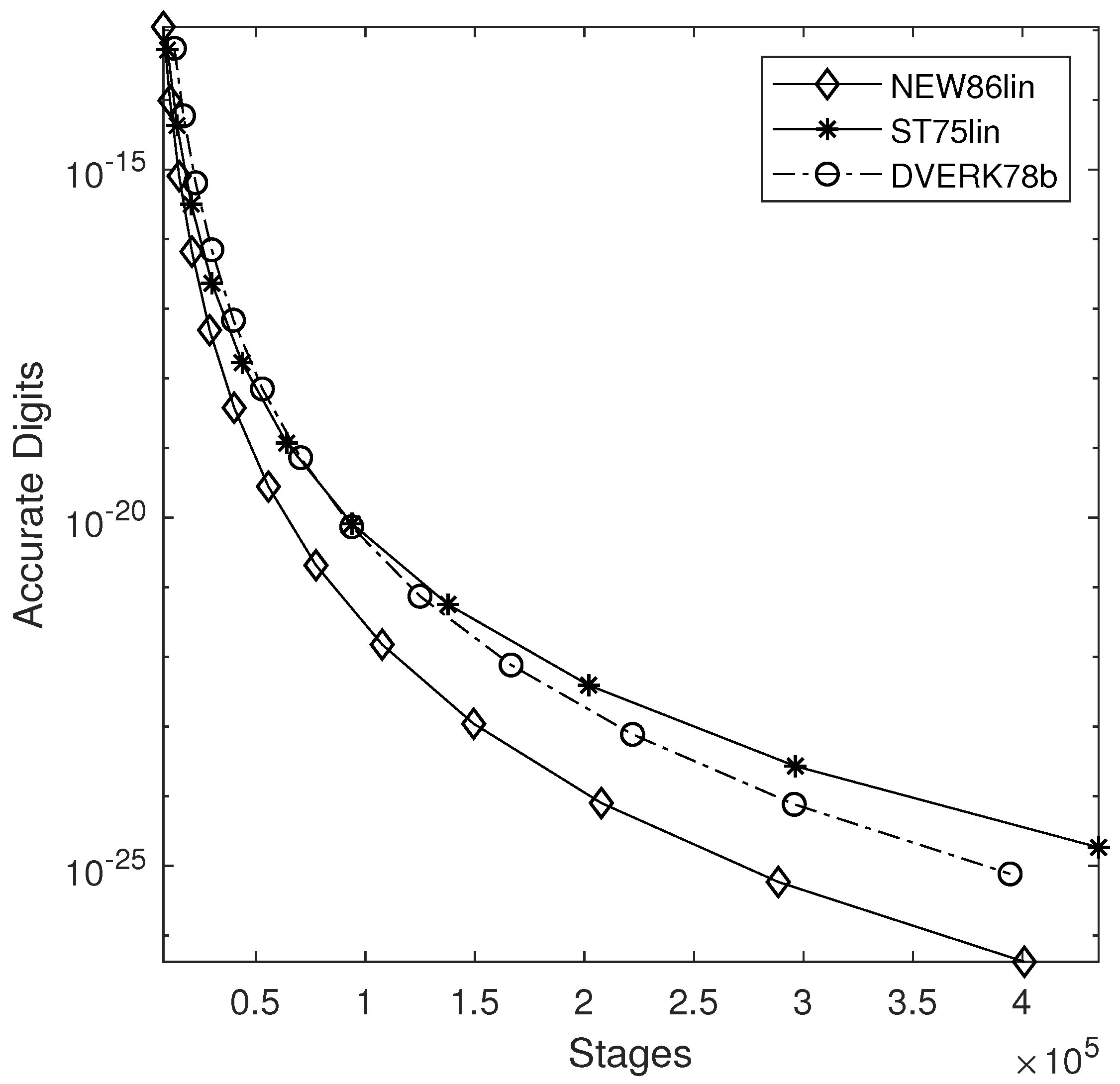
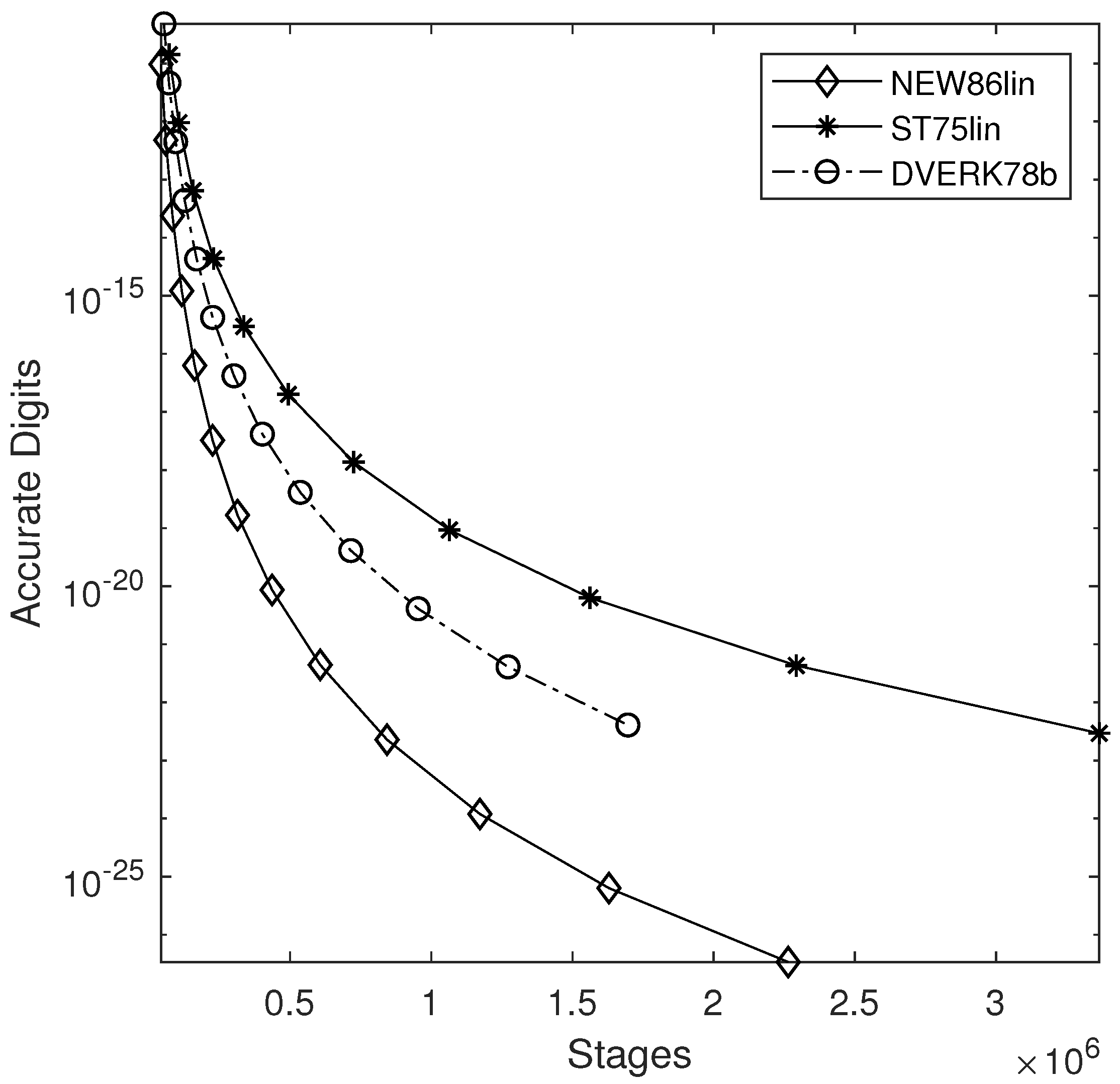
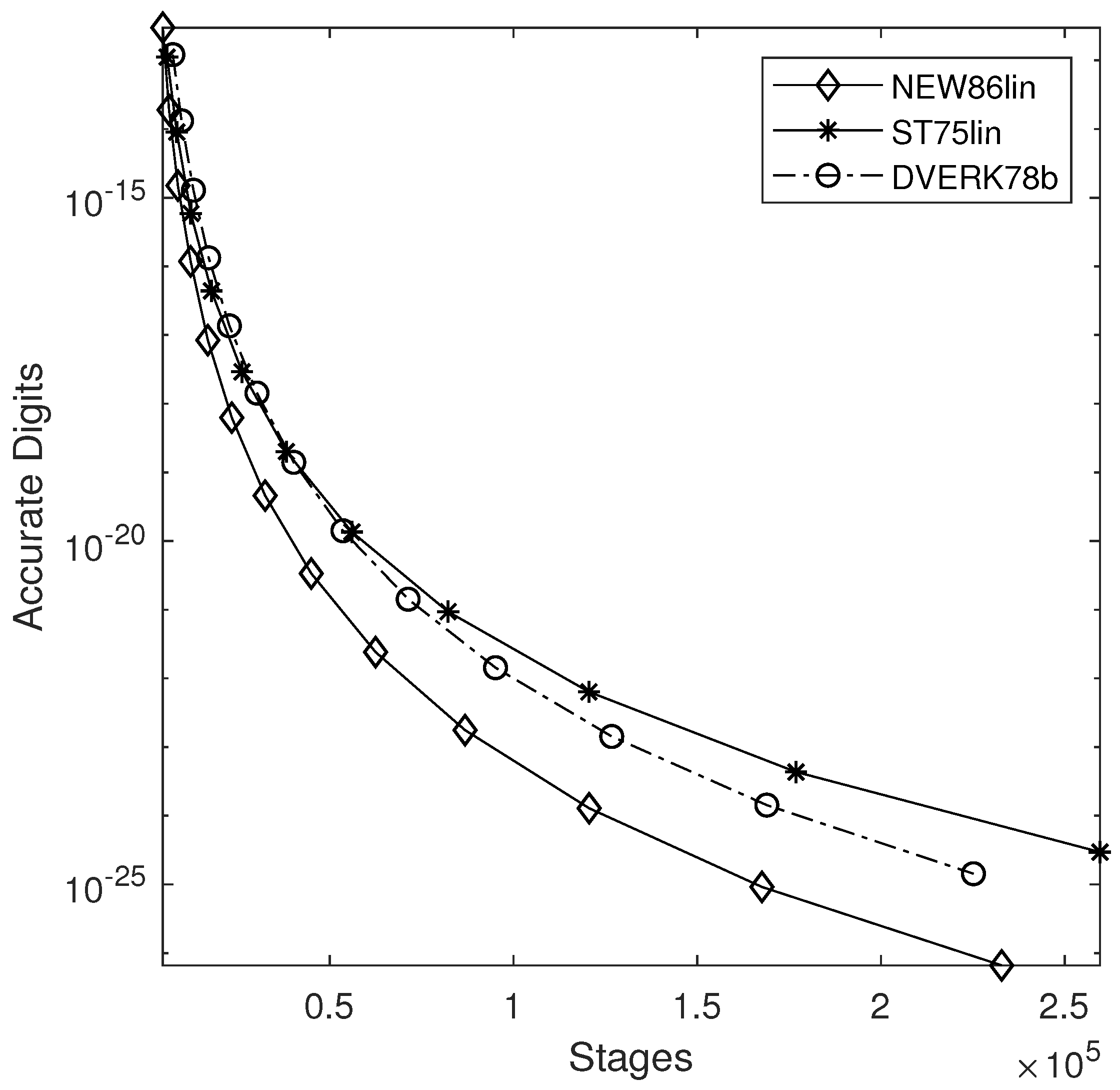
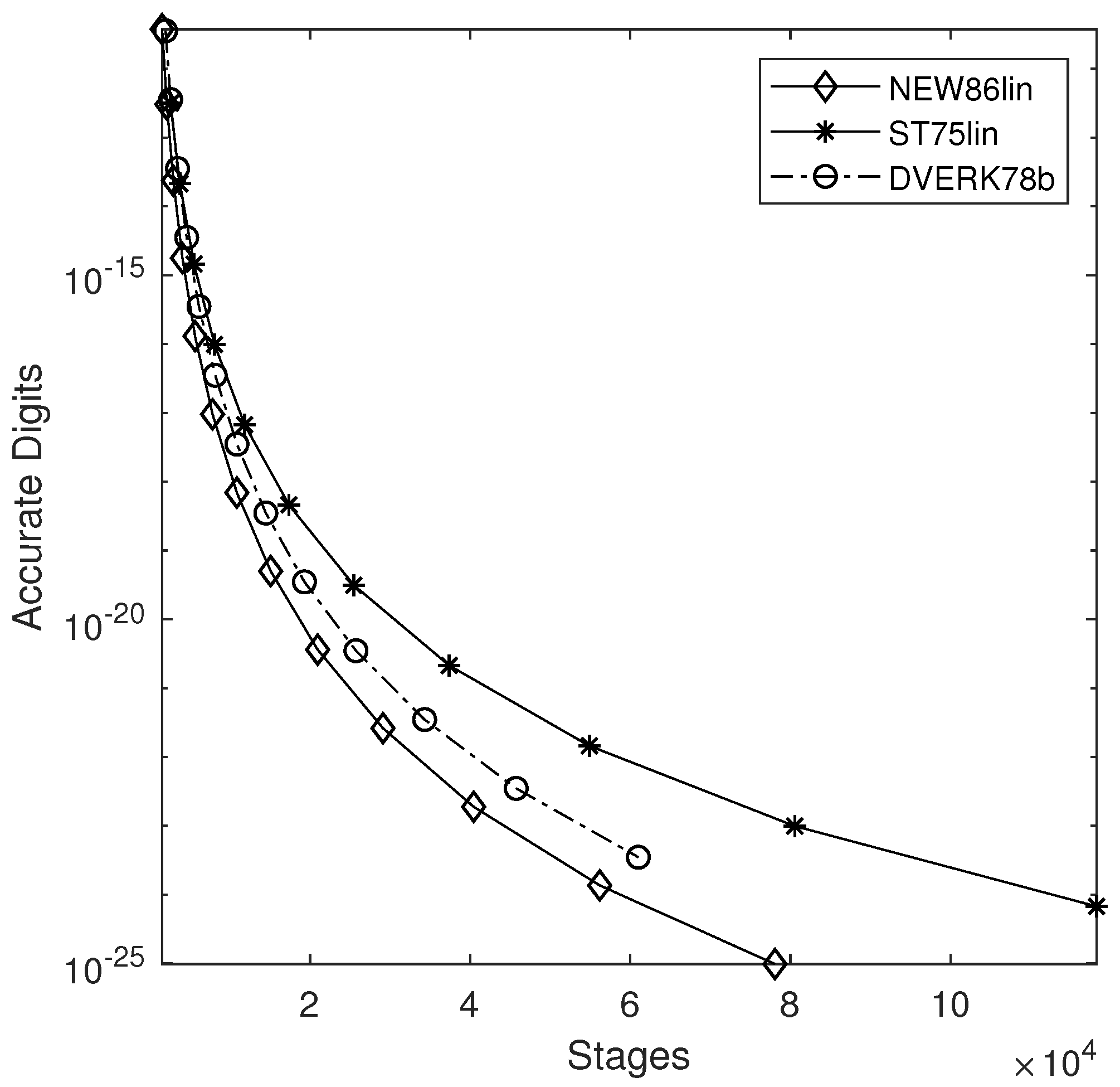
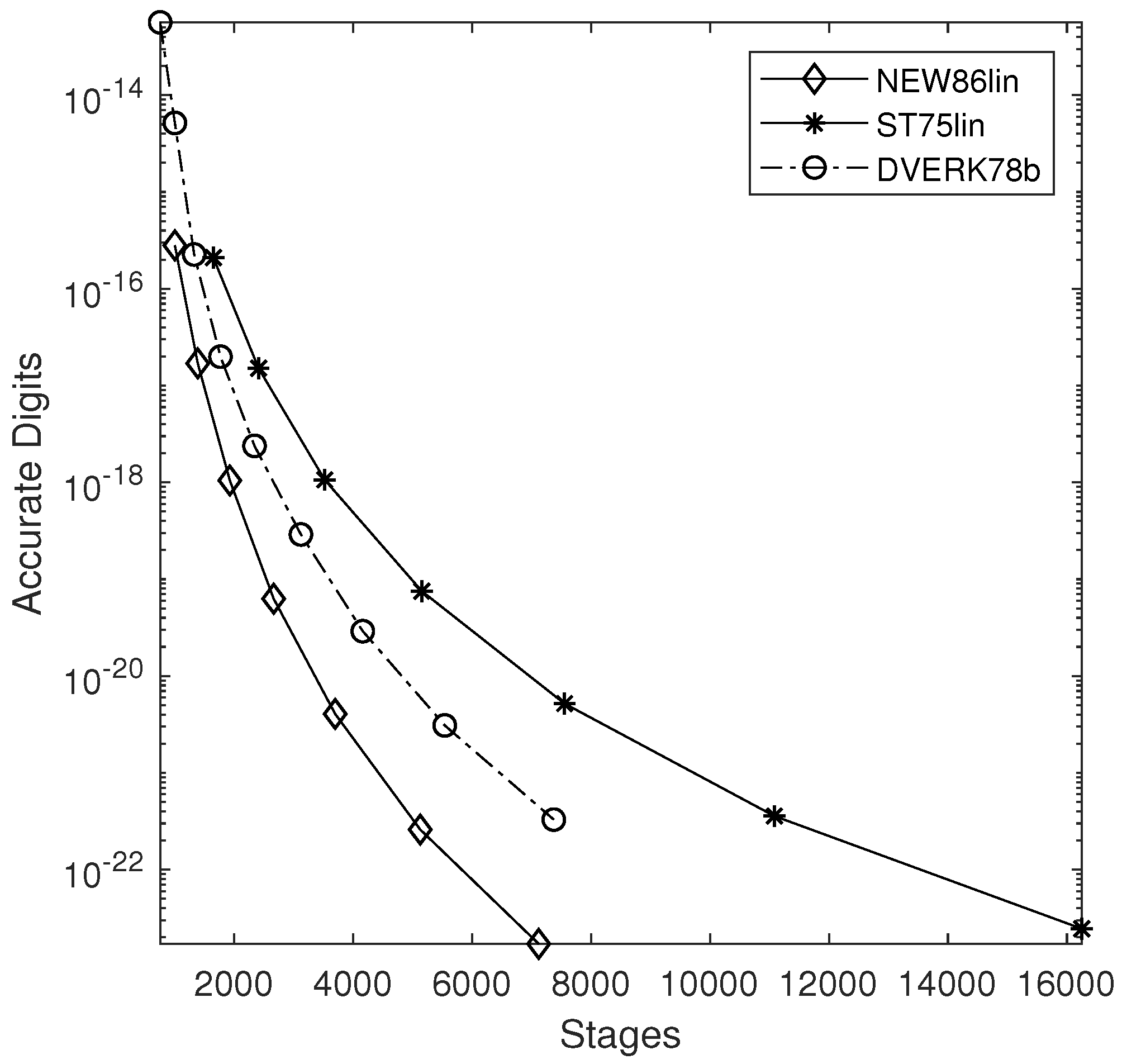
4. Numerical Results
- DVERK78b: 13 stages pair of orders proposed in [26].
- NEW8(6)lin: Effectively 10 stages FSAL pair given in Table 3.
- 1.
- Scalar
- Equation:
- Initial values:
- Interval of integration:
- Exact Solution:
- 2.
- Linear Inhomogeneous
- Equation:
- Initial values:
- Interval of integration:
- Exact solution:
- 3.
- Simple system
- Equation:
- Initial values:
- Interval of integration:
- Exact solution:
- 4.
- Vibratory system
- Equation:
- as described in [30].
- Initial values: ,
- Interval of integration:
- Exact solution at the end point (found by a very accurate integration at tolerance using Mathematica):
- 5.
- Larger system
- Equation:
- Initial values:
- Interval of integration:
- Exact solution at the end point (found by a very accurate integration at tolerance using Mathematica):
- In[6]:= Needs[“DifferentialEquations‘NDSolveProblems’”];
- Needs[“DifferentialEquations‘NDSolveUtilities’”];
- In[8]:= T86={“ExplicitRungeKutta”,“Coefficients”->T86Coefficients,
- “DifferenceOrder”->8,“StiffnessTest”->False};
- In[9]:= system=NDSolveProblem[{{y’[t]==-10*y[t]+Cos[t]},{y[0]==1},
- {y[t]},{t,0,10*Pi},{},{},{}}];
- refsol={10/101};
- CompareMethods[system,refsol,{T86},WorkingPrecision->33,
- AccuracyGoal->22,PrecisionGoal->22]
- Out[11]= {{{36439,4},400875,4.170180*10^-27}}
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kovalnogov, V.N.; Fedorov, R.V.; Karpukhina, T.V.; Evgenievich, C.Y.; Simos, T.E.; Tsitouras, C. An Algorithmic approach to Runge–Kutta–Nystrom pairs. TWMS J. Pure Appl. Math. 2023, 14, 3–22. [Google Scholar]
- Li, R.; Lin, R.-L.; Simos, T.E.; Tsitouras, C. A novel approach on high order Runge-Kutta-Nystrom error estimators. Appl. Comput. Math. 2023, 22, 246–258. [Google Scholar]
- Simos, T.E.; Tsitouras, C.; Famelis, I.T. Explicit Numerov Type Methods with Constant Coefficients: A Review. Appl. Comput. Math. 2017, 16, 89–113. [Google Scholar]
- Simos, T.E.; Tsitouras, C. High phase–lag order, four–step methods for solving y″ = f(x,y). Appl. Comput. Math. 2018, 17, 307–316. [Google Scholar]
- Shampine, L.F. Cheaper integration of linear systems. Simulation 1973, 20, 17. [Google Scholar] [CrossRef]
- England, R. Error estimates for Runge–Kutta type solutions of systems of ordinary differential equations. Comput. J. 1969, 12, 166–170. [Google Scholar] [CrossRef]
- Enright, W.H. The efficient solution of linear constant-coefficient systems of differential equations. Simulation 1978, 30, 129–133. [Google Scholar] [CrossRef]
- Zingg, D.W.; Chisholm, T.T. Runge-Kutta methods for linear ordinary differential equations. Appl. Numer. Math. 1999, 31, 227–238. [Google Scholar] [CrossRef]
- Butcher, J.C. Implicit Runge-Kutta processes. Math. Comput. 1964, 18, 50–64. [Google Scholar]
- Butcher, J.C. On Runge-Kutta processes of high order. J. Austral. Math. Soc. 1964, 4, 179–194. [Google Scholar] [CrossRef]
- Tsitouras, C.; Papakostas, S.N. Cheap error estimation for Runge-Kutta methods. SIAM J. Sci. Comput. 1999, 20, 2067–2088. [Google Scholar] [CrossRef]
- Simos, T.E.; Tsitouras, C. Evolutionary derivation of Runge-Kutta pairs for addressing inhomogeneous linear problems. Numer. Algor. 2021, 21, 511–525. [Google Scholar] [CrossRef]
- Lambert, J.D. Numerical Methods for ODEs; Wiley: Chichester, UK, 1991. [Google Scholar]
- Butcher, J.C. The Numerical Analysis of ODEs: Runge-Kutta and General Linear Methods; Wiley: Chichester, UK, 1987. [Google Scholar]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Fehlberg, E. Low Order Classical Runge-Kutta Formulas with Step-Size Control and Their Application to Some Heat Transfer Problems; NASA Tech. Rep. TR R-315; NASA Marshall Space Flight Center: Huntsville, AL, USA, 1969.
- Shampine, L.F. Some practical Runge–Kutta formulas. Math. Comput. 1986, 46, 135–150. [Google Scholar]
- Houwen, P.J.V.D.; Sommeijer, B.P. Explicit Runge-Kutta-Nyström methods with reduced phase errors for computing oscillating solutions. SIAM J. Numer. Anal. 1987, 24, 595–617. [Google Scholar] [CrossRef]
- Chawla, M.M.; Rao, P.S. An explicit sixth-order method with phase-iag of order eight for y″ = f(x,y). J. Comput. Appl. Math. 1987, 17, 365–368. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-540-20950-8. [Google Scholar]
- Feoktistov, V. Differential Evolution: In Search of Solutions; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-0-387-36895-5. [Google Scholar]
- Wolfram Research, Inc. Mathematica, Version 11.3.0; Wolfram Research, Inc.: Champaign, IL, USA, 2018. [Google Scholar]
- NDSolve: Mathematica Function. Available online: https://reference.wolfram.com/language/ref/NDSolve.html?q=NDSolve (accessed on 17 March 2025).
- “ExplicitRungeKutta” for NDSolve. Available online: https://reference.wolfram.com/language/tutorial/NDSolveExplicitRungeKutta.html (accessed on 17 March 2025).
- Verner, J.H. Available online: https://www.sfu.ca/~jverner/RKV87.IIa.Robust.00000754677.081208.FLOAT40OnWeb (accessed on 17 March 2025).
- Verner, J.H. Numerically optimal Runge–Kutta pairs with interpolants. Numer. Algor. 2010, 53, 383–396. [Google Scholar] [CrossRef]
- MATLAB, version R2019b; The Mathworks, Inc.: Natick, MA, USA, 2019.
- ode78: Matlab Function. Available online: https://www.mathworks.com/help/matlab/ref/ode78.html (accessed on 17 March 2025).
- Low, K.H. Displacement and Frequency analyses of vibratory systems. Comput. Struct. 1995, 54, 743–755. [Google Scholar] [CrossRef]
| Order Conditions | Elementary Differential | Valid for (2) |
|---|---|---|
| OK | ||
| OK | ||
| OK | ||
| OK | ||
| OK | ||
| OK | ||
| no | ||
| OK | ||
| OK | ||
| no | ||
| no | ||
| no | ||
| no | ||
| OK | ||
| no | ||
| OK | ||
| OK |
| , | ||
| In[1]:= T86bvec={314527/4021920,0,0,5727/1232,−87349/5670,45545/1764,−1227/49, 93395/6048,−2543/378,1730048/829521,1/10,0}; T86amat={{1/5},{3/40,9/40}, {−40355761601083472/266140230441105939,379205628299487986/443567050735176565, −80711523202166944/266140230441105939}, {−695463111469361764/1500196446724802203,1260442490511067231/788875102592301206, −270448114268444353/457441976633771789,−27251633927536895/634169504640478649}, {−324985794948140570/279362987511647517,2067789770618503777/539709130919242078, −1024281445080204601/271760704640117271,1267426191530190207/414089865092880655, −312635769063330587/229931829445938805}, {−1991868306773221465/988006971090061434,2066883310365527951/280309913359190828, −1149915980509893214/105627821090836979,5877046745400870627/551178302290848343, −2307633641349644207/534928889341982614,−19336393482604757/161379954985036024}, {3421988792443320320/409958906743348487,−7719526057460011553/583879427237260871, −14327944929325885917/974705522708371870,5169381944138214741/193127113008949648, −3485110191323692511/454226838873771266,954500654845243233/243523757961617086, −1194811460443290403/452590789241887404}, {17264226447133602112/272996897031641451,−32295720487824629515/241904388356288873, 2953206026652849252/303413816706367747,12956688961776592125/220733668141103896, −52264594687490789/8300814588386032,8242534511359177399/334193487031316324, −3550153210913076029/227155312778390915,−1532175456666191/388107427043540147}, {26688207385003289504/264585390926238097,−56507224747685848649/253583197096431440, 11428471378372210538/207643458100451045,22065085407467690258/509695469676088365, 1766268407864809339/156440651140379502,12163744429792102954/310450202476834919, −22159013041367309573/796071732134508657,1197252865130107127/509462498080681282, −63611354765744053/159614734793971724}, {114537892779893654389/192922971090262140,−510740282904871030564/415586341949265143, −47597666620490009567/897862996765222138,188835790411128503725/232069536271070424, −51119528850220842269/182287831866373472,168104550605285163532/542064106458782789, −35470180775173364810/256387766512111747,−3139869671811831263/170707935556822437, 206571767992602104/130392041890225475,865024/829521}, {314527/4021920,0,0,5727/1232,−87349/5670,45545/1764,−1227/49,93395/6048,−2543/378, 1730048/829521,1/10}}; T86cvec={1/5,3/10,2/5,1/2,3/5,7/10,4/5,9/10,19/20,1,1}; T86evec= {−2193001/205922304,0,0,27567979/14192640,−6553007/725760,8277295/451584, −11701679/564480,21853871/1548288,−6452/945,35430481/16590420,1/8,−1/20}; T86Coefficients[8, p_] := N[{T86amat, T86bvec, T86cvec, T86evec}, p]; |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jerbi, H.; Maali, S.; Aoun, S.B.; Aledaily, A.N.; Jeyamani, V.; Simos, T.E.; Tsitouras, C. On High-Order Runge–Kutta Pairs for Linear Inhomogeneous Problems. Axioms 2025, 14, 245. https://doi.org/10.3390/axioms14040245
Jerbi H, Maali S, Aoun SB, Aledaily AN, Jeyamani V, Simos TE, Tsitouras C. On High-Order Runge–Kutta Pairs for Linear Inhomogeneous Problems. Axioms. 2025; 14(4):245. https://doi.org/10.3390/axioms14040245
Chicago/Turabian StyleJerbi, Houssem, Sanaa Maali, Sondess Ben Aoun, Arwa N. Aledaily, Vijipriya Jeyamani, Theodore E. Simos, and Charalampos Tsitouras. 2025. "On High-Order Runge–Kutta Pairs for Linear Inhomogeneous Problems" Axioms 14, no. 4: 245. https://doi.org/10.3390/axioms14040245
APA StyleJerbi, H., Maali, S., Aoun, S. B., Aledaily, A. N., Jeyamani, V., Simos, T. E., & Tsitouras, C. (2025). On High-Order Runge–Kutta Pairs for Linear Inhomogeneous Problems. Axioms, 14(4), 245. https://doi.org/10.3390/axioms14040245










