Elliptic Quaternion Matrices: Theory and Algorithms
Abstract
1. Introduction
2. Preliminaries
- (a)
- ,
- (b)
- ,
- (c)
- ,
- (d)
- .
3. Eigenvalues and Eigenvectors, Singular Value Decomposition, Pseudoinverse, and Least Squares Problem for EQ Matrices
3.1. EC Matrices
3.2. EQ Matrices
3.2.1. Algorithms
| Algorithm 1 This algorithm calculates the eigenvalues and eigenvectors of the EQ matrix . |
|
| Algorithm 2 This algorithm performs the singular value decomposition of the EQ matrix . |
|
| Algorithm 3 This algorithm calculates the pseudoinverse of the EQ matrix . |
|
| Algorithm 4 This algorithm calculates the minimum norm least squares solution of the EQ matrix equation . |
|
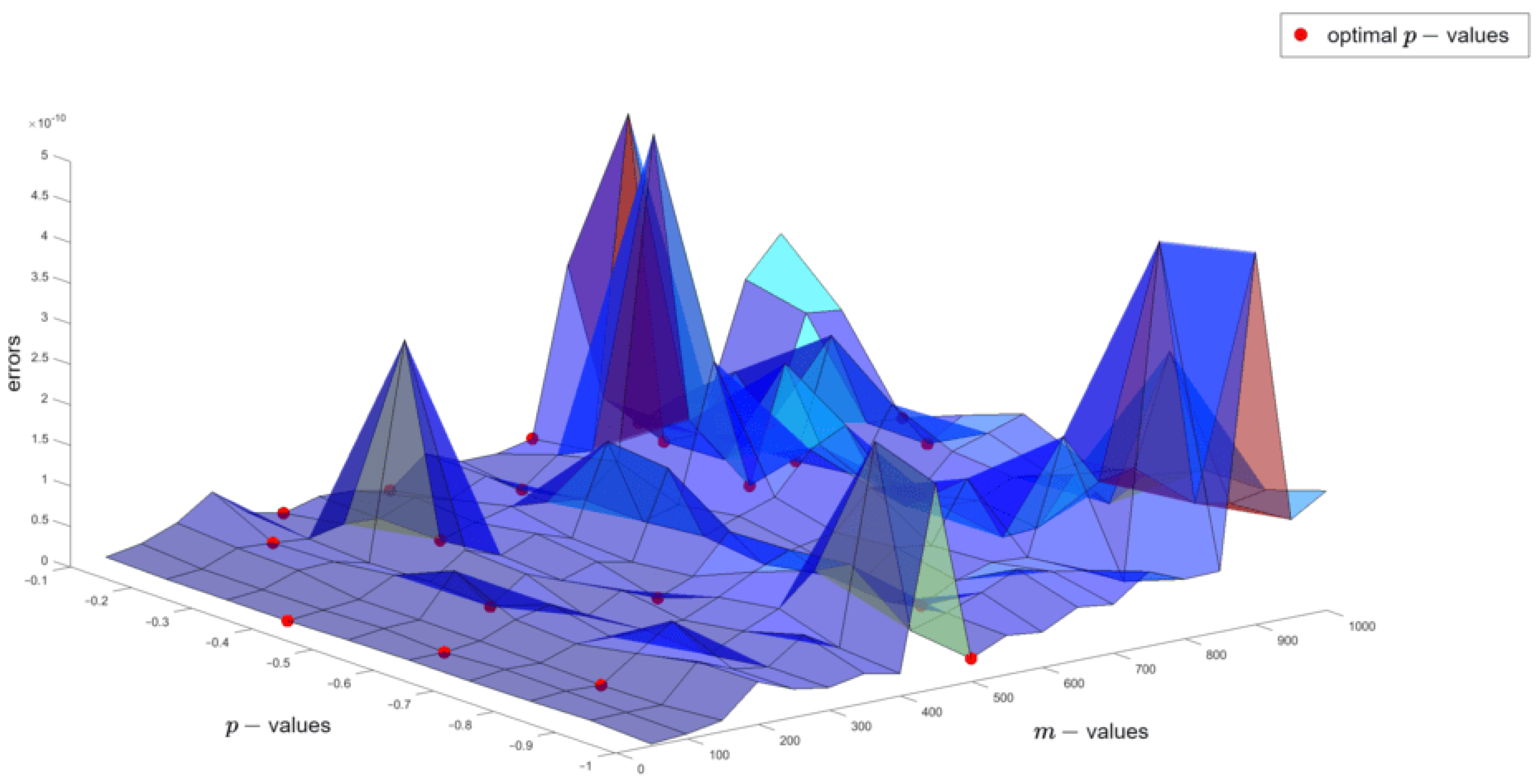
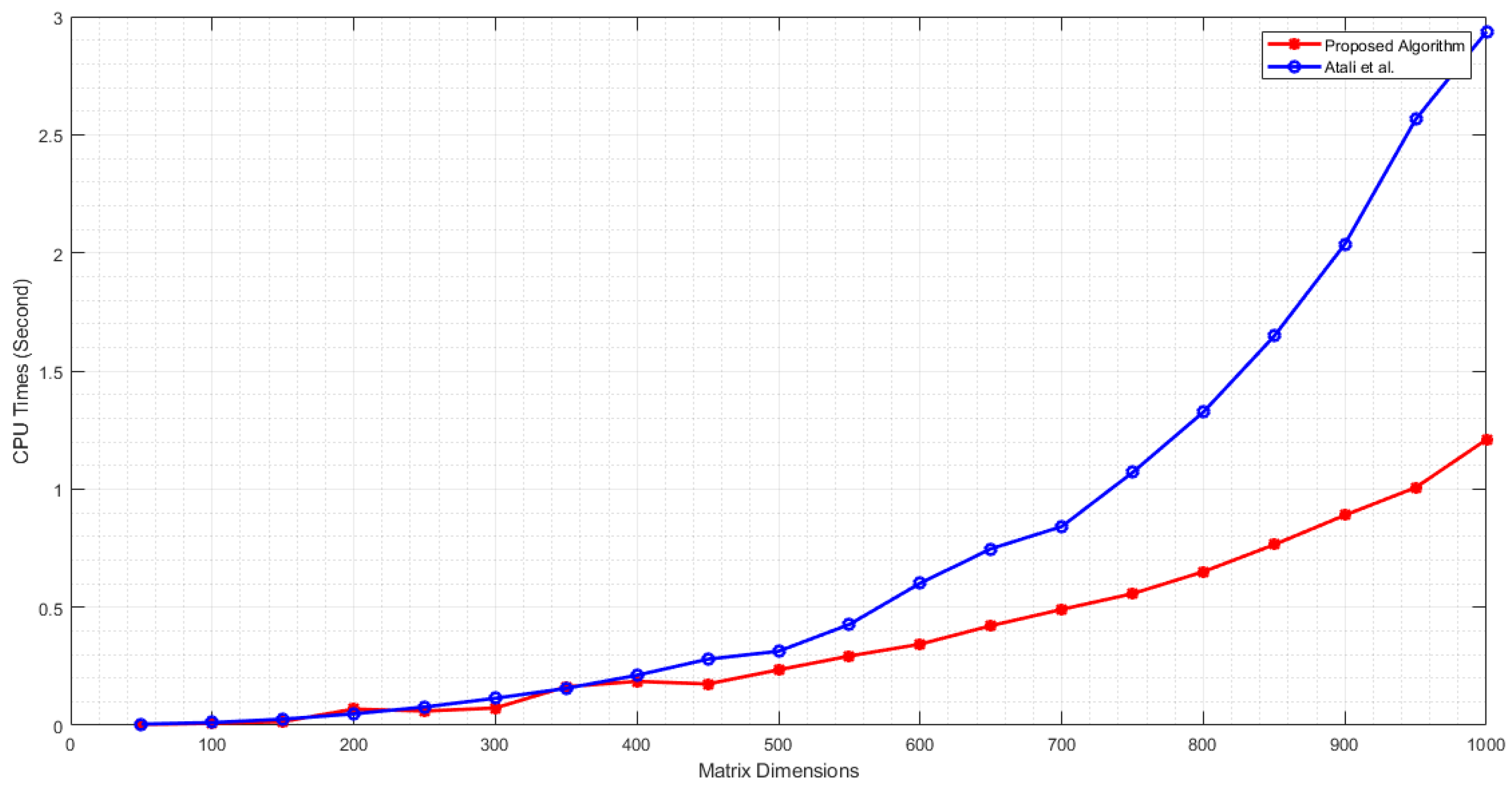
3.2.2. Numerical Examples
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ben-Israel, A.; Greville, T.N. Generalized Inverses: Theory and Applications; Springer Science Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Samar, M.; Li, H.; Wei, Y. Condition numbers for the K-weighted pseudoinverse and their statistical estimation. Linear Multilinear Algebra 2021, 69, 752–770. [Google Scholar] [CrossRef]
- Samar, M.; Zhu, X.; Xu, H. Conditioning Theory for -Weighted Pseudoinverse and -Weighted Least Squares Problem. Axioms 2021, 13, 345. [Google Scholar] [CrossRef]
- Simsek, S. Least-squares solutions of generalized Sylvester-type quaternion matrix equations. Adv. Appl. Clifford Algebr. 2023, 33, 28. [Google Scholar] [CrossRef]
- Dian, R.; Li, S.; Kang, X. Regularizing hyperspectral and multispectral image fusion by CNN denoiser. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1124–1135. [Google Scholar] [CrossRef] [PubMed]
- Hashemipour, N.; Aghaei, J.; Kavousi-Fard, A.; Niknam, T.; Salimi, L.; del Granado, P.C.; Shafie-Khah, M.; Wang, F.; Catalão, J.P.S. Optimal Singular value decomposition based big data compression approach in smart grids. IEEE Trans. Ind. Appl. 2021, 32, 1124–1135. [Google Scholar] [CrossRef]
- Wang, Y.C.; Zhu, L. Research and implementation of SVD in machine learning. In Proceedings of the 2017 IEEE/ACIS 16th International Conference on Computer and Information Science, Wuhan, China, 24–26 May 2017; pp. 471–475. [Google Scholar]
- Harkin, A.A.; Harkin, J.B. Geometry of generalized complex numbers. Math. Mag. 2004, 77, 118–129. [Google Scholar] [CrossRef]
- Catoni, F.; Cannata, R.; Zampetti, P. An introduction to commutative quaternions. Adv. Appl. Clifford Algebr. 2006, 16, 1–28. [Google Scholar] [CrossRef]
- Yaglom, I.M. A Simple Non-Euclidean Geometry and Its Physical Basis; Springer: New York, NY, USA, 1979. [Google Scholar]
- Condurache, D.; Burlacu, A. Dual tensors based solutions for rigid body motion parameterization. Mech. Mach. Theory 2014, 74, 390–412. [Google Scholar] [CrossRef]
- Ozdemir, M. An alternative approach to elliptical motion. Adv. Appl. Clifford Algebr. 2016, 26, 279–304. [Google Scholar] [CrossRef]
- Dundar, F.S.; Ersoy, S.; Pereira, N.T.S. Bobillier formula for the elliptical harmonic motion. An. St. Univ. Ovidius Constanta 2018, 26, 103–110. [Google Scholar] [CrossRef]
- Derin, Z.; Gungor, M.A. Elliptic biquaternionic equations of gravitoelectromagnetism. Math. Methods Appl. Sci. 2022, 45, 4231–4243. [Google Scholar] [CrossRef]
- Catoni, F.; Cannata, R.; Zampetti, P. An introduction to constant curvature spaces in the commutative (Segre) quaternion geometry. Adv. Appl. Clifford Algebr. 2006, 16, 85–101. [Google Scholar] [CrossRef]
- Guo, L.; Zhu, M.; Ge, X. Reduced biquaternion canonical transform, convolution and correlation. Signal Process. 2011, 91, 2147–2153. [Google Scholar] [CrossRef]
- Yuan, S.F.; Tian, Y.; Li, M.Z. On Hermitian solutions of the reduced biquaternion matrix equation (AXB, CXD) = (E, G). Linear Multilinear Algebra 2020, 68, 1355–1373. [Google Scholar] [CrossRef]
- Tosun, M.; Kosal, H.H. An algorithm for solving the Sylvester s-conjugate elliptic quaternion matrix equations. In Algorithms as a Basis of Modern Applied Mathematics; Hošková-Mayerová, Š., Flaut, C., Maturo, F., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 279–292. [Google Scholar]
- Gai, S.; Huang, X. Reduced biquaternion convolutional neural network for color image processing. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 1061–1075. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, D.; Vasiliev, V.I.; Jiang, T. Algebraic techniques for Maxwell’s equations in commutative quaternionic electromagnetics. Eur. Phys. J. Plus 2022, 137, 577–1075. [Google Scholar]
- Atali, G.; Kosal, H.H.; Pekyaman, M. A new image restoration model associated with special elliptic quaternionic least-squares solutions based on LabVIEW. J. Comput. Appl. Math. 2023, 425, 115071. [Google Scholar] [CrossRef]
- Catoni, F.; Boccaletti, D.; Cannata, R.; Catoni, V.; Nichelatti, E.; Zampetti, P. The Mathematics of Minkowski Space–Time: With an Introduction to Commutative Hypercomplex Numbers; Birkhäuser: Basel, Switzerland, 2008. [Google Scholar]
- Surekci, A.; Kosal, H.H.; Gungor, M.A. A Note on Gershgorin disks in the elliptic plane. J. Math. Sci. Model. 2021, 4, 104–109. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kösal, H.H.; Kişi, E.; Akyiğit, M.; Çelik, B. Elliptic Quaternion Matrices: Theory and Algorithms. Axioms 2024, 13, 656. https://doi.org/10.3390/axioms13100656
Kösal HH, Kişi E, Akyiğit M, Çelik B. Elliptic Quaternion Matrices: Theory and Algorithms. Axioms. 2024; 13(10):656. https://doi.org/10.3390/axioms13100656
Chicago/Turabian StyleKösal, Hidayet Hüda, Emre Kişi, Mahmut Akyiğit, and Beyza Çelik. 2024. "Elliptic Quaternion Matrices: Theory and Algorithms" Axioms 13, no. 10: 656. https://doi.org/10.3390/axioms13100656
APA StyleKösal, H. H., Kişi, E., Akyiğit, M., & Çelik, B. (2024). Elliptic Quaternion Matrices: Theory and Algorithms. Axioms, 13(10), 656. https://doi.org/10.3390/axioms13100656





