Abstract
In this paper, we introduce the “Walk on Equations” (WE) Monte Carlo algorithm, a novel approach for solving linear algebraic systems. This algorithm shares similarities with the recently developed WE MC method by Ivan Dimov, Sylvain Maire, and Jean Michel Sellier. This method is particularly effective for large matrices, both real- and complex-valued, and shows significant improvements over traditional methods. Our comprehensive comparison with the Gauss–Seidel method highlights the WE algorithm’s superior performance, especially in reducing relative errors within fewer iterations. We also introduce a unique dominancy number, which plays a crucial role in the algorithm’s efficiency. A pivotal outcome of our research is the convergence theorem we established for the WE algorithm, demonstrating its optimized performance through a balanced iteration matrix. Furthermore, we incorporated a sequential Monte Carlo method, enhancing the algorithm’s efficacy. The most-notable application of our algorithm is in solving a large system derived from a finite-element approximation in constructive mechanics, specifically for a beam structure problem. Our findings reveal that the proposed WE Monte Carlo algorithm, especially when combined with sequential MC, converges significantly faster than well-known deterministic iterative methods such as the Jacobi method. This enhanced convergence is more pronounced in larger matrices. Additionally, our comparative analysis with the preconditioned conjugate gradient (PCG) method shows that the WE MC method can outperform traditional methods for certain matrices. The introduction of a new random variable as an unbiased estimator of the solution vector and the analysis of the relative stochastic error structure further illustrate the potential of our novel algorithm in computational mathematics.
MSC:
60J22; 62P12; 65C05; 68W20
1. Introduction
Linear systems play a pivotal role in various fields of mathematics, science, engineering, and technology, showcasing their fundamental significance [1,2,3,4,5]. The study and solution of linear systems of algebraic equations provide a versatile framework for modeling and analyzing a wide array of real-world phenomena [6,7,8,9,10,11,12,13,14]. These systems offer a structured approach to represent relationships and dependencies among variables, enabling the formulation of mathematical models for diverse applications, including physics, economics, biology, and computer science. Linear systems also serve as the foundation for understanding more-complex mathematical structures, paving the way for advanced techniques and methodologies in numerical analysis, optimization, and data analysis. The ability to efficiently solve linear systems is crucial for addressing practical problems, making them an indispensable tool in the toolkit of researchers, scientists, and engineers across various disciplines. Whether in simulating physical systems, optimizing resource allocation, or processing data, the significance of linear systems lies in their capacity to provide a systematic and powerful framework for problem-solving and decision-making.
Beyond their foundational role in mathematics, linear systems offer a practical and indispensable tool for solving real-world problems [15,16,17,18]. The linear nature of these systems simplifies their mathematical representation, making them particularly amenable to analytical and computational methods. In engineering, for instance, linear systems are pervasive in control theory, signal processing, and structural analysis. The ability to solve linear systems efficiently contributes to the design and optimization of systems ranging from electronic circuits to mechanical structures. Moreover, in economics and finance, linear models are frequently employed to analyze relationships between variables, aiding in decision-making processes. The significance of linear systems extends to scientific research, where they are utilized for data analysis, image processing, and simulations. In essence, the versatility and applicability of linear systems underscore their significance across a broad spectrum of disciplines, emphasizing their role as a cornerstone in the theoretical understanding and practical application of mathematical concepts in the real world.
The significance of linear systems transcends their mere existence as mathematical constructs; rather, they embody a fundamental and pervasive concept with profound implications across various domains of human inquiry. At its core, a linear system encapsulates relationships, dependencies, and interactions within a structured framework, providing a mathematical language to express and decipher complex phenomena. In physics, the laws governing many natural phenomena exhibit linearity, allowing scientists to model and predict behavior. In the intricate world of engineering, linear systems are the backbone of control theory, enabling the design of stable and efficient systems, whether in aerospace engineering or telecommunications.
Moreover, linear systems [19,20,21] serve as a gateway to understanding more-sophisticated mathematical structures. The study of linear algebra and the solutions to linear systems lay the groundwork for advanced mathematical techniques that underpin numerical analysis, optimization, and statistical modeling. In essence, linear systems act as a bridge between theoretical abstraction and real-world problem-solving, facilitating a deeper comprehension of intricate mathematical concepts. The practical implications of efficiently solving linear systems are profound. From the optimization of resource allocation in logistics to the simulation of complex physical processes, the ability to navigate and manipulate linear systems empowers researchers and engineers to tackle challenges of increasing complexity. In economics, linear models elucidate intricate relationships within financial systems, offering insights crucial for informed decision-making.
Linear Algebraic Equations (LAEs) [22,23,24,25] establish the fundamental scaffolding for an array of scientific and engineering pursuits, effectively translating abstract concepts into tangible, real-world applications. Whether navigating intricate simulations in the realm of computational fluid dynamics or delving into intricate optimizations within the field of structural engineering, LAEs provide a mathematical prism that allows us to not only comprehend but also address a diverse range of complex challenges. As computational power continues to burgeon and the intricacy of problems intensifies, attention has gravitated towards large-scale LAEs. These expansive systems not only push the boundaries of analytical methods but also necessitate a computational infrastructure capable of grappling with their sheer magnitude. Within these vast systems lie intricate interrelationships and voluminous datasets, amplifying the critical nature and complexity of their resolution. Successfully addressing these extensive systems often hinges on the application of sophisticated stochastic techniques, highlighting the necessity for advanced and nuanced approaches [26,27].
LAEs serve as a foundational framework in mathematics and its applications, enabling the modeling and analysis of diverse systems and phenomena. The widespread use of LAEs underscores their significance as a foundational and unifying mathematical framework. As computational power continues to advance, the application of linear algebra in interdisciplinary research and problem-solving is likely to expand, further cementing its role as an indispensable tool in both theoretical and applied mathematics. Their broad applicability and the development of specialized techniques for their solution make them a central topic in both theoretical and applied mathematics. The application of linear algebraic equations extends across a wide array of fields, demonstrating their versatility in addressing complex problems and providing essential tools for understanding, modeling, and solving diverse systems and phenomena. Here are some broader perspectives on the applications of LAEs [28,29,30,31,32].
In engineering disciplines, LAEs are fundamental to the analysis and design of structures, circuits, and mechanical systems. They play a pivotal role in solving problems related to fluid dynamics, heat transfer, and electrical networks. In physics, linear algebra is essential for describing quantum mechanics, classical mechanics, and the behavior of physical systems. Linear algebra is at the core of many algorithms and techniques in computer science. From image processing and computer graphics to machine learning and artificial intelligence, linear algebraic equations are used for tasks like image transformation, data representation, and solving systems of equations arising in algorithmic processes. LAEs are applied in economic modeling and financial analysis. Systems of linear equations are used to model economic relationships, optimize resource allocation, and analyze market trends. Techniques such as input-output analysis and linear programming rely on linear algebraic methods. Linear algebra is a fundamental tool in statistics and data analysis. Methods such as linear regression, principal component analysis, and singular value decomposition involve solving and manipulating systems of linear equations. These techniques are crucial for extracting meaningful information from large datasets. LAEs play a central role in optimization problems and control systems engineering. Techniques like linear programming and control theory heavily rely on linear algebraic methods to optimize processes, design controllers, and ensure stability in dynamic systems. Cryptography, the science of secure communication, employs linear algebra in areas such as coding theory and the design of encryption algorithms. Techniques like error-correcting codes and cryptographic protocols often involve solving linear algebraic equations to ensure the security and integrity of transmitted information. LAEs find applications in biomedical imaging, genetics, and bioinformatics. Techniques like image reconstruction in medical imaging, genetic mapping, and the analysis of biological networks involve solving linear systems to interpret and understand complex biological phenomena. Environmental scientists use LAEs to model and analyze environmental systems. This includes studying the flow of pollutants in ecosystems, analyzing climate models, and optimizing resource management strategies to address environmental challenges.
Monte Carlo (MC) algorithms [33,34,35] for LAPs leverage probabilistic sampling techniques to address challenges associated with large-scale linear systems. These algorithms are particularly useful when traditional methods become computationally expensive or impractical. MC methods are often incorporated into randomized numerical linear algebra algorithms. These methods introduce randomness into the computation, allowing for efficient approximations of matrix factorizations and solutions to linear systems. These techniques are useful for tasks like low-rank approximation, singular value decomposition, and solving linear systems. MC algorithms for LAPs can be applied to solve systems of linear equations. Instead of directly computing the solution, these algorithms use random sampling to approximate the solution or components of the solution vector. This is especially advantageous when dealing with large and sparse matrices. MC integration techniques are adapted for LAPs, where the goal is to approximate integrals involving high-dimensional vectors or matrices. This approach involves random sampling to estimate expectations or integrals, offering a stochastic alternative to deterministic methods. In some applications, matrices involved in linear algebraic problems are too large to be explicitly formed or stored. Matrix-free MC methods address this challenge by performing matrix-vector products on-the-fly, utilizing random samples to compute these products without explicitly representing the entire matrix. MC algorithms provide a stochastic approximation framework for solving LAPs. By iteratively updating the solution based on random samples, these algorithms converge to an approximate solution over multiple iterations. This approach is particularly relevant for large-scale problems where deterministic methods may be impractical. MC algorithms naturally lend themselves to estimating errors and confidence intervals in the computed solutions. By generating multiple random samples and observing the variability in the results, these algorithms provide insights into the uncertainty associated with the computed solution. MC algorithms for LAPs are well-suited for parallel and distributed computing environments. The inherent randomness and independence of MC samples make it possible to perform computations concurrently, improving the scalability of these algorithms for large-scale problems. MC techniques for LAPs find applications in data science and machine learning, especially in tasks involving large datasets and high-dimensional spaces. These algorithms are used for tasks such as approximating covariance matrices, solving linear regression problems, and conducting randomized dimensionality reduction. Some MC algorithms for LAEs incorporate adaptive sampling strategies, where the sampling distribution is adjusted based on the observed outcomes. This adaptability allows the algorithm to focus computational efforts on the most influential components of the problem. MC algorithms for LAPs provide a powerful and flexible approach to handling large-scale computations. Their stochastic nature and adaptability make them well-suited for addressing challenges in diverse fields, ranging from scientific computing to data-driven applications. As computational resources continue to advance, the role of MC methods in addressing complex LAPs is likely to expand further.
A comprehensive overview of these algorithms is provided in [36]. The renowned Power method [37] furnishes an evaluation for the main eigenvalue , employing the well-known Rayleigh quotient In [38], the authors delve into matrix powers’ bilinear forms, employing them to devise their solution. Both theoretical and experimental examinations delve into the algorithm’s robustness. It is elucidated that as perturbations in the entries of perfectly balanced matrices increase, both error and variance witness a corresponding escalation. Particularly, smaller matrices exhibit a heightened variance. As the power of A increases, a rise in the relative error becomes apparent.
Iterative Monte Carlo (IMC) methods [36,39,40] are a class of computational techniques that utilize iterative processes inspired by Monte Carlo (MC) simulations to solve complex problems, particularly those involving probabilistic or random elements. These methods are iterative in nature, meaning that they involve repeated cycles of computation to refine an estimate or solution. IMC methods are powerful tools that provide flexible and efficient solutions to a wide range of problems across different disciplines. Their ability to handle complex, high-dimensional problems makes them particularly valuable in situations where traditional analytical methods may be impractical or infeasible. As computational resources continue to advance, the application of Iterative Monte Carlo methods is likely to expand further, contributing to advancements in scientific research, optimization, and data-driven decision-making. IMC methods designed to solve LAEs (LAEs) can be conceptualized as truncated Markov chains [41]:
where each state for represents an absorbing state in the chain.
To devise an algorithm for assessing the minimal eigenvalue by modulus, denoted as , a matrix polynomial is essential. Here, represents binomial coefficients, and q serves as an acceleration parameter [23,42,43]. This approach aligns with a discrete analog of the resolvent analytical continuation method utilized in [44]. There are instances where the polynomial converges to the resolvent matrix [25,36,42]. Notably, implementing an acceleration parameter taking into account the resolvent is one avenue for reducing computational complexity. Alternatively, employing a variance reduction technique [45] serves to achieve the required solution approximation with fewer operations. The variance reduction technique proposed in [45] for eigenvalue calculations in particle transport utilizes MC approximations of fluxes. In [46], an unbiased estimator for solving linear algebraic systems (LAS) is introduced. This estimator is adept at finding specific components of the solution, accompanied by comprehensive results elucidating its quality and properties. The author leverages this estimator to establish error bounds and construct confidence intervals for the solution components. Furthermore, ref. [47] introduces a MC method for matrix inversion, rooted in the solution of simultaneous LAEs. In our subsequent exploration, insights from both [36,47] will be incorporated to demonstrate how the proposed algorithm can effectively approximate the inverse of a matrix.
2. Problem Formulation
Examine the subsequent LAP:
- Computing elements of the solution vector, which could involve a subset of components or all components.
- Assessing linear functionals of the solution.
- Performing matrix inversion.
- Determining the extremal eigenvalues.
Let A and B are matrices of size , i.e., .
where . Norms of vectors (-norm): and matrices Consider a matrix and a vector The matrix A can be treated as a linear operator ; the linear transformation determines a new vector in .
Suppose that this LAE is given:
Let the matrix , such that
D is a diagonal matrix is a parameter for accelerating the convergence. The system (2) can be expressed as:
where
Let’s assume that the matrix B exhibits diagonal dominance. However, it’s worth noting that the algorithms presented are applicable to a broader class of matrices, as demonstrated later. Specifically, if B is diagonally dominant, certain conditions on the matrix’ elements of A must be met:
2.1. Problem Settings
We shall consider the following problems.
Problem 1
where is a given matrix; and are given vectors.
(Evaluating the inner product).
of the solution of the LAS
It is feasible to select a non-singular matrix for which , is the identity matrix and , .
Then
It is taken into consideration that
- (i)
so, every value of for which
is met. If the criteria outlined in are satisfied, then a stationary linear iterative algorithm can be employed:
and the solution x could be expressed as known as von Neumann series.
Problem 2
(Assessing all components of the solution vector).
Here, we express the Equation (7) with , and likewise, .
Problem 3
(Inverting of matrices). This consists of computation: where a specified real matrix.
It is presupposed that
- (ii)
Here the subsequent iterative matrix: can be defined. When (ii) are met, can be expressed as
2.2. Almost Optimal Monte Carlo Algorithm
We will employ the algorithm known as the MAO algorithm. It is an algorithm that defines Almost Optimal Method (Method Almost Optimal, (MAO)) according the definition given by I. Dimov in [48].
Take an initial density vector , where and . Also, contemplate a matrix representing transition density , where and , for any . Establish sets of permissible densities and .
Definition 1.
The initial density vector is called permissible to the vector , i.e., , if
The transition density matrix is called permissible to the matrix , i.e., , if
In this study, we will focus on densities that adhere to the defined criteria. This strategy ensures that the generated random trajectories, designed to address the problems at hand, consistently avoid encountering elements with zero values in the matrix. This method not only reduces the computational intricacies of the algorithms but also proves advantageous, particularly when handling large sparse matrices.
Suppose we have a Markov chain:
with n states. The random trajectory (chain) of length k originating from the initial state , is specified as:
Here refers to the state selected, indicating .
Assume that
where represents the probability of the chain initiating in state , and is the transition probability to state after being in state . These probabilities collectively form a transition matrix P.
So our MAO WE algorithm, is configured with a distinctive selection of absorbing states, entails the presence of states denoted as .
The transition density matrix is designed in a way that , and the probability of absorption at each stage, excluding the initial one, is
.
2.3. Absorbing States Monte Carlo Algorithm
Rather than dealing with the finite random trajectory , we examine an infinite trajectory characterized by a state coordinate . Suppose if the trajectory is broken (absorbed) and otherwise. Let
Thus, equals 1 until the trajectory’s first termination, and thereafter, becomes 0.
It can be demonstrated that, given conditions (i) and (ii), these equalities hold:
3. Probabilistic Representation for the WE Algorithm
3.1. Simple Examples
- The positive case:. We also assume that .
Consider a system of two equations:
with unknowns and Clearly, we have , where
and , where
To estimate , we start with an initial score of 1 in our walk. Subsequently, we either terminate with a probability of since we already know the value of X (which is zero), or we proceed to approximate either or again with probabilities or . If the walk continues and the goal is to approximate , we add 2 to the current score. We then stop with a probability of or continue to approximate or again with a probability of . This procedure persists until either of the random variables X or Y reaches zero. The score increases incrementally during the walk as outlined. The score functions as an impartial estimator of , and by averaging scores obtained from independent walks, we derive the Monte Carlo estimation of .
This algorithm shares a striking similarity with those utilized in calculating Feynman-Kac boundary value problems’ representation, employing walks that are either discrete or continuous such as the discrete grids’ walk or the spheres method’ walk. At walk’ each step, the current position solution x corresponds to the anticipated value of the solution on a discrete or continuous set, potentially augmented by a source term. The pivotal concept is the double randomization principle, asserting that the expected solution on this set can be substituted by the solution at a randomly selected point, following the appropriate distribution.
3.2. Probabilistic Representation for Real Matrices
Consider a system , where and Define a Markov chain with states , with
if and
Let c be a vector defined as if and Represent as a random trajectory that initiates at the initial state and traverses through until reaching the absorbing state . The probability of following the trajectory is given by . Use the MAO algorithm: and for the transition density matrix . Define the weights:
The estimator can be expressed as with .
An example of the general MC method for LAP is shown on Figure 1. For the new algorithm the following theorem can be proved.
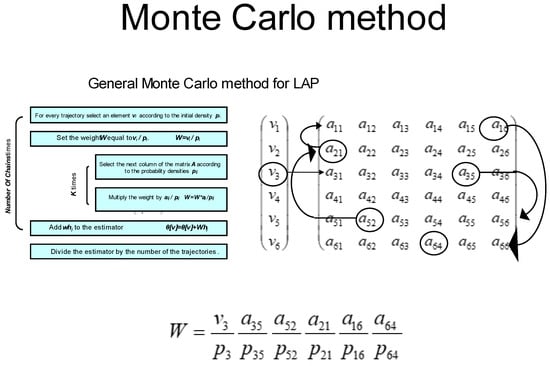
Figure 1.
MC-scheme explanation.
Theorem 1.
The random variable is an unbiased estimator of , i.e.,
Proof.
Since , the last sum is finite and
Thus,
□
The conjugate to random variable has the same mean value, i.e., . This could be established by the same technique used above.
Suppose it is possible to calculate N values of , namely . Taking into account as a MC approximation of the component of the solution. For the random variable one may prove [1]:
Theorem 2.
The random variable is an unbiased estimator of , i.e.,
and the variance vanishes when N goes to infinity, i.e.,
Proof.
The equation can be readily demonstrated by employing the mean value’s properties. Similarly, the validity of (22) can be established using the variance properties. □
Furthermore, by applying the Kolmogorov theorem and considering the independence of the sequences , which are also independently distributed with a finite mathematical expectation of , it can be shown that almost surely converges to :
The following theorem provides the composition of the variance in the proposed algorithm [1].
Theorem 3.
3.3. Balancing
The robustness of the MC algorithm is demonstrated in [38] with balanced matrices possessing matrix norms much smaller than 1, showcasing significant variance improvement compared to cases where matrices have norms close to 1. This underscores the crucial importance of input matrix balancing in MC computations, suggesting that a balancing procedure should serve as an initial preprocessing step to enhance the MC algorithms’ overall quality. Furthermore, for matrices that are close to stochastic matrices, the MC algorithm’ accuracy remains notably high.
Theorem 4.
Consider a perfectly balanced stochastic matrix
and the vector . Then MC algorithm defined by trajectory probability is a zero-variance MC algorithm.
It is sufficient to show that the variance is zero. Obviously,
and also,
Since
and we have: Thus, we proved that .
It is feasible to explore matrix-vector iterations as they form the foundation for Neumann series, which serves as an approximation for solving systems of linear algebraic equations. The underlying concept is to illustrate that as the matrix A approaches a perfectly balanced matrix, the probability error of the algorithm diminishes. The theorem implies that the initial algorithm can be enhanced by achieving balance in the iteration matrix.
3.4. Interpolation MC Algorithms
Definition 2.
A MC algorithm with a probability error of zero is referred to as an interpolation MC algorithm.
The subsequent theorem outlines the variance structure for the MAO algorithm. Let’s introduce the following symbols: ,
Theorem 5.
Corrolary 1.
For a stochastic matrix A and vectors , the MC algorithm, characterized by the density distributions outlined earlier, is classified as an interpolation MC algorithm.
The well-known Power method brings an approximation for the dominant eigenvalue . It uses the so-called Rayleigh quotient :
where are arbitrary vectors. The Rayleigh quotient is used to obtain an approximation to :
where k is arbitrary large natural number.
Considering the MAO density distributions, the random variable can be expressed in the following manner:
We deal with the variance
The following equalities are true:
Obviously,
and
Theorem 6.
The Markov chain trajectory length to absorption is less than 1 over the smallest absorption probability.
Proof.
The chance for absorption at each step is at least m (where m is the smallest absorption probability). Thus, interpreting the steps to absorption as a geometrically distributed random variable, we see that the expected length of a trajectory is at most 1/m. Moreover, the standard deviation is finite and at most 1/m as well. □
3.5. Eigenvalue Problems
For the Randomized Inverse Shifted Power Method the iteration is replaced by , where A and B have the same eigenvectors. The power iteration converges to the eigenvector associated with B’s dominant eigenvalue. Since A and B have the same eigenvectors, we have also computed an eigenvector of A. Letting denote a scalar, there are 3 common choices for B: named as the shifted power method, named as the inverse power method, and named as the inverse shifted power method. These observations are shown on Table 1.

Table 1.
Relationship between eigenvalues of A and B.
3.6. Convergence and Mapping
To analyze the MC algorithms’ convergence, taking into account the following functional equation
where is some parameter. Observe that the matrices can be treated as linear operators. Determine resolvent operator (matrix) by
in which I is the identity operator.
Let be the eigenvalues of (23), where it is supposed that
MC algorithms rely on the depiction
where
In the neighborhood of the point () the resolvent can be determined by the series
where
Contemplate the variable situated within the unit circle on the complex plane .
The function
maps the domain into .
where and .
Let us assume that all eigenvalues are real and , where . Contemplate a mapping for the case ():
The sequence for the transformation given by (27) exhibits both absolute and uniform convergence.
where
The coefficients
and can be calculated in advance.
If , then
where is the minimal by modulo eigenvalue, and is the approximation to the dominant eigenvalue of .
If , then
where is the dominant
4. Description of the WE MC Algorithms
Now we will give the description of the new WE MC algorithm, the old WE MC algorithm, and a combination between the two algorithms—the hybrid WE MC algorithm.
4.1. The First Monte Carlo Algorithm for Computing One Component of the Solution
In this Section 4.1 we will give the description of the first (old) WE algorithm for linear systems described in details in [1]. For the Algorithm 1 we need in advance as input data the matrix B, the vector , the constant parameter and the number of random trajectories N.
| Algorithm 1: Computing one component of the solution . |
Initialization Input B, , N. Preliminary calculations (preprocessing): Compute the matrix A using : Compute the vector : compute the vector of initial probabilities,
Compute the transition probability matrix ,
Set . for to N do (MC loop) set . set . while do: generate a udr variable if then ; else chose the index j according to ; set ; update ; endif. endwhile enddo |
4.2. The First WE Monte Carlo Algorithm for Evaluating the Solution’ All Components
In this Section 4.2, to simplify the situation in Algorithm 2, let’s assume that all the entries in the matrix are nonnegative, i.e., , for .
4.3. The New WE Monte Carlo Algorithm for Computing One Component of the Solution
In this Section 4.3, we introduce the novel Monte Carlo algorithm designed for computing a specific component of the solution in a linear system with real coefficients. The algorithm initiates its walk on row of the system, adding to the walk’s score. Subsequently, the walk either undergoes absorption or moves to another equation based on probabilities outlined in Algorithm 3 below. The contributions to the score are adjusted in accordance with the signs of the coefficients in the system. Further details are provided in the following Algorithm 3.
| Algorithm 2: Computing all components of the solution. |
Initialization. Preprocessing. for
to
n
do ; for to N do (MC loop) set . set ; ; while do: ; ; ; for do: ; if , then ; else chose j according to ; set . endif endwhile enddo for do: ; . |
| Algorithm 3: Computing one component of the solution . |
Initialization Input initial data: the matrix A, the vector , and the number of random trajectories N. Preliminary calculations (preprocessing): Compute the vector : Compute the sum of elements in vector b: Set . for to N do (MC loop) choose the index j, according to the probability density vector ; ; while do: choose the new value of the index j, according to the probability density vector ; If then else ; endif endwhile enddo . |
4.4. The New WE Monte Carlo Algorithm for Computing All Components of the Solution
In this Section 4.4, we present the novel Algorithm 4 designed for the computation of all components of the solution. The core idea is to calculate scores for all states, treated as new starting points, encountered throughout a given trajectory. The initial equation is randomly selected from the n equations with uniform probability. Subsequently, for each state i, we define the total score and the total number of visits , both of which are adjusted whenever state i is visited during a walk. The parameter represents the number of trajectories for component of the solution. The algorithm’s key element involves the application of the Sequential Monte Carlo (Sequential MC) method for linear systems, as introduced by John Halton [49,50,51,52], based on the control variate method [39].
| Algorithm 4: Computing all components of the solution . |
Initialization Input initial data: the matrix A, the vector , and the number of random trajectories N. Preliminary calculations (preprocessing): Compute the vector : Compute the sum of elements in vector b: Set and for to n. for to N do (MC loop) choose component to be estimated uniformly at random from increment by 1. . choose the index j, according to the probability density vector ; ; while do: choose the new value of the index j, according to the probability density vector ; If then else ; endif endwhile enddo for to n do . |
4.5. The Hybrid Monte Carlo Algorithm for Computing One Component of the Solution
In this Section 4.5 we will give the description of the hybrid WE algorithm for linear systems. The hybrid WE Algorithm 5 seems like the old algorithm WE but used if you got into an absorbing state (the state where the trajectory is broken) like the new algorithm.
| Algorithm 5: Computing one component of the solution . |
Initialization Input: B, , N. Preliminary calculations (preprocessing): Compute A using : Compute the vector : compute Compute , where
Set . for to N do (MC loop) set . set . while do: generate a udr variable choose the new value of the index j, according to the probability density vector ; if then ; else ; update ; endif. endwhile enddo |
4.6. The Hybrid WE Monte Carlo Algorithm for Computing All Components of the Solution
Finally, in this Section 4.6 we will give the description of the Hybrid WE MC algorithm for computing all components of the solution. Later we will see that in some situations this hybrid Algorithm 6 gives the best results compared to the new and the old algorithm.
4.7. Sequential Monte Carlo
The Sequential Monte Carlo (SMC) approach for LAEs was initially pioneered by John Halton in the 1960s [49] and has seen subsequent advancements in more recent publications [50,51,52]. This technique has been applied across various domains, including the computation of approximations on orthogonal bases [39] and the precise solution of linear partial differential equations [53].
| Algorithm 6: Computing all components of the solution. |
Initialization. Preprocessing. for
to
n
do ; for to N do (MC loop) set . set ; ; while do: ; ; ; for do: ; choose the new value of the index j, according to the probability density vector ; if , then ; set . endif endwhile enddo for do: ; . |
The SMC method is based on the simple yet highly efficient concept of iteratively applying the control variate method. In the realm of linear systems, where the objective is to determine the vector solution u for the equation , the method capitalizes on the fact that minimizing the variance of the algorithm is achieved when b is small, and when , the variance becomes zero. Exploiting the linearity of our problem, a new system is constructed, with its solution representing the residual of the original system and having a small b. Let denote the approximate solution obtained using the aforementioned algorithm. The residual
satisfies the new equation
where is expected to be close to zero. We calculate the approximation for this equation using our algorithm, resulting in the approximation
for the original equation. This iterative process is applied to obtain the estimate after k steps of the algorithm.
Demonstrated in [53], it has been established that when the number of samples N utilized in computing is sufficiently large, the variance of decreases exponentially with respect to k. This form of convergence, referred to as zero-variance algorithms [36,38,39,48,54,55,56], enables these algorithms to effectively compete with optimal deterministic algorithms based on Krylov subspace methods and conjugate gradient methods (CGM), which have numerous variations.
However, a critical consideration is warranted. Performing the matrix-vector multiplication deterministically requires operations. This implies that for a high-quality WE algorithm combined with SMC to be efficient, only a small number of sequential steps is necessary. The subsequent section will present numerical results showcasing high accuracy achieved in just a few sequential steps.
4.8. Dominancy Number
One of the key novelties in our paper is that we will introduce the special dominancy parameter .
The condition number is consistently positive when dealing with diagonally dominant matrices, providing a rough indication of the dominance strength of the matrix’s diagonal over the remaining elements. This concept is closely intertwined with the absorption probabilities in the Markov chain employed for the stochastic computation of solutions to linear systems. It is noteworthy that when then the newly developed algorithm performs with a several orders of magnitude higher accuracy compared to the old one. Later we will give experiments when is below and above to see the behavior of the three algorithms under consideration.
We may introduce the following statement
Theorem 7.
If the dominancy number is closer to 1, then the new algorithm is significantly better than the previous algorithm.
Proof.
When the dominancy number is close to 1, the preconditioned matrix has high absorption probabilities at each step. Thus, the length of each trajectory is small. Observe that in the new algorithm, the variable which estimates the solution is calculated once—at the end of each trajectory, and is irrespective of the length of the trajectory. On the other hand, in the old algorithm, the variable estimating the solution is updated along each step of a trajectory. Thus, it is natural to observe that more lengthy trajectories would produce better estimating variables. Whereas in the new algorithm, the length of a trajectory does not affect the calculation of the estimating variable. Thus, it is expected that the new algorithm performs better when the dominancy number is closer to 1. □
5. Numerical Tests
In this section we give ample numerical simulations to demonstrate the capabilities of the proposed approaches. The algorithms are implemented and run in a MATLAB® R2021b environment, using a mobile computer with 6-core processor and 16 GB RAM.
5.1. The New Algorithm versus Deterministic Algorithms
On the graphs we will illustrate the value of
where we check the accuracy of a computed solution , while is the exact solution-vector. One may observe that the results for all other components exhibit similar trends.
To assess whether the weighted residual [57,58]:
can serve as a reliable indicator of error, we juxtapose the relative error against the residual for a matrix of dimensions (refer to Figure 2). It is evident [1] that the curves representing the relative error and the residual closely align. The number of random trajectories for MC is . It is already established in [1] that for much large dense matrix of size n = 25,000 the WE method is clearly better than the Jacobi method—see Figure 3.
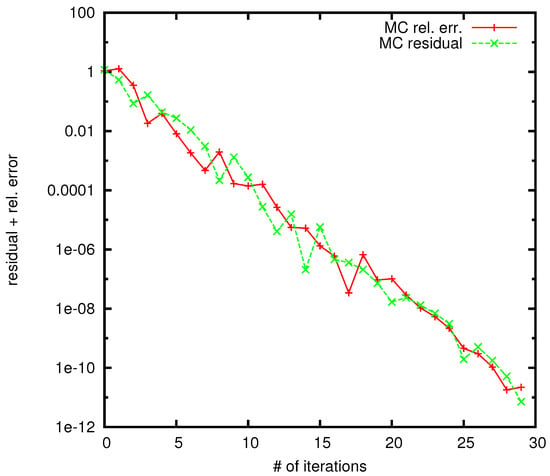
Figure 2.
Comparison the relative error with the residual for the WE MC.
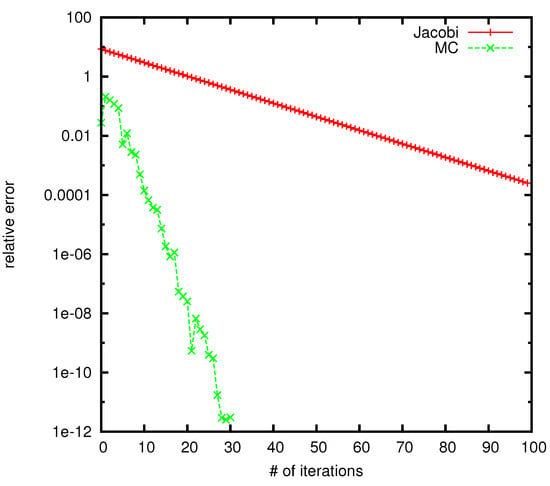
Figure 3.
Relative error for the WE MC and Jacobi method for a matrix of size 25,000 × 25,000.
Here we conduct a number of numerical experiments with dense matrices of size n = 10, 100, 1000, 10,000. A comparative analysis is conducted with well-established deterministic methods, specifically Gauss–Seidel and Jacobi algorithms. Key observations are as follows. Firstly, across all experiments, Gauss–Seidel consistently outperforms the Jacobi method by a margin of at least three orders of magnitude. Notably, this study introduces a comparison with Gauss–Seidel for the first time, as previous comparisons in [1] exclusively involved the Jacobi method. For the matrix of size on Figure 4 for 20 iterations, the relative error produced by the Monte Carlo approach is about two magnitudes better than the relative error for Gauss–Seidel method and 7 magnitudes better than the Jacobi approach. For the matrix of size on Figure 4 after just 15 iterations, the relative error from the Monte Carlo approach is approximately six orders of magnitude better than the Gauss–Seidel method and ten orders of magnitude better than the Jacobi method.
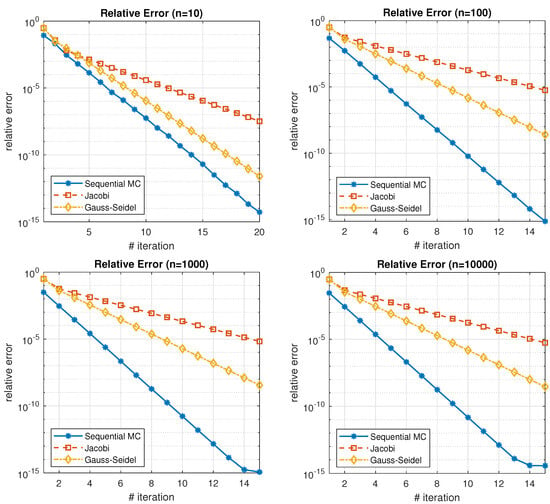
Figure 4.
Relative error of random dense matrices for (top left), (top right), (bottom left) and n = 10,000 (bottom right).
As we increase the matrix dimension to the new Monte Carlo approach continues to exhibit superior performance. In Figure 4, after 15 iterations, the relative error from the Monte Carlo approach is approximately seven orders of magnitude better than that of the Gauss–Seidel method and ten orders of magnitude better than the Jacobi method. This trend becomes even more pronounced with higher matrix dimensions. The most interesting case will be very high dimensional matrix of size 10,000 × 10,000. The results for this case are presented on Figure 4. Here, just for 14 iterations, the Monte Carlo method achieves a relative error of , while for the same number iterations Gauss–Seidel achieves and Jacobi produces . Consequently, for very high dimensions, the developed Monte Carlo approach emerges as the most accurate, surpassing other methods by a significant margin across multiple orders of magnitude.
We conduct also a range of computational experiments involving dense matrices with dimensions . These experiments are compared against well-established deterministic algorithms, specifically the Gauss–Seidel and Jacobi methods, to facilitate a thorough analysis. Notably, the results reveal consistent superiority in accuracy for the Gauss–Seidel algorithm compared to the Jacobi method, with a minimum difference of three orders of magnitude in each computational test. This juxtaposition with Gauss–Seidel is a distinctive contribution, as prior studies such as [1] exclusively focused on comparing with the Jacobi method. Taking the example of a matrix (illustrated in Figure 5) after 15 iterations, our Monte Carlo approach demonstrates a relative error approximately five orders of magnitude lower than Gauss–Seidel and eight orders of magnitude lower than Jacobi.
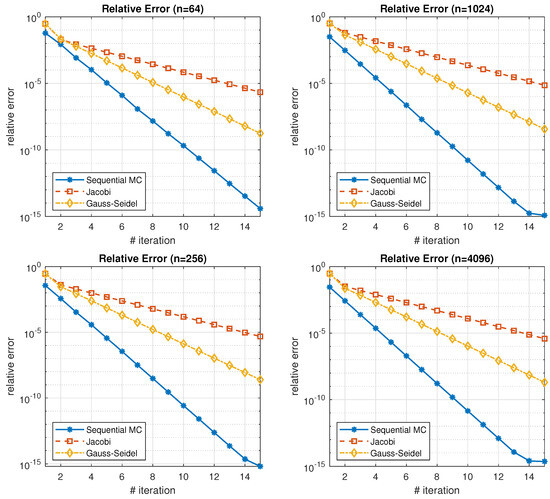
Figure 5.
Relative error of random dense matrices for (top left), (top right), (bottom left) and (bottom right).
Examining a larger matrix with dimensions (illustrated in Figure 5) and restricting the iterations to just 15, we observe that the Monte Carlo approach outperforms Gauss–Seidel by roughly six orders of magnitude and surpasses the Jacobi method by approximately ten orders of magnitude in relative error.
As we further elevate the matrix size to , the performance differential becomes even more striking. With just 15 iterations (see Figure 5), the Monte Carlo method demonstrates a relative error that is seven orders of magnitude superior to Gauss–Seidel and ten orders of magnitude better than Jacobi. Hence, we can affirm that the performance disparity between our Monte Carlo approach and the Gauss–Seidel algorithm expands as we increase the matrix dimensions.
The apex of our analysis is focused on the colossal matrix, the outcomes for which are illustrated in Figure 5. In a mere 14 iterations, the Monte Carlo methodology achieved an impressively low relative error of . Comparatively, Gauss–Seidel registered a relative error of and Jacobi languished further behind with . Hence, for exceedingly large-scale problems, our developed Monte Carlo approach stands out, surpassing other algorithms by a substantial margin in terms of accuracy.
5.2. WE versus PCG
We evaluate our outcomes against the optimal deterministic preconditioned conjugate gradient (PCG) method [57,59,60].
Here’s more detailed information regarding our PCG method implementation. Our objective is to address a linear system of equations, , utilizing the PCG iterative method. The matrix B in our context is the square and sizable matrix from the widely recognized Harwell-Boeing collection, with the requirement that B is symmetric and positive definite. The NOS4 matrix is a notable example from this collection, primarily because of its distinct characteristics and the challenges it presents in computational processing.
The NOS4 matrix is a sparse matrix, a common type found in the Harley-Boeing collection, known for its large size and sparsity. This matrix is particularly representative of structural engineering problems, often derived from finite element analysis. The specific features of the NOS4 matrix are as follows.
The NOS4 matrix exhibits a highly sparse structure, which is characteristic of matrices derived from finite element methods in engineering. This sparsity is a significant factor in computational processing, as it requires specialized algorithms that can efficiently handle non-dense data distributions.
The matrix is relatively large, which adds to the computational challenge. Its size and the complexity of its elements make it an ideal candidate for testing the scalability and efficiency of our algorithm.
The matrix typically contains numerical values that represent physical properties in structural engineering contexts, such as stiffness and material properties. These values are crucial for accurately simulating and analyzing structural behavior under various conditions.
Specifically, in the context of our study, the NOS4 matrix is utilized to model problems in constructive mechanics. This involves simulations that are critical for understanding and predicting the behavior of structures, particularly in the design and analysis of buildings, bridges, and other infrastructural elements.
In our implementation, the parameters employed are as follows: b represents the right-hand side vector; stands for the required relative tolerance for the residual error, denoted as , signifying that the iteration halts if ; denotes the maximum permissible number of iterations; corresponds to the (left) preconditioning matrix, ensuring that the iteration is theoretically equivalent to solving by PCG , with ; and signifies the initial guess.
Some detailed information about heaviest diagonals and conditioning for the matrix NOS4 is given on Figure 6. The illustration of the PCG for NOS4 is given on Figure 7. Our approach, devoid of such an optimization process, yields superior results. It is noteworthy that the specific matrix (NOS4) appears to pose a challenging test for PCG, but generalizing this observation is complex, as PCG success depends on the specific functional minimized in the method. Further analysis is required to determine the conditions under which the IWE and WE Monte Carlo methods outperform the widely used PCG.
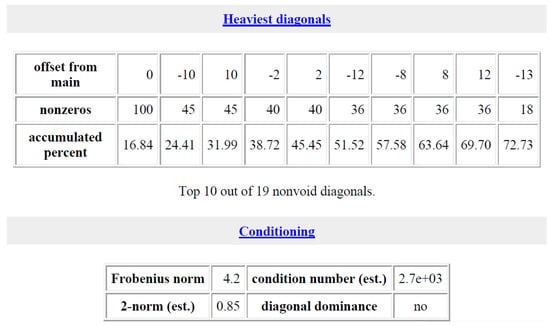
Figure 6.
Info for NOS4.
Figure 7.
Illustration of PCG for NOS4 matrix.
Figure 8 depicts the convergence analysis of the WE Monte Carlo and PCG methods when applied to the matrix This matrix originates from an application involving the finite element approximation of a problem associated with a beam structure in structural mechanics [61].
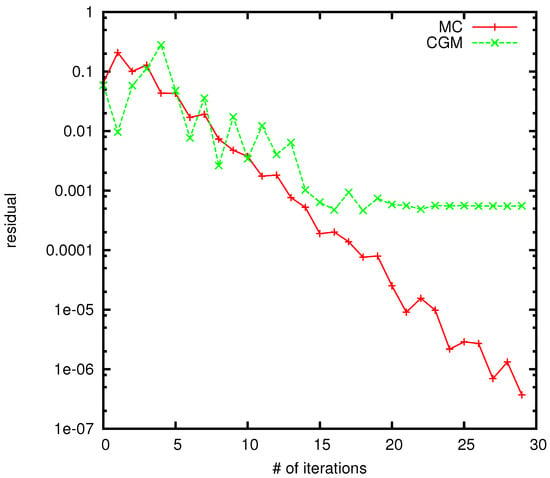
Figure 8.
Comparison of the WE MC and the PCG method for .
The outcomes depicted in Figure 8 indicate that the WE Monte Carlo exhibits superior convergence. The curve representing the residual with the number of iterations is smoother, reaching values as low as or compared to the PCG curve, which achieves an accuracy of . It is important to emphasize that, for the experiments showcased, the desired accuracy is specified as . One of the most significant distinctions between the Preconditioned Conjugate Gradient (PCG) method and our Walk on Equations (WE) Monte Carlo algorithm lies in their respective operational mechanisms within Krylov subspaces. While both methods operate within these optimal subspaces, the approach each takes is fundamentally different, leading to a crucial advantage for the WE algorithm.
The PCG method is fundamentally an optimization-based approach. It seeks to minimize the residual of the solution iteratively within the Krylov subspace. This process, while effective under certain conditions, inherently runs the risk of becoming ensnared in local minima. These local minima, which are close but not equivalent to the global minimum, can significantly hinder the convergence of the PCG method towards the most accurate solution. This susceptibility is illustrated in Figure 8, where the PCG method’s trajectory towards convergence is impeded by the presence of a local minimum.
In contrast, our WE algorithm operates within the same Krylov subspaces but diverges from the PCG method by eschewing the optimization paradigm entirely. Instead, it leverages the probabilistic nature of Monte Carlo methods to traverse the solution space. This approach inherently bypasses the pitfalls of optimization-based methods, such as getting trapped in local minima. The WE algorithm, by not being constrained to follow the gradient descent pathway that optimization methods inherently use, is not prone to stalling or slowing in areas that only represent local solutions. This attribute allows the WE algorithm to explore the solution space more freely and thoroughly, increasing the likelihood of reaching the global solution without the hindrance of local minima.
Therefore, the fundamental difference in operational philosophy between the PCG and WE methods not only delineates their theoretical underpinnings but also translates into a practical advantage for the WE algorithm. By navigating the solution space without the constraints of an optimization problem, the WE algorithm demonstrates a robustness and efficiency in finding the global solution, particularly in complex linear algebraic systems where local minima can be a significant obstacle.
5.3. Testing the Balancing
It is noteworthy that matrix balancing is a crucial concern for deterministic algorithms. Consequently, an arbitrary matrix necessitates a balancing procedure as part of the preprocessing steps. While MC algorithms are generally less sensitive to balancing, balancing does influence the convergence of the WE MC algorithm. As it is already established in [1], in the first instance, illustrated in Figure 9 (top left), we examine two small matrices with size . The balanced matrix is characterized by , resulting in a parameter a of . On the other hand, the unbalanced matrix has , with an extreme level of imbalance (the ratio between the largest and smallest elements by magnitude is 40). It is worth noting that a ratio is considered large when it reaches 5.
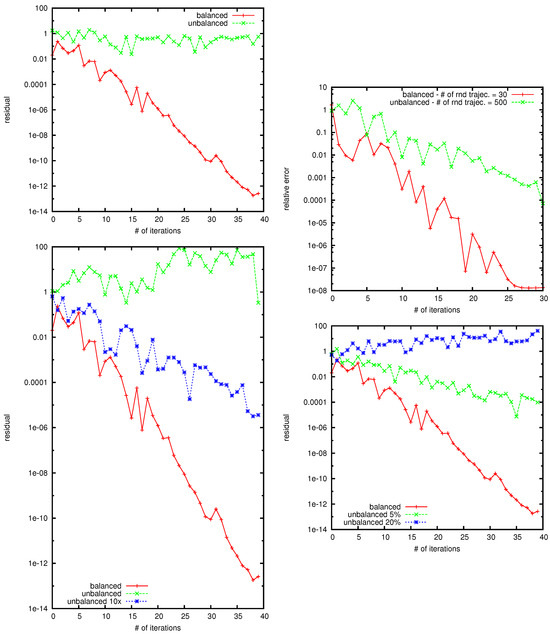
Figure 9.
Residual for the WE MC for balanced and extremity unbalanced matrix of size . The number of random trajectories is (top left); Residual for the WE Monte Carlo for balanced and extremity unbalanced matrix of size . The number of random trajectories for the balanced matrix is ; for the unbalanced matrix there two cases: (i) —red curve; (ii) —green curve. (top right); Residual for the WE MC, the matrix of size is . The number of random MC trajectories is (bottom left); Residual for the WE MC, the matrix of size is . Matrix elements are additionally perturbed by and by (bottom right).
Certainly, for the unbalanced matrix, convergence is entirely absent. In contrast, the balanced matrix exhibits rapid convergence, albeit with a somewhat erratic red curve, attributable to the limited number of random trajectories. To explore this further, we revisited the same matrices, this time augmenting the number of random trajectories to . Concurrently, we reduced the number of random trajectories (and consequently the computational time) for the balanced matrix from to . The outcomes of this experiment are illustrated in Figure 9 (top right).
The results clearly indicate that the WE algorithm initiates convergence, reaching three correct digits after approximately 35 to 40 iterations. While the balanced matrix still demonstrates swift convergence, the red curve retains its roughness, reflective of the limited number of random trajectories.
For randomly generated matrices of size , akin results are presented in Figure 9 (bottom left). The unbalanced matrix results from random perturbations to the elements of the balanced matrix. Both the green and blue curves pertain to the same unbalanced matrix, with the latter achieved by leveraging ten times more random trajectories. This demonstrates that increasing the number N of random trajectories can enhance convergence, aligning with theoretical expectations.
In our specific numerical experiments depicted in Figure 9 (bottom left), the green curve is derived from a set of trajectories with , while the blue curve is based on trajectories. It is evident that, in the former case, the algorithm fails to converge, whereas in the latter case, convergence is achieved. These experiments underscore that the WE Monte Carlo exhibits an additional degree of freedom, absent in deterministic algorithms, allowing for enhanced convergence even with severely imbalanced matrices. However, this improvement in convergence comes at the cost of increased complexity, or computational time, due to the augmented number of simulation trajectories.
To explore the impact of matrix imbalance on the convergence of the WE Monte Carlo, we conducted a noteworthy experiment. By randomly generating matrices of varying sizes, we introduced random perturbations to the matrix elements, progressively increasing the matrix’s imbalance. The results for a matrix of size are illustrated in Figure 9 (bottom right). The matrix’s randomly generated entries were additionally perturbed by and .
Matrix balancing plays a pivotal role in the performance of many computational algorithms, particularly in solving linear algebraic systems. While MC algorithms, including our WE MC algorithm, are generally less sensitive to matrix balancing compared to deterministic algorithms, the impact of balancing on convergence is non-negligible.
To provide a concrete context for the necessity of matrix balancing, let us consider a practical example from structural engineering. In finite element analysis, matrices often represent stiffness or connectivity matrices of a physical structure, like a bridge or building. These matrices can become imbalanced due to variations in material properties or non-uniform loading conditions. An imbalanced matrix in such scenarios could lead to inaccurate or inefficient computational analysis, impacting the reliability of the structural assessment.
Given the practical implications, it is vital to establish criteria for when and how to apply matrix balancing:
- Magnitude of Element Variation: Balancing should be considered when there is a significant disparity in the magnitude of matrix elements. A practical threshold could be set; for instance, a ratio of 5 or more between the largest and smallest elements by magnitude indicates a need for balancing.
- Application-Specific Needs: In fields such as structural engineering or fluid dynamics, where matrices represent physical phenomena, the need for balancing should be assessed based on the physical realism of the matrix. If imbalances in the matrix do not correspond to realistic physical conditions, balancing may be necessary.
- Computational Efficiency: If preliminary runs of the algorithm show a slow convergence rate, this could signal the need for balancing, especially in large matrices where computational efficiency is paramount.
5.4. Comparison between the Three WE Algorithms
This subsection is very important, because it will address the issue in which cases the new algorithm is better than the old algorithm.
We consider randomly chosen matrix and with values of the dominancy parameter . While in the case of lower the two algorithms produce similar results with the new algorithm being better at high sequential steps, for higher the advantage of the new algorithm can be clearly seen—see Table 2. The apex of our analysis is focused on the matrix, the outcomes for which are illustrated in Table 2. In a mere 5 iterations, the new Monte Carlo algorithm achieved an impressively low relative error of . Comparatively, the old WE registered a relative error of . Hence, for exceedingly large-scale problems, our developed Monte Carlo approach stands out, surpassing the old algorithm by a substantial margin in terms of accuracy.

Table 2.
Weighted residual for the matrix (1) with a dominancy parameter and (2) with a dominancy parameter .
We can see the comparison between the three algorithms on Figure 10. The corresponding dominancy numbers are . We can observe similar behavior between the three algorithms with the slight advantage to the hybrid and the new WE algorithm due to the fact that the dominancy number is closer to . When we increase the dominancy number the advantage of the new algorithm versus the old algorithm become more evident—see the results on Figure 11. The corresponding dominancy numbers are . When we augment the dominancy number, the superiority of the new algorithm over the old algorithm becomes increasingly pronounced. As the dominancy number, which characterizes the influence of the diagonal elements within a system, grows, the effectiveness and efficiency of the new algorithm become more evident in comparison to the older method. This trend suggests that the performance gap between the two algorithms widens as the system’s key features gain greater prominence, underscoring the enhanced adaptability and efficacy of the new algorithm in handling scenarios with elevated dominancy numbers. This observation reinforces the notion that the advantages of the new algorithm are particularly prominent and advantageous in situations where dominant factors play a more significant role. When we decrease the dominancy number the advantage of the hybrid algorithm versus the old and new algorithm become more evident—see the results on Figure 12. The corresponding dominancy numbers are . It is worth mentioning that in case of low dominancy numbers the difference between the old and the new algorithm is very similar. This fact could be explained by the proof of Theorem 7, but needs more careful analysis and will be an object of a future study.
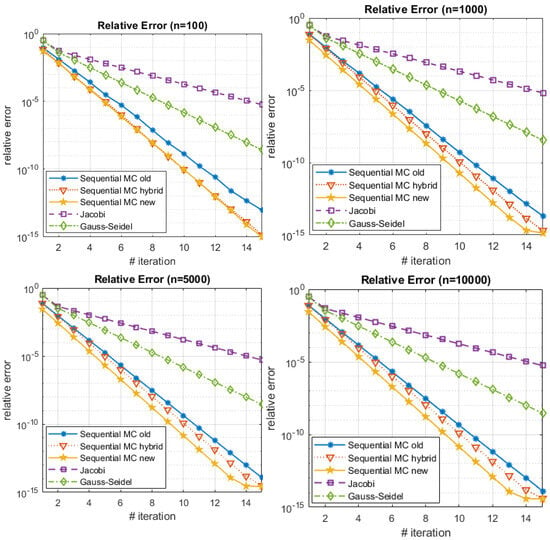
Figure 10.
Relative error of random dense matrices for (top left), (top right), (bottom left) and n = 10,000 (bottom right).
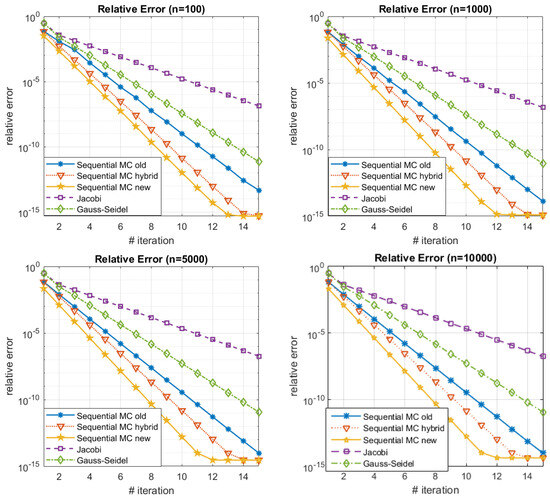
Figure 11.
Relative error of random dense matrices for (top left), (top right), (bottom left) and n = 10,000 (bottom right).
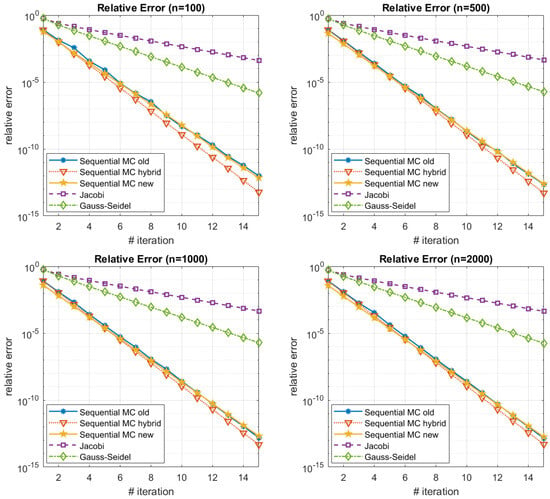
Figure 12.
Relative error of random dense matrices for (top left), (top right), (bottom left) and (bottom right).
Here we describe the significance of the dominancy number and its impact on the performance of our new Monte Carlo algorithm compared to traditional methods. To provide a clearer understanding of how the dominancy number relates to real-world systems, we will establish a link between the bands of this parameter and their applications in various scenarios.
5.4.1. Dominancy Number in Real Systems
1. Structural Engineering and Mechanics: In structural engineering, matrices derived from finite element analysis often have dominancy numbers reflecting the stiffness of the structure. A higher dominancy number (closer to 1) might indicate a structure with more uniform material properties or loading conditions, whereas a lower dominancy number (closer to 0) could represent a structure with highly variable stiffness or irregular load distribution. For instance, in a uniformly loaded beam, the stiffness matrix would likely exhibit a higher dominancy number, indicating the potential effectiveness of our new algorithm in such scenarios.
2. Electrical Networks and Circuit Analysis: In electrical engineering, matrices representing circuit networks often have dominancy numbers that reflect the distribution of resistances or impedances. A circuit with evenly distributed resistances across components may present a higher dominancy number, suggesting a system where our new algorithm could be particularly efficient.
3. Fluid Dynamics and Heat Transfer: Systems modeled for fluid dynamics or heat transfer can have matrices with varying dominancy numbers depending on the homogeneity of the medium or the boundary conditions. For example, a heat transfer problem in a homogenous medium might have a higher dominancy number, indicating the suitability of our new algorithm for such cases.
5.4.2. Practical Implications of Dominancy Number Bands
- -
- High Dominancy Band ( ≈ 0.6–1.0): Systems with high dominancy numbers are likely to benefit more from our new algorithm. These systems typically exhibit more uniform properties or conditions, making our algorithm more efficient in handling them.
- -
- Medium Dominancy Band ( ≈ 0.4–0.6): In this range, the performance of our new algorithm is comparable to traditional methods, with slight advantages in certain scenarios. Systems in this band often exhibit moderate variability in their properties.
- -
- Low Dominancy Band ( ≈ 0.0–0.4): Systems with low dominancy numbers might not exhibit a significant performance difference between our new algorithm and traditional methods. These systems often represent highly variable or irregular conditions.
The dominancy number is a critical parameter in determining the suitability and efficiency of our new Monte Carlo algorithm for various real-world systems. By understanding the implications of different dominancy number bands, practitioners can better assess the applicability of our algorithm to specific scenarios, ranging from structural engineering to electrical networks.
6. Discussion
In this section we will discuss the most important features of the new algorithm. We will discuss its advantages over the original algorithm. As can be seen the advantage of the new algorithm versus the old one depends on the newly presented parameter in this paper—the so called dominancy number.
We may observe the following key elements of the presented algorithms.
- Performance enhancement through strategic relaxation parameter selection, leading to reduced computation time and relative errors within a fixed number of iterations.
- Optimization potential by balancing the iteration matrix, demonstrating improvements in the algorithm’s original form.
- The introduced random variable serves as an unbiased estimator for the solution vector. The stochastic error’s structure is analyzed in detail.
- The analysis of the stochastic error structure reveals that the convergence rate of the proposed WE Monte Carlo algorithm is influenced by matrix balancing. Although this influence is less pronounced compared to deterministic algorithms, it is still a factor to consider.
- Application of a sequential Monte Carlo method by John Halton, based on the control variate method, for further optimization.
- Analysis of the relative stochastic error structure, revealing a dependency on matrix balancing for the convergence rate of the WE algorithm.
- Comparative analysis of numerical outcomes with the most optimal deterministic method, the Preconditioned Conjugate Gradient (PCG), indicating superior results for the WE Monte Carlo method in certain cases.
- The proposed WE Monte Carlo algorithm, in conjunction with the sequential Monte Carlo for computing all solution components, demonstrates significantly faster convergence compared to certain well-known deterministic iterative methods, such as the Jacobi and Gauss–Seidel methods.
- The proposed WE Monte Carlo algorithm, in conjunction with the sequential Monte Carlo for computing all solution components, shows faster convergence compared to the old algorithm when the dominancy number is close to 1. This trend is consistent across matrices of various sizes, with a more pronounced effect observed for larger matrices.
Now, when we consider the impact of the dominancy number on the performance of algorithms, particularly the comparison between a new and an old algorithm, the following dynamics come into play:
The dominancy number reflects the diagonally dominance in the system. As this number increases, it implies that specific elements or features have a more substantial influence on the overall system behavior.
The old algorithm might have been designed or optimized based on certain assumptions or characteristics of the problem. However, if the dominancy number is low, the impact of the dominance may not have been fully exploited or addressed by the old algorithm.
The new algorithm, on the other hand, may have been specifically developed or adapted to handle scenarios with higher dominancy numbers. It could incorporate techniques that capitalize on the influence of diagonally dominance. As the dominancy number increases, the advantages of these tailored approaches become more apparent.
The observed performance difference between the old and new algorithms is indicative of the latter’s adaptability and efficacy in scenarios where certain factors play a more critical role. The new algorithm may dynamically adjust or scale its strategies based on the prominence of diagonally dominance, leading to improved outcomes in these situations.
In essence, the correlation between the dominancy number and algorithmic performance emphasizes the importance of algorithmic design that considers and leverages the influential factors within a given problem. As the dominancy number grows, the advantages of the new and the hybrid algorithm specifically crafted to handle such conditions become increasingly evident, showcasing the importance of adaptability and specialization in algorithmic solutions.
However, there is another issue to be addressed. The need for increased simulation trajectories to achieve convergence, especially when dealing with imbalanced matrices, raises questions about efficiency and practicality, particularly in comparison to canonical methods.
To address this critical point, it is possible to apply a number of strategies to achieve a balance between convergence speed and the number of simulation trajectories:
- Adaptive Trajectory Sampling: By implementing an adaptive sampling technique, the algorithm can dynamically adjust the number of trajectories based on the convergence rate. When the algorithm is far from convergence, fewer trajectories can be used. As it approaches the solution, the algorithm can increase the number of trajectories to fine-tune the accuracy. This adaptive approach helps in reducing unnecessary computational overhead in the early stages of the algorithm.
- Parallel Computing and Optimization: The inherently parallel nature of Monte Carlo simulations makes our WE algorithm particularly amenable to parallel computing techniques. By distributing the simulation trajectories across multiple processors or a GPU, we can significantly reduce the overall CPU time. Furthermore, optimizing the code for specific hardware architectures can also lead to substantial improvements in computational efficiency.
- Hybrid Methodologies: Combining the WE algorithm with deterministic methods can offer a compromise between the robustness of Monte Carlo approaches and the speed of traditional methods. Starting with a deterministic method to reach a closer approximation to the solution and then switching to the WE algorithm for fine-tuning could reduce the total number of simulation trajectories required.
- Improving the Dominancy Number Calculation: As our research highlights the importance of the dominancy number in the algorithm’s performance, refining the calculation or estimation of this number can lead to a more efficient trajectory planning. This could involve developing predictive models that estimate the optimal dominancy number based on matrix characteristics.
- Advanced Stochastic Techniques: Incorporating advanced stochastic techniques, such as importance sampling or variance reduction strategies, could improve the efficiency of the simulation trajectories. These techniques aim to focus computational effort on the most critical parts of the solution space, thereby reducing the number of trajectories required for a given level of accuracy.
To summarize, while the increase in CPU time due to additional simulation trajectories is a valid concern, especially for imbalanced matrices, the strategies outlined above provide viable pathways to optimize the trade-off between convergence speed and computational effort. Our future work will focus on further investigating and implementing these strategies to enhance the practical applicability of the WE algorithm.
7. Conclusions
Linear systems hold significance not just for their mathematical elegance but for their pervasive influence across various disciplines, serving as a foundational language to articulate and comprehend the complexities of the world. Linear Algebraic Equations are more than mere problems to solve; they act as a vital link between abstract theories and practical realities in scientific and engineering applications. Whether navigating simulations in computational fluid dynamics or optimizing structures in engineering, they offer a mathematical framework to perceive, understand, and tackle intricate challenges. As computational capabilities expand, addressing large-scale linear algebraic problems has become a focal point, pushing the boundaries of both analytical techniques and computational hardware.
In our research, we have introduced and thoroughly investigated a novel Monte Carlo method designed explicitly for large systems of algebraic linear equations. This innovative approach is based on the “Walk on Equations” Monte Carlo model, a recent development attributed to Ivan Dimov, Sylvain Maire, and Jean Michel Sellier. Additionally, we present a new hybrid algorithm, a combination of the two methods, introducing a crucial element—the dominancy number—for algorithmic performance. Notably, our study breaks new ground by providing a comparative analysis with the Jacobi and Gauss–Seidel algorithms, focusing on matrices of considerable dimensions—an aspect largely unexplored in existing scholarly discussions.
To validate our approach, we conduct numerical experiments, including a significant case involving a large system from finite element approximation in structural mechanics, specifically addressing a beam structure problem. Our work contributes to advancing the understanding and effective solution of large-scale linear algebraic problems, showcasing the relevance and potential applications of our proposed Monte Carlo method in practical, real-world scenarios.
Looking ahead to the future landscape of scholarly endeavors in this field, we anticipate a comprehensive and rigorous evaluation that juxtaposes traditional computational methods with our cutting-edge Monte Carlo technique. Moreover, we need to investigate how the proposed method change to nonlinearities, and what possible criteria can be done in this case. Additionally, we aim to broaden the scope of our innovative algorithm by applying it to various matrices drawn from the well-known Harwell-Boeing collection. This initiative seeks to underscore the adaptability and effectiveness of our approach in solving linear algebraic equations crucial to a variety of practical, real-world scenarios.
Author Contributions
Conceptualization, V.T. and I.D.; methodology, V.T. and I.D.; software, V.T. and I.D.; validation, V.T.; formal analysis, V.T. and I.D.; investigation, V.T.; resources, V.T.; data curation, V.T.; writing—original draft preparation, V.T.; writing—review and editing, V.T.; visualization, V.T; supervision, V.T. and I.D.; project administration, V.T. and I.D.; funding acquisition, V.T. and I.D. All authors have read and agreed to the published version of the manuscript.
Funding
The methodology for investigation is supported by the Project BG05M2OP001-1.001-0004 UNITe, funded by the Operational Programme “Science and Education for Smart Growth”, co-funded by the European Union trough the European Structural and Investment Funds. The development of the stochastic methods is supported by the Bulgarian National Science Fund (BNSF) under Project KP-06-N52/5 “Efficient methods for modeling, optimization and decision making”. The computational experiments are supported by the BNSF under Project KP-06-N52/2 “Perspective Methods for Quality Prediction in the Next Generation Smart Informational Service Networks”. The simulations are supported by the BNSF under Project KP-06-N62/6 “Machine learning through physics-informed neural networks”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dimov, I.T.; Maire, S.; Sellier, J.M. A New Walk on Equations Monte Carlo Method for Linear Algebraic Problems. Appl. Math. Model. 2015, 39, 4494–4510. [Google Scholar] [CrossRef]
- Zheng, Z.C.; Ren, G.X.; Wang, W.J. A reduction method for large scale unsymmetric eigenvalue problems in structural dynamics. J. Sound Vib. 1997, 199, 253–268. [Google Scholar] [CrossRef]
- Stüben, K. A review of algebraic multigrid. J. Comput. Appl. Math. 2001, 128, 281–309. [Google Scholar] [CrossRef]
- Audu, K.J.; Essien, J.N. An Accelerated Iterative Technique: Third Refinement of Gauss–Seidel Algorithm for Linear Systems. Comput. Sci. Math. Forum 2023, 7, 7. [Google Scholar] [CrossRef]
- Lukyanenko, D. Parallel Algorithm for Solving Overdetermined Systems of Linear Equations, Taking into Account Round-Off Errors. Algorithms 2023, 16, 242. [Google Scholar] [CrossRef]
- Ishii, G.; Yamamoto, Y.; Takaishi, T. Acceleration and Parallelization of a Linear Equation Solver for Crack Growth Simulation Based on the Phase Field Model. Mathematics 2021, 9, 2248. [Google Scholar] [CrossRef]
- Georgiev, S.; Vulkov, L. Parameters Identification and Numerical Simulation for a Fractional Model of Honeybee Population Dynamics. Fractal Fract. 2023, 7, 311. [Google Scholar] [CrossRef]
- Georgiev, S.G.; Vulkov, L.G. Coefficient identification in a SIS fractional-order modelling of economic losses in the propagation of COVID-19. J. Comput. Sci. 2023, 69, 102007. [Google Scholar] [CrossRef] [PubMed]
- Atanasov, A.Z.; Georgiev, S.G.; Vulkov, L.G. Reconstruction analysis of honeybee colony collapse disorder modeling. Optim. Eng. 2021, 22, 2481–2503. [Google Scholar] [CrossRef]
- Georgiev, I.K.; Kandilarov, J. An immersed interface FEM for elliptic problems with local own sources. AIP Conf. Proc. 2009, 1186, 335–342. [Google Scholar] [CrossRef]
- Veleva, E.; Georgiev, I.R. Seasonality of the levels of particulate matter PM10 air pollutant in the city of Ruse, Bulgaria. AIP Conf. Proc. 2020, 2302, 030006. [Google Scholar] [CrossRef]
- Boutchaktchiev, V. Inferred Rate of Default as a Credit Risk Indicator in the Bulgarian Bank System. Entropy 2023, 25, 1608. [Google Scholar] [CrossRef]
- Traneva, V.; Tranev, S. Intuitionistic Fuzzy Model for Franchisee Selection. In Intelligent and Fuzzy Systems. INFUS 2022; Kahraman, C., Tolga, A.C., Cevik Onar, S., Cebi, S., Oztaysi, B., Sari, I.U., Eds.; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2022; Volume 504, pp. 632–640. [Google Scholar] [CrossRef]
- Traneva, V.; Tranev, S. Intuitionistic Fuzzy Two-factor Variance Analysis of Movie Ticket Sales. J. Intell. Fuzzy Syst. 2021, 42, 563–573. [Google Scholar] [CrossRef]
- Dimov, I.; Tonev, O. Performance Analysis of Monte Carlo Algorithms for Some Models of Computer Architectures. In International Youth Workshop on Monte Carlo Methods and Parallel Algorithms—Primorsko; Sendov, B., Dimov, I., Eds.; World Scientific: Singapore, 1990; pp. 91–95. [Google Scholar]
- Spanier, J.; Gelbard, E. Monte Carlo Principles and Neutron Transport Problem; Addison-Wesley: Boston, MA, USA, 1969. [Google Scholar]
- Curtiss, J.H. Monte Carlo methods for the iteration of linear operators. J. Math Phys. 1954, 32, 209–232. [Google Scholar] [CrossRef]
- Curtiss, J.H. A Theoretical Comparison of the Efficiencies of Two Classical Methods and a Monte Carlo Method for Computing One Component of the Solution of a Set of Linear Algebraic Equations; John Wiley and Sons: Hoboken, NJ, USA, 1956; pp. 191–233. [Google Scholar]
- Arafat, A.; El-Mikkawy, M. A Fast Novel Recursive Algorithm for Computing the Inverse of a Generalized Vandermonde Matrix. Axioms 2023, 12, 27. [Google Scholar] [CrossRef]
- Alexandrov, V.; Atanassov, E.; Dimov, I. Parallel Quasi-Monte Carlo Methods for Linear Algebra Problems. Monte Carlo Methods Appl. 2004, 10, 213–219. [Google Scholar]
- Dimov, I. Monte Carlo Algorithms for Linear Problems. Pliska (Studia Math. Bulg.) 2000, 13, 57–77. [Google Scholar]
- Dimov, I.; Tonev, O. Monte Carlo algorithms: Performance analysis for some computer architectures. J. Comput. Appl. Math. 1993, 48, 253–277. [Google Scholar] [CrossRef][Green Version]
- Dimov, I.; Alexandrov, V.; Karaivanova, A. Parallel resolvent Monte Carlo algorithms for linear algebra problems. J. Math. Comput. Simul. 2001, 55, 25–35. [Google Scholar] [CrossRef]
- IDimov, T.; Karaivanova, A.N. Iterative Monte Carlo algorithms for linear algebra problems. In Numerical Analysis and Its Applications, Proceedings of the First Workshop on Numerical Analysis and Applications, Rousse, Bulgaria, 24–27 June 1996; Springer Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1196, pp. 150–160. [Google Scholar]
- Dimov, I.T.; Alexandrov, V. A New Highly Convergent Monte Carlo Method for Matrix Computations. Math. Comput. Simul. 1998, 47, 165–181. [Google Scholar] [CrossRef]
- Hammersley, J.M.; Handscomb, D.C. Monte Carlo Methods; John Wiley & Sons, Inc.: New York, NY, USA; London, UK; Sydney, Australia; Methuen, MA, USA, 1964. [Google Scholar]
- Shyamkumar, N.; Banerjee, S.; Lofgren, P. Sublinear estimation of a single element in sparse linear systems. In Proceedings of the 2016 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016. [Google Scholar]
- Choudalakis, S.; Mitrouli, M.; Polychronou, A.; Roupa, P. Solving High-Dimensional Problems in Statistical Modelling: A Comparative Study. Mathematics 2021, 9, 1806. [Google Scholar] [CrossRef]
- Hached, M.; Jbilou, K.; Koukouvinos, C.; Mitrouli, M. A Multidimensional Principal Component Analysis via the C-Product Golub–Kahan–SVD for Classification and Face Recognition. Mathematics 2021, 9, 1249. [Google Scholar] [CrossRef]
- Angelova, V.; Hached, M.; Jbilou, K. Sensitivity of the Solution to Nonsymmetric Differential Matrix Riccati Equation. Mathematics 2021, 9, 855. [Google Scholar] [CrossRef]
- Delgado, J.; Peña, G.; Peña, J.M. Green Matrices, Minors and Hadamard Products. Axioms 2023, 12, 774. [Google Scholar] [CrossRef]
- Zhou, W.; Xiong, Z.; Qin, Y. Forward Order Law for the Reflexive Inner Inverse of Multiple Matrix Products. Axioms 2022, 11, 123. [Google Scholar] [CrossRef]
- Li, M.; Feng, Y.; Wang, G. Estimating Failure Probability with Neural Operator Hybrid Approach. Mathematics 2023, 11, 2762. [Google Scholar] [CrossRef]
- Abud, T.P.; Augusto, A.A.; Fortes, M.Z.; Maciel, R.S.; Borba, B.S.M.C. State of the Art Monte Carlo Method Applied to Power System Analysis with Distributed Generation. Energies 2023, 16, 394. [Google Scholar] [CrossRef]
- Tomczyk, K. Monte Carlo-Based Procedure for Determining the Maximum Energy at the Output of Accelerometers. Energies 2020, 13, 1552. [Google Scholar] [CrossRef]
- Dimov, I.T. Monte Carlo Methods for Applied Scientists; World Scientific: Hackensack, NJ, USA; London, UK; Singapore, 2008; 291p, ISBN-10 981-02-2329-3. [Google Scholar]
- Golub, G.V.; Loon, C.F.V. Matrix Computations, 3rd ed.; Johns Hopkins Univ. Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Dimov, I.T.; Philippe, B.; Karaivanova, A.; Weihrauch, C. Robustness and applicability of Markov chain Monte Carlo algorithms for eigenvalue problems. Appl. Math. Model. 2008, 32, 1511–1529. [Google Scholar] [CrossRef]
- Maire, S. Reducing variance using iterated control variates. J. Stat. Comput. Simul. 2003, 73, 1–30. [Google Scholar] [CrossRef]
- Straßburg, J.; Alexandrov, V.N. A Monte Carlo Approach to Sparse Approximate Inverse Matrix Computations. Procedia Comput. Sci. 2013, 18, 2307–2316. [Google Scholar] [CrossRef][Green Version]
- Sobol, I.M. Monte Carlo Numerical Methods; Nauka: Moscow, Russia, 1973. [Google Scholar]
- Dimov, I.; Karaivanova, A. Parallel computations of eigenvalues based on a Monte Carlo approach. J. Monte Carlo Method Appl. 1998, 4, 33–52. [Google Scholar] [CrossRef]
- Dimov, I.; Karaivanova, A. A Power Method with Monte Carlo Iterations, Recent Advances in Numerical Methods and Applications; Iliev, O., Kaschiev, M., Sendov, B., Vassilevski, P., Eds.; World Scientific: Singapore, 1999; pp. 239–247. [Google Scholar]
- Kantorovich, L.W.; Krylov, V.I. Approximate Methods of Higher Analysis; Interscience: New York, NY, USA, 1964. [Google Scholar]
- Densmore, J.D.; Larsen, E.W. Variational variance reduction for particle transport eigenvalue calculations using Monte Carlo adjoint simulation. J. Comput. Phys. 2003, 192, 387–405. [Google Scholar] [CrossRef]
- Rosca, N. A New Monte Carlo Estimator for Systems of Linear Equations. Stud. Univ. Babes-Bolyai Math. 2006, 51, 97–107. [Google Scholar]
- Forsythe, G.E.; Leibler, R.A. Matrix Inversion by a Monte Carlo Method. Math. Comput. 1950, 4, 127–129. [Google Scholar] [CrossRef]
- Dimov, I. Minimization of the Probable Error for Some Monte Carlo methods. In Proceedings of the International Conference on Mathematical Modeling and Scientific Computation, Albena, Bulgaria, 23–28 September 1990; Publishing House of the Bulgarian Academy of Sciences: Sofia, Bulgaria, 1991; pp. 159–170. [Google Scholar]
- Halton, J. Sequential Monte Carlo. Math. Proc. Camb. Philos. Soc. 1962, 58, 57–78. [Google Scholar] [CrossRef]
- Halton, J. Sequential Monte Carlo; University of Wisconsin: Madison, WI, USA, 1967; Mathematics Research Center Technical Summary Report No. 816; 38p. [Google Scholar]
- Halton, J.; Zeidman, E.A. Monte Carlo Integration with Sequential Stratification; University of Wisconsin: Madison, WI, USA, 1969; Computer Sciences Department Technical Report No. 61; 31p. [Google Scholar]
- Halton, J. Sequential Monte Carlo for linear systems—A practical summary. Monte Carlo Methods Appl. 2008, 14, 1–27. [Google Scholar] [CrossRef]
- Gobet, E.; Maire, S. Sequential control variates for functionals of Markov processes. SIAM J. Numer. Anal. 2005, 43, 1256–1275. [Google Scholar] [CrossRef]
- Kollman, C.; Baggerly, K.; Cox, D.; Picard, R. Adaptive importance sampling on discrete Markov chains. Ann. Appl. Probab. 1999, 9, 391–412. [Google Scholar]
- L’Ecuyer, P.; Blanchet, J.H.; Tuffin, B.; Glynn, P.W. Asymptotic robustness of estima- tors in rare-event simulation. ACM Trans. Model. Comput. Simul. 2010, 20, 6. [Google Scholar]
- L’Ecuyer, P.; Tuffin, B. Approximate zero-variance simulation. In Proceedings of the 2008 Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; pp. 170–181. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003; p. 195. ISBN 978-0-89871-534-7. [Google Scholar]
- Westlake, J.R. A Handbook of Numerical Matrix Inversion and Solution of Linear Equations; John Wiley & Sons, Inc.: New York, NY, USA; London, UK; Sydney, Australia, 1968. [Google Scholar]
- Golub, G.H.; Ye, Q. Inexact Preconditioned Conjugate Gradient Method with Inner-Outer Iteration. SIAM J. Sci. Comput. 1999, 21, 1305. [Google Scholar] [CrossRef]
- Knyazev, A.V.; Lashuk, I. Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning. SIAM J. Matrix Anal. Appl. 2008, 29, 1267. [Google Scholar] [CrossRef]
- Website: Matrix Market. NOS4: Lanczos with Partial Reorthogonalization. Finite Element Approximation to a Beam Structure. Available online: http://math.nist.gov/MatrixMarket/data/Harwell-Boeing/lanpro/nos4.html (accessed on 1 January 2004).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).