Hybrid Quantum Genetic Algorithm with Fuzzy Adaptive Rotation Angle for Efficient Placement of Unmanned Aerial Vehicles in Natural Disaster Areas
Abstract
1. Introduction
- 1.
- We introduce the first algorithm that is capable of running on a quantum computer, efficiently addressing the challenge of locating UAVs in disaster zones.
- 2.
- To enhance the performance of our HQGAFARA (Hybrid Quantum Genetic Algorithm with Fuzzy Adaptive Rotation Angle), we incorporate fuzzy logic, a technique that effectively manages uncertainties in complex mathematical models. Implementing a fuzzy adaptive rotation angle enables flexible manipulation of the quantum gate rotation angle. In contrast, using an adaptive rotation angle based on a mathematical equation restricts qubit-state rotation to a single direction.
- 3.
- Our approach integrates a quantum recombination operator based on the Deutsch–Jozsa circuit. This addition endows the algorithm with quantum advantages, including quantum parallelism, entanglement, and quantum haploid recombination and mutation, which all synergistically enhance its capabilities. These attributes are unattainable with classical computing methods.
2. Theoretical Framework
2.1. Quantum Computing
2.2. Quantum Inspired Algorithms
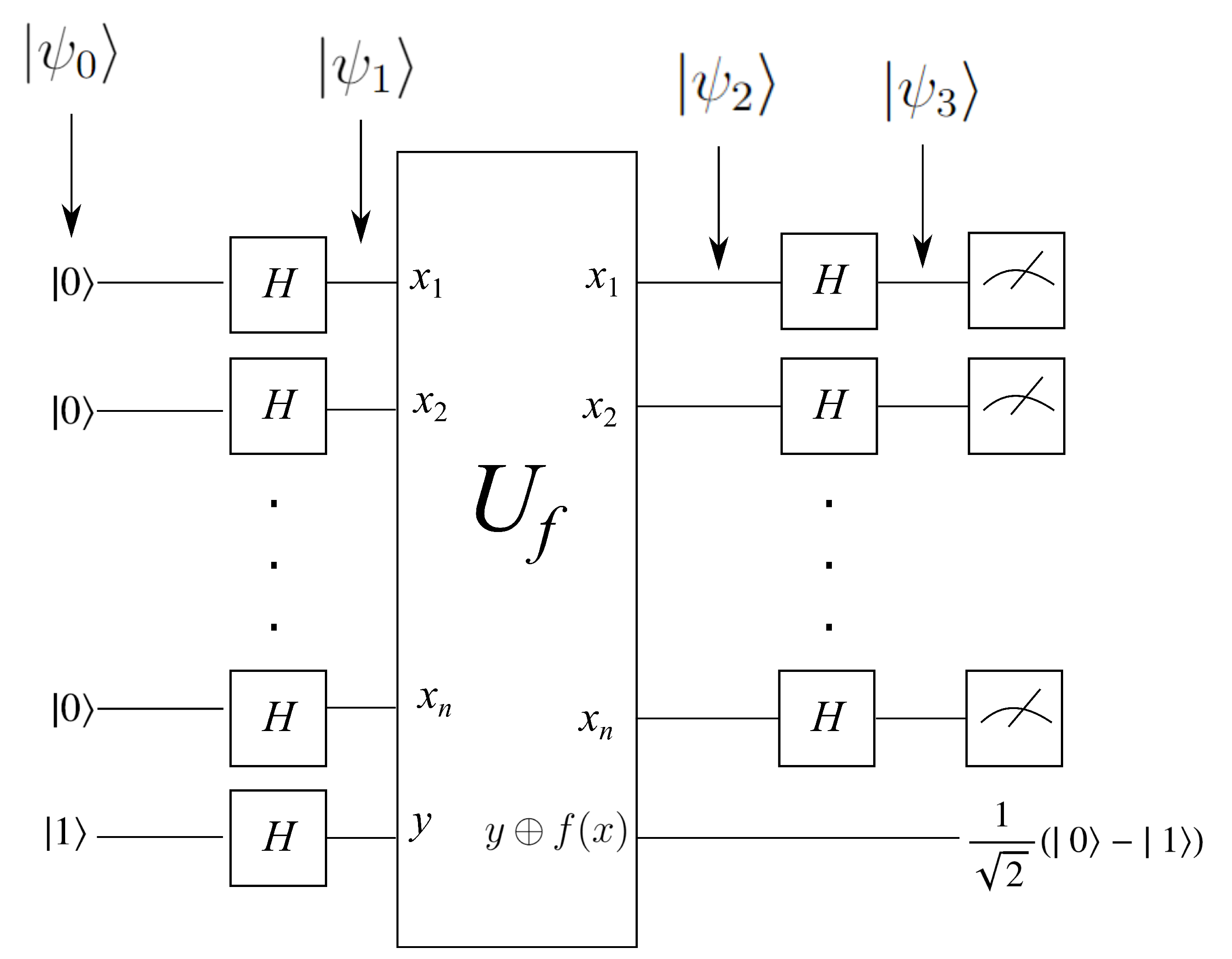
2.3. The Deutsch–Jozsa Algorithm
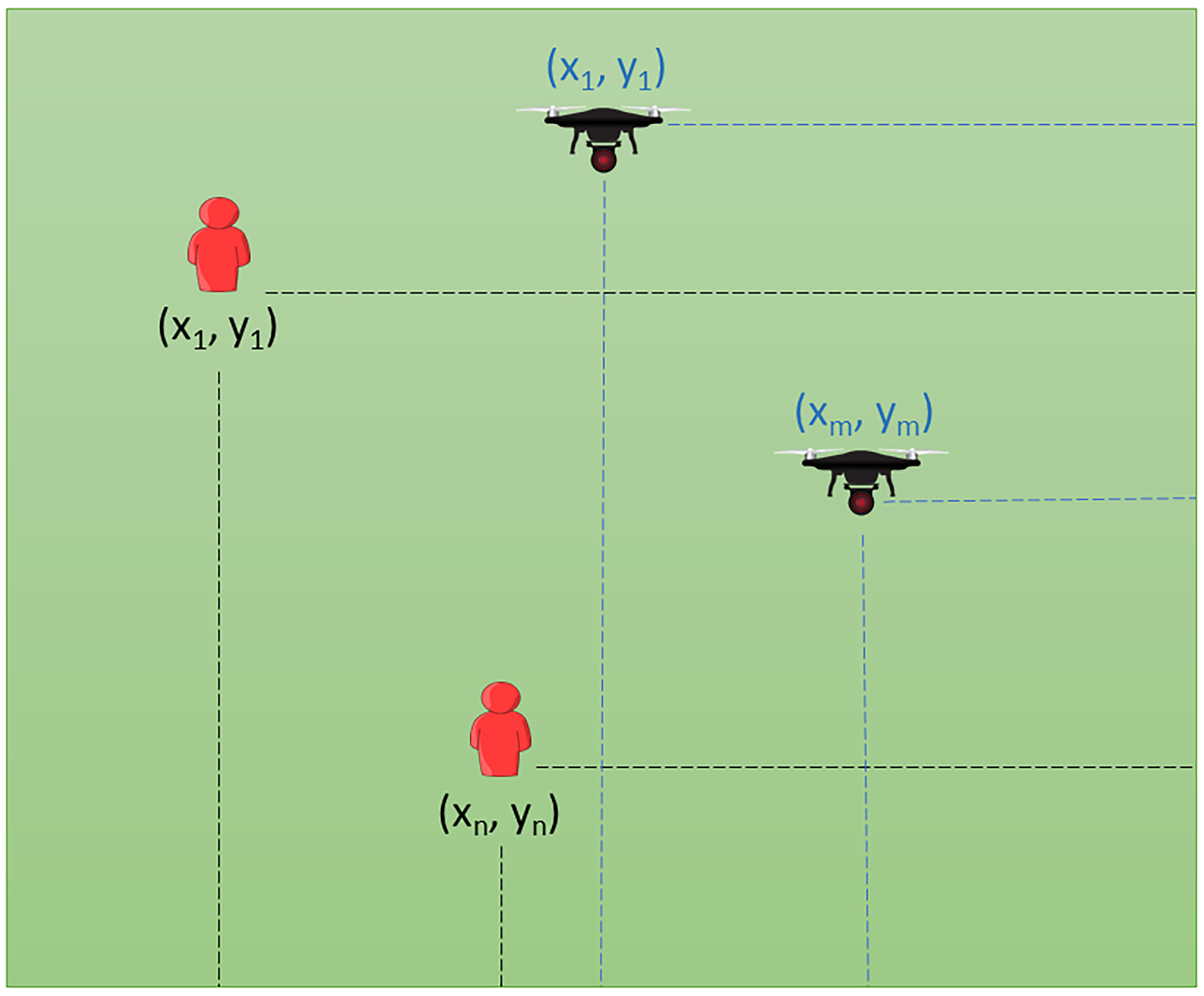
2.4. Disaster Zone Model
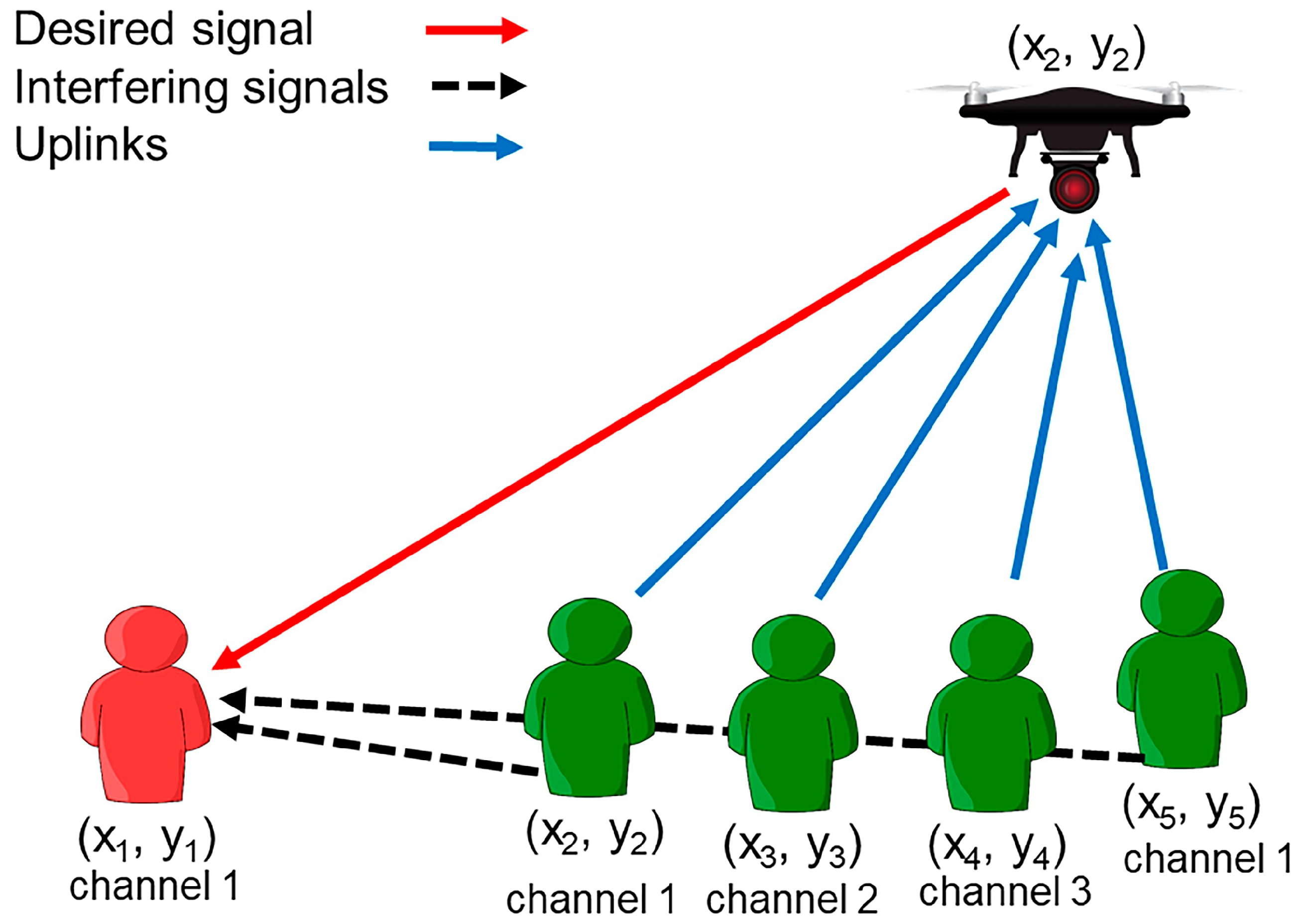
2.5. Objective Function and Restrictions
3. Materials and Methods
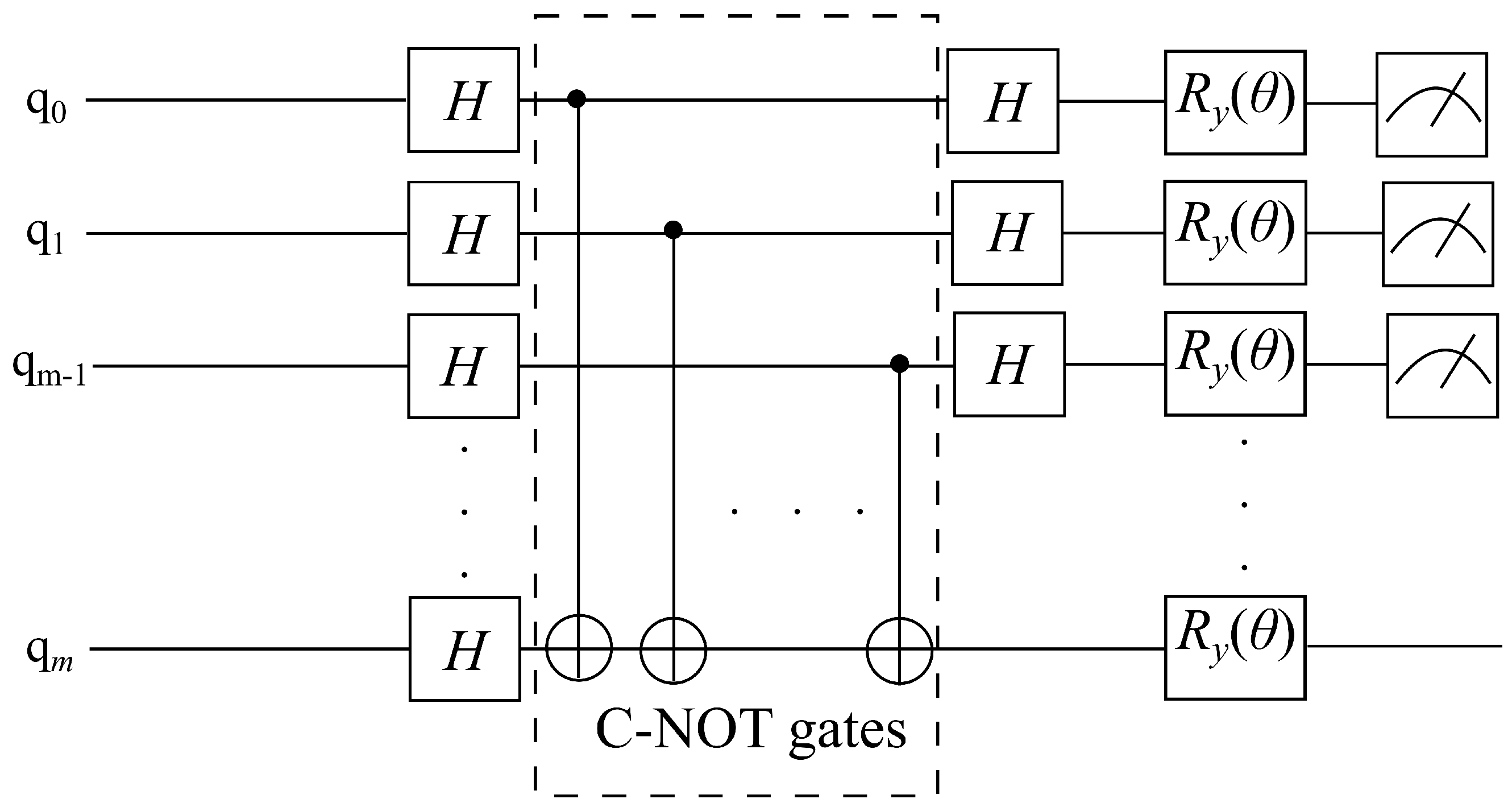
Hybrid Quantum Genetic Algorithm with Fuzzy Adaptive Rotation Angle
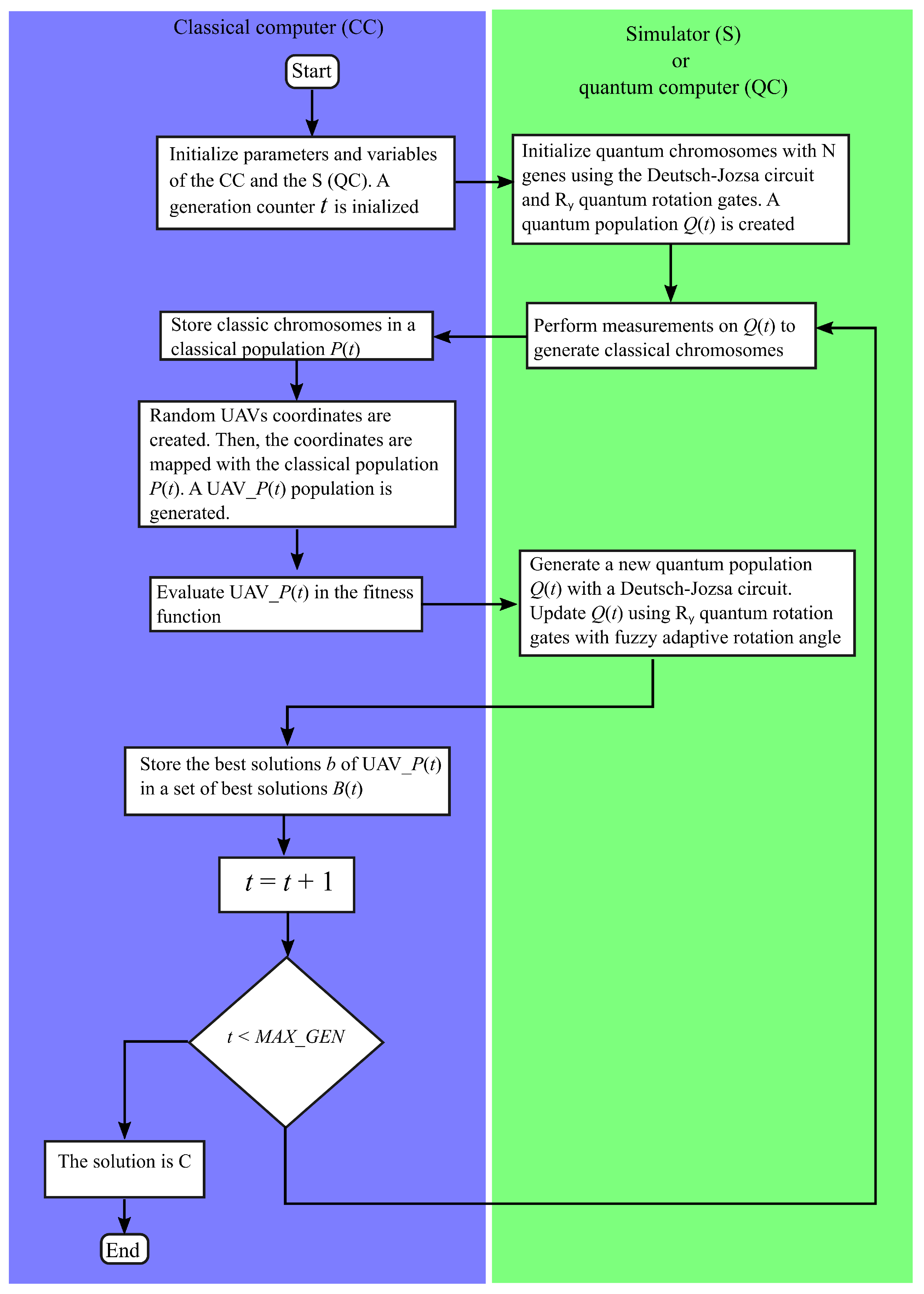
| Algorithm 1 Hybrid Quantum Genetic Algorithm with Fuzzy Adaptive Rotation Angle |
| Require:
The number p of quantum chromosomes, the maximal number of generations , the total number of mobile users N, the total number of UAVs M Ensure: Maximum coverage C as shown in Equation (7) Begin ; Randomly generate the positions of N Initialize using a Deutsch–Jozsa circuit and quantum rotation gates while do Measure using Equation (19) to generate Map with random UAVs’ coordinates. A UAV_ population is created Evaluate UAV_ using the fitness function in Equation (7) Generate the new population using the Deutsch–Jozsa circuit Update using quantum rotation gates with a fuzzy adaptive rotation angle Store the best solution b of UAV_ in End |
| Algorithm 2 Fitness function used to evaluate UAV_ |
| Require:
Number of mobile users N, number of UAVs M Ensure: Maximum coverage C as shown in Equation (7) 1: Begin 2: 3: while do 4: 5: if then 6: while do 7: if then 8: Compute the Euclidean distance between and 9: if then 10: Compute the pathloss 11: if then 12: Compute the SIR of the 13: if then 14: Associate with 15: 16: Add the associated 17: 18: Calculate C 19: End |
4. Results
- Case 1: The worst-case scenario where the UAVs had only one transmission channel to provide connectivity to mobile users.
- Case 2: The best case scenario is that the UAVs had more than one transmission channel to assist the affected area.
- 1.
- Perform the Shapiro–Wilk test to determine if the results have a normal distribution (H0 equals True) or not. Afterward, a parametric or non-parametric test should be applied. A significant level of was used in all experiments, meaning that the probability of rejecting the H0 hypothesis when it is true is 0.01. Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16 and Table 17 show these results. The variables N and W in the tables mentioned above represent the number of samples and the statistical value in the Shapiro–Wilk test, respectively.
- 2.
- At this point, three possible cases are considered.
- (a)
- All results obtained by the Shapiro–Wilk test are true (H0 is True); this means that the results presented by the algorithms have a normal distribution. We use a parametric Welch t-student test with .
- (b)
- All the results obtained by the Shapiro–Wilk test are false (H0 is False); this means the results presented by the algorithms have a non-normal distribution. Here, we use a non-parametric Wilcoxon signed ranks test with .
- (c)
- Some results have a normal distribution, while others do not. In this case, we perform a Bootstrapping procedure to convert non-normally distributed data into a normal distribution. Then, we can apply a Welch t-student test. These results are shown in tables, with a ”boots” label next to the algorithm name.
5. Discussion
- 1.
- The inclusion of the Deutsch–Jozsa quantum circuit within quantum meta-heuristics. This circuit was employed to generate new individuals mimicking a haploid recombination and the mutation operation. This expedited the evolutionary process by leveraging the superposition to generate new individuals, a concept that is applicable to solve various problems.
- 2.
- A novel fuzzy operator was introduced to adapt the rotation angle effectively. The proposal yielded better average results compared to existing methods, particularly in the worst-case experiments, where the conditions challenged the efficiency and robustness of the algorithms.
- 3.
- The introduction of a novel meta-heuristic named HQGAFARA, which was statistically proven to outperform the classical GA.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| C | Coverage |
| GA | Genetic algorithm |
| HQGAFARA | Hybrid Quantum Genetic Algorithm with Fuzzy Adaptive Rotation Angle |
| UAV | Unmanned Aerial Vehicle |
| GQA | Genetic Quantum Algorithms |
| KP | Knapsack Problem |
| QEA | Quantum Evolutionary Algorithm |
| NISQ | Noisy Intermediate-Scale Quantum |
| MU | Mobile Users |
| SIR | Signal-to-Interference Ratio |
References
- Cangialosi, J.P.; Kimberlain, T.B. Hurricane Odile (EP152014). In National Hurricane Center Tropical Cyclone Report; National Hurricane Center: Miami, FL, USA, 2015. [Google Scholar]
- Sapkota, S.N.; Bollinger, L.; Perrier, F. Fatality rates of the Mw~8.2, 1934, Bihar–Nepal earthquake and comparison with the April 2015 Gorkha earthquake. Earth Planets Space 2016, 68, 40. [Google Scholar] [CrossRef]
- Yabe, T.; Ukkusuri, S.V.C.; Rao, P.S. Mobile phone data reveals the importance of pre-disaster inter-city social ties for recovery after Hurricane Maria. Appl. Netw. Sci. 2019, 4, 98. [Google Scholar] [CrossRef]
- Nakata, K.; Katsumata, A.; Muhari, A. Submarine landslide source models consistent with multiple tsunami records of the 2018 Palu tsunami, Sulawesi, Indonesia. Earth Planets Space 2020, 72, 44. [Google Scholar] [CrossRef]
- Cavallo, E.A.; Giles-Aĺvarez, L.; Powell, A. Estimating the Potential Economic Impact of Haiti’s 2021 Earthquake; Inter-American Development Bank: Washington, DC, USA, 2021; p. 11. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M. Natural Disasters. Our World in Data. 2014. Available online: https://ourworldindata.org/natural-disasters (accessed on 1 March 2023).
- Sambo, Y.A.; Klaine, P.V.; Nadas, J.P.B.; Imran, M.A. Energy Minimization UAV Trajectory Design for Delay-Tolerant Emergency Communication. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, D.; Cui, M.; Zhang, G.; Chu, X.; Lin, F. Trajectory optimization and resource allocation for UAV base stations under in-band backhaul constraint. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 83. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Chen, S.Y.; Ling, H.F. Evolutionary optimization for disaster relief operations: A survey. Appl. Soft Comput. 2015, 27, 553–566. [Google Scholar] [CrossRef]
- Talbi, E. Metaheuristics: From Design to Implementation; Wiley Series on Parallel and Distributed Computing; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Martínez-Vargas, A.; Rodríguez-Cortés, G.L.; Montiel-Ross, O. Comparative Representations of a Genetic Algorithm to Locate Unmanned Aerial Vehicles in Disaster Zones. Eng. Lett. 2019, 27, 374–384. [Google Scholar]
- Rodríguez-Cortés, G.L.; Martínez-Vargas, A.; Montiel-Ross, O.H.; Cosío-León, M.; Martínez, D.M. Deployment of Unmanned Aerial Vehicles for Maximum Coverage in Emergency Scenarios Using the (1+1) Evolution Strategy with One-Fifth Success Rule. In Proceedings of the 2021 Mexican International Conference on Computer Science (ENC), Morelia, Mexico, 9–11 August 2021; pp. 1–7. [Google Scholar] [CrossRef]
- ur Rahman, S.; Kim, G.H.; Cho, Y.Z.; Khan, A. Positioning of UAVs for throughput maximization in software-defined disaster area UAV communication networks. J. Commun. Netw. 2018, 20, 452–463. [Google Scholar] [CrossRef]
- Munawar, H.S.; Hammad, A.W.; Waller, S.T. Disaster Region Coverage Using Drones: Maximum Area Coverage and Minimum Resource Utilisation. Drones 2022, 6, 96. [Google Scholar] [CrossRef]
- Yan, T.; Lu, F.; Wang, S.; Wang, L.; Bi, H. A hybrid metaheuristic algorithm for the multi-objective location-routing problem in the early post-disaster stage. J. Ind. Manag. Optim. 2023, 19, 4663–4691. [Google Scholar] [CrossRef]
- Gupta, M.; Varma, S. Optimal placement of UAVs of an aerial mesh network in an emergency situation. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 343–358. [Google Scholar] [CrossRef]
- Peer, M.; Bohara, V.A.; Srivastava, A. Multi-UAV placement strategy for disaster-resilient communication network. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–7. [Google Scholar]
- Liu, G.; Shakhatreh, H.; Khreishah, A.; Guo, X.; Ansari, N. Efficient deployment of UAVs for maximum wireless coverage using genetic algorithm. In Proceedings of the 2018 IEEE 39th Sarnoff Symposium, Newark, NJ, USA, 24–25 September 2018; pp. 1–6. [Google Scholar]
- Kumbhar, A.; Güvenç, I.; Singh, S.; Tuncer, A. Exploiting LTE-Advanced HetNets and FeICIC for UAV-assisted public safety communications. IEEE Access 2017, 6, 783–796. [Google Scholar] [CrossRef]
- Hassan, A.; Ahmad, R.; Ahmed, W.; Magarini, M.; Alam, M.M. Managing Critical Nodes in UAV assisted Disaster Networks. In Proceedings of the 2020 17th Biennial Baltic Electronics Conference (BEC), Tallinn, Estonia, 6–8 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Lai, X.; Hao, J.; Yue, D.; Gao, H. A Diversification-based Quantum Particle Swarm Optimization Algorithm for the Multidimensional Knapsack Problem. In Proceedings of the 2018 5th IEEE International Conference on Cloud Computing and Intelligence Systems (CCIS), Nanjing, China, 23–25 November 2018; pp. 315–319. [Google Scholar] [CrossRef]
- Pradhan, K.; Basu, S.; Thakur, K.; Maity, S.; Maiti, M. Imprecise modified solid green traveling purchaser problem for substitute items using quantum-inspired genetic algorithm. Comput. Ind. Eng. 2020, 147, 106578. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- LaValle, S. Planning Algorithms; Cambridge University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Zhang, X.; Xia, S.; Li, X. Quantum Behavior-Based Enhanced Fruit Fly Optimization Algorithm with Application to UAV Path Planning. Int. J. Comput. Intell. Syst. 2020, 13, 1315–1331. [Google Scholar] [CrossRef]
- Hu, C.; Xia, Y.; Zhang, J. Adaptive Operator Quantum-Behaved Pigeon-Inspired Optimization Algorithm with Application to UAV Path Planning. Algorithms 2019, 12, 3. [Google Scholar] [CrossRef]
- Li, S.; Deng, Y. Quantum-entanglement pigeon-inspired optimization for unmanned aerial vehicle path planning. Aircr. Eng. Aerosp. Technol. 2019, 91, 171–181. [Google Scholar] [CrossRef]
- Mousavi, S.; Afghah, F.; Ashdown, J.D.; Turck, K. Use of a quantum genetic algorithm for coalition formation in large-scale UAV networks. Ad Hoc Netw. 2019, 87, 26–36. [Google Scholar] [CrossRef]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Wu, Y.; Bao, W.S.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef]
- Zhong, H.S.; Deng, Y.H.; Qin, J.; Wang, H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Wu, D.; Gong, S.Q.; Su, H.; et al. Phase-Programmable Gaussian Boson Sampling Using Stimulated Squeezed Light. Phys. Rev. Lett. 2021, 127, 180502. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Yanofsky, N.; Manucci, M. Quantum Computing for Computer Scientists; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Zhang, G.; Jin, W.; Li, N. An Improved Quantum Genetic Algorithm and Its Application. In Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. RSFDGrC 2003. Lecture Notes in Computer Science; Wang, G., Liu, Q., Yao, Y., Skowron, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2639. [Google Scholar] [CrossRef]
- Narayanan, A.; Moore, M. Quantum-Inspired Genetic Algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 61–66. [Google Scholar] [CrossRef]
- Narayanan, A. Quantum computing for beginners. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; (Cat. No. 99TH8406). Volume 3, pp. 2231–2238. [Google Scholar]
- Han, K.-H.; Kim, J.-H. Genetic quantum algorithm and its application to combinatorial optimization problem. In Proceedings of the 2000 Congress on Evolutionary Computation CEC00 (Cat. No.00TH8512), La Jolla, CA, USA, 16–19 July 2000; Volume 2, pp. 1354–1360. [Google Scholar]
- Han, K.-H.; Kim, J.-H. Quantum-inspired evolutionary algorithm for a class of combinatorial optimization. IEEE Trans. Evol. Comput. 2002, 6, 580–593. [Google Scholar] [CrossRef]
- Montiel Ross, O.H. A Review of Quantum-Inspired Metaheuristics: Going From Classical Computers to Real Quantum Computers. IEEE Access 2020, 8, 814–838. [Google Scholar] [CrossRef]
- Zhang, G. Quantum-inspired evolutionary algorithms: A survey and empirical study. J. Heuristics 2011, 17, 303–351. [Google Scholar] [CrossRef]
- Montiel Ross, O.; Rubio, Y.; Olvera, C.; Rivera, A. Quantum-Inspired Acromyrmex Evolutionary Algorithm. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum Supremacy using a Programmable Superconducting Processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Pednault, E.; Gunnels, J.A.; Nannicini, G.; Horesh, L.; Wisnieff, R. Leveraging Secondary Storage to Simulate Deep 54-qubit Sycamore Circuits. arXiv 2019. [Google Scholar]
- King, J.; Yarkoni, S.; Raymond, J.; Ozfidan, I.; King, A.D.; Nevisi, M.M.; Hilton, J.P.; McGeoch, C.C. Quantum Annealing amid Local Ruggedness and Global Frustration. arXiv 2017. [Google Scholar] [CrossRef]
- Hirzel, T. Building the Quantum Stack for the NISQ Era. Available online: https://www.hpcwire.com/2020/08/24/building-the-quantum-stack-for-the-nisq-era/ (accessed on 12 January 2023).
- Williams, C. Explorations in Quantum Computing; Springer: London, UK, 2011. [Google Scholar]
- Deutsch, D.; Jozsa, R. Rapid solution of problems by quantum computation. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1992, 439, 553–558. [Google Scholar]
- Cao, Z.; Uhlmann, J.; Liu, L. Analysis of Deutsch-Jozsa Quantum Algorithm. IACR Cryptol. EPrint Arch. 2018, 2018, 249. [Google Scholar]
- Johansson, N.; Larsson, J.A. Efficient classical simulation of the Deutsch–Jozsa and Simon’s algorithms. Quantum Inf. Process. 2017, 16, 233. [Google Scholar] [CrossRef]
- Paredes López, M.; Meneses Viveros, A.; Morales-Luna, G. Algoritmo cuántico de Deutsch y Jozsa en GAMA. Rev. Mex. Física 2018, 64, 181–189. [Google Scholar] [CrossRef]
- Martínez-Vargas, A.; Andrade, Á.G. Deployment analysis and optimization of heterogeneous networks under the spectrum underlay strategy. EURASIP J. Wirel. Commun. Netw. 2015, 2015, 55. [Google Scholar] [CrossRef]
- Wittek, P. 3-Quantum Mechanics. In Quantum Machine Learning; Wittek, P., Ed.; Academic Press: Boston, MA, USA, 2014; pp. 25–39. [Google Scholar] [CrossRef]
- Rubio, Y.; Olvera, C.; Montiel, O. Quantum-inspired evolutionary algorithms on ibm quantum experience. Eng. Lett. 2021, 29, 1573–1584. [Google Scholar]
- Kumbhar, A.; Koohifar, F.; Güvenç, I.; Mueller, B. A Survey on Legacy and Emerging Technologies for Public Safety Communications. IEEE Commun. Surv. Tutor. 2017, 19, 97–124. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Yu, Y.; Qian, C. Evolutionary Learning: Advances in Theories and Algorithms, 1st ed.; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2019. [Google Scholar]

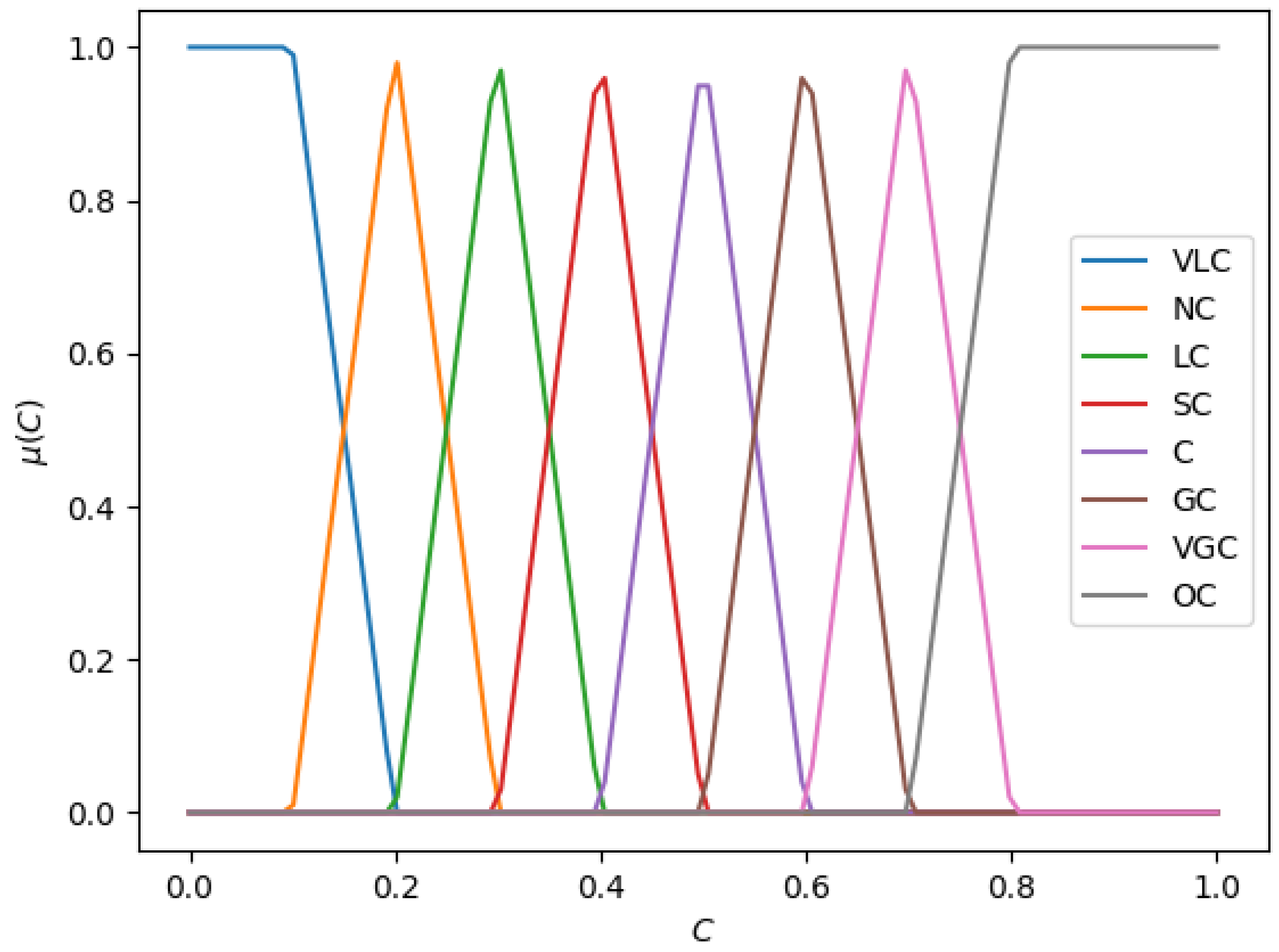
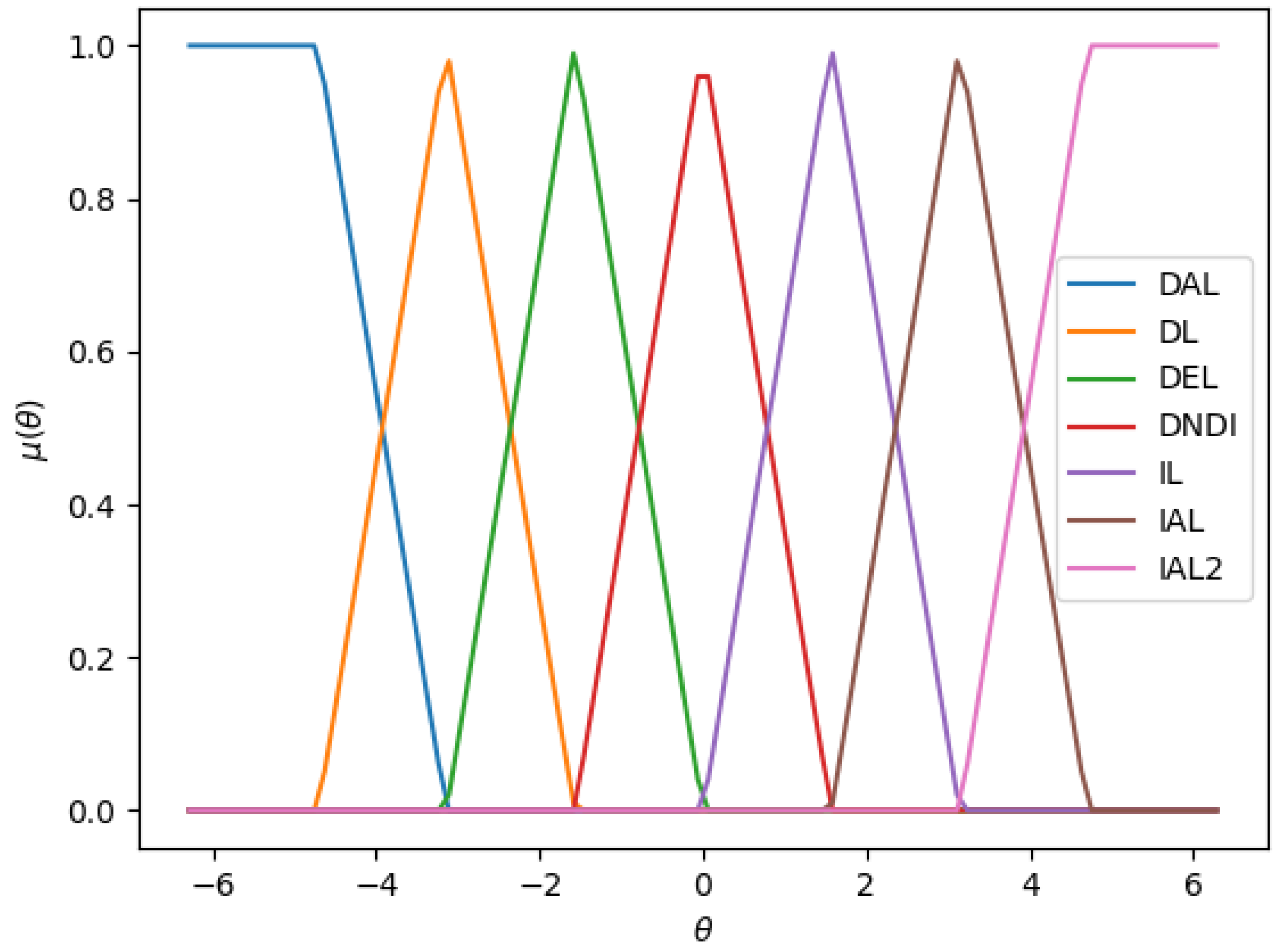
| Variable Name | Term Name | Type | Parameters |
|---|---|---|---|
| C | VLC | Trapezoidal | [0, 0, 0.1, 0.2] |
| C | NC | Triangular | [0.1, 0.2, 0.3] |
| C | LC | Triangular | [0.2, 0.3, 0.4] |
| C | SC | Triangular | [0.3, 0.4, 0.5] |
| C | C | Triangular | [0.4, 0.5, 0.6] |
| C | GC | Triangular | [0.5, 0.6, 0.7] |
| C | VGC | Triangular | [0.6, 0.7, 0.8] |
| C | OC | Trapezoidal | [0.7, 0.8, 1, 1] |
| DAL | Trapezoidal | [−2, −2, −3/2, −] | |
| DL | Triangular | [−3/2, −, −/2] | |
| DEL | Triangular | [−, −/2, 0] | |
| DNDI | Triangular | [−/2, 0 , /2] | |
| IL | Triangular | [0, /2, ] | |
| IAL | Triangular | [/2, , 3/2] | |
| IAL2 | Trapezoidal | [, 3/2, 2, 2] |
| VLC | NC | LC | SC | C | GC | VGC | OC |
|---|---|---|---|---|---|---|---|
| IAL2 | IAL | IL | DEL | DL | DEL | DNDI | DNDI |
| Parameter | Values |
|---|---|
| transmit power | 24 dBm |
| transmit power | 73 dBm |
| Altitude of | 150 m |
| Height of | 1.5 m |
| Frequency | 700 MHz |
| M | Algorithm | Best | Mean | Worst | Std | CI |
|---|---|---|---|---|---|---|
| 5 | GA | 0.36 | 0.33 | 0.296 | 1.47 × 10 | 6.92 × 10 |
| HQGAARA- | 0.356 | 0.338 | 0.328 | 6.65 × 10 | 3.13 × 10 | |
| HQGAARA- | 0.358 | 0.336 | 0.322 | 8.78 × 10 | 4.13 × 10 | |
| HQGAFARA | 0.348 | 0.33 | 0.318 | 7.48 × 10 | 3.52 × 10 | |
| 10 | GA | 0.604 | 0.539 | 0.496 | 2.64 × 10 | 1.24 × 10 |
| HQGAARA- | 0.578 | 0.556 | 0.532 | 1.22 × 10 | 5.74 × 10 | |
| HQGAARA- | 0.582 | 0.551 | 0.532 | 1.37 × 10 | 6.46 × 10 | |
| HQGAFARA | 0.572 | 0.550 | 0.532 | 9.62 × 10 | 4.52 × 10 | |
| 20 | GA | 0.534 | 0.457 | 0.36 | 5.06 × 10 | 2.38 × 10 |
| HQGAARA- | 0.538 | 0.470 | 0.422 | 2.46 × 10 | 1.16 × 10 | |
| HQGAARA- | 0.49 | 0.447 | 0.416 | 1.70 × 10 | 8.01 × 10 | |
| HQGAFARA | 0.538 | 0.462 | 0.426 | 2.44 × 10 | 1.15 × 10 |
| M | Algorithm | Best Case | Worst Case |
|---|---|---|---|
| 5 | HQGAARA- | ||
| HQGAARA- | |||
| HQGAFARA | |||
| 10 | HQGAARA- | ||
| HQGAARA- | |||
| HQGAFARA | |||
| 20 | HQGAARA- | ||
| HQGAARA- | |||
| HQGAFARA |
| M | Algorithm | Best | Mean | Worst | Std | CI |
|---|---|---|---|---|---|---|
| 5 | GA | 0.174 | 0.155 | 0.142 | 7.27 × 10 | 3.42 × 10 |
| HQGAARA- | 0.168 | 0.160 | 0.152 | 3.82 × 10 | 1.80 × 10 | |
| HQGAARA- | 0.17 | 0.159 | 0.148 | 6.23 × 10 | 2.93 × 10 | |
| HQGAFARA | 0.172 | 0.160 | 0.154 | 5.31 × 10 | 2.50 × 10 | |
| 10 | GA | 0.266 | 0.246 | 0.22 | 1.20 × 10 | 5.66 × 10 |
| HQGAARA- | 0.268 | 0.253 | 0.242 | 6.11 × 10 | 2.88 × 10 | |
| HQGAARA- | 0.274 | 0.253 | 0.238 | 7.54 × 10 | 3.55 × 10 | |
| HQGAFARA | 0.264 | 0.253 | 0.242 | 5.42 × 10 | 2.55 × 10 | |
| 20 | GA | 0.246 | 0.207 | 0.156 | 2.50 × 10 | 1.18 × 10 |
| HQGAARA- | 0.256 | 0.214 | 0.198 | 1.24 × 10 | 5.82 × 10 | |
| HQGAARA- | 0.238 | 0.208 | 0.19 | 1.03 × 10 | 4.86 × 10 | |
| HQGAFARA | 0.244 | 0.206 | 0.19 | 1.20 × 10 | 5.62 × 10 |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA |
| N | 30 | 30 | 30 | 30 |
| W | 0.978 | 0.960 | 0.964 | 0.942 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 0.758 | 0.303 | 0.398 | 0.101 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA |
| d.o.f. | 40 | 47 | 43 | |
| t-value | −2.830 | −2.038 | −0.045 | |
| Critical value | 3.551 | 3.515 | 3.538 | |
| Hypothesis H0 | True | True | True | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA |
| N | 30 | 30 | 30 | 30 |
| W | 0.970 | 0.973 | 0.940 | 0.972 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 0.533 | 0.627 | 0.089 | 0.583 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA |
| d.o.f. | 41 | 44 | 37 | |
| t-value | −3.150 | −2.257 | −2.169 | |
| Critical value | 3.551 | 3.526 | 3.574 | |
| Hypothesis H0 | True | True | True | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA_boots |
| N | 30 | 30 | 30 | 30 |
| W | 0.950 | 0.965 | 0.964 | 0.986 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 0.171 | 0.408 | 0.386 | 0.953 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA_boots |
| d.o.f. | 42 | 35 | 29 | |
| t-value | −1.284 | 1.011 | −0.741 | |
| Critical value | 3.538 | 3.591 | 3.659 | |
| Hypothesis H0 | True | True | True | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA |
| N | 30 | 30 | 30 | 30 |
| W | 0.962 | 0.955 | 0.962 | 0.849 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 0.356 | 0.223 | 0.347 | 0.0006 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA |
| d.o.f. | 44 | 57 | 53 | |
| t-value | −3.512 | −2.441 | −3.365 | |
| Critical value | 3.526 | 3.46 | 3.496 | |
| Hypothesis H0 | True | True | True | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA |
| N | 30 | 30 | 30 | 30 |
| W | 0.972 | 0.974 | 0.945 | 0.972 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 0.601 | 0.655 | 0.125 | 0.598 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA |
| d.o.f. | 43 | 49 | 40 | |
| t-value | −2.970 | −2.771 | −3.262 | |
| Critical value | 3.526 | 3.496 | 3.551 | |
| Hypothesis H0 | True | True | True | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA | HQGAARA-_boots | HQGAARA- | HQGAFARA_boots |
| N | 30 | 30 | 30 | 30 |
| W | 0.952 | 0.967 | 0.930 | 0.968 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 0.194 | 0.468 | 0.051 | 0.480 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA | HQGAARA-_boots | HQGAARA- | HQGAFARA_boots |
| d.o.f. | 29 | 39 | 29 | |
| t-value | −1.541 | −0.233 | 0.057 | |
| Critical value | 3.659 | 3.558 | 3.659 | |
| Hypothesis H0 | True | True | True | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA |
| Mean | 233 | 346 | 310 | 449 |
| N | 30 | 30 | 30 | 30 |
| W | 0.723 | 0.820 | 0.773 | 0.901 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 3.39 × 10 | 1.55 × 10 | 2.16 × 10 | 8.83 × 10 |
| Hypothesis H0 | False | False | False | False |
| Wilcoxon signed ranks test ( = 0.001) | ||||
| Algorithms | GA | HQGAARA- | HQGAARA- | HQGAFARA |
| N | 30 | 30 | 30 | |
| W | 174.5 | 186.5 | 102.5 | |
| Critical value | 78 | 78 | 78 | |
| R+ | 174.5 | 186.5 | 102.5 | |
| R- | 290.5 | 278.5 | 362.5 | |
| p-value | 2.37 × 10 | 3.49 × 10 | 6.19 × 10 | |
| Hypothesis H0 | True | True | True | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA | HQGAARA-_boots | HQGAARA-_boots | HQGAFARA |
| Mean | 368 | 470 | 198 | 556 |
| N | 30 | 30 | 30 | 30 |
| W | 0.959 | 0.980 | 0.906 | 0.950 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 0.287 | 0.828 | 0.011 | 0.167 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA | HQGAARA-_boots | HQGAARA-_boots | HQGAFARA |
| d.o.f. | 36 | 34 | 57 | |
| t-value | −2.570 | 4.369 | −3.342 | |
| Critical value | 3.582 | 3.601 | 3.46 | |
| Hypothesis H0 | True | False | True | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA-boots | HQGAARA-_boots | HQGAARA- | HQGAFARA |
| Mean | 851 | 458 | 163 | 464 |
| N | 30 | 30 | 30 | 30 |
| W | 0.980 | 0.949 | 0.973 | 0.948 |
| Critical value | 0.817 | 0.163 | 0.9 | 0.9 |
| p-value | 8.17 × 10 | 0.1625 | 0.618 | 0.148 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA-boots | HQGAARA-_boots | HQGAARA- | HQGAFARA |
| d.o.f. | 48 | 38 | 30 | |
| t-value | 42.638 | 53.478 | 7.882 | |
| Critical value | 3.505 | 3.566 | 3.646 | |
| Hypothesis H0 | False | False | False | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA_boots | HQGAARA-_boots | HQGAARA-_boots | HQGAFARA |
| Mean | 211 | 490 | 449 | 500 |
| N | 30 | 30 | 30 | 30 |
| W | 0.964 | 0.949 | 0.959 | 0.962 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 0.398 | 1.58 × 10 | 2.94 × 10 | 3.47 × 10 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA_boots | HQGAARA-_boots | HQGAARA-_boots | HQGAFARA |
| d.o.f. | 40 | 35 | 30 | |
| t-value | −23.451 | −14.840 | −6.385 | |
| Critical value | 3.551 | 3.591 | 3.646 | |
| Hypothesis H0 | False | False | False | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA | HQGAARA-_boots | HQGAARA-_boots | HQGAFARA |
| Mean | 391 | 424 | 202 | 502 |
| N | 30 | 30 | 30 | 30 |
| W | 0.916 | 0.948 | 0.964 | 0.953 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 2.11 × 10 | 1.46 × 10 | 3.87 × 10 | 2.08 × 10 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA | HQGAARA-_boots | HQGAARA-_boots | HQGAFARA |
| d.o.f. | 37 | 31 | 54 | |
| t-value | −0.770 | 4.753 | −1.692 | |
| critical value | 3.574 | 3.633 | 3.496 | |
| Hypothesis H0 | True | False | True | |
| Shapiro–Wilk test ( = 0.01) | ||||
| Algorithms | GA-boots | HQGAARA-_boots | HQGAARA- | HQGA-Fuzzy |
| Mean | 846 | 522 | 148 | 498 |
| N | 30 | 30 | 30 | 30 |
| W | 0.911 | 0.979 | 0.965 | 0.972 |
| Critical value | 0.9 | 0.9 | 0.9 | 0.9 |
| p-value | 1.61 × 10 | 8.00 × 10 | 4.23 × 10 | 5.95 × 10 |
| Hypothesis H0 | True | True | True | True |
| Welch t-student test ( = 0.001) | ||||
| Algorithms | GA-boots | HQGAARA-_boots | HQGAARA- | HQGA-Fuzzy |
| d.o.f. | 35 | 34 | 29 | |
| t-value | 27.006 | 52.306 | 7.413 | |
| Critical value | 3.591 | 3.601 | 3.659 | |
| Hypothesis H0 | False | False | False | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballinas, E.; Montiel, O.; Martínez-Vargas, A.; Rodríguez-Cortés, G. Hybrid Quantum Genetic Algorithm with Fuzzy Adaptive Rotation Angle for Efficient Placement of Unmanned Aerial Vehicles in Natural Disaster Areas. Axioms 2024, 13, 48. https://doi.org/10.3390/axioms13010048
Ballinas E, Montiel O, Martínez-Vargas A, Rodríguez-Cortés G. Hybrid Quantum Genetic Algorithm with Fuzzy Adaptive Rotation Angle for Efficient Placement of Unmanned Aerial Vehicles in Natural Disaster Areas. Axioms. 2024; 13(1):48. https://doi.org/10.3390/axioms13010048
Chicago/Turabian StyleBallinas, Enrique, Oscar Montiel, Anabel Martínez-Vargas, and Gabriela Rodríguez-Cortés. 2024. "Hybrid Quantum Genetic Algorithm with Fuzzy Adaptive Rotation Angle for Efficient Placement of Unmanned Aerial Vehicles in Natural Disaster Areas" Axioms 13, no. 1: 48. https://doi.org/10.3390/axioms13010048
APA StyleBallinas, E., Montiel, O., Martínez-Vargas, A., & Rodríguez-Cortés, G. (2024). Hybrid Quantum Genetic Algorithm with Fuzzy Adaptive Rotation Angle for Efficient Placement of Unmanned Aerial Vehicles in Natural Disaster Areas. Axioms, 13(1), 48. https://doi.org/10.3390/axioms13010048







