Abstract
This tutorial delves into the application of proportional odds-type ordinal logistic regression to assess the impact of incorporating both fixed and random effects when predicting the rankings of Brazilian universities in a well-established international academic assessment utilizing authentic data. In addition to offering valuable insights into the estimation of ordinal logistic models, this study underscores the significance of integrating random effects into the analysis and addresses the potential pitfalls associated with the inappropriate treatment of phenomena exhibiting categorical ordinal characteristics. Furthermore, we have made the R language code and dataset available as supplementary resources for the replication.
Keywords:
ordinal logistic regression; proportional odds; random coefficient model; repeated measures; intra-class correlations; higher education institution MSC:
6201; 62H12; 62H86; 62H99; 62J12; 62J99
1. Introduction
Ordinal variables are commonly assumed to be composed of categories that present semantic differences with a sense of order without the possibility of gauging the distance between these categories [1,2]. Manifestations of their occurrence are usually amalgamated in surveys that use Likert scales and/or in the organization of observations into positions in a ranking [3].
Although prevalent across diverse scientific domains, it is not uncommon for researchers to use transformations that disregard the existence of a sense of order in their analysis and subsequent modeling. Fullerton and Anderson [4] point out that these transformations concern (i) the arbitrary recoding of ordinal categories so that they are understood as metric values, applying estimates aimed at continuous variables or count data, or (ii) the use of binary models after the dichotomization of a given polychotomous phenomenon.
Disregarding the sense of order of a given phenomenon can lead to unreformable problems in the data analysis process and in the interpretation of the results with the intention of underpinning the decision-making process. Liddell and Kruschke [5] conducted an analysis across articles in the Journal of Personality and Social Psychology (JPSP), Psychological Science (PS), and Journal of Experimental Psychology: General (JEP:G). The authors revealed a consistent trend where whenever the term “Likert” was referenced, ordinal data were incorrectly analyzed as if they were a metric. Their findings suggest an elevated risk of Type I and Type II errors, signifying the potential for false positives or negatives. Moreover, these errors may be compounded by the inversion of model parameter signs.
However, following an analysis of ordinal data with binary models would depend on an arbitrary dichotomization of possible polychotomous Y. Let us take a general example of a survey using a Likert scale with the following response options: “very bad”, “bad”, “neutral”, “good” and “excellent”. Following the controversial line of reasoning proposed, similar categories such as “very bad” and “bad” would be merged into a single category; as well as “good” and “excellent” categories being merged into another category. For the dichotomization of the phenomenon to be effective, there would still be a problem with what to do with the neutral category. Nadler et al. [6] point out that researchers often find themselves at the following crossroads when they take the undesirable path described above (i) or arbitrarily add observations from neutral categories to a given category (in the proposed example, either the one formed by combining “very bad” and “bad”, or the one generated by combining “good” and “excellent”); (ii) or assume that the observations in the neutral categories are missing values.
Therefore, this research is motivated by the current and latent need to disseminate ordinal logistic regressions to young researchers as well as to remind more experienced researchers of their existence. Moreover, the aim was to demonstrate the advantages of considering the contexts (nestings) that exist in the data. In the words of Bauer and Sterba [7] (p. 374), researchers may be reluctant to use multilevel models for two main reasons: (1) they felt more familiar with linear fixed-effects models and, as such, were unsure of how to interpret non-linear models; (2) it is not always obvious to practitioners in the field that ordinal multilevel options exist, and there is a gap in the literature regarding the definition of an ordinal variable [1,3]. This raises questions regarding which functional forms should be used to model a phenomenon that behaves in an ordinal manner.
In fact, any query in scientific portals, such as Google Scholar, Scopus, Web of Science, and PubMed, among others, about any subject shows a predilection for the use of linear models by researchers, regardless of the period considered. To give you an idea, as of December 2023, a search for keywords encompassing the subject “ordinal logistic regressions” returned only 24,600 results in the Google Scholar tool, 12,704 results in the Scopus portal, 11,195 results in the Web of Science and 23,647 results in the PubMed portal (Considering the following naïve query: “ordinal regression” OR “ordered regression” OR “ordinal logistic regression” OR “ordered logistic regression” OR “ordinal logit regression” OR “ordered logit regression” OR “ordinal probit regression” OR “ordered probit regression” OR “adjacent-category” OR “cumulative-odds” OR “proportional odds” OR “non proportional odds” OR “partial odds”. Only scientific articles published in English were counted. No filter was run on the publication date of the articles counted).
In addition, this study shares, free of charge, its unprecedented and real-world database, as well as the commented codes in the R computer language, which is also free and open source.
The necessary and brilliant contributions of Hedeker and Gibbons [8], Fielding et al. [9], Li et al. [10], and Hedeker [11] are worth mentioning.
The studies by Hedeker and Gibbons [8] focused, from a practical point of view, on educating readers about ordinal probit regressions considering fixed and random effects. Li et al. [10] drew an interesting comparison between binary and ordinal logistic estimations, also considering fixed and random effects but for dichotomous phenomena.
Fielding et al. [9] compare linear and ordinal logistic regressions from a multilevel perspective. Hedeker [11] worked with ordinal logistic regressions of the proportional odds type and compared them with ordinal nonproportional odds logistic regressions, both from a multilevel perspective.
This study, although similar to the aforementioned studies, differs in the following aspects: (i) assumes a polychotomous ordinal phenomenon; (ii) based on this polychotomous ordinal phenomenon, it is proposed to consider it concurrently from the perspectives and premises of linear models, binary logistic models and ordinal logistic models; (iii) the phenomenon is first modeled without taking its contexts into account (nesting) and then taking them into account; (iv) with the exception of the time of Hedeker’s [11] studies, data processing capacity, with an emphasis on using the EM algorithm for multilevel estimations, was a considerable problem, which prevented many studies from using this type of approach; (v) most of the aforementioned studies have used software that is not free and is not open source; and (vi) although this study is a tutorial, it uses real and unpublished data from Brazilian universities and, although this was not the central objective of the study, it can be said that this research contributes with insights and ideas regarding modeling aimed at improving the positions of these institutions in national and international rankings.
Returning to the core of this study, considering a phenomenon that behaves in an ordinal polytomous way to avoid incurring the difficulties mentioned above (arbitrary recoding and dichotomization), ordinal logistic regressions are an interesting solution for statistical analysis and inference.
According to Hilbe [12], there are various types of ordinal logistic models, such as adjacent-category, cumulative odds, and continuation-ratio models. This study delves into estimations using the proportional odds type of ordinal logistic regression for three main reasons: (i) it is the most commonly used model for analyzing ordinal data [13,14,15]; (ii) it enables the measurement of covariate effects on the studied phenomenon via coefficients, facilitating the calculation of probability ratios [16,17,18]; and (iii) compared with other ordinal logistic models, the presentation of the results is notably simplified and straightforward [19].
In addition to ordinal logistic models, the study also drew comparisons between a classic linear regression model and binary logistic estimation. In this way, the reader can see the limitations and advantages of each approach, as well as the consequences of arbitrary recoding [4,5] and the arbitrary dichotomization described [6]. This research also aims to explore the main guidelines for ordinal logistic estimations from a multilevel perspective in order to take into account idiosyncrasies and observational contexts [20,21,22].
The remainder of this paper is organized as follows. Section 2 introduces the conventional proportional odds methodology for ordinal logistic regressions. Section 3 discusses a multilevel perspective, considering inherent data nesting. Section 4 extends the proportional odds models within a multilevel framework, addressing nested data structures involving repeated measures. Section 5 describes the datasets used in this study. Section 6 presents an exploration and a comparative analysis of the models estimated in this study. Section 7 discusses and interprets the results. Finally, Section 8 provides concluding remarks based on the findings of the study.
2. Ordinal Logit Regression—A Traditional Proportional Odds Approach
In ordinal logistic regression models, the dependent variable () manifests in a latent form with a sense of order between its categories, and the outcome of the estimation is the chance of the occurrence of the event studied. Therefore, represents an ordinal categorical variable, and the estimation yields the probability of occurrence for each of its respective categories, where . The prevailing method for conducting ordinal logistic regression typically involves Generalized Linear Models (GLM).
As elucidated by Hilbe [12], within the framework of the proportional odds model, there is a comparison between the probability of an equal or lower response () and the probability of a higher response (). Agresti [23] points out that estimations via proportional odds generate models that concomitantly use the logits () of cumulative probabilities, as shown in Equation (1):
being .
Following Agresti [23], cumulative logits are defined according to Equation (2):
where , and each logit uses all the response categories of .
From Equation (2), the proportional odds model can be described mathematically according to Equation (3).
where .
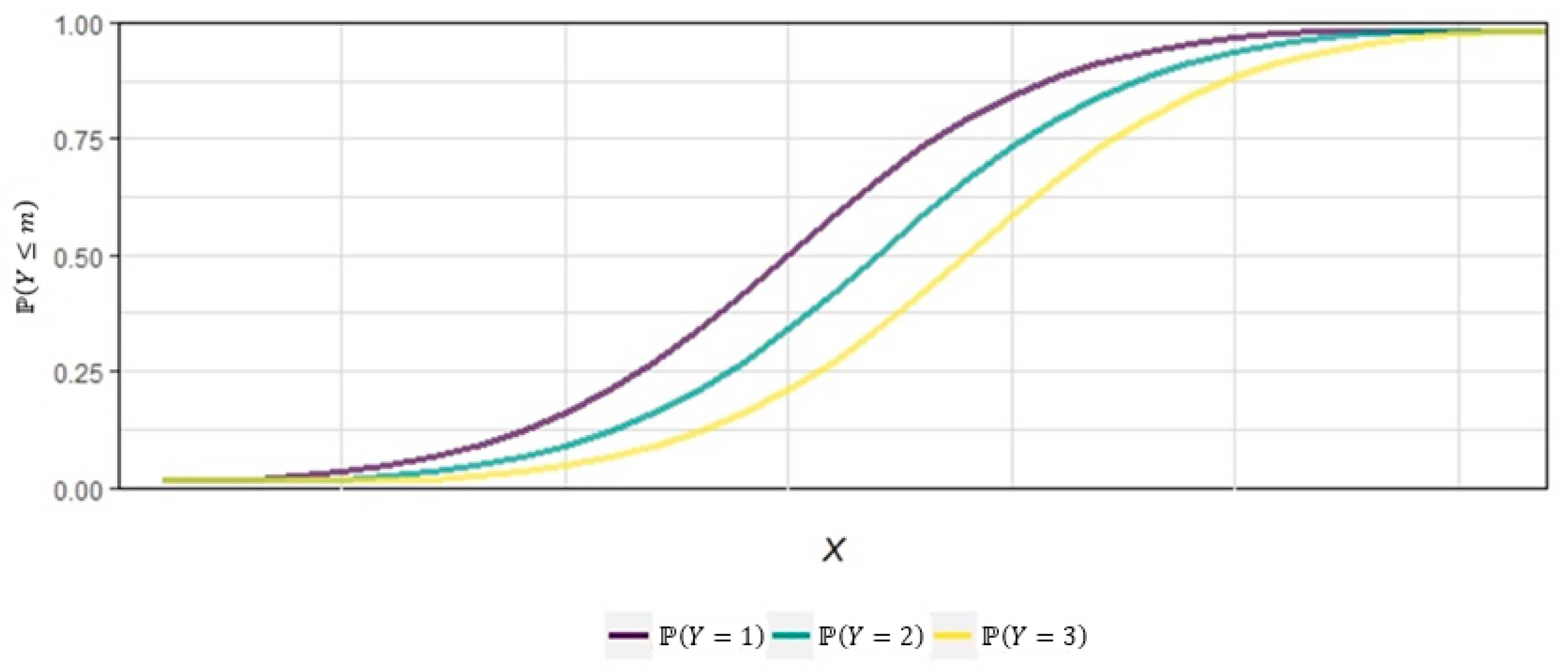
The application of Equation (3) yields identical slope coefficients () for each response level of but with different angular coefficients () depending on the change in the category studied. Figure 1 explains the postulate, assuming a theoretical model with a dependent variable with categories and a single continuous predictor variable.

Figure 1.
Theoretical ordinal logistic model with cumulative logits.
Hosmer et al. [24] stated that owing to the demonstrated uniqueness of the technique discussed, cumulative probabilities are present for this type of modeling, and it is possible to calculate the probabilities of each category of the phenomenon according to Equations (4)–(7), as illustrated in Figure 1.
where ; represents the values of the first to the k-th predictor variable of the observations; indicates the cut points (thresholds) of , where ; and refers to the multiplicative effects in their respective explanatory variables .
As already mentioned, given that , then in ordinal logistic models, there will be the estimation of logits. Therefore, the predicted probability curve for the case of Equation (7) is not shown in Figure 1.
Thus, as asserted by Hosmer et al. [24], the log-likelihood function () used to calculate the parameters and of a given GLM ordinal logistic estimation of the proportional odds model can be described by Equation (8).
However, it is crucial to underscore the fundamental premise implicit in Equations (2) and (3) for the application of proportional odds models. Expressions (2) and (3), as already mentioned, postulate as true that the type of estimation discussed is a model with parallel or equal slopes. Therefore, Liu et al. [14] explained that the odds ratio (OR) of these models when considering two theoretical predictor variables (i.e., and ), can be obtained according to Equation (9).
The authors elucidate that the assumption known as the proportional odds property emanates from the components of expression (9), from which the OR must be independent of the cut point of the category . In other words, for a proportional odds estimation, all are expected to be statistically equal, as proposed in (10).
To test the premise explained in (10), we used the Brant test [25]. In short, the test consists of estimating binary logistic regressions, whose dependent variables () must be considered according to (11):
with the expected probability for the ordinal model satisfying .
Based on binary logistic models calculated independently, the Brant test [25] aims to verify whether the differences between the of the independent models at the different cut points are relatively small as a function of the maximum likelihood estimate.
3. Multilevel Perspective
Based on the aforementioned, it should be remembered that GLM models estimate the fixed effects of a given phenomenon; that is, it is assumed that the heterogeneity of the individuals in the sample is constant, either as a function of time or as a function of natural nesting of the observations [26]. Therefore, as discussed by Headley and Plano Clark [27] and Mathieu and Chen [28], the levels of data analysis, that is, their contexts, also called nestings (latent or non-latent), are not considered in GLM estimations. On the other hand, estimates made from a multilevel perspective are natural expansions of GLM models, allowing fixed and random effects to be modeled simultaneously for the observations in a given database [20,21,22].
Studying the specific case of Brazilian universities, which constitute the central focus of this tutorial database, it becomes evident that these institutions operate within diverse contextual frameworks. These contexts encompass several facets, such as varying academic orientations [29], differing levels of public or private investment [30], differences in the quality of professor training [31], geographical locations with distinct demographic characteristics [32], different social demands for which their existence is justified [33], and different aspirations for internationalization [34], among other factors.
Consequently, employing an identical yardstick to compare, for instance, the University of São Paulo (USP), recognized as the leading university in Latin America, with another national university not ranked among the country’s top institutions, without considering similar social, economic, and demographic contexts, would be inherently inequitable.
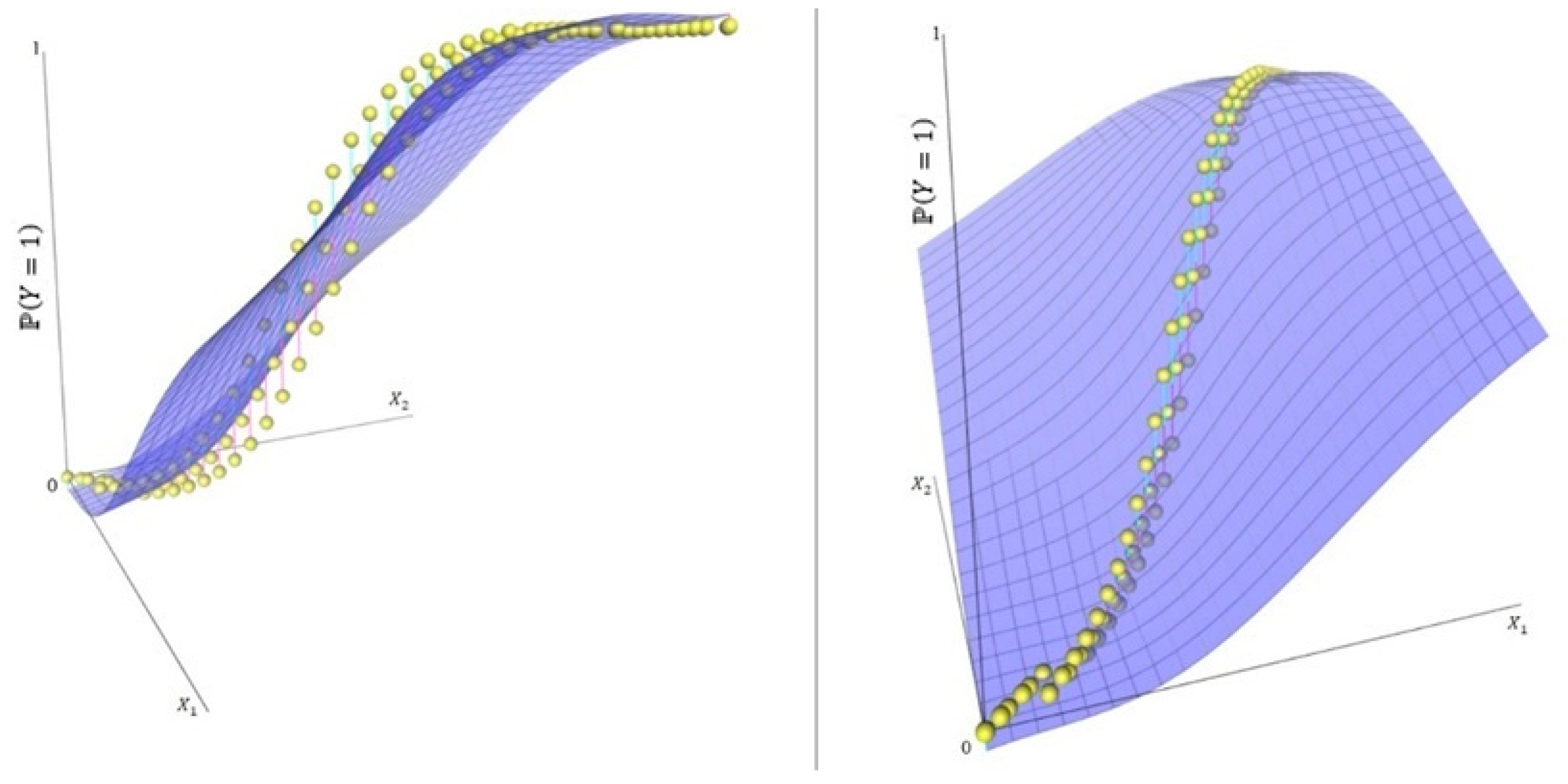
A fixed-effects model tailored to this scenario would advocate for the approach described in the preceding paragraph. Hence, for instructional clarity and to elucidate the rationale we critique, Figure 2 illustrates the hypothetical representation of Brazilian university performance using a model that exclusively accommodates fixed effects.

Figure 2.
Possible theoretical ordinal logistic GLM estimation considering a single cumulative logit for didactic purposes. The two images belong to the same model; they are different rotations of the same graph.
Figure 2 illustrates that a model assuming constant heterogeneity among individuals within the sample would attempt to gauge the performance of Brazilian universities by encompassing all national institutions within a singular framework. Consequently, this model fails to acknowledge the distinct contextual realities that differentially impact performance. As per Courgeau [26], employing a GLM model for the addressed issue might yield results that lack a connection between observations and the diverse environments in which these institutions operate.
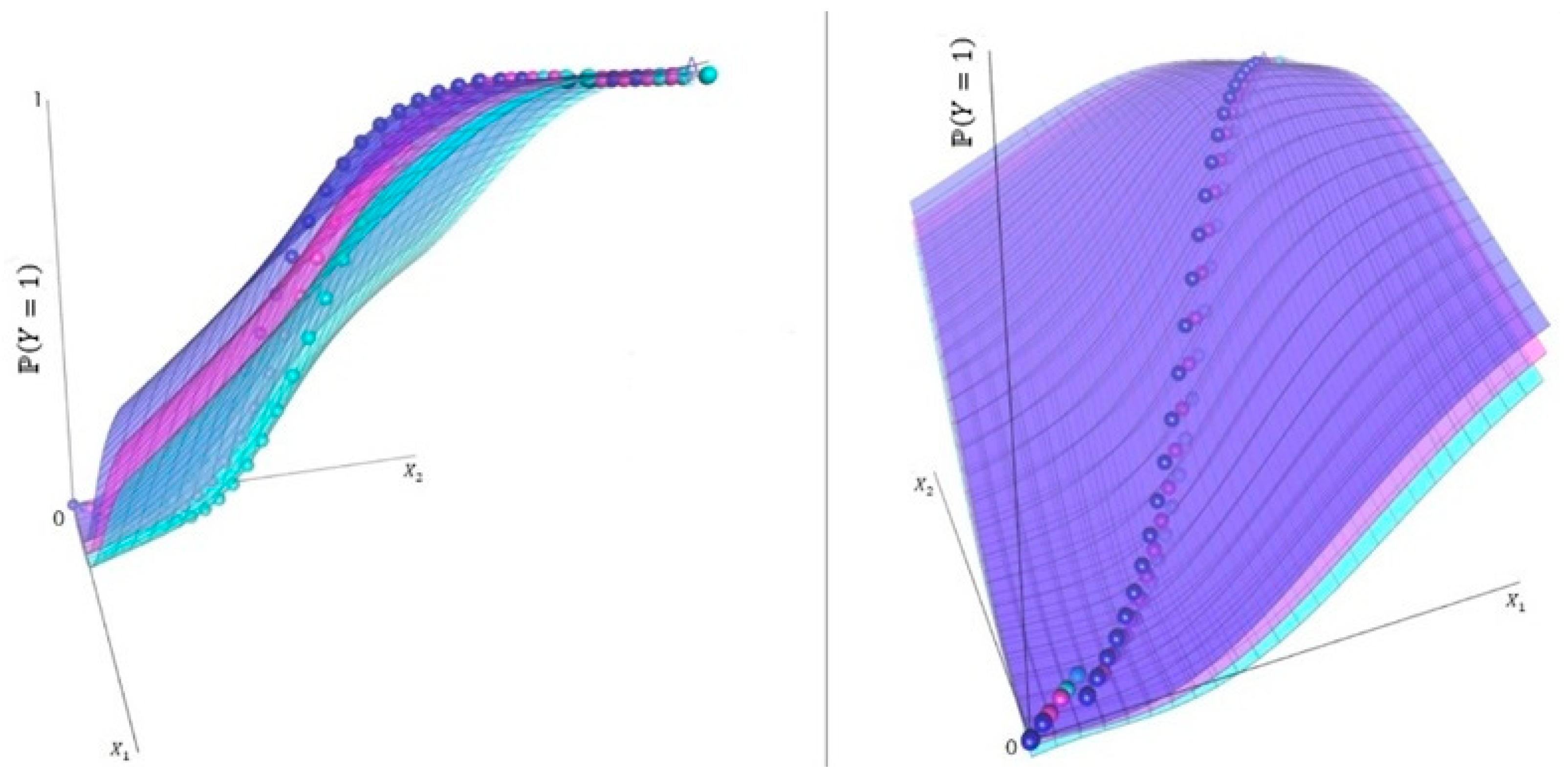
Conversely, Figure 3 aims to portray a similar theoretical endeavor to evaluate the performance of Brazilian universities, as depicted in Figure 2, but with consideration of the hierarchical structures (referred to as levels of analysis or nesting) inherent in the dataset.

Figure 3.
A conceivable theoretical multilevel ordinal logistic model featuring a single cumulative logit nested within a particular level presented for instructional purposes. Both images pertain to an identical multilevel model, showing distinct perspectives obtained using the rotational adjustments of the same graph.
The following section presents the mathematical descriptions of multilevel ordinal logistic regression.
4. A Multilevel Proportional Odds Approach
As delineated by Mahmoud et al. [35] and Palardy [36], estimations for nested data, alternatively known as hierarchical regression models, mixed regression models, nested data models, and random coefficient models, are categorized within the realm of Generalized Linear Latent and Mixed Models (GLLAMM). This approach enables the concurrent examination of both fixed and random effects associated with the observed phenomenon.
Data structured using nested relationships are ubiquitous across various human knowledge domains. For instance, patients experiencing heart-related ailments may exhibit nesting in hospitals in which they receive treatment. Moreover, these hospitals could be nested within specific regional contexts in which they operate [37]. Similarly, employees might be nested within their respective departments, which, in turn, can be nested within larger organizational entities such as firms [38]. In both scenarios, the passage of time during patient treatment and the temporal effects on employees could potentially manifest as nested attributes within these individuals [39], showcasing the progression of observations at the individual and/or group levels.
The examples presented illustrate that GLLAMM estimations facilitate the examination of a phenomenon concerning explanatory variables that exhibit variation at the individual observation level while remaining constant across higher levels of nesting without repetition across other superior nesting levels [40,41,42]. Essentially, this form of estimation enables the comprehension of a variable-represented phenomenon in relation to defined predictor variables, wherein alterations may or may not emerge because of delineated nesting structures encompassing recurring measurements stemming from a chronological sequence.
Thus, following Rabe-Hesketh and Skrondal [42], when considering an ordinal categorical phenomenon organized into two levels, the mathematical description of the probability of its occurrence is represented by Equation (12).
where is the subscript representing Level 1 observations; is the subscript indicating Level 2 observations; is the -th explanatory variable of the first level; is the -th second-level predictor variable (therefore invariant for Level 1); and h is the ordinal logistic cumulative distribution function that represents the cumulative probability of an event.
From Equation (12), we can calculate the probability of observing a category according to Equation (13) [24].
where .
Thus, following Bauer and Sterba [7], a possible theoretical multilevel ordinal logistic model with two levels can be described by expanding Equations (4)–(7) in terms of Equations (14)–(17).
- Level 1:where refers to the logits of an event of interest for the observations belonging to the group ; and refers to the level 1 parameters of the estimation.
- Level 2:where and correspond to the level 2 parameters; corresponds to the intercept random effects of the second level, and indicates the slope random effects of level 2.
When the equations for Levels 1 and 2 are combined, the general model described by (18) to (21) is obtained.
- General Model:
Multilevel ordinal logistic regressions can be estimated using the maximum likelihood criterion [42]. For the first level of this type of model, Equation (8) should be followed. For higher estimation levels, the conditional distribution of for a set of random effects is described by Equation (22).
where .
Because the multivariate distribution of is assumed to adhere to the Gaussian distribution with mean equal to zero and with the variance matrix [43], the contribution of the log-likelihood to nesting above the first level () can be obtained by integrating from the joint density function as shown in Equation (23).
where .
The ordinal logistic models of the GLLAMM family also allow ORs calculations as well as the estimation of intra-class correlations (ICC), which quantifies the extent to which variance at a lower level can be attributed to variability across higher levels (s) [44]. Agresti [23], assuming an ordinal logistic model with two levels, proposed calculating the ICC according to Equation (24).
where indicates the variance of the upper-level errors, and the variance for the first level is approximated by [23,44].
5. Data
The dataset employed in this study comprises an unbalanced panel incorporating repeated measures, encompassing all Brazilian universities listed on the Ranking Web of Universities (WEBOMETRICS (Available at https://www.webometrics.info/en, accessed on 12 July 2023)) from 2012 to 2018. The explanatory variables were obtained from the Brazilian Higher Education Census (CES) (Available at https://www.gov.br/inep/pt-br/areas-de-atuacao/pesquisas-estatisticas-e-indicadores/censo-da-educacao-superior, accessed on 24 September 2023), an initiative run by the country’s Ministry of Education.
The primary aim of WEBOMETRICS is to rank HEIs by assessing their online presence and visibility. Currently, WEBOMETRICS incorporates four indicators that gauge the research and teaching impact of these institutions, reflecting their dissemination of knowledge and resultant influence in terms of university visibility and the consequent impact of this visibility [45]. Essentially, WEBOMETRICS utilizes HEI visibility as a surrogate measure of academic performance.
As per Aguillo et al. [46], the online exposure of institutions is evaluated using comprehensive databases accessed via independent web search engines. These engines, notably Google, Google Scholar, Majestic, Ahrefs, and Scimago Institutions Ranking, are frequently used for cybermetric evaluation. Figure 4 visually represents the documents retrieved from these databases, which were deemed pertinent for inclusion in the ranking process.

Figure 4.
Online documents retrieved from the Internet are employed to assess the online visibility and presence of Higher Education Institutes (HEIs), specifically in the context of WEBOMETRICS. Source: Aguillo et al. [47].
The dependent variable involves the categorization of universities into five groups, denoted as , , , and . These groups were established using a specific methodology: Brazilian universities listed in the WEBOMETRICS ranking for each year of the study were arranged in ascending order based on their respective rankings, that is, from top to bottom. Subsequently, considering the subsets delineated for each year under examination, the original ranking positions of HEIs in WEBOMETRICS were considered. These subsets were further subdivided into five relatively homogeneous segments that were as homogeneous as possible in terms of the number of observations: , , , and . Universities mentioned only within the ranking in a single year and/or those lacking pertinent data within the CES were subsequently excluded. Table 1 provides an overview of the distribution of HEIs across the groups.

Table 1.
The distribution of the number of Brazilian HEIs in the strata proposed by the research.
Thus, in Table 1, the HEIs in Group represent the best-placed Brazilian academies in the WEBOMETRICS ranking, whereas the universities in Group represent the worst placed in the ranking. Table 1 also shows the imbalance in the repeated measures panel used in this study. Table 2 lists the explanatory variables selected for the estimations.

Table 2.
Description of the research’s predictor variables.
With this context in mind, this tutorial aims to investigate a particular construct: can the performance of Brazilian universities, considering performance as the position (strata A to E) in the WEBOMETRICS ranking, be concurrently elucidated over time, the proportion of students engaged in doctoral programs concerning the total count of professors, and the classification of an HEI as a federal university?
Table 3 shows the univariate descriptive statistics for the study’s metric variables and the frequency tables for the survey’s categorical variables.

Table 3.
Univariate descriptive statistics of the study variables.
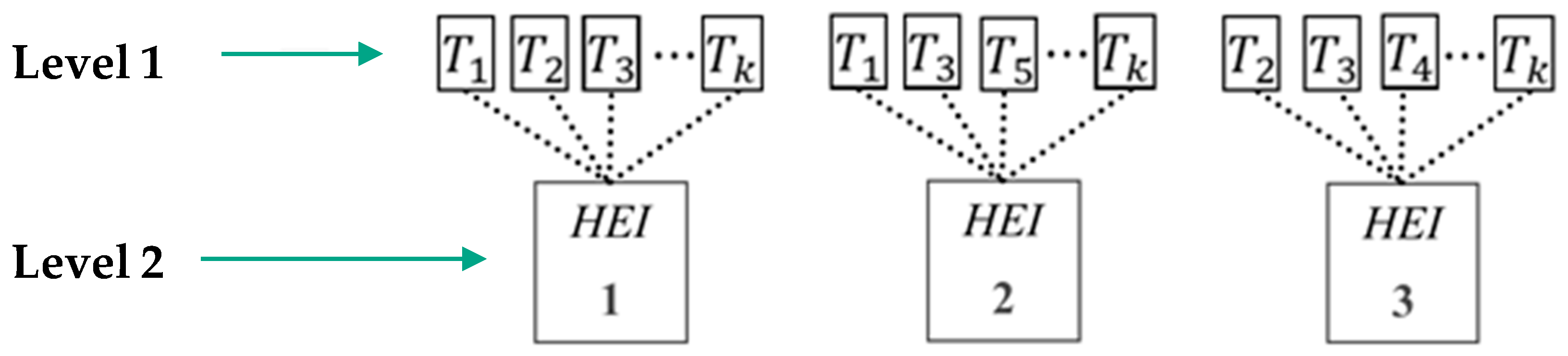
Given the above explanations, the model considered the context of the passage of time nested in each university, as shown in Figure 5.
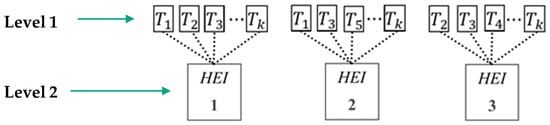
Figure 5.
Illustrative example showcasing the nested structures postulated by the research within an unbalanced theoretical panel.
The next section presents the models considered in this study.
6. Empirical Application
A total of four models were estimated: two of them using arbitrary recoding and/or arbitrary dichotomization approaches, both from the GLM family, respectively a classical linear regression model (Linear GLM) and a binary logistic model (Binary GLM); the other two estimations correspond to ordinal logistic regressions, the first being from the GLM family, and the other GLLAMM (Ordinal GLM and Ordinal GLLAMM, respectively).
For the Linear GLM model, the dependent variable was assumed to be a metric, considering classes to in the study as values from to , as follows: , , , , and . It could be argued that, for this type of estimation, the use of regression techniques for discrete variables (for example, Poisson, Gamma, Poisson-Gamma) would be more useful, as discussed in Section 5, in which the proposition of classes from to in the research was made by prioritizing the homogeneity of the number of HEIs in each category. As such, calculating the density probability of the phenomenon, when in metric form, would show a curve similar to that of a uniform distribution, creating difficulties for the regression models for the count data mentioned above.
However, for the Binary GLM estimation, groups and were joined to form a new stratum called “”. The groups and were combined to create a “” stratum. For this model, the individuals in the Group were considered to be missing values.
Finally, for the ordinal models (Ordinal GLM and Ordinal GLLAMM), the dependent variable was considered in accordance with Section 5; that is, considering all groups from to , categorically and in that precise order. Table 4 summarizes the transformations proposed for the dependent variable of the research, depending on the model generated.

Table 4.
Transformations applied to the study’s dependent variable.
Table 5 shows the algorithms, packages, and their respective versions in the R computer language. The codes and databases can be found in the Supplementary Materials.

Table 5.
The algorithms and packages used in the research.
Table 6 compares the parameters of the estimates produced by this study. In Table 6, the first three columns show the parameters of the models that only consider the fixed effects of the predictor variables on the phenomenon studied, while the last column shows the model from a multilevel perspective, that is, considering fixed effects and random intercept effects simultaneously. For the Ordinal GLLAMM estimation, there was no algorithmic convergence for the estimation of the slope random effects.

Table 6.
Comparison of the calculated parameters of the study’s regression models.
Table 6 provides the mathematical transcriptions of the GLM models and GLLAMM estimation, which considers fixed effects and random intercept effects. For didactic reasons, in the case of ordinal models, we present the equations for calculating the probability of class; after all, for the other classes, it would be enough to change the values of the intercepts.
- Linear GLM estimation:
- Binary GLM estimation:
- Ordinal GLM estimation:
- GLLAMM estimation:
The next section presents discussions and comparisons of the models proposed by the research.
7. Comparison of Research Models and Discussion
The analysis of the results presented in Table 6 begins with the statistics . This statistical metric serves a similar purpose to the likelihood-ratio test (LR test) [42], seeking to compare the researchers’ final model with its null model analog using the same dependent variable and the same number of observations. Mathematically, the calculation of the statistic is described by Equation (29):
The of the test described by (29) indicates that there are no statistically significant differences between a given research model and its respective null model. The results are presented in Table 7.

Table 7.
results.
According to the results shown in Table 7, it can be said that all the research models were statistically different from their analogous null estimates at a 1% significance level, i.e., the phenomenon as a function of the intercept only. In other words, the results in Table 7 reinforce that at least one predictor variable, ceteris paribus, proved to be statistically different from zero for all models.
Subsequently, a second round of LR tests [50,51] was proposed to check which of the estimations in Table 6 best suited the research data, that is, the modeling of the rankings of Brazilian universities in WEBOMETRICS. Thus, the value of , in order to check whether the gain between two different models is statistically equal to zero, is calculated by adapting expression (29), described by Equation (30).
Using Equation (30), all the values from all the models shown in Table 6 were compared with each other pair by pair. The of the discussed LR test is that the two models compared are not statistically different from each other; however, indicates that a given estimate is more appropriate for the case studied. The LR test results are presented in Table 8.

Table 8.
LR test results.
In Table 8, it is not possible to present the results of the LR tests involving Binary GLM estimation because of the difference in the sampling considered by the models (see Table 6). In any case, Section 7.2 discusses Binary GLM estimation as well as the problems with the methodological choice of disregarding the observations present in Group . It is also true that Section 7.4 will compare the accuracies of all the models, as well as considerations regarding the non-parametric Kolmogorov–Smirnov Predictive Accuracy (KSPA) test [52], to verify the adequacy of the estimates for the phenomenon studied.
In the next section, discussions and considerations regarding the GLM Linear estimation are discussed.
7.1. The GLM Linear Estimation
At this point, it should be remembered that, for didactic purposes, the survey’s dependent variable, which is ordinal categorical, was arbitrarily recoded to a metric specification, where 1 indicates stratum HEIs, and 5 indicates Group HEIs (see Table 4).
From the analysis of the parameters of the Linear GLM model with its intercept, as shown in Table 6 and in Equation (25), it can be seen that this model is optimistic in generating difficulties for any HEI to be classified in a category lower than , given its value of . In other words, even if all predictor variables were mathematically equal to 0, the GLM Linear estimation would not classify any HEI in the Group of the research. According to Table 1, 246 individuals belong to the aforementioned stratum .
Table 6 also shows that an increase in one unit in the variable year would cause a reduction of −0.03336 in the measurement of the dependent variable, and all other conditions remain constant. On the other hand, if the HEI was a federal university (), the dependent variable would receive an increase of 0.77469 in its unit of measurement, ceteris paribus; if it was not a federal university (), the increase would be equal to zero, while the other conditions remaining constant. Finally, an increase in one unit in the variable would lead, ceteris paribus, to an increase of 1.86460 in the dependent variable.
It is interesting to note that although the maximum value of the dependent variable studied for the GLM Linear model is mathematically equal to 5 (which represents the Group of HEIs), there were 76 observations with their respective fitted values greater than 5. The highest fitted value recorded was approximately 7.25, whereas the lowest fitted value recorded was approximately 2.18.
The estimation of fitted values that extrapolate the observed values, given the occurrence of arbitrary recoding for a given variable to be assumed as a metric, is expected in the literature. Both Bauer and Sterba [7] and Long and Freese [53] agree that arbitrary metric recoding for an ordinal phenomenon can generate fitted values below or above the categories existing in the phenomenon. The authors also pointed out that, as the fitted values extrapolate (upward or downwards) the observed values, there is a compression of the variability of the residues, generating the problems of heteroscedasticity and non-adherence of the residues to normality.
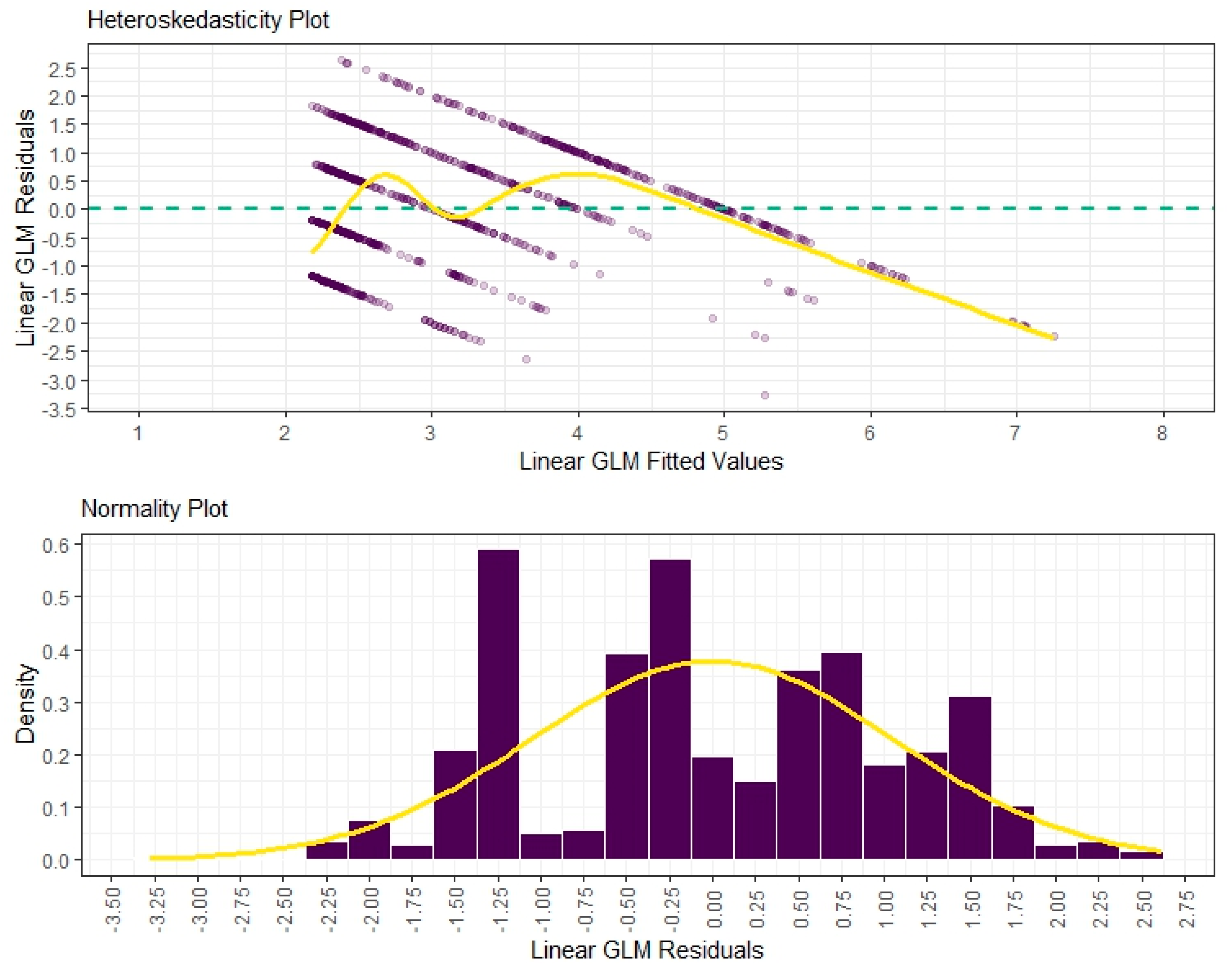
In fact, the postulates by Bauer and Sterba [7] and Long and Freese [53] regarding the condition of homoscedasticity and the non-existence of adherence to the normality of the residuals were observed in the Linear GLM estimation of the research.
To confirm this, the Breusch-Pagan test (BP test) was performed to verify the absence of heteroscedasticity [54]. The of this test indicates that the assumption of homoscedasticity for GLM linear regressions is met. Because , with 3 degrees of freedom, we have a p-value = 0.000. Therefore, it can be said that the Linear GLM model is heteroscedastic at a 1% significance level. The upper portion of Figure 6 illustrates the situation described above.
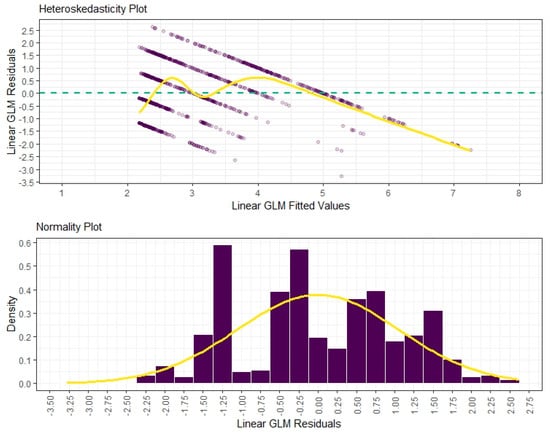
Figure 6.
Visualizations of the Linear GLM estimation residuals.
The Shapiro-Francia normality test (SF test) was also performed to check whether the assumption was met [55]. The indicates adherence to the Gaussian distribution for a given significance level. Because , with the respective p-value = 0.000, it can be said that in the GLM Linear estimation, its residuals do not adhere to normality at the 1% significance level. The lower part of Figure 6 illustrates this situation.
More than that predicted by Bauer and Sterba [7] and Long and Freese [53], the researchers noted the existence of autocorrelation in the residuals of the Linear GLM model. The Durbin-Watson test (DW test) was used to diagnose the autocorrelation of the error terms [56], where the indicates the non-existence of the situation discussed for a given significance level. The DW test indicated the presence of autocorrelation in the residuals of the Linear GLM estimation for up to 9-time lags at a 1% significance level.
Below are some considerations and discussions regarding the Binary GLM model.
7.2. The GLM Binary Estimation
Before discussing the interpretability of the parameters of the Binary GLM estimation, it should be recalled that the ordinal polytomous dependent variable with five levels was dichotomized, as shown in Table 4.
Binary models require the phenomenon of a dichotomous nature, which is where the crossroads began for the authors of the study. Groups and were assumed to be the upper strata of the database, forming the group, while groups and were combined to form the category.
However, the researchers understand that if the intention of the modeling was to support the managerial decision-making process, whether of a policymaker or a university manager, this decision would raise questions that would be difficult to answer.
- ▪
- If the intention is to try to study, based on the variables present in the database, which factors lead an HEI to be in the top positions of the WEBOMETRICS ranking (Group , in this case), why should the stratum be mixed with the stratum ?
- ▪
- On the other hand, if the intention is to understand what leads an HEI to fall into the very bottom positions of the ranking studied, why mix group with stratum ?
- ▪
- However, if the intention is to study the composition of the Group or the Group , what should be performed with the HEIs in the groups , , and ?
- ▪
- If we assume the conjunction of groups and , forming a new category, and the mixture of and generating another category, what should we do with the individuals in the Group ?
To illustrate the problems that can be generated by the chosen path, it was decided to disregard the individuals in the Group , i.e., missing values were considered. To do so, 244 rows of the database were not used to train the algorithm. In other words, the model’s supervised learning was deprived of information on 244 individuals.
The analysis of the parameters of a logistic model, be it binary, ordinal, or multinomial, unlike a classic linear regression model, is based on the calculation of ORs. As such, it can be said that according to Table 6, the Binary GLM estimation indicates that the chance of a federal university being considered part of the group (strata and ) is 2411 times greater () compared to an HEI that is not a federal university, ceteris paribus. However, there is no way to determine whether such an HEI will be classified into the original groups or .
Table 6 also indicates that a one-unit increase in the variable , with all other conditions held constant, increases the chance of a given HEI being categorized as Group by 71,816.53 times (). Finally, with regard to the variable year, the passage of one year, ceteris paribus, decreases the chance of a university being inferred as the category by 13.49%, i.e., it must be multiplied by a factor of 0.8651, since .
7.3. The GLM and GLLAMM Ordinal Estimations
7.3.1. OR Analysis
Following Table 6, according to the Ordinal GLM estimation, the chance of a Brazilian academy, other than a federal university, being in Group , of the WEBOMETRICS ranking is 2.313 times greater () than federal universities. However, for the estimation that considers both fixed and random effects (Ordinal GLLAM), the chance of a Brazilian university, other than a federal academy, being classified in the Group must be multiplied by a factor of 488.735 (), i.e., 487.7% higher than that for a federal university.
The proposed interpretation can also be achieved via the predicted probabilities of different values when versus , as presented in Table 9.

Table 9.
Predicted probability that a given Brazilian university will occupy performance groups to , whether or not it is a federal university.
From Table 9, and using Equation (9), when comparing the probabilities of a given Brazilian HEI being in group, because it is not a federal university against the fact that it is a federal university, we have:
- For Ordinal GLM estimation:
- For Ordinal GLLAMM estimation:
Still, on the results in Table 9, if the attempt at analysis was based on the question of what the chance of a Brazilian HEI, being a federal university, being categorized in the or or or strata, and not being categorized in the stratum, we would still have:
- For Ordinal GLM estimation:
- For Ordinal GLLAMM estimation:
Another way of analyzing the variable , following the estimation proposed in Table 6 and Equations (27) and (28), is to directly calculate the chance of a Brazilian HEI being categorized in the Group , being a federal university. The answer to this question would be , all other conditions being equal. In other words, for Ordinal GLM modeling, the chance of a Brazilian federal academy being categorized in group E must be multiplied by a factor of 0.43232; that is, it is 56.768% lower than if this HEI were not a federal university, ceteris paribus.
On the other hand, when proposing the previous question for the Ordinal GLLAMM estimation, the chance of a Brazilian HEI being categorized in the Group , being a federal university, should be multiplied by a factor of 0.00205 (), i.e., for the GLLAMM estimation, it would be 99.795% lower than if this HEI were not a federal university, with other conditions remaining constant.
When looking at the time span considered by the variable , it is interesting to note that, according to the results in Table 6, the estimated coefficients are close for both models. In the case of the estimation presented in (27), adding one unit to the variable year increases the chance of a given Brazilian university being categorized in the stratum E by 13.785% (), ceteris paribus. In the case of the model in (28), the passage of one year implies an increase in the chance of a given Brazilian HEI being categorized in the stratum of 11.905% (), ceteris paribus.
Finally, when generating an increment of one unit in the variable , the Ordinal GLM modeling—Equation (27)—points out that the chance of a given Brazilian HEI being classified in the Group is 99.917% lower (). The Ordinal GLLAMM estimation indicates that this chance is 99.999% lower ().
7.3.2. Intercept (Threshold) Analysis
Another important point is the possibility of analyzing the intercepts of the models as well as the differences between the intercepts of the estimates proposed by the research.
In the case of the ordinal logistic regressions in the survey (Ordinal GLM and Ordinal GLLAMM), the first consideration to make is that the intercept values indicate the probability of a given Brazilian HEI being categorized in any stratum proposed by the survey (from to ) when the other predictor variables are equal to 0. These probabilities for the data studied can be found in rows 1 and 3 of Table 9.
Table 9 also explains the problem of not considering the observational idiosyncrasies of the data. The calculated probabilities, in the case of the Ordinal GLM estimation (see row 1 of Table 5), are more evenly distributed between the groups , , , and . In other words, the Ordinal GLM model is optimistic for those HEIs that have low values of the variable , guaranteeing easier predictions of reasonable ratings in the WEBOMETRICS ranking (e.g., or ) for this type of university.
On the other hand, when a similar analysis is carried out for the Ordinal GLLAMM estimation (see line 3 of Table 9), its probability distributions between the groups adopted by the research leave homogeneity aside and penalize universities with low values of the variable more heavily. It is also true that, in this case, the Ordinal GLLAMM model also penalizes, considerably, the predictions of positions in the WEBOMETRICS ranking for HEIs that are not federal universities, which leads to the discussion of the consideration of random effects, which must be analyzed on a case-by-case basis. This implies that the intercepts proposed by the Ordinal GLLAMM model must be corrected using the values of their random effects (), as presented in Appendix A, following the logic of (28). The values are therefore adjusted to the values of the GLLAMM estimation thresholds, made because of the peculiarities and observational nesting, for the intercepts of the multilevel model.
As previously mentioned, the values are presented in Appendix A of this study. Therefore, when considering the Ordinal GLLAMM estimation for the two levels modeled, the intercept for Group , in the case of the Federal University of Western Pará (UFOP), presented in the first line of Table A1, should not be considered equal to (see Table 6), but equal to .
The next section discusses the accuracy and suitability of these estimates.
7.4. Accuracy and Suitability of Estimates
Different modeling methodologies typically employ specific techniques to measure the accuracy. In the case of classic regression models, the R2 statistic is commonly utilized for this purpose [57], as well as the mean squared error (MSE) or root mean square error (RMSE), among others [58]. Binary logistic models make it possible to propose confusion matrices by assuming some cutoff (including analyses of sensitivity, specificity, etc.), as well as calculating the area under the ROC curve or the Gini coefficient [12,23]. Finally, ordinal logistic models usually assume, according to the trained algorithm, the category with the highest probability of occurrence, and the classification error or hit rate is evaluated. As these methods of measuring accuracy between models are considerably different, it was decided to adapt all estimates so that they could be evaluated in terms of classification accuracy rates.
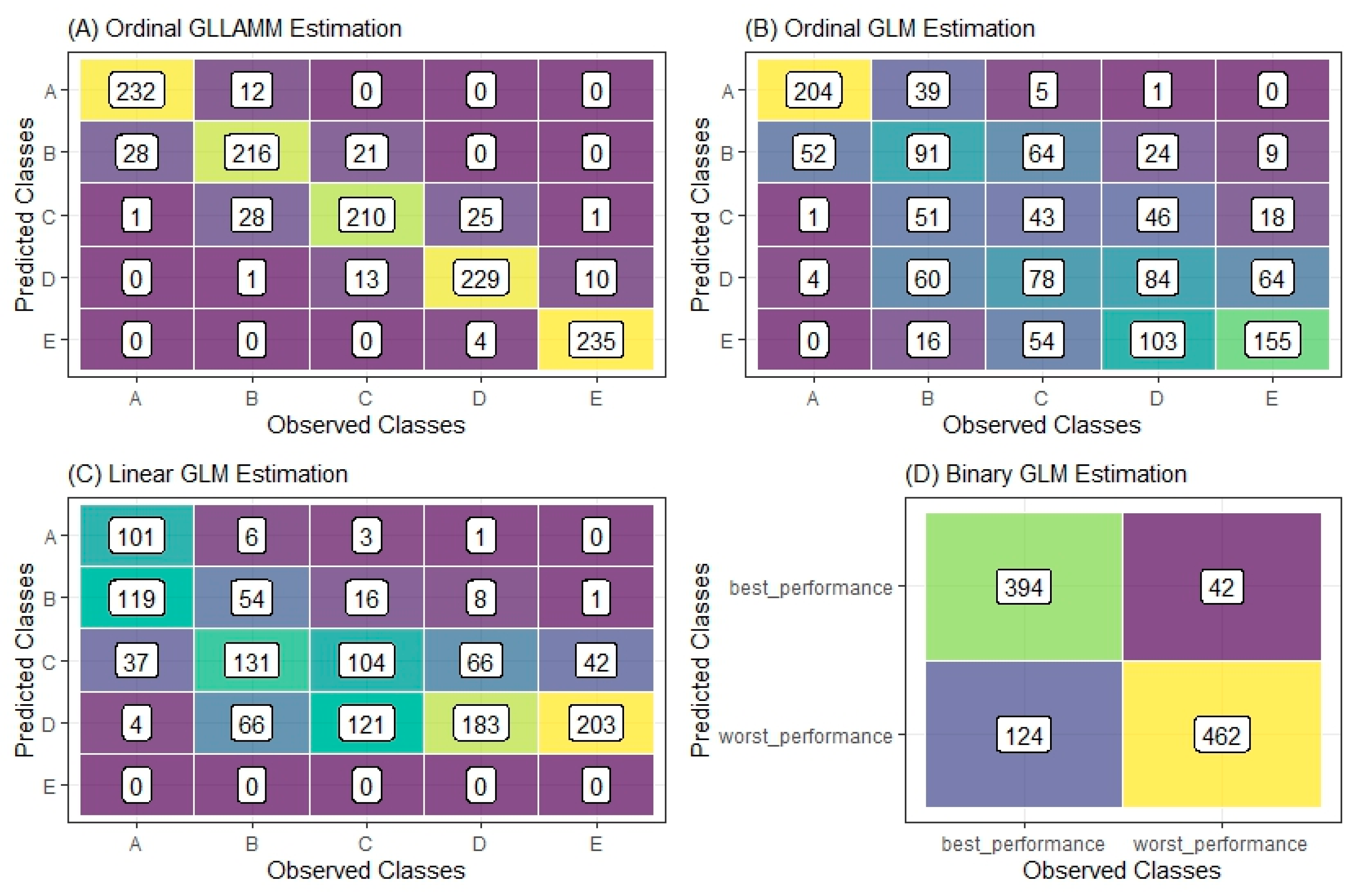
Figure 7 shows the cross between the observed (abscissa axis) and predicted categories (ordinate axis). From this image, it would be difficult to advocate disregarding the nesting present in the study data by presenting the intersections between predicted classes and observed classes for the research estimates, considering the possibility of a guess for each model.

Figure 7.
Predicted versus observed classes.
To measure the accuracy of the models, considering a single guess from Figure 7, we simply calculate the sum of its main diagonal and divide the result by the total sample. Therefore, the Ordinal GLLAMM estimation has an accuracy of , whereas for the Ordinal GLM estimation, we have an accuracy of .
The lowest accuracy was observed in the Linear GLM model, with (. This value was obtained by considering fitted values greater than 5 to be equal to 5 (group ).
This difference in predictive power between the Ordinal GLM and Ordinal GLLAMM models can be explained using the ICC value of the Ordinal GLLAMM estimate. For the aforementioned model, the calculated ICC was 94.29%; that is, 94.29% of the total variability in the performance of the Brazilian HEIs studied was related to changes between HEIs (correlations within repeated measurements of ranking classes).
The Binary GLM estimation achieved an accuracy of . However, it should be remembered that 244 observations were disregarded in the modeling, and groups were combined to create a dichotomous phenomenon, and there is no way of predicting which of the groups assumed by the study (from to ) a given Brazilian HEI might be classified in.
A non-parametric KSPA test [52] was used for all the estimations. According to the authors, the KPSA test allows the distances between the cumulative distributions (CDF) of the observed values and the predicted values to be measured without being impacted by any autocorrelation that may be present in the forecast errors. The of the KSPA test proposes that two samples (in this case, the observed values from the database and the predicted values from each model) belong to the same CDF at a given significance level. The results of the KSPA test are summarized in Table 10.

Table 10.
KSPA test results.
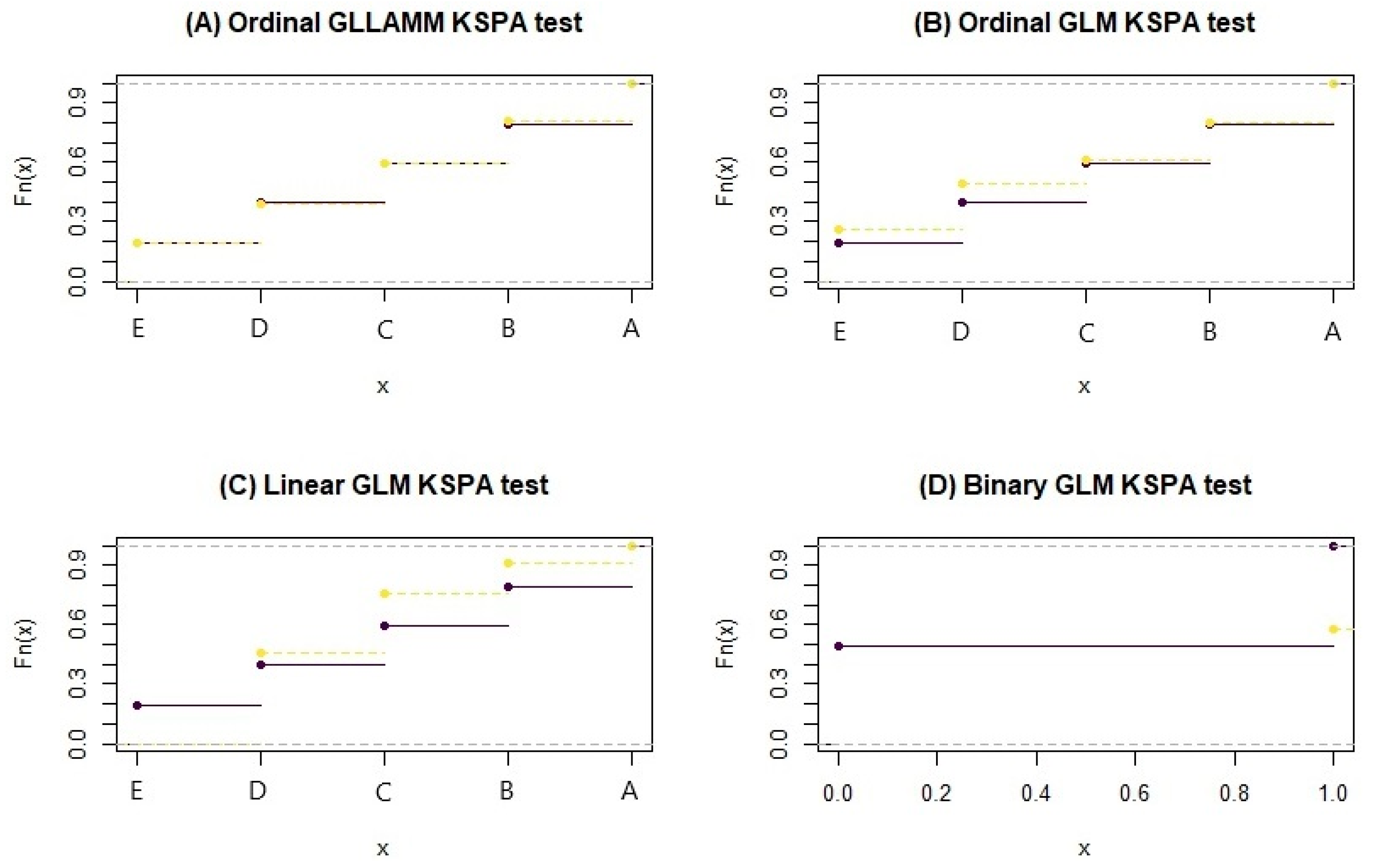
Table 10 suggests, at the 1% significance level, that the predictions of the GLM models are not suitable for this case, ceteris paribus. Figure 8 shows the CDF distances between the observed values (purple and solid dashes) and the predicted values (yellow dashed color) of the research estimates.

Figure 8.
KSPA test results visualization for each model of the research.
Therefore, Figure 8 reinforces the suitability of the Ordinal GLLAMM estimation for the data studied. The following is a discussion of the expected values of the phenomenon as a function of the predictor variables of the study.
7.5. The Expected Values as a Function of the Study’s Predictor Variables
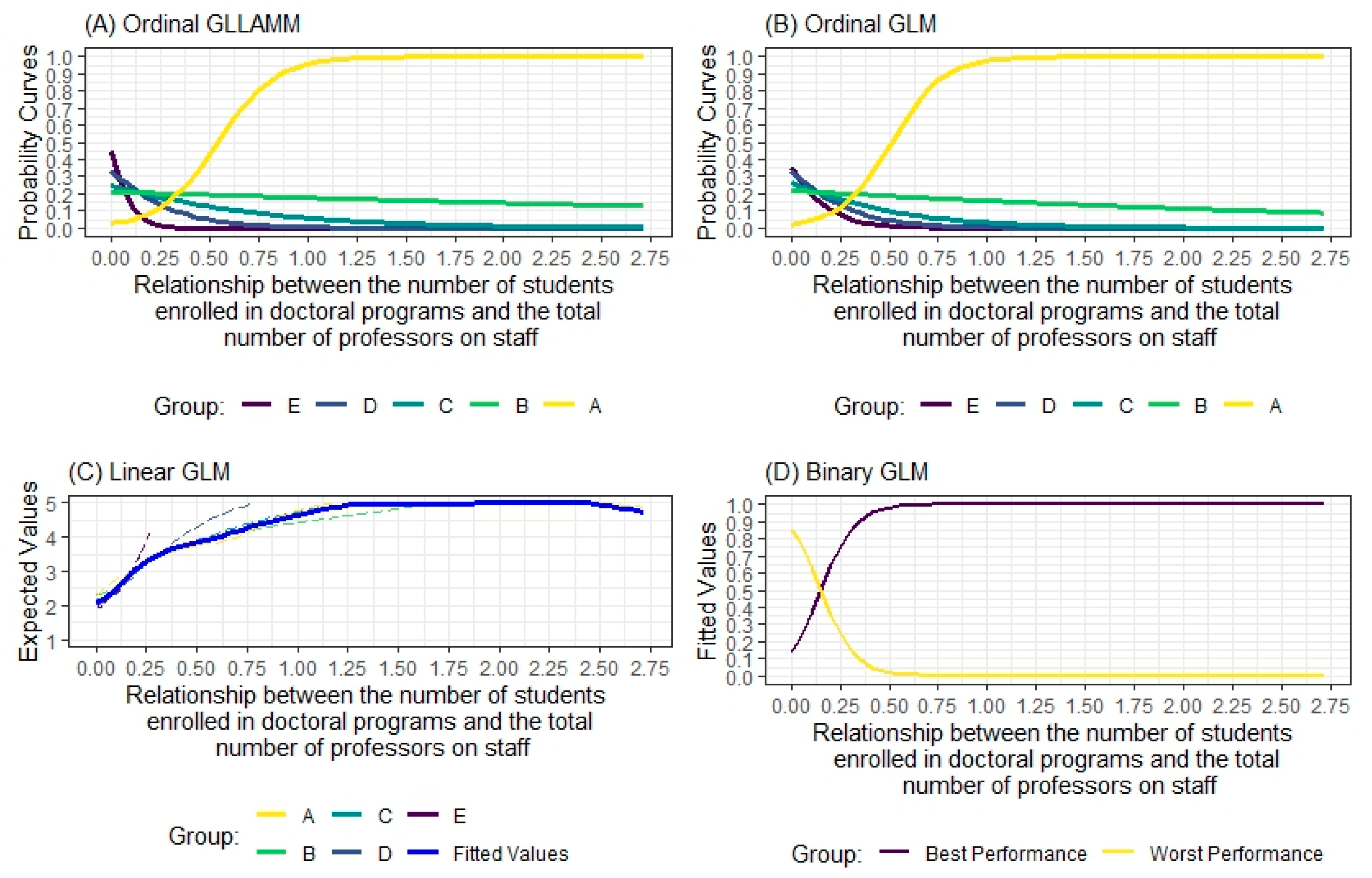
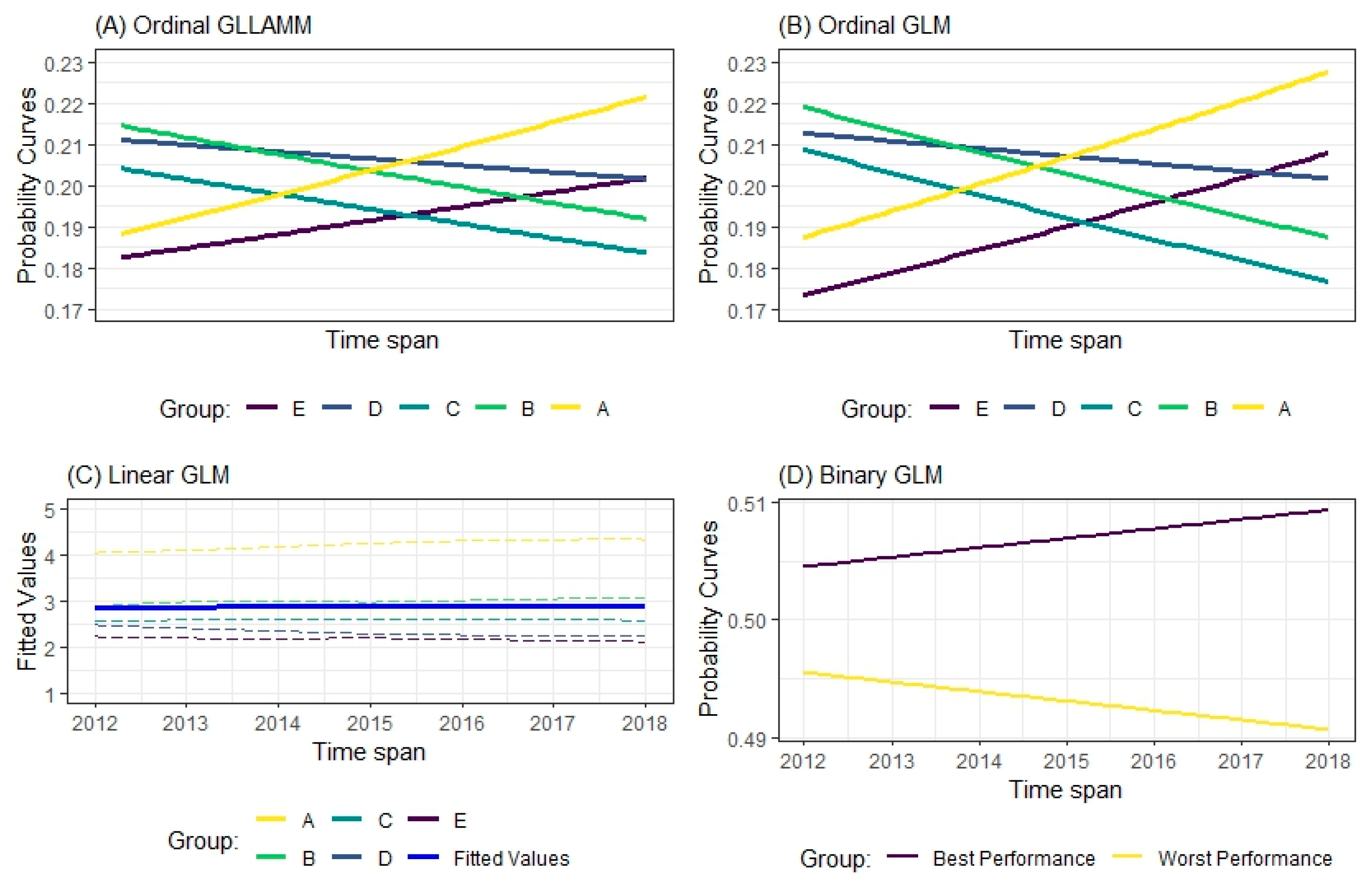
Figure 9, Figure 10 and Figure 11 show the estimated probability curves for the Ordinal GLLAMM, Ordinal GLM, and Binary GLM models, respectively that Section 7.2 and Section 7.3 deal with variations in the probability of occurrence of the phenomenon for the models discussed, and not their probabilities of occurrence for each category of the dependent variable.
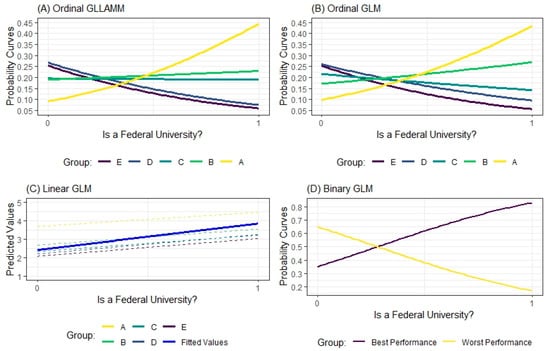
Figure 9.
Predicted values for the dependent variable as a function of variable.

Figure 10.
Predicted values for dependent variable as a function of variable.

Figure 11.
Predicted values for dependent variable as a function of variable.
Figure 9, Figure 10 and Figure 11 also show the behavior of the fitted values of the Linear GLM model as a function of each of the predictor variables used in the study. Section 7.1 presented the marginal effects of each explanatory variable on this phenomenon. In this section, we present the fitted values for the Linear GLM model (solid blue curve) as well as the fitted values for each Group of HEIs that were assumed by the research.
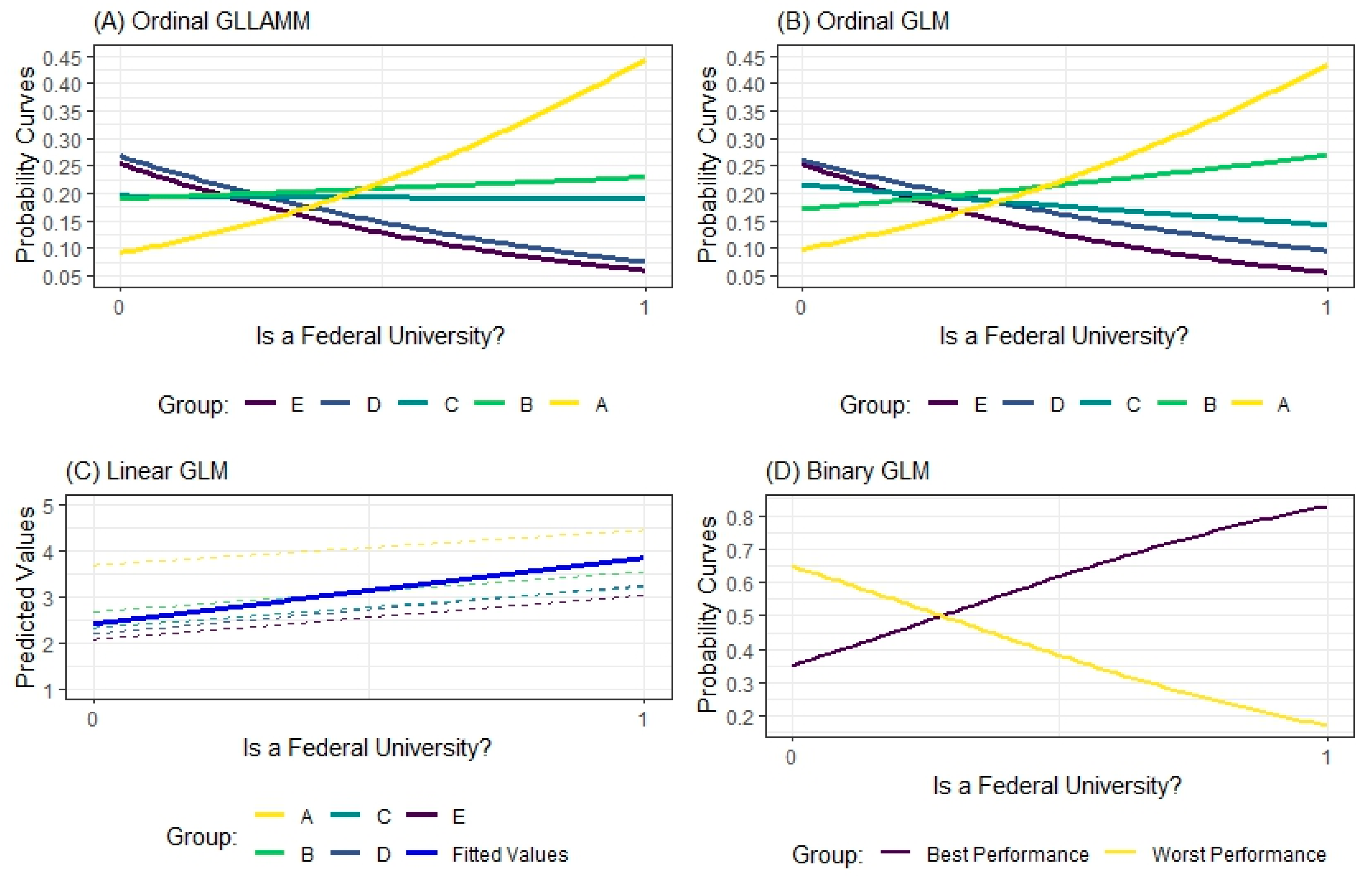
Figure 9 shows that when Ordinal GLLAMM, Ordinal GLM, and Binary GLM estimations are adopted, the fact that a Brazilian HEI is a federal university increases its likelihood of being classified in the upper strata of the research.
According to Figure 9, ceteris paribus, for the Ordinal GLLAM estimation, it is also true that there is a certain probability that the university in question, even though it is a federal university, will be classified in strata or and probably there will be no classification in strata or . On the other hand, other conditions remain constant; for the Ordinal GLM model, the growth rate of the probability curve of a given federal university being considered to belong to category is higher compared to the Ordinal GLLAM estimation, as well as a higher decay rate for the probability of a given federal university being considered in Group , compared to the Ordinal GLLAMM estimation.
As shown in Figure 9, when looking at the behavior of the probability curves of the Binary GLM model, the probability of a given HEI being considered part of the upper strata of the research (B and A), being a federal university, exceeds 80%, ceteris paribus. However, the model points out that the fact that a Brazilian HEI is not a federal university can cause it to be classified in the lower strata of the study ( and ) with a probability of approximately 65%, all other conditions remaining constant.
The biggest problem with the Binary GLM estimation observed in this study is that the simplification of the phenomenon, thanks to an arbitrary dichotomization, together with the disregard of almost 20% of the observations in the database, creates a false sense of ease in interpreting the model’s results. For this estimation, nothing is known about what makes an HEI in Group different from an HEI in Group in terms of increases or decreases in the explanatory variables of the research—the same can be said for groups and .
More incisively, from the researchers’ perspective, by assuming arbitrary dichotomization in place of a phenomenon that manifests itself in an ordinal polychotomous way, there is disregard for the extremes of the phenomenon assumed to be original. There is no way to understand what led a given HEI to be in the top positions in the ranking studied and, as such, no way for the HEIs in an immediately lower group to understand what needs to be performed for them to climb up the WEBOMETRICS rankings. The opposite is also true; that is, there is no way to diagnose the reasons why a given HEI has been categorized as group E, and therefore, little could be performed to help it.
It could be argued that if the Binary GLM model indicates the important variables for achieving the category, then it would be sufficient to apply the same conditions abstracted from it to universities belonging to the group. The fallacy of this argument lies in the fact that it ignores that there is an unknown distance between category and category , as well as observational idiosyncrasies; the same can be said between categories and , whose distances are unknown (in fact, category was disregarded by the estimate discussed), as well as differences in regional, social, political, and economic realities, and so on, up to category .
The behavior of the Linear GLM model, as shown in Figure 9, also indicates a tendency for Brazilian federal universities to be classified in the highest groups of HEIs. However, the interpretability of the Linear GLM model in this case is the most intricate. It has already been discussed that the Linear GLM estimation did not classify any HEI in the stratum , but there is also the difficulty of establishing a cutoff point that indicates the point from which the change in category will be considered.
What is meant is that starting from the two-dimensional visualization proposed in Figure 9, imagine that a given HEI has a calculated fitted value of 2.5. Strictly speaking, a priori, the Linear GLM model would not have considered this observation as part of category , nor as part of category —but rather, the estimation would classify this HEI somewhere between these two groups. The data analyst would be left with the arbitrary decision of “adjusting” the model’s prediction (i.e., some kind of rounding) so that it converges on the categories being studied—something similar to what the researchers did in Section 7.1 because, for 76 observations, there were fitted values greater than 5.
However, for researchers, this attitude seems to go against the reasons why a machine learning model exists or is estimated. If the central idea of modeling is to support the decision-making process, regardless of the field of science being considered and regardless of the activity being observed, the estimation discussed would help less (not to say that it would be in the way) in deciding on a certain course of action in relation to the other models in the study. This situation occurred, it must be stressed, due to the arbitrary recoding of the ordinal categorical dependent variable so that it could take on metric values and, therefore, so that a classical linear regression algorithm could be trained.
Figure 10 shows that small values of the ratio of students involved in doctoral programs to the total number of professors can lead to an average probability of 45%, ceteris paribus, of a Brazilian HEI being classified as a stratum , according to the Ordinal GLLAM estimation. According to the Ordinal GLM model, this average probability drops to approximately 35% on average, and all the other conditions are equal.
Figure 10 also demonstrates that, for the Ordinal GLM estimation, values close to 0 and 0.1 of the variable do not differentiate the classification of a given Brazilian HEI in the , , and strata. However, the situation narrated occurs to a lesser extent for the Ordinal GLLAM model.
In addition, according to Figure 10, the Ordinal GLLAM and Ordinal GLM estimates, indicate an average probability of approximately 50% for a given Brazilian HEI to be predicted in the stratum . For the same modeling, the values of points to a given university being considered in the stratum with an average probability of more than 85%, ceteris paribus.
On the other hand, according to the Binary GLM estimation and its results are shown in Figure 10, values of would already be a strong indicator for a given Brazilian university to appear in the upper strata of the WEBOMETRICS ranking. Linear GLM estimation indicates that the higher the value of the variable, the greater the possibility of an HEI moving up the categories, and when , ceteris paribus, a given HEI should be placed in the stratum of the study.
In Figure 11, in relation to the Ordinal GLLAMM and Ordinal GLM models, it can be said that the passage of time benefits universities at the extremes of classification—groups and , with higher growth rates in the case of the Ordinal GLM estimation. It is also true that Ordinal GLM estimation has higher decay rates for predicting groups , and when compared to Ordinal GLLAMM estimation. Although there is little mathematical difference in the values of the slope coefficient for the variable year (see Equations (27) and (28)), the fact that the Ordinal GLLAMM estimation considers observational idiosyncrasies may justify the smoother growth and decay rates, depending on the case.
In the case of the Linear GLM estimation, according to Figure 11, the passage of time seems to benefit HEIs in groups and ; to harm universities in groups and , and not to change the status of HEIs belonging to Group . According to Figure 11, the model’s general fitted values (solid blue line) indicate a slight downward trend in the categorization of Brazilian universities over time.
Finally, for Binary GLM modeling, the passage of time is perceived as beneficial for universities in the top stratum and detrimental for HEIs in the other Group. However, according to Figure 11, the changes in the classification probabilities, ceteris paribus, were small.
8. Final Considerations
In this study, we demonstrated the application of proportional odds-type ordinal logistic regression to assess the impact of incorporating both fixed and random effects when predicting the rankings of Brazilian universities using an unprecedented, real-world database that is now freely available to the academic community.
The research also compared the proportional odds-type ordinal logistic regression (GLM and GLLAMM) estimates with a classic linear regression model and with a binary logistic regression model, using the following construct: Can the performance of Brazilian universities, considering performance as in the WEBOMETRICS ranking, be concurrently elucidated over time, the proportion of students engaged in doctoral programs concerning the total count of professors, and the classification of an HEI as a Brazilian federal university? All codes in the R computer language have been provided and are commented in English for teaching purposes.
The Ordinal GLLAMM estimation showed the highest accuracy of all models (88.63% correct; see Section 7.4 and Figure 7). The Binary GLM model achieved 83.76% accuracy, the Ordinal GLM estimation showed 45.58% accuracy, and the Linear GLM model showed the lowest accuracy of all the estimations in the study (34.91%).
When comparing the Binary GLM and Ordinal GLLAMM models, it should be noted that the dependent variable in the binary logistic estimation underwent transformations to dichotomize the phenomenon under study [5]. Groups B and A of the dependent variable formed the “best performance” group, while the combination of strata D and E generated the “worst performance” category. The estimates for Group C were missing values, totaling 244 observations.
In this sense, the considerable accuracy of the Binary GLM model tells us a lot about the HEIs grouped according to the extremes of the strata studied, but it does not tell us anything about what makes a given Brazilian university belong to Group C.
This may be of interest to the HEIs originally grouped in stratum A to maintain the status quo of their performance level, but it does not seem to help other universities. For example, when using the Binary Model, an HEI belonging to group B would extract little information on how to climb positions and would know little (or almost nothing) about falling to a position belonging to stratum C. On the subject of the Binary Model, a given HEI originally belonging to group E would have little understanding of the factors that keep it from the top positions in the ranking, given that its information was mixed with stratum D and the model discussed, knowing nothing about the central position in the ranking, the C group. In our view, the use of Binary GLM estimation in this case could generate a cult of real-world performative average mediocrity.
However, when looking at the so-called Linear GLM model, it should be remembered that the phenomenon in this case was assumed to be a discrete metric, with a value from 1 (for group E) to 5 (for stratum A) [4]. For the dataset studied, this estimation generated 76 fitted values greater than 5 [7,53], forcing the researchers to consider these observations as members of group A. For the case studied, the Linear GLM model was not capable of categorizing observations in stratum E. In the case of the Linear GLM model, it was also found that its residuals did not adhere to normality, heteroscedasticity, and autocorrelation for up to nine lags, at 1% significance, ceteris paribus [7,53,54,55,56,57,58].
When comparing the Ordinal GLM and Ordinal GLLAMM models, the study’s findings suggest that due to the oversight of observational intricacies, particularly within the GLM model, in contrast to the GLLAMM model, there was an inability to comprehend the diverse contexts encountered by the HEIs featured in the dataset, resulting in the lower accuracy observed. Furthermore, the calculated ICC of 94.29% within a panel database incorporating repeated measures served as a robust indicator of the heterogeneous behavior evident within the observations.
Nevertheless, it is important to emphasize that this scientific article adopts a tutorial format, explicitly avoiding any assertion that the enclosed models comprehensively encapsulate a wide array of realities within Brazilian Higher Education Institutes (HEIs). Brazil is well known for its extensive heterogeneity across various dimensions and is particularly highlighted by its stark income inequality. This socioeconomic disparity inevitably exerts a profound influence on the development trajectory of educational institutions, regardless of whether they are public or private or government funding.
Moreover, the manner in which the researchers categorized Brazilian universities into groups E to A is subject to limitations, much like other methodological approaches. For any subsequent researcher intending to further this study, determining the appropriate distribution of universities across categories, as well as establishing the optimal number of categories for stratification, presents itself as a set of challenges to be addressed.
Indeed, the genuine intent of the researchers engaged in this study in disseminating the discussed guidelines for ordinal logistic estimations, along with the R programming language code, is to encourage further exploration. The aspiration is for subsequent research endeavors to delve deeper, encompassing both multilevel perspectives and the accurate handling of ordinal categorical data.
In situations where researchers encounter challenges in explicitly identifying existing contexts (nestings) in their data, the suggested approach involves generating clusters based on the observations themselves. This can encompass methodologies such as centroid-based/partition clustering, hierarchical clustering, and fuzzy-based clustering. It is plausible that the resultant groupings could be regarded as latent nestings, facilitating the estimation of the random effects. However, it is important to acknowledge that cluster analysis is an unsupervised technique. If the outcomes are integrated into a multilevel model, the predictive capacity of the model may be lost. Nonetheless, these results offer more precise diagnostic insights into the researchers’ dataset.
Continuing from the preceding suggestion, to avoid losing the predictive power of ordinal regression, it may make sense to show unobservable nesting. For example, the use of classificatory Support Vector Machines, or if the amount of data is not a problem, the use of deep artificial neural networks aimed at classifying observations could serve as viable strategies.
Supplementary Materials
The following supporting information can be downloaded at: https://drive.google.com/file/d/1vBv6msnV_yBapGmvOw-WRtb0oARzMxM1/view?usp=sharing. (accessed on 6 January 2024).
Author Contributions
Conceptualization, R.d.F.S., F.G.L. and H.L.C.; methodology, R.d.F.S., F.G.L. and H.L.C.; software, R.d.F.S.; validation, R.d.F.S., F.G.L. and H.L.C.; formal analysis, R.d.F.S. and F.G.L.; investigation, R.d.F.S. and H.L.C.; resources, R.d.F.S., F.G.L. and H.L.C.; data curation, R.d.F.S.; writing—original draft preparation, R.d.F.S., F.G.L. and H.L.C.; writing—review and editing, R.d.F.S. and F.G.L.; visualization, R.d.F.S. and F.G.L.; supervision, R.d.F.S.; project administration, R.d.F.S.; funding acquisition, R.d.F.S., F.G.L. and H.L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the School of Economics, Business and Accounting of Ribeirao Preto, University of São Paulo—USP.
Data Availability Statement
CES data can be found at https://www.gov.br/inep/pt-br/areas-de-atuacao/pesquisas-estatisticas-e-indicadores/censo-da-educacao-superior (accessed on 6 January 2024). Data on university positions in WEBOMETRICS can be found at https://www.webometrics.info/en (accessed on 6 January 2024).
Acknowledgments
The author is grateful for the comments of four anonymous reviewers. This work is dedicated to the memory of Gabriel Castella Cardoso, a dear friend.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Calculated values of for the individuals in the research.
Table A1.
Calculated values of for the individuals in the research.
| HEI Names | Is It a Federal University? | |
|---|---|---|
| Federal University of Western Para | yes | −14.99009635 |
| Federal University of The Southern Border | yes | −13.73180070 |
| Darcy Ribeiro North Fluminense State University | no | −13.67610299 |
| Federal University of Latin American Integration | yes | −13.51506685 |
| University of the International Integration of Afro-Brazilian Lusophony | yes | −13.27160473 |
| Federal University of Health Sciences of Porto Alegre | yes | −10.37416534 |
| Sao Francisco University | no | −9.752614271 |
| Catholic University of Petropolis | no | −9.506667313 |
| Municipal University of Sao Caetano Do Sul | no | −9.215742952 |
| University of the Sapucai Valley | no | −9.123246743 |
| Federal University Of Lavras | yes | −8.436202000 |
| Vila Velha University | no | −8.411085314 |
| Nilton Lins University | no | −8.354072711 |
| Candido Mendes University | no | −8.347125089 |
| Marilia University | no | −8.234944757 |
| Cuiaba University | no | −8.232441189 |
| Metropolitan University of Santos | no | −8.188602961 |
| Amapa State University | no | −8.079419237 |
| State University of Health Sciences of Alagoas | no | −8.064994723 |
| Severino Sombra University | no | −8.064994723 |
| Santa Ursula University | no | −8.064994723 |
| Presidente Antonio Carlos University | no | −8.064994723 |
| Camilo Castelo Branco University | no | −8.064994723 |
| Iguacu University | no | −8.064994723 |
| Ibirapuera University | no | −8.064994723 |
| Vale do Rio Doce University | no | −8.064994723 |
| Planalto Catarinense University | no | −8.064994723 |
| State University of Rio Grande Do Sul | no | −8.064994723 |
| Rio Verde University | no | −8.064994723 |
| State University of Roraima | no | −8.064994723 |
| State University of Alagoas | no | −8.064994723 |
| University of the Campanha Region | no | −7.974555746 |
| Braz Cubas University | no | −7.974555746 |
| Itauna University | no | −7.860477850 |
| Federal University of Amapa | yes | −7.677428376 |
| Grande ABC University | no | −7.174835087 |
| Jose do Rosario Vellano University | no | −6.468046656 |
| Joinville Region University | no | −6.242757024 |
| Federal University of Roraima | yes | −6.143240450 |
| State University of Northern Parana | no | −6.006872575 |
| Cruz Alta University | no | −5.891714847 |
| Federal Rural University of the Amazon | yes | −5.795563090 |
| Cruzeiro do Sul University | no | −5.657494653 |
| Foundation Federal University of Grande Dourados | yes | −5.334567978 |
| Catholic University of Salvador | no | −5.089159010 |
| Federal University of Triangulo Mineiro | yes | −5.007426154 |
| Federal Rural University of The Semi-Arid Region | yes | −4.281043460 |
| Federal University of the Jequitinhonha and Mucuri Valleys | yes | −4.252152738 |
| Federal University of Alfenas | yes | −3.731053337 |
| Sorocaba University | no | −3.492989706 |
| Federal University of Itajuba | yes | −3.298113673 |
| Anhanguera University | no | −3.133556781 |
| Federal University of Acre | yes | −2.978102075 |
| Dom Bosco Catholic University | no | −2.976272160 |
| Franca University | no | −2.805512911 |
| Federal Rural University of Pernambuco | yes | −2.636823118 |
| Salgado de Oliveira University | no | −2.629415418 |
| Ribeirao Preto University | no | −2.601152707 |
| Potiguar University | no | −2.475139817 |
| Federal Rural University of Rio De Janeiro | yes | −2.434885013 |
| Sagrado Coracao University | no | −2.421717770 |
| Acarau Valley State University | no | −2.386904761 |
| Tocantins University | no | −2.386904761 |
| Rondonia Federal University | yes | −2.321180703 |
| Federal University of The Sao Francisco Valley | yes | −2.268085483 |
| Pontifical Catholic University of Sao Paulo | no | −2.203539879 |
| Santos Catholic University | no | −2.185315550 |
| Federal University of Alagoas | yes | −2.143302503 |
| Bandeirante University of Sao Paulo | no | −2.123308368 |
| Federal University of the State of Rio De Janeiro | yes | −2.080315766 |
| Federal University of Tocantins Foundation | yes | −1.859696753 |
| Pampa Federal University Foundation | yes | −1.700680157 |
| Tuiuti University Of Parana | no | −1.658723722 |
| Professor “Jose De Souza Herdy” University of Grande Rio | no | −1.652905607 |
| Mogi Das Cruzes University | no | −1.619034111 |
| Fumec University | no | −1.516993675 |
| State University of Mato Grosso Do Sul | no | −1.436778710 |
| City of Sao Paulo University | no | −1.424392798 |
| Sao Judas Tadeu University | no | −1.415667314 |
| Minas Gerais State University | no | −1.007623742 |
| Regional University of Cariri | no | −0.936288606 |
| Reconcavo da Bahia Federal University | yes | −0.889593824 |
| Rio Verde Valley University | no | −0.866415961 |
| State University of Piaui | no | −0.866415961 |
| Santa Cecilia University | no | −0.866415961 |
| Amazonia University | no | −0.383843188 |
| State University of Campinas | no | 0.000001716 |
| Federal University of Rio Grande Do Sul | yes | 0.000441941 |
| University of Sao Paulo | no | 0.001643641 |
| Federal University of Rio De Janeiro | yes | 0.026150447 |
| Federal University of Minas Gerais | yes | 0.085981454 |
| Federal University of Santa Catarina | yes | 0.091604285 |
| University of Western Paulista | no | 0.126200469 |
| Federal University of Ceara | yes | 0.294389265 |
| Federal University of Sao Carlos | yes | 0.310381033 |
| Federal University of Rio Grande | yes | 0.343443136 |
| State University of Maranhao | no | 0.485721407 |
| Federal University of Pernambuco | yes | 0.547950963 |
| University of Western Santa Catarina | no | 0.576139939 |
| Castelo Branco University | no | 0.630102533 |
| Santo Amaro University | no | 0.630102533 |
| Contestado University | no | 0.630102533 |
| Federal University of Vicosa | yes | 0.822644994 |
| Federal University of Sao Paulo | yes | 0.919583062 |
| Brasilia University | yes | 1.214990312 |
| ABC Federal University | yes | 1.272662705 |
| Methodist University of Piracicaba | no | 1.299548471 |
| Positivo University | no | 1.455745927 |
| Paraiba Valley University | no | 1.553119688 |
| Federal University of Parana | yes | 1.624846845 |
| Federal University of Pelotas | yes | 1.638422371 |
| Federal University of Mato Grosso | yes | 1.884384028 |
| Mato Grosso State University | no | 1.939326056 |
| Catholic University of Pernambuco | no | 2.036981661 |
| Federal University of Piaui | yes | 2.120003238 |
| Federal University of Maranhao | yes | 2.139401048 |
| Amazonas State University | no | 2.336524924 |
| Federal University of Ouro Preto | yes | 2.394441009 |
| Regional University of Northwestern Rio Grande do Sul State | no | 2.616960817 |
| Technological Federal University of Parana | yes | 2.619387447 |
| Tiradentes University | no | 2.622135482 |
| Federal University of Mato Grosso Do Sul | yes | 2.632919886 |
| Federal University of Bahia | yes | 2.876477055 |
| Julio de Mesquita Filho Paulista State University | no | 3.132439958 |
| Federal University of Campina Grande | yes | 3.140551802 |
| North Parana University | no | 3.439539019 |
| Guarulhos University | no | 3.574697821 |
| Para State University | no | 3.587890006 |
| Uberaba University | no | 3.729799680 |
| Federal University of Rio Grande Do Norte | yes | 3.999376018 |
| Federal University of Amazonas | yes | 4.036775310 |
| Federal University of Sergipe | yes | 4.067316504 |
| Feevale University | no | 4.121768718 |
| Federal University of Santa Maria | yes | 4.145951484 |
| Federal University of Sao Joao Del Rei | yes | 4.185864581 |
| Veiga de Almeida University | no | 4.203584165 |
| Anhembi Morumbi University | no | 4.301687824 |
| Rio Grande do Norte State University | no | 4.318800807 |
| Paranaense University | no | 4.318800807 |
| Community University of the Chapeco Region | no | 4.318800807 |
| Alto Uruguai e das Missões Integrated Regional University | no | 4.345878060 |
| Federal University of Para | yes | 4.491504554 |
| Taubate University | no | 4.634044812 |
| Federal University of Uberlandia | yes | 4.804616760 |
| Fluminense Federal University | yes | 4.852823692 |
| Federal University of Paraiba | yes | 4.985137105 |
| Santa Cruz State University | no | 5.038850317 |
| State University of Southwest Bahia | no | 5.041621224 |
| Salvador University | no | 5.164845860 |
| State University of Midwest | no | 5.309082320 |
| Pontifical Catholic University Of Goias | no | 5.457353354 |
| State University of Ceara | no | 5.626526798 |
| Paulista University | no | 5.709381079 |
| Federal University of Goias | yes | 5.752312579 |
| State University of Goias | no | 5.802286719 |
| University of Extreme South Catarinense | no | 5.833866187 |
| Federal University of Juiz De Fora | yes | 5.948009565 |
| Santa Cruz do Sul University | no | 6.024406003 |
| Regional University of Blumenau | no | 6.220647133 |
| Federal University of Espírito Santo | yes | 6.229696268 |
| Catholic University of Pelotas | no | 6.237231979 |
| Pontifical Catholic University of Rio de Janeiro | no | 6.599206352 |
| Rio dos Sinos Valley University | no | 6.699586880 |
| Mackenzie Presbyterian University | no | 6.703518715 |
| Fortaleza University | no | 7.200753664 |
| Itajai Valley University | no | 7.296747253 |
| Lutheran University Of Brazil | no | 7.47832689 |
| Pernambuco University | no | 7.481812386 |
| Bahia State University | no | 7.512211886 |
| Brazilian Catholic University | no | 7.566038025 |
| State University of Western Parana | no | 7.654403455 |
| Pontifical Catholic University Of Rio Grande Do Sul | no | 7.961440315 |
| Nove de Julho University | no | 7.996981951 |
| Pontifical Catholic University of Campinas | no | 8.087346315 |
| State University of Feira de Santana | no | 8.281796599 |
| Rio de Janeiro State University | no | 8.606858437 |
| Santa Catarina State University | no | 8.611956177 |
| Ponta Grossa State University | no | 8.637562072 |
| Caxias do Sul University | no | 8.711704534 |
| Methodist University of Sao Paulo | no | 8.908381972 |
| Paraiba State University | no | 9.227040499 |
| Pontifical Catholic University of Minas Gerais | no | 9.310656616 |
| University of Southern Santa Catarina | no | 9.448175941 |
| State University Of Maringa | no | 9.515227693 |
| Estacio de Sa University | no | 9.615633159 |
| Passo Fundo University | no | 10.12255267 |
| State University of Montes Claros | no | 11.46164999 |
| State University of Londrina | no | 11.51611222 |
| Pontifical Catholic University of Parana | no | 12.82779457 |
References
- Lalla, M. Fundamental characteristics and statistical analysis of ordinal variables: A review. Qual. Quant. 2017, 51, 435–458. [Google Scholar] [CrossRef]
- Vogt, W.P.; Johnson, R.B. The SAGE Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences, 5th ed.; SAGE Publications: London, UK, 2015. [Google Scholar]
- Kampen, J.; Swyngedouw, M. The Ordinal Controversy Revisited. Qual. Quant. 2000, 34, 87–102. [Google Scholar] [CrossRef]
- Fullerton, A.S.; Anderson, K.F. Ordered Regression Models: A Tutorial. Prev. Sci. 2023, 24, 431–443. [Google Scholar] [CrossRef]
- Liddell, T.M.; Kruschke, J.K. Analyzing ordinal data with metric models: What could possibly go wrong? Exp. Soc. Psychol. 2018, 79, 328–348. [Google Scholar] [CrossRef]
- Nadler, J.T.; Weston, R.; Voyles, E.C. Stuck in the Middle: The Use and Interpretation of Mid-Points in Items on Questionnaires. J. Gen. Psychol. 2015, 142, 71–89. [Google Scholar] [CrossRef] [PubMed]
- Bauer, D.J.; Sterba, S.K. Fitting multilevel models with ordinal outcomes: Performance of alternative specifications and methods of estimation. Psychol. Methods 2011, 16, 373–390. [Google Scholar] [CrossRef] [PubMed]
- Hedeker, D.; Gibbons, R.D. A Random-Effects Ordinal Regression Model for Multilevel Analysis. Biometrics 1994, 50, 933. [Google Scholar] [CrossRef]
- Fielding, A.; Yang, M.; Goldstein, H. Multilevel ordinal models for examination grades. Stat. Model. 2003, 3, 127–153. [Google Scholar] [CrossRef]
- Li, B.; Lingsma, H.F.; Steyerberg, E.W.; Lesaffre, E. Logistic random effects regression models: A comparison of statistical packages for binary and ordinal outcomes. BMC Med. Res. Methodol. 2011, 11, 77. [Google Scholar] [CrossRef]
- Hedeker, D. Methods for Multilevel Ordinal Data in Prevention Research. Prev. Sci. 2015, 16, 997–1006. [Google Scholar] [CrossRef]
- Hilbe, J.M. Logistic Regression Models; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Fernandes, A.J.; Shukla, B.; Fardoun, H. Indian Higher Education in World University Rankings—The Importance of Reputation and Branding. J. Stat. Appl. Probab. 2022, 11, 673–681. [Google Scholar] [CrossRef]
- Liu, A.; He, H.; Tu, X.M.; Tang, W. On testing proportional odds assumptions for proportional odds models. Gen. Psychiatr. 2023, 36, e101048. [Google Scholar] [CrossRef] [PubMed]
- Verwaeren, J.; Waegeman, W.; de Baets, B. Learning partial ordinal class memberships with kernel-based proportional odds models. Comput. Stat. Data Anal. 2012, 56, 928–942. [Google Scholar] [CrossRef]
- Abrudan, I.-N.; Pop, C.-M.; Lazăr, P.-S. Using a General Ordered Logit Model to Explain the Influence of Hotel Facilities, General and Sustainability-Related, on Customer Ratings. Sustainability 2020, 12, 9302. [Google Scholar] [CrossRef]
- Bender, R.; Grouven, U. Ordinal logistic regression in medical research. J. R. Coll. Physicians Lond. 1997, 31, 546–551. [Google Scholar] [PubMed]
- Ma, C.; Zhou, J.; Yang, D. Causation Analysis of Hazardous Material Road Transportation Accidents Based on the Ordered Logit Regression Model. Int. J. Environ. Res. Public Health 2020, 17, 1259. [Google Scholar] [CrossRef] [PubMed]
- Jayawardena, S.; Epps, J.; Ambikairajah, E. Ordinal Logistic Regression with Partial Proportional Odds for Depression Prediction. IEEE Trans. Affect. 2023, 14, 563–577. [Google Scholar] [CrossRef]
- Humphrey, S.E.; LeBreton, J.M. The Handbook of Multilevel Theory, Measurement, and Analysis; American Psychological Association: Worcester, MA, USA, 2018. [Google Scholar]
- Wu, L. Mixed Effects Models for Complex Data; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Singmann, H.; Kellen, D. An Introduction to Mixed Models for Experimental Psychology. In New Methods in Cognitive Psychology; Spieler, D., Schumacher, E., Eds.; Routledge: London, UK, 2019; pp. 4–27. [Google Scholar]
- Agresti, A. Categorical Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Brant, R. Assessing Proportionality in the Proportional Odds Model for Ordinal Logistic Regression. Biometrics 1990, 46, 1171–1178. [Google Scholar] [CrossRef]
- Courgeau, D. Methodology and Epistemology of Multilevel Analysis: Approaches from Different Social Sciences; Springer: London, UK, 2003. [Google Scholar]
- Headley, M.G.; Plano Clark, V.L. Multilevel Mixed Methods Research Designs: Advancing a Refined Definition. J. Mix. Methods Res. 2020, 14, 145–163. [Google Scholar] [CrossRef]
- Mathieu, J.E.; Chen, G. The Etiology of the Multilevel Paradigm in Management Research. J. Manag. 2011, 37, 610–641. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, F.; Wang, D.; Ang, S. Efficiency evaluation for higher education institutions in China considering unbalanced regional development: A meta-frontier super-SBM model. Socio-Economic. Plan. Sci. 2023, 88, 101648. [Google Scholar] [CrossRef]
- Benito, M.; Gil, P.; Romera, R. Funding, is it key for standing out in the university rankings? Scientometrics 2019, 121, 771–792. [Google Scholar] [CrossRef]
- Salmi, J.; D’Addio, A. Policies for achieving inclusion in higher education. Policy Rev. High. Educ. 2021, 5, 47–72. [Google Scholar] [CrossRef]
- Yang, J.; Wang, C.; Liu, L.; Croucher, G.; Moore, K.; Coates, H. The Productivity of Leading Global Universities. In Responsibility of Higher Education Systems; Broucker, B., Borden, V.M.H., Kallenberg, T., Milsom, C., Eds.; BRILL: Leiden, The Netherlands, 2020; pp. 224–249. [Google Scholar] [CrossRef]
- Núnez Chicharro, M.; Mangena, M.; Alonso Carrillo, M.I.; Priego De La Cruz, A.M. The effects of stakeholder power, strategic posture and slack financial resources on sustainability performance in UK higher education institutions. Sustain. Account. Manag. 2024, 15, 171–206. [Google Scholar] [CrossRef]
- Lepori, B.; Borden, V.M.H.; Coates, H. Opportunities and challenges for international institutional data comparisons. Eur. J. High. Educ. 2022, 12 (Suppl. S1), 373–390. [Google Scholar] [CrossRef]
- Mahmoud, N.; Abdel-Aty, M.; Cai, Q.; Abuzwidah, M. Analyzing the Difference Between Operating Speed and Target Speed Using Mixed-Effect Ordered Logit Model. Transp. Res. Rec. J. Transp. Res. Board 2022, 2676, 596–607. [Google Scholar] [CrossRef]
- Palardy, G.J. Review of HLM 7. Soc. Sci. Comput. Rev. 2011, 29, 515–520. [Google Scholar] [CrossRef]
- Austin, P.C. A Tutorial on Multilevel Survival Analysis: Methods, Models and Applications. Int. Stat. Rev. 2017, 85, 185–203. [Google Scholar] [CrossRef]
- Molina-Azorín, J.F.; Pereira-Moliner, J.; López-Gamero, M.D.; Pertusa-Ortega, E.M.; José Tarí, J. Multilevel research: Foundations and opportunities in management. BRQ Bus. Res. Q. 2020, 23, 319–333. [Google Scholar] [CrossRef]
- Volpert-Esmond, H.I.; Page-Gould, E.; Bartholow, B.D. Using multilevel models for the analysis of event-related potentials. Int. J. Psychophysiol. 2021, 162, 145–156. [Google Scholar] [CrossRef]
- Kim, M.; van Horn, M.L.; Jaki, T.; Vermunt, J.; Feaster, D.; Lichstein, K.L.; Taylor, D.J.; Riedel, B.W.; Bush, A.J. Repeated measures regression mixture models. Behav. Res. Methods 2020, 52, 591–606. [Google Scholar] [CrossRef] [PubMed]
- Nezlek, J.B.; Mroziński, B. Applications of multilevel modeling in psychological science: Intensive repeated measures designs. L’Année Psychol. 2020, 120, 39–72. [Google Scholar] [CrossRef]
- Rabe-Hesketh, S.; Skrondal, A. Multilevel and Longitudinal Modeling Using Stata; Stata Press: College Station, TX, USA, 2022. [Google Scholar]
- Demidenko, E. Mixed Models: Theory and Application; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Bliese, P. Within-group agreement, non-independence, and reliability: Implications for data aggregation and analysis. In Multilevel Theory, Research, and Methods in Organizations: Foundations, Extensions, and New Directions; Klein, K., Kozlowski, S., Eds.; Jossey-Bass: San Francisco, CA, USA; pp. 349–381.
- WEBOMETRICS. Ranking Web of Universities 2019; WEBOMETRICS: Madrid, Spain, 2019. [Google Scholar]
- Aguillo, I.F.; Granadino, B.; Ortega, J.L.; Prieto, J.A. Scientific research activity and communication measured with cybermetrics indicators. J. Am. Soc. Inf. Sci. 2006, 57, 1296–1302. [Google Scholar] [CrossRef]
- Aguillo, I.F.; Ortega, J.L.; Fernández, M. Webometric Ranking of World Universities: Introduction, Methodology, and Future Developments. High. Educ. Eur. 2008, 33, 233–244. [Google Scholar] [CrossRef]
- McManus, C.; Neves, A.A.B.; Diniz Filho, J.A.; Maranhão, A.Q.; Souza Filho, A.G. Profiles not metrics: The case of Brazilian universities. An. Da Acad. Bras. De Ciências 2021, 93, 1–23. [Google Scholar] [CrossRef]
- McCowan, T.; Bertolin, J. Inequalities in Higher Education Access and Completion in Brazil (No. 3). Working Paper 2020. Available online: https://www.econstor.eu/handle/10419/246235 (accessed on 12 November 2023).
- Doi, S.A.R.; Kostoulas, P.; Glasziou, P. Likelihood ratio interpretation of the relative risk. BMJ Evid.-Based Med. 2023, 28, 241–243. [Google Scholar] [CrossRef]
- Dörnemann, N. Likelihood ratio tests under model misspecification in high dimensions. J. Multivar. Anal. 2023, 193, 105122. [Google Scholar] [CrossRef]
- Hassani, H.; Silva, E. A Kolmogorov-Smirnov Based Test for Comparing the Predictive Accuracy of Two Sets of Forecasts. Econometrics 2015, 3, 590–609. [Google Scholar] [CrossRef]
- Long, J.S.; Freese, J. Regression Models for Categorical Dependent Variables Using Stata; Stata Press: College Station, TX, USA, 2014. [Google Scholar]
- Onifade, O.C.; Olanrewaju, S.O. Investigating Performances of Some Statistical Tests for Heteroscedasticity Assumption in Generalized Linear Model: A Monte Carlo Simulations Study. Open J. Stat. 2020, 10, 453–493. [Google Scholar] [CrossRef]
- Mbah, A.K.; Paothong, A. Shapiro–Francia test compared to other normality test using expected p-value. J. Stat. Comput. Simul. 2015, 85, 3002–3016. [Google Scholar] [CrossRef]
- Turner, P. Critical values for the Durbin-Watson test in large samples. Appl. Econ. Lett. 2020, 27, 1495–1499. [Google Scholar] [CrossRef]
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach; Cengage Learning: Boston, MA, USA, 2018. [Google Scholar]
- Shmueli, G.; Bruce, P.C.; Stephens, M.L.; Anandamurthy, M.; Nitin, R. Machine Learning for Business Analytics: Concepts, Techniques and Applications with JMP Pro; Wiley: Hoboken, NJ, USA, 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).