Exploring Dynamic Structures in Matrix-Valued Time Series via Principal Component Analysis
Abstract
1. Introduction
2. Cross-Autocorrelation Functions
3. Principal Component Analysis
3.1. Principal Components for Time Series
3.2. Interpretation—Correlations Circles
- (i)
- Pearson product moment correlationThe Pearson product moment covariance function between and is defined aswhere , , is as defined in Equation (3) andwhere the principal components are calculated from Equation (19). Hence, the Pearson correlation function between and iswhere are the sample variances of and , respectively, given by
- (ii)
- Moran correlationIn the context of spatial neighbors, Ref. [63] introduced an index to measure spatial correlations. The Moran correlation is commonly employed to measure the correlation between variables while considering a predefined spatial, geographical, or temporal structure. Extending this concept to time series and focusing the correlation measure on lagged observations (i.e., neighbors), we refer to it as Moran’s correlation measure. To define the Moran covariance function, we consider ,where represents the set of neighboring observations. For a lag of k, , meaning that the neighbors are observations (and similarly for principal components ) separated by k units.Then, the Moran correlation between the variable and principal component is calculated aswhere
- (iii)
- Loadings based dependenceIn a standard principal component analysis of non-time-series data, the correlation or measure of loadings-based dependence between and is given byIn this equation, is estimated using as defined in Equation (23). The expression of Equation (29) provides the contribution or the weight of each original variable to the calculation of the principal component. This weight can be interpreted as a measure of dependence. The same definition applies directly to time-series data, although the eigenvectors and eigenvalues indirectly incorporate the time structure through the variance–covariance matrix .
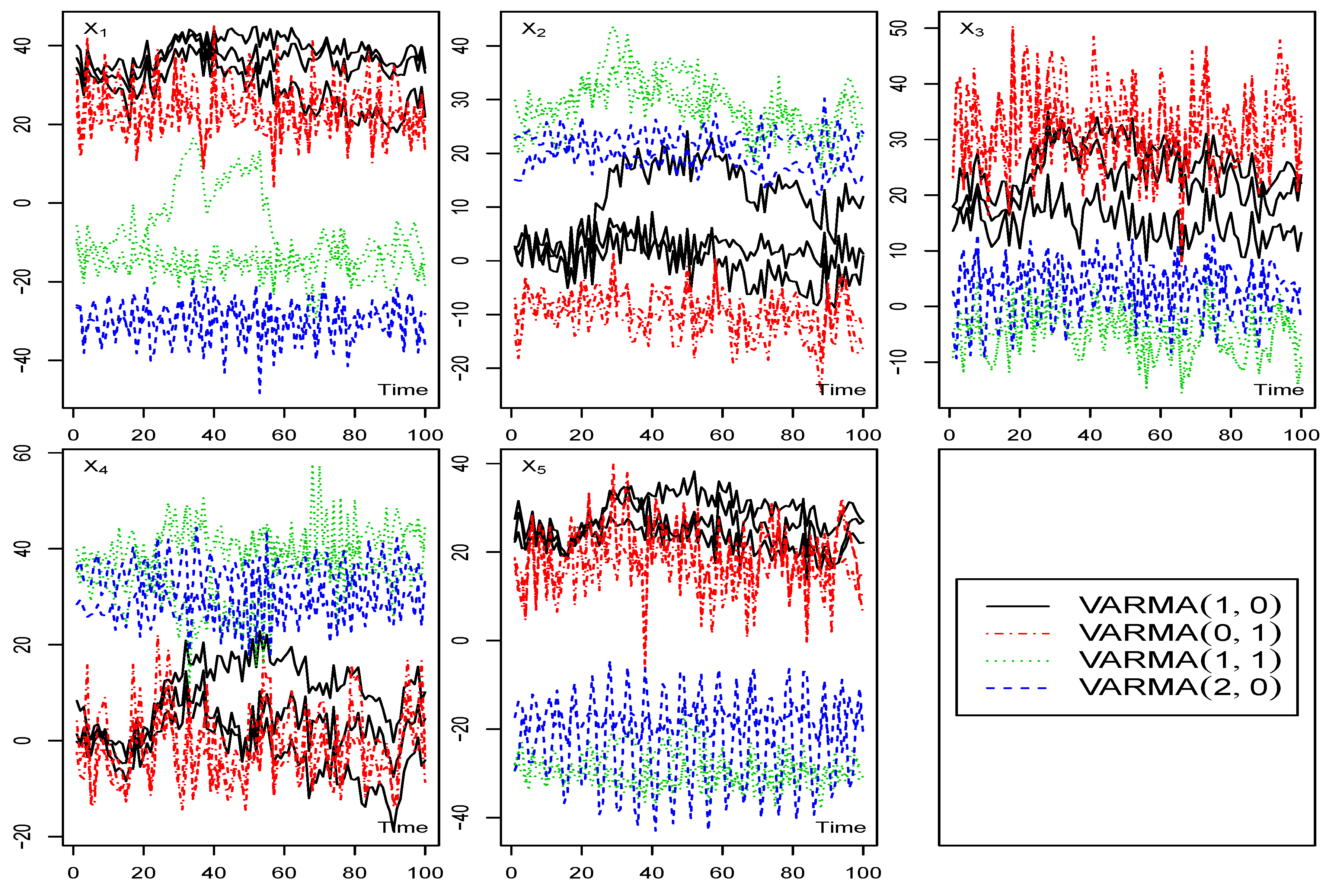
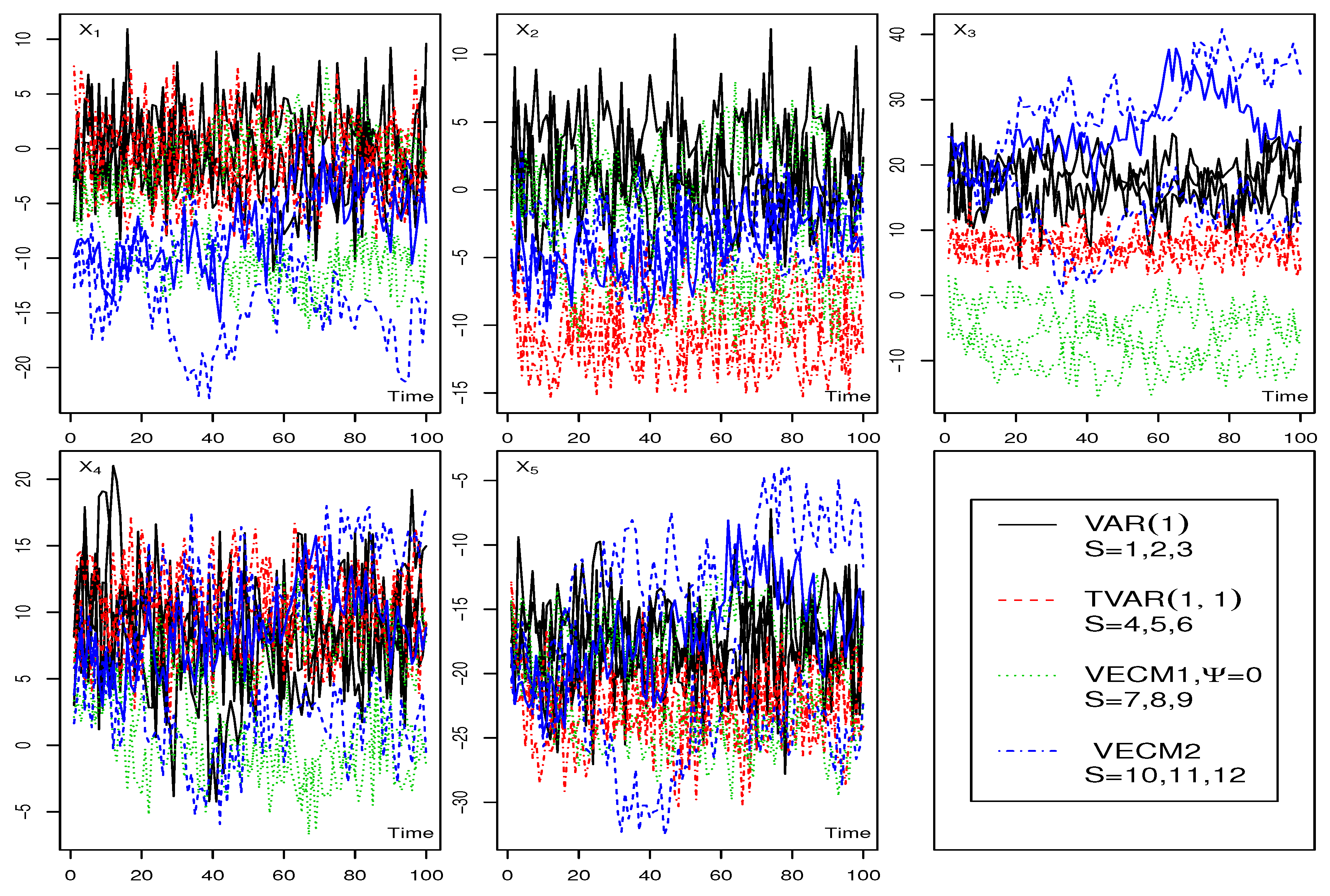
4. Simulation Studies
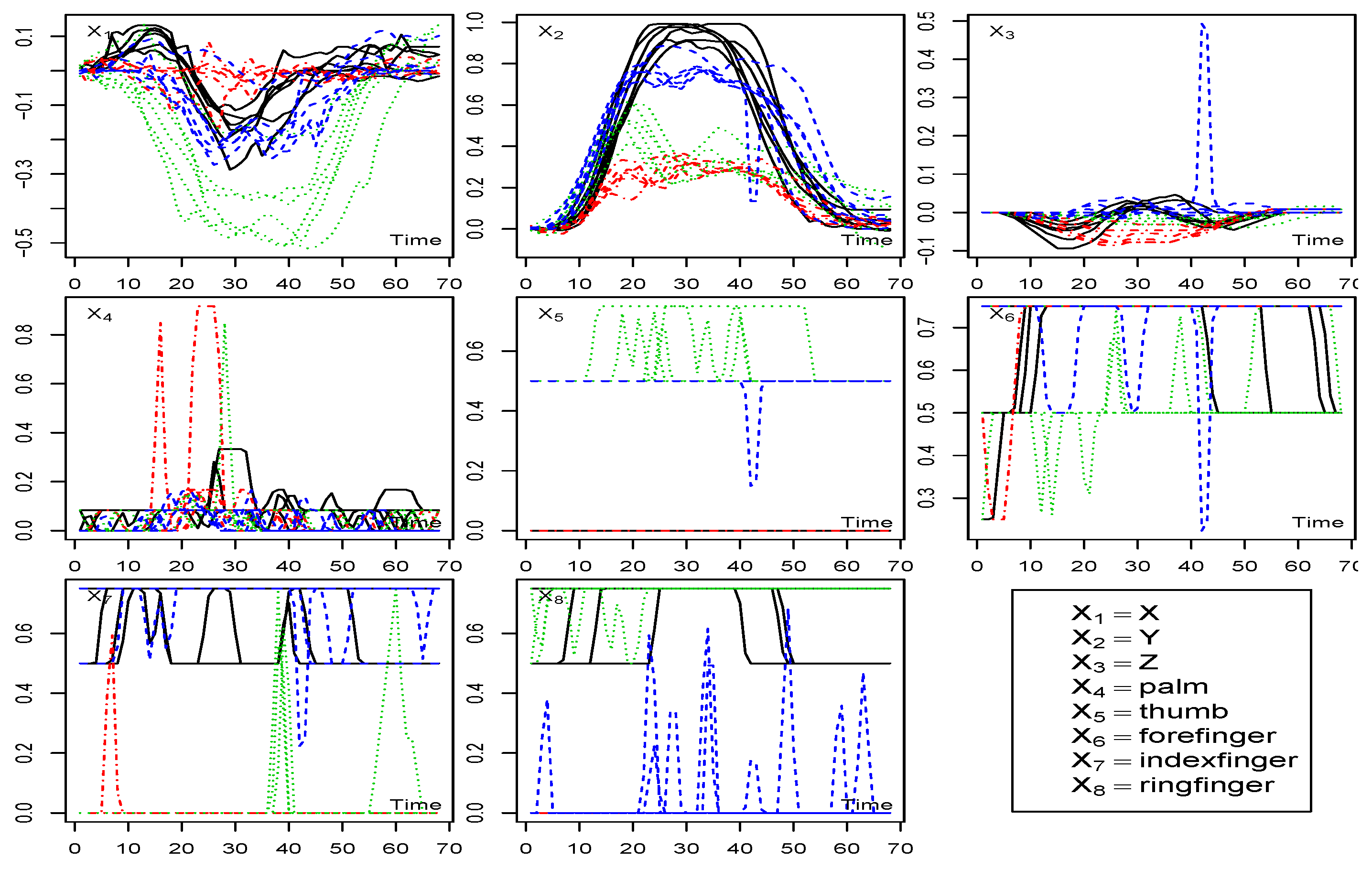
5. Illustration
5.1. Auslan Sign Language Data
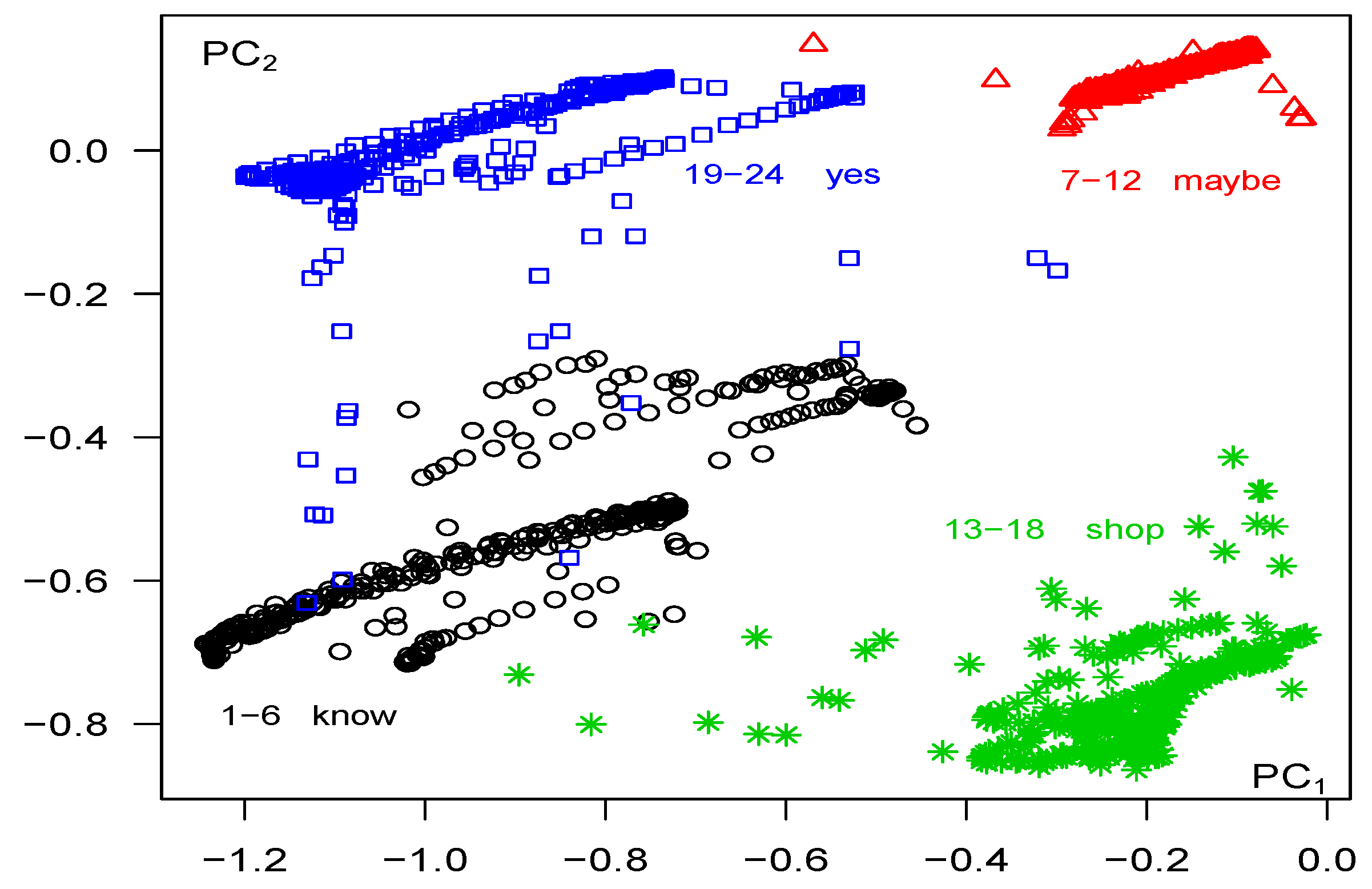
5.2. Analysis Based on Total Variations
5.3. Within Variations and
5.3.1. Principal Components Based on within Variations
5.3.2. Lag
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, J.; Michailidis, G. Regularized estimation and testing for high-dimensional multi- block vector-autoregressive models. J. Mach. Learn. Res. 2017, 18, 4188–4236. [Google Scholar]
- Mills, T.C. The Econometric Modelling of Financial Time Series; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Samadi, S.Y.; Billard, L. Analysis of dependent data aggregated into intervals. J. Multivar. Anal. 2021, 186, 104817. [Google Scholar] [CrossRef]
- Samadi, S.Y.; Herath, H.M.W.B. Reduced-rank envelope vector autoregressive models. 2023; preprint. [Google Scholar]
- Seth, A.K.; Barrett, A.B.; Barnett, L. Granger causality analysis in neuroscience and neuroimaging. J. Neurosci. 2015, 35, 3293–3297. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Li, L.; Zhu, H. Tensor regression with applications in neuroimaging data analysis. J. Am. Stat. Assoc. 2013, 108, 540–552. [Google Scholar] [CrossRef] [PubMed]
- Liao, T.W. Clustering of time series—A survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Košmelj, K.; Batagelj, V. Cross-sectional approach for clustering time varying data. J. Classif. 1990, 7, 99–109. [Google Scholar] [CrossRef]
- Goutte, C.; Toft, P.; Rostrup, E. On clustering fMRI time series. Neuroimage 1999, 9, 298–310. [Google Scholar] [CrossRef] [PubMed]
- Policker, S.; Geva, A.B. Nonstationary time series analysis by temporal clustering. IEEE Trans. Syst. Man Cybernet-B Cybernet 2000, 30, 339–343. [Google Scholar] [CrossRef]
- Prekopcsák, Z.; Lemire, D. Time series classification by class-specific Mahalanobis distance measures. Adv. Data Anal. Classif. 2012, 6, 185–200. [Google Scholar]
- Harrison, L.; Penny, W.D.; Friston, K. Multivariate autoregressive modeling of fMRI time series. Neuroimage 2003, 19, 1477–1491. [Google Scholar] [CrossRef]
- Maharaj, E.A. Clusters of time series. J. Classif. 2000, 17, 297–314. [Google Scholar] [CrossRef]
- Piccolo, D. A distance measure for classifying ARIMA models. J. Time Ser. Anal. 1990, 11, 153–164. [Google Scholar] [CrossRef]
- Alonso, A.M.; Berrendero, J.R.; Hernández, A.; Justel, A. Time series clustering based on forecast densities. Comput. Stat. Data Anal. 2006, 51, 762–776. [Google Scholar] [CrossRef]
- Vilar, J.A.; Alonso, A.M.; Vilar, J.M. Non-linear time series clustering based on non-parametric forecast densities. Comput. Stat. Data Anal. 2010, 54, 2850–2865. [Google Scholar] [CrossRef]
- Owsley, L.M.D.; Atlas, L.E.; Bernard, G.D. Self-organizing feature maps and hidden Markov models for machine-tool monitoring. IEEE Trans. Signal Process. 1997, 45, 2787–2798. [Google Scholar] [CrossRef]
- Douzal-Chouakria, A.; Nagabhushan, P. Adaptive dissimilarity index for measuring time series proximity. Adv. Data Anal. Classif. 2007, 1, 5–21. [Google Scholar] [CrossRef]
- Jeong, Y.; Jeong, M.; Omitaomu, O. Weighted dynamic time warping for time series classification. Pattern Recognit. 2011, 44, 2231–2240. [Google Scholar] [CrossRef]
- Yu, D.; Yu, X.; Hu, Q.; Liu, J.; Wu, A. Dynamic time warping constraint learning for large margin nearest neighbor classification. Inf. Sci. 2011, 181, 2787–2796. [Google Scholar] [CrossRef]
- Liao, T.W. A clustering procedure for exploratory mining of vector time series. Pattern Recognit. 2007, 40, 2550–2562. [Google Scholar] [CrossRef]
- Košmelj, K.; Zabkar, V. A methodology for identifying time-trend patterns: An application to the advertising expenditure of 28 European countries in the 1994–2004 period. In Lecture Notes in Computer Science, KI: Advances in Artificial Inteligence; Furbach, U., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 92–106. [Google Scholar]
- Kalpakis, K.; Gada, D.; Puttagunta, V. Distance measures for effective clustering of ARIMA time-series. Data Min. 2001, 1, 273–280. [Google Scholar]
- Kakizawa, Y.; Shumway, R.H.; Taniguchi, N. Discrimination and clustering for mulitvariate time series. J. Am. Stat. Assoc. 1998, 93, 328–340. [Google Scholar] [CrossRef]
- Shumway, R.H. Time-frequency clustering and discriminant analysis. Stat. Probab. Lett. 2003, 63, 307–314. [Google Scholar] [CrossRef]
- Vilar, J.M.; Vilar, J.A.; Pértega, S. Classifying time series data: A nonparametric approach. J. Classif. 2009, 26, 3–28. [Google Scholar] [CrossRef]
- Forni, M.; Hallin, M.; Lippi, M.; Reichlin, L. The generalized dynamic factor model: Identification and estimation. Rev. Econ. Stat. 2000, 82, 540–554. [Google Scholar] [CrossRef]
- Forni, M.; Lippi, M. The generalized factor model: Representation theory. Econom. Theory 2001, 17, 1113–1141. [Google Scholar] [CrossRef]
- Garcia-Escudero, L.A.; Gordaliza, A. A proposal for robust curve clustering. J. Classif. 2005, 22, 185–201. [Google Scholar] [CrossRef]
- Hebrail, G.; Hugueney, B.; Lechevallier, Y.; Rossi, F. Exploratory analysis of functional data via clustering and optimal segmentation. Neurocomputing 2010, 73, 1125–1141. [Google Scholar] [CrossRef]
- Huzurbazar, S.; Humphrey, N.F. Functional clustering of time series: An insight into length scales in subglacial water flow. Water Resour. Res. 2008, 44, W11420. [Google Scholar] [CrossRef]
- Serban, N.; Wasserman, L. CATS: Clustering after transformation and smoothing. J. Am. Stat. Assoc. 2005, 100, 990–999. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics; Le Cam, L., Neyman, J., Eds.; University of California Press: Oakland, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Asoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Dunn, J. A fuzzy relative of the ISODATA process and its use in detecting compact, well separated clusters. J. Cybern. 1974, 3, 32–57. [Google Scholar] [CrossRef]
- Beran, J.; Mazzola, G. Visualizing the relationship between time series by hierarchical smoothing models. J. Comput. Graph. Stat. 1999, 8, 213–228. [Google Scholar]
- Wismüller, A.; Lange, O.; Dersch, D.R.; Leinsinger, G.L.; Hahn, K.; Pütz, B.; Auer, D. Cluster analysis of biomedical image time series. Int. J. Comput. Vis. 2002, 46, 103–128. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control, 4th ed.; Holden-Day: San Francisco, CA, USA, 2015. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods; Springer: New York, NY, USA, 1991. [Google Scholar]
- Park, J.H.; Samadi, S.Y. Heteroscedastic modelling via the autoregressive conditional variance subspace. Can. J. Stat. 2014, 42, 423–435. [Google Scholar] [CrossRef]
- Park, J.H.; Samadi, S.Y. Dimension Reduction for the Conditional Mean and Variance Functions in Time Series. Scand. J. Stat. 2020, 47, 134–155. [Google Scholar] [CrossRef]
- Samadi, S.Y.; Hajebi, M.; Farnoosh, R. A semiparametric approach for modelling multivariate nonlinear time series. Can. J. Stat. 2019, 47, 668–687. [Google Scholar] [CrossRef]
- Walden, A.; Serroukh, A. Wavelet Analysis of Matrix-valued Time Series. Proc. Math. Phys. Eng. Sci. 2002, 458, 157–179. [Google Scholar] [CrossRef]
- Wang, H.; West, M. Bayesian analysis of Matrix Normal Graphical Models. Biometrika 2009, 96, 821–834. [Google Scholar] [CrossRef]
- Samadi, S.Y. Matrix Time Series Analysis. Ph.D. Dissertation, University of Georgia, Athens, GA, USA, 2014. [Google Scholar]
- Samadi, S.Y.; Billard, L. Matrix time series models. 2023; preprint. [Google Scholar]
- Cryer, J.D.; Chan, K.-S. Time Series Analysis; Springer: New York, NY, USA, 2008. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications; Springer: New York, NY, USA, 2011. [Google Scholar]
- Whittle, P. On the fitting of multivariate autoregressions, and the approximate canonical factorization of a spectral density matrix. Biometrika 1963, 50, 129–134. [Google Scholar] [CrossRef]
- Jones, R.H. Prediction of multivariate time series. J. Appl. Meteorol. 1964, 3, 285–289. [Google Scholar] [CrossRef]
- Webb, A. Statistical Pattern Recognition; Hodder Headline Group: London, UK, 1999. [Google Scholar]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 7th ed.; Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
- Joliffe, I.T. Principal Component Analysis; Springer: New York, NY, USA, 1986. [Google Scholar]
- Anderson, T.W. An Introduction to Multivariate Statistical Analysis, 2nd ed.; John Wiley: New York, NY, USA, 1984. [Google Scholar]
- Samadi, S.Y.; Billard, L.; Meshkani, M.R.; Khodadadi, A. Canonical correlation for principal components of time series. Comput. Stat. 2017, 32, 1191–1212. [Google Scholar] [CrossRef]
- Billard, L.; Douzal-Chouakria, A.; Samadi, S.Y. An Exploratory Analysis of Multiple Multivariate Time Series. In Proceedings of the 1st International Workshop Advanced Analytics Learning on Temporal Data AALTD 2015, Porto, Portugal, 11 September 2015; Volume 3, pp. 1–8. [Google Scholar]
- Jäckel, P. Monte Carlo Methods in Finance; John Wiley: New York, NY, USA, 2002. [Google Scholar]
- Rousseeuw, P.; Molenberghs, G. Transformation of non positive semidefnite correlation matrices. Commun. Stat. Theory Methods 1993, 22, 965–984. [Google Scholar] [CrossRef]
- Cai, T.T.; Ma, Z.; Wu, Y. Sparse PCA: Optimal rates and adaptive estimation. Ann. Stat. 2013, 41, 3074–3110. [Google Scholar] [CrossRef]
- Guan, Y.; Dy, J.G. Sparse probabilistic principal component analysis. J. Mach. Learn. Res. 2009, 5, 185–192. [Google Scholar]
- Lu, M.; Huang, J.Z.; Qian, X. Sparse exponential family Principal Component Analysis. Pattern Recognit. 2016, 60, 681–691. [Google Scholar] [CrossRef] [PubMed]
- Moran, P.A.P. The interpretation of statistical maps. J. R. Stat. Soc. A 1948, 10, 243–251. [Google Scholar] [CrossRef]
- Lo, C.M.; Zivot, E. Threshold cointegration and nonlinear adjustment to the law of one price. Macroecon. Dyn. 2001, 5, 533–576. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W.J. Co-integration and error correction: Representation, estimation and testing. Econometrica 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Kadous, M.W. Recognition of Australian Sign Language Using Instrumented Gloves. Bachelor’s Thesis, University of South Wales, Newport, UK, 1995; 136p. [Google Scholar]
- Kadous, M.W. Learning comprehensible descriptions and multivariate time series. In Proceedings of the Sixteenth International Conference on Machine Learning, Bled, Slovenia, 27–30 June 1999; Bratko, I., Dzeroski, S., Eds.; Morgan Kaufmann Publishers: San Fransisco, CA, USA, 1999; pp. 454–463. [Google Scholar]



| Percent Variation | Cumulative Variation | Percent Variation | Cumulative Variation | ||||
|---|---|---|---|---|---|---|---|
| (a) Total Variations—lag | (b) Within Variations—lag | ||||||
| 1 | 2.31907 | 0.49939 | 0.49939 | 1 | 1.96330 | 0.48941 | 0.48941 |
| 2 | 1.10152 | 0.23720 | 0.73659 | 2 | 0.79967 | 0.19934 | 0.68876 |
| 3 | 0.84684 | 0.18236 | 0.91895 | 3 | 0.63151 | 0.15742 | 0.84619 |
| 4 | 0.28645 | 0.06168 | 0.98064 | 4 | 0.35461 | 0.08839 | 0.93459 |
| 5 | 0.08990 | 0.01935 | 1.00000 | 5 | 0.26238 | 0.06540 | 1.00000 |
| Cross-Autocorrelations | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.986 | −0.299 | −0.010 | −0.071 | −0.410 | 0.414 | 0.205 | −0.274 | |
| −0.330 | 0.977 | 0.071 | 0.244 | 0.065 | 0.215 | 0.418 | 0.111 | |
| 0.015 | 0.042 | 0.849 | −0.108 | 0.238 | −0.072 | 0.253 | 0.017 | |
| −0.101 | 0.247 | −0.132 | 0.820 | −0.184 | 0.028 | 0.039 | 0.131 | |
| −0.413 | 0.065 | 0.238 | −0.184 | 0.984 | −0.355 | 0.011 | 0.092 | |
| 0.403 | 0.217 | −0.071 | 0.022 | −0.353 | 0.945 | 0.376 | −0.494 | |
| 0.202 | 0.421 | 0.250 | 0.038 | 0.012 | 0.383 | 0.978 | −0.033 | |
| −0.273 | 0.111 | 0.016 | 0.128 | 0.092 | −0.498 | −0.032 | 0.979 | |
| Percent Variation | Cumulative Variation | Percent Variation | Cumulative Variation | ||||
|---|---|---|---|---|---|---|---|
| (a) Total Variations—lag | (b) Within Variations—lag | ||||||
| 1 | 2.11118 | 0.28087 | 0.28087 | 1 | 1.92391 | 0.28656 | 0.28656 |
| 2 | 1.62876 | 0.21669 | 0.49756 | 2 | 1.07780 | 0.16053 | 0.44709 |
| 3 | 1.26361 | 0.16811 | 0.66567 | 3 | 0.95661 | 0.14248 | 0.58957 |
| 4 | 0.90345 | 0.12019 | 0.78587 | 4 | 0.77506 | 0.11544 | 0.70501 |
| 5 | 0.58972 | 0.07846 | 0.86432 | 5 | 0.63006 | 0.09384 | 0.79885 |
| 6 | 0.48044 | 0.06392 | 0.92824 | 6 | 0.54432 | 0.08107 | 0.87992 |
| 7 | 0.29035 | 0.03863 | 0.96687 | 7 | 0.44756 | 0.06666 | 0.94659 |
| 8 | 0.24902 | 0.03313 | 1.00000 | 8 | 0.35862 | 0.05341 | 1.00000 |
| (a) Pearson Correlation Circle | ||||||||
| 0.653 | −0.235 | −0.161 | −0.216 | −0.121 | 0.083 | −0.323 | −0.177 | |
| 0.028 | 0.855 | 0.273 | 0.069 | 0.448 | −0.087 | 0.194 | −0.534 | |
| −0.040 | 0.190 | −0.295 | −0.082 | 0.103 | 0.249 | −0.123 | −0.032 | |
| −0.004 | 0.203 | 0.487 | −0.124 | −0.139 | −0.095 | 0.070 | −0.061 | |
| −0.560 | 0.211 | −0.584 | 0.287 | 0.196 | 0.740 | 0.320 | 0.186 | |
| 0.799 | 0.230 | −0.139 | 0.254 | −0.082 | −0.078 | −0.360 | −0.358 | |
| 0.456 | 0.784 | −0.251 | −0.275 | 0.616 | 0.513 | −0.674 | −0.325 | |
| −0.700 | 0.202 | 0.589 | −0.807 | 0.690 | −0.003 | 0.416 | 0.670 | |
| (b) Moran Correlation Circle | ||||||||
| 0.273 | −0.263 | −0.121 | −0.247 | −0.023 | 0.153 | 0.195 | −0.097 | |
| 0.144 | 0.716 | 0.211 | 0.384 | 0.268 | 0.011 | 0.352 | −0.323 | |
| −0.383 | −0.507 | −0.001 | −0.413 | −0.449 | −0.469 | −0.062 | −0.064 | |
| −0.033 | 0.220 | 0.797 | −0.081 | −0.768 | 0.509 | 0.009 | 0.098 | |
| 0.076 | 0.394 | −0.229 | 0.347 | 0.286 | 0.578 | 0.160 | 0.161 | |
| 0.587 | 0.403 | −0.040 | 0.368 | 0.311 | 0.282 | 0.210 | 0.522 | |
| 0.487 | 0.735 | −0.243 | −0.147 | 0.436 | 0.635 | −0.699 | 0.000 | |
| −0.656 | 0.103 | 0.416 | −0.818 | 0.347 | −0.048 | 0.314 | 0.617 | |
| (c) Loadings Based Dependence Circle | ||||||||
| 0.742 | −0.310 | −0.129 | −0.416 | 0.026 | 0.210 | 0.265 | −0.169 | |
| −0.009 | 0.863 | 0.249 | 0.190 | 0.084 | −0.161 | 0.232 | −0.221 | |
| −0.078 | 0.290 | −0.567 | −0.332 | −0.465 | −0.349 | 0.057 | 0.046 | |
| 0.002 | 0.271 | 0.641 | −0.056 | −0.499 | 0.247 | 0.002 | 0.037 | |
| −0.594 | 0.240 | −0.538 | 0.293 | 0.050 | 0.419 | 0.175 | 0.066 | |
| 0.824 | 0.204 | −0.010 | 0.224 | 0.064 | −0.035 | 0.135 | 0.354 | |
| 0.401 | 0.706 | −0.211 | −0.272 | 0.201 | 0.225 | −0.313 | −0.021 | |
| −0.602 | 0.180 | 0.344 | −0.609 | 0.265 | 0.002 | 0.126 | 0.195 | |
| (a) Pearson Correlation Circle | ||||||||
| 0.540 | 0.620 | 0.065 | 0.397 | 0.232 | 0.175 | −0.307 | 0.126 | |
| −0.860 | −0.002 | 0.222 | −0.211 | 0.416 | 0.406 | −0.127 | −0.849 | |
| −0.083 | 0.090 | −0.172 | −0.349 | 0.270 | −0.143 | −0.030 | −0.115 | |
| −0.266 | −0.082 | 0.305 | 0.338 | 0.145 | −0.030 | 0.070 | −0.062 | |
| −0.323 | −0.258 | −0.741 | −0.746 | −0.057 | −0.523 | 0.167 | −0.384 | |
| 0.019 | 0.466 | 0.019 | 0.329 | 0.350 | 0.636 | −0.712 | −0.129 | |
| −0.451 | 0.771 | −0.142 | −0.407 | 0.983 | 0.263 | −0.349 | −0.287 | |
| −0.474 | 0.124 | 0.519 | −0.472 | −0.086 | −0.695 | 0.930 | 0.011 | |
| (b) Moran Correlation Circle | ||||||||
| 0.390 | 0.268 | 0.039 | 0.103 | −0.006 | −0.151 | 0.065 | −0.243 | |
| −0.743 | 0.035 | −0.011 | 0.011 | 0.000 | 0.433 | −0.225 | −0.796 | |
| 0.570 | −0.484 | 0.502 | 0.048 | 0.047 | −0.345 | 0.303 | 0.356 | |
| −0.302 | −0.342 | 0.146 | 0.889 | 0.471 | −0.671 | 0.017 | 0.267 | |
| −0.435 | 0.313 | −0.626 | −0.197 | −0.034 | −0.001 | −0.187 | −0.347 | |
| −0.515 | 0.614 | −0.217 | −0.064 | −0.197 | 0.145 | −0.426 | −0.127 | |
| −0.410 | 0.670 | −0.480 | −0.299 | 0.765 | 0.166 | −0.312 | 0.072 | |
| −0.299 | 0.284 | 0.661 | −0.268 | −0.102 | −0.568 | 0.901 | 0.132 | |
| (c) Loadings Based Dependence Circle | ||||||||
| 0.740 | 0.529 | 0.069 | 0.230 | 0.062 | −0.126 | 0.064 | −0.378 | |
| −0.802 | −0.211 | 0.250 | 0.036 | 0.023 | 0.267 | −0.060 | −0.398 | |
| 0.245 | −0.373 | 0.513 | −0.405 | 0.335 | −0.334 | −0.188 | −0.033 | |
| −0.370 | −0.224 | 0.063 | 0.615 | 0.302 | −0.376 | 0.002 | 0.086 | |
| −0.308 | −0.029 | −0.654 | −0.321 | −0.070 | −0.329 | 0.047 | −0.180 | |
| −0.451 | 0.566 | 0.158 | −0.021 | −0.281 | −0.051 | −0.334 | 0.098 | |
| −0.240 | 0.421 | −0.191 | −0.203 | 0.577 | 0.039 | −0.139 | 0.075 | |
| −0.425 | 0.258 | 0.365 | −0.185 | −0.075 | −0.302 | 0.522 | 0.028 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Billard, L.; Douzal-Chouakria, A.; Samadi, S.Y. Exploring Dynamic Structures in Matrix-Valued Time Series via Principal Component Analysis. Axioms 2023, 12, 570. https://doi.org/10.3390/axioms12060570
Billard L, Douzal-Chouakria A, Samadi SY. Exploring Dynamic Structures in Matrix-Valued Time Series via Principal Component Analysis. Axioms. 2023; 12(6):570. https://doi.org/10.3390/axioms12060570
Chicago/Turabian StyleBillard, Lynne, Ahlame Douzal-Chouakria, and S. Yaser Samadi. 2023. "Exploring Dynamic Structures in Matrix-Valued Time Series via Principal Component Analysis" Axioms 12, no. 6: 570. https://doi.org/10.3390/axioms12060570
APA StyleBillard, L., Douzal-Chouakria, A., & Samadi, S. Y. (2023). Exploring Dynamic Structures in Matrix-Valued Time Series via Principal Component Analysis. Axioms, 12(6), 570. https://doi.org/10.3390/axioms12060570






