Abstract
This study introduces a new two-parameter Liu estimator (PMTPLE) for addressing the multicollinearity problem in the Poisson regression model (PRM). The estimation of the PRM is traditionally accomplished through the Poisson maximum likelihood estimator (PMLE). However, when the explanatory variables are correlated, thus leading to multicollinearity, the variance or standard error of the PMLE is inflated. To address this issue, several alternative estimators have been introduced, including the Poisson ridge regression estimator (PRRE), Liu estimator (PLE), and adjusted Liu estimator (PALE), each of them relying on a single shrinkage parameter. The PMTPLE uses two shrinkage parameters, which enhances its adaptability and robustness in the presence of multicollinearity between explanatory variables. To assess the performance of the PMTPLE compared to the four existing estimators (the PMLE, PRRE, PLE, and PALE), a simulation study is conducted that encompasses various scenarios and two empirical applications. The evaluation of the performance is based on the mean square error (MSE) criterion. The theoretical comparison, simulation results, and findings of the two applications consistently demonstrate the superiority of the PMTPLE over the other estimators, establishing it as a robust solution for count data analysis under multicollinearity conditions.
MSC:
62J07; 62J12
1. Introduction
The Poisson regression model (PRM) is a crucial statistical tool applied in various fields for the analysis of count data. It is particularly valuable when examining the relationships between one or more explanatory variables and a response variable that represents rare events or non-negative integer counts. The significance of the PRM lies in its ability to accommodate data with distinct characteristics, such as the distribution of event occurrences. This makes it a fundamental component in epidemiology, ecology, economics, and numerous scientific disciplines. The Poisson regression model is not only the most commonly employed model for count data, but it is also highly popular for estimating the parameters of multiplicative models [1,2]. By employing the maximum likelihood estimation (MLE) method, the PRM enables researchers to estimate regression coefficients. This makes it an indispensable asset for precise modeling and hypothesis testing in data analysis.
In the context of multiple regression modeling, interpreting individual parameter estimates becomes difficult when the explanatory variables are highly correlated with each other—a phenomenon known as multicollinearity. This presents a significant challenge when estimating the unknown regression coefficients, especially in the PRM (which relies on MLE). Månsson and Shukur [3] emphasized the sensitivity of MLE to multicollinearity, highlighting the need to address this concern in statistical analysis. When multicollinearity is present, constructing robust inferences becomes complex as the variances and standard errors of the regression estimates increase, thus potentially leading to incorrect indications of the sign. Additionally, the t and F ratios, which are crucial for hypothesis testing, often lose their statistical significance in the presence of severe multicollinearity. This further underscores the importance of addressing this issue in multiple regression analysis.
Multicollinearity presents a challenge by causing an inflated variance in the estimated coefficient vectors, making interpreting parameter estimates difficult. This leads to unreliable statistical inferences and limits the ability to assess the impact of various economic factors on the dependent variable. To address this issue, ridge regression (RR) analysis is widely used. RR was introduced by Hoerl and Kennard [4], and it involves adding a positive value k, known as the ridge parameter, to the variance–covariance matrix. Alkhamisi et al. [5]; Alkhamisi and Shukur [6]; Khalaf and Shukur [7]; Kibria [8]; Manson and Shukur [3]; and Muniz and Kibria [9] have proposed different techniques for estimating k. These studies compared the performance of the RR estimator through simulations and found it to be an effective analysis method. Manson and Shukur [3] introduced the Poisson ridge regression estimator (PRRE) method for addressing multicollinearity and demonstrated that the PRRE outperformed the MLE method in Poisson regression analysis. Another approach to combat multicollinearity is the Liu estimator (LE) [10], which has gained popularity due to its linear function of the shrinkage parameter (d). Månsson et al. [11] extended this concept to propose the Poisson Liu regression (PLE) method, thereby showing its superior performance to the PRRE in Poisson regression analysis. Amin et al. [12] introduced the adjusted Liu estimator for Poisson regression, referred to as the PALE, which is a modified version of the one-parameter LE for linear regression models [13]. The PALE has proven effective in addressing multicollinearity challenges and is considered superior to both the PRRE and PLE methods in managing multicollinearity concerns, thereby enhancing the toolkit for robust statistical analysis according to the current literature.
Several research articles have suggested new two-parameter estimators for various regression models as a solution to the problem of multicollinearity. These articles have demonstrated that estimators relying on two parameters outperform those relying on only one parameter. Notable studies include those of Algamal and Abonazel [14]; Yang and Chang [15]; Abonazel et al. [16]; Omara [17]; and Abonazel et al. [18]. The objective of this article was to introduce a new modified two-parameter Liu estimator for the Poisson model, and to propose methods for selecting its parameters. Additionally, the maximum likelihood, ridge, Liu, and adjusted Liu estimators were compared with the proposed estimator.
The structure of this paper is as follows: Section 1 provides a definition of the Poisson distribution and its regression model. Section 2 introduces the PRRE, PLE, and PALE, as well as presents our proposed estimator. Section 3 offers theoretical comparisons of the proposed estimator and other estimators. Section 4 presents the optimal value of the biasing parameter. Section 5 discusses the simulation study conducted to evaluate the performance of the proposed estimator. Section 6 provides the results of the real-world application. Finally, Section 7 concludes the paper.
2. Methodology
2.1. Poisson Regression Model
The PRM was used to analyze data, which consist of counts. In this model, the response variable, denoted as , follows a Poisson distribution. The Poisson distribution is characterized by its probability density function, which is expressed as follows:
where for all , and the expected value and the variance of are equal to , i.e., . The expression for is represented using the canonical log link function and a linear combination of the explanatory variables. This can be written as , where represents the ith row of the data matrix X. The data matrix X has dimensions of , where n represents the number of observations and p the number of explanatory variables. The vector has dimensions of and contains the coefficients for the linear combination.
The maximum likelihood method is a widely recognized technique for estimating model parameters in the PRM. The log-likelihood function for the PRM is provided below.
The PMLE is determined by calculating the first derivative of Equation (2) and equating it to zero. This process can be expressed as follows:
where it is given that Equation (3) presents a nonlinear relationship with respect to . To overcome this nonlinearity, the iteratively weighted least squares (IWLS) algorithm can be employed. This algorithm allows for the estimation of the PMLE values for the Poisson regression parameters as follows:
where , is an n-dimensional vector with the ith element , and .
The MLE follows a normal distribution, with a covariance matrix that is equal to the inverse of the second derivative, which is given by
The mean square error can calculated as follows:
Given the equation , one can observe that G represents an orthogonal matrix with its columns corresponding to the eigenvectors of the matrix H. Moreover, refers to the eigenvalue associated with the position of the matrix H.
The correlation of the predictor variables significantly affects the H value, thus resulting in the high variance and instability of the PMLE estimator. The biased estimators proposed in the literature to deal with the multicollinearity problem in the PRM are addressed below.
2.2. Poisson Ridge Regression Estimator (PRRE)
In response to the multicollinearity issues in generalized linear models (GLMs), Segerstedt [19] introduced, inspired by Hoerl and Kannard [4], the RR estimator. Multicollinearity arises when explanatory variables in the PRM are correlated, which causes problems with MLE. To address this, Manson and Shukur [3] proposed the RR estimator for the PRM, thus offering a solution to the multicollinearity challenges. The formulation and characterization of the PRRE are as follows:
The ridge parameter, denoted as k, and the identity matrix of order , denoted as I, play a crucial role in Equation (7). When k equals zero, the biased corrected PRRE is equivalent to the PMLE. To define the bias vector and covariance matrix in Equation (7), the following expressions are used:
The formulation of the MSE and the matrix mean square error (MMSE) related to the PRRE is as follows:
In the given expression, the matrix is formed as a diagonal matrix . Here, k is added to each diagonal element of the original diagonal matrix U. Using the trace operator in Equation (10), Manson and Shukur [3] introduced a formulation for the MSE of the PRRE. This MSE acts as a metric for evaluating the accuracy and precision of the PRRE in estimating true parameter values, even in the presence of multicollinearity and other influencing factors.
where represents the element of the vector . This vector is derived by multiplying the transpose of the matrix G by the parameter vector . The matrix G is an orthogonal matrix composed of the eigenvectors of a particular matrix H.
2.3. Poisson Liu Estimator (PLE)
Månsson et al. [20] introduced an alternative estimator known as the PLE to address multicollinearity more effectively than the previously mentioned PRRE. The PLE is defined by the following equation:
The behavior of the Liu estimator depends on the value of the shrinkage parameter, d, as follows:
- When , the PLE is the same as the PMLE.
- When , the PLE tends to produce parameter estimates that are closer to zero than the PMLE. This effect helps reduce the impact of multicollinearity in the data.
The formulae for the bias vector, covariance matrix, and MMSE related to the PLE are as follows:
The MSE attributed to the PLE is expressed as follows:
The Liu parameter, denoted as d, can be determined by taking the derivative of Equation (16) with respect to d and setting it equal to zero. This process allows one to find the optimal value for the Liu parameter as follows:
2.4. Poisson-Adjusted Liu Estimator (PALE)
Expanding on the work of Lukman et al. [13], Amin et al. [12] proposed a modified version of the Liu estimator designed for the Poisson regression model called the Poisson-adjusted Liu estimator. This adaptation aimed to improve the effectiveness of the original Liu estimator when applied in the context of the Poisson model. The modified estimator is defined as follows:
The parameter is referred to as the adjusted Liu parameter. This modification significantly enhanced the effectiveness of the new PALE. The recommended estimator consistently achieves a lower MSE compared to the PMLE, PRRE, and PLE. The bias, covariance, and MMSE of the PALE can be expressed as follows:
The MSE of the PALE can be defined as follows:
The procedure for determining the optimal value of involves calculating the partial derivative of Equation (22) with respect to , setting it equal to zero, and then solving for . The outcome provides the jth term for the biasing parameter as follows:
2.5. Proposed Poisson Modified Two-Parameter Liu Estimator (PMTPLE)
Based on the research conducted by Abonazel [21], we propose a modified two-parameter Liu estimator for the PRM. This modified estimator, referred to as the PMTPLE, is constructed using a pair of parameters . The PMTPLE formulation is summarized as follows:
The bias vector, variance–covariance matrix, and MSE matrix for the PMTPLE are given by the following expressions:
Then, the MSE of the PMTPLE is
Following Abonazel [21], we provide a definition for the optimal values of and for by equating the partial differentiation of with respect to and to zero. This yields the following equations:
and
3. Comparison of the Estimators
In this section, we make theoretical comparisons between the above estimators based on the MMSE and extract the main conditions that make the proposed PMTPLE estimator more efficient than other estimators. The following lemma is useful for theoretical comparisons between the proposed PMTPLE estimator and other estimators.
Lemma 1.
Assume two estimators for β: and , where and are non-stochastic matrices. If the covariance matrix difference , where and are the covariance matrices of and , respectively, then if and only if . Here, , with representing the bias vector of for , as discussed by [22].
Theorem 1.
, if and only if , and for and , where .
Proof.
Using Lemma (1), if and only if under the assumption that is a positive definite (pd) matrix (). Therefore , if , and this is achieved when for and . This means that is favored over if and only if and . □
Theorem 2.
, if and only if and for , , and , where .
Proof.
Using Lemma (1), if and only if , under the assumption that . Therefore, , if , and this is achieved when for , and . This means that is favored over if and only if and for , , and . □
Theorem 3.
, if and only if and for , and , where .
Proof.
Using Lemma (1), if and only if , under the assumption that . Therefore, , if , and this is achieved when for , and . This means that is favored over if and only if and for , and . □
Theorem 4.
, if and only if and for , and , where .
Proof.
Using Lemma (1), if and only if , under the assumption that . Therefore, , if , and this is achieved when for , , and . This means that is favored over if and only if and for , and . □
4. Selection of the Biasing Parameter
4.1. Ridge Parameter
Given the abundance in the literature addressing multicollinearity in the PRM, the optimal value of k for ridge regression is used, as outlined in the relevant scholarly works.
According to Lukman et al. [23] and Aladeitan et al. [24], the preferred value of k can be determined as follows:
Amin et al. [12] proposed an alternative optimal value of k:
Furthermore, Kibria et al. [25]; Ertan and Akay [26]; Akay and Ertan [27]; and Türkan and Özel [28] used the optimal value of k, which is described by the following equation:
4.2. Liu Parameter
According to the research conducted by Akay and Ertan [27], Qasim et al. [29], Amin et al. [12], Abonazel et al. [16], and Lukman et al. [23], the optimal value of d can be determined as follows:
4.3. Adjusted Liu Parameter
Lukman et al. [13], Amin et al. [12], and Abonazel et al. [16] determined the most suitable value of as follows:
4.4. Proposed Estimator Parameters
Based on the research conducted by Abonazel et al. [16] and Abonazel [21], we suggest using the estimator for the parameter in the PMTPLE. This can be achieved by incorporating the value of within Equation (29), as outlined below:
when it is given that .
Initially, the most suitable value of can be used as the value of k in the ridge estimator for the modified two-parameter Liu estimator as follows:
Given that , one can substitute for to calculate the value of . Therefore, we propose defining the parameter as follows:
5. Monte Carlo Simulation
5.1. Simulation Design
In this section, we present the Monte Carlo simulation study that was conducted to evaluate the performance of the different estimators in the context of a Poisson regression model when dealing with multicollinearity. This study involved generating a response variable based on a Poisson distribution [12,23], where the mean () is represented as , the variable i ranges from 1 to n, and consists of coefficients (). The matrix X represents the design matrix, and corresponds to the row of this matrix. The explanatory variables were obtained from McDonald and Galarneau [30] and obeyed the following pattern:
In this equation, is derived from a standard normal distribution, while represents the correlation between explanatory variables. The impact of was examined by considering different values of 0.85, 0.90, 0.95, and 0.99. Mean functions were established for scenarios with 3, 6, 9, and 12 explanatory variables. The intercept () values were strategically set to −1, 0, and 1, which influenced the average intensity of the Poisson process. The slope coefficients were chosen such that and across various sample sizes (50, 100, 150, 200, 250, 300, and 400). The simulation experiments were conducted using the R programming language. For each replicate, the MSE of the estimators was calculated using the following formula:
Here, represents the vector of estimated values for the lth simulation experiment of one of the four estimators (PMLE, PRRE, PLE, and PMTPLE), and the estimator with the lowest MSE is considered the most suitable.
5.2. Simulation Results
To organize the presentation of the simulation results, Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 show the MSE values for each estimator in the case of p = 3 and p = 6. Meanwhile, the results for the case of p = 9 and p = 12 are listed in Tables S1–S6 in the Supplementary Material section. The smallest MSE value in each row is highlighted in bold. The results of the simulation study provide a comprehensive analysis of the performance of the different estimators for the PRM when dealing with multicollinearity. The results offer valuable insights into the challenges and potential solutions for parameter estimation in complex regression scenarios. It is important to note that the PMLE consistently underperforms in these scenarios, thus indicating the need for caution or alternative approaches when multicollinearity is a concern. One of the key findings from this study was the significant impact of multicollinearity () on estimation accuracy. As the level of multicollinearity increased, all the estimators experienced an observable increase in MSE. This confirmed the well-established notion that multicollinearity adversely affects the precision of parameter estimation. Researchers should be aware of this effect and consider strategies to mitigate multicollinearity’s influence on their models. An increasing sample size (n) was identified as a critical factor for improving estimation accuracy, as larger sample sizes consistently led to a decrease in the MSE across all estimators. This emphasized the importance of having ample data when aiming for precise parameter estimates. Another noteworthy observation was the impact of the number of explanatory variables (p) on the simulated MSE. As the number of explanatory variables increased from 3 to 12, the MSE rose across all estimators. This suggested that additional variables introduce higher levels of multicollinearity. While the effect of changing the intercept value () was modest compared to that of other factors, shifting from −1 to +1 resulted in a decrease in the MSE. Furthermore, the proposed estimator consistently outperformed other estimators, such as the PMLE, PRRE, PLE, and PALE, across various sample sizes (n), numbers of explanatory variables (p), levels of multicollinearity (), and intercept values (). The proposed estimator, PMTPLE, demonstrated superior performance in the presence of multicollinearity. Additionally, though and were used for the proposed estimator, the approach still offered more favorable values in terms of MSE, thus making it a reliable choice for researchers facing similar regression challenges. However, it is important to note that the PMTPLE works for all values of (, , , , and ). Interestingly, emerged as the most effective choice across the various scenarios as it consistently yielded the minimum MSE. This highlighted the robust and optimal performance of , which was related to the PMTPLE and arose from its derivative of the MSE.

Table 1.
Computed MSE for the difference estimators and .

Table 2.
Computed MSE for the difference estimators and .

Table 3.
Computed MSE for the difference estimators and .

Table 4.
Computed MSE for the difference estimators and .

Table 5.
Computed MSE for the difference estimators and .

Table 6.
Computed MSE for the difference estimators and .
5.3. Relative Efficiency
An alternative metric for evaluating the performance of biasing estimators is relative efficiency (RE). Relative efficiency offers an objective means for comparing the precision and accuracy of different estimators in a given context. It provides a quantitative measure through which to assess the effectiveness of one estimator relative to another. The MSE is a crucial factor in calculating relative efficiency as it captures both bias and variance. A lower MSE indicates more a favorable performance when evaluating estimators comprehensively. In many cases, the reference estimator is used as a benchmark due to its desirable asymptotic properties, including efficiency. The results of Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 and Tables S1–S6 were used to calculate the relative efficiency. The calculation of the relative efficiency involved determining the MSE for both the reference estimator and other estimators, as described in Equation (42). The formula for calculating relative efficiency can be found in authoritative references such as [31,32] as follows:
where denotes either the PRRE, PLE, PALE, or PMTPLE.
In Figure 1, Figure 2, Figure 3 and Figure 4, the RE of the various estimators is plotted against different variables, such as the sample size (n), correlation between explanatory variables (), explanatory variable count (p), and intercept value (). The PMTPLE consistently demonstrated the highest RE values across various n, , , and p levels. This finding highlighted the superior efficiency of the PMTPLE compared to the other four estimators under evaluation. In essence, the PMTPLE emerged as the preferred choice in various scenarios, including , , and . It consistently outperformed the other estimators in terms of precision and efficiency, with showing the highest RE across all cases.
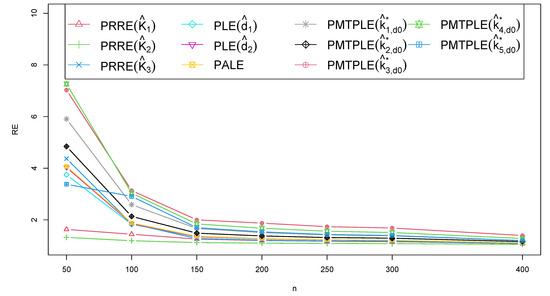
Figure 1.
The RE when applied to different estimators and when classified by sample size.
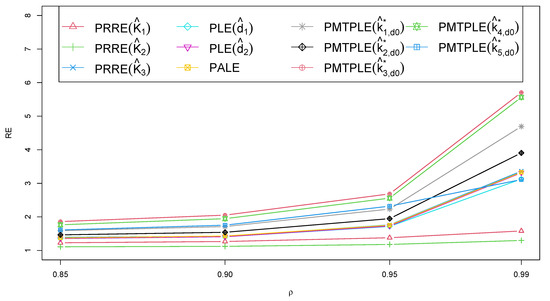
Figure 2.
The RE when applied to different estimators and when classified by correlation between the explanatory variables.
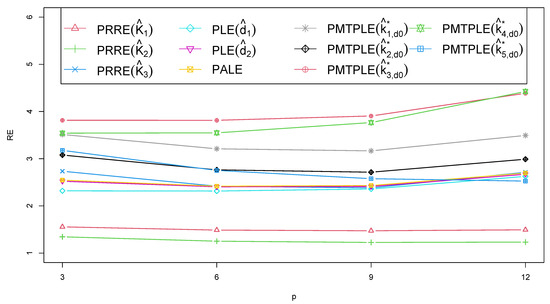
Figure 3.
The RE when applied to different estimators and when classified by the number of explanatory variables.
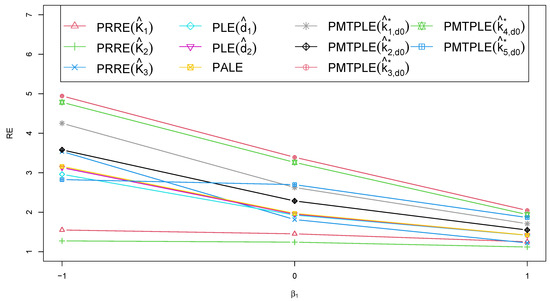
Figure 4.
The RE when applied to different estimators and when classified by the intercept value.
6. Applications
In this section, we present the two real-world applications used to evaluate the effectiveness of the proposed estimator.
6.1. Mussel Data
In this subsection, the empirical study conducted by Asia et al. [33] is considered. The researchers employed a mussel dataset and Poisson inverse Gaussian regression modeling to address the issue of multicollinearity. The mussel dataset, initially introduced by Sepkoski and Rex [34], contains valuable insights into the factors that influence the count of mussel species in coastal rivers within the southeastern United States. This dataset includes 35 observations (after removing outlier values), with a single response variable and six explanatory variables. These variables are as follows: the number of mussel species (y); the area of drainage basins (A, ); the count of stepping stones to four major species–source river systems, namely the Alabama-Coosa River System (AC, ), the Apalachicola River (AP, ), the St. Lawrence River (SL, ), and the Savannah River (SV, ); and the natural logarithm of the area of drainage basins (ln(A), ).
The data show that the mean of y (10.285) equals the variance of y (10.327). Anderson–Darling and Pearson chi-square goodness-of-fit tests were conducted to evaluate the response variable’s probability distribution. Both tests indicated that the response variable y followed a Poisson distribution. The computed statistics (p-value) for the Anderson–Darling and Pearson chi-square tests were 0.604 (0.643) and 2.409 (0.996), respectively.
The correlation plot in Figure 5 provides a visual representation of the data, whereby a significant intercorrelation among most of the variables was revealed. A careful examination of the plot showed that the variables were highly correlated with each other, which raised concerns about the potential multicollinearity issues within the data. To validate the presence of multicollinearity, two commonly used measures were employed: the variance inflation factor (VIF) and the condition number (CN). Both the VIF and CN were applied to evaluate the strength of the linear association (correlation) between the predictor variables in a regression model. The condition number (CN) was calculated by taking the square root of the ratio between the maximum eigenvalue (3.2 × 1010) and the minimum eigenvalue (0.15984), thus resulting in a value of 445737. In addition, the variance inflation factors (VIFs) for the explanatory variables were 8.804, 271.929, 132.136, 59.234, 2.369, and 6.423. The correlation matrix, CN, and VIF collectively indicated the presence of the multicollinearity among the explanatory variables.
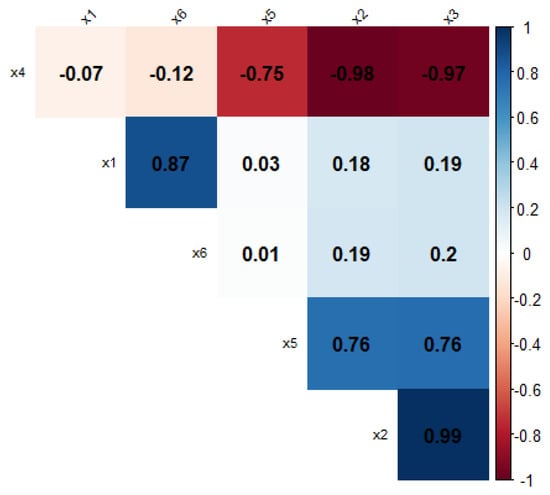
Figure 5.
Correlation matrix for the six explanatory variables in the mussel dataset.
Table 7 provides a summary of the various estimators, including their associated biasing parameters, intercepts, coefficients for predictor variables through , and MSEs. Below is a brief overview of the results presented in the table:

Table 7.
The coefficients and MSE for different estimators in the mussel dataset.
- PMLE: This estimator had an intercept of 2.09378 and coefficient values for each predictor variable ( through ). The associated MSE was 6.27306.
- PRRE: We considered three variations of the PRRE, each with a different biasing parameter—, , and . These estimators had varying intercepts and coefficient values for the predictor variables. The MSE values ranged from 0.15981 to 0.97892.
- PLE: We considered two variations of the PLE, both with the same biasing parameter . These estimators had consistent intercepts and coefficient values for the predictor variables, thereby resulting in an identical MSE of 0.13671.
- PALE: This estimator, represented by , had consistent intercept and coefficient values for the predictor variables. The MSE was 0.13671, thus matching the PLE.
- PMTPLE: We considered five variations of the PMTPLE, denoted by through . These estimators had varying intercepts and coefficient values for the predictor variables. The MSE values ranged from 0.01931 to 0.88043.
Overall, the table provides a comprehensive comparison of the different estimation techniques in the context of the mussel data. It allows for an assessment of the biasing parameters, and it shows that the PMLE had the highest MSE. The PRRE had a lower MSE than the PLE for all biasing parameters, thus indicating that the PLE introduced a lower MSE compared to the PRRE. The PALE and PLE yielded the same MSE in this case. The PMTPLE demonstrated the lowest MSE of all estimators, especially for , , and . The optimal MSE was observed at for the PMTPLE, which supports the simulation results.
6.2. Recreation Demand Data
An additional practical application is presented to demonstrate the enhanced performance of the proposed estimator. This application’s dataset pertained to entertainment demand, a field that has previously been explored by Abonazel et al. [16]. These data, originally introduced by Cameron and Trivedi [35], were employed to estimate a function representing recreation demand. The dataset was collected through a survey conducted in 1980, which gathered information about the number of recreational boating trips taken to Somerville Lake in East Texas. The main focus of our analysis was the response variable denoted as y, which represents the count of recreational boating excursions. This dataset consists of 179 observations (after removing outlier values) and includes three explanatory variables, , , and , which represent the expenditure (measured in USD) associated with visiting Lake Conroe, Lake Somerville, and Lake Houston, respectively.
The analysis of the data indicated that the mean of the response variable (y) was 2.788, which was nearly equivalent to its variance of 2.864. To evaluate the goodness of fit for the probability distribution of the response variable, two statistical tests were performed: the Anderson–Darling and Pearson chi-square tests. Both tests yielded similar results, indicating that the response variable y closely followed a Poisson distribution. The p-values calculated for these tests were 10.909 (0.164) (Anderson–Darling) and 4.064 (0.760) (Pearson chi-square), thus confirming the compatibility of y with a Poisson distribution. The correlation coefficients between explanatory variables :, :, and : were 0.97, 0.98, and 0.94, respectively, thereby indicating a significant interrelationship between most of the variables. A careful examination of this plot highlighted a strong correlation between these variables, which raised concerns about the potential multicollinearity within the dataset. To confirm the presence of multicollinearity, two commonly used measures were employed: the variance inflation factor (VIF) and the condition number (CN). Both the VIF and CN are diagnostic tools for assessing the strength of linear association or correlation among predictor variables within a regression model. The condition number (CN) was computed by taking the square root of the ratio between the maximum eigenvalue (1147.54) and the minimum eigenvalue (1.006), thereby resulting in a value of 33.771. Additionally, the variance inflation factors (VIFs) for the explanatory variables were computed as 43.840, 14.619, and 24.63566, respectively. Overall, the correlation matrix, CN, and VIFs provided substantial evidence for the presence of multicollinearity among the explanatory variables.
Table 8 provides an insightful overview of the various estimators and their performance when modeling recreation demand data. To summarize the results, the first estimator, PMLE, yielded an intercept of 1.20525 and coefficients for the three predictor variables (, , and ), with an associated MSE of 1.22355 and no biasing parameter. The PRRE estimator was divided into three variations (, , and ), each offering distinct intercepts, coefficients, and MSE values ranging from 0.57949 to 0.92717. The PLE, represented by two variations ( and ), maintained consistent intercepts, coefficients, and identical MSE values of 0.54352. The PALE () also resulted in the same intercepts, coefficients, and MSE as the PLE. The PMTPLE, with five variations ( through ), exhibited varying intercepts, coefficients, and MSE values between 0.49054 and 0.60474. In summary, the table serves as a valuable resource for comparing the estimation techniques when using recreation demand data, demonstrating that the PMLE had the highest MSE; the PRRE outperformed the PMLE for all biasing parameters; the PALE matched the PLE’s MSE; and the PMTPLE, particularly and , showed the lowest MSE, thus supporting the simulation results and indicating their optimality.

Table 8.
The coefficients and MSE for the different estimators when using the recreation demand data.
Through two applications, we verified the theoretical conditions of Theorems 1–4 and found that all conditions were satisfied on both datasets. This explained the superiority of the proposed PMTPLE estimator over the rest of the estimators.
7. Conclusions
This article introduced a new Liu estimator (PMTPLE) with two shrinkage parameters for the Poisson regression model to address the multicollinearity challenges in the Poisson maximum likelihood estimator (PMLE). The proposed PMTPLE was compared to four existing estimators (the PMLE, PRRE, PLE, and PALE) through a Monte Carlo simulation study and two empirical applications with a focus on evaluating the MSE. This study revealed that higher levels of multicollinearity () lead to less accurate parameter estimates, while larger sample sizes (n) resulted in more reliable estimates. Additionally, increasing the number of explanatory variables (p) also increased the estimation errors due to multicollinearity. However, varying the intercept value from −1 to +1 led to a decrease in the MSE. Both the Monte Carlo simulation and empirical applications consistently demonstrated the superiority of the proposed PMTPLE over the PMLE, PRRE, PLE, and PALE in various scenarios. Therefore, we strongly recommend that practitioners use the shrinkage parameter when applying the PMTPLE to the Poisson regression model with significant multicollinearity. This recommendation holds practical significance and highlights the importance of the PMTPLE as the preferred choice for accurate parameter estimation in the presence of multicollinearity-related issues in statistical modeling. Researchers and practitioners are encouraged to consider as the optimal choice for enhancing parameter estimation accuracy in such scenarios.
In future studies, we will integrate cross-validation and model selection techniques with the proposed PMTPLE, especially in cases where many predictors are involved in the model. Furthermore, to increase the efficiency of the PMTPLE, the generalized cross-validation (GCV) criterion will be used to select the biasing parameters.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/axioms13010046/s1, Table S1: Computed MSE for difference estimators p = 9 and = −1; Table S2: Computed MSE for difference estimators p = 9 and = 0; Table S3: Computed MSE for difference estimators p = 9 and = 1; Table S4: Computed MSE for difference estimators p = 12 and = −1; Table S5: Computed MSE for difference estimators p = 12 and = 0; Table S6: Computed MSE for difference estimators p = 12 and = 1.
Author Contributions
Conceptualization, M.M.A., M.R.A. and A.T.H.; methodology, M.R.A., A.T.H. and A.M.E.-M.; software, M.R.A. and A.T.H.; validation, M.M.A. and M.R.A.; formal analysis, M.M.A., M.R.A. and A.T.H.; investigation, M.M.A., M.R.A. and A.M.E.-M.; resources, M.R.A. and A.M.E.-M.; data curation, A.T.H.; writing—original draft preparation, A.T.H. and A.M.E.-M.; writing—review and editing, M.M.A., M.R.A. and A.T.H.; visualization, A.M.E.-M.; supervision, M.M.A. and M.R.A.; project administration, M.M.A. and M.R.A.; funding acquisition, M.M.A. and M.R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-RP23097).
Data Availability Statement
Datasets are mentioned along the paper.
Acknowledgments
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Silva, J.S.; Tenreyro, S. The log of gravity. Rev. Econ. Stat. 2006, 88, 641–658. [Google Scholar] [CrossRef]
- Manning, W.G.; Mullahy, J. Estimating log models: To transform or not to transform? J. Health Econ. 2001, 20, 461–494. [Google Scholar] [CrossRef] [PubMed]
- Månsson, K.; Shukur, G. A Poisson ridge regression estimator. Econ. Model. 2011, 28, 1475–1481. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Alkhamisi, M.; Khalaf, G.; Shukur, G. Some modifications for choosing ridge parameters. Commun. Stat. Theory Methods 2006, 35, 2005–2020. [Google Scholar] [CrossRef]
- Alkhamisi, M.A.; Shukur, G. Developing ridge parameters for SUR model. Commun. Stat. Theory Methods 2008, 37, 544–564. [Google Scholar] [CrossRef]
- Khalaf, G.; Shukur, G. Choosing ridge parameter for regression problems. Commun. Stat. Theory Methods 2005, 34, 1177–1182. [Google Scholar] [CrossRef]
- Kibria, B.G. Performance of some new ridge regression estimators. Commun. Stat. Simul. Comput. 2003, 32, 419–435. [Google Scholar] [CrossRef]
- Muniz, G.; Kibria, B.G. On some ridge regression estimators: An empirical comparisons. Commun. Stat. Simul. Comput. 2009, 38, 621–630. [Google Scholar] [CrossRef]
- Kejian, L. A new class of biased estimate in linear regression. Commun. Stat. Theory Methods 1993, 22, 393–402. [Google Scholar] [CrossRef]
- Månsson, K.; Kibria, B.G.; Sjölander, P.; Shukur, G. Improved Liu estimators for the Poisson regression model. Int. J. Stat. Probab. 2012, 1, 2. [Google Scholar] [CrossRef]
- Amin, M.; Akram, M.N.; Kibria, B.G. A new adjusted Liu estimator for the Poisson regression model. Concurr. Comput. Pract. Exp. 2021, 33, e6340. [Google Scholar] [CrossRef]
- Lukman, A.F.; Kibria, B.G.; Ayinde, K.; Jegede, S.L. Modified one-parameter Liu estimator for the linear regression model. Model. Simul. Eng. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Algamal, Z.Y.; Abonazel, M.R. Developing a Liu-type estimator in beta regression model. Concurr. Comput. Pract. Exp. 2022, 34, e6685. [Google Scholar] [CrossRef]
- Yang, H.; Chang, X. A new two-parameter estimator in linear regression. Commun. Stat. Theory Methods 2010, 39, 923–934. [Google Scholar] [CrossRef]
- Abonazel, M.R.; Awwad, F.A.; Tag Eldin, E.; Kibria, B.G.; Khattab, I.G. Developing a two-parameter Liu estimator for the COM—Poisson regression model: Application and simulation. Front. Appl. Math. Stat. 2023, 9, 956963. [Google Scholar] [CrossRef]
- Omara, T.M. Modifying two-parameter ridge Liu estimator based on ridge estimation. Pak. J. Stat. Oper. Res. 2019, 15, 881–890. [Google Scholar] [CrossRef]
- Abonazel, M.R.; Algamal, Z.Y.; Awwad, F.A.; Taha, I.M. A new two-parameter estimator for beta regression model: Method, simulation, and application. Front. Appl. Math. Stat. 2022, 7, 780322. [Google Scholar] [CrossRef]
- Segerstedt, B. On ordinary ridge regression in generalized linear models. Commun. Stat. Theory Methods 1992, 21, 2227–2246. [Google Scholar] [CrossRef]
- Månsson, K.; Kibria, B.G.; Sjölander, P.; Shukur, G.; Sweden, V. New Liu Estimators for the Poisson Regression Model: Method and Application; Technical Report; HUI Research: Stockholm, Swizerland, 2011. [Google Scholar]
- Abonazel, M.R. New modified two-parameter Liu estimator for the Conway—Maxwell Poisson regression model. J. Stat. Comput. Simul. 2023, 93, 1976–1996. [Google Scholar] [CrossRef]
- Trenkler, G.; Toutenburg, H. Mean squared error matrix comparisons between biased estimators—An overview of recent results. Stat. Pap. 1990, 31, 165–179. [Google Scholar] [CrossRef]
- Lukman, A.F.; Aladeitan, B.; Ayinde, K.; Abonazel, M.R. Modified ridge-type for the Poisson regression model: Simulation and application. J. Appl. Stat. 2022, 49, 2124–2136. [Google Scholar] [CrossRef] [PubMed]
- Aladeitan, B.B.; Adebimpe, O.; Lukman, A.F.; Oludoun, O.; Abiodun, O.E. Modified Kibria-Lukman (MKL) estimator for the Poisson Regression Model: Application and simulation. F1000Research 2021, 10, 548. [Google Scholar] [CrossRef]
- Kibria, B.G.; Månsson, K.; Shukur, G. A simulation study of some biasing parameters for the ridge type estimation of Poisson regression. Commun. Stat. Simul. Comput. 2015, 44, 943–957. [Google Scholar] [CrossRef]
- Ertan, E.; Akay, K.U. A new class of Poisson Ridge-type estimator. Sci. Rep. 2023, 13, 4968. [Google Scholar] [CrossRef] [PubMed]
- Akay, K.U.; Ertan, E. A new improved Liu-type estimator for Poisson regression models. Hacet. J. Math. Stat. 2022, 51, 1484–1503. [Google Scholar] [CrossRef]
- Türkan, S.; Özel, G. A new modified Jackknifed estimator for the Poisson regression model. J. Appl. Stat. 2016, 43, 1892–1905. [Google Scholar] [CrossRef]
- Qasim, M.; Kibria, B.; Månsson, K.; Sjölander, P. A new Poisson Liu regression estimator: Method and application. J. Appl. Stat. 2020, 47, 2258–2271. [Google Scholar] [CrossRef]
- McDonald, G.C.; Galarneau, D.I. A Monte Carlo evaluation of some ridge-type estimators. J. Am. Stat. Assoc. 1975, 70, 407–416. [Google Scholar] [CrossRef]
- Farghali, R.A.; Qasim, M.; Kibria, B.G.; Abonazel, M.R. Generalized two-parameter estimators in the multinomial logit regression model: Methods, simulation and application. Commun. Stat. Simul. Comput. 2023, 52, 3327–3342. [Google Scholar] [CrossRef]
- Abonazel, M.R.; Taha, I.M. Beta ridge regression estimators: Simulation and application. Commun. Stat. Simul. Comput. 2023, 52, 4280–4292. [Google Scholar] [CrossRef]
- Batool, A.; Amin, M.; Elhassanein, A. On the performance of some new ridge parameter estimators in the Poisson-inverse Gaussian ridge regression. Alex. Eng. J. 2023, 70, 231–245. [Google Scholar] [CrossRef]
- Sepkoski, J.J., Jr.; Rex, M.A. Distribution of freshwater mussels: Coastal rivers as biogeographic islands. Syst. Biol. 1974, 23, 165–188. [Google Scholar] [CrossRef]
- Cameron, A.C.; Trivedi, P.K. Regression Analysis of Count Data; Cambridge University Press: Cambridge, UK, 2013; Volume 53. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).