A Review of Optimization Studies for System Appointment Scheduling
Abstract
:1. Introduction
2. System Structure of AS
2.1. AS Characteristics
- Uncertainty AS performance;
- 2.
- ASs can be extended to represent other industries.
2.2. System Structure of AS
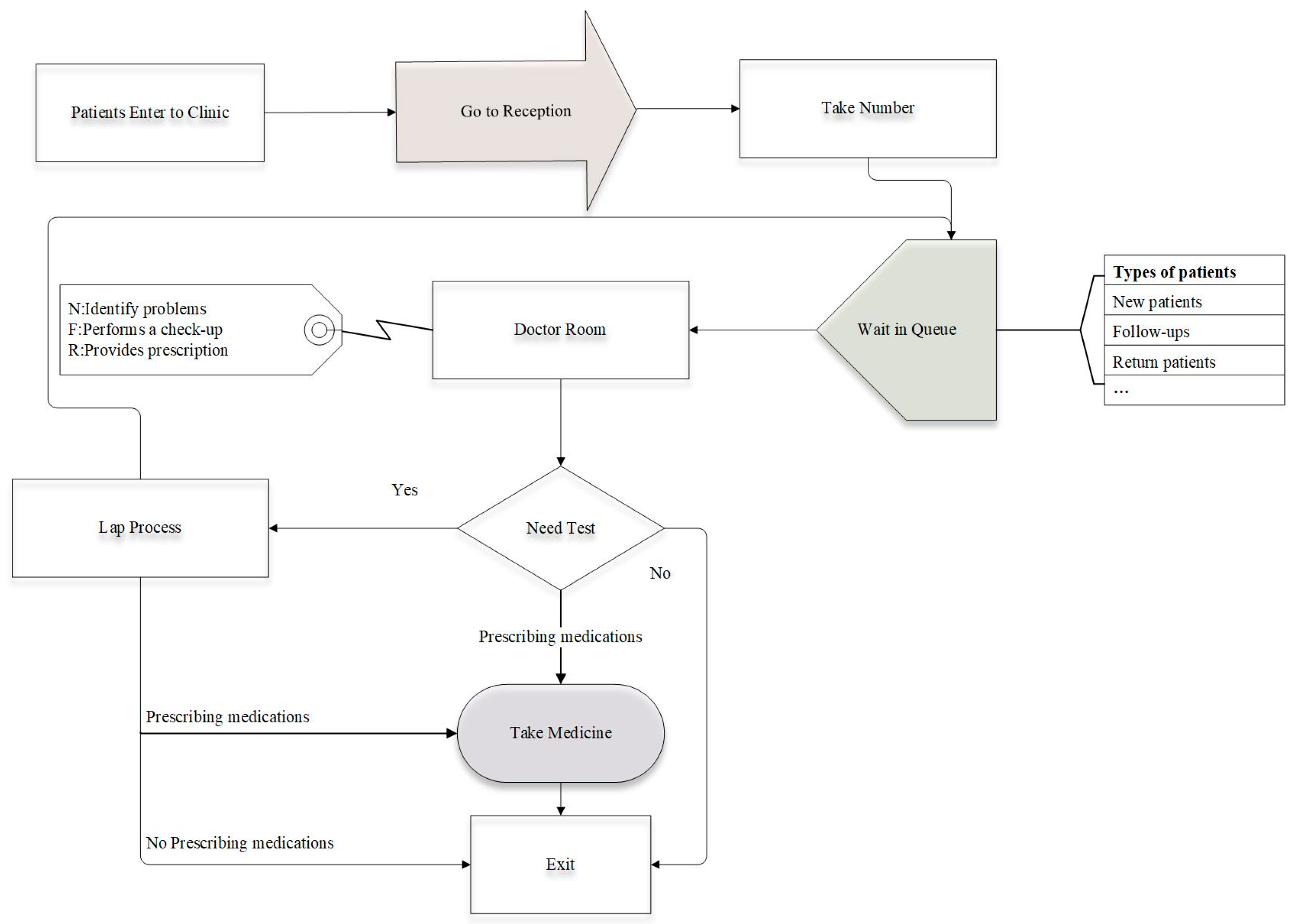
2.2.1. Appointment Rules
- Fixed-interval rules.
- 2.
- Variable-interval rules.
- The “offset” rule.
- The “dome” appointment rule.
- The “plateau-dome” appointment rule.
2.2.2. Patient Classification
2.3. AS System Decision Framework
2.3.1. Strategic Decisions
2.3.2. Tactical Decisions
2.3.3. Operational Decisions
3. Optimization Framework
3.1. Optimization Objective
3.1.1. Societal Benefit
3.1.2. Economic Performance
3.1.3. Resource Utilization
3.1.4. Other Objectives
3.2. Decision Variable
3.3. Constraints
3.3.1. Queue Balance Constraints
3.3.2. Capacity Constraints
- Surgeon availability constraint:
- Operating room availability constraint:
3.3.3. The Completion Time Constraint
4. Optimization Algorithms
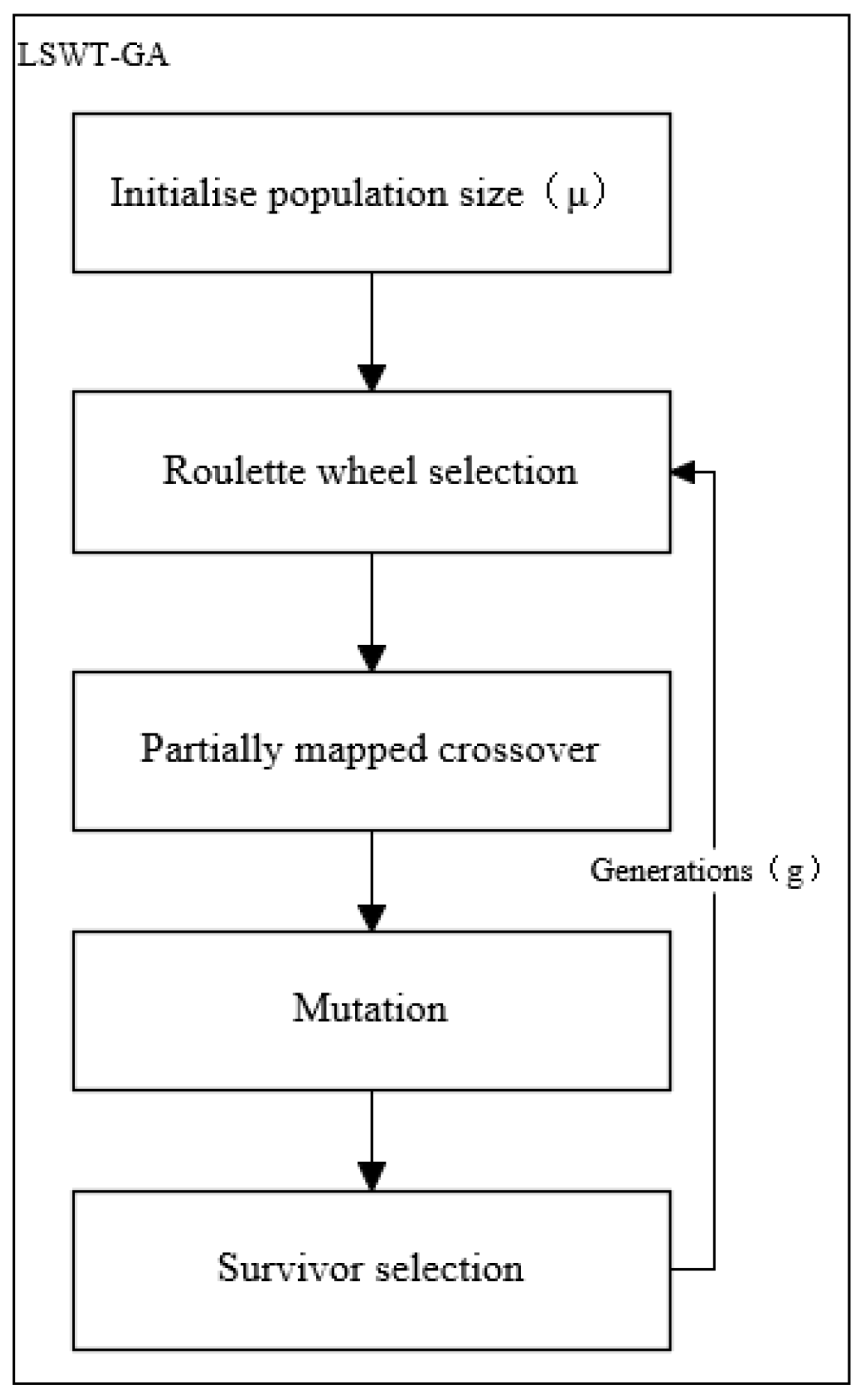
4.1. Genetic Algorithm
4.1.1. Objective Function and Constraint
4.1.2. Optimization Process
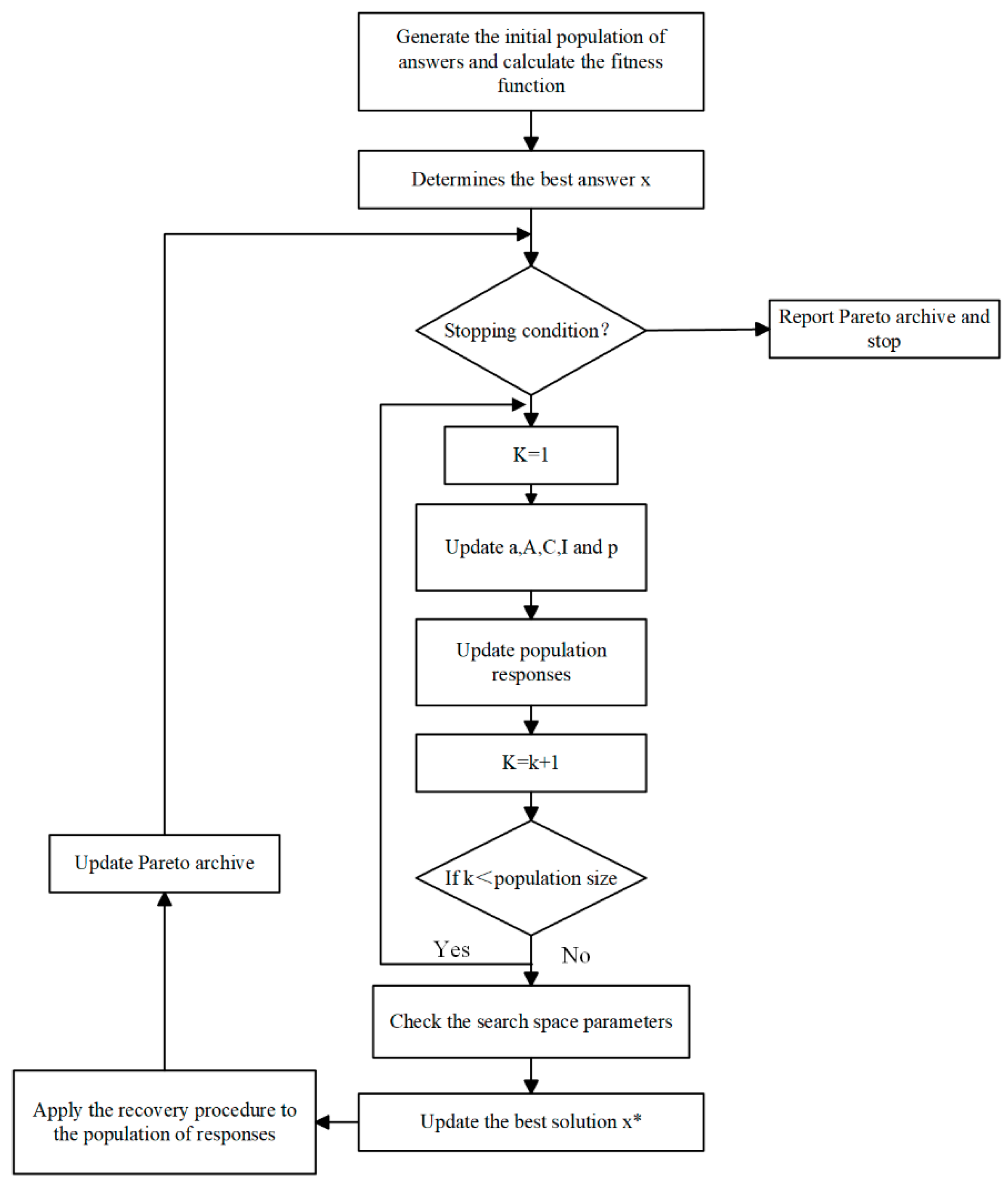
4.2. Whale Optimization Algorithm
4.2.1. Optimization Model
4.2.2. Objective Function
4.2.3. Constraint
4.2.4. Model Solving
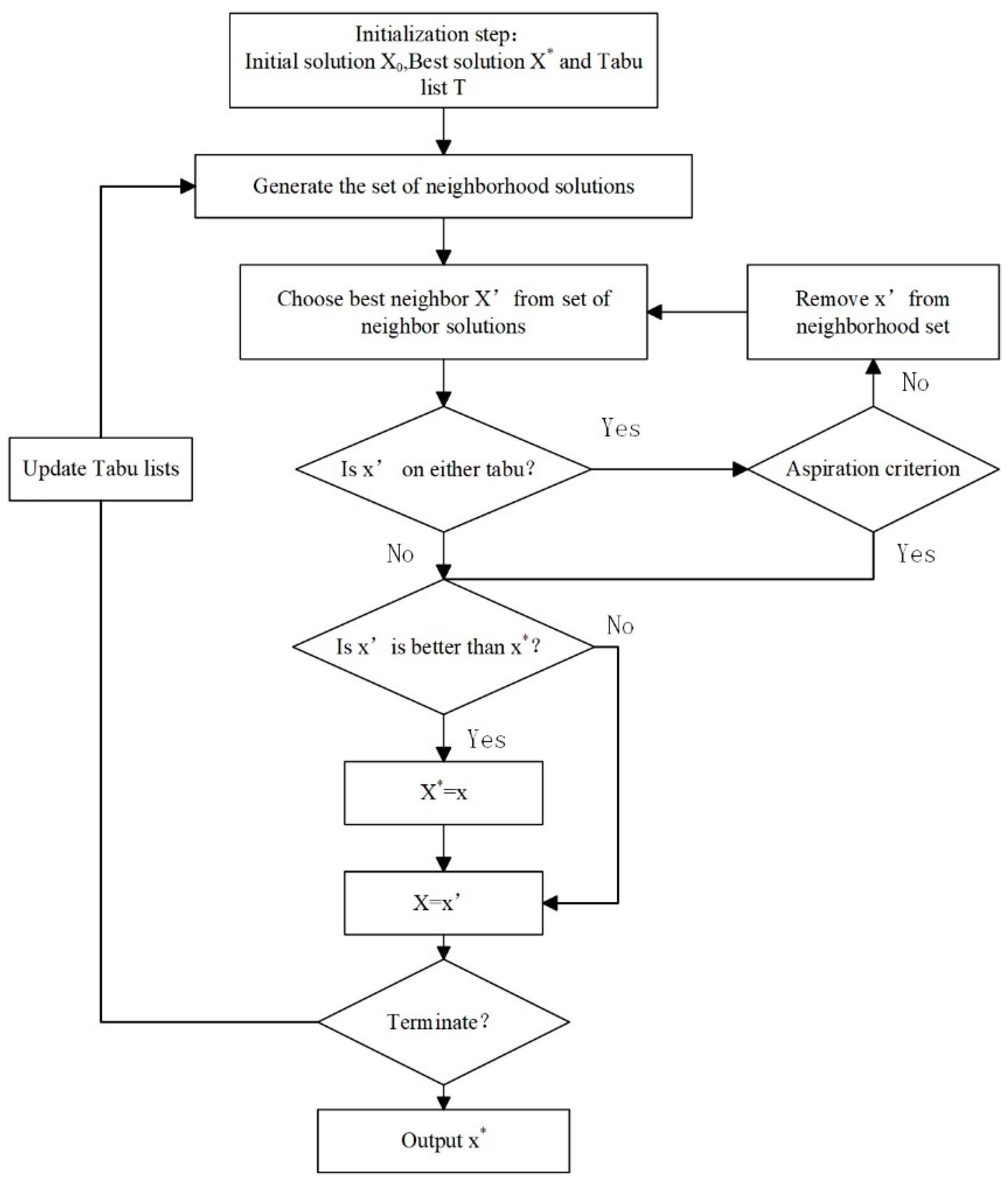
4.3. Tabu Search Algorithm
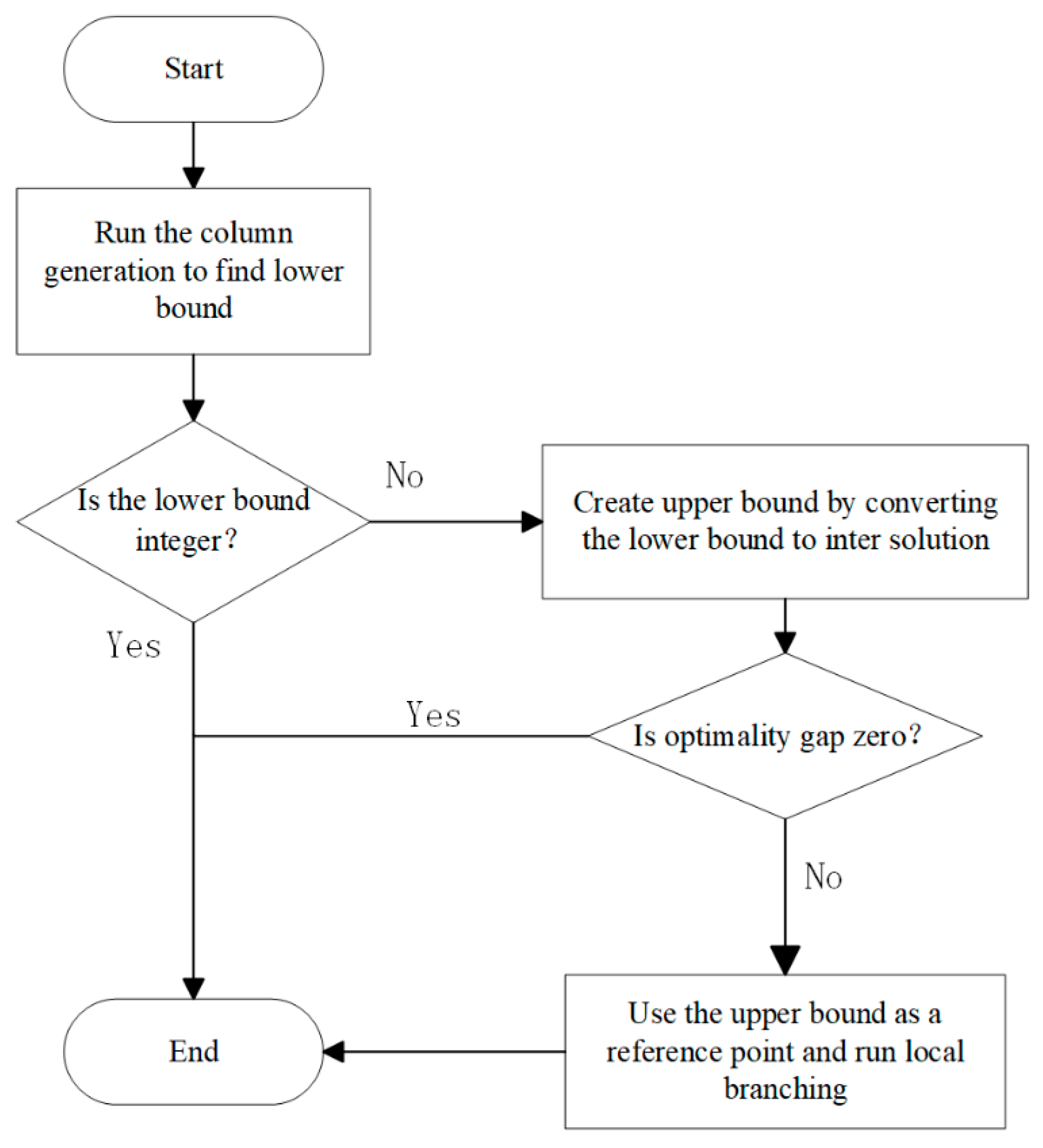
4.3.1. The Integer Programming Model in a Definitive Model
4.3.2. Algorithm Optimal Progress
4.4. Other Heuristic Algorithm
4.4.1. Problem Description
4.4.2. Constraint
4.4.3. Solution Methodology
5. Bibliometric Analysis of Literature
5.1. Methods and Data
5.1.1. Methods
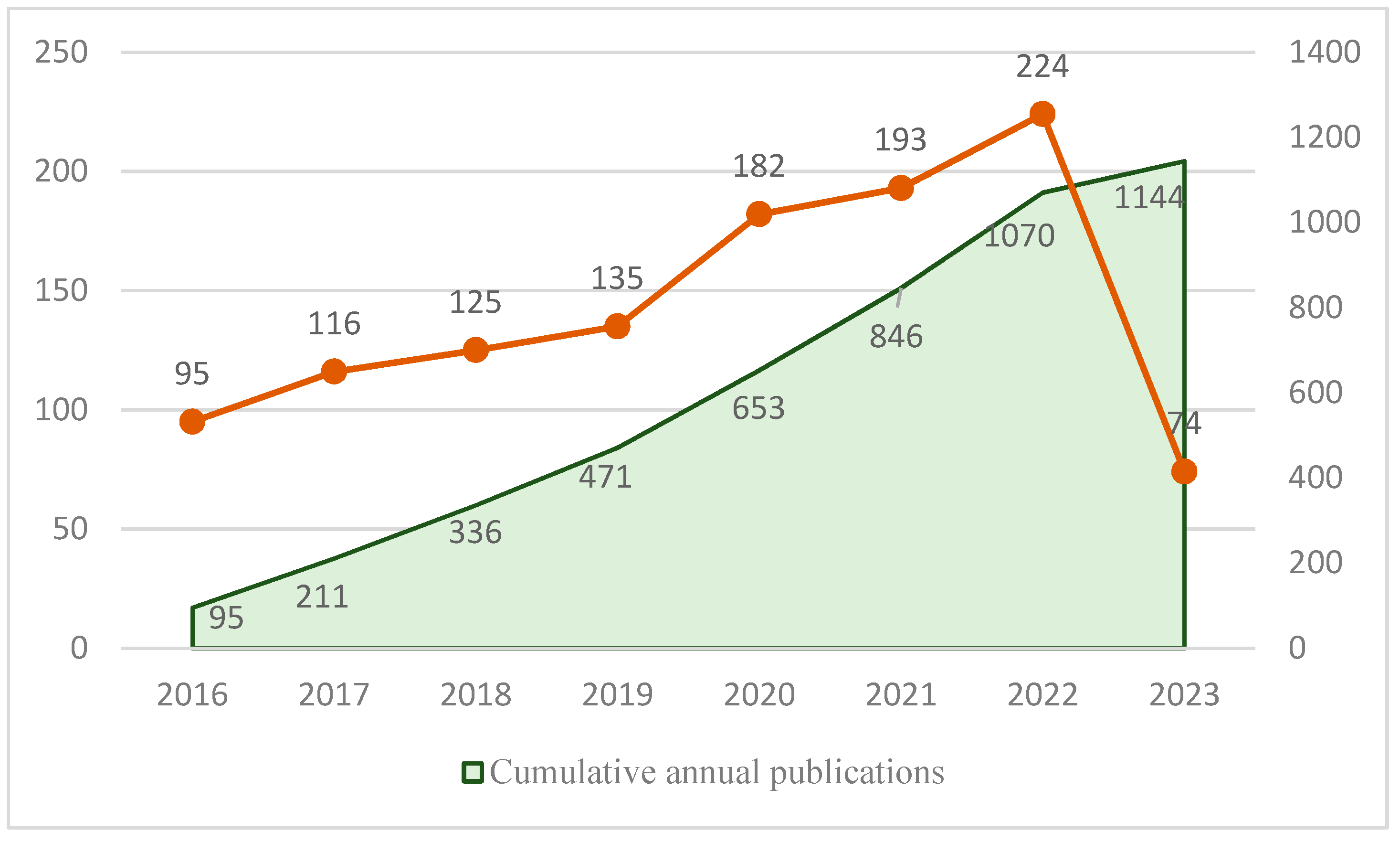
5.1.2. Data
5.2. Operational Results
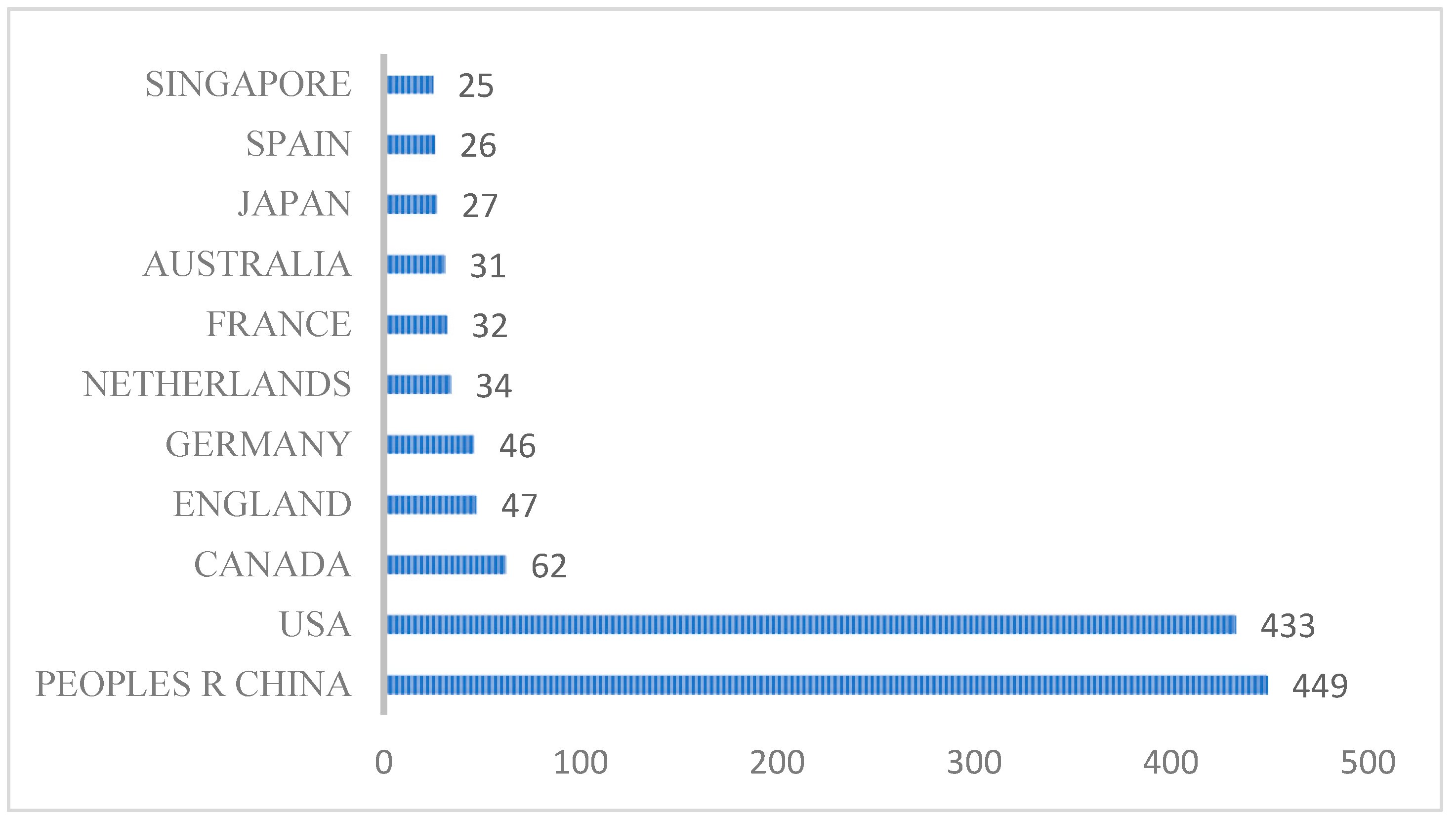
5.2.1. Country and Publisher
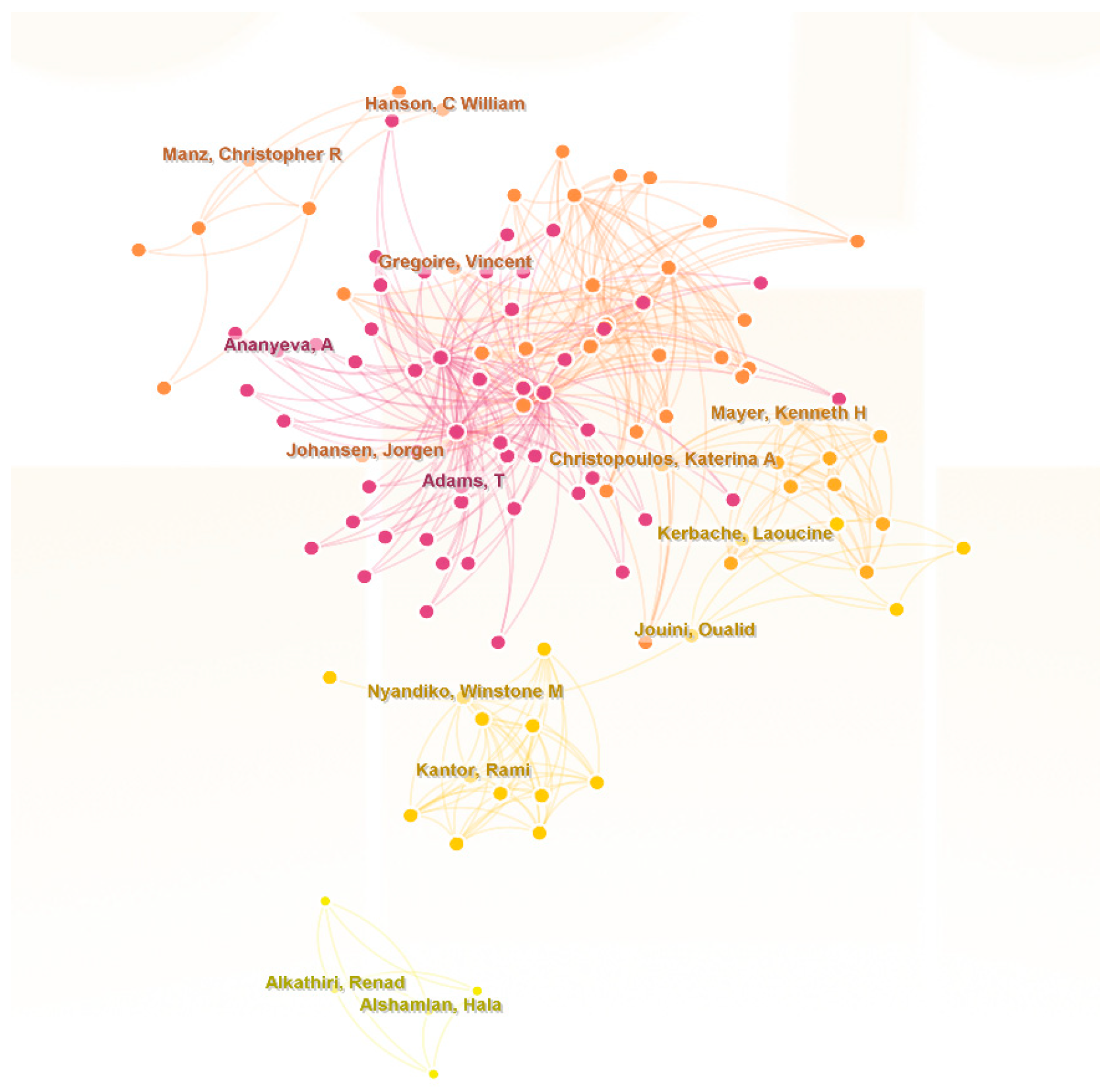
5.2.2. Author
5.2.3. Thematic Trends
5.2.4. Cited Journals
6. Discussion
6.1. Specifics of Healthcare
6.2. Differences of Related Methods
6.3. Tendencies and Scientific Methods
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L. Development of China’s Health Care System in the Time of COVID-19: Challenges, Opportunities, and Call for Actions. Health Care Sci. 2022, 1, 33–40. [Google Scholar] [CrossRef]
- Batko, K.; Ślęzak, A. The Use of Big Data Analytics in Healthcare. J. Big Data 2022, 9, 3. [Google Scholar] [CrossRef] [PubMed]
- Gupta, D.; Denton, B. Appointment Scheduling in Health Care: Challenges and Opportunities. IIE Trans. 2008, 40, 800–819. [Google Scholar] [CrossRef]
- Gao, K.; Shi, X.; Wang, W. The Life-Course Impact of Smoking on Hypertension, Myocardial Infarction and Respiratory Diseases. Sci. Rep. 2017, 7, 4330. [Google Scholar] [CrossRef] [PubMed]
- Qu, L.; Gao, K.; Chen, X.; He, Q.; Ma, Y.; Peng, R. Optimal Quarantine Duration for Preventing Epidemic with Window Period. J. Infect. Non Infect. Dis. 2020, 5, 28. [Google Scholar]
- Alrefaei, M.H.; Diabat, A. Modelling and Optimization of Outpatient Appointment Scheduling. RAIRO-Oper. Res. 2015, 49, 435–450. [Google Scholar] [CrossRef]
- Hulshof, P.J.H.; Vanberkel, P.T.; Boucherie, R.J.; Hans, E.W.; Van Houdenhoven, M.; Van Ommeren, J.-K.C.W. Analytical Models to Determine Room Requirements in Outpatient Clinics. OR Spectr. 2012, 34, 391–405. [Google Scholar] [CrossRef]
- Huang, Y.-L.; Marcak, J. Grid Patient Appointment Template Design to Improve Scheduling Effectiveness. J. Healthc. Eng. 2015, 6, 239–258. [Google Scholar] [CrossRef]
- Liu, N.; Finkelstein, S.R.; Kruk, M.E.; Rosenthal, D. When Waiting to See a Doctor Is Less Irritating: Understanding Patient Preferences and Choice Behavior in Appointment Scheduling. Manag. Sci. 2018, 64, 1975–1996. [Google Scholar] [CrossRef]
- Wright, P.D.; Bretthauer, K.M.; Cote, M.J. Reexamining the Nurse Scheduling Problem: Staffing Ratios and Nursing Shortages. Decis. Sci. 2006, 37, 39–70. [Google Scholar] [CrossRef]
- Talluri, K.; Van Ryzin, G. Revenue Management Under a General Discrete Choice Model of Consumer Behavior. Manag. Sci. 2004, 50, 15–33. [Google Scholar] [CrossRef]
- Gao, K.; Wang, T.; Peng, K.; Wang, Z.; He, Q.; Peng, R. A Recursive Model of Residual Life Prediction for Human Beings with Health Information from Activities of Daily Living and Memory. Syst. Sci. Control Eng. 2021, 9, 529–541. [Google Scholar] [CrossRef]
- Gao, K.; Peng, R.; Qu, L.; Xing, L.; Wang, S.; Wu, D. Linear System Design with Application in Wireless Sensor Networks. J. Ind. Inf. Integr. 2022, 27, 100279. [Google Scholar] [CrossRef]
- Feldman, J.; Liu, N.; Topaloglu, H.; Ziya, S. Appointment Scheduling Under Patient Preference and No-Show Behavior. Oper. Res. 2014, 62, 794–811. [Google Scholar] [CrossRef]
- Gupta, D.; Wang, W.-Y. Patient appointments in ambulatory care. In Handbook of Healthcare System Scheduling; Hall, R., Ed.; International Series in Operations Research & Management Science; Springer US: Boston, MA, USA, 2012; Volume 168, pp. 65–104. ISBN 978-1-4614-1733-0. [Google Scholar]
- Vieira, B.; Hans, E.W.; Van Vliet-Vroegindeweij, C.; Van De Kamer, J.; Van Harten, W. Operations Research for Resource Planning and -Use in Radiotherapy: A Literature Review. BMC Med. Inf. Decis. Mak. 2016, 16, 149. [Google Scholar] [CrossRef] [PubMed]
- Cayirli, T.; Veral, E. Outpatient Scheduling in Health Care: A Review of Literature. Prod. Oper. Manag. 2009, 12, 519–549. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A.; Jalali, Z.; Klassen, K.J. Outpatient Appointment Systems in Healthcare: A Review of Optimization Studies. Eur. J. Oper. Res. 2017, 258, 3–34. [Google Scholar] [CrossRef]
- Woodcock, E.W. Barriers to and Facilitators of Automated Patient Self-Scheduling for Health Care Organizations: Scoping Review. J. Med. Internet Res. 2022, 24, e28323. [Google Scholar] [CrossRef]
- Marynissen, J.; Demeulemeester, E. Literature Review on Multi-Appointment Scheduling Problems in Hospitals. Eur. J. Oper. Res. 2019, 272, 407–419. [Google Scholar] [CrossRef]
- Ala, A.; Chen, F. Appointment Scheduling Problem in Complexity Systems of the Healthcare Services: A Comprehensive Review. J. Healthc. Eng. 2022, 2022, 5819813. [Google Scholar] [CrossRef]
- Ala, A.; Simic, V.; Deveci, M.; Pamucar, D. Simulation-Based Analysis of Appointment Scheduling System in Healthcare Services: A Critical Review. Arch. Comput. Methods Eng. 2023, 30, 1961–1978. [Google Scholar] [CrossRef]
- Dantas, L.F.; Fleck, J.L.; Cyrino Oliveira, F.L.; Hamacher, S. No-Shows in Appointment Scheduling—A Systematic Literature Review. Health Policy 2018, 122, 412–421. [Google Scholar] [CrossRef] [PubMed]
- Wilson, R.; Winnard, Y. Causes, Impacts and Possible Mitigation of Non-Attendance of Appointments within the National Health Service: A Literature Review. J. Health Organ. Manag. 2022, 36, 892–911. [Google Scholar] [CrossRef] [PubMed]
- Donthu, N.; Kumar, S.; Mukherjee, D.; Pandey, N.; Lim, W.M. How to Conduct a Bibliometric Analysis: An Overview and Guidelines. J. Bus. Res. 2021, 133, 285–296. [Google Scholar] [CrossRef]
- Leeftink, A.G.; Vliegen, I.M.H.; Hans, E.W. Stochastic Integer Programming for Multi-Disciplinary Outpatient Clinic Planning. Health Care Manag. Sci. 2019, 22, 53–67. [Google Scholar] [CrossRef] [PubMed]
- Green, L.V.; Savin, S. Reducing Delays for Medical Appointments: A Queueing Approach. Oper. Res. 2008, 56, 1526–1538. [Google Scholar] [CrossRef]
- Bobbie, A.; Karwowski, W. Simulation-Based Evaluation of Patient Appointment Policies for a Primary Care Clinic with Unscheduled Visits: A Case Study. Int. J. Hum. Factors Model. Simul. 2019, 7, 152. [Google Scholar] [CrossRef]
- Lin, C.K.Y.; Ling, T.W.C.; Yeung, W.K. Resource Allocation and Outpatient Appointment Scheduling Using Simulation Optimization. J. Healthc. Eng. 2017, 2017, 9034737. [Google Scholar] [CrossRef]
- Robinson, L.W.; Chen, R.R. Scheduling Doctors’ Appointments: Optimal and Empirically-Based Heuristic Policies. IIE Trans. 2003, 35, 295–307. [Google Scholar] [CrossRef]
- Shonick, W. An Approach to Reducing the Adverse Effects of Broken Appointments in Primary Care Systems. Med. Care 1977, 15, 419–429. [Google Scholar] [CrossRef]
- Chen, P.-S.; Hong, I.-H.; Hou, Y.; Shao, Y.-C. Healthcare Scheduling Policies in a Sequence-Number Based Appointment System for Outpatients’ Arrivals: Early, on Time, or Late? Comput. Ind. Eng. 2019, 130, 298–308. [Google Scholar] [CrossRef]
- Tomkins, A.; Naylor, S.; Morgan, E. Short Message Service Cancellation Intervention to Reduce Integrated Sexual Health and HIV ‘Did Not Attend’ Appointment Rates. Int. J. STD AIDS 2019, 30, 201–203. [Google Scholar] [CrossRef] [PubMed]
- Williamson, A.E.; Ellis, D.A.; Wilson, P.; McQueenie, R.; McConnachie, A. Understanding Repeated Non-Attendance in Health Services: A Pilot Analysis of Administrative Data and Full Study Protocol for a National Retrospective Cohort. BMJ Open 2017, 7, e014120. [Google Scholar] [CrossRef] [PubMed]
- Dickey, W.; Morrow, J.I. Can Outpatient Non-Attendance Be Predicted from the Referral Letter? An Audit of Default at Neurology Clinics. J. R. Soc. Med. 1991, 84, 662–663. [Google Scholar] [CrossRef] [PubMed]
- Barz, C.; Rajaram, K. Elective Patient Admission and Scheduling under Multiple Resource Constraints. Prod. Oper. Manag. 2015, 24, 1907–1930. [Google Scholar] [CrossRef]
- Burke, E.K.; De Causmaecker, P.; Berghe, G.V.; Van Landeghem, H. The State of the Art of Nurse Rostering. J. Sched. 2004, 7, 441–499. [Google Scholar] [CrossRef]
- Jansson, B. Choosing a Good Appointment System—A Study of Queues of the Type (D, M, 1). Oper. Res. 1966, 14, 292–312. [Google Scholar] [CrossRef]
- Chiu, C.-K. Understanding Relationship Quality and Online Purchase Intention in E-Tourism: A Qualitative Application. Qual. Quant. 2009, 43, 669–675. [Google Scholar] [CrossRef]
- Mak, H.-Y.; Rong, Y.; Zhang, J. Sequencing Appointments for Service Systems Using Inventory Approximations. Manuf. Serv. Oper. Manag. 2014, 16, 251–262. [Google Scholar] [CrossRef]
- Denton, B.; Gupta, D. A Sequential Bounding Approach for Optimal Appointment Scheduling. IIE Trans. 2003, 35, 1003–1016. [Google Scholar] [CrossRef]
- Klassen, K.J.; Rohleder, T.R. Outpatient Appointment Scheduling with Urgent Clients in a Dynamic, Multi-period Environment. Int. J. Serv. Ind. Manag. 2004, 15, 167–186. [Google Scholar] [CrossRef]
- Cayirli, T.; Veral, E.; Rosen, H. Designing Appointment Scheduling Systems for Ambulatory Care Services. Health Care Manag. Sci. 2006, 9, 47–58. [Google Scholar] [CrossRef]
- Patrick, J.; Puterman, M.L.; Queyranne, M. Dynamic Multipriority Patient Scheduling for a Diagnostic Resource. Oper. Res. 2008, 56, 1507–1525. [Google Scholar] [CrossRef]
- Solmaz, H. Comparison of Patients’ Admissions to the Cardiology Outpatient Clinics Between the Appointment System and the Queue System. Arch. Turk. Soc. Cardiol. 2023, 51, 188–195. [Google Scholar] [CrossRef] [PubMed]
- Afrane, S.; Appah, A. Queuing Theory and the Management of Waiting-Time in Hospitals: The Case of Anglo Gold Ashanti Hospital in Ghana. Int. J. Acad. Res. Bus. Soc. Sci. 2014, 4, 34–44. [Google Scholar] [CrossRef]
- Soriano, A.; Cayirli, T.; Yang, K.K.; Kong, Q.; Lee, C.-Y.; Teo, C.-P.; Zheng, Z.; Robinson, L.W.; Chen, R.R.; Denton, B.T.; et al. Comparison of Two Scheduling Systems. Oper. Res. 1966, 14, 388–397. [Google Scholar] [CrossRef]
- LaGanga, L.R.; Lawrence, S.R. Appointment Overbooking in Health Care Clinics to Improve Patient Service and Clinic Performance. Prod. Oper. Manag. 2012, 21, 874–888. [Google Scholar] [CrossRef]
- Shnits, B.; Bendavid, I.; Marmor, Y.N. An Appointment Scheduling Policy for Healthcare Systems with Parallel Servers and Pre-Determined Quality of Service. Omega 2020, 97, 102095. [Google Scholar] [CrossRef]
- Cayirli, T.; Yang, K.K. Altering the Environment to Improve Appointment System Performance. Serv. Sci. 2019, 11, 138–154. [Google Scholar] [CrossRef]
- Rohleder, T.; Klassen, K.J. Using Client-Variance Information to Improve Dynamic Appointment Scheduling Performance. Omega 2000, 28, 293–302. [Google Scholar] [CrossRef]
- Creemers, S.; Lambrecht, M.R.; Beliën, J.; Van Den Broeke, M. Evaluation of Appointment Scheduling Rules: A Multi-Performance Measurement Approach. Omega 2021, 100, 102231. [Google Scholar] [CrossRef]
- Bosch, P.M.V.; Dietz, D.C. Minimizing Expected Waiting in a Medical Appointment System. IIE Trans. 2000, 32, 841–848. [Google Scholar] [CrossRef]
- Cayirli, T.; Yang, K.K.; Quek, S.A. A Universal Appointment Rule in the Presence of No-Shows and Walk-Ins. Prod. Oper. Manag. 2012, 21, 682–697. [Google Scholar] [CrossRef]
- Klassen, K.J.; Yoogalingam, R. An Assessment of the Interruption Level of Doctors in Outpatient Appointment Scheduling. Oper. Manag. Res. 2008, 1, 95–102. [Google Scholar] [CrossRef]
- Klassen, K.J.; Yoogalingam, R. Improving Performance in Outpatient Appointment Services with a Simulation Optimization Approach. Prod. Oper. Manag. 2009, 18, 447–458. [Google Scholar] [CrossRef]
- Peng, Y.; Qu, X.; Shi, J. A Hybrid Simulation and Genetic Algorithm Approach to Determine the Optimal Scheduling Templates for Open Access Clinics Admitting Walk-in Patients. Comput. Ind. Eng. 2014, 72, 282–296. [Google Scholar] [CrossRef]
- Meersman, T.; Maenhout, B. Multi-Objective Optimisation for Constructing Cyclic Appointment Schedules for Elective and Urgent Patients. Ann. Oper. Res. 2022, 312, 909–948. [Google Scholar] [CrossRef]
- Cayirli, T.; Yang, K.K. A Universal Appointment Rule with Patient Classification for Service Times, No-Shows, and Walk-Ins. Serv. Sci. 2014, 6, 274–295. [Google Scholar] [CrossRef]
- Salzarulo, P.A.; Mahar, S.; Modi, S. Beyond Patient Classification: Using Individual Patient Characteristics in Appointment Scheduling. Prod. Oper. Manag. 2016, 25, 1056–1072. [Google Scholar] [CrossRef]
- Robinson, L.W.; Chen, R.R. A Comparison of Traditional and Open-Access Policies for Appointment Scheduling. Manuf. Serv. Oper. Manag. 2010, 12, 330–346. [Google Scholar] [CrossRef]
- Qu, X.; Rardin, R.L.; Williams, J.A.S. Single versus Hybrid Time Horizons for Open Access Scheduling. Comput. Ind. Eng. 2011, 60, 56–65. [Google Scholar] [CrossRef]
- Turkcan, A.; Zeng, B.; Lawley, M. Chemotherapy Operations Planning and Scheduling. IIE Trans. Healthc. Syst. Eng. 2012, 2, 31–49. [Google Scholar] [CrossRef]
- Gocgun, Y.; Bresnahan, B.W.; Ghate, A.; Gunn, M.L. A Markov Decision Process Approach to Multi-Category Patient Scheduling in a Diagnostic Facility. Artif. Intell. Med. 2011, 53, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Saghafian, S.; Austin, G.; Traub, S.J. Operations Research/Management Contributions to Emergency Department Patient Flow Optimization: Review and Research Prospects. IIE Trans. Healthc. Syst. Eng. 2015, 5, 101–123. [Google Scholar] [CrossRef]
- Sauré, A.; Puterman, M.L. The Appointment Scheduling Game. INFORMS Trans. Educ. 2014, 14, 73–85. [Google Scholar] [CrossRef]
- Pérez, E.; Ntaimo, L.; Wilhelm, W.E.; Bailey, C.; McCormack, P. Patient and Resource Scheduling of Multi-Step Medical Procedures in Nuclear Medicine. IIE Trans. Healthc. Syst. Eng. 2011, 1, 168–184. [Google Scholar] [CrossRef]
- Wang, W.-Y.; Gupta, D. Adaptive Appointment Systems with Patient Preferences. Manuf. Serv. Oper. Manag. 2011, 13, 373–389. [Google Scholar] [CrossRef]
- Kong, Q.; Lee, C.-Y.; Teo, C.-P.; Zheng, Z. Scheduling Arrivals to a Stochastic Service Delivery System Using Copositive Cones. Oper. Res. 2013, 61, 711–726. [Google Scholar] [CrossRef]
- Erdogan, S.A.; Denton, B. Dynamic Appointment Scheduling of a Stochastic Server with Uncertain Demand. INFORMS J. Comput. 2013, 25, 116–132. [Google Scholar] [CrossRef]
- Turkcan, A.; Zeng, B.; Muthuraman, K.; Lawley, M. Sequential Clinical Scheduling with Service Criteria. Eur. J. Oper. Res. 2011, 214, 780–795. [Google Scholar] [CrossRef]
- Ozen, A.; Balasubramanian, H. The Impact of Case Mix on Timely Access to Appointments in a Primary Care Group Practice. Health Care Manag. Sci. 2013, 16, 101–118. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, H.; Biehl, S.; Dai, L.; Muriel, A. Dynamic Allocation of Same-Day Requests in Multi-Physician Primary Care Practices in the Presence of Prescheduled Appointments. Health Care Manag. Sci. 2014, 17, 31–48. [Google Scholar] [CrossRef] [PubMed]
- Conforti, D.; Guerriero, F.; Guido, R. Optimization Models for Radiotherapy Patient Scheduling. 4OR 2008, 6, 263–278. [Google Scholar] [CrossRef]
- Truong, V.-A. Optimal Advance Scheduling. Manag. Sci. 2015, 61, 1584–1597. [Google Scholar] [CrossRef]
- Anderson, K.; Zheng, B.; Yoon, S.W.; Khasawneh, M.T. An Analysis of Overlapping Appointment Scheduling Model in an Outpatient Clinic. Oper. Res. Health Care 2015, 4, 5–14. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, Y.; Leung, E.; Liu, X. Outpatient Appointment Scheduling with Unpunctual Patients. Int. J. Prod. Res. 2018, 56, 1982–2002. [Google Scholar] [CrossRef]
- Kaandorp, G.C.; Koole, G. Optimal Outpatient Appointment Scheduling. Health Care Manag. Sci. 2007, 10, 217–229. [Google Scholar] [CrossRef]
- Dharmadhikari, N.; Zhang, D.J. Simulation Optimization of Blocking Appointment Scheduling Policies for Multi-Clinic Appointments in Centralized Scheduling Systems. Ph.D. Thesis, North Dakota State University, Fargo, ND, USA, 2013. Volume 2. [Google Scholar]
- Cordier, J.-P.; Riane, F. Towards a Centralised Appointments System to Optimise the Length of Patient Stay. Decis. Support. Syst. 2013, 55, 629–639. [Google Scholar] [CrossRef]
- Aslani, N.; Zhang, J. Integration of Simulation and DEA to Determine the Most Efficient Patient Appointment Scheduling Model for a Specific Healthcare Setting. J. Ind. Eng. Manag. 2014, 7, 785–815. [Google Scholar] [CrossRef]
- Shuang, M.; Songlin, C.; Xiaotian, C. A Two-stage stochastic programming model for outpatient appointment scheduling. In Proceedings of the 2019 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Macao, China, 15–18 December 2019; pp. 79–83. [Google Scholar]
- El-Sharo, M.; Zheng, B.; Yoon, S.W.; Khasawneh, M.T. An Overbooking Scheduling Model for Outpatient Appointments in a Multi-Provider Clinic. Oper. Res. Health Care 2015, 6, 1–10. [Google Scholar] [CrossRef]
- Salemi Parizi, M.; Ghate, A. Multi-Class, Multi-Resource Advance Scheduling with No-Shows, Cancellations and Overbooking. Comput. Oper. Res. 2016, 67, 90–101. [Google Scholar] [CrossRef]
- Chakraborty, S.; Muthuraman, K.; Lawley, M. Sequential Clinical Scheduling with Patient No-Shows and General Service Time Distributions. IIE Trans. 2010, 42, 354–366. [Google Scholar] [CrossRef]
- Chakraborty, S.; Muthuraman, K.; Lawley, M. Sequential Clinical Scheduling with Patient No-Show: The Impact of Pre-Defined Slot Structures. Socio-Econ. Plan. Sci. 2013, 47, 205–219. [Google Scholar] [CrossRef]
- Muthuraman, K.; Lawley, M. A Stochastic Overbooking Model for Outpatient Clinical Scheduling with No-Shows. IIE Trans. 2008, 40, 820–837. [Google Scholar] [CrossRef]
- Geng, N.; Xie, X. Optimal Dynamic Outpatient Scheduling for a Diagnostic Facility With Two Waiting Time Targets. IEEE Trans. Automat. Contr. 2016, 61, 3725–3739. [Google Scholar] [CrossRef]
- Patrick, J. A Markov Decision Model for Determining Optimal Outpatient Scheduling. Health Care Manag. Sci. 2012, 15, 91–102. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Yan, C.; Wang, L.; Lu, D.; Ma, L. Optimization methods for joint capacity and appointment scheduling problem with walk-in patients. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 9600–9604. [Google Scholar]
- Nguyen, T.B.T.; Sivakumar, A.I.; Graves, S.C. A Network Flow Approach for Tactical Resource Planning in Outpatient Clinics. Health Care Manag. Sci. 2015, 18, 124–136. [Google Scholar] [CrossRef] [PubMed]
- Zeng, B.; Turkcan, A.; Lin, J.; Lawley, M. Clinic Scheduling Models with Overbooking for Patients with Heterogeneous No-Show Probabilities. Ann. Oper. Res. 2010, 178, 121–144. [Google Scholar] [CrossRef]
- Yan, C.; Tang, J.; Jiang, B.; Fung, R.Y.K. Sequential Appointment Scheduling Considering Patient Choice and Service Fairness. Int. J. Prod. Res. 2015, 53, 7376–7395. [Google Scholar] [CrossRef]
- Tsai, P.-F.J.; Teng, G.-Y. A Stochastic Appointment Scheduling System on Multiple Resources with Dynamic Call-in Sequence and Patient No-Shows for an Outpatient Clinic. Eur. J. Oper. Res. 2014, 239, 427–436. [Google Scholar] [CrossRef]
- Jiang, B.; Tang, J.; Yan, C. Outpatient Capacity Allocation Considering Adding Capacity to Match High Patient Demand. J. Syst. Sci. Syst. Eng. 2017, 26, 487–516. [Google Scholar] [CrossRef]
- Jiang, B.; Yu, M. Optimal Outpatient Capacity Allocation under the Capacity-Addition Policy. Comput. Ind. Eng. 2022, 174, 108791. [Google Scholar] [CrossRef]
- Sevinc, S.; Sanli, U.A.; Goker, E. Algorithms for Scheduling of Chemotherapy Plans. Comput. Biol. Med. 2013, 43, 2103–2109. [Google Scholar] [CrossRef] [PubMed]
- Savelsbergh, M.; Smilowitz, K. Stratified Patient Appointment Scheduling for Mobile Community-Based Chronic Disease Management Programs. IIE Trans. Healthc. Syst. Eng. 2016, 6, 65–78. [Google Scholar] [CrossRef]
- Zhu, H.; Hou, M.; Wang, C.; Zhou, M. An Efficient Outpatient Scheduling Approach. IEEE Trans. Autom. Sci. Eng. 2012, 9, 701–709. [Google Scholar] [CrossRef]
- Erdelyi, A.; Topaloglu, H. Computing Protection Level Policies for Dynamic Capacity Allocation Problems by Using Stochastic Approximation Methods. IIE Trans. 2009, 41, 498–510. [Google Scholar] [CrossRef]
- Gao, K.; Peng, R.; Qu, L.; Wu, S. Jointly Optimizing Lot Sizing and Maintenance Policy for a Production System with Two Failure Modes. Reliab. Eng. Syst. Saf. 2020, 202, 106996. [Google Scholar] [CrossRef]
- Bai, G.; Chi, Y.; Gao, K.; Peng, R. Reliability Evaluation of Multi-State Systems with Common Bus Performance Sharing Considering Performance Excess. IEEE Access 2022, 10, 19174–19185. [Google Scholar] [CrossRef]
- Lei, B.; Ren, Y.; Luan, H.; Dong, R.; Wang, X.; Liao, J.; Fang, S.; Gao, K. A Review of Optimization for System Reliability of Microgrid. Mathematics 2023, 11, 822. [Google Scholar] [CrossRef]
- Gao, K.; Wang, T.; Han, C.; Xie, J.; Ma, Y.; Peng, R. A Review of Optimization of Microgrid Operation. Energies 2021, 14, 2842. [Google Scholar] [CrossRef]
- Ren, Y.; Jin, C.; Fang, S.; Yang, L.; Wu, Z.; Wang, Z.; Peng, R.; Gao, K. A Comprehensive Review of Key Technologies for Enhancing the Reliability of Lithium-Ion Power Batteries. Energies 2023, 16, 6144. [Google Scholar] [CrossRef]
- Homem-de-Mello, T.; Kong, Q.; Godoy-Barba, R. A Simulation Optimization Approach for the Appointment Scheduling Problem with Decision-Dependent Uncertainties. INFORMS J. Comput. 2022, 34, 2845–2865. [Google Scholar] [CrossRef]
- Liu, N.; Ziya, S. Panel Size and Overbooking Decisions for Appointment-Based Services under Patient No-Shows. Prod. Oper. Manag. 2014, 23, 2209–2223. [Google Scholar] [CrossRef]
- Zhang, Z.; Berg, B.P.; Denton, B.T.; Xie, X. Appointment Scheduling and the Effects of Customer Congestion on Service. IISE Trans. 2019, 51, 1075–1090. [Google Scholar] [CrossRef]
- Luo, J.; Kulkarni, V.G.; Ziya, S. Appointment Scheduling Under Patient No-Shows and Service Interruptions. Manuf. Serv. Oper. Manag. 2012, 14, 670–684. [Google Scholar] [CrossRef]
- Gao, K.; Yan, X.; Peng, R.; Xing, L. Economic Design of a Linear Consecutively Connected System Considering Cost and Signal Loss. IEEE Trans. Syst. Man. Cybern. Syst. 2021, 51, 5116–5128. [Google Scholar] [CrossRef]
- Saremi, A.; Jula, P.; ElMekkawy, T.; Wang, G.G. Appointment Scheduling of Outpatient Surgical Services in a Multistage Operating Room Department. Int. J. Prod. Econ. 2013, 141, 646–658. [Google Scholar] [CrossRef]
- Braune, R.; Gutjahr, W.J.; Vogl, P. Stochastic Radiotherapy Appointment Scheduling. Cent. Eur. J. Oper. Res. 2022, 30, 1239–1277. [Google Scholar] [CrossRef]
- Fan, X.; Tang, J.; Yan, C.; Guo, H.; Cao, Z. Outpatient Appointment Scheduling Problem Considering Patient Selection Behavior: Data Modeling and Simulation Optimization. J. Comb. Optim. 2021, 42, 677–699. [Google Scholar] [CrossRef]
- Alizadeh, R.; Rezaeian, J.; Abedi, M.; Chiong, R. A Modified Genetic Algorithm for Non-Emergency Outpatient Appointment Scheduling with Highly Demanded Medical Services Considering Patient Priorities. Comput. Ind. Eng. 2020, 139, 106106. [Google Scholar] [CrossRef]
- Dehghanimohammadabadi, M.; Rezaeiahari, M.; Seif, J. Multi-Objective Patient Appointment Scheduling Framework (MO-PASS): A Data-Table Input Simulation–Optimization Approach. Simulation 2023, 99, 363–383. [Google Scholar] [CrossRef]
- Ala, A.; Alsaadi, F.E.; Ahmadi, M.; Mirjalili, S. Optimization of an Appointment Scheduling Problem for Healthcare Systems Based on the Quality of Fairness Service Using Whale Optimization Algorithm and NSGA-II. Sci. Rep. 2021, 11, 19816. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Wang, D.; Wang, Y.; Yin, Y. MRI Appointment Scheduling with Uncertain Examination Time. J. Comb. Optim. 2019, 37, 62–82. [Google Scholar] [CrossRef]
- Garaix, T.; Rostami, S.; Xie, X. Daily Outpatient Chemotherapy Appointment Scheduling with Random Deferrals. Flex. Serv. Manuf. J. 2020, 32, 129–153. [Google Scholar] [CrossRef]
- Corsini, R.R.; Costa, A.; Fichera, S.; Parrinello, V. Hybrid Harmony Search for Stochastic Scheduling of Chemotherapy Outpatient Appointments. Algorithms 2022, 15, 424. [Google Scholar] [CrossRef]
- Ala, A.; Chen, F. An appointment scheduling optimization method in healthcare with simulation approach. In Proceedings of the 2020 IEEE 7th International Conference on Industrial Engineering and Applications (ICIEA), Bangkok, Thailand, 16–21 April 2020; pp. 833–837. [Google Scholar]
- Rajakumari, K.; Madhunisha, M. Intelligent and convolutional-neural-network based smart hospital and patient scheduling system. In Proceedings of the 2020 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 22–24 January 2020; pp. 1–5. [Google Scholar]
- Dogru, A.K.; Melouk, S.H. Adaptive Appointment Scheduling for Patient-Centered Medical Homes. Omega 2019, 85, 166–181. [Google Scholar] [CrossRef]
- Squires, M.; Tao, X.; Elangovan, S.; Gururajan, R.; Zhou, X.; Acharya, U.R. A Novel Genetic Algorithm Based System for the Scheduling of Medical Treatments. Expert. Syst. Appl. 2022, 195, 116464. [Google Scholar] [CrossRef]
- Akbarzadeh, B.; Moslehi, G.; Reisi-Nafchi, M.; Maenhout, B. The Re-Planning and Scheduling of Surgical Cases in the Operating Room Department after Block Release Time with Resource Rescheduling. Eur. J. Oper. Res. 2019, 278, 596–614. [Google Scholar] [CrossRef]
- Chen, C. CiteSpace II: Detecting and Visualizing Emerging Trends and Transient Patterns in Scientific Literature. J. Am. Soc. Inf. Sci. 2006, 57, 359–377. [Google Scholar] [CrossRef]
- Fragidis, L.L.; Chatzoglou, P.D.; Aggelidis, V.P. Integrated Nationwide Electronic Health Records System: Semi-Distributed Architecture Approach. Technol. Health Care 2016, 24, 827–842. [Google Scholar] [CrossRef]
- Kallos, A.; Perez, A.; O’Neill, M.G.; Holt, N.L.; Bruce, A.; Childs, M.; Kane Poitras, S.; Kherani, T.; Ladha, T.; Majaesic, C.; et al. Recommendations from Parents, Administrative Staff and Clinicians to Improve Paediatric Ambulatory Appointment Scheduling. Child 2021, 47, 834–843. [Google Scholar] [CrossRef] [PubMed]
- Krzyzanowski, B.; Manson, S.M. Twenty Years of the Health Insurance Portability and Accountability Act Safe Harbor Provision: Unsolved Challenges and Ways Forward. JMIR Med. Inf. 2022, 10, e37756. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, C.-J.; King, J.; Hing, E.; Simon, A.E. The Role of Health Information Technology in Care Coordination in the United States. Med. Care 2015, 53, 184–190. [Google Scholar] [CrossRef] [PubMed]
- Novillo-Ortiz, D.; Dumit, E.M.; D’Agostino, M.; Becerra-Posada, F.; Kelley, E.T.; Torrent-Sellens, J.; Jiménez-Zarco, A.; Saigí-Rubió, F. Digital Health in the Americas: Advances and Challenges in Connected Health. BMJ Innov. 2018, 4, 123–127. [Google Scholar] [CrossRef] [PubMed]
- Lv, Z.; Qiao, L. Analysis of Healthcare Big Data. Future Gener. Comput. Syst. 2020, 109, 103–110. [Google Scholar] [CrossRef]
- Lee, J.; Park, Y.-T.; Park, Y.R.; Lee, J.-H. Review of National-Level Personal Health Records in Advanced Countries. Healthc. Inf. Res. 2021, 27, 102–109. [Google Scholar] [CrossRef]
- Ratwani, R.M. Electronic Health Records and Improved Patient Care: Opportunities for Applied Psychology. Curr. Dir. Psychol. Sci. 2017, 26, 359–365. [Google Scholar] [CrossRef]
- Yogesh, M.J.; Karthikeyan, J. Health Informatics: Engaging Modern Healthcare Units: A Brief Overview. Front. Public Health 2022, 10, 854688. [Google Scholar] [CrossRef]


| Decision Types | Features | Related Studies |
|---|---|---|
| Strategic decisions |
| Robinson et al. [61]; Qu et al. [62]; Turkcan et al. [63]; Gocgun et al. [64]; Saghafian et al. [65]; Sauréet al. [66]; Pérez et al. [67] |
| ||
| ||
| Tactical decisions |
| Wang et al. [68]; Kong et al. [69]; Erdogan et al. [70]; Turkcan et al. [71]; Ozen et al. [72] |
| ||
| ||
| Operational decisions |
| Balasubramanian et al. [73]; Conforti et al. [74]; Truong et al. [75]; Feldman et al. [14]; Cayirli et al. [17] |
| ||
|
| Objectives | Contributions | Related Studies |
|---|---|---|
| Societal benefit |
| Anderson et al. [76]; Han et al. [77]; Guido et al. [78]; Dharmadhikari et al. [79]; Cordier et al. [80]; Nazanin et al. [81]; Ma et al. [82] |
| ||
| ||
| Economic performance |
| El-Sharo et al. [83]; Parizi et al. [84]; Chakraborty et al. [85,86]; Muthuraman et al. [87]; Geng et al. [88]; Patrick et al. [89]; Wang et al. [90] |
| ||
| ||
| ||
| Resource utilization |
| Nguyen et al. [91];Zeng et al. [92]; Yan et al. [93]; Tsai et al. [94]; Jiang et al. [95,96]; Sevinc et al. [97] |
| ||
| ||
| Other objectives |
| Savelsbergh et al. [98]; Ozen et al. [72] Zhu et al. [99]; Erdelyi et al. [100] |
| ||
| ||
|
| Algorithms | Features | Related Studies |
|---|---|---|
| GA |
| Braune et al. [112]; Fan et al. [113]; Alizadeh et al. [114]; Squires et al. [123] |
| ||
| ||
| WOA |
| Mohammad et al. [115]; Ali et al. [116]; Qiu et al. [117]; |
| ||
| ||
| TSA |
| Meersman et al. [58]; Garaix et al. [118]; Corsini et al. [119]; Ali et al. [120]; |
| ||
| ||
| Other algorithms (GRASP, contraindicated search approach, etc.). | Rajakumari et al. [121]; Ali et al. [122]; Akbarzadeh et al. [124] | |
| Keywords | Year | Strength | Begin | End | 2016–2023 |
|---|---|---|---|---|---|
| patient flow | 2016 | 4.64 | 2016 | 2017 |  |
| discrete event simulation | 2016 | 2.95 | 2016 | 2018 |  |
| overbooking model | 2017 | 2.8 | 2017 | 2018 |  |
| time windows | 2017 | 2.58 | 2017 | 2018 |  |
| metanalysis | 2018 | 2.59 | 2018 | 2019 |  |
| simulation | 2017 | 2.56 | 2018 | 2019 |  |
| digital health | 2019 | 3.31 | 2019 | 2020 |  |
| health information technology | 2019 | 2.48 | 2019 | 2020 |  |
| electronic health record | 2020 | 2.93 | 2020 | 2021 |  |
| robust optimization | 2017 | 2.39 | 2021 | 2023 |  |
| operations research | 2021 | 2.27 | 2021 | 2023 |  |
| COVID-19 pandemic | 2021 | 2.27 | 2021 | 2023 |  |
| Country | AS Methods | Advantages | Disadvantages |
|---|---|---|---|
| China |
| Rapid adoption of digital technologies Integration of traditional Chinese medicine | Higher requirements for system arithmetic operations and maintenance |
| |||
| |||
| United States |
| Convenient for patients Improved accessibility with telemedicine | Insurance dependence Complex verification |
| |||
| |||
| Canada |
| Universal healthcare coverage | Variation in healthcare services across provinces |
| |||
| Germany |
| Well-established healthcare infrastructure | Gatekeeping may lead to delays in specialty care access |
| |||
| Japan |
| Prevention and early intervention | Aging population strain healthcare resources |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, T.; Lei, B.; Guo, L.; Fang, S.; Li, Q.; Gao, B.; Yang, L.; Gao, K. A Review of Optimization Studies for System Appointment Scheduling. Axioms 2024, 13, 16. https://doi.org/10.3390/axioms13010016
Niu T, Lei B, Guo L, Fang S, Li Q, Gao B, Yang L, Gao K. A Review of Optimization Studies for System Appointment Scheduling. Axioms. 2024; 13(1):16. https://doi.org/10.3390/axioms13010016
Chicago/Turabian StyleNiu, Tiantian, Bingyin Lei, Li Guo, Shu Fang, Qihang Li, Bingrui Gao, Li Yang, and Kaiye Gao. 2024. "A Review of Optimization Studies for System Appointment Scheduling" Axioms 13, no. 1: 16. https://doi.org/10.3390/axioms13010016
APA StyleNiu, T., Lei, B., Guo, L., Fang, S., Li, Q., Gao, B., Yang, L., & Gao, K. (2024). A Review of Optimization Studies for System Appointment Scheduling. Axioms, 13(1), 16. https://doi.org/10.3390/axioms13010016










