Heuristic Ensemble Construction Methods of Automatically Designed Dispatching Rules for the Unrelated Machines Environment

Abstract

Dynamic scheduling represents an important class of combinatorial optimisation problems that are usually solved with simple heuristics, the so-called dispatching rules (DRs). Designing efficient DRs is a tedious task, which is why it has been automated through the application of genetic programming (GP). Various approaches have been used to improve the results of automatically generated DRs, with ensemble learning being one of the best-known. The goal of ensemble learning is to create sets of automatically designed DRs that perform better together. One of the main problems in ensemble learning is the selection of DRs to form the ensemble. To this end, various ensemble construction methods have been proposed over the years. However, these methods are quite computationally intensive and require a lot of computation time to obtain good ensembles. Therefore, in this study, we propose several simple heuristic ensemble construction methods that can be used to construct ensembles quite efficiently and without the need to evaluate their performance. The proposed methods construct the ensembles solely based on certain properties of the individual DRs used for their construction. The experimental study shows that some of the proposed heuristic construction methods perform better than more complex state-of-the-art approaches for constructing ensembles.

1. Introduction

The unrelated machines scheduling problem represents an important combinatorial optimisation problem that frequently arises in various real-world domains, such as multiprocessor task scheduling [1], equipment scheduling [2], and manufacturing [3]. In this problem, it is necessary to schedule a set of jobs on a limited number of machines by optimising one or more user-defined criteria [4]. Due to its importance, many researchers have addressed this problem and usually solved it with a variety of metaheuristic and heuristic methods [5,6]. In many situations, however, the problem must be solved under dynamic conditions, which means that jobs are released into the system during execution, making it difficult to apply standard metaheuristic methods because not all information about the problem is known in advance. For such situations, dispatching rules (DRs) and simple greedy heuristics are the methods of choice [7].

DRs build the schedule incrementally by determining which job to schedule each time a scheduling decision is made. Over the years, various DRs have been developed that base their decisions on some characteristics of the job or the entire scheduling system. For example, these DRs might use strategies such as scheduling the job with the fastest processing time or the earliest due date [7]. Although DRs can create schedules quite efficiently and can be used under dynamic conditions, their performance is limited as they make decisions based on very simple rules. Unfortunately, manually creating complex DRs is quite a difficult task that requires extensive expertise. Therefore, research on the application of hyper-heuristic methods for the automatic generation of such DRs has gradually increased.

Genetic programming (GP) is a hyperheuristic method [8,9] that is most commonly used for the automated design of DRs for various combinatorial optimisation problems, starting with scheduling problems [10,11], the travelling salesman problem [12,13], vehicle and arc routing problems [14,15], the container relocation problem [16], and the cutting-stock problem [17,18]. Although GP enables the automatic design of DRs and thus eliminates the extensive and tedious task of manually designing DRs, the performance of the designed DRs is still limited. Even though these automatically designed DRs regularly perform better than the manually designed rules, there are still many ways to improve their performance. Therefore, much research has been conducted in the field of automatic design of DRs to develop methods that can increase the performance of such DRs.

One of the most popular and efficient methods to improve the performance of automatically designed DRs from the literature is the application of ensemble learning to construct ensembles of DRs [19]. This approach has repeatedly demonstrated that it can improve the performance of individual DRs by simply combining them into ensembles of rules that jointly make their scheduling decisions. Many methods for creating ensembles have been proposed and applied in the literature over the years [20]. However, many of these methods have the disadvantage that they are quite computationally intensive and require the evaluation of several hundreds or thousands of ensembles to create good ensembles. Therefore, the construction process of ensembles is usually quite computationally intensive, and a lot of time must be invested to create good ensembles.

In classical ensemble construction methods, the constructed ensembles are evaluated to determine their quality and select better ensembles to direct the search to promising areas [20]. However, the evaluation process of ensembles is the most costly part of the whole ensemble construction method and leads to long execution times. Therefore, the aim of this study is to propose novel heuristics for ensemble construction that can be used to construct ensembles almost instantaneously. This is achieved by not evaluating the constructed ensembles but by constructing the ensembles based on the properties of the individual rules used to construct them. However, since no complete or partial ensembles are evaluated, strategies have to be defined for how such ensembles should be constructed, i.e., according to which strategies the DRs should be selected to be included in the ensemble. For this reason, we propose 10 simple deterministic ensemble construction methods that incrementally construct the ensemble by selecting suitable DRs to form the ensemble using different strategies. The ensembles constructed with the proposed heuristics are compared with the results of the current best ensemble construction method to evaluate their performance. The results show that, in many cases, simple heuristics can design ensembles that perform equally well or even better compared to those constructed using a more complex ensemble construction method. Moreover, the time required by the proposed heuristics to construct the ensembles is almost negligible (less than a millisecond), which illustrates their rather low computational complexity. The obtained results show that the proposed heuristic ensemble construction methods are a viable alternative to the existing and more computationally intensive ensemble construction methods.

The rest of the paper is organised as follows. Section 2 provides a literature review on the application of ensemble learning methods in the context of automatically designed DRs. The background of the topics relevant to this study is presented in Section 3. The proposed heuristic ensemble construction methods are described in detail in Section 4. Section 5 describes the design of the experiments, outlines the results obtained, and discusses them. Finally, Section 6 concludes the study and suggests possible future research avenues.

2. Literature Review

Since the first studies dealing with the application of GP for the automated design of DRs [21,22], this research area has received more and more attention from various researchers [10,11,23]. Over the years, researchers have studied many topics in this area, including experimenting with different solution representations [24,25], solving multi-objective problems [26,27,28,29], the use of multitask GP approaches [30,31], surrogate models [32,33] and many other research directions [34,35,36,37].

The first application of ensemble learning to create ensembles of automatically designed DRs was undertaken in [19]. In this study, the authors applied a cooperative coevolution GP approach, where each DR in the ensemble was evolved in a separate subpopulation and combined with other rules to evaluate its performance. The results obtained showed that the constructed ensembles performed significantly better than the individual DRs. This study was extended in [38] with a multi-level GP method, but the experiments showed no improvement in the performance of the method. In [39,40], a novel approach called NELLI-GP was proposed for the development of DRs. This method develops individual rules specialised for solving specific subproblems and then combines them into ensembles that perform better than previous ensemble learning methods. In addition to the method used to construct the ensemble, the methods used to combine the ensemble, i.e., the method used to combine the individual decisions of the rules in the ensemble into a single decision, must also be specified. Therefore, several ensemble combination methods were investigated in [41], and it was shown that the standard sum and voting combination methods achieve the best performance.

In addition to the methods already mentioned, which both develop DRs and construct ensembles, there is also an alternative approach to ensemble learning in which the ensembles are constructed from DRs that have already been generated. In this way, the method only needs to focus on selecting suitable DRs to form the ensemble, reducing the complexity of the problem. One method that works in this way is simple ensemble combination (SEC) [42], which constructs ensembles by sampling from a large number of ensembles and selecting the one that performs best. Compared to approaches that both evolve DRs and construct ensembles, such as BagGP, BoostGP, and cooperative coevolution, SEC has been shown to regularly achieve significantly better results [20,43].

Another way of applying ensembles, which only applies to static scheduling conditions, was proposed in [44]. In this type of ensemble, each rule is applied independently of the other rules, and the best solution obtained by one of the rules in the ensemble is selected. The problem is, therefore, finding such a set of rules that perform well individually in a large number of instances. This ensemble type was further studied in [45,46], where ensembles of manually designed DRs were tested, and different methods for creating such ensembles were investigated. These ensembles were compared to the traditional type of ensembles (suitable for dynamic problems) in [47], and it was shown that they perform significantly better compared to them in static scheduling problems. Furthermore, in [48], this ensemble type was adapted for dynamic scheduling conditions, and it was shown that such ensembles are competitive and better than some standard ensemble combination methods, but with the disadvantage that they are more computationally intensive.

Another recent research direction is the use of ensembles to solve multi-objective problems. In [49], the authors constructed ensembles of DRs designed to solve multi-objective problems to improve not only their performance but also the coverage of the search space and obtain better Pareto fronts of solutions. The experimental results have shown that using ensembles in this way leads to better results and better Pareto fronts than using single DRs. The multi-objective problem was also addressed in [50] but in a completely different way. In this study, the authors used DRs that were developed for the optimisation of single objectives but then combined them into ensembles that are suitable for the simultaneous optimisation of multiple objectives. The results of this line of research have shown that such a methodology leads to ensembles that perform significantly better than single DRs developed directly for multi-objective optimisation and that such ensembles can be created in less time than it takes to develop DRs for a new multi-objective optimisation problem.

In addition to scheduling, ensemble learning has also been combined with hyperheuristic methods in other optimisation problems such as the capacitated arc routing problem [15,51] or the travelling salesman problem [13]. This shows that ensemble learning is a viable approach that can be used in various problem domains.

3. Background

This section provides the required background information of the considered topics.

3.1. The Unrelated Machines Scheduling Problem

The unrelated machines environment consists of n jobs that must be scheduled on one of the m available machines [52]. Each job j has a different processing time on each machine i, denoted by $p_{ij}$. In addition, each job j also has an associated release time $r_j$, which specifies the time at which the job is released in the system (i.e., it becomes available), a weight $w_j$, which specifies the importance of the job, and a due date $d_j$, which defines the time by which the job should finish its execution. In the problem considered here, no preemption is allowed, i.e., as soon as a job is scheduled on a machine, it must be completed and cannot be interrupted. Furthermore, each machine can only execute a single job at any time, and each machine can process any of the available jobs. If a machine is free, a job does not necessarily have to be scheduled on it immediately, i.e., it is permitted to introduce idle times on machines. The optimised criterion is the total weighted tardiness, which can be defined as follows: $TWT={\sum }_i^n{w}_{j}max(C_j-d_j,0)$, where $C_j$ denotes the time at which job j is finished with its execution. The aim of this criterion is to reduce the time that jobs spend executing after their respective due date. The problem to be analysed can be defined as $R|r_j|\sum w_j{T}_j$ using the standard notation for scheduling problems [53].

Finally, the problem described above is considered under dynamic conditions, which means that no information about the jobs is available until they are actually released in the system. This means that the system does not know when the next job will arrive nor what properties it will have (e.g., processing time or weight). Therefore, the problem cannot be solved with traditional improvement-based methods (such as metaheuristics) as the solution space is not known before or even during most of the execution of the system. Therefore, dispatching rules (DRs) are an alternative for solving problems under dynamic conditions. DRs are simple constructive heuristic methods that build the schedule incrementally by selecting the job to be scheduled next at each decision time (when at least one machine is available). They can usually be divided into two parts: the schedule building scheme and the prioritisation function.

The schedule generation scheme (SGS) represents the design of the DR and determines how and when the scheduling decision is made. This means that the SGS determines when a scheduling decision should be made and which jobs and machines should be considered so that the assignment of a job to a machine is feasible and the created schedule is valid in the end. However, to determine which job should be scheduled on which machine, it uses a PF that assigns a numerical value to each scheduling decision (assignment of a job to a machine). This numerical value, often called a priority, is used to rank all scheduling decisions, and the SGS selects the decision with the best rank (the lowest or highest, depending on the implementation). In most cases, the SGS is easy to design, as it only needs to ensure that the decisions it is considering are feasible. However, designing good PFs is a difficult and time-consuming task, as there are many possibilities that need to be considered. Therefore, the design of PFs has often been automated in the literature to obtain PFs of better quality and for various scheduling problems.

Algorithm 1 outlines a possible SGS (the one used by the automatically designed DRs). This SGS is executed throughout the execution of the system. Each time a machine becomes available and there is at least one free machine, it determines which job should be scheduled on which machine. To do this, it uses a PF to rank all possible assignments of jobs to the machines and then selects the one with the best priority. When a particular decision has been made, the selected job is simply scheduled on the appropriate machine, and the whole process is repeated.

Algorithm 1 SGS used by generated DRs

1: while true do  2:    Wait until at least one job and machine are available  3:    for all available jobs j and each machine i in m do  4:      Calculate the priority ${\pi }_{ij}$ of scheduling j on machine i  5:    end for  6:    for all available jobs do  7:      Determine the machine with the best ${\pi }_{ij}$ value  8:    end for  9:    while jobs whose best machine is available exist do 10:      Determine the best priority of all such jobs 11:      Schedule the job with the best priority 12:    end while 13: end while

3.2. Automated Design of DRs with GP

Genetic programming (GP) is a powerful evolutionary computational method [54,55] that has proven over the years the ability to obtain human competitive results in many areas [56]. The basic features of the algorithm are presented in Algorithm 2 and follow the structure of standard genetic algorithms [57]. First, the algorithm randomly initialises the initial population of potential solutions by randomly constructing a certain number of solutions using the ramped half-and-half method [55]. These solutions are then evaluated against a set of problems to determine their quality, i.e., how suitable they are for solving the problem in question. This quality measure is usually called fitness, and the function used to calculate it is called the fitness function.

Algorithm 2 Standard steady state GP algorithm

1: Randomly initialise the population P  2: Evaluate all individuals in the population  3: while termination criterion is not met do  4:    Randomly select 3 individuals from the population that compete in a tournament  5:    Select the better two individuals from the tournament, which are denoted as parents  6:    Perform the crossover operator on the parents and create a new child individual  7:    Perform the mutation operator on the child individual with a certain probability  8:    Evaluate the child individual  9:    Replace the remaining individual in the tournament with the child individual 10: end while

After this initial phase, the algorithm iteratively executes a series of steps until a certain termination criterion, such as the maximum number of iterations or the maximum execution time, is met. In each step, the algorithm executes several genetic operators to search for better solutions. First, the three-tournament selection operator is applied to randomly select three individuals from the population in a tournament. The better of the two individuals, called parents, are used in the crossover operator to create a new individual, the child, based on the traits of both parents. This individual is then subjected to the mutation operator, which introduces random changes into the individual with a certain probability in order to maintain the diversity of the population and reduce the possibility of being trapped in local optima. The child is then inserted into the population in place of the remaining individual selected in the tournament, which is the worst of the three selected individuals. After the termination condition is met, the best individual in the population is returned as the final solution.

The main difference between GP and genetic algorithms lies in the way the solutions are coded. While in standard genetic algorithms, the solutions are usually represented as arrays of floating point numbers of permutations, in GP the solutions are represented as expression trees. Expression trees consist of two types of nodes: function nodes and terminal nodes. Function nodes are inner nodes of the expression tree and represent various types of operators that are executed on their child nodes, such as mathematical or logical operators. Terminal nodes, on the other hand, are leaves of the expression tree and represent constants or variables. They are important because they provide all relevant information about the problem or the current state of the system in execution. By using appropriate sets of functions and terminal nodes, GP can construct expressions to solve various types of problems.

In the automated development of DRs, GP is used to automatically develop a new PF that is used by a predefined SGS (the one in Algorithm 1) to rank all decisions and determine which job should be scheduled next and on which machine. Therefore, it is necessary to define the terminal and function nodes that GP will use to develop an appropriate PF that prioritises the jobs.

Table 1. The set of terminal nodes used by GP to evolve PFs.

Terminal	Description
$pt$	processing time of job j on machine i
$pmin$	minimal processing time (MPT) of job j
$pavg$	average processing time of job j across all machines
$PAT$	time until machine with the MPT for job j becomes available
$MR$	time until machine i becomes available
$age$	time which job j spent in the system
$dd$	time until which job j has to finish with its execution
w	weight of job j ($w_j$)
$SL$	slack of job j, $-max(d_j-p_{ij}-t,0)$

outlines the set of terminal nodes that are used to generate PFs for the problem under consideration. These terminals contain both simple features of the problem, such as the processing times or due dates of the jobs, as well as some more complicated features, such as the slack of the job, which indicates how much time is left until the job is overdue. As for the function nodes, GP has used the addition, subtraction, multiplication, protected division (returns 1 if the division is by 0), and positive (unary function that returns 0 if the argument is a positive number; otherwise, it returns 0) functions to construct the PFs.

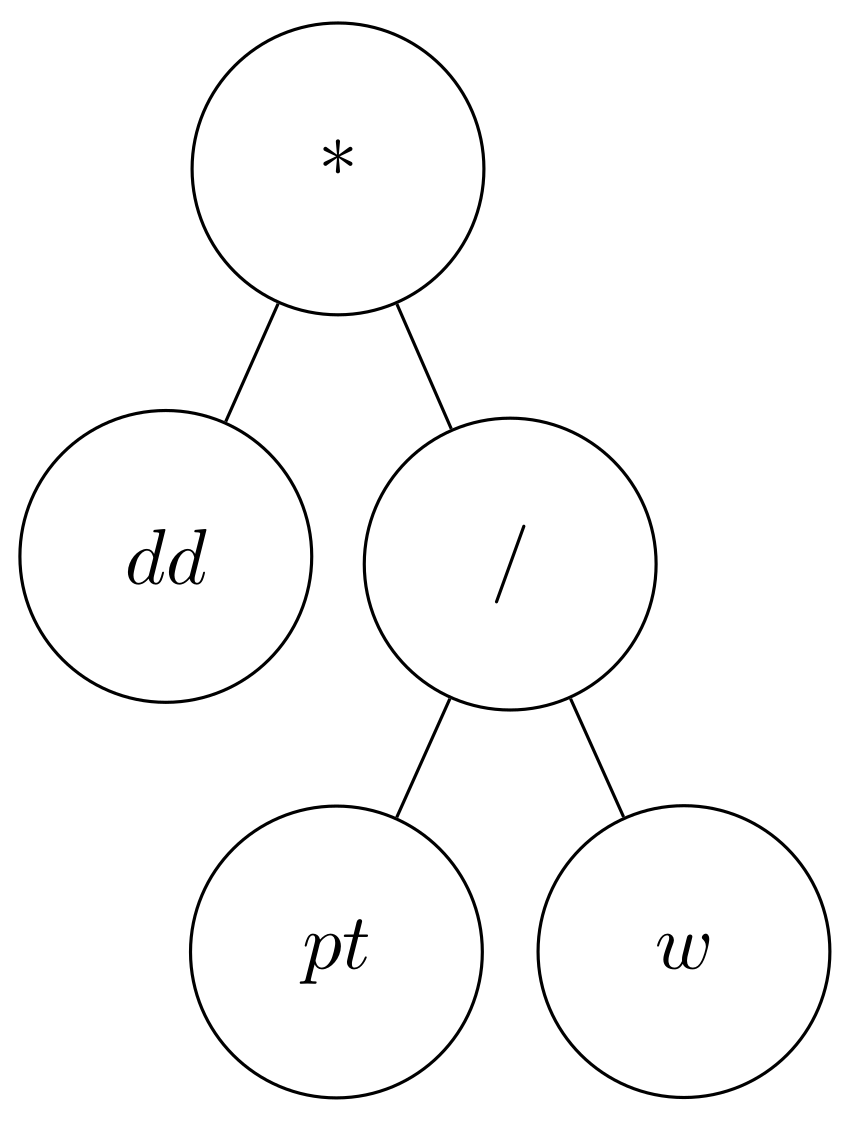
An example of an individual that represents an expression interpreted as PF is shown in Figure 1. The figure shows the structure that this expression would have in the individual in the form of an expression tree. This expression tree represents the expression $dd\frac{pt}{w}$, represented in infix notation, which is interpreted as a PF to calculate the priorities of all available jobs that need to be scheduled. Based on this PF, the jobs with the lowest priority value would be selected first, as the rule multiplies the processing time of the job with its due date and divides the product by the weight of the job. This means that the rule would prioritise the jobs with a shorter processing time and a closer due date, as well as a higher weight (meaning that the job is more important). Of course, the PFs that GP develops can be much more complex, which depends on the maximum size of expressions it can construct. In this study, the depth of the expression tree is limited to 5, which means that expressions with up to 63 nodes can be constructed (since the root node is at depth 0). However, for this size, it is already impossible to enumerate all possible expressions that can be represented, thus prohibiting us from using an exact method to find an expression that represents a suitable PF. Furthermore, since the GP algorithm and all its operators ensure that each individual represents a syntactically correct expression (all operators have the required number of operands), each solution represents a valid PF, and no infeasible solutions can occur.

3.3. Ensemble Learning for Automatically Designed DRs

In the context of DRs, ensemble learning is a method that constructs sets of DRs that jointly make scheduling decisions and thus jointly solve a scheduling problem [19]. To apply ensemble learning to create DR ensembles, three things must be defined: the size of the ensemble, the ensemble combination method and the ensemble construction method [20]. The ensemble size parameter, as the name suggests, determines how many DRs will be included in the ensemble. The value of this parameter has a significant impact on the performance of the ensemble, as larger ensembles usually perform better, but at the cost of longer execution time and lower interpretability. On the other hand, smaller ensembles execute scheduling decisions faster and may be easier to interpret. Therefore, the size of the ensemble is usually kept smaller in order to find a compromise between performance and efficiency.

The ensemble combination method determines how the individual decisions of the DRs in the ensemble are aggregated into a single scheduling decision. Although a number of combination methods have been used over the years, the two most commonly used are the sum and vote [41]. The sum combination method defines that all priority values calculated by each DR in the ensemble for each decision time are simply summed up. Then, the decision with the best overall priority value is selected and executed. Although it might seem that this method has a serious problem because the DRs in the ensemble can assign different priority values, this has not proven to be a problem in previous studies, and the method has regularly achieved good results. The voting combination method, on the other hand, works in such a way that each DR casts a single vote for the scheduling decision that received the best prioritisation value. These votes are then accumulated, and the scheduling decision with the most votes is then selected and executed. In this combination method, the decision that is considered the best by most DRs in the ensemble is executed. In this study, both the sum and voting combination methods are used to aggregate the decisions of the DRs in the ensemble and investigate how both work with the proposed ensemble construction methods.

Finally, the ensemble construction method is used to select the DRs that will form the ensemble. Over the years, many ensemble construction methods have been proposed [19,20], but they all have a common goal, which is to find those DRs that perform well together. In this study, ensemble construction methods that construct ensembles from previously generated DRs are considered, as several previous studies have shown their efficiency compared to approaches that both develop new DRs and construct ensembles simultaneously [20,43]. The simplest but also one of the most efficient ensemble construction methods is the simple ensemble combination method (SEC) [42]. In this method, a certain number of ensembles are generated from a set of previously developed DRs by randomly selecting the DRs from the set of available DRs. All generated ensembles are evaluated, and the best one is selected. Despite its simplicity, this method has achieved good performance in several studies. However, its main drawback is its high computational complexity, as many (at least several thousand) ensembles need to be evaluated to ensure that good ensembles have been generated. The SEC method is used as a baseline to evaluate the performance of the proposed deterministic heuristic ensemble construction methods.

4. Deterministic Ensemble Construction Methods

This section describes the proposed deterministic ensemble construction methods. All proposed construction heuristics require the same inputs to construct an ensemble of DRs. The first parameter required by the heuristics is the size k of the ensemble to be constructed. Secondly, they require a set of DR candidates R to be used for the construction of the ensemble. Finally, they need the calculated fitness values $f_{r,i}$ of each rule r from R for each instance i of a given problem instance set D. These fitness values are usually available immediately after the generation of the DRs by GP, as they were used to calculate the fitness of the individuals during evolution. Based on these input values, the proposed heuristic methods then construct an ensemble of DRs and return it as a result. The main difference between the proposed methods lies in the strategy used to select the DRs that will form the ensemble. If there is a tie in the selection of different rules, the one with the lower index is selected (the index denotes its position in the set). Of course, other tie-breaking methods could have been used, but for the sake of simplicity, this basic tie-breaking strategy has been used.

4.1. Fitness-Based Ensemble Construction

The first and simplest construction method for ensembles is the fitness-based heuristic (FBH). This heuristic selects the DRs based on the fitness values of the entire data set D. This means that the DR with the best fitness value is selected first, then the DR with the second best fitness value and so on until an ensemble of the desired size is constructed. Since the fitness of the DRs is represented as the total TWT value of the data set, the best rule is the one that achieves the lowest fitness value. The motivation for this heuristic method is that DRs that perform well individually should also perform well in ensembles, i.e., high-quality ensembles should consist of high-quality DRs. The basic features of this heuristic procedure are shown in Algorithm 3. The algorithm first calculates the overall fitness for all DRs and then selects the rules according to their fitness values and adds them to the ensemble until the ensemble of the desired size is created.

Algorithm 3 Outline of the fitness-based heuristic

Input: k—ensemble size, R—set of DRs, $f_{r,i}$—fitness of rule r on instance i in dataset D  Output: E—the constructed ensemble  1: $E=⌀$  2: for rule r in R do  3:     $f_r=0$  4:     for instance i in the dataset D do  5:       $f_r+=f_{r,i}$  6:     end for  7: end for  8: while  $\left|E\right|<k$  do  9:    $r\leftarrow$ DR with the lowest fitness value $f_r$ 10:    $E\leftarrow r$ 11:    $R\leftarrow R\setminus \left\{r\right\}$ 12: end while

4.2. Optimal Count Heuristic

The optimal count heuristic (OCH) specifies that DRs should be included in the ensemble depending on the number of problem instances they solve “optimally”. Of course, there is no guarantee that the DRs will solve an instance optimally. In this context, optimal means that the DR achieves the best result for a problem instance within the given set of DRs, i.e., that the DR under consideration r achieves the smallest TWT value within the set of rules R. On this basis, the number of problem instances that it solves optimally within the rule set is determined for each DR. The DRs are then sorted by this number in descending order (meaning that rules that optimally solve more problem instances are considered better), and then the number of rules corresponding to the ensemble size is selected. The motivation for this construction heuristic is that it is preferable to select rules that achieve the best results for the most problem instances. Algorithm 4 outlines the steps of OCH, where, first, the number of instances that each rule optimally solves is calculated and then the DRs are simply selected based on this metric and added to the ensemble.

Algorithm 4 Outline of the optimal count heuristic

Input: k—ensemble size, R—set of DRs, $f_{r,i}$—fitness of rule r on instance i in dataset D  Output: E—the constructed ensemble  1: $E=⌀$  2: for rule r in R do  3:    $op{t}_r=0$  4:    for instance i in the dataset D do  5:      if $f_{r,i}={min}_s{f}_{s,i}$ then  6:        $op{t}_r+=1$  7:      end if  8:    end for  9: end for 10: while  $\left|E\right|<k$  do 11:    $r\leftarrow$ DR from R with the largest value of $op{t}_r$ 12:    $E\leftarrow r$ 13:    $R\leftarrow R\setminus \left\{r\right\}$ 14: end while

4.3. Optimal Unique Count Heuristic

The optimal unique count heuristic (OUCH) is similar to the OCH with one main difference. Instead of counting the number of instances for each DR that it optimally solves, in this case, the number of unique instances that a rule optimally solves is counted. This means that if two or more DRs optimally solve a single instance, this instance is not counted for any of the rules. However, if an instance is optimally solved by only one rule in the set, it is counted for this rule. The intuition behind this heuristic is that we can assume that the instance is easier to solve if multiple rules optimally solve a single instance. On the other hand, if an instance is optimally solved by a single rule, this may mean that either the instance is more difficult to solve or that the rule has specialised in solving this type of instance. In either case, it would make sense to select this DR and add it to the ensemble. Algorithm 5 outlines the steps of the OUCH selection of the rules for the ensemble, with the only difference to OCH being the part where the number of optimally solved instances is calculated for each DR.

4.4. Remaining Optimal Count Heuristic

The remaining optimal count heuristic (ROCH) is similar to the previous two heuristics but attempts to solve a potential problem that could arise with OCH. Namely, it is possible that there are rules that optimally solve the same set of instances and are, therefore, included in the ensemble only because they optimally solve a large number of instances. However, this could mean that the ensemble consists of rules that have an overlap in the instances that they optimally solve. Therefore, it might be better to select rules that optimally solve more different instances. To avoid this situation, this would mean that when selecting a DR to add to the ensemble, the instances that this rule solves optimally are not taken into account when selecting the next rules for the ensemble. This means that when selecting the next rule for the ensemble, only the instances that are not optimally solved by any rule that has been selected for the ensemble so far are taken into account when counting the number of optimally solved instances. The logic of this heuristic, therefore, consists of selecting those rules that optimally solve instances that are not optimally solved by the rules previously selected in the ensemble. This heuristic, therefore, attempts to select the rules that offer the best coverage of the optimally solved problem instances in the data set. The main features of this method are shown in Algorithm 6, where the calculation of the optimally solved instances must simply be performed each time a new rule is selected, and the instances that have been optimally solved by any rule in the ensemble must be disregarded.

Algorithm 5 Outline of the optimal unique count heuristic

Input: k—ensemble size, R—set of DRs, $f_{r,i}$—fitness of rule r on instance i in dataset D  Output: E—the constructed ensemble  1: $E=⌀$  2: for Rule r in R do  3:    $op{t}_i=0$  4:    for Instance i in the dataset D do  5:      if $f_{r,i}={min}_s{f}_{s,i}$ and rule r uniquely achieves this value then  6:        $op{t}_r+=1$  7:      end if  8:    end for  9: end for 10: while  $\left|E\right|<k$  do 11:    $r\leftarrow$ DR from R with the largest value of $op{t}_r$ 12:    $E\leftarrow r$ 13:    $R\leftarrow R\setminus \left\{r\right\}$ 14: end while

Algorithm 6 Outline of the remaining optimal count heuristic

Input: k—ensemble size, R—set of DRs, $f_{r,i}$—fitness of rule r on instance i in dataset D  Output: E—the constructed ensemble  1: $E=⌀$  2: while  $\left|E\right|<k$  do  3:    for rule r in R do  4:      $op{t}_i=0$  5:      for instance i in the dataset D do  6:        if no rule in E achieves the optimal result for i then  7:          if $f_{r,i}={min}_s{f}_{s,i}$ then  8:            $op{t}_r+=1$  9:          end if 10:        end if 11:      end for 12:    end for 13:    $r\leftarrow$ DR from R with the largest value of $op{t}_r$ 14:    $E\leftarrow r$ 15:    $R\leftarrow R\setminus \left\{r\right\}$ 16: end while

4.5. Fitness Coverage Heuristic

The fitness coverage heuristic (FCH) selects the rules for the ensemble based on their fitness values for the individual instances. This means that when the ensemble is created, a rule is added to the ensemble and the quality of the ensemble is determined by summing the best fitness values obtained by each of the rules in the ensemble for each instance. This means that in this heuristic, the rules are added to the ensemble to achieve the best coverage of the problem set based on the best fitness value for each individual problem instance. Thus, instead of evaluating the ensemble as a whole, only its individual parts (DRs) are considered, and their best performances are aggregated over the entire dataset. This heuristic is, therefore, similar to ROCH, but it uses the fitness values of the problem instances for the selection instead of the number of optimal instances. The logic behind this heuristic is to select the rules that best cover the problem set, i.e., if each rule is applied to the dataset and the minimum values of each rule are selected for each instance, the target value obtained should be the lowest. The steps of FCH are outlined in Algorithm 7, which shows that in each iteration, each of the rules is considered with the current ensemble to determine the rule that gives the lowest overall fitness value when taking the minimum fitness values of the rules in the ensemble for each problem instance. The rule for which this is true is then selected and added to the ensemble.

Algorithm 7 Outline of the fitness coverage heuristic

Input: k—ensemble size, R—set of DRs, $f_{r,i}$—fitness of rule r on instance i in dataset D  Output: E—the constructed ensemble  1: $E=⌀$  2: for instance i in dataset D do  3:    $f{e}_i=\infty$  4: end for  5: while  $\left|E\right|<k$  do  6:    for rule r in R do  7:      $f{t}_r=fe$  8:      for instance i in the dataset D do  9:        if $f{e}_i>f_{r,i}$ then 10:          $f{t}_r=f_{r,i}$ 11:        end if 12:      end for 13:    end for 14:    $r\leftarrow$ DR from R with the smallest value of $f{t}_r$ 15:    $E\leftarrow r$ 16:    $R\leftarrow R\setminus \left\{r\right\}$ 17: end while

4.6. Remaining Fitness Heuristic

The remaining fitness heuristic (RFH) selects the rules in the ensemble according to their fitness for instances that are not optimally solved by the rules that are already in the ensemble. This means that in each iteration of the heuristic, the fitness value of the candidate rules is only calculated based on the rules that are not optimally solved by the rules already selected in the ensemble. Therefore, this heuristic favours the selection of those rules that achieve the best fitness for instances that are not yet optimally solved by the rules in the ensemble. In this way, the heuristic attempts to select rules that achieve the lowest fitness for the remaining instances that are not optimally solved. The steps of this heuristic method are outlined in Algorithm 8, where in each step, the fitness of each rule is calculated only for non-optimally solved instances, and then the rule with the smallest such fitness is selected.

4.7. Weighted Fitness Heuristic

The weighted fitness heuristic (WFH) combines the fitness value and number of optimally solved instances metric. The idea of this heuristic method is that the fitness of each rule for each instance is adjusted by the number of rules that optimally solve that instance. This is achieved in a way that the fitness of the individual problem instances is reduced proportionally by the number of rules that solve that problem instance optimally. This means that the greater the number of rules that solve a problem instance optimally, the lower the fitness score an individual will receive for this instance, i.e., its influence in the selection process of the appropriate DR for the ensemble will be reduced. Therefore, this heuristic will favour the selection of those rules that perform well in instances in which a lower number of other rules performed well. Algorithm 9 outlines the steps of this heuristic construction method, where the fitness of each instance is simply adjusted by the number of rules that optimally solve the considered problem instance.

Algorithm 8 Outline of the remaining fitness heuristic

Input: k—ensemble size, R—set of DRs, $f_{r,i}$—fitness of rule r on instance i in dataset D  Output: E—the constructed ensemble  1: $E=⌀$  2: while  $\left|E\right|<k$  do  3:    for rule r in R do  4:      $f_r=0$  5:      for instance i in the dataset D do  6:        if no rule in E achieves the optimal result for i then  7:          if $f_{r,i}={min}_s{f}_{s,i}$ then  8:            $f_r+=f_{r,i}$  9:          end if 10:        end if 11:      end for 12:    end for 13:    $r\leftarrow$ DR from R with the smallest value of $f_r$ 14:    $E\leftarrow r$ 15:    $R\leftarrow R\setminus \left\{r\right\}$ 16: end while

Algorithm 9 Outline of the weighted fitness heuristic

Input: k—ensemble size, R—set of DRs, $f_{r,i}$—fitness of rule r on instance i in dataset D  Output: E—the constructed ensemble  1: $E=⌀$  2: for Rule r in R do  3:    $op{t}_i=0$  4:    for instance i in the dataset D do  5:      if $f_{r,i}={min}_s{f}_{s,i}$ then  6:        $op{t}_i+=1$  7:      end if  8:    end for  9: end for 10: for Rule r in R do 11:    $f_r=0$ 12:    for instance i in the dataset D do 13:      $f_r+=f_{r,i}/op{t}_i$ 14:    end for 15: end for 16: while  $\left|E\right|<k$  do 17:    $r\leftarrow$ DR from R with the largest value of $op{t}_r$ 18:    $E\leftarrow r$ 19:    $R\leftarrow R\setminus \left\{r\right\}$ 20: end while

4.8. Adjusted Fitness Heuristic

The adjusted fitness heuristic (AFH) can be seen as a simplification of the WFH, where the fitness is not adjusted for each instance individually, but only the overall fitness is adjusted. In this case, the fitness of a rule is divided by the number of instances that this rule has optimally solved. This means that the more instances a rule has optimally solved, the lower its fitness value, which makes the rule more desirable for selection. The rules are then sorted according to the resulting value, and the number of rules corresponding to the ensemble size is selected. In this way, the heuristic attempts to select rules by considering both metrics: the fitness of the individual and the number of instances it optimally solves. The steps of this heuristic are outlined in Algorithm 10, which shows that the fitness value of each instance is simply additionally scaled by the number of optimally solved instances.

Algorithm 10 Outline of the adjusted fitness heuristic

Input: k—ensemble size, R—set of DRs, $f_{r,i}$—fitness of rule r on instance i in dataset D  Output: E—the constructed ensemble  1: $E=⌀$  2: for rule r in R do  3:    $op{t}_r=0$  4:    $f_r=0$  5:    for instance i in the dataset D do  6:      $f_r+=f_{r,i}$  7:      if rule r uniquely achieves the lowest $TWT$ value out of all rules in R then  8:        $op{t}_r+=1$  9:      end if 10:    end for 11: end for 12: while  $\left|E\right|<k$  do 13:    $r\leftarrow$ DR from R with the largest value of $f_r/op{t}_r$ 14:    $E\leftarrow r$ 15:    $R\leftarrow R\setminus \left\{r\right\}$ 16: end while

4.9. Standard Deviation Heuristic

The standard deviation heuristic (SDH) determines the standard deviation of the fitness values obtained by the rules for each problem instance. The rules are then selected using these standard deviation values. This is applied so that the rule that optimally solves the instance with the largest standard deviation is selected first and added to the ensemble. The rule that optimally solves the instance with the second largest deviation is then selected and added to the ensemble. This continues until the required number of rules is selected. If there are several rules that optimally solve a problem instance at a given time, the one with the better overall fitness value is selected. The motivation for this heuristic lies in the fact that a large standard deviation of fitness values for a problem instance means that the DRs for this instance have achieved quite inconsistent results. It would, therefore, be better to select the rules that perform best in these instances, as not selecting such a rule could easily lead to selecting a rule that performs quite poorly in this problem instance. The main features of this heuristic method are shown in Algorithm 11, where, first, the standard deviations for each problem instance are calculated. Then, the rules are selected and added to the ensemble based on these values.

4.10. Optimal Match Based Heuristic

The optimal match-based heuristic (OMBH) is a method similar to ROBH. However, instead of selecting the rules that perform optimally on disjoint sets of instances, this heuristic uses the reverse logic. It selects the rules that have the greatest overlap with the rules already included in the ensemble for the optimally solved instances. The motivation for this heuristic is the attempt to select rules that perform well in similar instances and should, therefore, exhibit similar behaviour. In this way, the rules should mostly be scheduling and, thus, make mostly good scheduling decisions when creating the plan. The steps of the algorithm are outlined in Algorithm 12, wherein the first step, the rule that optimally solves the most problem instances is added to the ensemble. The procedure then selects the rules that have the greatest overlap with the ensemble in the optimally solved instances.

Algorithm 11 Outline of the standard deviation heuristic

Input: k—ensemble size, R—set of DRs, $f_{r,i}$—fitness of rule r on instance i in dataset D  Output: E—the constructed ensemble  1: $E=⌀$  2: for Instance i in the dataset D do  3:    for Rule r in R do  4:      $f_{i,r}=\mathrm{TWT}\mathrm{of}\mathrm{rule}r\mathrm{on}\mathrm{instance}i$  5:      $av{g}_i+=f_{i,r}$  6:    end for  7:    $av{g}_i=av{g}_i/\left|R\right|$  8:    $st{d}_i=0$  9:    for Rule r in R do 10:      $st{d}_i+={(f_{i,r}-av{g}_i)}^2$ 11:    end for 12:    $av{g}_i=st{d}_i/\left|R\right|$ 13: end for 14: $i=1$ 15: while  $\left|E\right|<k$  do 16:    $r\leftarrow$ DR from R which optimally solves the instance with the i-th largest $st{d}_i$ value 17:    $i\leftarrow i+1$ 18:    $E\leftarrow r$ 19:    $R\leftarrow R\setminus \left\{r\right\}$ 20: end while

Algorithm 12 Outline of the optimal match-based heuristic

Input: k—ensemble size, R—set of DRs, $f_{r,i}$—fitness of rule r on instance i in dataset D  Output: E—the constructed ensemble  1: $E=⌀$  2: for rule r in R do  3:    for instance i in the dataset D do  4:      if $f_{r,i}={min}_s{f}_{s,i}$ then  5:        $op{t}_{r,j}=1$  6:      end if  7:    end for  8: end for  9: $r\leftarrow$ DR from R with the largest value of $op{t}_r$ 10: $E\leftarrow r$ 11: $R\leftarrow R\setminus \left\{r\right\}$ 12: while  $\left|E\right|<k$  do 13:    $r\leftarrow$ DR from R with the largest overlap of $op{t}_r$ with those from the rules in E 14:    $E\leftarrow r$ 15:    $R\leftarrow R\setminus \left\{r\right\}$ 16: end while

5. Experimental Analysis

This section provides an overview of the experiments conducted to evaluate the effectiveness of the proposed methods. Firstly, the experimental setup is described, and then, the results of the experiments are outlined and discussed.

5.1. Experimental Setup

For the experimental analysis, a set of 120 problem instances from a previous study was used to evaluate the proposed methods [42]. The set contains instances of different sizes, with the number of jobs ranging from 12 to 100 and the number of machines ranging from 3 to 10. Moreover, the instances were generated with different characteristics regarding the due dates of the jobs, i.e., the set contains both easy and difficult instances. These instances were divided into two disjoint sets, the training set and the test set, each consisting of 60 instances. The training set was used to evolve the DRs and compute their properties (such as their fitness or the number of instances that optimally solve them). The training set was also used by the presented heuristics to create DR ensembles. On the other hand, the test set was used to evaluate the performance of the ensembles generated by the different heuristics to construct ensembles, and all ensemble results presented in this section were obtained with this set.

The set of DRs used for the construction of ensembles comes from an earlier study in which GP was used to develop them [42]. This set consists of 50 DRs, each of which comes from a separate GP run from the best individual, which was selected at the end of evolution. The ensemble construction methods then use this set of DRs to construct ensembles of different sizes, specifically ensembles of sizes 2 to 10. These sizes are considered because previous studies have shown that ensembles of this size already work quite well and that using larger ensembles provides little additional benefit [42,48]. Since all proposed heuristic ensemble construction methods are deterministic, it is sufficient to run them only once, as they will always give the same result. The methods are tested using both the sum and the vote ensemble combination methods. All methods were coded in the C++ programming language using the ECF framework (http://ecf.zemris.fer.hr/, accessed on 4 December 2022) for the purpose of developing DRs with GP. All experiments were performed on a Windows 10 PC with an AMD Ryzen Threadripper 3990X 64-core processor and 128 GB RAM.

In order to evaluate the performance of the ensemble construction methods proposed in this paper, which are described in Algorithms 3–12, their performance is compared with the performance of the individual automatically generated DRs from [58], as well as the ATC rule [59], which is the best manually designed DR for Twt minimisation. In addition, the results are also compared with several other ensemble learning methods from the literature, such as the SEC ensemble construction method previously proposed in [42], BagGP [60], BoostGP [61], and a memetic genetic algorithm (MGA) designed to evolve ensembles [48]. SEC requires an additional parameter that specifies the number of ensembles to be sampled, which was set to 20,000 based on previous experiments. GP, BagGP, and BoostGP use a population size of 1000 individuals, a mutation probability of 0.3, a tournament size of 3 individuals, and 80,000 function evaluations as the termination condition. The MGA uses a population of 1000 individuals, the crossover probability of 0.8, mutation probability of 0.2, and the local search is executed for 5 iterations with a ratio of 0.2 (it is applied on every fifth individual), and it executes for 1000 generations. Since both GP, SEC, BagGP, BoostGP, and MGA are stochastic methods, they were run multiple times (50 in the case of individual DRs and 30 in the case of SEC, BagGP, BoostGP, and MGA), and the results shown in the tables represent the median values obtained over multiple runs. The median values were used because the Shapiro–Wilk normality test showed that the results obtained did not follow the normal distribution. Therefore, we considered it more appropriate to use the median in order to avoid a possible bias (due to too good or too bad solutions) that could arise from using the mean.

5.2. Experimental Results

Table 2. Results obtained by ensemble construction methods using the sum combination method.

	2	3	4	5	6	7	8	9	10
ATC	16.63
DR	16.09
BagGP	16.28	16.11	16.05	16.04	16.05	16.00	16.00	16.02	16.07
BoostGP	15.82	15.76	15.87	15.89	15.89	15.85	15.86	15.86	15.89
MGA	15.66	15.46	15.49	15.48	15.47	15.46	15.45	15.45	15.77
SEC	15.68	15.68	15.65	15.52	15.43	15.29	15.38	15.32	15.34
FBH (3)	16.09	15.53	15.05	15.07	15.13	14.95	14.92	14.91	14.99
OCH (4)	15.55	16.07	15.99	16.01	15.95	15.86	15.91	15.93	16.21
OUCH (5)	15.70	15.65	15.38	16.48	16.82	16.17	16.86	16.89	15.79
ROCH (6)	15.27	15.15	15.12	15.10	15.28	15.31	14.90	15.38	15.90
FCH (7)	15.55	15.16	15.27	15.11	15.40	15.48	15.45	15.60	15.59
RFH (8)	15.55	15.52	15.91	15.31	15.29	15.32	15.29	15.45	15.88
WFH (9)	16.09	14.94	15.12	14.94	15.01	15.01	15.02	15.02	15.02
AFH (10)	15.27	15.32	15.48	15.45	15.31	15.44	15.43	15.47	15.38
SDH (11)	15.46	15.73	15.48	15.84	15.57	15.66	15.66	15.66	15.67
OMBH (12)	15.95	15.38	16.00	15.60	15.67	15.68	15.68	15.68	15.70

shows the results of the ensembles obtained using the sum combination method. At the top of the table, the results for other existing DRs or ensemble learning methods are outlined. This is followed by the results for each of the proposed deterministic heuristic methods, with the reference to the algorithm describing the methods given in the parenthesis next to its name. Each row represents the results of ensembles created using one of the proposed ensemble construction methods, while the columns represent the size of the ensembles created using the respective methods. Each entry in the table gives the value of the minimised optimisation criterion, which in this case is the total weighted tardiness that was obtained by the ensemble constructed using a particular ensemble construction method for the given ensemble size. For each ensemble size, the best result is denoted in bold. In addition, the cases where a heuristic ensemble construction method performed better than any of the outlined existing methods are underlined. First of all, the results show that almost all ensembles created with the proposed heuristic methods perform better on average than the individual DRs, be it automatically designed or the manually designed ATC rule. The only exceptions are the ensembles created with the OUCH heuristic, which performs quite poorly for larger ensemble sizes. In other cases, the performance of the ensembles was even up to 7% better compared to the individual DRs. This result shows that the proposed heuristic ensemble construction methods are valid, as they can construct ensembles that perform better than the individual rules from which they were developed.

If we compare the results of the heuristics with those of the existing methods, we see that the heuristics were able to obtain better ensembles in around 40% of cases. This is especially true for smaller ensemble sizes, where most methods produced better ensembles than those constructed by existing methods. However, as the ensemble size increases, the SEC method generally performed the best. Nevertheless, it is interesting to observe that for each ensemble size, one of the proposed constructive heuristics always achieved the best result for a given ensemble size. The best result obtained by the heuristic ensemble construction methods outperformed the ensembles of the SEC method by about 2.5%.

Table 3. Results obtained by ensemble construction methods using the vote combination method.

	2	3	4	5	6	7	8	9	10
ATC	16.63
DRs	16.09
BagGP	16.38	15.81	15.82	15.70	15.68	15.58	15.65	15.58	15.57
BoostGP	16.02	15.72	15.67	15.50	15.64	15.56	15.68	15.53	15.55
MGA	15.59	15.54	15.79	15.51	15.53	15.51	15.59	15.50	15.50
SEC	15.76	15.60	15.67	15.67	15.64	15.55	15.57	15.52	15.55
FBH (3)	15.73	15.80	15.80	15.87	15.80	15.66	15.51	15.74	15.52
OCH (4)	15.43	15.71	15.52	15.74	15.71	15.60	15.65	15.46	15.50
OUCH (5)	15.73	15.61	15.64	15.20	15.21	15.11	15.27	15.67	15.69
ROCH (6)	16.17	15.46	15.49	15.29	15.34	15.32	15.50	15.49	15.58
FCH (7)	15.62	15.73	15.56	15.24	15.08	15.89	15.42	15.77	15.45
RFH (8)	15.62	15.53	15.24	15.67	15.71	15.59	15.56	15.31	15.58
WFH (9)	15.73	15.52	15.29	15.33	15.57	16.03	15.26	15.94	16.23
AFH (10)	16.17	15.64	15.54	15.39	15.53	15.59	15.40	15.75	15.61
SDH (11)	16.65	16.14	16.04	15.75	15.81	15.96	15.98	15.87	15.90
OMBH (12)	16.01	15.88	16.10	15.77	16.44	15.62	16.02	15.52	15.95

shows the results of the ensembles obtained with the vote method. The structure of the table is the same as in the case of Table 2. In this case, it can also be seen that most of the constructed ensembles perform better on average than the individual DRs. However, some construction methods have again constructed ensembles with poor performance, such as OMBH and SDH, which in a few cases have not produced ensembles that perform better than the individual DRs and, in one case, even perform worse than the manually designed ATC rule. Nonetheless, other heuristics for constructing ensembles consistently perform better compared to single rules for all ensemble sizes tested. The best ensemble constructed using the heuristic construction methods achieved an improvement of 6.3% over the individual DRs.

If we compare the results between the ensembles created with the heuristic ensemble construction methods and existing ensemble construction methods, we see that the heuristic methods perform better in more than one-third of the cases. This time, the methods seem to perform better when ensembles of medium size are constructed, while the performance seems to decrease again for the largest sizes. The best ensemble created with the heuristic methods outperforms the MGA method by about 2.8%. This shows that the heuristic ensemble construction methods also perform quite well with the vote combination method.

For both ensemble construction methods, it was found that the performance of the methods was not as good for larger ensemble sizes, suggesting that these methods have more problems when more DRs are selected. However, this is to be expected since the rules are never evaluated collectively but are only selected based on their individual properties. While this may be feasible for smaller ensembles, it is more difficult to expect a larger set of DRs to perform well collectively if they are only selected based on their individual properties. Therefore, the proposed methods seem to be more suitable for creating ensembles of smaller sizes.

When comparing the performance of the ensembles with respect to the ensemble combination method used for evaluation, we found that the ensembles performed better in two-thirds of the experiments when the sum combination method was used. Furthermore, all heuristic ensemble construction methods, with the exception of OCH and OUCH, mostly performed better when the sum combination method was used. OCH and OUCH were the only methods where better results were obtained in most cases with the vote combination method. Moreover, it was possible to obtain ensembles with a better overall fitness, i.e., a smaller TWT value, with the sum combination. From these observations, we can conclude that the sum combination method is a better choice for combining the decisions of the individual rules in the ensembles constructed by the proposed heuristics.

To obtain a better impression of the performance of the proposed methods,

Table 4. Ranking of the deterministic ensemble construction methods.

	Sum			Vote			Both
	#	Avg. Rank	Tot. Rank	#	Avg. Rank	Tot. Rank	Avg. Rank	Tot. Rank
FBH (3)	7	2.89	2	1	6.67	8	4.78	6
OCH (4)	1	8.67	10	4	4.56	5	6.61	8
OUCH (5)	1	8.56	9	5	3.67	2	6.11	7
ROCH (6)	6	3	3	7	3.55	1	3.28	1
FCH (7)	5	4.78	5	5	4.33	4	4.56	4
RFH (8)	4	5.22	6	4	3.67	2	4.44	3
WFH (9)	8	2.56	1	4	5.33	7	3.94	2
AFH (10)	5	4.44	4	4	5.11	6	4.78	5
SDH ¨(11)	2	6.56	7	0	9	10	7.78	9
OMBH (12)	1	7.56	8	0	8.22	9	7.89	10

shows the ranking of all heuristics for the two ensemble construction methods considered. The column “#” indicates how often each heuristic performed better than any of the existing methods, ‘Avg. rank’ indicates the average rank of the heuristic construction method over the tested ensemble sizes (lower is better), and ‘Tot. rank’ indicates the overall rank of the method calculated based on the average rank. These properties are described separately for the sum and vote combination as well as for the combination of both methods.

The table shows that the WFH, FBH, and ROCH methods achieve the best results with the sum combination method. The first two, in particular, perform quite well, as they achieve better results than any existing method for eight and seven of the nine ensemble sizes tested, respectively. All three methods perform quite well across all ensemble sizes, with WFH and FBH performing poorly only on the smallest ensemble sizes, while ROCH performs well on the smaller ensemble sizes but not as well as on the largest ensemble size (10). In general, it seems that better results are obtained with methods that construct the ensemble based on the fitness of the DRs.

For the voting method of combining voices, we see a completely different behaviour. In this case, the ROCH method achieves the best performance, closely followed by the RFH and OCH methods. The FBH method, on the other hand, which performed excellently in the sum combination, now performs quite poorly and only ranks eighth. Unlike the sum combination method, in this case, the methods that form the ensemble based on the number of optimally solved instances appear to achieve better results, as both ROCH and OCH base their decision on this metric.

When looking at both combination methods, ROCH seems to be the most robust heuristic, as it performed very well in both cases. The second best heuristic would be WFH, which achieved the best results with the summation method, but only came seventh with the vote combination method. Similarly, RFH performed quite well with the vote combination method but was again inferior with the sum combination. These observations show that ROCH seems to be the only viable choice for creating ensembles that perform well with both ensemble combination methods, while the other heuristics perform well with only one combination method or poorly with both.

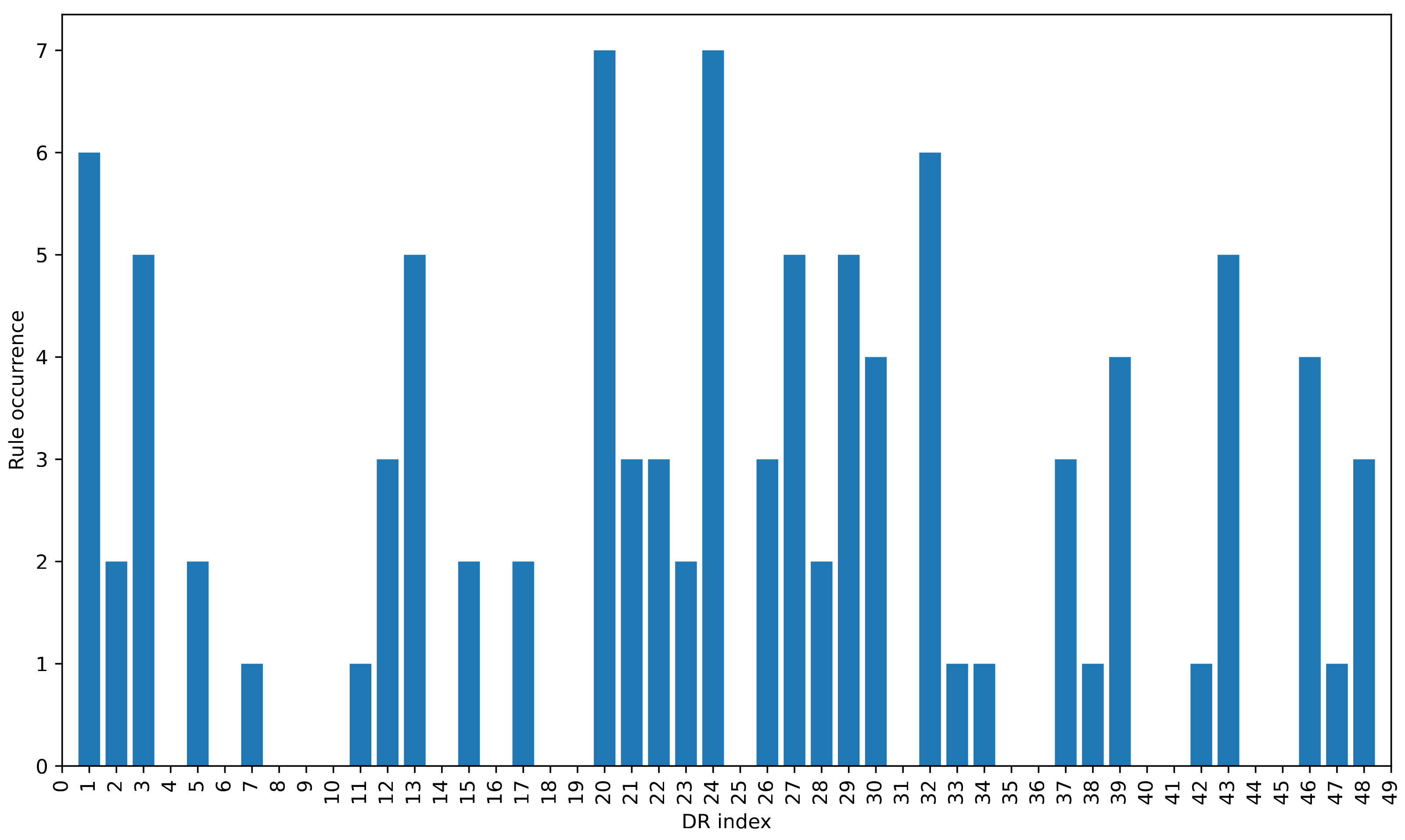
The frequency of selection of the individual DRs when creating ensembles of size 10 by the heuristic methods is shown in Figure 2. The figure shows that certain DRs are selected more frequently than others, which is to be expected since all construction methods use quite similar strategies to select DRs. The fact that some rules are selected more frequently than others seems to indicate that they are favoured by different heuristic selection methods, regardless of the different strategies used to select them. This suggests that there is some overlap between the features, meaning that a rule is considered good based on different features.

Table 5. Characteristics of the eight DRs most commonly selected by the ensemble construction methods.

DR Index	Fitness	# Optimal	# Unique Optimal
1	14.494	37	1
3	14.3753	36	1
13	14.6812	37	0
20	14.297	37	3
24	14.3575	35	1
27	14.5239	38	0
29	14.7101	37	1
32	14.6285	37	1
43	14.43 7	35	1
Average	14.5969	35.14	0.32

outlines the properties of the DRs that are most frequently selected by the proposed heuristic for ensemble formation. The table shows the fitness of each DR, the number of instances that solve it optimally, and the number of instances that solve it uniquely optimally. In addition, the table also shows the average values of all DRs for all three characteristics. The table shows that half of the rules have a better performance than the average of all rules, but half of these rules have a worse performance. Most of the selected rules have an above-average number of uniquely solved instances, which shows that this feature does not have to correlate with the fitness of the rules. However, most of the rules that are selected most frequently solve at least one problem instance uniquely.

An important aspect that has not yet been mentioned is the time required to create the ensembles since the existing ensemble learning methods usually require a substantially larger execution time. For example, the SEC approach works by examining a number of ensembles and selecting the one with the best performance. Of course, the performance of the method depends on the number of ensembles sampled and usually improves with a greater number of sampled ensembles. For example, if 20,000 ensembles (as in the experiments in this paper) of size 3 are sampled, the method requires about 40 min to perform SEC. On the other hand, all the proposed heuristic ensemble construction methods require only 0.1 milliseconds to construct the ensemble. Given that the ensembles constructed using these heuristics have shown competitive results, these simple heuristic ensemble construction methods are a viable alternative to the more computationally intensive methods.

6. Conclusions

Ensemble learning in the context of DRs has become an increasingly investigated topic over the last several years. As such, there is a growing need to improve the results obtained by ensemble methods further and improve their applicability. This study proposes ten novel ensemble construction heuristics that construct ensembles without the need to evaluate their fitness. Unlike the current methods that are used to construct ensembles, these heuristics construct ensembles by solely using characteristics of the DRs that are selected for the ensemble. The experimental results demonstrate that several of the proposed heuristic ensemble construction methods can construct ensembles that perform equally well or even better than ensembles constructed by a more complex and computationally expensive method. This represents a significant result as it demonstrates that it is possible to use very simple heuristic methods that can construct highly efficient ensembles in time that can be considered negligible when compared to the more complex methods.

The results obtained in this study open up several possible future research directions. One possibility is to try to define more complex rules according to which DRs should be selected for the ensemble, which should possibly lead to the construction of even better ensembles. The second possibility is to extend the SEC method with heuristic rules to improve its performance. This could be achieved either by using them to adjust the probability of selecting rules or by combining both methods so that part of the ensemble is created by randomly selecting DRs and the other part with a heuristic rule. Another line of research would be to apply GP itself to develop the heuristic rule according to which the DRs should be selected to form the ensemble.