Estimation of Entropy for Generalized Rayleigh Distribution under Progressively Type-II Censored Samples
Abstract
1. Introduction
2. Preliminary Knowledge
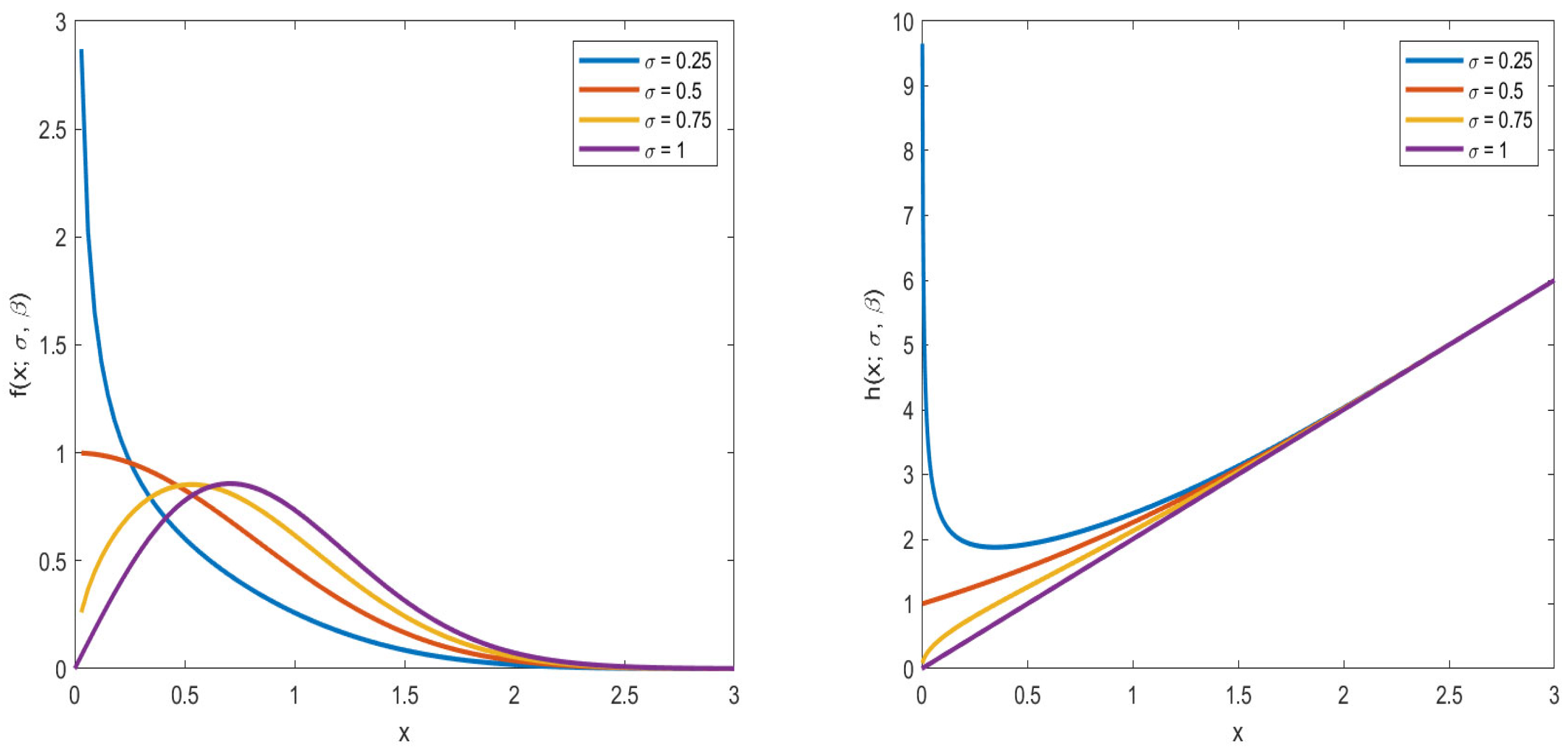
2.1. Shannon Entropy of
2.2. Maximum Likelihood Estimation
- (i)
- Determine the LF and take the logarithm to obtain the log-LF.
- (ii)
- Calculate the first derivative and the second derivative of the log-LF.
- (iii)
- Initialize parameter values, usually using sample mean or other empirical values as initial values.
- (iv)
- Calculate the first and second derivatives using the current parameter values.
- (v)
- Update the parameter values using Newton’s iterative formula:where represents the new parameter values and represents the initial parameter values.
- (vi)
- Repeat steps (iv) and (v) until the parameter values converge or reach the preset number of iterations.
- (vii)
- The final parameter values obtained are the ML estimates.
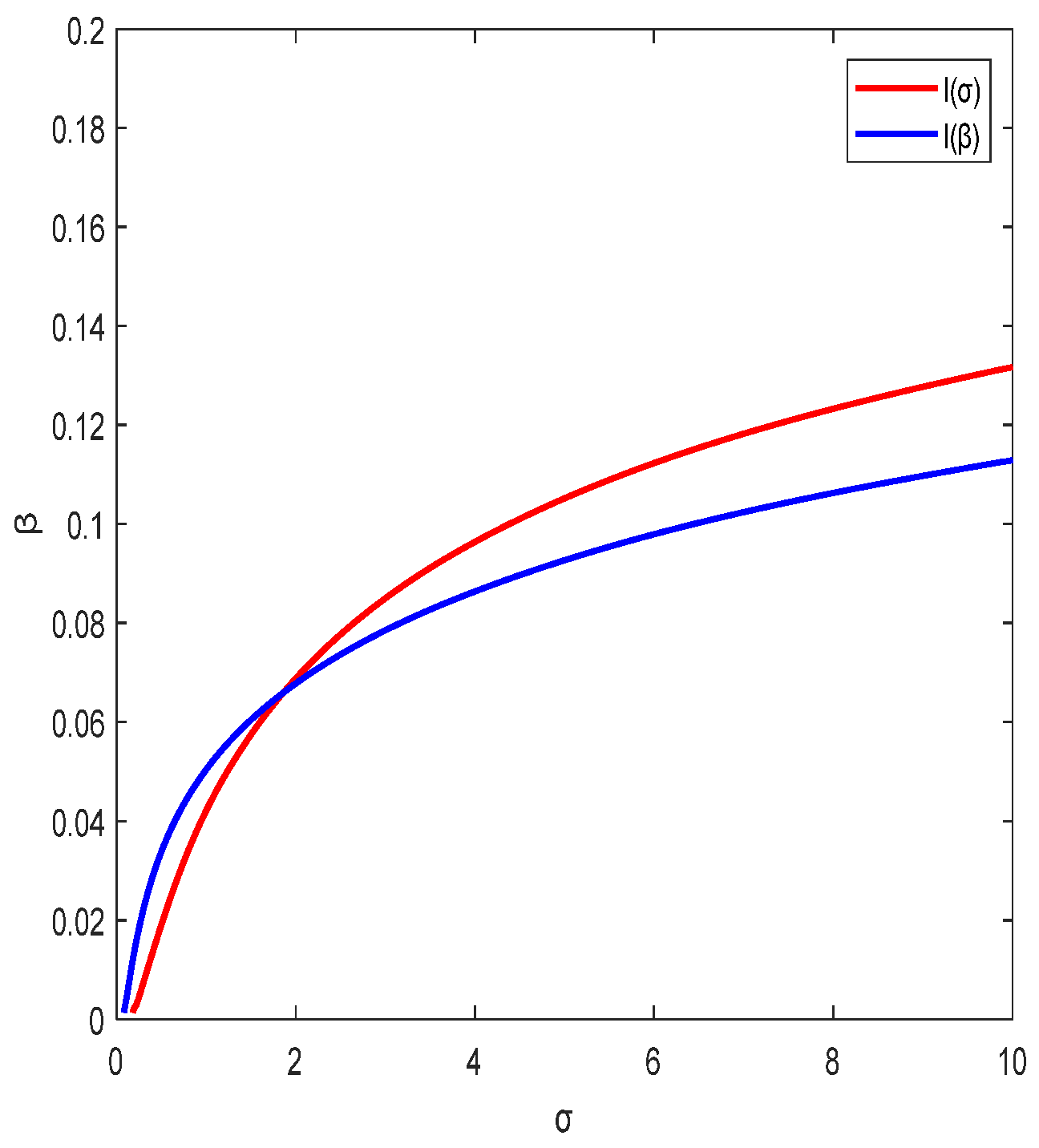
2.3. Asymptotic Confidence Interval of Shannon Entropy
3. Bayes Estimation
3.1. Prior and Posterior Distributions
- (i)
- WSELF [31]:
- (ii)
- PLF [32]:
- (iii)
- KLF [33]:
3.2. Lindley’s Approximation
- (i)
- BE under WSELF.
- (ii)
- BE under PLF.
- (iii)
- BE under KLF.
3.3. MCMC Method for Mixed Gibbs Sampling
- (1)
- Using the M-H algorithm to extract samples from .
- (i)
- Extract samples from . When , resample. Next, calculate the acceptance probability:
- (ii)
- Extract sample from uniformly distributed , set
- (iii)
- Let k = k + 1, and return to step (i).
- (2)
- Using the M-H algorithm to extract samples from .
- (i)
- Extract samples from . When , resample. Next, calculate the acceptance probability:
- (ii)
- Extract sample from uniformly distributed , and set
- (iii)
- Let k = k + 1, and return to step (i).
4. Monte Carlo Simulation
- (1)
- First, set the PC-II schemes (See Table 1).
- (2)
- According to the set PC-II scheme, the PC-II data can be obtained through the following algorithm (Algorithm 1):
| Algorithm 1. Generating PC-II data under |
| 1. Generate observations that follow a (0,1) uniform distribution. . . 4. Given the initial parameters , set ; then, is the asymptotic Type-II censored data. 5. Calculate the ML estimates of using Equations (8) and (9), and calculate the ML estimates of entropy and ACI using Equation (12). 6. Set the superparameters . For different loss functions, use Lindley’s approximation method to calculate the exact value of the entropy of Equations (14)–(16) 7. Repeat steps 1 to 6 a total of 1000 times, and calculate the ML estimates, MSE, coverage probability (CV), and variance; the calculation results are shown in the table below. |
- (1)
- For Shannon entropy, Bayesian estimation performs better overall than ML estimation.
- (2)
- In Bayesian estimation, the overall performance of the MCMC method is superior to Lindley’s approximation method.
- (3)
- When the number of observed faults is fixed, MSE shows an upward trend as the sample size increases; when the sample size is fixed, MSE shows a decreasing trend as the number of observed faults increases.
- (4)
- In Lindley’s approximation, the Bayesian estimate under PLF is superior to the other two loss functions; in MCMC sampling, the performance of Bayesian estimates under WSELF and KLF is similar, both of which are better than those under PLF.
- (5)
- As shown in Table 3, the coverage probability at that time tended to be more at a confidence level.
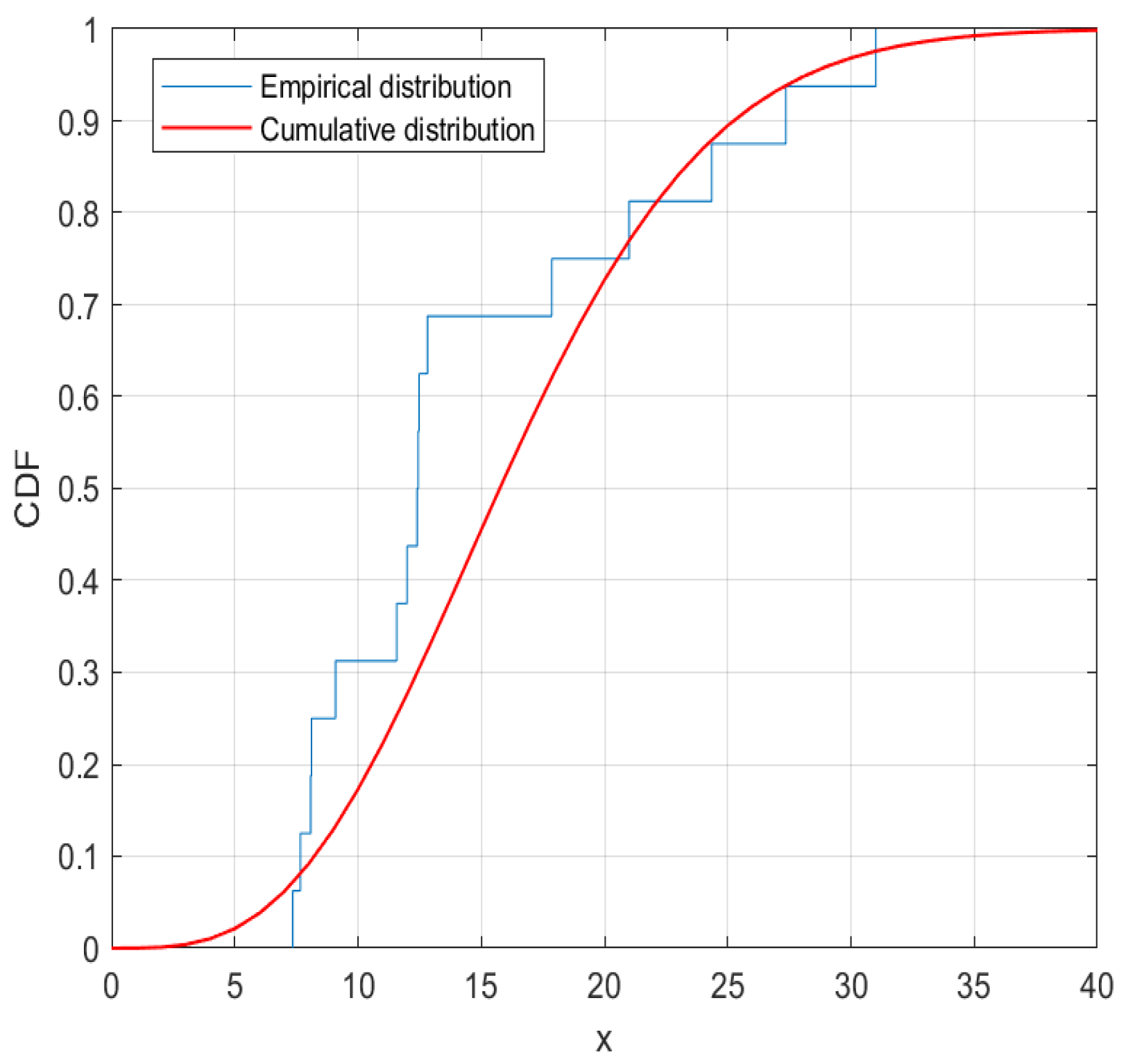
5. Real Data Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kundu, D.; Raqab, M.Z. Generalized Rayleigh distribution: Different methods of estimations. Comput. Stat. Data Anal. 2005, 49, 187–200. [Google Scholar] [CrossRef]
- Surles, J.G.; Padgett, W.J. Inference for reliability and stress-strength for a scaled Burr Type X distribution. Lifetime Data Anal. 2001, 7, 187–200. [Google Scholar] [CrossRef]
- Yan, W.A.; Li, P.; Yu, Y.X. Statistical inference for the reliability of Burr-XII distribution under improved adaptive Type-II progressive censoring. Appl. Math. Model. 2021, 95, 38–52. [Google Scholar] [CrossRef]
- Jamal, F.; Chesneau, C.; Nasir, M.A.; Saboor, A.; Altun, E.; Khan, M.A. On a modified Burr XII distribution having flexible hazard rate shapes. Math. Slovaca 2020, 70, 193–212. [Google Scholar] [CrossRef]
- Chang, H.; Ding, J.J.; Wu, L.N. Performance of EBPSK demodulator in AWGN channel. J. Southeast Univ. Natural Sci. 2012, 42, 14–19. [Google Scholar]
- Fu, R.L.; Ma, Y.X.; Dong, G.H. Researches on statistical properties of freak waves in uni-directional random waves in deep water. Acta Oceanologica Sin. 2021, 43, 81–89. [Google Scholar]
- Feng, Y.; Song, S.; Xu, C.Q. Two-parameter generalized Rayleigh distribution. Math. Appl. 2022, 35, 128–136. [Google Scholar]
- Çolak, A.B.; Sindhu, T.N.; Lone, S.A.; Shafiq, A.; Abushal, T.A. Reliability study of generalized Rayleigh distribution based on inverse power law using artificial neural network with Bayesian regularization. Tribol. Int. 2023, 185, 108544. [Google Scholar] [CrossRef]
- Shen, B.L.; Chen, W.X.; Wang, S.; Chen, M. Fisher information for generalized Rayleigh distribution in ranked set sampling design with application to parameter estimation. Appl. Math. Ser. B 2022, 37, 615–630. [Google Scholar] [CrossRef]
- Shen, Z.J.; Alrumayh, A.; Ahmad, Z.; Abu-Shanab, R.; Al-Mutairi, M.; Aldallal, R. A new generalized rayleigh distribution with analysis to big data of an online community. Alex. Eng. J. 2022, 61, 11523–11535. [Google Scholar] [CrossRef]
- Rabie, A.; Hussam, E.; Muse, A.H.; Aldallal, R.A.; Alharthi, A.S.; Aljohani, H.M. Estimations in a constant-stress partially accelerated life test for generalized Rayleigh distribution under Type-II hybrid censoring scheme. J. Math.-UK 2022, 2022, 6307435. [Google Scholar] [CrossRef]
- Raqab, M.Z.; Kundu, D. Burr Type X distribution: Revisited. J. Probab. Stat. Sci. 2006, 4, 179–193. [Google Scholar]
- Xu, R.; Gui, W.H. Entropy estimation of inverse Weibull distribution under Adaptive Type-II progressive hybrid censoring schemes. Symmetry 2019, 11, 1463. [Google Scholar]
- Chacko, M.; Asha, P.S. Estimation of entropy for generalized exponential distribution based on record values. J. Indian Soc. Prob. St. 2018, 19, 79–96. [Google Scholar] [CrossRef]
- Shrahili, M.; El-Saeed, A.R.; Hassan, A.S.; Elbatal, I.; Elgarhy, M. Estimation of entropy for Log-Logistic distribution under progressive Type-II censoring. J. Nanomater. 2022, 2022, 2739606. [Google Scholar] [CrossRef]
- Wang, X.J.; Gui, W.H. Bayesian estimation of entropy for Burr type XII distribution under progressive Type-II censored data. Mathematics 2021, 9, 313. [Google Scholar] [CrossRef]
- Al-Babtain, A.A.; Elbatal, I.; Chesneau, C.; Elgarhy, M. Estimation of different types of entropies for the Kumaraswamy distribution. PLoS ONE 2021, 16, e0249027. [Google Scholar] [CrossRef] [PubMed]
- Bantan, R.A.R.; Elgarhy, M.; Chesneau, C.; Jamal, F. Estimation of entropy for inverse Lomax distribution under multiple censored data. Entropy 2020, 22, 601. [Google Scholar] [CrossRef]
- Shi, X.L.; Shi, Y.M.; Zhou, K. Estimation for entropy and parameters of generalized Bilal distribution under adaptive Type-II progressive hybrid censoring scheme. Entropy 2021, 23, 206. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.H.; Gui, W.H. Estimating the entropy for Lomax distribution based on generalized progressively hybrid censoring. Symmetry 2019, 11, 1219. [Google Scholar] [CrossRef]
- Zhou, X.D.; Qi, X.R.; Yue, R.X. Statistical analysis for Type-II progressive interval censored data based on Weibull survival regression models. J. Syst. Sci. Math. Sci. Chin. Ser. 2023, 43, 1346–1361. [Google Scholar]
- Almarashi, A.; Abd-Elmougod, G. Accelerated competing risks model from Gompertz lifetime distributions with Type-II censoring scheme. Therm. Sci. 2020, 24, 165–175. [Google Scholar] [CrossRef]
- Ramadan, D.A. Assessing the lifetime performance index of weighted Lomax distribution based on progressive Type-II censoring scheme for bladder cancer. Int. J. Biomath. 2022, 14, 2150018. [Google Scholar] [CrossRef]
- Hashem, A.F.; Alyami, S.A. Inference on a new lifetime distribution under progressive Type-II censoring for a parallel-series structure. Complexity 2021, 2021, 6684918. [Google Scholar] [CrossRef]
- Luo, C.L.; Shen, L.J.; Xu, A.C. Modelling and estimation of system reliability under dynamic operating environments and lifetime ordering constraints. Reliab. Eng. Syst. Saf. 2022, 218, 108136. [Google Scholar] [CrossRef]
- Ren, J.; Gui, W. Statistical analysis of adaptive Type-II progressively censored competing risks for Weibull models. Appl. Math. Model. 2021, 98, 323–342. [Google Scholar] [CrossRef]
- Zhou, S.R.; Xu, A.C.; Tang, Y.C.; Shen, L.J. Fast Bayesian inference of reparameterized Gamma process with random effects. IEEE Trans. Reliab. 2023, 1–14. [Google Scholar] [CrossRef]
- Zhuang, L.L.; Xu, A.C.; Wang, X.L. A prognostic driven predictive maintenance framework based on Bayesian deep learning. Reliab. Eng. Syst. Saf. 2023, 234, 109181. [Google Scholar] [CrossRef]
- Wang, X.; Song, L. Bayesian estimation of Pareto distribution parameter under entropy loss based on fixed time censoring data. J. Liaoning Tech. Univ. (Nat. Sci. Edit.) 2013, 32, 245–248. [Google Scholar]
- Renjini, K.R.; Abdul-Sathar, E.I.; Rajesh, G. A study of the effect of loss functions on the Bayes estimates of dynamic cumulative residual entropy for Pareto distribution under upper record values. J. Stat. Comput. Simul. 2016, 86, 324–339. [Google Scholar] [CrossRef]
- Han, M. E-Bayesian estimations of parameter and its evaluation standard: E-MSE (expected mean square error) under different loss functions. Commun Stat.-Simul. Comput. 2021, 50, 1971–1988. [Google Scholar] [CrossRef]
- Rasheed, H.A.; Abd, M.N. Bayesian Estimation for two parameters of exponential distribution under different loss functions. Ibn Al-Haitham J. Pure Appl. Sci. 2023, 36, 289–300. [Google Scholar] [CrossRef]
- Hassan, A.S.; Elsherpieny, E.A.; Mohamed, R.E. Classical and Bayesian estimation of entropy for Pareto distribution in presence of outliers with application. Sankhya A 2022, 85, 707–740. [Google Scholar] [CrossRef]
- Kohansal, A. On estimation of reliability in a multicomponent stress-strength model for a Kumaraswamy distribution based on progressively censored sample. Stat. Pap. 2019, 60, 2185–2224. [Google Scholar] [CrossRef]
- Luengo, D.; Martino, L.; Bugallo, M.; Elvira, V.; Särkkä, S. A survey of Monte Carlo methods for parameter estimation. Eurasip J. Adv. Signal Process. 2020, 2020, 101186. [Google Scholar] [CrossRef]
- Das, A.; Debnath, N. Sampling-based techniques for finite element model updating in bayesian framework using commercial software. Lect. Notes Civ. Eng. 2021, 81, 363–379. [Google Scholar]
- Karunarasan, D.; Sooriyarachchi, R.; Pinto, V. A comparison of Bayesian Markov chain Monte Carlo methods in a multilevel scenario. Commun. Stat.-Simul. Comput. 2021, 81, 1–17. [Google Scholar] [CrossRef]
- Raqab Mohammad, Z. Discriminating between the generalized Rayleigh and Weibull distributions. J. Appl. Stat. 2013, 40, 1480–1493. [Google Scholar] [CrossRef]
| Scheme | |
|---|---|
| a | |
| b | |
| c |
| MLE | Lindley | MCMC | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 30 | 10 | a b c | 0.4103 (0.0951) 0.4354 (0.0721) 0.4868 (0.0503) | 0.3930 (0.0977) 0.4144 (0.0753) 0.4599 (0.0548) | 0.4568 (0.0665) 0.4698 (0.0514) 0.5141 (0.0296) | 0.3173 (0.1125) 0.3252 (0.0923) 0.3651 (0.0799) | 0.7545 (0.0498) 0.6278 (0.0052) 0.7792 (0.0500) | 0.8294 (0.0749) 0.7333 (0.0315) 0.8092 (0.0643) | 0.7788 (0.0749) 0.6621 (0.0113) 0.7891 (0.0544) |
| 15 | a b c | 0.4825 (0.0466) 0.4876 (0.0414) 0.5043 (0.0325) | 0.4688 (0.0490) 0.4726 (0.0439) 0.4852 (0.0350) | 0.4999 (0.0419) 0.5054 (0.0380) 0.5205 (0.0292) | 0.3603 (0.0804) 0.3640 (0.0744) 0.3729 (0.0635) | 0.6821 (0.0160) 0.6216 (0.0043) 0.6807 (0.0156) | 0.7243 (0.0284) 0.6441 (0.0078) 0.7122 (0.0245) | 0.6961 (0.0197) 0.6291 (0.0054) 0.6914 (0.0184) | |
| 20 | a b c | 0.5044 (0.0290) 0.5100 (0.0313) 0.5083 (0.0243) | 0.4926 (0.0305) 0.4987 (0.0327) 0.4946 (0.0256) | 0.5159 (0.0278) 0.5214 (0.0298) 0.5207 (0.0234) | 0.3739 (0.0609) 0.3783 (0.0623) 0.3737 (0.0545) | 0.6649 (0.0119) 0.5896 (0.0011) 0.5670 (0.0002) | 0.6827 (0.0161) 0.6142 (0.0034) 0.6121 (0.0032) | 0.6708 (0.0132) 0.5976 (0.0018) 0.5841 (0.0008) | |
| 40 | 10 | a b c | 0.4130 (0.1044) 0.4483 (0.0722) 0.4870 (0.0452) | 0.3955 (0.1702) 0.4267 (0.0751) 0.4590 (0.0495) | 0.4631 (0.0757) 0.4866 (0.0533) 0.5121 (0.0330) | 0.3289 (0.1196) 0.3413 (0.0971) 0.3614 (0.0739) | 0.6840 (0.0165) 0.7307 (0.0306) 0.6416 (0.0074) | 0.7163 (0.0258) 0.7932 (0.0564) 0.6936 (0.0190) | 0.6949 (0.0194) 0.7524 (0.0387) 0.6593 (0.0107) |
| 15 | a b c | 0.4702 (0.0565) 0.4842 (0.0413) 0.5060 (0.0328) | 0.4574 (0.0583) 0.4693 (0.0435) 0.4873 (0.0351) | 0.4910 (0.0495) 0.5015 (0.0376) 0.5223 (0.0303) | 0.3533 (0.0881) 0.3597 (0.0743) 0.3731 (0.0633) | 0.6292 (0.0054) 0.6748 (0.0142) 0.5874 (0.0010) | 0.6587 (0.0106) 0.6919 (0.0186) 0.6208 (0.0042) | 0.6391 (0.0069) 0.6807 (0.0156) 0.5984 (0.0018) | |
| 20 | a b c | 0.4934 (0.0332) 0.5077 (0.0313) 0.5201 (0.0249) | 0.4829 (0.0346) 0.4964 (0.0330) 0.5066 (0.0264) | 0.5049 (0.0315) 0.5193 (0.0299) 0.5324 (0.0234) | 0.3645 (0.0658) 0.3759 (0.0662) 0.3861 (0.0557) | 0.6097 (0.0030) 0.6580 (0.0105) 0.5681 (0.0002) | 0.6329 (0.0060) 0.6880 (0.0175) 0.5948 (0.0015) | 0.6174 (0.0038) 0.6680 (0.0126) 0.5772 (0.0005) | |
| 50 | 15 | a b c | 0.4728 (0.0611) 0.4860 (0.0470) 0.5160 (0.0257) | 0.4610 (0.0630) 0.4709 (0.0494) 0.4975 (0.0277) | 0.4926 (0.0542) 0.5042 (0.0403) 0.5319 (0.0241) | 0.3562 (0.0931) 0.3629 (0.0782) 0.3840 (0.0565) | 0.6316 (0.0058) 0.6450 (0.0080) 0.6145 (0.0035) | 0.6636 (0.0116) 0.6739 (0.0140) 0.6757 (0.0144) | 0.6422 (0.0075) 0.6543 (0.0097) 0.6341 (0.0061) |
| 20 | a b c | 0.4929 (0.0391) 0.5058 (0.0316) 0.5205 (0.0217) | 0.4832 (0.0403) 0.4946 (0.0330) 0.5069 (0.0232) | 0.5056 (0.0372) 0.5176 (0.0296) 0.5329 (0.0200) | 0.3687 (0.0707) 0.3752 (0.0634) 0.3865 (0.0515) | 0.6039 (0.0023) 0.6432 (0.0077) 0.6048 (0.0024) | 0.6260 (0.0049) 0.6528 (0.0094) 0.6559 (0.0100) | 0.6112 (0.0031) 0.6465 (0.0082) 0.6215 (0.0043) | |
| 30 | a b c | 0.5222 (0.0209) 0.5236 (0.0175) 0.5265 (0.0168) | 0.5147 (0.0216) 0.5162 (0.0180) 0.5174 (0.0176) | 0.5294 (0.0203) 0.5310 (0.0172) 0.5346 (0.0164) | 0.3884 (0.0527) 0.3876 (0.0456) 0.3891 (0.0464) | 0.5792 (0.0006) 0.5778 (0.0005) 0.5769 (0.0004) | 0.5921 (0.0013) 0.5910 (0.0012) 0.5909 (0.0011) | 0.5836 (0.0008) 0.5822 (0.0007) 0.5816 (0.0006) | |
| 30 | 10 | a b c | 0.7480 0.8240 0.9110 | 0.7160 0.7480 0.8750 | 0.0219 0.0095 0.0149 |
| 15 | a b c | 0.8110 0.8560 0.9170 | 0.7650 0.7950 0.8590 | 0.0063 0.0076 0.0135 | |
| 20 | a b c | 0.8570 0.8880 0.8940 | 0.7960 0.8090 0.8740 | 0.0064 0.0069 0.0089 | |
| 40 | 10 | a b c | 0.7290 0.8220 0.9230 | 0.6970 0.7510 0.8820 | 0.0090 0.0219 0.0112 |
| 15 | a b c | 0.7930 0.8420 0.9100 | 0.7240 0.7700 0.8770 | 0.0069 0.0087 0.0171 | |
| 20 | a b c | 0.8390 0.8310 0.9190 | 0.7690 0.8270 0.8780 | 0.0044 0.0037 0.0070 | |
| 50 | 15 | a b c | 0.7620 0.8510 0.9410 | 0.7160 0.8020 0.8880 | 0.0030 0.0107 0.0099 |
| 20 | a b c | 0.8060 0.8590 0.9200 | 0.7530 0.8120 0.8950 | 0.0040 0.0055 0.0061 | |
| 30 | a b c | 0.8520 0.8720 0.9270 | 0.7810 0.8300 0.8810 | 0.0050 0.0028 0.0052 |
| ML Estimates | Bayesian Estimates | |||||
|---|---|---|---|---|---|---|
| Lindley | MCMC | |||||
| under WSEKF | under PLF | under KLF | under WSEKF | under PLF | under KLF | |
| 3.2815 | 3.2704 | 3.2844 | 5.9348 | 3.1649 | 3.1737 | 3.1678 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, H.; Gong, Q.; Hu, X. Estimation of Entropy for Generalized Rayleigh Distribution under Progressively Type-II Censored Samples. Axioms 2023, 12, 776. https://doi.org/10.3390/axioms12080776
Ren H, Gong Q, Hu X. Estimation of Entropy for Generalized Rayleigh Distribution under Progressively Type-II Censored Samples. Axioms. 2023; 12(8):776. https://doi.org/10.3390/axioms12080776
Chicago/Turabian StyleRen, Haiping, Qin Gong, and Xue Hu. 2023. "Estimation of Entropy for Generalized Rayleigh Distribution under Progressively Type-II Censored Samples" Axioms 12, no. 8: 776. https://doi.org/10.3390/axioms12080776
APA StyleRen, H., Gong, Q., & Hu, X. (2023). Estimation of Entropy for Generalized Rayleigh Distribution under Progressively Type-II Censored Samples. Axioms, 12(8), 776. https://doi.org/10.3390/axioms12080776






