Solvability, Approximation and Stability of Periodic Boundary Value Problem for a Nonlinear Hadamard Fractional Differential Equation with $\mathcal{p}$-Laplacian

Abstract

The fractional order $\mathcal{p}$-Laplacian differential equation model is a powerful tool for describing turbulent problems in porous viscoelastic media. The study of such models helps to reveal the dynamic behavior of turbulence. Therefore, this article is mainly concerned with the periodic boundary value problem (BVP) for a class of nonlinear Hadamard fractional differential equation with $\mathcal{p}$-Laplacian operator. By virtue of an important fixed point theorem on a complete metric space with two distances, we study the solvability and approximation of this BVP. Based on nonlinear analysis methods, we further discuss the generalized Ulam-Hyers (GUH) stability of this problem. Eventually, we supply two example and simulations to verify the correctness and availability of our main results. Compared to many previous studies, our approach enables the solution of the system to exist in metric space rather than normed space. In summary, we obtain some sufficient conditions for the existence, uniqueness, and stability of solutions in the metric space.

1. Introduction

The $\mathcal{p}$-Laplacian differential equation is one of the famous and important second-order nonlinear ordinary differential equations (ODEs). This equation first appeared in Leibenson’s study [1] of turbulence in porous media in 1983. The underlying form of $\mathcal{p}$-Laplacian differential equation is written as

$${\mathsf{\Phi }}_{\mathcal{p}}{\left(u^{\prime }\left(t\right)\right)}^{\prime }=f(t,u\left(t\right)),t\in (0,1),$$

where ${\mathsf{\Phi }}_{\mathcal{p}}:x\to {\left|x\right|}^{p-2}x(\mathcal{p}>1)$ is called the $\mathcal{p}$-Laplacian operator. Its inverse is ${\mathsf{\Phi }}_{\mathcal{p}}^{-1}={\mathsf{\Phi }}_{\mathcal{q}}$ with $\frac{1}{\mathcal{p}}+\frac{1}{\mathcal{q}}=1$. Due to its description of fundamental mechanical problems in turbulence, $\mathcal{p}$-Laplacian differential equations have been extensively and deeply studied. In recent years, some scholars have begun to focus on the nonlinear fractional differential system with $\mathcal{p}$-Laplacian. For example, the authors in [2] investigated the multiple positive solutions of a nonlinear high order Riemann-Liouville fractional $\mathcal{p}$-Laplacian equation with integral boundary value conditions. In [3], the author explored the existence and GUH-stability of a nonlinear Caputo-Fabrizio fractional coupled Laplacian equations. In [4], based on the Guo-Krasnosel’skii fixed point theorem, the authors probed into the multiple positive solutions of a system of mixed Hadamard fractional BVP with $({\mathcal{p}}_1,{\mathcal{p}}_2)$-Laplacian. In fact, some articles have been disposed of the BVP of $\mathcal{p}$-Laplacian system involving Riemann-Liouville or Caputo fractional derivatives (see [5,6,7,8,9,10,11,12,13]).

Hadamard [14] raised a novel fractional integral and derivative in 1892, which was later named Hadamard-type fractional calculus. There are some obvious differences between Hadamard fractional calculus and Riemann-Liouville fractional calculus. For example, $k_H(t,s)$ = ${(log\frac{t}{s})}^{\gamma -1}$ is the integral kernel corresponding to $\gamma$-order Hadamard fractional derivative, while $k_R(t,s)={(t-s)}^{\gamma -1}$ is the integral kernel corresponding to $\gamma$-order Riemann-Liouville fractional derivative. Furthermore, for any $\lambda >0$, $k_H(\lambda t,\lambda s)=k_H(t,s)$ is different from $k_R(\lambda t,\lambda s)={\lambda }^{\gamma -1}{k}_R(t,s)\ne k_R(t,s)$. The study on Hadamard fractional differential equations has attracted the attention of many scholars. There have been a series of fruitful achievements (see [15,16,17,18,19,20,21]). In 1940s, Ulam and Hyers [22,23] put forward a new stability that describes the stationarity of the exact and approximate solutions of system. Subsequently, extensive and in-depth research was conducted on the Ulam-Hyers stability of various systems. Especially, many excellent research results have emerged regarding the Ulam-Hyers stability of fractional order differential systems (see some of them [3,21,24,25,26,27,28,29,30,31,32]). Moreover, it is rare to combine the Hadamard fractional derivative with Laplacian operator. Therefore, it is novel and interesting to probe these problems.

Illuminated by the above arguments, this manuscript deals with the periodic BVP of a nonlinear Hadamard fractional differential equation with $\mathcal{p}$-Laplacian operator as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\alpha }\left[{\mathsf{\Phi }}_{\mathcal{p}}\left({}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(t\right)\right)\right]=f(t,u\left(t\right)),t\in (1,e],\hfill \\ u\left(1\right)=u\left(e\right),{}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(1\right)={}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(e\right),\hfill \end{array}\right.\end{array}$$

(1)

where $0<\alpha \le 1$, $1<\beta \le 2$, $\mathcal{p}>1$, ${}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{*}$ is the *-order Hadamard fractional derivative, ${\mathsf{\Phi }}_{\mathcal{p}}={\left|x\right|}^{\mathcal{p}-2}x$, and its inverse ${\mathsf{\Phi }}_{\mathcal{p}}^{-1}={\mathsf{\Phi }}_{\mathcal{q}}$ with $\frac{1}{\mathcal{p}}+\frac{1}{\mathcal{q}}=1$, $f\in C\left(\right[1,e]\times \mathbb{R},\mathbb{R})$. In addition, our study has also been inspired by the latest achievements in fractional differential equations, such as numerical algorithms and simulations [33,34,35,36,37,38], as well as the application of some nonsingular fractional derivative models [34,37,38,39,40,41,42,43].

The paper aims to discuss the approximation and GUH-stability of BVP (1). The novelty of this paper is mainly reflected as follows: (a) Since there is no paper dealing with the approximation problem of nonlinear Hadamard fractional differential systems with Laplace operator, we first consider the system (1) to fill this gap. (b) By applying a fixed point theorem on complete metric space with two kinds of distance, we obtain some sufficient conditions to ensure that system (1) has a unique solution. In addition, we build the generalized Ulam-Hyers stability of system (1) based on nonlinear analysis methods and inequality techniques. (c) Many previous papers (see [2,3,4,5,6,7,8,9,10,11,12,13,17,18,19,24,25]) usually used some fixed-point theorems on Banach spaces to study the existence of solutions of fractional differential equations. However, we handle the existence of solutions to fractional order differential equations by defining two different distances on a complete distance space. This allows for the discussion of the existence of solutions in a broader space, and there are relatively few restrictions on the existence of solutions. Therefore, our research methods and results are novel and interesting.

The rest sections of this paper are organized as follows. In Section 2, we recollect the definition of Hadamard fractional integrals and derivatives and some necessary lemmas. In Section 3, we discuss the existence, uniqueness, and approximation of solutions to BVP (1) by constructing two different distances and applying an important fixed point theorem on metric space. Furthermore, we use nonlinear analysis methods and inequality techniques to establish the GUH-stability of BVP (1) in Section 4. Section 5 provides the numerical solutions and simulations for two examples by means of ODE113 toolbox in MATLAB. Finally, we have made a brief summary in Section 6.

2. Preliminaries

This portion mainly introduces some important concepts and lemmas.

Definition 1 

([44]). For $a>0$, the left-sided Hadamard fractional integral of order $\gamma >0$ for a function $\xi :[a,\infty )\to \mathbb{R}$ is defined by

$$\begin{array}{c}\hfill {}^{\mathrm{H}}{\mathcal{J}}_{a^{+}}^{\gamma }\xi \left(t\right)=\frac{1}{\Gamma \left(\gamma \right)}{\int }_a^t{\left(log\frac{t}{s}\right)}^{\gamma -1}\xi \left(s\right)\frac{ds}{s},\end{array}$$

provided the integral exists, where $\Gamma \left(\gamma \right)={\int }_0^{\infty }{t}^{\gamma -1}{e}^{-t}dt$ and $log(·)={log}_e(·)$.

Definition 2 

([44]). Let $a,\gamma >0$ and $\xi \in C^m[a,\infty )$, the γ-order left-sided Hadamard fractional derivative is defined by

$$\begin{array}{c}\hfill {}^{\mathrm{H}}{\mathcal{D}}_{a^{+}}^{\alpha }\xi \left(t\right)=\frac{1}{\Gamma (m-\gamma )}{\left(t\frac{d}{dt}\right)}^m{\int }_a^t{\left(log\frac{t}{s}\right)}^{m-\gamma -1}\xi \left(s\right)\frac{ds}{s},\end{array}$$

where $m-1<\alpha \le m$, $m=\left[\gamma \right]+1$, and $[·]$ is the Gaussian truncating integer function.

Lemma 1 

([44]). Let $a,b,\gamma >0$ and $\xi \in C^m(a,b)\cap L^1(a,b)$, then

$$\begin{array}{c}\hfill {}^{\mathrm{H}}{\mathcal{J}}_{a^{+}}^{\gamma }{(}^{\mathrm{H}}{\mathcal{D}}_{a^{+}}^{\gamma }\xi \left(t\right))=\xi \left(t\right)+{\displaystyle \sum _{i=1}^m}{c}_i{\left(log\frac{t}{a}\right)}^{\gamma -i},\end{array}$$

where $c_1,c_2,\dots ,c_m$ are some real constants, and $m=\left[\gamma \right]+1$.

Lemma 2. 

Let $\mathcal{p}>1$. The $\mathcal{p}$-Laplacian operator ${\mathsf{\Phi }}_{\mathcal{p}}\left(z\right)={\left|z\right|}^{\mathcal{p}-2}z$ has the followings:

$\left(\mathrm{i}\right)$

If $z\ge 0$, then ${\mathsf{\Phi }}_{\mathcal{p}}\left(z\right)=z^{\mathcal{p}-1}$, and ${\mathsf{\Phi }}_{\mathcal{p}}\left(z\right)$ is increasing with respect to $z;$

$\left(\mathrm{ii}\right)$

For all $z,w\in \mathbb{R}$, ${\mathsf{\Phi }}_{\mathcal{p}}\left(zw\right)={\mathsf{\Phi }}_{\mathcal{p}}\left(z\right){\mathsf{\Phi }}_{\mathcal{p}}\left(w\right);$

$\left(\mathrm{iii}\right)$

If $\frac{1}{\mathcal{p}}+\frac{1}{\mathcal{q}}=1$, then ${\mathsf{\Phi }}_{\mathcal{q}}\left[{\mathsf{\Phi }}_{\mathcal{p}}\left(z\right)\right]={\mathsf{\Phi }}_{\mathcal{p}}\left[{\mathsf{\Phi }}_{\mathcal{q}}\left(z\right)\right]=z$, for all $z\in \mathbb{R};$

$\left(\mathrm{iv}\right)$

For all $z,w\ge 0$, $z\le w$⇔${\mathsf{\Phi }}_{\mathcal{q}}\left(z\right)\le {\mathsf{\Phi }}_{\mathcal{q}}\left(w\right);$

$\left(\mathrm{v}\right)$

$0\le z\le {\mathsf{\Phi }}_{\mathcal{q}}^{-1}\left(w\right)$⇔$0\le {\mathsf{\Phi }}_{\mathcal{q}}\left(z\right)\le w;$

$\left(\mathrm{vi}\right)$

$|{\mathsf{\Phi }}_{\mathcal{q}}\left(z\right)-{\mathsf{\Phi }}_{\mathcal{q}}\left(w\right)|\le \left\{\begin{array}{cc}(\mathcal{q}-1){\overline{M}}^{\mathcal{q}-2}|z-w|,\hfill & \mathcal{q}\ge 2,0\le z,w\le \overline{M},\hfill \\ (\mathcal{q}-1){\underline{M}}^{\mathcal{q}-2}|z-w|,\hfill & 1<\mathcal{q}<2,z,w\ge \underline{M}\ge 0.\hfill \end{array}\right.$

Now we introduce the following important fixed point theorem on a complete metric space involving two different distances, which will be used to prove the existence and uniqueness of solution to BVP (1).

Lemma 3 

([45]). Let ρ and ϱ be two different metrics on a nonempty set $\mathbb{X}$, and define an operator $\mathcal{T}:\mathbb{X}\to \mathbb{X}$. Assume that

$\left(\mathrm{a}1\right)$

For all $x,y\in \mathbb{X}$, there has a constant $\iota >0$ such that $\varrho (\mathcal{T}x,\mathcal{T}y)\le \iota \rho (x,y)$;

$\left(\mathrm{a}2\right)$

$(\mathbb{X},\varrho )$ is a complete metric space;

$\left(\mathrm{a}3\right)$

$\mathcal{T}:(\mathbb{X},\varrho )\to (\mathbb{X},\varrho )$ is continuous;

$\left(\mathrm{a}4\right)$

For all $x,y\in \mathbb{X}$, there has a constant $0<\kappa <1$ such that $\rho (\mathcal{T}x,\mathcal{T}y)\le \kappa \rho (x,y)$.

Then there has a unique $x^{*}\in \mathbb{X}$ such that $\mathcal{T}{x}^{*}=x^{*}$, and ${lim}_{k\to \infty }{\mathcal{T}}^k{x}_0=x^{*}$ for any $x_0\in \mathbb{X}$.

It is worth noting that the application techniques and related generalization of Lemma 3 can also be found in [46,47,48,49] and the references therein.

3. Solvability and Approximation

In this portion, we will prove the existence of a unique solution for system (1) based on Lemma 3. To this end, we need the following important lemma.

Lemma 4. 

Assume that $0<\alpha \le 1$, $1<\beta \le 2$ and $\mathcal{p}>1$ are some constants, $f\in C\left(\right[1,e]\times \mathbb{R},\mathbb{R})$. Then BVP (1) is equivalent to the following integral equation

$$\begin{array}{c}\hfill u\left(t\right)=-A_u\left(e\right){(logt)}^{\beta -1}+A_u\left(t\right),\end{array}$$

(2)

where $A_u\left(t\right)={}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u\left(t\right))\right)\right]$.

Proof. 

If $u\left(t\right)\in C\left(\right(1,e],\mathbb{R})$ is a solution of system (1), then it follows from Lemma 1 that

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_{\mathcal{p}}\left({}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(t\right)\right)=c{(logt)}^{\alpha -1}+{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u\left(t\right)),\end{array}$$

(3)

which implies that

$$\begin{array}{c}\hfill {}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(t\right)={\mathsf{\Phi }}_{\mathcal{q}}[c{(logt)}^{\alpha -1}+{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u\left(t\right))].\end{array}$$

(4)

According to the existence of ${}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(1\right)$ and (4), we know that $c=0$ and ${}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(1\right)=0$. By Lemma 1 and (4), we have

$$\begin{array}{c}\hfill u\left(t\right)=d_1{(logt)}^{\beta -1}+d_2{(logt)}^{\beta -2}+{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u\left(t\right))\right)\right].\end{array}$$

(5)

Similarly, we drive from $u\left(1\right)=u\left(e\right)$ and (5) that $d_2=0$ and

$$\begin{array}{c}\hfill d_1=-{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u\left(t\right))\right)\right]{|}_{t=e}=-A_u\left(e\right).\end{array}$$

(6)

In view of (5) and (6), we have

$$\begin{array}{c}\hfill u\left(t\right)=-A_u\left(e\right){(logt)}^{\beta -1}+A_u\left(t\right).\end{array}$$

(7)

Thus, $u\left(t\right)\in C\left(\right(1,e],\mathbb{R})$ is a solution of system (2). Vice versa, if $u\left(t\right)\in C\left(\right(1,e],\mathbb{R})$ is a solution of (2), then it is also a solution of (1) because the above derivation is completely reversible. The proof is completed. □

Let $\mathbb{X}=C\left(\right[1,e],\mathbb{R})$, two different distances $\rho ,\varrho :\mathbb{X}\to \mathbb{X}$ are respectively defined by

$$\begin{array}{c}\hfill \rho (u\left(t\right),v\left(t\right))={\displaystyle \underset{t\in [1,e]}{sup}}|u\left(t\right)-v\left(t\right)|,\varrho (u\left(t\right),v\left(t\right))={\int }_1^e|u\left(t\right)-v\left(t\right)|dt,\end{array}$$

(8)

for all $u\left(t\right),v\left(t\right)\in \mathbb{X}$. It is easy to prove that $(\mathbb{X},\rho )$ and $(\mathbb{X},\varrho )$ are all complete metric spaces. In addition, we need the following underlying assumptions in the whole paper.

$\left(\mathrm{H}1\right)$

$0<\alpha \le 1$, $1<\beta \le 2$ and $1<\mathcal{p}\le 2$ are some constants, $f\in C\left(\right[1,e]\times \mathbb{R},\mathbb{R})$.

$\left(\mathrm{H}2\right)$

There has a constant $M>0$ such that

$$0\le f(t,u)\le M,\forall t\in [1,e],u\in \mathbb{R}.$$

$\left(\mathrm{H}3\right)$

There has a function $0\le \mathcal{l}\left(t\right)\in C[1,e]$ such that, for all $t\in [1,e]$ and $u,v\in \mathbb{R}$,

$$\left|f\right(t,u)-f(t,v\left)\right|\le \mathcal{l}\left(t\right)|u-v|.$$

$\left(\mathrm{H}4\right)$

$\kappa =\frac{2(\mathcal{q}-1)}{\Gamma (\alpha +\beta +1)}{\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{\parallel \mathcal{l}\parallel }_e<1$, where ${\parallel \mathcal{l}\parallel }_e=\underset{1\le t\le e}{max}\left\{\mathcal{l}\left(t\right)\right\}$.

Theorem 1. 

If $\left(\mathrm{H}1\right)$–$\left(\mathrm{H}4\right)$ are fulfilled, then BVP (1) has a unique solution $u^{*}\left(t\right)\in \mathbb{X}$.

Proof. 

In what follows, we will apply Lemma 3 to prove Theorem 1. Two different distances $\rho ,\varrho :\mathbb{X}\to \mathbb{X}$ are defined as (8), then $(\mathbb{X},\rho )$ and $(\mathbb{X},\varrho )$ are all complete metric spaces, which indicates that the condition $\left(\mathrm{a}2\right)$ holds. According to Lemma 4, for all $u\left(t\right)\in \mathbb{X}$, an operator $\mathcal{T}:\mathbb{X}\to \mathbb{X}$ is defined by

$$\begin{array}{c}\hfill \mathcal{T}\left(u\left(t\right)\right)=-A_u\left(e\right){(logt)}^{\beta -1}+A_u\left(t\right),\end{array}$$

(9)

where $A_u\left(t\right)={}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u\left(t\right))\right)\right]$.

From the continuity of ${\mathsf{\Phi }}_{\mathcal{q}}$ and Hadamard fractional integral, we know that $\mathcal{T}:(\mathbb{X},\varrho )$→$(\mathbb{X},\varrho )$ is continuous, which means that the condition $\left(\mathrm{a}3\right)$ holds. By $\left(\mathrm{H}2\right)$, we have

$$\begin{array}{c}\hfill 0\le {}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u\left(t\right),u(t-\tau \left(t\right)))\le \frac{M}{\Gamma (\alpha +1)}{(logt)}^{\alpha }\le \frac{M}{\Gamma (\alpha +1)},t\in [1,e].\end{array}$$

(10)

For all $u,v\in \mathbb{X}$, $t\in [1,e]$, we derive from $\left(\mathrm{vi}\right)$ in Lemma 2, $\left(\mathrm{H}3\right)$ and (10) that

$$\begin{array}{cc}\hfill & |A_u\left(t\right)-A_v\left(t\right)|=|{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u\left(t\right))\right)-{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,v\left(t\right))\right)\right]|\hfill \\ \hfill \le & {}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }|{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u\left(t\right))\right)-{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,v\left(t\right))\right)|\hfill \\ \hfill \le & (\mathcal{q}-1){\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }|{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u\left(t\right))-{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,v\left(t\right))|\hfill \\ \hfill \le & (\mathcal{q}-1){\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }|f(t,u\left(t\right))-f(t,v\left(t\right))|\right]\hfill \\ \hfill \le & (\mathcal{q}-1){\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha +\beta }\left[\mathcal{l}\left(t\right)\right|u\left(t\right)-v\left(t\right)\left|\right]\hfill \\ \hfill \le & (\mathcal{q}-1){\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}\frac{1}{\Gamma (\alpha +\beta +1)}{\parallel \mathcal{l}\parallel }_e·\rho (u,v).\hfill \end{array}$$

(11)

It follows from (9) and (11) that

$$\begin{array}{cc}\hfill & |\mathcal{T}\left(u\left(t\right)\right)-\mathcal{T}\left(v\left(t\right)\right)|=|-(A_u\left(e\right)-A_v\left(e\right)){(logt)}^{\beta -1}+(A_u\left(t\right)-A_v\left(t\right))|\hfill \\ \hfill \le & |A_u\left(e\right)-A_v{\left(e\right)|(logt)}^{\beta -1}+\left|(A_u\left(t\right)-A_v\left(t\right))\right|\hfill \\ \hfill \le & \frac{2(\mathcal{q}-1)}{\Gamma (\alpha +\beta +1)}{\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{\parallel \mathcal{l}\parallel }_e·\rho (u,v)=\kappa \rho (u,v).\hfill \end{array}$$

(12)

In light of (12), we have

$$\begin{array}{c}\hfill \rho \left(\mathcal{T}\right(u),\mathcal{T}(v\left)\right)\le \kappa \rho (u,v),\forall u,v\in \mathbb{X},t\in [1,e].\end{array}$$

(13)

According to $\left(\mathrm{H}4\right)$ and (13), we know that $\left(\mathrm{a}4\right)$ in Lemma 3 holds.

Similar to (11), noticing that ${\left(log\frac{t}{s}\right)}^{\alpha +\beta -1}$ and $\frac{1}{s}$ are monotonically decreasing with respect to s in $[1,e]$, we have

$$\begin{array}{cc}\hfill & |A_u\left(t\right)-A_v\left(t\right)|\le (\mathcal{q}-1){\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha +\beta }\left[\mathcal{l}\left(t\right)\right|u\left(t\right)-v\left(t\right)\left|\right]\hfill \\ \hfill =& (\mathcal{q}-1){\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}\frac{1}{\Gamma (\alpha +\beta )}{\parallel \mathcal{l}\parallel }_e{\int }_1^t{\left(log\frac{t}{s}\right)}^{\alpha +\beta -1}|u\left(s\right)-v\left(s\right)|\frac{ds}{s}\hfill \\ \hfill \le & (\mathcal{q}-1){\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}\frac{1}{\Gamma (\alpha +\beta )}{\parallel \mathcal{l}\parallel }_e·{\left(logt\right)}^{\alpha +\beta -1}{\int }_1^t|u\left(s\right)-v\left(s\right)|ds\hfill \\ \hfill \le & \frac{\mathcal{q}-1}{\Gamma (\alpha +\beta )}{\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{\parallel \mathcal{l}\parallel }_e·{\left(loge\right)}^{\alpha +\beta -1}{\int }_1^e|u\left(s\right)-v\left(s\right)|ds\hfill \\ \hfill =& \frac{\mathcal{q}-1}{\Gamma (\alpha +\beta )}{\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{\parallel \mathcal{l}\parallel }_e·\varrho (u,v).\hfill \end{array}$$

(14)

Similar to (12), we derive from (14) that

$$\begin{array}{c}\hfill |\mathcal{T}\left(u\left(t\right)\right)-\mathcal{T}\left(v\left(t\right)\right)|\le \frac{2(\mathcal{q}-1)}{\Gamma (\alpha +\beta )}{\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{\parallel \mathcal{l}\parallel }_e·\varrho (u,v).\end{array}$$

(15)

From (15), we get

$$\begin{array}{cc}\hfill & \varrho (\mathcal{T}\left(u\right),\mathcal{T}\left(v\right))={\int }_1^e|\mathcal{T}\left(u\left(t\right)\right)-\mathcal{T}\left(v\left(t\right)\right)|dt\hfill \\ \hfill \le & \frac{2(\mathcal{q}-1)e}{\Gamma (\alpha +\beta )}{\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{\parallel \mathcal{l}\parallel }_e·\varrho (u,v).\hfill \end{array}$$

(16)

Equation (16) indicates that $\left(\mathrm{a}1\right)$ in Lemma 3 also holds. Thus, it follows from Lemma 3 that $\mathcal{T}$ exists a unique fixed point $u^{*}\left(t\right)\in \mathbb{X}$, which is the unique solution of (1). The proof is completed. □

Next, we shall discuss the approximation of solution for system (1). In fact, from Lemma 3, we conclude that the unique solution $u^{*}\left(t\right)\in \mathbb{X}$ of (1) satisfies $u^{*}\left(t\right)={lim}_{n\to \infty }{\mathcal{T}}^n{u}_0$ for any $u_0\in \mathbb{X}$. Denote $u_n\left(t\right)={\mathcal{T}}^n{u}_0$, then $\left\{u_n\left(t\right)\right\}$ is a approximation sequence of solution to system (1). Based on (9), $u_n\left(t\right)$ can be represented as

$$\begin{array}{c}\hfill u_n\left(t\right)=-A_{u_{n-1}}\left(e\right){(logt)}^{\beta -1}+A_{u_{n-1}}\left(t\right),\end{array}$$

(17)

where $A_{u_{n-1}}\left(t\right)={}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u_{n-1}\left(t\right))\right)\right]$.

Similar to (12), we derive from (17) that

$$\begin{array}{cc}\hfill & |u_{n+1}\left(t\right)-u_n\left(t\right)|\le \kappa |u_n\left(t\right)-u_{n-1}\left(t\right)|,\hfill \end{array}$$

which implies that

$$\begin{array}{c}\hfill \rho (u_{n+1},u_n)\le \kappa \rho (u_n,u_{n-1}).\end{array}$$

(18)

By virtue of $\left(\mathrm{H}4\right)$ and (18), we know that $\left\{u_n\left(t\right)\right\}$ converges exponentially on $(\mathbb{X},\rho )$.

4. Generalized Ulam-Hyers Stability

This section centres on the GUH-stability of BVP (1). We first provide the concept of GUH-stability for BVP (1).

For all $\delta >0$, consider the following fractional differential inequality

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\alpha }\left[{\mathsf{\Phi }}_{\mathcal{p}}\left({}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(t\right)\right)\right]-f(t,u\left(t\right))\le \delta ,t\in (1,e],\hfill \\ u\left(1\right)=u\left(e\right),{}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(1\right)={}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(e\right).\hfill \end{array}\right.\end{array}$$

(19)

Definition 3. 

BVP (1) is said to be generalized Ulam-Hyers (GUH) stable on the metric space $(\mathbb{X},\rho )$, provided that, for all $\delta >0$ and any solution $u\in \mathbb{X}$ of (19), there have an $\omega \in C(\mathbb{R},{\mathbb{R}}^{+})$ with $\omega \left(0\right)=0$ and a unique solution $u^{*}\in \mathbb{X}$ of (1) such that

$$\begin{array}{c}\hfill \rho (u,u^{*})\le \omega \left(\delta \right).\end{array}$$

Remark 1. 

$u\left(t\right)\in \mathbb{X}$ solves the inequality 19) iff there has a continuous function $\phi \left(t\right)$ such that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left|\phi \right(t\left)\right|\le \delta ,t\in (1,e],\hfill \\ {}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\alpha }\left[{\mathsf{\Phi }}_{\mathcal{p}}\left({}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(t\right)\right)\right]=f(t,u\left(t\right))+\phi \left(t\right),t\in (1,e],\hfill \\ u\left(1\right)=u\left(e\right),{}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(1\right)={}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(e\right).\hfill \end{array}\right.\end{array}$$

(20)

Theorem 2. 

If $\left(\mathrm{H}1\right)$–$\left(\mathrm{H}4\right)$ are satisfied, then BVP (1) is GUH-stable.

Proof. 

On the basis of Lemma 4 and Remark 1, the solution $u\left(t\right)$ of inequality (19) is written by

$$\begin{array}{c}\hfill u\left(t\right)=-A_u^{\phi }\left(e\right){(logt)}^{\beta -1}+A_u^{\phi }\left(t\right),\end{array}$$

(21)

where $A_u^{\phi }\left(t\right)={}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }[f(t,u\left(t\right))+\phi \left(t\right)]\right)\right]$. In the light of Theorem 1 and Lemma 4, the unique solution $u^{*}\left(t\right)$ of BVP (1) is read as

$$\begin{array}{c}\hfill u^{*}\left(t\right)=-A_{u^{*}}\left(e\right){(logt)}^{\beta -1}+A_{u^{*}}\left(t\right),\end{array}$$

(22)

where $A_{u^{*}}\left(t\right)={}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u^{*}\left(t\right))\right)\right]$.

Similar to (11), we obtain

$$\begin{array}{cc}\hfill & |A_u^{\phi }\left(t\right)-A_{u^{*}}\left(t\right)|=|{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }[f(t,u\left(t\right))+\phi \left(t\right)]\right)-{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u^{*}\left(t\right))\right)\right]|\hfill \\ \hfill \le & {}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }|{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }[f(t,u\left(t\right))+\phi \left(t\right)]\right)-{\mathsf{\Phi }}_{\mathcal{q}}\left({}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u^{*}\left(t\right))\right)|\hfill \\ \hfill \le & (\mathcal{q}-1){\left(\frac{M+\delta }{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }|{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }[f(t,u\left(t\right))+\phi \left(t\right)]-{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }f(t,u^{*}\left(t\right))|\hfill \\ \hfill \le & (\mathcal{q}-1){\left(\frac{M+\delta }{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\beta }\left[{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha }\left[\right|f(t,u\left(t\right))-f(t,u^{*}\left(t\right))|+|\phi \left(t\right)\left|\right]\right]\hfill \\ \hfill \le & (\mathcal{q}-1){\left(\frac{M+\delta }{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{}^{\mathrm{H}}{\mathcal{J}}_{1^{+}}^{\alpha +\beta }\left[\mathcal{l}\left(t\right)\right|u\left(t\right)-u^{*}\left(t\right)|+|\phi \left(t\right)\left|\right]\hfill \\ \hfill \le & (\mathcal{q}-1){\left(\frac{M+\delta }{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}\frac{1}{\Gamma (\alpha +\beta +1)}{[\parallel \mathcal{l}\parallel }_e·\rho (u,u^{*})+\delta ].\hfill \end{array}$$

(23)

By the same manner of (12), we derive from (21)–(23) that

$$\begin{array}{cc}\hfill & |u\left(t\right)-u^{*}\left(t\right)|=|-(A_u^{\phi }\left(e\right)-A_{u^{*}}\left(e\right)){(logt)}^{\beta -1}+(A_u^{\phi }\left(t\right)-A_{u^{*}}\left(t\right))|\hfill \\ \hfill \le & |A_u^{\phi }\left(e\right)-A_{u^{*}}{\left(e\right)|(logt)}^{\beta -1}+\left|(A_u^{\phi }\left(t\right)-A_{u^{*}}\left(t\right))\right|\hfill \\ \hfill \le & \frac{2(\mathcal{q}-1)}{\Gamma (\alpha +\beta +1)}{\left(\frac{M+\delta }{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{[\parallel \mathcal{l}\parallel }_e·\rho (u,u^{*})+\delta ]\hfill \\ \hfill =& \kappa \left(\delta \right)\rho (u,u^{*})+\lambda \left(\delta \right),\hfill \end{array}$$

(24)

where $\kappa \left(\delta \right)=\frac{2(\mathcal{q}-1)}{\Gamma (\alpha +\beta +1)}{\left(\frac{M+\delta }{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{\parallel \mathcal{l}\parallel }_e$, $\lambda \left(\delta \right)=\frac{2(\mathcal{q}-1)\delta }{\Gamma (\alpha +\beta +1)}{\left(\frac{M+\delta }{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}$.

For any sufficiently small $\delta >0$, the condition $\left(\mathrm{H}4\right)$ ensures that $0<\kappa \left(\delta \right)<1$. Thus, we know from (24) that

$$\begin{array}{c}\hfill \rho (u,u^{*})\le \frac{\lambda \left(\delta \right)}{1-\kappa \left(\delta \right)}=\omega \left(\delta \right).\end{array}$$

(25)

Obviously, $\kappa \left(0\right)=\kappa <1$, $\lambda \left(0\right)=0$ and $\omega \left(\delta \right)=\frac{\lambda \left(\delta \right)}{1-\kappa \left(\delta \right)}>0$ with $\omega \left(0\right)=0$. By virtue of Definition 3, (25) shows that BVP (1) is GUH-stable. The proof is completed. □

5. Two Examples and Simulations

This section provides two examples and simulations to inspect the correctness and validity of our main results. Consider the following nonlinear Hadamard fractional differential equation with $\mathcal{p}$-Laplacian operator

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\alpha }\left[{\mathsf{\Phi }}_{\mathcal{p}}\left({}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(t\right)\right)\right]=f(t,u\left(t\right)),t\in (1,e],\hfill \\ u\left(1\right)=u\left(e\right),{}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(1\right)={}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(e\right),\hfill \end{array}\right.\end{array}$$

(26)

Example 1. 

In (26), we take $\mathcal{p}=\frac{5}{4}$, $\alpha =0.2$, $\beta =1.4$, $f(t,u)=\frac{2+sin\left(3t\right)}{20}[\frac{3\pi }{4}+arctan\left(u\right)]$, then a simple computation gives that $\mathcal{q}=5>2$, and

$$\frac{\pi }{80}\le f(t,u)\le \frac{3\pi }{16},|f(t,u)-f(t,v)|\le \frac{2+sin\left(3t\right)}{20}|u-v|.$$

In consequent, the conditions $\left(\mathrm{H}1\right)$–$\left(\mathrm{H}3\right)$ are fulfilled. In addition, $M=\frac{3\pi }{16}$, $\mathcal{l}\left(t\right)=\frac{2+sin\left(3t\right)}{20}$, ${\parallel \mathcal{l}\parallel }_e=\frac{3}{20}$, and

$$\kappa =\frac{2(\mathcal{q}-1)}{\Gamma (\alpha +\beta +1)}{\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{\parallel \mathcal{l}\parallel }_e\approx 0.1716<1.$$

Thus, $\left(\mathrm{H}4\right)$ holds. From Theorem 1 and Theorem 2, we claim that Example 1 has a unique solution, which is GUH-stable.

Remark 2. 

In Example 1, $\mathcal{p},\alpha ,\beta$ are all rational number. $\alpha =0.2$ is close to 0, and $\beta =1.4$ is close to 1.5. To further verify the correctness of our results and the sensitivity of numerical simulation to parameters, we choose $\mathcal{p},\alpha ,\beta$ as irrational number satisfying α close to 1 and β close to 2 in the following example.

Example 2. 

In (26), Choose $\mathcal{p}=\frac{\sqrt{15}}{2}$, $\alpha =\sqrt{0.9}$, $\beta =\sqrt{3.9}$, and $f(t,u)$ be same as Example 1. Then $\mathcal{q}=2.0678>2$, and the conditions $\left(\mathrm{H}1\right)$–$\left(\mathrm{H}3\right)$ also hold. M, $\mathcal{l}\left(t\right)$ and ${\parallel \mathcal{l}\parallel }_e$ are same as Example 1. In addition,

$$\kappa =\frac{2(\mathcal{q}-1)}{\Gamma (\alpha +\beta +1)}{\left(\frac{M}{\Gamma (\alpha +1)}\right)}^{\mathcal{q}-2}{\parallel \mathcal{l}\parallel }_e\approx 0.0567<1.$$

Thus, $\left(\mathrm{H}4\right)$ is also true. From Theorems 1 and 2, we claim that Example 2 also has a unique GUH-stable solution.

To perform the numerical simulation on Examples 1 and 2, we need to give a concise algorithm below. Let $v\left(t\right)={}^{\mathrm{H}}{\mathcal{D}}_{1^{+}}^{\beta }u\left(t\right)$, then the Equation (2) can be rewritten as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}u\left(t\right)=-\frac{1}{\Gamma \left(\beta \right)}{\int }_1^e{\left(log\frac{e}{s}\right)}^{\beta -1}v\left(s\right)\frac{ds}{s}·{(logt)}^{\beta -1}\hfill \\ +\frac{1}{\Gamma \left(\beta \right)}{\int }_1^t{\left(log\frac{t}{s}\right)}^{\beta -1}v\left(s\right)\frac{ds}{s},\hfill \\ v\left(t\right)={\left[\frac{1}{\Gamma \left(\alpha \right)}{\int }_1^t{\left(log\frac{t}{s}\right)}^{\alpha -1}f(s,u\left(s\right))\frac{ds}{s}\right]}^{\mathcal{q}-1}.\hfill \end{array}\right.\end{array}$$

(27)

Taking the derivative at both sides of (27), we get

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{du\left(t\right)}{dt}=-\frac{\beta -1}{\Gamma \left(\beta \right)}{\int }_1^e{\left(log\frac{e}{s}\right)}^{\beta -1}v\left(s\right)\frac{ds}{s}·\frac{{(logt)}^{\beta -2}}{t}\hfill \\ +\frac{\beta -1}{t\Gamma \left(\beta \right)}{\int }_1^t{\left(log\frac{t}{s}\right)}^{\beta -2}v\left(s\right)\frac{ds}{s},\hfill \\ \frac{dv\left(t\right)}{dt}=(\mathcal{q}-1){\left[\frac{1}{\Gamma \left(\alpha \right)}{\int }_1^t{\left(log\frac{t}{s}\right)}^{\alpha -1}f(s,u\left(s\right))\frac{ds}{s}\right]}^{\mathcal{q}-2}\hfill \\ \times \frac{\alpha -1}{t\Gamma \left(\alpha \right)}{\int }_1^t{\left(log\frac{t}{s}\right)}^{\alpha -2}f(s,u\left(s\right))\frac{ds}{s}.\hfill \end{array}\right.\end{array}$$

(28)

For (28), we can apply the appropriate ODE toolbox in MATLAB to perform numerical solutions and simulations.

Based on the above algorithm, we employ the ODE113 toolbox in MATLAB R2019b on two examples to give their numerical solutions and simulations. Example 1 is shown as Table 1 and Table 2, Figure 1 and Figure 2. Example 2 is shown as Table 3 and Table 4, Figure 3 and Figure 4. Figure 2 and Table 1 and Table 2 show that Example 1 is GUH-stable. Figure 4 and Table 3 and Table 4 show that Example 2 is GUH-stable.

Table 1. The numerical solution $u\left(t\right)$ to Example 1 which needs to multiply by ${10}^{10}$.

	t	1.2	1.4	1.6	1.8	2.0	2.2	2.4	2.6	2.7183
u
$\delta =0$		0.0079	0.0314	0.0497	0.0645	0.0786	0.0963	0.1210	0.1448	0.1501
$\delta =0.001$		0.0080	0.0318	0.0501	0.0650	0.0790	0.0971	0.1218	0.1447	0.1498

Table 2. The numerical solution $v\left(t\right)$ to Example 1 which needs to multiply by $-{10}^{10}$.

	t	1.2	1.4	1.6	1.8	2.0	2.2	2.4	2.6	2.7183
u
$\delta =0$		0.1653	0.2690	0.3344	0.4302	0.7319	1.7307	4.0310	7.5843	9.7746
$\delta =0.001$		0.1671	0.2720	0.3355	0.4327	0.7319	1.7749	3.9019	7.2621	9.3765

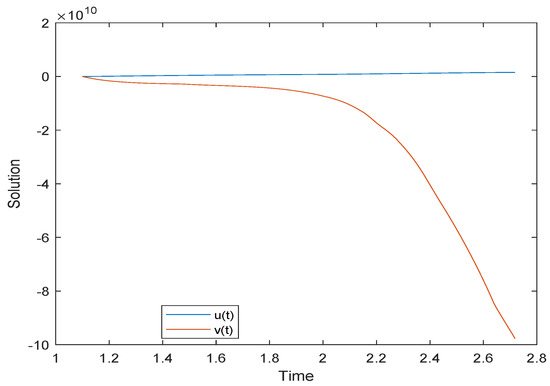
Figure 1. Simulation of solutions to Example 1.

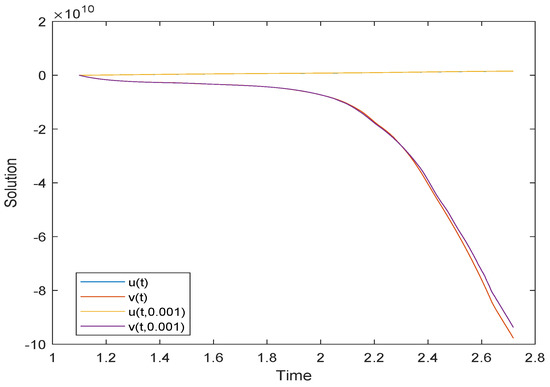
Figure 2. Evolution of the GUH-stability of Example 1.

Table 3. The numerical solution $u\left(t\right)$ to Example 2.

	t	1.2	1.4	1.6	1.8	2.0	2.2	2.4	2.6	2.7183
u
$\delta =0$		0.0018	0.0121	0.0252	0.0384	0.0507	0.0614	0.0699	0.0749	0.0757
$\delta =0.001$		0.0019	0.0122	0.0254	0.0387	0.0511	0.0619	0.0704	0.0754	0.0763

Table 4. The numerical solution $v\left(t\right)$ to Example 2 which needs to multiply by $-1$.

	t	1.2	1.4	1.6	1.8	2.0	2.2	2.4	2.6	2.7183
u
$\delta =0$		0.0818	0.1947	0.2757	0.3530	0.4481	0.5721	0.7189	0.8741	0.9639
$\delta =0.001$		0.0824	0.1960	0.2779	0.3556	0.4516	0.5767	0.7244	0.8828	0.9723

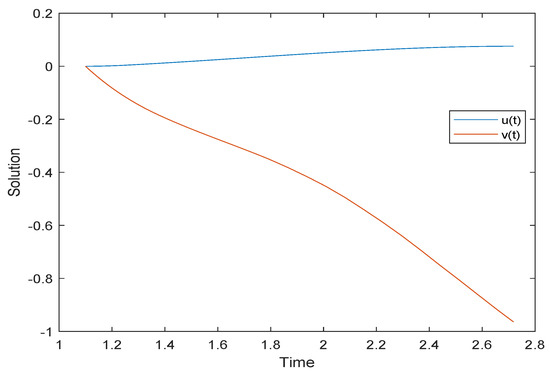
Figure 3. Simulation of solutions to Example 2.

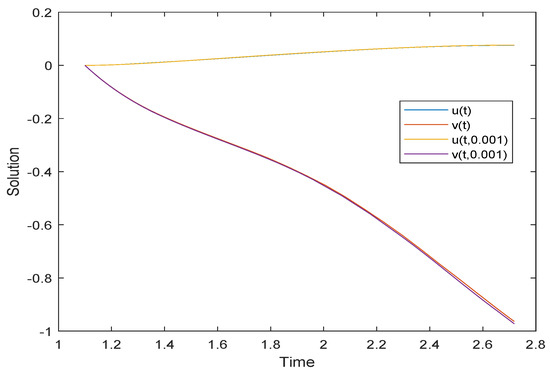
Figure 4. Evolution of the GUH-stability of Example 2.

6. Summaries

It is well known that the $\mathcal{p}$-Laplacian differential equation arises from the turbulence problem in porous medium. In viscoelastic mechanics, some studies have shown that fractional order differential equation models are more accurate than integer order differential equation models. Therefore, the fractional $\mathcal{p}$-Laplacian differential model has greater advantages in the study of viscoelastic porous medium turbulence. In this article, we study BVP (1) of a nonlinear $\mathcal{p}$-Laplacian Hadamard fractional differential equation. Unlike many published papers, we have established the existence, uniqueness, stability, and sequence approximation of solutions for fractional order differential equations on a wide range of complete metric spaces rather than Banach spaces. We have obtained some concise and easily verifiable sufficient criteria. Examples 1 and 2 and simulations demonstrate that our main results are correct and available. Meanwhile, Figure 1 and Figure 2 also indicate that the solution of BVP (1) is sensitive and dependent on parameters $\mathcal{p},\alpha$ and $\beta$. Our results provide theoretical support for revealing the mechanical problems of viscoelastic porous medium turbulence. The mathematical theories and methods used in the article have certain generality in solving similar problems. In addition, based on our recent research findings [50,51,52,53], we plan to study some ecosystems involving fractional derivatives or reaction diffusion effects in the future.