Weighted Pseudo-θ-Almost Periodic Sequence and Finite-Time Guaranteed Cost Control for Discrete-Space and Discrete-Time Stochastic Genetic Regulatory Networks with Time Delays
Abstract
1. Introduction
- (1)
- (2)
- (3)
- Finite-time cost-preserving controllers are designed for this class of SGRNs.
2. Problem Formulation
2.1. Space–Time Discrete Stochastic GRNs
2.2. Weighted Pseudo-Almost Periodicity
3. Mean Square -Pseudo--Almost Periodic Sequence
- and are -valued almost periodic sequences; , , and are -valued almost periodic sequences; , , , , and are -valued -pseudo-almost periodic sequences.
- and there exist positive numbers , and such thatfor any , .
- .
3.1. -Pseudo--Almost Periodicity of Operator
3.2. Weighted Pseudo-Almost Periodic Sequence Solution to GRNs Equation (1)
- , where
4. Finite-Time Guaranteed Cost Controls in Exponential Form
4.1. The Frame of Controlling GRNs
4.2. Design of Finite-Time Guaranteed Cost Controllers
- The control gains and , where and are positive constants,
- It holds that , where and ,
- (a)
- There exist and such that
- (b)
- There exist and ensuring
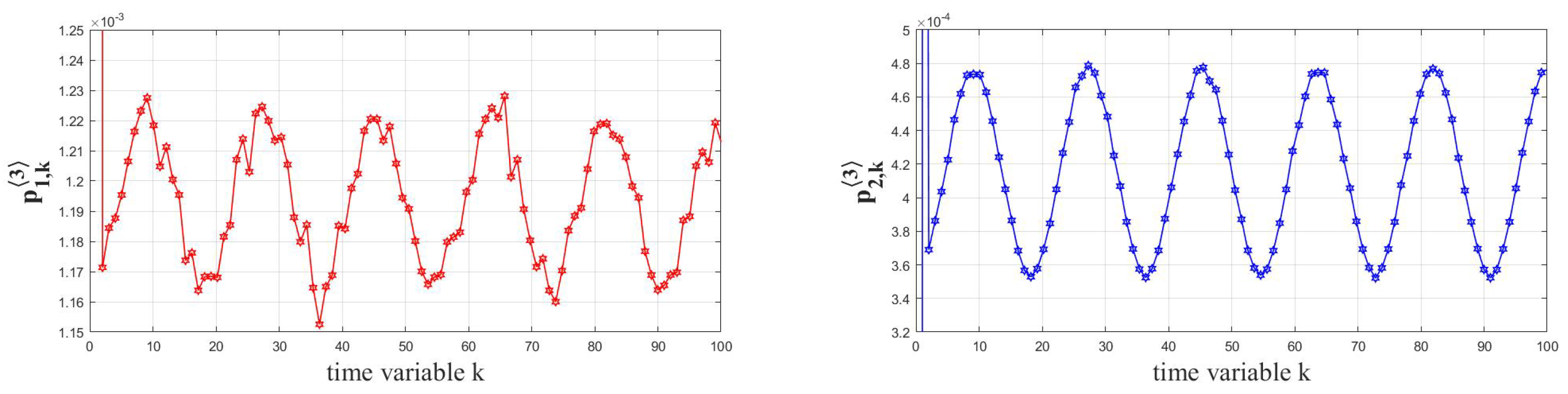
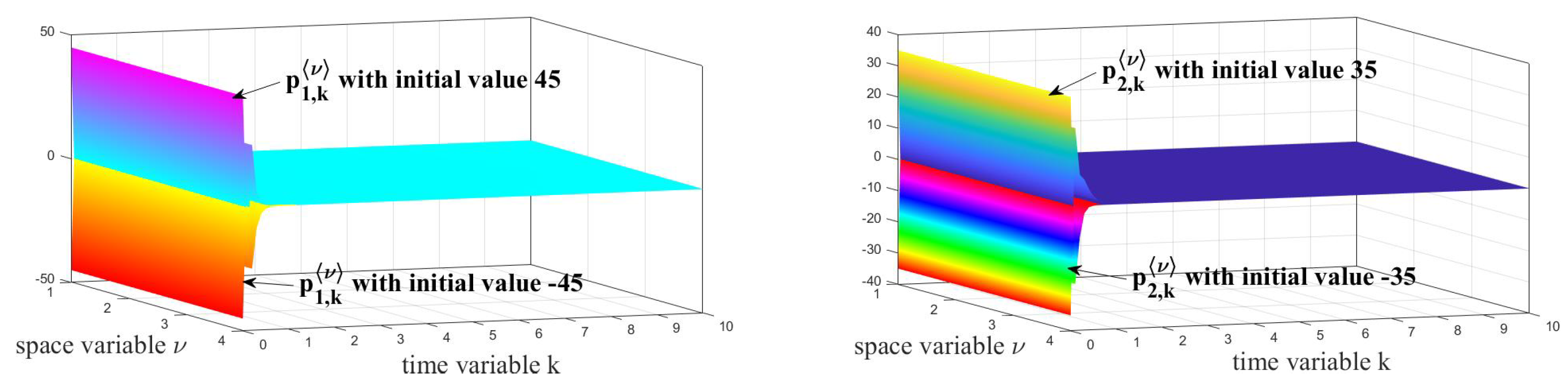
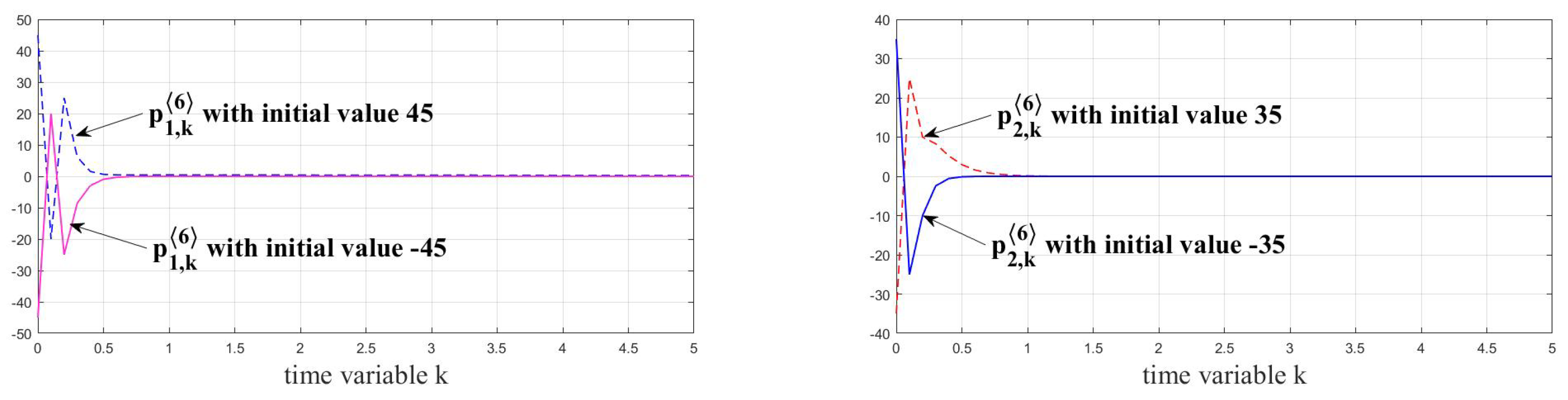
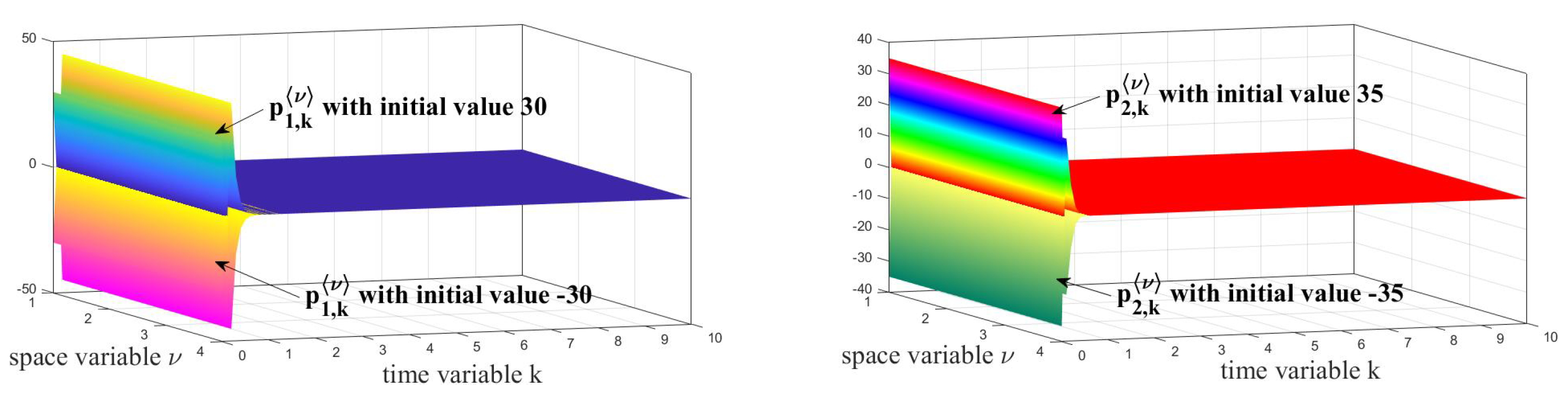
5. Example
6. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alon, U. An Introductin to Systems Biology: Design Principles of Biological Circuits; CRC: London, UK, 2006. [Google Scholar]
- Thieffry, D.; Thomas, R. Qualitative analysis of gene networks. Proc. Pac. Symp. Biocomput. 1998, 3, 77–88. [Google Scholar]
- Bao, W.Z.; Yuan, C.A.; Zhang, Y.H. Mutli-features prediction of protein translational modification sites. IEEE/ACM Trans. Comput. Biol. Bioinf. 2018, 15, 1453–1460. [Google Scholar] [CrossRef] [PubMed]
- Somogyi, R.; Sniegoski, C. Modeling the complexity of genetic networks: Understanding multigenic and pleiotropic regulation. Complexity 1996, 1, 45–63. [Google Scholar] [CrossRef]
- de Jong, H. Modeling and simuation of genetic regulatory systems: A literature review. J. Comput. Biol. 2002, 9, 67–103. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.; Gulbahce, N.; Loscalzo, J. Network medicien: A network-based approach to human disease. Nat. Rev. Genet. 2011, 12, 56–68. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Long, L.; Zhao, Z.; Liu, Y.; Alsaadi, F.E. Stability criteria of quatemion-valued neutral-type delayed neural networks. Neurocomputing 2020, 412, 287–294. [Google Scholar] [CrossRef]
- Hood, L.; Health, J.; Phelps, M.; Lin, B. Systems biology and new technologies enable predictive and preventative medicine. Science 2004, 306, 640–643. [Google Scholar] [CrossRef]
- Liu, R.J.; Lu, J.Q.; Lou, J.G.; Alsaedi, A.; Alsaedi, F.E. Set stabiliation of Boolean networks under pinning contril strategy. Neurocomputing 2017, 260, 142–148. [Google Scholar] [CrossRef]
- Possieri, C.; Teel, A.R. Asymptotic stability in probability for stochastic Boolean Networks. Automatica 2017, 83, 1–9. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Wang, Y.T.; Zhang, X. Improved stochastic integral inequalities to stability analysis of stochastic genetic regulatory networks with mixed time-varying delays. IET Control Theory Appl. 2020, 14, 2439–2448. [Google Scholar] [CrossRef]
- Ayachi, M. Existence and exponential stability of weighted pseudo-almost periodic solutions for genetic regulatory networks with time-varying delays. Int. J. Biomath. 2021, 14, 2150006. [Google Scholar] [CrossRef]
- Chen, T.; He, H.Y.; Church, G.M. Modeling gene expression with differential equations. Pac. Symp. Biocomput. 1999, 4, 29–40. [Google Scholar]
- Han, Y.Y.; Zhang, X.; Wang, Y.T. Asymptotic Stability Criteria for genetic regulatory networks with time-varying delays and reaction-diffusion terms. Circ. Syst. Signal Process 2015, 34, 3161–3190. [Google Scholar] [CrossRef]
- Zou, C.Y.; Zhou, C.J.; Zhang, Q.; He, V.Y.; Huang, C. State emstimation for delayed genetic regulatory networks with reaction diffusion terms and Markovian jump. Complex Intell. Syst. 2023, 1–15. [Google Scholar] [CrossRef]
- Xie, Y.P.; Xiao, L.; Wang, L.M.; Wang, G.H. Algebriaic Stability Criteria of Reaction Diffusion Genetic Regulatory Neteorks With Discrete and Distrubted Delays. IEEE Access 2021, 9, 16410–16418. [Google Scholar] [CrossRef]
- Xue, Y.; Liu, C.Y.; Zhang, X. State bounding description and reachable set estimation for discrete-time genetic regulatory networks with time-varying delays and bounded disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6652–6661. [Google Scholar] [CrossRef]
- Liu, C.Y.; Wang, X.; Xue, Y. Global exponential stability analysis of discrete-time genetic regulatory networks with time-varying discrete delays and unbounded distributed delays. Neurocomputing 2020, 372, 100–108. [Google Scholar] [CrossRef]
- Yue, D.D.; Guan, Z.H.; Chen, J.; Ling, G.; Wu, Y. Bifurcations and chaos of a discrete-time model in genetic regulatory networks. Nonlinear Dyn. 2017, 87, 567–586. [Google Scholar] [CrossRef]
- Zhang, T.W.; Li, Y.K. Global exponential stability of discrete-time almost automorphic Caputo—Fabrizio BAM fuzzy neural networks via exponential Euler technique. Knowl.-Based Syst. 2022, 246, 108675. [Google Scholar] [CrossRef]
- Huang, Z.K.; Mohamad, S.; Gao, F. Multi-almost periodicity in semi-discretizations of a general class of neural networks. Math. Comput. Simul. 2014, 101, 43–60. [Google Scholar] [CrossRef]
- Zhang, T.W.; Han, S.F.; Zhou, J.W. Dynamic behaviours for semi-discrete stochastic Cohen-Grossberg neural networks with time delays. J. Frankl. Inst. 2020, 357, 13006–13040. [Google Scholar] [CrossRef]
- Zhang, T.W.; Qu, H.Z.; Liu, Y.T.; Zhou, J.W. Weighted pseudo θ-almost periodic sequence solution and guaranteed cost control for discrete-time and discrete-space stochastic inertial neural networks. Chaos Solitons Fractals 2023, 173, 113658. [Google Scholar] [CrossRef]
- Zhang, T.W.; Li, Z.H. Switching clusters’ synchronization for discrete space-time complex dynamical networks via boundary feedback controls. Pattern Recognit. 2023, 143, 109763. [Google Scholar] [CrossRef]
- Zhang, T.W.; Liu, Y.T.; Qu, H.Z. Global mean-square exponential stability and random periodicity of discrete-time stochastic inertial neural networks with discrete spatial diffusions and Dirichlet boundary condition. Comput. Math. Appl. 2023, 141, 116–128. [Google Scholar] [CrossRef]
- Xu, G.X.; Bao, H.B.; Cao, J.D. Mean-square exponential input-to-state stability of stochastic gene regulatory networks with maltiple time delays. Neural Process. Lett. 2020, 51, 271–286. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, S.; Shen, H. Finite-time robust stochastic stability of uncertain stochastic delayed reaction-diffusion genetic regulatory networks. Neurocomputing 2011, 74, 2790–2796. [Google Scholar] [CrossRef]
- Wang, W.Q.; Zhong, S.M.; Liu, F. Robust filtering of uncertain stochastic genetic regulatory networks with time-varying delays. Chaos Solitons Fract. 2012, 45, 915–929. [Google Scholar] [CrossRef]
- Wang, B. Random periodic sequence of globally mean-square exponentially stable discrete-time stochastic genetic regulatory networks with discrete spatial diffusions. Electron. Res. Arch. 2023, 31, 3097–3122. [Google Scholar] [CrossRef]
- Zhang, G.P.; Zhu, Q.X. Finite-time guaranteed cost control for uncertain delayed switched nonlinear stochastic systems. J. Frankl. Institeu 2022, 359, 8802–8818. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, H.B.; Shi, K.B.; Zhou, K. Event-triggered finite-time guaranteed cost control for networked Takagi-Sugeno (T-S) fuzzy switched systems under denial of service attacks. Int. J. Robust Nolinear Control 2022, 32, 5764–5775. [Google Scholar] [CrossRef]
- Liu, L.P.; Di, Y.F.; Shang, Y.L.; Fu, Z.M.; Fan, B. Guaranteed Cost and Finite-Time Non-fragile Control of Fractional-Order Positive Switched Systems with Asynchronous Switching and Impulsive Moments. Circuits Syst. Signal Process. 2021, 40, 3143–3160. [Google Scholar] [CrossRef]
- Liu, M.X.; Wu, B.W.; Wang, Y.E.; Liu, L.L. Dynamic Output Feedback Control and Guaranteed Cost Finite-time Boundedness for Uncertain Switched Linear Systems. Int. J. Control Autom. Syst. 2023, 21, 400–409. [Google Scholar] [CrossRef]
- Liu, M.X.; Wu, B.W.; Wang, Y.E.; Liu, L.L. Dynamic Output Feedback control and Guaranteed Cost Finite-Time Boundedness for Switched Linear Systems. Circuits Syst. Signal Process. 2022, 41, 2653–2668. [Google Scholar] [CrossRef]
- Liu, X.K.; Li, W.C.; Yao, C.X.; Li, Y. Finite-Time Guaranteed Cost Control for Markovian Jump Systems with Time-Varying Delays. Mathematics 2022, 10, 2028. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, Y.Y.; Wang, H.; He, S.P. Finite-time dissipative control for time-delay Markov jump systems with conic-type non-linearities under guaranteed cost controller and quantiser. IET Control Theory Appl. 2021, 15, 489–498. [Google Scholar] [CrossRef]
- Luo, Y.P.; Wang, X.E.; Cao, J.D. Guaranteed-cost finite-time consensus of multi-agent systems via intermittent control. Math. Methods Appl. Sci. 2022, 45, 697–717. [Google Scholar] [CrossRef]
- Duan, L.; Di, F.J.; Wang, Z.Y. Existence and global exponential stability of almost periodic solutions of genetic regulatory networks with time-varying delays. J. Exp. Theor. Artif. Intell. 2020, 32, 453–463. [Google Scholar] [CrossRef]
- Luo, Q.; Zhang, R.B.; Liao, X.X. Unconditional global exponential stability in Lagrange sense of genetic regulatory networks with SUM regulatory logic. Cogn. Neurodyn. 2010, 4, 251–261. [Google Scholar] [CrossRef]
- Li, Y.J.; Zhang, X.; Tan, C. Global exponential stability analysis of discrete-time genetic regulatory networks with time delays. Asian J. Control 2013, 15, 1448–1475. [Google Scholar] [CrossRef]
- Xie, Y.P.; Xiao, L.; Ge, M.F.; Wang, L.M.; Wang, G.H. New results on global exponential stability of genetic regulatory networks with diffusion effect and time-varying hybird delays. Neural Process. Lett. 2021, 53, 3947–3963. [Google Scholar] [CrossRef]
- Liu, Z.X.; Yang, X.; Yu, T.T.; Zhang, X.; Wang, X. Global Exponential Satbility Analysis of Coupled Cyclic Genentic Regulatory Networks With Constant Delays. IEEE Trans. Control Netw. Syst. 2021, 8, 1811–1821. [Google Scholar] [CrossRef]
- Zhang, W.L.; Zheng, Z.H. Random almost periodic solutions of random dynamical systems. arXiv 2019, arXiv:1909.01586. [Google Scholar]
- de Fitte, P.R. Almost periodicity and periodicity for nonautonomous random dynamical systems. Stochastics Dyn. 2020, 21, 2150034. [Google Scholar] [CrossRef]
- Marie, N.; Fitte, P.R.D. Almost periodic and periodic solutions of differential equations driven by the fractional Brownian motion with statistical application. Stochastics 2020, 93, 886–906. [Google Scholar] [CrossRef]
- Zhang, C. Pseudo almost periodic solutions of some differential equations. J. Math. Anal. Appl. 1994, 181, 62–76. [Google Scholar] [CrossRef]
- Diagana, T. Weighted pseudo-almost periodic functions and applications. Comptes Rendus Math. 2006, 343, 643–646. [Google Scholar] [CrossRef]
- Es-saiydy, M.; Zitane, M. New composition theorem for weighted stepanov-like pseudo almost periodic functions on time scales and applications. Bol. Soc. Parana. Mat. 2023, in press. [CrossRef]
- Yan, Z. Sensitivity analysis for a fractional stochastic differential equation with S-p-weighted pseudo almost periodic coefficients and infinite delay. Fract. Calc. Appl. Anal. 2022, 25, 2356–2399. [Google Scholar] [CrossRef]
- M’Hamdi, M.S. On the weighted pseudo almost-periodic solutions of static DMAM neural network. Neural Process. Lett. 2022, 54, 4443–4464. [Google Scholar] [CrossRef]
- Hu, P.; Huang, C.M. Delay dependent asymptotic mean square stability analysis of the stochastic exponential Euler method. J. Comput. Appl. Math. 2021, 382, 113068. [Google Scholar] [CrossRef]
- Zhang, T.W.; Li, Y.K. Exponential Euler scheme of multi-delay Caputo-Fabrizio fractional-order differential equations. Appl. Math. Lett. 2022, 124, 107709. [Google Scholar] [CrossRef]
- Bessaih, H.; Garrido-Atienza, M.J.; Köpp, V.; Schmalfuß, B.; Yang, M. Synchronization of stochastic lattice equations. Nonlinear Differ. Equ. Appl. Nodea 2020, 27, 36. [Google Scholar] [CrossRef]
- Han, X.Y.; Kloeden, P.E. Sigmoidal approximations of Heaviside functions in neural lattice models. J. Differ. Equ. 2020, 268, 5283–5300. [Google Scholar] [CrossRef]
- Han, X.Y.; Kloden, P.E.; Usman, B. Upper semi-continuous convergence of attractors for a Hopfield-type lattice model. Nonlinearity 2020, 33, 1881–1906. [Google Scholar] [CrossRef]
- Kuang, J.C. Applied Inequalities; Shandong Science and Technology Press: Shandong, China, 2012. [Google Scholar]
- Arnold, L. Random Dynamical Systems; Springer: Berlin, Germany, 1998. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Zhang, T.; Li, Z. Weighted Pseudo-θ-Almost Periodic Sequence and Finite-Time Guaranteed Cost Control for Discrete-Space and Discrete-Time Stochastic Genetic Regulatory Networks with Time Delays. Axioms 2023, 12, 682. https://doi.org/10.3390/axioms12070682
Sun S, Zhang T, Li Z. Weighted Pseudo-θ-Almost Periodic Sequence and Finite-Time Guaranteed Cost Control for Discrete-Space and Discrete-Time Stochastic Genetic Regulatory Networks with Time Delays. Axioms. 2023; 12(7):682. https://doi.org/10.3390/axioms12070682
Chicago/Turabian StyleSun, Shumin, Tianwei Zhang, and Zhouhong Li. 2023. "Weighted Pseudo-θ-Almost Periodic Sequence and Finite-Time Guaranteed Cost Control for Discrete-Space and Discrete-Time Stochastic Genetic Regulatory Networks with Time Delays" Axioms 12, no. 7: 682. https://doi.org/10.3390/axioms12070682
APA StyleSun, S., Zhang, T., & Li, Z. (2023). Weighted Pseudo-θ-Almost Periodic Sequence and Finite-Time Guaranteed Cost Control for Discrete-Space and Discrete-Time Stochastic Genetic Regulatory Networks with Time Delays. Axioms, 12(7), 682. https://doi.org/10.3390/axioms12070682





