Statistical Analysis of Type-II Generalized Progressively Hybrid Alpha-PIE Censored Data and Applications in Electronic Tubes and Vinyl Chloride

Abstract

A new Type-II generalized progressively hybrid censoring strategy, in which the experiment is ensured to stop at a specified time, is explored when the lifetime model of the test subjects follows a two-parameter alpha-power inverted exponential (Alpha-PIE) distribution. Alpha-PIE’s parameters and reliability indices, such as reliability and hazard rate functions, are estimated via maximum likelihood and Bayes estimation methodologies in the presence of the proposed censored data. The estimated confidence intervals of the unknown quantities are created using the normal approximation of the acquired classical estimators. The Bayesian estimators are also produced using independent gamma density priors under symmetrical (squared-error) loss. The Bayes’ estimators and their associated highest posterior density intervals cannot be calculated theoretically since the joint likelihood function is derived in a complicated form, but they can potentially be assessed using Monte Carlo Markov-chain algorithms. We next go through four optimality criteria for identifying the best progressive design. The effectiveness of the suggested estimation procedures is assessed using Monte Carlo comparisons, and certain recommendations are offered. Ultimately, two different applications, one focused on the failure times of electronic tubes and the other on vinyl chloride, are analyzed to illustrate the effectiveness of the proposed techniques that may be employed in real-world scenarios.

1. Introduction

Inverted exponential distribution has been popularly used in several sectors such as engineering, biology, medicine, and others. It has an inverted bathtub failure rate, which describes the relative failure rate, which initially increases, comes to a head after some time, and then decreases over time. A new simple two-parameter alpha power-inverted exponential distribution (denoted as Alpha-PIE($\alpha ,\mu$)) has been proposed by Ünal et al. [1] as an extension of the conventional inverted exponential distribution. They also stated, by making use of two lifetime data sets, that the Alpha-PIE model offers superior fits to some other lifetime models, namely, Lindley, inverted exponential, generalized inverted exponential, and inverted Rayleigh distributions. However, a lifetime random variable X is said to have the Alpha-PIE$(\alpha ,\mu )$ distribution, where $\vartheta ={(\alpha ,\mu )}^{\mathsf{T}}$ is a vector of the model parameters, if its probability density function (PDF) $f(·)$; cumulative distribution function, say $F(·)$ (CDF); reliability function, say $R(·)$ (RF); and hazard rate function, say $h(·)$ (HRF), are provided by

$$f(x;\vartheta )=\frac{\mu log\left(\alpha \right)}{\alpha -1}{x}^{-2}exp\left(-\frac{\mu }{x}\right){\alpha }^{exp\left(-\frac{\mu }{x}\right)},x>0,\alpha \ne 1,$$

(1)

$$F(x;\vartheta )=\frac{{\alpha }^{exp\left(-\frac{\mu }{x}\right)}-1}{\alpha -1},$$

(2)

$$R(x;\vartheta )=\frac{\alpha }{\alpha -1}\left(1-{\alpha }^{exp\left(-\frac{\mu }{x}\right)-1}\right),x>0,$$

(3)

and

$$h(x;\vartheta )=\frac{\mu log\left(\alpha \right)x^{-2}exp\left(-\frac{\mu }{x}\right){\alpha }^{exp\left(-\frac{\mu }{x}\right)-1}}{\left(1-{\alpha }^{exp\left(-\frac{\mu }{x}\right)-1}\right)},$$

(4)

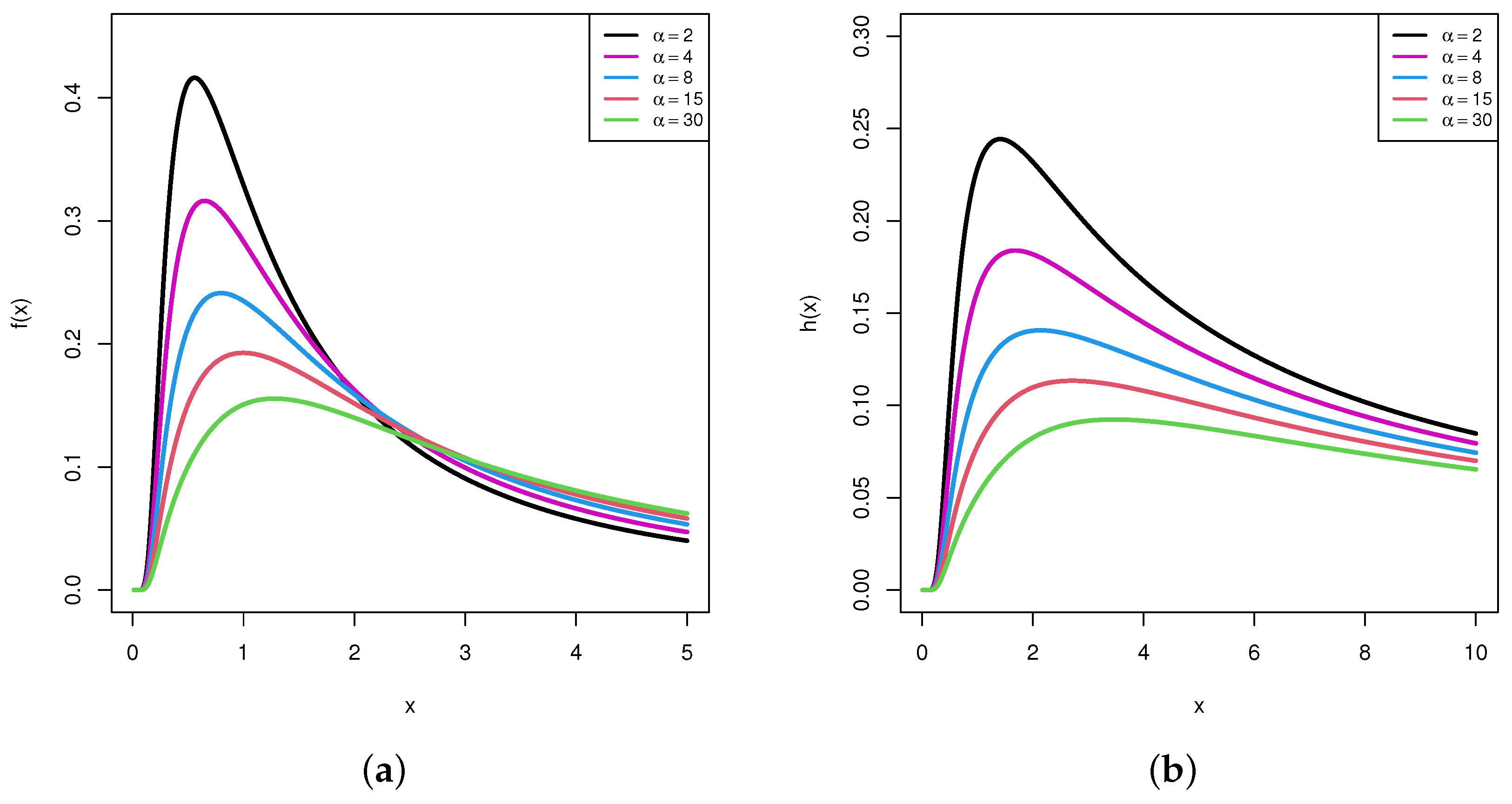
respectively, where $\alpha >0$ and $\mu >0$ are the shape and scale parameters, respectively. Obviously, when we put $\alpha \to 1$, the alpha-PIE distribution is reduced to the inverted exponential distribution by Keller et al. [2]. When we fix $\mu =1$ and consider different values of $\alpha$, in Figure 1, several shapes for the PDF and HRF of the Alpha-PIE distribution are demonstrated. This shows that the density of the alpha-PIE distribution is unimodal, while its HRF is a monotonically increasing function. Recently, in the presence of complete data, Amjad et al. [3] derived various Bayes estimators of the alpha-PIE parameters and stated that the alpha-PIE model behaved better than the inverted exponential and generalized inverted exponential models.

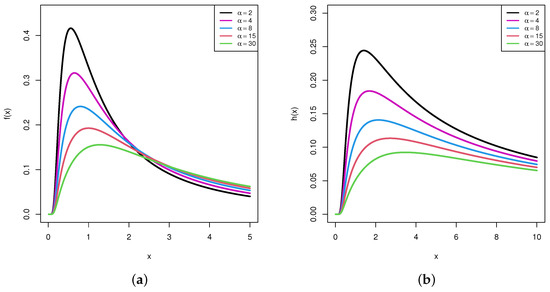
Figure 1. Plots for the PDF (a) and HRF (b) of the alpha-PIE distribution when $\mu =1$.

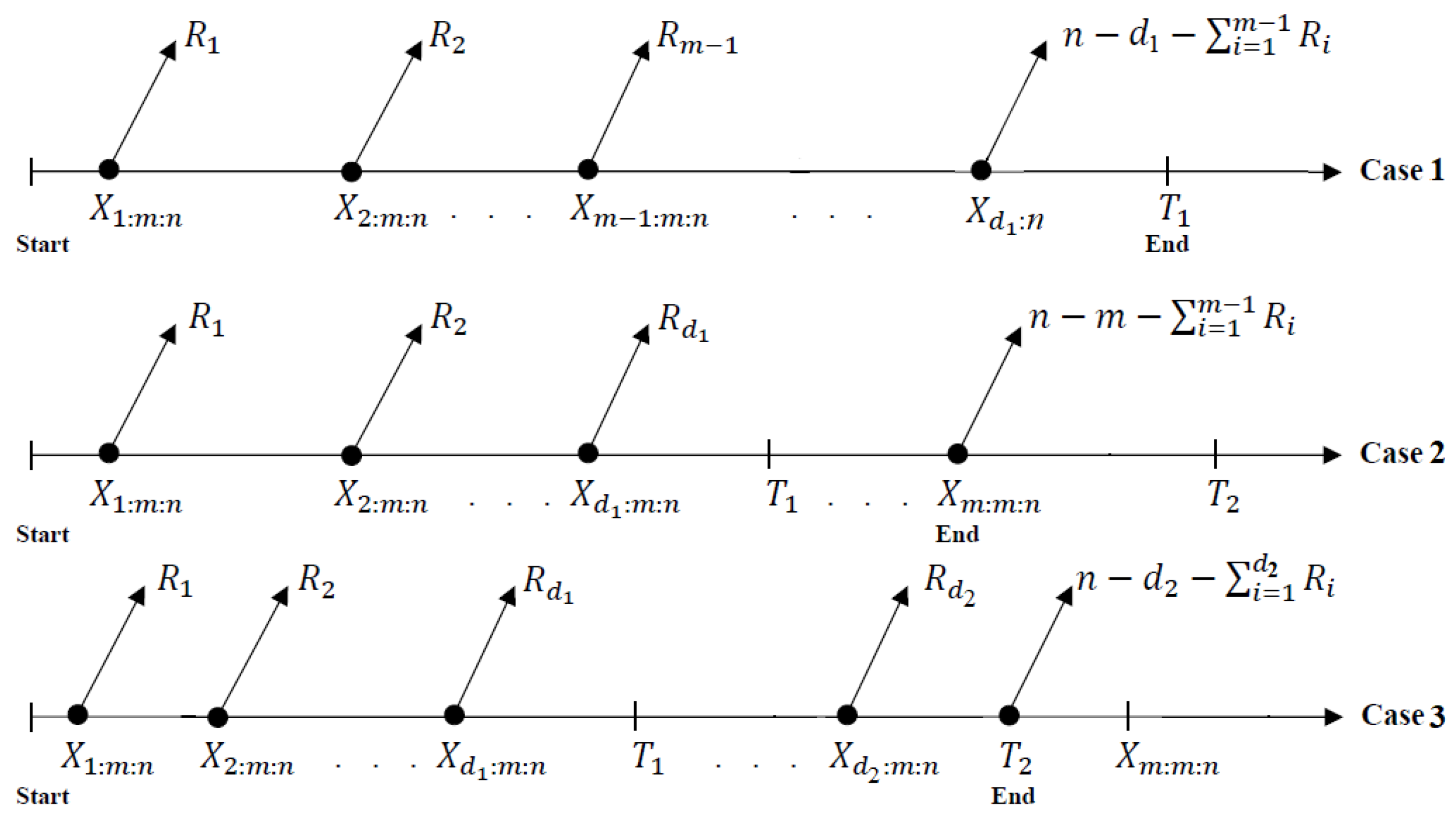
In a reliability context, the failure time data of the experimental objects are frequently not totally accessible, so minimizing both the expense and duration of the experiment is critical for any researcher. Progressive Type-II censoring (PTIIC) was proposed to allow the experimenter to remove items at times other than the stop time. This technique may be advantageous when some of the live test objects that are removed early on can be used again for future tests or when a balance between observing even some extreme lifetimes and reducing testing duration is desired, one may refer to Balakrishnan and Cramer [4] for additional details. Recently, if PCS-II is applied, because of the lengthy lifespan of many items, particularly electronics, the total experimental time might be quite long. This is the main drawback of PTIIC sampling. Therefore, to ensure that the experiment is completed at a specified optimal time without losing the ability to collect an effective number of observable failures, a generalized Type-II progressively hybrid censored (GTIIPHC) strategy was introduced by Lee et al. [5]. This strategy starts with putting n independent items into a test at time zero, specifying two threshold points of failures, $T_i,i=1,2$ and the desired number m, where ($1<m\le n$), and designing the progressive censoring $\mathbf{R}=(R_1,R_2,\dots ,R_m)$. When the experimenter records the first failure (say $X_{1:m:n}$), $R_1$ items are randomly chosen from $n-1$ and removed from the test; next, at the second failure (say $X_{2:m:n}$), $R_2$ items are randomly chosen from $n-R_1-2$ and out of the test, and so on. At ${\mathcal{T}}^{*}=\max \left\{\min \left\{X_{m:m:n},T_2\right\},T_1\right\}$, where $0<T_1<T_2$, the test is stopped and all remaining survival subjects are removed. Note that ($d_1,d_2$) represents the size of recorded failures up to ($T_1,T_2$).

If $X_{m:n}<T_1$, the test is stopped at $T_1$ (Case 1) without any additional removals. If $T_1<X_{m:m:n}<T_2$, similar to the PTIIC, the test is stopped at $X_{m:m:n}$ (Case-2); otherwise, the test is stopped at $T_2$ (Case-3). Thus, the partitioner will collect one of the samples:

$$\{\mathbf{X},\mathbf{R}\}=\left\{\begin{array}{ccc}\{(X_{1:m:n},R_1),\dots ,(X_{m-1:m:n},R_{m-1}),(X_{m:m:n},0),\dots ,(X_{d_1:n},0)\};\hfill & & \mathrm{Case-}1,\\ \{(X_{1:m:n},R_1),\dots ,(X_{d_1:n},R_{d_1}),\dots ,(X_{m-1:m:n},R_{m-1}),(X_{m:m:n},R_m)\};\hfill & & \mathrm{Case-}2,\\ \{(X_{1:m:n},R_1),\dots ,(X_{d_1:n},R_{d_1}),\dots ,(X_{d_2-1:n},R_{d_2-1}),(X_{d_2:n},R_{d_2})\};\hfill & & \mathrm{Case-}3.\end{array}\right.$$

Let $\{\mathbf{X},\mathbf{R}\}$ be the censoring members of GTIIPHC in a distribution with a PDF and CDF. Therefore, the joint likelihood function, say ${\mathcal{L}}_q(·)$, of the proposed censoring mechanism can be expressed as

$${\mathcal{L}}_q\left(\vartheta \right|\mathbf{X})=K_q{\Re }_q(T_{\tau };\vartheta )\prod _{i=1}^{D_q}f(x_{i:m:n};\vartheta ){\left[1-F(x_{i:m:n};\vartheta )\right]}^{R_i},q=1,2,3,$$

(5)

where ${\Re }_q(·)$ is a composite term of reliability functions and $\tau =1,2$.

It is critical to note that the GTIIPHC modifies the Type-II progressive hybrid censoring (PHC), proposed by Childs et al. [6], by guaranteeing that the test is completed at the specified time $T_2$. Thus, $T_2$ is the greatest duration that the examiner is willing to allow the test to continue. Table 1 lists the GTIIPHC notations. Furthermore, from (5), six sampling plans can be introduced and provided in Table 2. A diagrammatic demonstration of GTIIPHC sampling is depicted in Figure 2.

Table 1. The GTIIPHC notations.

q	${\mathit{K}}_{\mathit{q}}$	${\mathit{D}}_{\mathit{q}}$	${\mathit{\Re }}_{\mathit{q}}({\mathit{T}}_{\mathit{\tau }};\mathit{\vartheta })$	${\mathit{R}}_{{\mathit{d}}_{\mathit{\tau }}+1}^{*}$
1	${\Pi }_{i=1}^{d_1}{\sum }_{k=i}^m\left(R_k+1\right)$	$d_1$	${\left[1-F\left(T_1\right)\right]}^{R_{d_1+1}^{*}}$	$n-d_1-{\sum }_{k=1}^{m-1}{R}_k$
2	${\Pi }_{i=1}^m{\sum }_{k=i}^m\left(R_k+1\right)$	m	1	0
3	${\Pi }_{i=1}^{d_2}{\sum }_{k=i}^m\left(R_k+1\right)$	$d_2$	${\left[1-F\left(T_2\right)\right]}^{R_{d_2+1}^{*}}$	$n-d_2-{\sum }_{k=1}^{d_2}{R}_k$

Table 2. Special sampling plans from GTIIPHC.

Plan	Author(s)	Setting
Type-I PHC	Kundu and Joarder [7]	$T_1\to 0$
Type-II PHC	Childs et al. [6]	$T_2\to \infty$
Type-I Hybrid	Epstein [8]	$T_1\to 0$, $R_i=0,i=1, 2, \dots , m-1,$ and $R_m=n-m$
Type-II Hybrid	Childs et al. [9]	$T_2\to \infty$, $R_i=0,i=1, 2, \dots , m-1,$ and $R_m=n-m$
Type-I censoring	Epstein and Sobel [10]	$T_1=0$, $m=n$, $R_i=0,i=1, 2, \dots , m-1,$ and $R_m=n-m$
Type-II censoring	Epstein and Sobel [10]	$T_1=0$, $T_2\to \infty$, $R_i=0,i=1, 2, \dots , m-1,$ and $R_m=n-m$

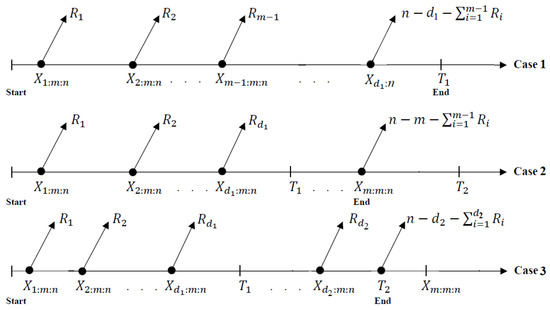
Figure 2. Diagram of GTIIPHC sampling.

In the context of GTIIPHC data, several researchers have carried out important research on the statistical estimation of unknown parameter(s) and/or reliability time functions in various lifetime models; for example, Ashour and Elshahhat [11] studied both frequentist and Bayes estimators of the Weibull parameters; Ateya and Mohammed [12] studied the prediction issue of the Burr-XII failure times; Seo [13] discussed the Bayesian inference of Weibull’s model; Cho and Lee [14] analyzed the competing risks from exponential data; Nagy et al. [15] pointed out different estimates of the Burr-XII parameters; Wang et al. [16] derived various estimators of the Kumaraswamy parameters; Elshahhat et al. [17] addressed the Nadarajah–Haghighi parameters; later, Alotaibi et al. [18] estimated the Fréchet Parameters.

Although there are many studies that give a mathematical treatment to the proposed distribution, they do not shed light on the application aspects of the alpha-PIE distribution, especially in reliable practice. To our understanding, no study has been performed to evaluate the parameters or reliability features of the alpha-PIE lifetime model when an incomplete dataset is available. Thus, to resolve this issue, our objectives in this work are fourfold:

• Derive the maximum likelihood estimators (MLEs) in addition to their two-sided approximate confidence intervals (ACIs), using observed Fisher’s information, of the alpha-PIE parameters $\alpha$ and $\mu$ or any associated function such as $R\left(t\right)$ and $h\left(t\right)$.
• Derive the Bayes’ estimators in addition to their two-sided highest posterior density (HPD) intervals, under independent gamma priors assumption, of $\alpha$, $\mu$, $R\left(t\right)$, and $h\left(t\right)$ using the squared error loss (SEL) function.
• To select the best progressive censoring patterns among various competing strategies, several criteria of optimality are proposed.
• Via extensive Monte Carlo simulations, on the basis of four accuracy criteria, namely, (i) root mean squared-errors, (ii) mean relative absolute biases, (iii) average confidence lengths, and (iv) coverage percentages, the performance of the acquired estimators is examined. Additionally, two real-word applications from the engineering and chemistry sectors, to evaluate how the offered approaches operate in practice and to choose the best censoring strategy, are examined.

The organization of the article is as follows: Section 2 and Section 3 provide the point and interval inferences using frequentist and Bayes approaches. Simulation results are obtained and discussed in Section 4. Section 5 examines two applications of actual data sets. Optimum criteria of progressive patterns are presented in Section 6. Lastly, Section 7 lists the study’s conclusions.

2. Classical Inference

This section investigates the maximum likelihood and approximate asymptotic interval estimators of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$.

2.1. Maximum Likelihood Estimators

Suppose $\mathbf{x}=\{x_{i:m:n},R_i\}$ for $i=1, \dots , d_2$ is a GTIIPHC sample of size $d_2$ collected from the alpha-PIE population with PDF (1) and CDF (2). Substitute (1) and (2) into (5). Utilizing $x_i$ in place of $x_{i:m:n}$, the likelihood function of GTIIPHC (5), ignoring the constant term, can be expressed as

$$\begin{array}{c}\hfill {\mathcal{L}}_q\left(\vartheta \right|\mathbf{x})\propto {\xi }_q\left(T_{\tau };\vartheta \right){\left(\frac{\alpha }{\alpha -1}\right)}^n{\left(\frac{\mu log\left(\alpha \right)}{\alpha }\right)}^{D_q}{e}^{-{\sum }_{i=1}^{D_q}\eta \left(x_i,R_i;\vartheta \right)},q=1,2,3,\end{array}$$

(6)

where ${\xi }_1\left(T_1;\vartheta \right)={\left[\frac{\alpha }{\alpha -1}\left(1-{\alpha }^{exp(-\mu T_1^{-1})-1}\right)\right]}^{R_{d_1+1}^{*}}$, ${\xi }_3\left(T_2;\vartheta \right)={\left[\frac{\alpha }{\alpha -1}\left(1-{\alpha }^{exp(-\mu T_2^{-1})-1}\right)\right]}^{R_{d_2+1}^{*}}$, ${\xi }_2\left(T_{\tau };\vartheta \right)=1$ and $\eta \left(x_i,R_i;\vartheta \right)=\mu x_i^{-1}-exp(-\mu x_i^{-1})\log \left(\alpha \right)-R_i\log \left(1-{\alpha }^{exp(-\mu x_i^{-1})-1}\right).$

Consequently, the natural logarithm of (6) becomes

$$log{\mathcal{L}}_q\left(\vartheta \right|\mathbf{x})\propto {\zeta }_q\left(T_{\tau };\vartheta \right)+nlog\left(\frac{\alpha }{\alpha -1}\right)+D_{q}log\left(\frac{\mu log\left(\alpha \right)}{\alpha }\right)-{\sum }_{i=1}^{D_q}\eta \left(x_i,R_i;\vartheta \right),$$

(7)

where ${\zeta }_1\left(T_1;\vartheta \right)=R_{d_1+1}^{*}log\left[\frac{\alpha }{\alpha -1}\left(1-{\alpha }^{exp(-\mu T_1^{-1})-1}\right)\right],$ ${\zeta }_2\left(T_{\tau };\vartheta \right)=0$, and ${\zeta }_3\left(T_2;\vartheta \right)=R_{d_2+1}^{*}log\left[\frac{\alpha }{\alpha -1}\left(1-{\alpha }^{exp(-\mu T_2^{-1})-1}\right)\right].$

To acquire the MLEs $\widehat{\alpha }$ and $\widehat{\mu }$ of $\alpha$ and $\mu$, respectively, by differentiating (7) with regard to $\alpha$ and $\mu$, we obtain the following normal equations:

$$\frac{\partial }{\partial \alpha }log{\mathcal{L}}_q\left(\left.\vartheta \right|\mathbf{x}\right)={\zeta }_q^{\circ }\left(T_{\tau };\vartheta \right)+\frac{1}{\alpha }\left[D_q\left({log}^{-1}\left(\alpha \right)-1\right)-\frac{n}{\alpha -1}\right]-{\sum }_{i=1}^{D_q}{\eta }^{\circ }\left(x_i,R_i;\vartheta \right),$$

(8)

and

$$\frac{\partial }{\partial \mu }log{\mathcal{L}}_q\left(\left.\vartheta \right|\mathbf{x}\right)={\zeta }_q^{•}\left(T_{\tau };\vartheta \right)+D_q{\mu }^{-1}-{\sum }_{i=1}^{D_q}{\eta }^{•}\left(x_i,R_i;\vartheta \right),$$

(9)

where ${\zeta }_2^{\circ }\left(T_{\tau };\vartheta \right)={\zeta }_2^{•}\left(T_{\tau };\vartheta \right)=0,$ ${\zeta }_q^{\circ }\left(T_{\tau };\vartheta \right)=-\frac{R_{d_{\tau }+1}^{*}}{(\alpha -1)R\left(T_{\tau };\alpha ,\mu \right)}\{{\alpha }^{exp(-\mu T_{\tau }^{-1})-1}{e}^{-\mu T_{\tau }^{-1}}-{(\alpha -1)}^{-1}$$[{\alpha }^{exp(-\mu T_{\tau }^{-1})-1}-1]\}$, and ${\zeta }_q^{•}\left(T_{\tau };\vartheta \right)=\frac{R_{d_{\tau }+1}^{*}}{(\alpha -1)T_{\tau }R\left(T_{\tau };\alpha ,\mu \right)}{\alpha }^{exp(-\mu T_{\tau }^{-1})}log\left(\alpha \right)e^{-\mu T_{\tau }^{-1}}.$

It is more clear, due to the complex expressions in (8) and (9), that the MLEs $\widehat{\alpha }$ and $\widehat{\mu }$ cannot be derived in closed form. Applying the Newton–Raphson procedure via the ’$\mathsf{maxLik}$’ package, proposed by Henningsen and Toomet [19], the offered estimators can be directly evaluated. Once $\widehat{\alpha }$ and $\widehat{\mu }$ are obtained, replacing $\alpha$ and $\mu$ in (3) and (4) by their MLEs $\widehat{\alpha }$ and $\widehat{\mu }$, the MLEs $\widehat{R}\left(t\right)$ and $\widehat{h}\left(t\right)$ of $R\left(t\right)$ and $h\left(t\right)$, for a mission time $t>0$, are

$$\widehat{R}\left(t\right)=\frac{\widehat{\alpha }}{\widehat{\alpha }-1}\left(1-{\widehat{\alpha }}^{exp\left(-\frac{\widehat{\mu }}{t}\right)-1}\right),$$

and

$$\widehat{h}\left(t\right)=\frac{\widehat{\mu }log\left(\widehat{\alpha }\right)t^{-2}exp\left(-\frac{\widehat{\mu }}{t}\right){\widehat{\alpha }}^{exp\left(-\frac{\widehat{\mu }}{t}\right)-1}}{\left(1-{\widehat{\alpha }}^{exp\left(-\frac{\widehat{\mu }}{t}\right)-1}\right)},$$

respectively.

In addition to obtaining a point estimate for an unknown parameter, it is also beneficial to obtain a limit of values that may include the real parameter with a given degree of confidence, this methodology is called interval estimation. Therefore, in the next subsection, we shall derive the ACIs of all unknown quantities of our interest.

2.2. Asymptotic Interval Estimators

To construct the $(1-ϵ)100\%$ ACIs for $\alpha$, $\mu$, $R\left(t\right)$ or $h\left(t\right)$, the asymptotic $2\times 2$ variance-covariance (inverted Fisher information) matrix must be first obtained. Following mild regularity conditions, we can say that $\widehat{\vartheta }$ has an approximately normal distribution, i.e., $\vartheta \sim N(\vartheta ,{\mathbf{I}}^{-1}\left(\vartheta \right))$. By replacing $\alpha$ and $\mu$ by $\widehat{\alpha }$ and $\widehat{\mu }$, respectively, one can estimate ${\mathbf{I}}^{-1}\left(\vartheta \right)$ by ${\mathbf{I}}^{-1}\left(\widehat{\vartheta }\right)$ (see Lawless [20]), as

$${\mathbf{I}}^{-1}\left(\widehat{\vartheta }\right)\cong {\left[\begin{array}{c}-{\mathcal{F}}_{11}-{\mathcal{F}}_{12}\\ -{\mathcal{F}}_{21}-{\mathcal{F}}_{22}\end{array}\right]}_{}^{-1}=\left[\begin{array}{c}{\widehat{v}}_{11}{\widehat{v}}_{12}\\ {\widehat{v}}_{21}{\widehat{v}}_{22}\end{array}\right],$$

(10)

where $\widehat{\vartheta }={(\widehat{\alpha },\widehat{\mu })}^{\mathsf{T}}$ and ${\mathcal{F}}_{ij},i,j=1,2$ are presented in Appendix A. Therefore, the two-sided $100(1-ϵ)100\%$ ACIs for $\alpha$ and $\mu$ are given by

$$\left(\widehat{\alpha }\mp z_{ϵ/2}\sqrt{{\widehat{v}}_{11}}\right)\mathrm{and}\left(\widehat{\mu }\mp z_{ϵ/2}\sqrt{{\widehat{v}}_{22}}\right),$$

respectively, where $z_{ϵ/2}$ refers to the upper $ϵ/2$ percentage level for the distribution of the standard normal.

On the other hand, to build the two-sided $100(1-ϵ)100\%$ ACIs of RF $R\left(t\right)$ and HRF $h\left(t\right)$, following Greene [21], the delta method is considered to derive the estimated variances ${\widehat{v}}_R$ and ${\widehat{v}}_h$ of $\widehat{R}\left(t\right)$ and $\widehat{h}\left(t\right)$, respectively, as

$${\widehat{v}}_R={\left.{\mathcal{C}}_R^{\mathsf{T}}{\mathbf{I}}^{-1}\left(\vartheta \right){\mathcal{C}}_R\right|}_{(\widehat{\alpha },\widehat{\mu })}\mathrm{and}{\widehat{v}}_h={\left.{\mathcal{C}}_h^{\mathsf{T}}{\mathbf{I}}^{-1}\left(\vartheta \right){\mathcal{C}}_h\right|}_{(\widehat{\alpha },\widehat{\mu })},$$

where ${\mathcal{C}}_R^{\mathsf{T}}=\left[\frac{\partial R\left(t\right)}{\partial \alpha }\frac{\partial R\left(t\right)}{\partial \mu }\right]$ and ${\mathcal{C}}_h^{\mathsf{T}}=\left[\frac{\partial h\left(t\right)}{\partial \alpha }\frac{\partial h\left(t\right)}{\partial \mu }\right]$.

Therefore, the $(1-ϵ)100\%$ ACIs of $R\left(t\right)$ and $h\left(t\right)$ are given by

$$\left(\widehat{R}\left(t\right)\mp z_{ϵ/2}\sqrt{{\widehat{v}}_R}\right)\mathrm{and}\left(\widehat{h}\left(t\right)\mp z_{ϵ/2}\sqrt{{\widehat{v}}_h}\right),$$

respectively.

3. Bayes Inference

In this section, the Bayes estimators of $\alpha$, $\mu$, $R\left(t\right)$, and $h\left(t\right)$, along with their HPD intervals, based on the SEL, are obtained.

3.1. Prior Functions

In practice, the Bayesian technique might leverage additional prior information, such as historical data or expertise in the statistical inferential process, to obtain more accurate estimates for tests with small sample sizes or when censored data are available. Regarding Bayes’ reliability analysis, several recent works have addressed this issue; see, for example, Chen and Ye [22], Wang et al. [23], Luo et al. [24], and Luo and Xu [25]. To acquire the Bayes point estimator of $\alpha$, $\mu$, $R\left(t\right)$ or $h\left(t\right)$, we suppose that $\alpha$ and $\mu$ are independent and distributed with gamma (G) density priors, i.e., $\alpha \sim G(a_1,b_1)$ and $\mu \sim G(a_2,b_2)$, respectively. We employ gamma priors, which are regarded as having greater adaptability than others, and adjust them to the parameters’ support. Furthermore, the independent gamma priors are plain and unambiguous, potentially avoiding many complex inferential concerns. Then, the joint prior PDF of $\alpha$ and $\mu$, denoted by $\rho (·)$, is

$$\rho (\alpha ,\mu )\propto {\alpha }^{a_1-1}{\mu }^{a_2-1}exp\left(-(\alpha b_1+\mu b_2)\right),$$

(11)

where $a_i>0$ and $b_i>0$ for $i=1,2,$ must be known. In the next subsections, we derive the Bayes point and HPD interval estimators of $\alpha$, $\mu$, $R\left(t\right)$, or $h\left(t\right)$.

3.2. Bayes Estimators

From (5) and (11), the joint posterior PDF (say $\mathcal{Q}(·)$) of $\alpha$ and $\mu$ becomes

$${\mathcal{Q}}_q\left(\left.\vartheta \right|\mathbf{x}\right)\propto \frac{{\alpha }^{n+a_1-D_q-1}{\mu }^{D_q-a_2-1}}{{\left(\alpha -1\right)}^n{\left(log\left(\alpha \right)\right)}^{D_q}}{\xi }_q\left(T_{\tau };\vartheta \right)e^{-\left(b_1\alpha +b_2\mu +{\sum }_{i=1}^{D_q}\eta \left(x_i,R_i;\vartheta \right)\right)},q=1,2,3,$$

(12)

where its normalizing term, say ${\mathcal{Q}}_q^{*}$, is given by

$${\mathcal{Q}}_q^{*}={\int }_0^{\infty }{\int }_0^{\infty }\frac{{\alpha }^{n+a_1-D_q-1}{\mu }^{D_q-a_2-1}}{{\left(\alpha -1\right)}^n{\left(log\left(\alpha \right)\right)}^{D_q}}{\xi }_q\left(T_{\tau };\vartheta \right)e^{-\left(b_1\alpha +b_2\mu +{\sum }_{i=1}^{D_q}\eta \left(x_i,R_i;\vartheta \right)\right)},\mathrm{d}\alpha \mathrm{d}\mu .$$

Under the SEL, the Bayes estimate (say $\tilde{\pi }(·)$) of any parametric function of $\alpha$ and $\mu$ (say $\pi (·)$) is known as the posterior mean of (12); for example,

$$\tilde{\pi }(\alpha ,\mu )={\int }_0^{\infty }{\int }_0^{\infty }\pi (\alpha ,\mu ){\mathcal{Q}}_q\left(\left.\vartheta \right|\mathbf{x}\right)\mathrm{d}\alpha \mathrm{d}\mu .$$

(13)

It is clear, from (13), that the Bayes estimate of $\alpha$ or $\mu$ cannot be extracted analytically because the posterior expectation involves double integrals in both the numerator and the denominator, and Bayes expressions of $\alpha$ and $\mu$ thus cannot be easily extracted. As a result, the Bayes Markov chain Monte Carlo (MCMC) process is used to create samples from which the offered Bayes estimates and HPD intervals can be obtained.

To start the MCMC technique, from (12), the full conditionals PDFs of $\alpha$ and $\mu$ are

$${\mathcal{Q}}_q^{\alpha }\left(\left.\alpha \right|\mathbf{x},\mu \right)\propto \frac{{\alpha }^{n+a_1-D_q-1}}{{\left(\alpha -1\right)}^n{\left(log\left(\alpha \right)\right)}^{D_q}}{\xi }_q\left(T_{\tau };\vartheta \right)e^{-\left(b_1\alpha +{\sum }_{i=1}^{D_q}\eta \left(x_i,R_i;\vartheta \right)\right)},$$

(14)

and

$${\mathcal{Q}}_q^{\mu }\left(\left.\mu \right|\mathbf{x},\alpha \right)\propto {\mu }^{D_q-a_2-1}{\xi }_q\left(T_{\tau };\vartheta \right)e^{-\left(b_2\mu +{\sum }_{i=1}^{D_q}\eta \left(x_i,R_i;\vartheta \right)\right)},$$

(15)

respectively.

Since Eqns. (14) and (15) of $\alpha$ and $\mu$, respectively, cannot be expressed analytically with any statistical model. Thus, the Metropolis-Hastings (M-H) algorithm discussed by Gelman et al. [26] and Lynch [27] is considered for this purpose. The following sampling process of M-H is adopted:

Step 1:

Set initial values ${\alpha }^{\left(0\right)}=\widehat{\alpha }$ and ${\mu }^{\left(0\right)}=\widehat{\mu }$.

Step 2:

Set $j=1$

Step 3:

Obtain ${\alpha }^{*}$ and ${\mu }^{*}$ from $N(\widehat{\alpha },{\widehat{v}}_{11})$ and $N(\widehat{\mu },{\widehat{v}}_{22})$, respectively.

Step 4:

Obtain ${\varphi }_{\alpha }=\frac{{\pi }_{\rho }^{\alpha }(\left.{\alpha }^{*}\right|{\mu }^{[j-1]},\mathbf{x})}{{\pi }_{\rho }^{\alpha }(\left.{\alpha }^{[j-1]}\right|{\mu }^{[j-1]},\mathbf{x})}$ and ${\varphi }_{\mu }=\frac{{\pi }_{\rho }^{\mu }\left(\left.{\mu }^{*}\right|{\alpha }^{\left[j\right]},\mathbf{x}\right)}{{\pi }_{\rho }^{\mu }\left(\left.{\mu }^{[j-1]}\right|{\alpha }^{\left[j\right]},\mathbf{x}\right)}$.

Step 5:

Obtain $u_1$ and $u_2$ from uniform $U(0,1)$ distribution.

Step 6:

If $u_{\alpha }⩽min\left\{1,{\varphi }_{\alpha }\right\}$ and $u_{\mu }⩽min\left\{1,{\varphi }_{\mu }\right\}$ set ${\alpha }^{\left[j\right]}={\alpha }^{*}$ and ${\mu }^{\left[j\right]}={\mu }^{*}$; else set ${\alpha }^{\left[j\right]}={\alpha }^{[j-1]}$ and ${\mu }^{\left[j\right]}={\mu }^{(j-1)}$, respectively.

Step 7:

Put $j=j+1$.

Step 8:

Redo Steps 3–7 for $\mathcal{B}$ times and obtain ${\alpha }^{\left[j\right]}$ and ${\mu }^{\left[j\right]}$ for $j=1, 2, \dots ,\mathcal{B}$.

Step 9:

Obtain the RF (3) and HRF (4) using $({\alpha }^{\left[j\right]},{\mu }^{\left[j\right]}),j=1, 2, \dots ,\mathcal{B}$, at $t>0$, respectively as

$$R^{\left[j\right]}\left(t\right)=\frac{{\alpha }^{\left[j\right]}}{{\alpha }^{\left[j\right]}-1}\left(1-{{\alpha }^{\left[j\right]}}^{exp\left(-{\mu }^{\left[j\right]}{t}^{-1}\right)-1}\right),$$

and

$$h^{\left[j\right]}\left(t\right)=\frac{{\mu }^{\left[j\right]}log\left({\alpha }^{\left[j\right]}\right)t^{-2}exp\left(-{\mu }^{\left[j\right]}{t}^{-1}\right){{\alpha }^{\left[j\right]}}^{exp\left(-{\mu }^{\left[j\right]}{t}^{-1}\right)-1}}{\left(1-{{\alpha }^{\left[j\right]}}^{exp\left(-{\mu }^{\left[j\right]}{t}^{-1}\right)-1}\right)}.$$

Step 10:

Obtain the Bayes estimate $\tilde{\pi }(·)$ of $\pi (·)$, after eliminating the first ${\mathcal{B}}^{*}$ samples as burn-in, as

$$\begin{array}{c}\hfill \tilde{\pi }(\alpha ,\mu )=\frac{1}{\mathcal{B}-{\mathcal{B}}^{*}}\sum _{j={\mathcal{B}}^{*}+1}^{\mathcal{B}}{\pi }^{\left[j\right]}(\alpha ,\mu ).\end{array}$$

Step 11:

Obtain the HPD interval of $\pi (·)$ via ordering ${\pi }^{\left[j\right]}(\alpha ,\mu )$ for $j={\mathcal{B}}^{*}+1,\dots ,\mathcal{B}$. Following Chen and Shao [28], the $(1-ϵ)100\%$ HPD interval of $\pi (\alpha ,\mu )$ is given by

$$\begin{array}{c}\hfill \left({\pi }^{\left(j^{*}\right)},{\pi }^{\left(j^{*}+\left(1-ϵ\right)\left(\mathcal{B}-{\mathcal{B}}^{*}\right)\right)}\right),\end{array}$$

where $j^{*}={\mathcal{B}}^{*}+1,\dots ,\mathcal{B}$ is specified such that

$${\delta }^{\left(j^{*}+\left[\left(1-ϵ\right)\left(\mathcal{B}-{\mathcal{B}}^{*}\right)\right]\right)}-{\pi }^{\left(j^{*}\right)}=\underset{1⩽j⩽ϵ\left(\mathcal{B}-{\mathcal{B}}^{*}\right)}{min}\left({\pi }^{\left(j+\left[\left(1-ϵ\right)\left(\mathcal{B}-{\mathcal{B}}^{*}\right)\right]\right)}-{\pi }^{\left[j\right]}\right),$$

where the highest integer less (or equal) than to y is denoted by $\left[y\right]$.

4. Monte Carlo Simulations

This section deals with comparing the behavior of the acquired frequentist and Bayes estimators of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$ obtained in the proceeding sections via extensive Monte Carlo simulations. This goal is developed based on large 1000 GPHC-T-II samples generated from two different groups of the alpha-PIE parameters, namely Set-1, Alpha-PIE$(1.2,0.2)$, and Set-2, Alpha-PIE$(1.5,0.5)$. For distinct time $t=0.1$, from Sets 1 and 2, the plausible values of ($R\left(t\right)$, $h\left(t\right)$) are (0.87509, 2.89008) and (0.99453, 0.27545), respectively. Several choices of $T_i,i=1,2$ (thresholds), n (total test items), m (effective test items), and $\mathbf{R}$ (progressive pattern) are also used, namely $(T_1,T_2)=(0.1,0.3)$ and (0.4,0.8), $n=(50,80)$. For each n, the value of m is determined as failure percentages (FPs) such as $\frac{m}{n}$ = (40,80)%. To assess the removal mechanism in GPHC-T-II, for each group $(n,m)$, three patterns of $(R_1,R_2,\dots ,R_m)$ are considered:

$$\begin{array}{cc}\mathrm{Scheme-}1:R_1\hfill & =n-m,R_i=0fori\ne 1,\hfill \\ \mathrm{Scheme-}2:R_{\frac{m}{2}}\hfill & =n-m,R_i=0fori\ne \frac{m}{2},\hfill \\ \mathrm{Scheme-}3:R_m\hfill & =n-m,R_i=0fori\ne m.\hfill \end{array}$$

As soon as 1000 GPHC-T-II data are collected, all suggested point (or interval) estimators created by maximum likelihood (or Bayes) inferential approaches of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$ are evaluated via $\mathsf{R}$ 4.2.2 programming software. Therefore, we recommend installing two statistical packages in $\mathsf{R}$, namely (i) ’$\mathsf{maxLik}$’ package (by Henningsen and Toomet [19]) to calculate the maximum likelihood estimates along with their 95% ACI estimates, (ii) ’$\mathsf{coda}$’ package (by Plummer et al. [29]) to evaluate the Bayes MCMC estimates for the same unknown parameters, as well as corresponding HPD interval estimations. Taking the classical estimates of $\alpha$ and $\mu$ as starting points, to compute the acquired Bayes point/interval estimates of $\alpha$, $\mu$, $R\left(t\right)$ or $h\left(t\right)$, we replicated the MCMC sampler 12,000 times and ignored the first 2000 times as burn-in. To demonstrate the performance of the Bayes findings on different gamma priors, following Kundu [30], two sets of the hyperparameters $(a_i,b_i),i=1,2$ are utilized, called

(a)

For Set-1:

• Prior-1:$(a_1,a_2)=(6,1)\mathrm{and}{b}_i=5\mathrm{for}i=1,2$;
• Prior-2:$(a_1,a_2)=(12,2)\mathrm{and}{b}_i=10\mathrm{for}i=1,2$.

(b)

For Set-2:

• Prior-1:$(a_1,a_2)=(7.5,2.5)\mathrm{and}{b}_i=5\mathrm{for}i=1,2$;
• Prior-2:$(a_1,a_2)=(15,5)\mathrm{and}{b}_i=10\mathrm{for}i=1,2$.

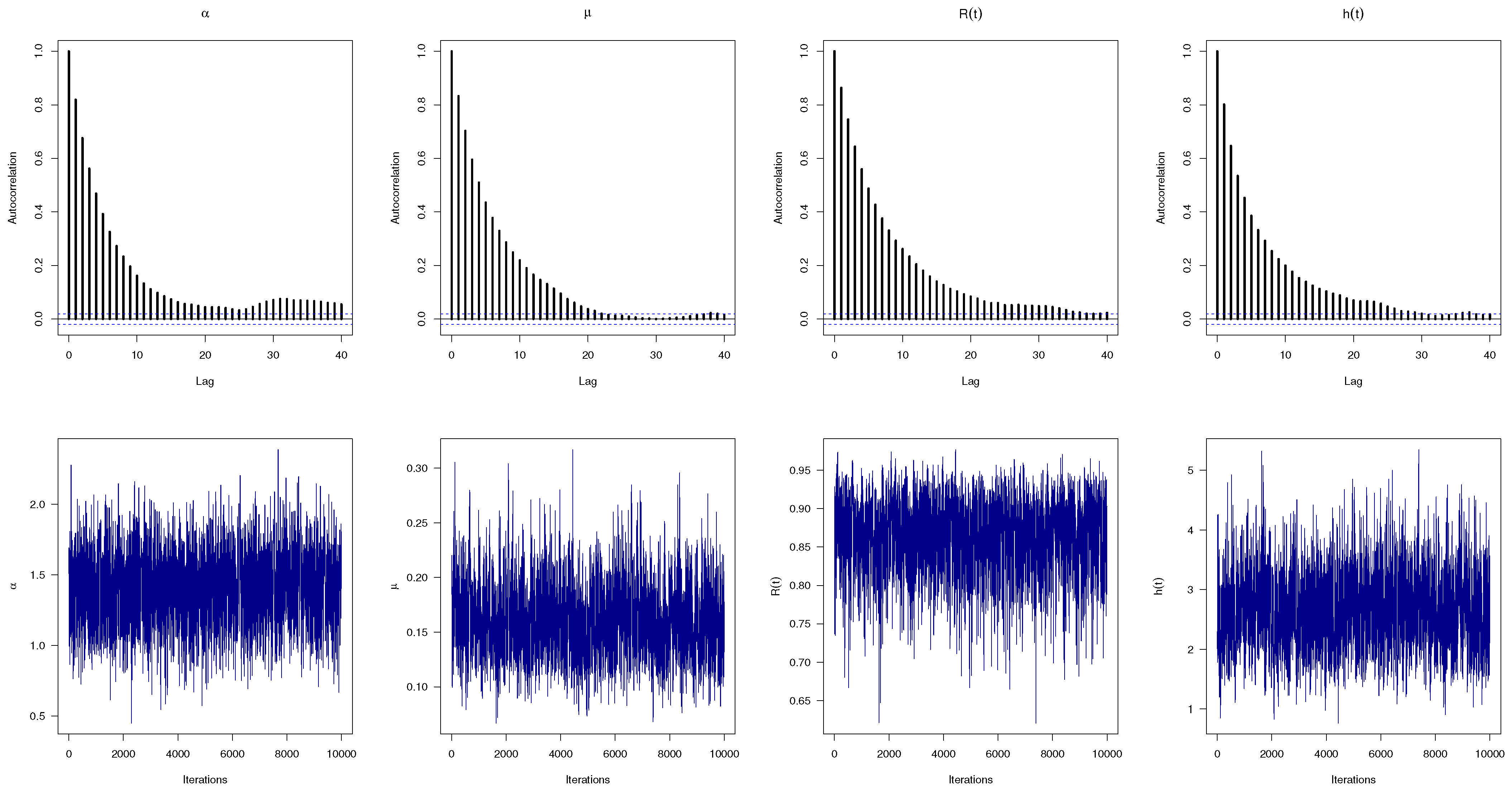
To examine the convergence status of the collected iterations of $\alpha$, $\mu$, $R\left(t\right)$, and $h\left(t\right)$ developed from the Bayes MCMC algorithm, for Set-1 along with Prior-1, $(T_1,T_2,n,m)=(0.1,0.3,50,20)$ and Scheme-1 as an example, the trace and autocorrelation plots are provided in Figure 3. Obviously, it is evident that the Markovian graphs of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$ are satisfactorily mixed, and thus, the results of the acquired points (or interval) become more significant.

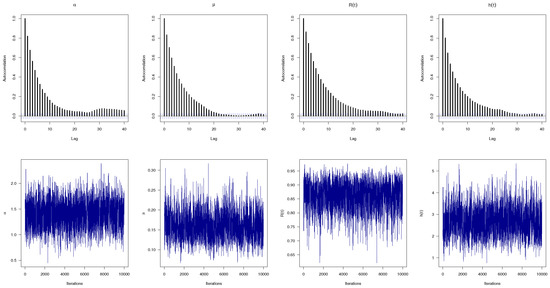
Figure 3. Autocorrelation (top) and trace (bottom) plots for MCMC draws of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$.

However, for each test, the average point estimates (Av.Es) of $\alpha$ are given by

$$\overline{\check{\alpha }}=\frac{1}{1000}{\sum }_{i=1}^{1000}{\check{\alpha }}^{\left(i\right)},$$

where ${\check{\alpha }}^{\left(i\right)}$ denotes the calculated estimate of $\alpha$ at the ith sample.

The acquired point estimates of $\alpha$ are compared based on their root mean squared-errors (RMSEs) and mean relative absolute biases (MRABs) as

$$\mathrm{RMSE}\left(\check{\alpha }\right)=\sqrt{\frac{1}{1000}{\sum }_{i=1}^{1000}{\left({\check{\alpha }}^{\left(i\right)}-\alpha \right)}^2},$$

and

$$\mathrm{MRAB}\left(\check{\alpha }\right)=\frac{1}{1000}{\sum }_{i=1}^{1000}\frac{1}{\alpha }\left|{\check{\alpha }}^{\left(i\right)}-\alpha \right|,$$

respectively.

Further, the acquired interval estimates of $\alpha$ are compared with regard to their average confidence lengths (ACLs) and coverage percentages (CPs) as

$${\mathrm{ACL}}_{(1-ϵ)\%}\left(\alpha \right)=\frac{1}{1000}{\sum }_{i=1}^{1000}\left({\mathcal{U}}_{{\check{\alpha }}^{\left(i\right)}}-{\mathcal{L}}_{{\check{\alpha }}^{\left(i\right)}}\right),$$

and

$${\mathrm{CP}}_{(1-ϵ)\%}\left(\alpha \right)=\frac{1}{1000}{\sum }_{i=1}^{1000}{\mathbf{1}}_{\left({\mathcal{L}}_{{\check{\alpha }}^{\left(i\right)}};{\mathcal{U}}_{{\check{\alpha }}^{\left(i\right)}}\right)}\left(\alpha \right),$$

respectively, where $\mathbf{1}(·)$ is the indicator function, $\left(\mathcal{L}\right(·),\mathcal{U}(·\left)\right)$ denote the (lower,upper) bounds of $(1-ϵ)\%$ ACI (or HPD) interval of $\alpha$. In a similar way, the Av.E, RMSE, BRAB, ACL, and CP values of $\mu$, $R\left(t\right)$, or $h\left(t\right)$ can be easily computed.

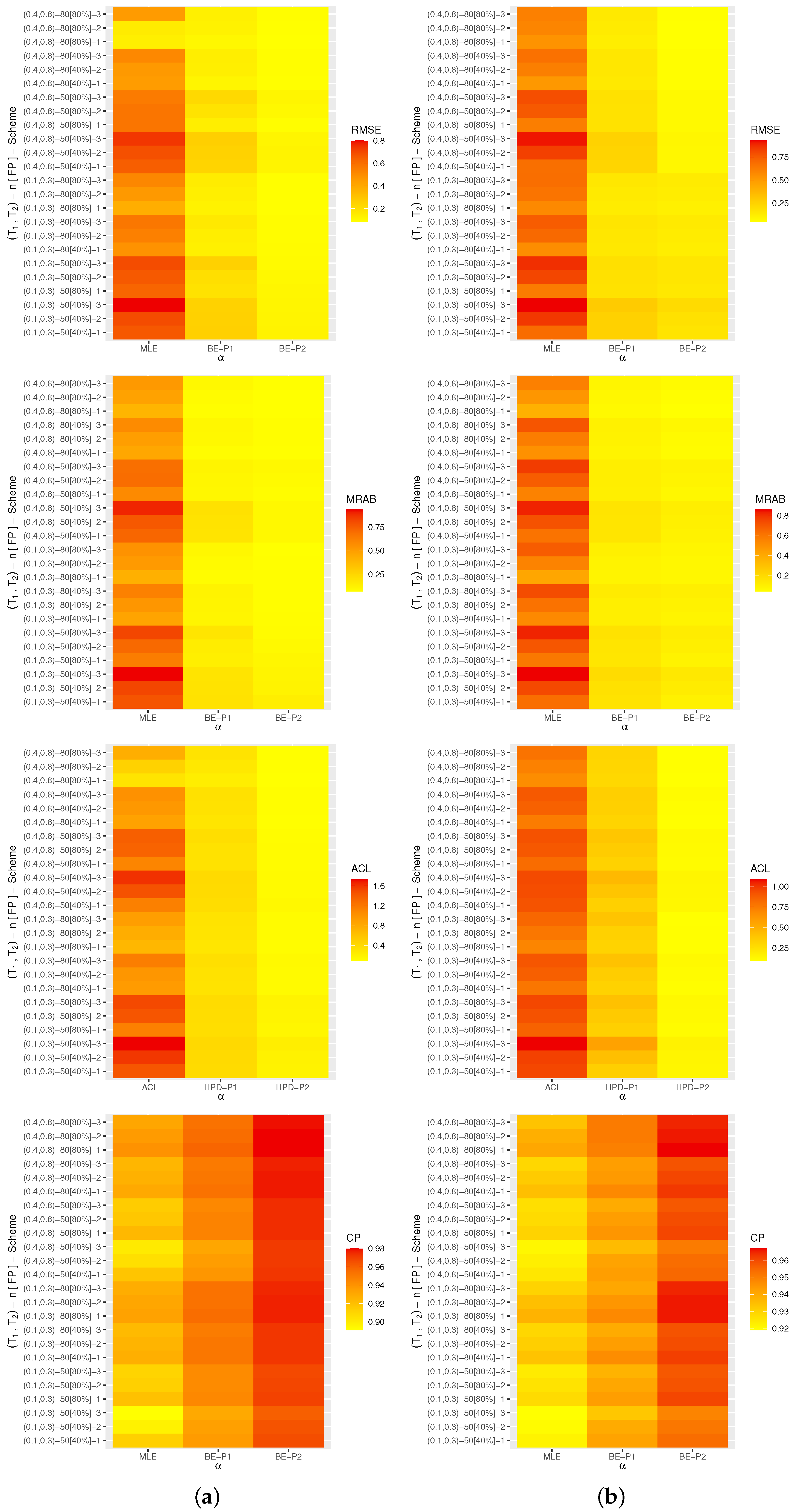
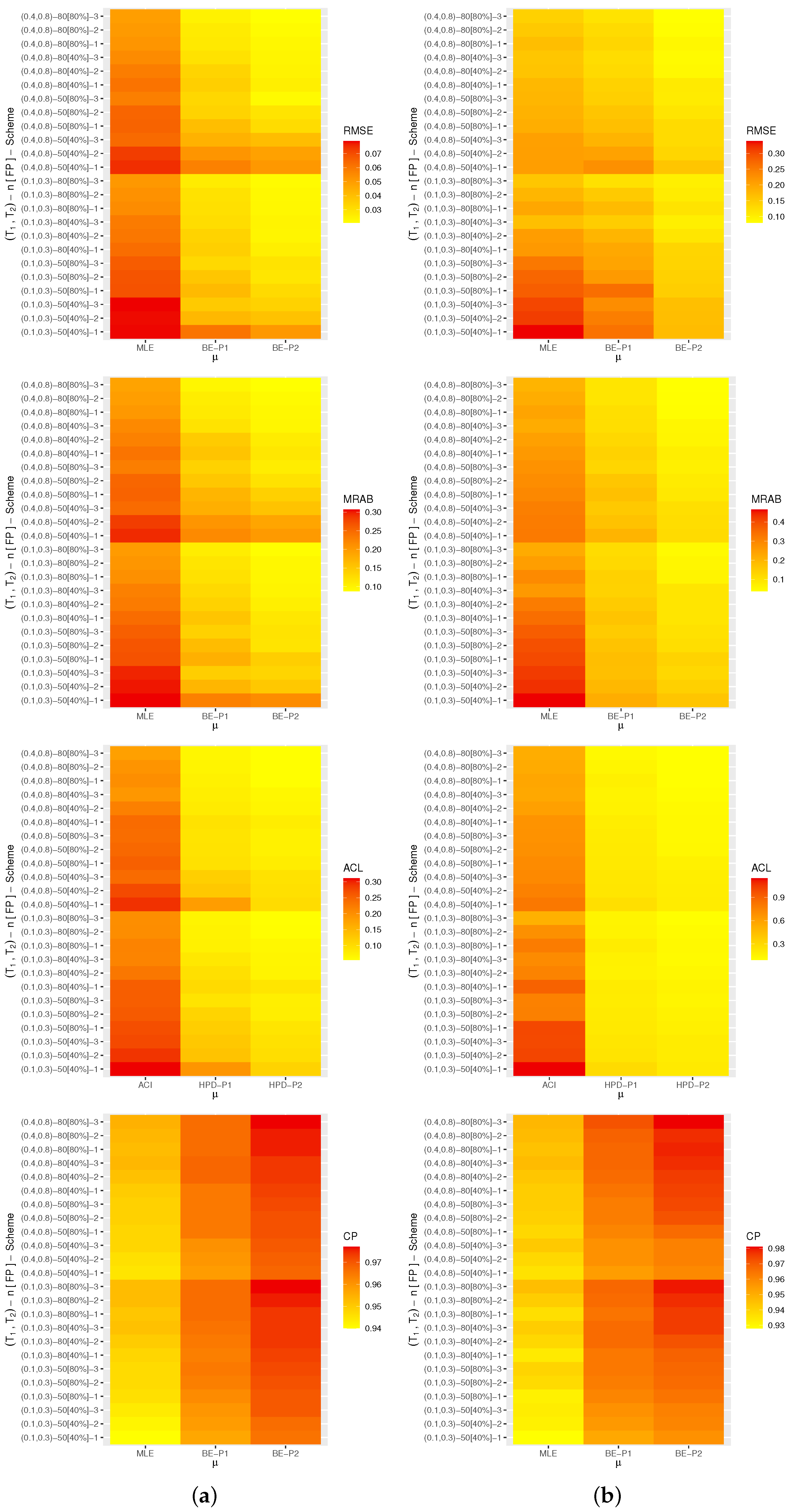
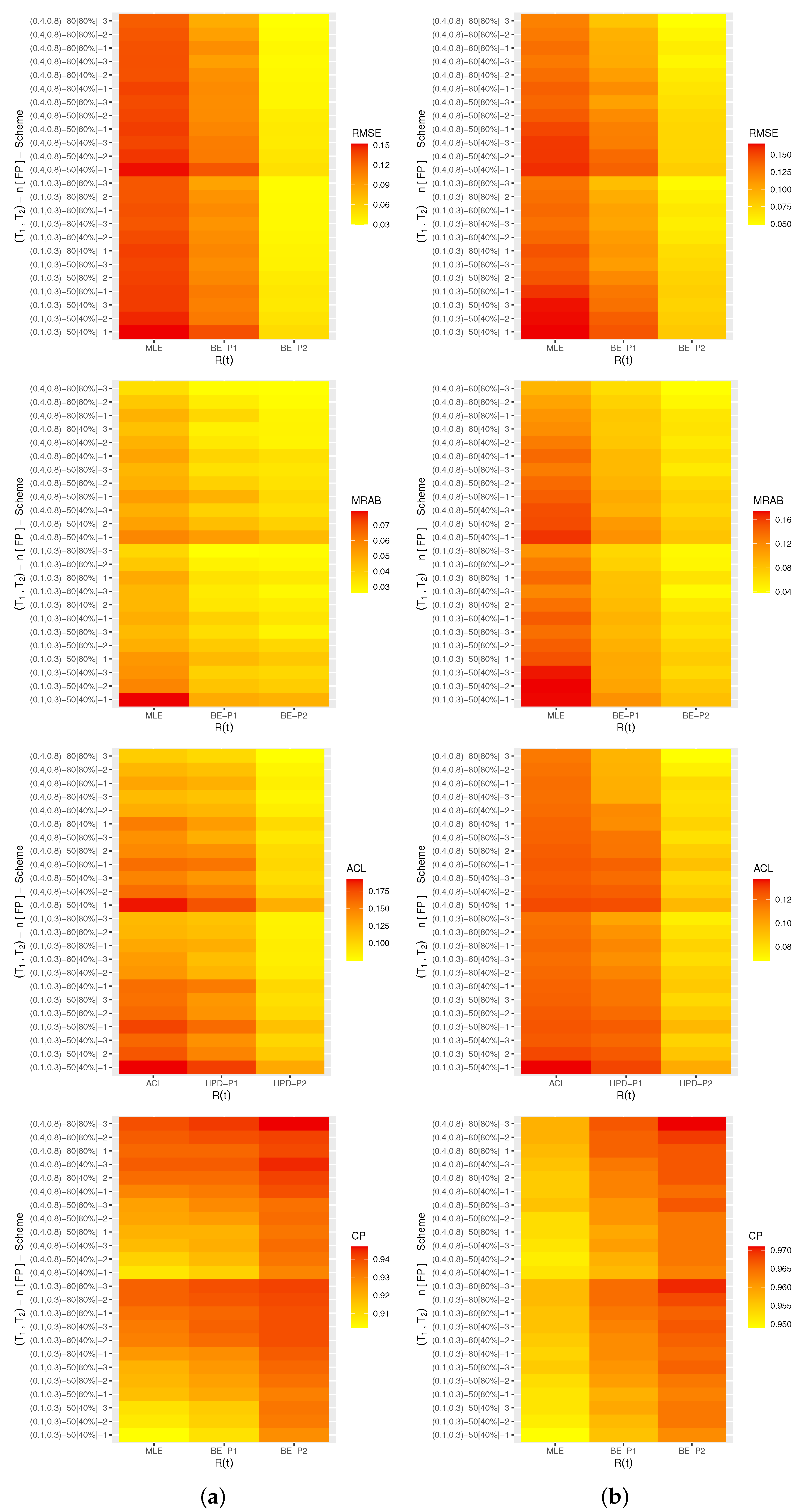
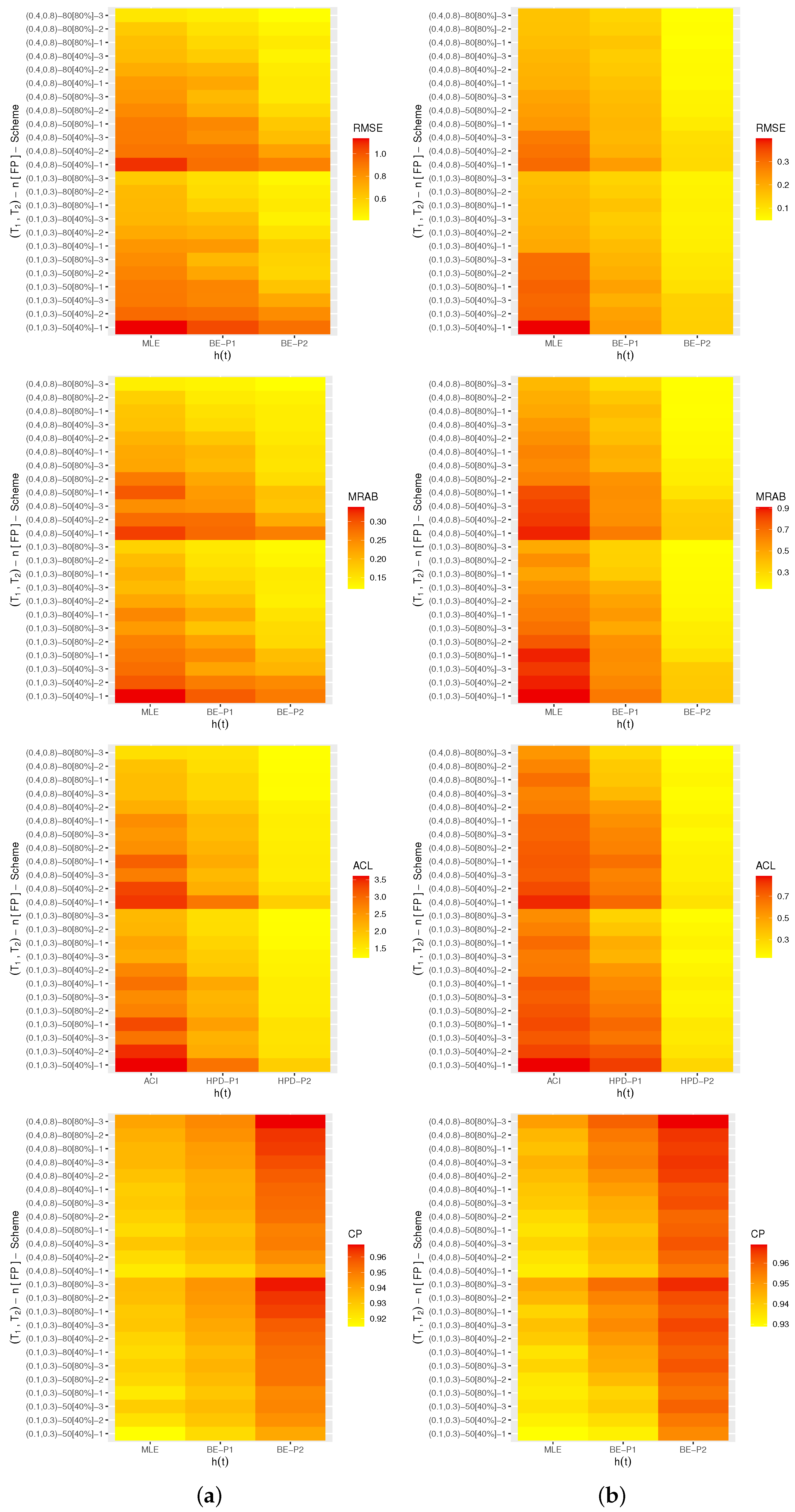
A heat map is a tool for graphically representing numerical data. Via $\mathsf{R}$ 4.2.2 software with the heat-map programming tool, the calculated criteria (including RMSEs, MRABs, ACLs, and CPs) of $\alpha$, $\mu$, $R\left(t\right)$, and $h\left(t\right)$ are represented in Figure 4, Figure 5, Figure 6 and Figure 7, respectively. As supplementary materials, all numerical values of $\alpha$, $\mu$, $R\left(t\right)$, or $h\left(t\right)$ are reported. To distinguish, for each plot in Figure 4, Figure 5, Figure 6 and Figure 7, the proposed approaches are displayed on the ‘x-axis’ line, whereas the censoring settings are displayed on the ‘y-axis’. In addition, as notations, the Bayes estimates (for Prior-I (say P1) as an example) are referred to as BE-P1, while the HPD interval is referred to as HPD-P1.

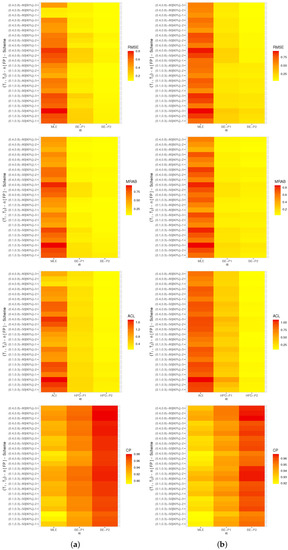
Figure 4. Heat-map for the Monte Carlo outputs of $\alpha$. (a) Set 1; (b) Set 2.

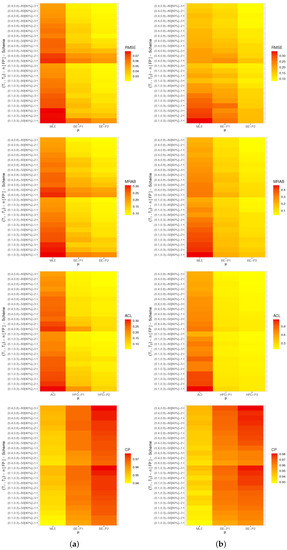
Figure 5. Heat-map for the Monte Carlo outputs of $\mu$. (a) Set 1; (b) Set 2.

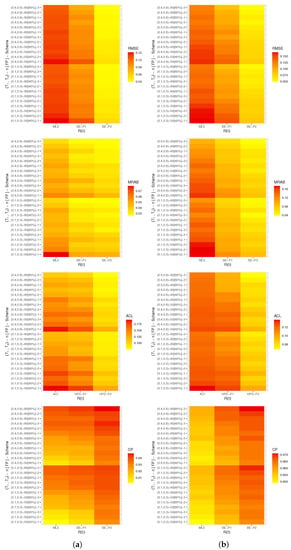
Figure 6. Heat-map for the Monte Carlo outputs of $R\left(t\right)$. (a) Set 1; (b) Set 2.

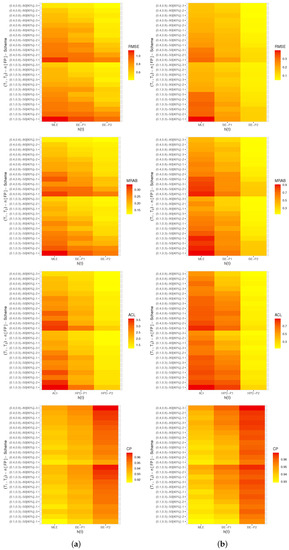
Figure 7. Heat-map for the Monte Carlo outputs of $h\left(t\right)$. (a) Set 1; (b) Set 2.

In terms of the smallest RMSE, MRAB, and ACL values as well as the largest CP values, from Figure 4, Figure 5, Figure 6 and Figure 7, the following comments are made:

• All acquired point and interval estimates of $\alpha$, $\mu$, $R\left(t\right)$ or $h\left(t\right)$ have good behavior; this is a general note.
• As n(or FP%) increases, all results of all unknown parameters of life perform satisfactorily. A similar point is also true when the spacing between n and m is reduced.
• As $T_i,i=1,2$ grow, for both Sets 1 and 2, the RMSEs, MRABs, and ACLs of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$ narrowed down, while their CPs increase.
• As anticipated, due to the gamma information, the Bayes point (or HPD interval) estimates of $\alpha$, $\mu$, $R\left(t\right)$, or $h\left(t\right)$ behave better compared to the others.
• All Bayesian computations performed based on Prior-2 provide more accurate results than those obtained based on Prior-1. This finding is due to the fact that the associated variance of Prior-2 is less than the associated variance of Prior-1.
• Comparing the suggested schemes 1, 2, and 3, for both Sets 1 and 2, it is seen that the point (or interval) estimates of $\delta$ have good results when all survival items $n-m$ are removed at the first stage (i.e., Scheme-1) and of $\mu$, $R\left(t\right)$, and $h\left(t\right)$ at the last stage (i.e., Scheme-3).
• In summary, it is advised to use MCMC samples to estimate the model parameters and reliability features of the alpha-PIE lifetime model when Type-II generalized progressively hybrid censored data are available.

5. Real Applications

To show the applicability of the suggested estimating methodologies and to illustrate the ability to adapt the study objectives to real-world situations, this section demonstrates two different applications from the engineering and chemistry fields. In each application, we prove that the offered model furnishes a good fit compared to five other competitive models in literature.

5.1. Electronic Tubes

An electron tube is a device that conducts electricity via electrons through a vacuum or a gas within a sealed glass or metal container and has a variety of popular applications, such as radio and television. For further applications of electron tubes, one may refer to Rosebury [31]. This application provides an analysis of a data set, taken from the engineering area, representing twenty lifetime values (in hundred hours) of electronic tubes; see Table 3. This data set has been first reported by Dixit and Nooghabi [32] and later discussed by Ibrahim et al. [33].

Table 3. Lifetimes of 20 electronic tubes.

0.1415	0.3484	0.3994	0.4174	0.5937	1.1045	1.7323	1.8348	2.3467	2.4651
2.6155	2.7425	3.1356	3.2259	3.4177	3.5551	3.5681	3.7287	9.2817	9.3208

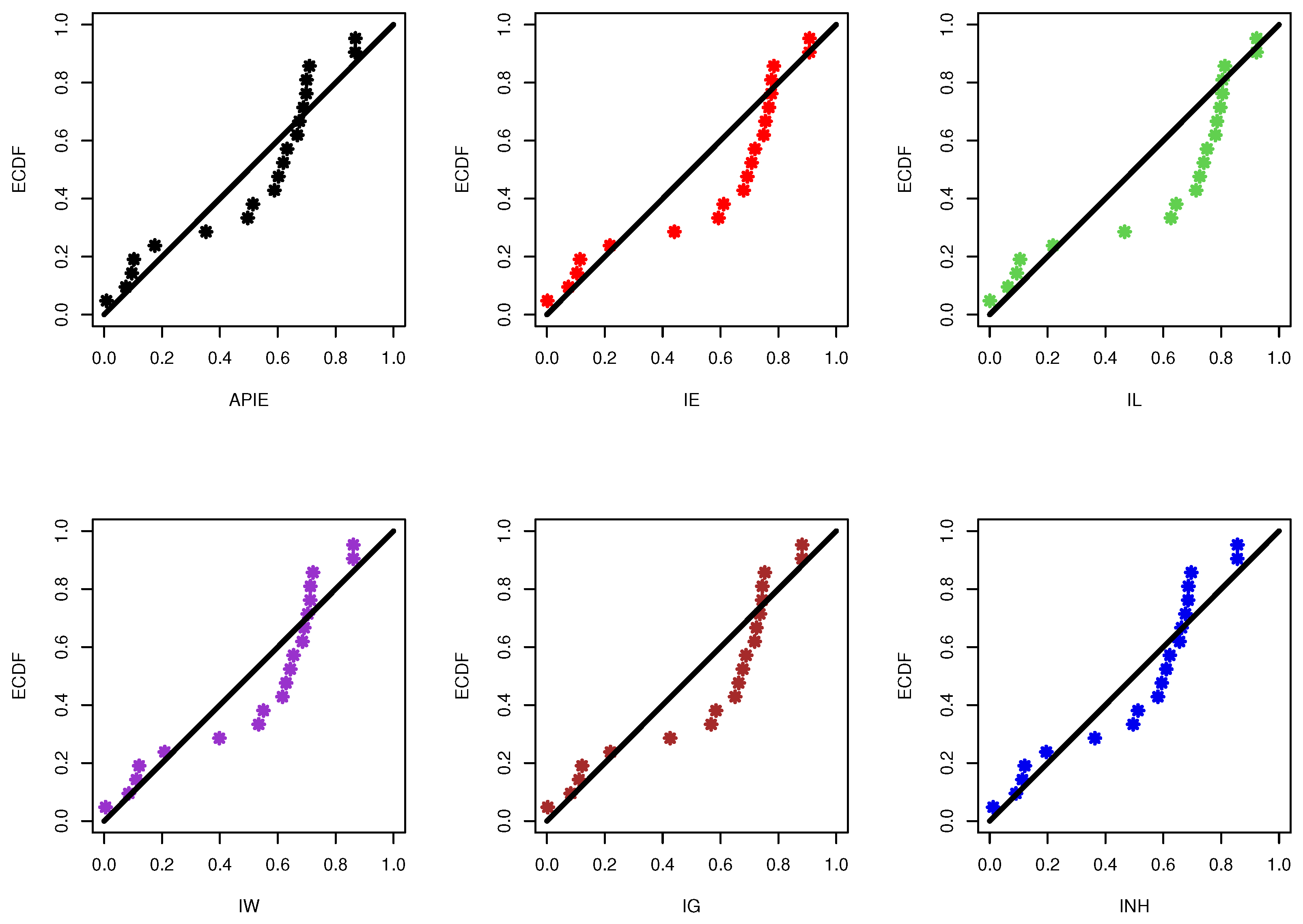
First, before proceeding, to highlight the utility of the offered model as competitors based on the complete data on electronic tubes, the alpha-PIE distribution is compared to five other inverted distributions (for $x>0$, $\alpha >0$ is a shape parameter and $\mu >0$ is a scale parameter), namely: inverted exponential (IE($\mu$)) by Keller et al. [2]; inverted Lindley (IL($\mu$)) by Sharma et al. [34]; inverted Weibull (IW($\alpha ,\mu$)) by Keller et al. [35]; inverted gamma (IG($\alpha ,\mu$)) by Glen [36]; and inverted Nadarajah–Haghighi (INH($\alpha ,\mu$)) by Tahir et al. [37]. The comparison of fits of the alpha-PIE (or simply, APIE) and other competitive models is made using several statistics, called negative log-likelihood (N-L), Akaike (A), Bayesian (B), consistent Akaike (C-A), Hannan-Quinn (H-Q), and Kolmogorov–Smirnov (K-S) statistic with its p-value. These measures are evaluated through the maximum likelihood estimates of $\alpha$ and $\mu$. Using Table 3, the MLEs (along with associated standard-errors (St.Ers)) of $\alpha$ and $\mu$, as well as the fitted values of N-L, A, B, C-A, H-Q, and K-S(p-value) are obtained and reported in Table 4. This indicates that the Alpha-PIE distribution has the lowest values of all given goodness-of-fit statistics, except that it has the highest p-value. This conclusion implies that the Alpha-PIE lifetime model provides a best fit than other distributions.

Table 4. Outputs of the fitting alpha-PIE and its competitive models from electronic tube data.

Model	MLE(St.Er)		N-L	A	B	C-A	H-Q	K-S (p-Value)
	$\mathsf{\alpha }$	$\mathsf{\mu }$
APIE	21.826 (55.135)	0.4149 (0.2867)	43.3798	90.7596	92.7511	91.4655	91.1484	0.1962 (0.375)
IE	-	0.9052 (0.2024)	45.0282	92.0564	93.0522	92.2787	92.2508	0.2930 (0.051)
IL	-	1.2990 (0.2240)	46.4118	94.8236	95.8194	95.0459	95.0180	0.3265 (0.0212)
IW	0.8531 (0.1361)	1.0019 (0.2383)	44.4847	92.9694	94.9609	93.6753	93.3581	0.2342 (0.1897)
IG	0.8692 (0.2390)	0.7869 (0.2871)	44.8932	93.7863	95.7778	94.4922	94.1751	0.2677 (0.0935)
INH	0.5622 (0.1660)	2.7258 (1.7357)	43.5167	91.0335	93.0249	91.7393	91.4222	0.2033 (0.3340)

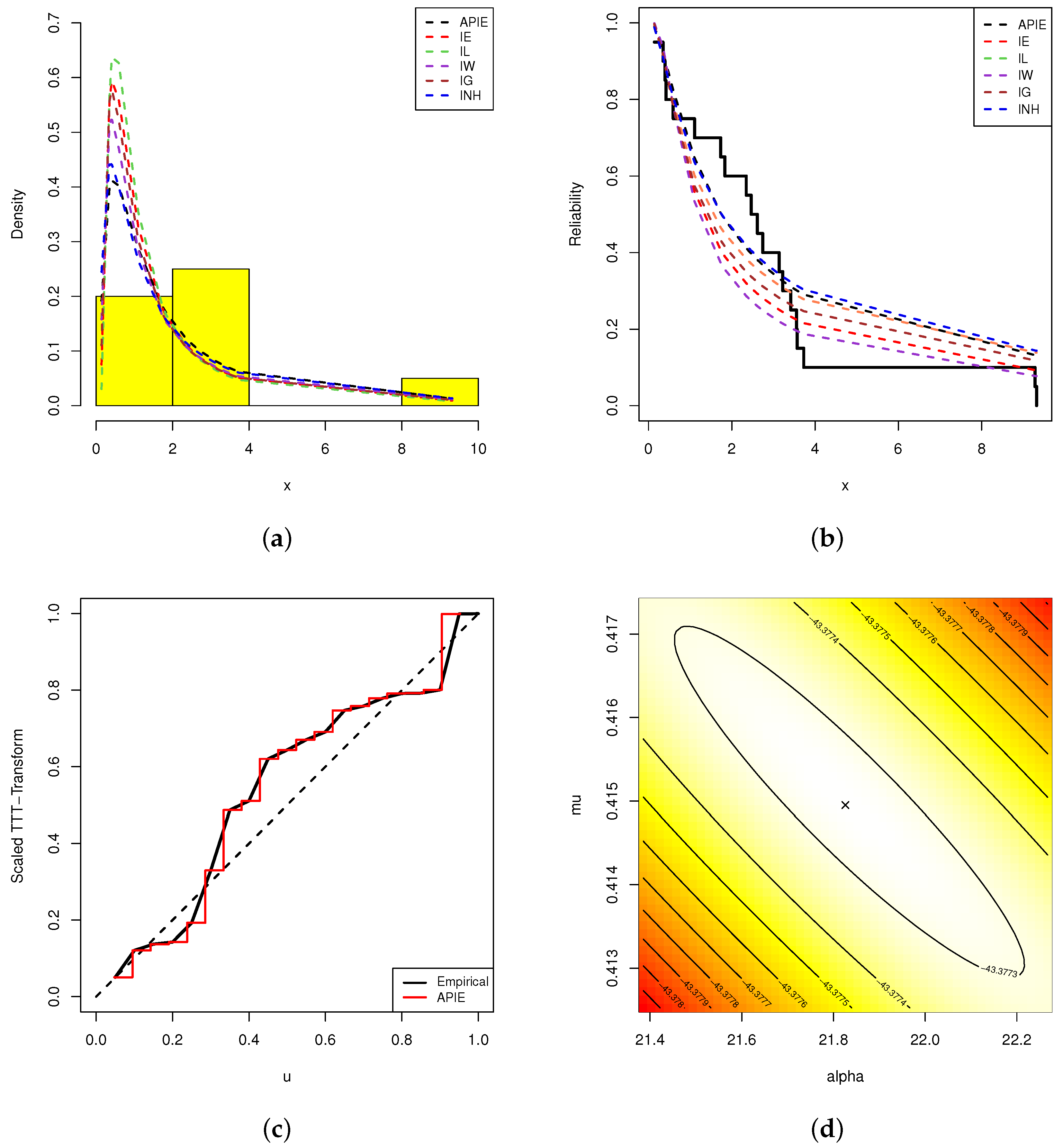
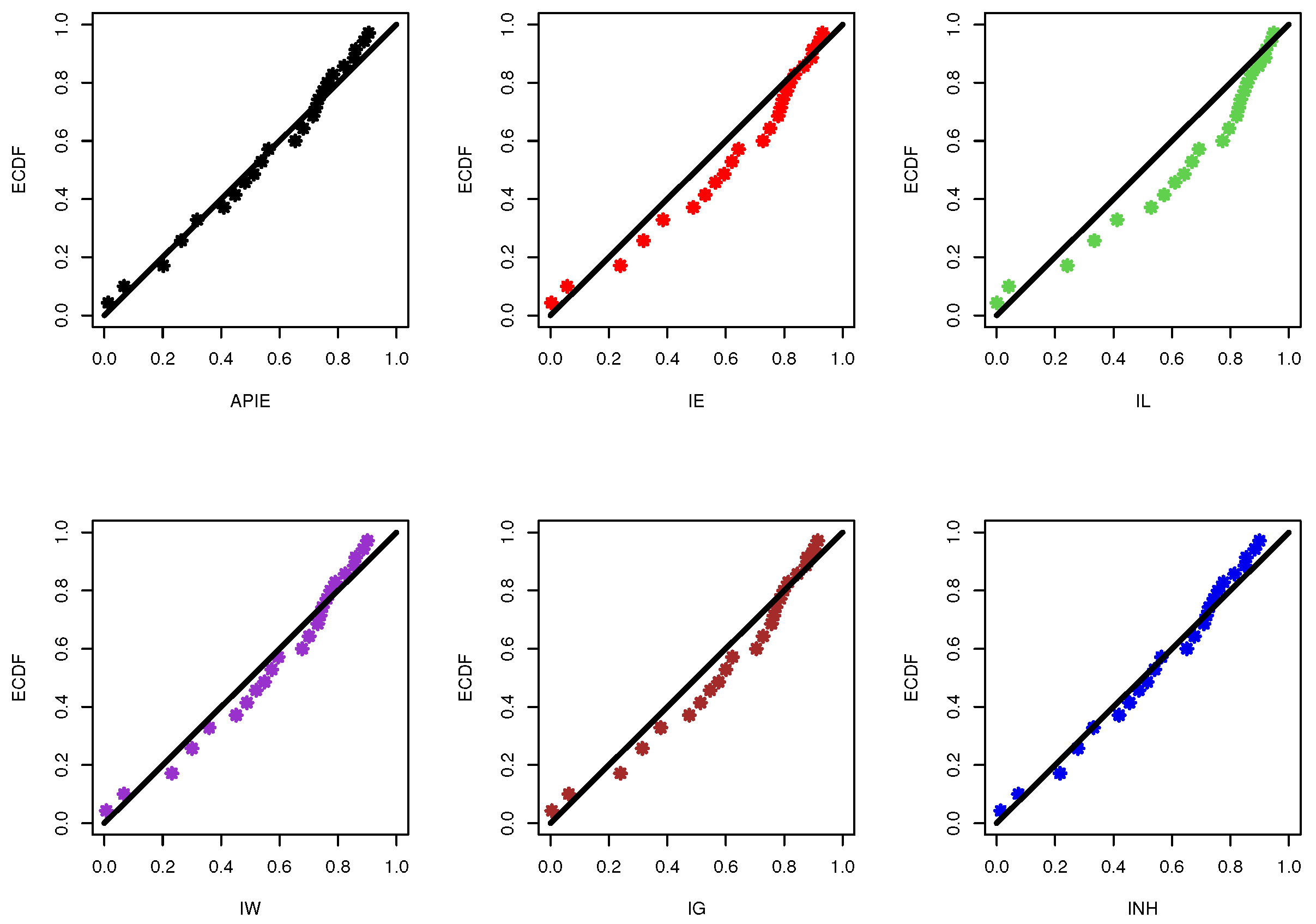
Graphically, in Figure 8, the probability–probability (PP) plots of alpha-PIE and their competitive distributions are displayed. Figure 8 supports the same numerical findings listed in Table 4. Moreover, in Figure 9, three different plots are also considered, called (i) fitted densities with relative histograms of given data; (ii) estimated/empirical reliability functions of alpha-PIE, IE, IL, IW, IG, and INH distributions; and (iii) estimated/empirical total time on test (TTT) transform plots.

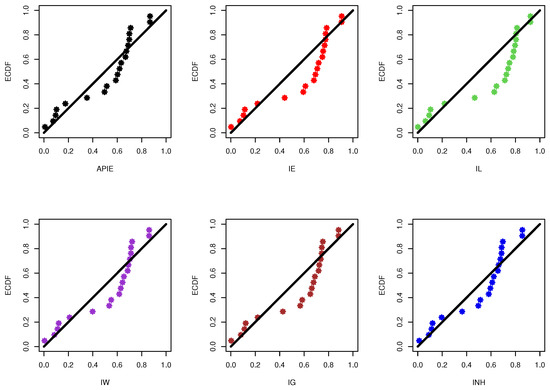
Figure 8. The PP plots of the alpha-PIE and its competitive models from electronic tube data.

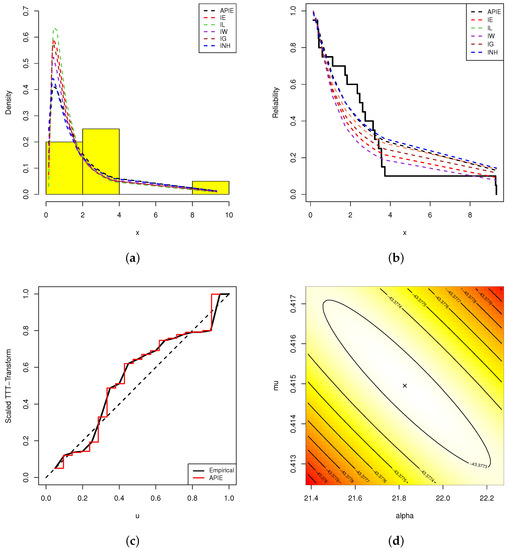
Figure 9. Fitted PDFs (a); fitted RFs (b); scaled TTT (c); contour (d); plots from electronic tubes data.

Each sub-plot in Figure 9 shows that the Alpha-PIE distribution provides a good fit compared to other competing models and indicates that the complete electronic tube data have an upside-down bathtub-shaped failure rate. In Figure 9, except for the alpha-PIE model, the fitted objects of other competitive models can be seen far away from the empirical ones. This observation is due to the fact that the estimated p-values of all compared models were lower than 0.5.

Additionally, to show the existence and uniqueness of $\widehat{\alpha }$ and $\widehat{\mu }$, the contour of the log-likelihood function under complete electronic tube data with respect to various choices of $\alpha$ and $\mu$ are also plotted and displayed in Figure 9, which provides evidence that the MLEs of $\widehat{\alpha }\cong 21.826$ and $\widehat{\mu }\cong 0.4149$ exist and are unique; in addition, they are considered starting points for forthcoming numerical evaluations.

To illustrate our acquired estimates of $\alpha$, $\mu$, $R\left(t\right)$, and $h\left(t\right)$ from the total data points of electronic tubes, various artificial GPHC-T-II samples of size $m=10$ are obtained based on different choices of times $T_i,i=1,2$ and censoring plans $R_i,i=1,2,\dots ,m$, namely, $\mathrm{Sch}\left[1\right]:\left(1^{10}\right)$, $\mathrm{Sch}\left[2\right]:(2^4,0^5,2)$, and $\mathrm{Sch}\left[3\right]:(2,0^5,2^4)$; see Table 5. Here, for brevity, the censoring plan $(1,1,1,1,1,1,1,1,1,1)$ is referred to as $\left(1^{10}\right)$. For each simulated sample in Table 5, Table 6 represents the point estimates (along their St.Ers) and the interval estimates (along their interval widths (IWs)) of $\alpha$, $\mu$, $R\left(t\right)$, and $h\left(t\right)$ at time $t=1$. Since we lack the prior information on $\alpha$ and $\mu$ from the electronic tubes data set, the improper gamma priors (where $a_i=b_i=0,i=1,2$) are used. Then, the Bayes estimates, along with their HPD intervals, are developed by repeating the MCMC technique 50,000 times and eliminating the first 10,000 times as burn-in. It can be seen, from Table 6, that the approximate Bayes estimates of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$ created from the MCMC sampler behave better than others in terms of the lowest St.Er and IW values.

Table 5. Artificial GPHC-T-II samples from electronic tube data.

Scheme	Sample	${\mathit{T}}_1\left({\mathit{d}}_1\right)$	${\mathit{T}}_2\left({\mathit{d}}_2\right)$	Generated Data	${\mathit{R}}^{*}$	${{\mathcal{T}}^{*}}^{*}$
Sch[1]	${\mathcal{S}}_1$	3.8 (10)	4.5 (10)	0.1415, 0.3994, 0.4174, 0.5937, 1.1045, 1.8348, 2.4651, 2.7425, 3.2259, 3.4177	1	3.8
	${\mathcal{S}}_2$	2.5 (6)	3.8 (10)	0.1415, 0.4174, 0.5937, 1.7323, 2.3467, 2.4651, 2.6155, 3.2259, 3.5551, 3.5681	0	3.5681
	${\mathcal{S}}_3$	1.5 (4)	3.3 (9)	0.1415, 0.4174, 0.5937, 1.1045, 1.7323, 1.8348, 2.6155, 2.7425, 3.2259	2	3.3
Sch[2]	${\mathcal{S}}_1$	2.8 (10)	3.5 (10)	0.1415, 0.4174, 0.5937, 1.1045, 1.7323, 1.8348, 2.3467, 2.4651, 2.6155, 2.7425	2	2.8
	${\mathcal{S}}_2$	1.8 (5)	3.6 (10)	0.1415, 0.3484, 0.5937, 1.1045, 1.7323, 2.3467, 2.4651, 2.6155, 3.1356, 3.5551	0	3.5551
	${\mathcal{S}}_3$	1.4 (4)	3.6 (9)	0.1415, 0.3994, 0.4174, 1.1045, 1.8348, 2.3467, 2.4651, 3.4177, 3.5551	3	3.6
Sch[3]	${\mathcal{S}}_1$	2.8 (10)	3.2 (10)	0.1415, 0.3994, 0.4174, 0.5937, 1.1045, 1.7323, 1.8348, 2.3467, 2.6155, 2.7425	2	2.8
	${\mathcal{S}}_2$	1.2 (6)	3.4 (10)	0.1415, 0.3484, 0.3994, 0.4174, 0.5937, 1.1045, 1.7323, 1.8348, 2.6155, 3.2259	0	3.2259
	${\mathcal{S}}_3$	1.9 (6)	3.5 (9)	0.1415, 0.4174, 0.5937, 1.1045, 1.7323, 1.8348, 2.3467, 2.7425, 3.4177	3	3.5

Table 6. Bayesian and classical estimates of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$ from electronic tube data.

Scheme	Sample	Par.	MLE		MCMC		ACI			HPD
			Est.	St.Er	Est.	St.Er	Lower	Upper	IW	Lower	Upper	IW
Sch[1]	${\mathcal{S}}_1$	$\alpha$	28.054	19.395	27.953	0.1417	0.0000	66.067	66.067	27.760	28.149	0.3884
		$\mu$	0.4391	0.1520	0.3742	0.0971	0.1411	0.7370	0.5960	0.2349	0.5154	0.2805
		$R\left(0.5\right)$	0.8892	0.0542	0.8500	0.0589	0.7831	0.9954	0.2123	0.7599	0.9247	0.1649
		$h\left(0.5\right)$	0.4043	0.1578	0.5098	0.1566	0.0949	0.7137	0.6187	0.3098	0.7522	0.4424
	${\mathcal{S}}_2$	$\alpha$	55.496	17.196	55.395	0.1431	21.792	89.200	67.408	55.193	55.588	0.3945
		$\mu$	0.5042	0.1509	0.4346	0.1038	0.2083	0.8000	0.5917	0.2847	0.5846	0.2999
		$R\left(0.5\right)$	0.9389	0.0344	0.9138	0.0383	0.8716	0.9923	0.1207	0.8589	0.9617	0.1029
		$h\left(0.5\right)$	0.2500	0.1179	0.3295	0.1197	0.0190	0.4810	0.4620	0.1770	0.5037	0.3267
	${\mathcal{S}}_3$	$\alpha$	48.976	17.349	48.875	0.1419	14.973	82.979	68.005	48.682	49.073	0.3905
		$\mu$	0.4676	0.1425	0.3995	0.1007	0.1884	0.7468	0.5584	0.2612	0.5477	0.2865
		$R\left(0.5\right)$	0.9248	0.0405	0.8942	0.0460	0.8454	0.9947	0.1493	0.8253	0.9521	0.1267
		$h\left(0.5\right)$	0.2965	0.1324	0.3888	0.1367	0.0371	0.5559	0.5188	0.2138	0.5946	0.3808
Sch[2]	${\mathcal{S}}_1$	$\alpha$	45.398	17.543	45.297	0.1430	11.015	79.782	68.767	45.095	45.488	0.3926
		$\mu$	0.3808	0.1221	0.3254	0.0877	0.1416	0.6200	0.4784	0.2005	0.4610	0.2605
		$R\left(0.5\right)$	0.8887	0.0557	0.8483	0.0630	0.7796	0.9979	0.2184	0.7560	0.9328	0.1768
		$h\left(0.5\right)$	0.4084	0.1657	0.5178	0.1689	0.0837	0.7332	0.6494	0.2937	0.7786	0.4849
	${\mathcal{S}}_2$	$\alpha$	36.008	17.983	35.909	0.1399	0.7610	71.254	70.493	35.712	36.105	0.3924
		$\mu$	0.4145	0.1378	0.3519	0.0950	0.1445	0.6845	0.5400	0.2173	0.4902	0.2729
		$R\left(0.5\right)$	0.8920	0.0551	0.8516	0.0613	0.7841	0.9989	0.2148	0.7588	0.9269	0.1681
		$h\left(0.5\right)$	0.3969	0.1633	0.5069	0.1649	0.0768	0.7171	0.6402	0.2890	0.7462	0.4572
	${\mathcal{S}}_3$	$\alpha$	30.437	18.638	30.333	0.1447	0.0000	66.966	66.966	30.125	30.523	0.3977
		$\mu$	0.4378	0.1532	0.3714	0.0989	0.1377	0.7380	0.6004	0.2271	0.5176	0.2905
		$R\left(0.5\right)$	0.8930	0.0555	0.8531	0.0600	0.7842	0.9919	0.2077	0.7596	0.9274	0.1678
		$h\left(0.5\right)$	0.3933	0.1638	0.5016	0.1608	0.0723	0.7144	0.6421	0.2955	0.7480	0.4525
Sch[3]	${\mathcal{S}}_1$	$\alpha$	34.013	18.493	33.913	0.1396	0.0000	70.259	70.259	33.728	34.109	0.3815
		$\mu$	0.4838	0.1496	0.4185	0.0987	0.1906	0.7770	0.5865	0.2725	0.5621	0.2896
		$R\left(0.5\right)$	0.9146	0.0423	0.8845	0.0459	0.8316	0.9975	0.1659	0.8152	0.9430	0.1278
		$h\left(0.5\right)$	0.3281	0.1321	0.4151	0.1312	0.0691	0.5871	0.5179	0.2417	0.6126	0.3709
	${\mathcal{S}}_2$	$\alpha$	17.027	11.353	16.926	0.1426	0.0000	39.279	39.279	16.7161	17.108	0.3920
		$\mu$	0.4427	0.1532	0.3787	0.0969	0.1425	0.7429	0.6004	0.2442	0.5259	0.2817
		$R\left(0.5\right)$	0.8615	0.0616	0.8184	0.0649	0.7406	0.9823	0.2417	0.7235	0.9072	0.1838
		$h\left(0.5\right)$	0.4831	0.1668	0.5907	0.1608	0.1562	0.8099	0.6537	0.3756	0.8365	0.4609
	${\mathcal{S}}_3$	$\alpha$	49.677	12.061	49.578	0.1383	26.038	73.315	47.277	49.392	49.767	0.3754
		$\mu$	0.5061	0.1499	0.4349	0.1053	0.2124	0.7999	0.5876	0.2904	0.5913	0.3009
		$R\left(0.5\right)$	0.9356	0.0356	0.9092	0.0400	0.8659	0.9967	0.1308	0.8499	0.9583	0.1084
		$h\left(0.5\right)$	0.2608	0.1201	0.3435	0.1233	0.0254	0.4963	0.4709	0.1896	0.5270	0.3374

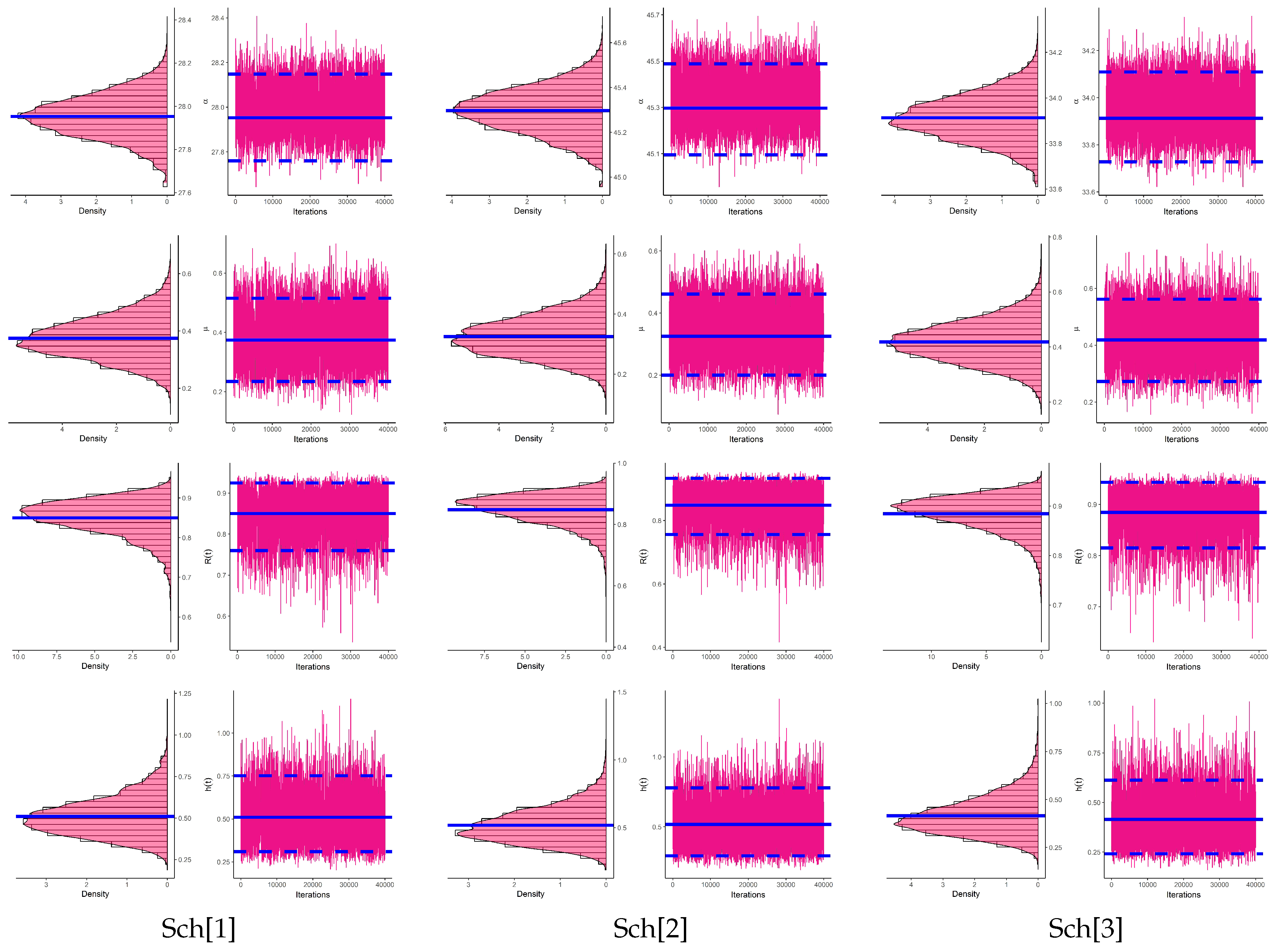
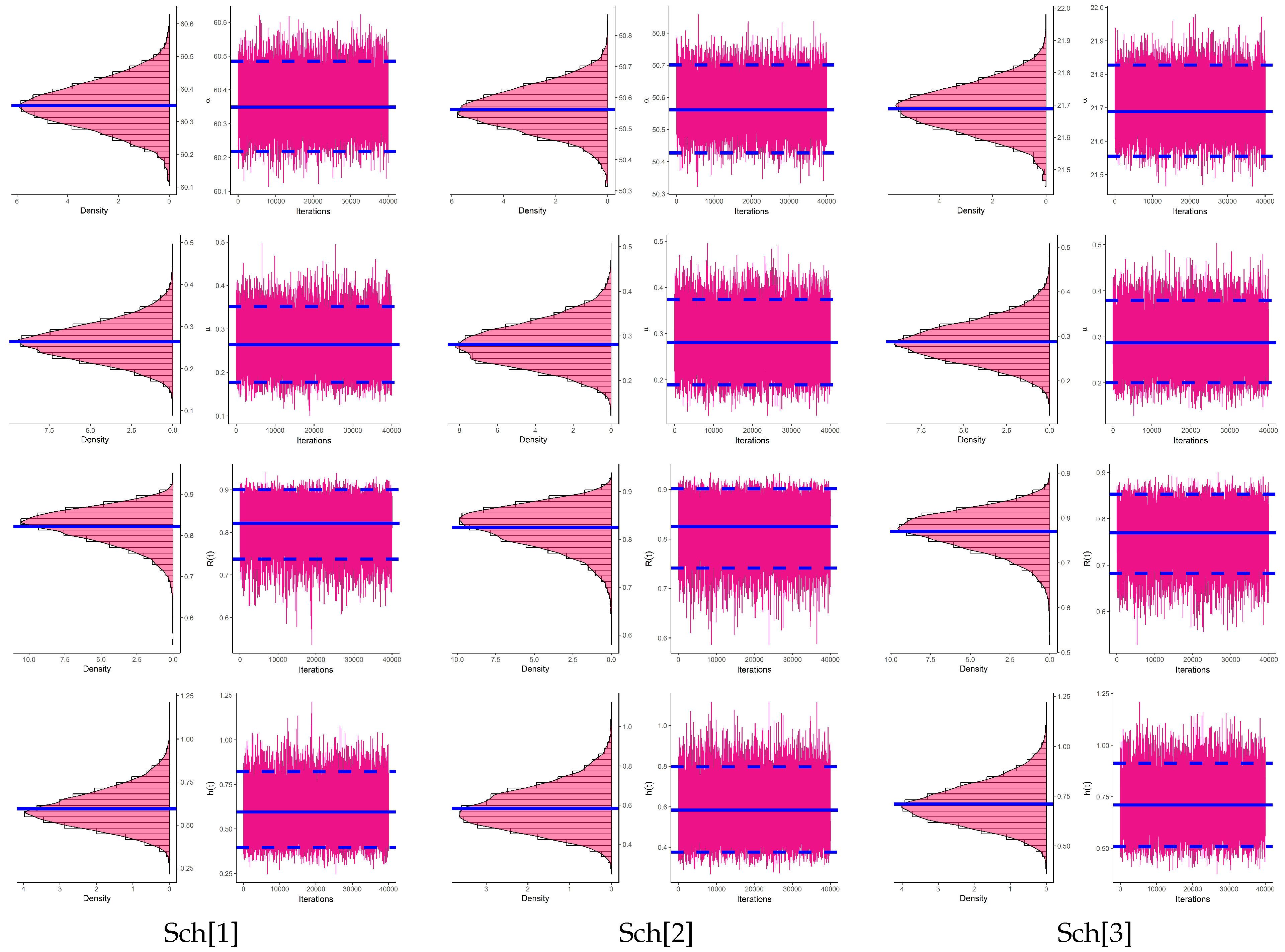
To emphasize the convergence of MCMC sequences of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$, from each sample ${\mathcal{S}}_1$ generated by $\mathrm{Sch}\left[i\right],i=1,2,3$ (as examples), Figure 10 displays the density and trace diagrams from 40,000 MCMC draws of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$. To distinguish THEM, for each plot in Figure 10, the Bayes estimate (posterior mean) and two 95% HPD interval bounds are represented by solid and dashed lines, respectively. It is clear, from Figure 10, that the MCMC strategy converges well and that the recommended size of the burn-in sample is adequate to ignore the impact of the starting points. The figure also demonstrates that the drawn estimates of $\alpha$ and $\mu$ are fairly symmetrical. Figure 10 also shows that the drawn estimates of $R\left(t\right)$ and $h\left(t\right)$ are negatively and positively skewed, respectively.

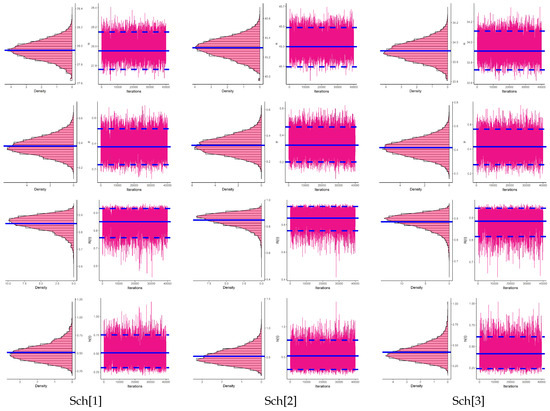
Figure 10. Density (left) and trace (right) plots of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$ from electronic tubes data.

5.2. Vinyl Chloride

Vinyl chloride is an organochloride, flammable gas with a sickly sweet odor, which is colorless at ambient temperature and is a recognized human carcinogen that burns readily. In 1835, it was first discovered by Justus von Liebig and Henri Victor Regnault. It is not produced naturally and must be produced industrially for its commercial uses, for example, pipes, packaging materials, and coatings for wire and cable; see Ware [38]. In this application, from clean up-gradient monitoring wells, we shall consider a data set consisting of thirty-four data points of vinyl chloride; see Table 7. This data set was given by Bhaumik et al. [39] and later, Elshahhat and Elemary [40] as well as Alotaibi et al. [41] also discussed it.

Table 7. Data point (in milligrams/liter) of vinyl chloride.

0.1	0.1	0.2	0.2	0.4	0.4	0.4	0.5	0.5	0.5	0.6	0.6	0.8	0.9	0.9	1.0	1.1
1.2	1.2	1.3	1.8	2.0	2.0	2.3	2.4	2.5	2.7	2.9	3.2	4.0	5.1	5.3	6.8	8.0

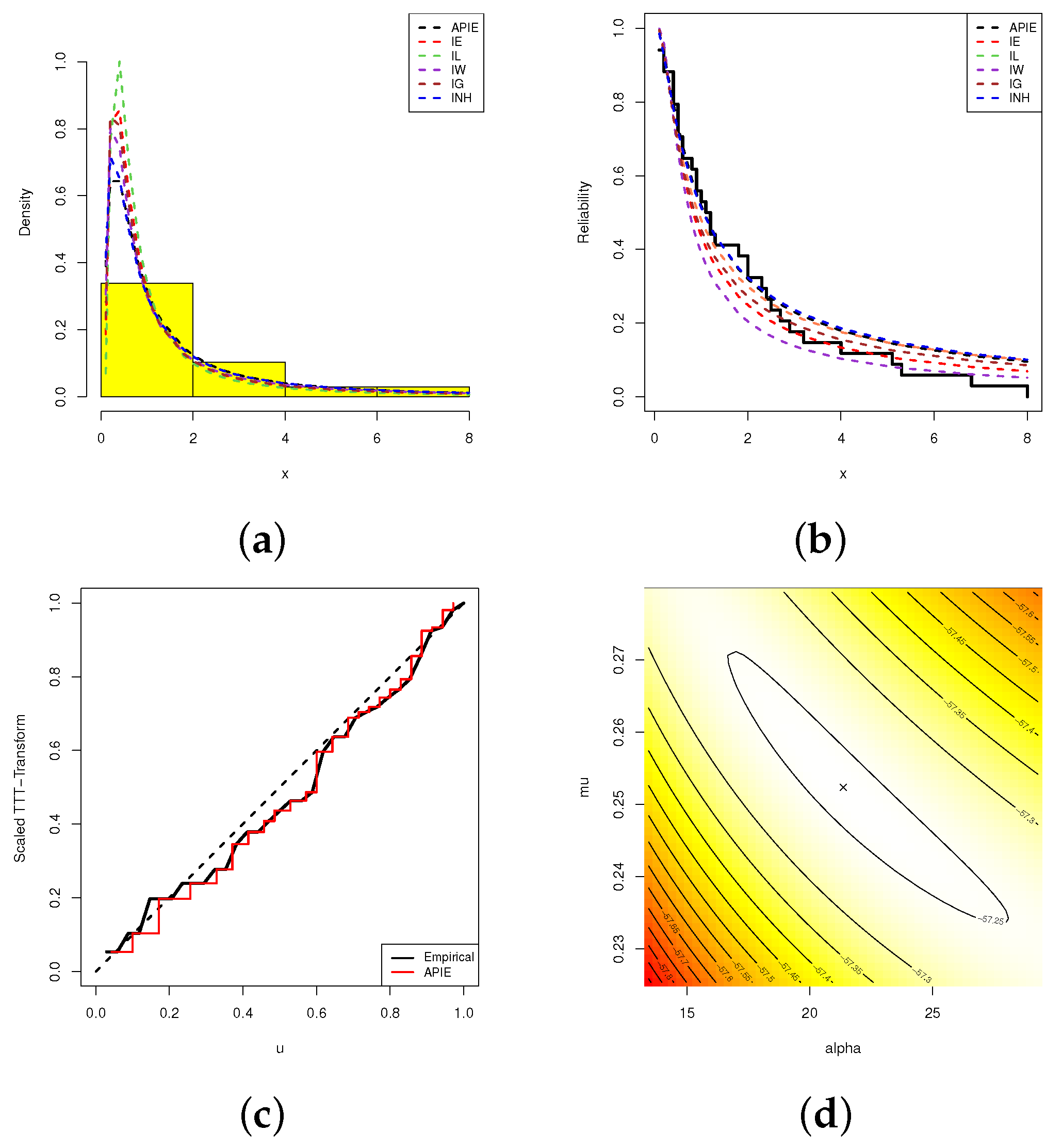
To monitor the adaptability and flexibility of the alpha-PIE distribution, from the complete vinyl chloride data, we compare its fits with several other competitive models reported in Section 5.1. For this purpose, the MLEs (with their St.Ers) of $\alpha$ and $\mu$, N-L, A, B, C-A, H-Q, and K-S(p-value) of alpha-PIE and its competing distributions are calculated and provided in Table 8. Furthermore, the corresponding PP plot of the alpha-PIE distribution and its five competitive models are shown in Figure 11. In Figure 12, the fitted density and reliability function of the alpha-PIE distribution and all studied models, as well as the TTT transform plot, are displayed. Figure 11 and Figure 12 indicate confirmed the same results presented in Table 8. Moreover, Figure 12 shows that a decreasing failure rate is appropriate for modeling vinyl chloride data. In addition, Figure 12 shows that the MLEs $\widehat{\alpha }\cong 21.364$ and $\widehat{\mu }\cong 0.2524$ developed from the vinyl chloride data exist and are unique. Therefore, in the forthcoming classical (or Bayesian) evaluations, these values are taken as initial guesses.

Table 8. Outputs of the fitting alpha-PIE and its competitive models from vinyl chloride data.

Model	MLE(St.Er)		N-L	A	B	C-A	H-Q	K-S (p-Value)
	$\mathsf{\alpha }$	$\mathsf{\mu }$
APIE	21.364 (52.796)	0.2524 (0.1725)	57.2457	118.4915	121.5442	118.8786	119.5325	0.0952 (0.918)
IE	-	0.5725 (0.0982)	59.1930	120.3860	121.9124	120.5110	120.9066	0.1470 (0.454)
IL	-	0.8774 (0.1127)	61.8136	125.6272	127.1535	125.7522	126.1477	0.1908 (0.168)
IW	0.8805 (0.1093)	0.6539 (0.1347)	58.6266	121.2532	124.3059	121.6403	122.2942	0.1134 (0.774)
IG	0.9002 (0.1904)	0.5154 (0.1434)	59.0659	122.1319	125.1846	122.5190	123.1729	0.1310 (0.604)
INH	0.6089 (0.1518)	1.4368 (0.7440)	57.5539	119.1079	122.1606	119.4950	120.1490	0.1004 (0.883)

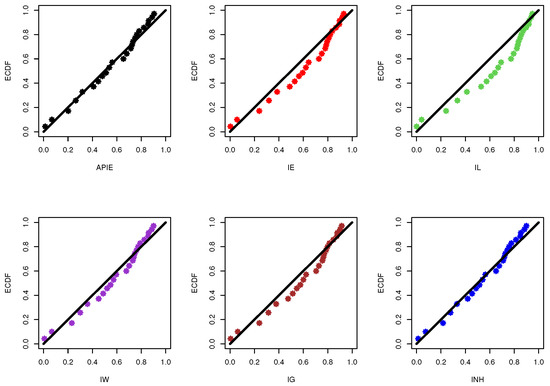
Figure 11. The PP plots of the alpha-PIE and its competitive distributions from vinyl chloride data.

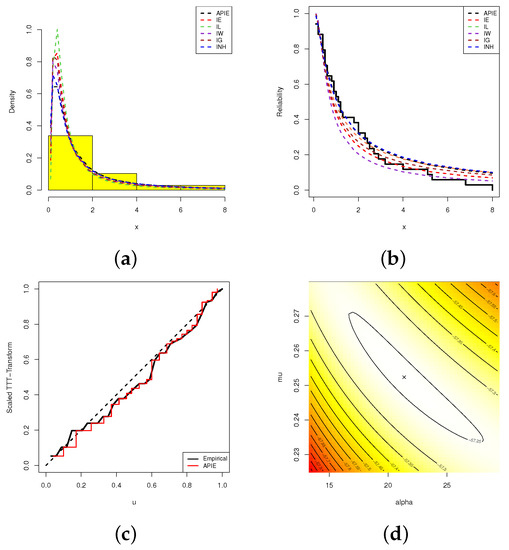
Figure 12. Fitted PDFs (a); fitted RFs (b); scaled-TTT (c); contour (d) plots from vinyl chloride data.

To assess the efficacy of the suggested inferential techniques in the chemical area, from the complete vinyl chloride data, several artificial GPHC-T-II samples (when $m=17$ and different choices of $T_i,i=1,2$ and $R_i,i=1,2,\dots ,m$ namely: $\mathrm{Sch}\left[1\right]:\left(1^{17}\right)$, $\mathrm{Sch}\left[2\right]:(2^8,0^8,1)$ and $\mathrm{Sch}\left[3\right]:(1,0^8,2^8)$) are created and listed in Table 9. From each GPHC-T-II sample reported Table 9, the maximum likelihood and Bayes MCMC estimates (along with their St.Ers) and the asymptotic and HPD interval estimates (along with their IWs) of $\alpha$, $\mu$, $R\left(t\right)$ or $h\left(t\right)$ (at $t=0.5$) are computed and provided in Table 10.

Table 9. Artificial GPHC-T-II samples from vinyl chloride data.

Scheme	Sample	${\mathit{T}}_1\left({\mathit{d}}_1\right)$	${\mathit{T}}_2\left({\mathit{d}}_2\right)$	Generated Data	${\mathit{R}}^{*}$	${{\mathcal{T}}^{*}}^{*}$
Sch[1]	${\mathcal{S}}_1$	4.2 (17)	4.8 (17)	0.1, 0.2, 0.4, 0.4, 0.5, 0.6, 0.8, 0.9, 0.9, 1.0, 1.1, 1.2, 1.3, 1.8, 2.3, 2.4, 4.0	1	4.2
	${\mathcal{S}}_2$	1.5 (12)	5.5 (17)	0.1, 0.2, 0.4, 0.4, 0.4, 0.5, 0.6, 0.6, 0.9, 1.0, 1.1, 1.2, 2.0, 2.0, 2.5, 2.7, 5.1	0	5.1
	${\mathcal{S}}_3$	1.1 (12)	1.3 (15)	0.1, 0.2, 0.4, 0.5, 0.5, 0.5, 0.6, 0.6, 0.8, 0.9, 0.9, 1.0, 1.1, 1.2, 1.2	4	1.3
Sch[2]	${\mathcal{S}}_1$	2.2 (11)	6.9 (17)	0.1, 0.2, 0.4, 0.5, 0.5, 0.6, 0.8, 0.9, 1.2, 1.3, 2.0, 2.3, 2.7, 4.0, 5.1, 5.3, 6.8	1	6.9
	${\mathcal{S}}_2$	1.7 (13)	5.4 (17)	0.1, 0.2, 0.5, 0.5, 0.6, 0.6, 0.8, 0.9, 0.9, 1.0, 1.1, 1.2, 1.2, 2.3, 2.4, 4.0, 5.3	0	5.3
	${\mathcal{S}}_3$	1.1 (12)	1.3 (14)	0.1, 0.2, 0.4, 0.4, 0.4, 0.5, 0.6, 0.6, 0.8, 0.9, 0.9, 1.0, 1.1, 1.2	4	1.3
Sch[3]	${\mathcal{S}}_1$	2.6 (17)	2.8 (17)	0.1, 0.2, 0.2, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5, 0.6,0.9, 0.9, 1.2, 1.2, 1.3, 2.0, 2.5	2	2.6
	${\mathcal{S}}_2$	1.4 (13)	4.4 (17)	0.1, 0.2, 0.2, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5, 0.6, 0.9, 1.1, 1.3, 1.8, 2.4, 2.9, 4.0	0	4.0
	${\mathcal{S}}_3$	0.8 (10)	1.4 (16)	0.1, 0.2, 0.2, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5, 0.6, 0.9, 1.0, 1.1, 1.2, 1.2, 1.3	3	1.4

Table 10. Bayesian and classical estimates of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$ from vinyl chloride data.

Scheme	Sample	Par.	MLE		MCMC		ACI			HPD
			Est.	St.Er	Est.	St.Er	Lower	Upper	IW	Lower	Upper	IW
Sch[1]	${\mathcal{S}}_1$	$\alpha$	60.396	8.489	60.349	0.0832	43.757	77.034	33.278	60.218	60.485	0.2670
		$\mu$	0.2862	0.0652	0.2641	0.0496	0.1584	0.4140	0.2556	0.1775	0.3515	0.1741
		$R\left(0.5\right)$	0.8466	0.0508	0.8216	0.0491	0.7471	0.9461	0.1990	0.7374	0.9003	0.1629
		$h\left(0.5\right)$	0.5326	0.1395	0.5956	0.1259	0.2592	0.8060	0.5467	0.3965	0.8226	0.4262
	${\mathcal{S}}_2$	$\alpha$	41.368	12.570	41.320	0.0844	16.730	66.006	49.275	41.188	41.459	0.2718
		$\mu$	0.3018	0.0729	0.2777	0.0521	0.1589	0.4447	0.2859	0.1888	0.3673	0.1785
		$R\left(0.5\right)$	0.8351	0.0532	0.8089	0.0502	0.7309	0.9393	0.2084	0.7238	0.8858	0.1620
		$h\left(0.5\right)$	0.5582	0.1415	0.6224	0.1253	0.2809	0.8354	0.5545	0.4174	0.8301	0.4127
	${\mathcal{S}}_3$	$\alpha$	183.76	6.8550	183.74	0.0554	170.33	197.20	26.871	183.64	183.83	0.1951
		$\mu$	0.1897	0.0421	0.1798	0.0321	0.1072	0.2721	0.1649	0.1232	0.2413	0.1181
		$R\left(0.5\right)$	0.8116	0.0581	0.7907	0.0521	0.6976	0.9255	0.2279	0.6979	0.8776	0.1797
		$h\left(0.5\right)$	0.6467	0.1513	0.6950	0.1274	0.3501	0.9433	0.5932	0.4717	0.9238	0.4521
Sch[2]	${\mathcal{S}}_1$	$\alpha$	50.611	17.847	50.562	0.0856	15.632	85.589	69.957	50.427	50.701	0.2738
		$\mu$	0.3078	0.0780	0.2810	0.0548	0.1549	0.4607	0.3058	0.1894	0.3741	0.1847
		$R\left(0.5\right)$	0.8522	0.0523	0.8250	0.0501	0.7497	0.9547	0.2050	0.7412	0.9015	0.1602
		$h\left(0.5\right)$	0.5146	0.1444	0.5837	0.1291	0.2315	0.7977	0.5662	0.3762	0.7973	0.4211
	${\mathcal{S}}_2$	$\alpha$	104.59	11.9356	104.55	0.0705	81.194	127.98	46.787	104.43	104.67	0.2364
		$\mu$	0.2352	0.0547	0.2195	0.0408	0.1280	0.3423	0.2143	0.1482	0.2958	0.1476
		$R\left(0.5\right)$	0.8333	0.0557	0.8096	0.0511	0.7241	0.9424	0.2184	0.7153	0.8896	0.1743
		$h\left(0.5\right)$	0.5785	0.1506	0.6362	0.1289	0.2834	0.8736	0.5902	0.4276	0.8757	0.4481
	${\mathcal{S}}_3$	$\alpha$	671.16	11.8650	670.21	663.50	647.91	694.42	46.510	664.45	675.78	11.3371
		$\mu$	0.1277	0.0286	0.1815	0.0584	0.0717	0.1837	0.1120	0.1410	0.2273	0.0863
		$R\left(0.5\right)$	0.7706	0.0665	0.8597	0.0938	0.6402	0.9010	0.2608	0.8009	0.9101	0.1092
		$h\left(0.5\right)$	0.7718	0.1604	0.5334	0.2528	0.4573	1.0862	0.6289	0.3851	0.7014	0.3163
Sch[3]	${\mathcal{S}}_1$	$\alpha$	21.738	9.609	21.689	0.0864	2.9050	40.572	37.667	21.554	21.828	0.2732
		$\mu$	0.3115	0.0788	0.2876	0.0515	0.1571	0.4659	0.3088	0.2005	0.3794	0.1789
		$R\left(0.5\right)$	0.7968	0.0572	0.7700	0.0517	0.6848	0.9088	0.2241	0.6825	0.8535	0.1710
		$h\left(0.5\right)$	0.6493	0.1400	0.7105	0.1200	0.3749	0.9237	0.5488	0.5081	0.9130	0.4049
	${\mathcal{S}}_2$	$\alpha$	20.378	9.7182	20.330	0.0849	1.3309	39.425	38.095	20.196	20.470	0.2736
		$\mu$	0.3529	0.0909	0.3248	0.0571	0.1749	0.5310	0.3562	0.2262	0.4203	0.1940
		$R\left(0.5\right)$	0.8230	0.0535	0.7972	0.0479	0.7182	0.9279	0.2097	0.7147	0.8689	0.1542
		$h\left(0.5\right)$	0.5834	0.1361	0.6450	0.1154	0.3166	0.8502	0.5336	0.4638	0.8403	0.3765
	${\mathcal{S}}_3$	$\alpha$	24.284	9.3539	24.234	0.0863	5.9510	42.618	36.667	24.103	24.374	0.2706
		$\mu$	0.2922	0.0720	0.2699	0.0495	0.1511	0.4332	0.2821	0.1868	0.3597	0.1728
		$R\left(0.5\right)$	0.7887	0.0584	0.7614	0.0538	0.6743	0.9031	0.2288	0.6685	0.8474	0.1788
		$h\left(0.5\right)$	0.6698	0.1418	0.7316	0.1239	0.3919	0.9478	0.5559	0.5268	0.9450	0.4182

By ignoring the first 10,000 iterations (burn-in) from the full MCMC 50,000 iterations, the Bayes’ estimates are approximated when the hyperparameter values are selected to be zero. Because we lacked additional historical information from the given data, which led to little to no difference between the proposed classical and Bayesian estimates, Table 10 stated that the offered estimates of $\alpha$, $\mu$, $R\left(t\right)$ or $h\left(t\right)$ behave similarly and seem to be close to one another.

From each sample ${\mathcal{S}}_1$ obtained by $\mathrm{Sch}\left[i\right],i=1,2,3$ (as examples), to display the convergence of 40,000 MCMC draws of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$, the density and trace pots of all unknown quantities are plotted and shown in Figure 13. This figure supports the same numerical findings reported in Table 10 and indicates that all MCMC iterations of $\alpha$, $\mu$, $R\left(t\right)$ or $h\left(t\right)$ converged satisfactorily. It also shows that the simulated MCMC estimates of $\alpha$ and $\mu$ are almost symmetrical, while those of $R\left(t\right)$ and $h\left(t\right)$ are negatively and positively skewed, respectively.

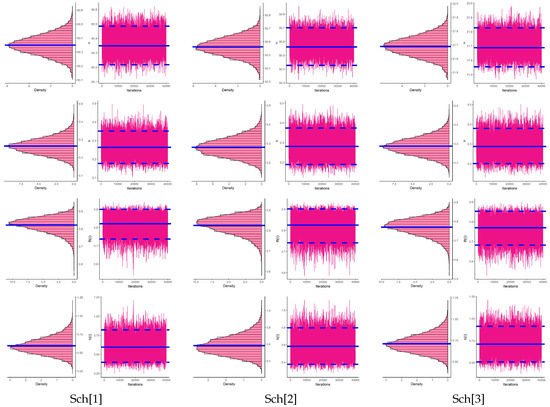
Figure 13. Density (left) and Trace (right) plots of $\alpha$, $\mu$, $R\left(t\right)$ and $h\left(t\right)$ from vinyl chloride data.

As a result, the reported discussions of real data sets representing 20 electron tubes and 34 vinyl chloride tubes, show that the derived estimators perform well in practical situations and proposed lifetime distribution is a suitable choice for modeling these data in the presence of Type-II generalized progressive hybrid censored data.

6. Optimal Progressive Designs

In regard to the context of reliability, the experimenter can decide to select the most effective censoring strategy from a group of all available progressive designs in order to offer as much information as possible about the parameter(s) under investigation. Independently, this issue was first addressed by Balakrishnan and Aggarwala [42] and Ng et al. [43]. The ideal censoring fashion $\mathbf{R}=(R_1,R_2,\dots ,R_m)$ such as ${\sum }_{j=1}^m{R}_j=n-m$, can be proposed, and the plausible choices of n, m and $T_i,i=1,2$ are predetermined in advance depending on unit capacity, experimentation facilities, and budgetary constraints. In the literature, several criteria, however, have been introduced, and numerous results on the optimum censoring systems have been investigated; for examples, see Pradhan and Kundu [44]; Sen et al. [45]; Elshahhat and Rastogi [46]; Ashour et al. [47]; and Elshahhat and Abu El Azm [48]. In Table 11, a list of commonly used metrics to help us choose the best censoring strategy is presented.

Table 11. Optimality criteria for the best censoring pattern.

Criterion	Aim
${\mathcal{O}}_1$	Maximize trace($\mathbf{I}\left(\widehat{\vartheta }\right)$)
${\mathcal{O}}_2$	Minimize trace(${\mathbf{I}}^{-1}\left(\widehat{\vartheta }\right)$)
${\mathcal{O}}_3$	Minimize det(${\mathbf{I}}^{-1}\left(\widehat{\vartheta }\right)$)
${\mathcal{O}}_4$	Minimize $\widehat{v}(\log ({\widehat{\mathcal{T}}}_{\varrho }))$

It should be noted that the objective of the studied criteria ${\mathcal{Q}}_i,i=2,3,4$ is to minimize the trace, determinant, and variance of the logarithmic MLE of the $\varrho$th quantile of the estimated variance–covariance ${\mathbf{I}}^{-1}(·)$ matrix, while the objective of criterion ${\mathcal{Q}}_1$ is to maximize the observed Fisher information ${\mathcal{F}}_{ii},i=1,2$ elements.

Obviously, the best censoring pattern must correspond to the largest value of ${\mathcal{Q}}_1$ and the smallest value of ${\mathcal{Q}}_i$ for $i=2,3,4$. Specifically, from (2), the logarithmic of the alpha-PIE lifetime distribution ${\mathcal{T}}_{\varrho }$ is given by

$$log({\widehat{\mathcal{T}}}_{\varrho })={\left.log\left(-\mu {\left[log\{{log}^{-1}\left(\alpha \right)log[\varrho (\alpha -1)+1]\}\right]}^{-1}\right)\right|}_{(\widehat{\alpha },\widehat{\mu })},0<\varrho <1.$$

(16)

Again, utilizing the delta method, the approximated variance of $log({\widehat{\mathcal{T}}}_{\varrho })$ is given by

$$\widehat{v}(log({\widehat{\mathcal{T}}}_{\varrho }))={\left.{\Sigma }_{log\left({\mathcal{T}}_{\varrho }\right)}^{\mathsf{T}}{\mathbf{I}}^{-1}\left(\vartheta \right){\Sigma }_{log\left({\mathcal{T}}_{\varrho }\right)}\right|}_{(\widehat{\alpha },\widehat{\mu })},$$

where

$${\Sigma }_{log({\widehat{\mathcal{T}}}_{\varrho })}^{\mathsf{T}}={\left.\left[\frac{\partial }{\partial \alpha }log({\mathcal{T}}_{\varrho })\phantom{\partial log\left({\mathcal{T}}_{\varrho }\right)},\frac{\partial }{\partial \mu }log\left({\mathcal{T}}_{\varrho }\right)\right]\right|}_{(\widehat{\alpha },\widehat{\mu })}.$$

6.1. Optimum from Electronic Tubes

This subsection aims to determine the best progressive censoring based on the generated samples, which are created from the electronic tube data, reported in Table 5. However, from Table 5, Table 6 and Table 11, the optimum criteria are evaluated; see Table 12.

Table 12. Optimum progressive plans from electronic tubes data.

Sample	Scheme	${\mathcal{O}}_1$	${\mathcal{O}}_2$	${\mathcal{O}}_3$	${\mathcal{O}}_4$
$\mathit{\varrho }\to$					0.3	0.6	0.9
${\mathcal{S}}_1$	Sch[1]	57.813	376.19	6.5069	0.1030	0.6945	18.150
	Sch[2]	73.399	307.77	4.1931	0.1051	0.7019	18.223
	Sch[3]	54.285	342.02	6.3005	0.1221	0.8200	21.367
${\mathcal{S}}_2$	Sch[1]	46.118	295.74	6.4126	0.1860	1.2338	31.917
	Sch[2]	58.574	323.42	5.3421	0.1128	0.7568	19.711
	Sch[3]	60.542	128.92	2.2010	0.0756	0.5160	13.586
${\mathcal{S}}_3$	Sch[1]	52.612	301.00	5.7118	0.1527	1.0162	26.337
	Sch[2]	46.011	347.39	6.6029	0.1183	0.7969	20.809
	Sch[3]	52.697	145.48	3.1619	0.1759	1.1714	30.362

Table 12 supports the same recommended censoring schemes considered in Section 4 and shows that

• According to ${\mathcal{O}}_i,i=1,2,3$, the design of Sch[2] (in Sample ${\mathcal{S}}_1$) and the design of Sch[3] (in Samples ${\mathcal{S}}_2$ and ${\mathcal{S}}_3$) are the optimum censoring plans compared to others.
• According to ${\mathcal{O}}_4$, the design of Sch[1] (in Sample ${\mathcal{S}}_1$), the design of Sch[3] (in Sample ${\mathcal{S}}_2$) and the design of Sch[2] (in Sample ${\mathcal{S}}_3$) are the optimum censoring plans compared to others.

6.2. Optimum from Vinyl Chloride

In this subsection, from the vinyl chloride data, we shall propose an optimal progressive censored plan based on the generated samples reported in Table 9. However, from Table 9, Table 10 and Table 11, the optimum criteria are evaluated and presented in Table 13.

Table 13. Optimum progressive plans from vinyl chloride data.

Sample	Scheme	${\mathcal{O}}_1$	${\mathcal{O}}_2$	${\mathcal{O}}_3$	${\mathcal{O}}_4$
$\mathit{\varrho }\to$					0.3	0.6	0.9
${\mathcal{S}}_1$	Sch[1]	240.82	72.074	0.2993	0.0371	0.2458	6.3534
	Sch[2]	185.93	318.51	1.7130	0.0439	0.2923	7.5784
	Sch[3]	211.50	92.340	0.4366	0.0241	0.1642	4.3147
${\mathcal{S}}_2$	Sch[2]	211.13	158.02	0.7485	0.0348	0.2328	6.0573
	Sch[2]	338.57	142.46	0.4208	0.0343	0.2240	5.7400
	Sch[3]	162.58	94.451	0.5810	0.0303	0.2061	5.4156
${\mathcal{S}}_3$	Sch[3]	566.15	46.993	0.0830	0.0262	0.1686	4.2879
	Sch[2]	1224.9	140.78	0.1149	0.0196	0.1227	3.0752
	Sch[3]	240.05	87.500	0.3645	0.0227	0.1540	4.0421

Table 13 shows that

• According to ${\mathcal{O}}_1$, the design of Sch[1] (in Sample ${\mathcal{S}}_1$) and the design of Sch[2] (in Samples ${\mathcal{S}}_i,i=2,3$) are the optimum censoring plans compared to others.
• According to ${\mathcal{O}}_i,i=2,3$, the design of Sch[1] (in Samples ${\mathcal{S}}_i,i=1,3$) are the optimum censoring plans compared to others.
• According to ${\mathcal{O}}_i,i=2,3$, the designs Sch[3] and Sch[2] (in Sample ${\mathcal{S}}_2$), respectively, are the optimum censoring plans compared to others.
• According to ${\mathcal{O}}_4$, the design of Sch[3] (in Samples ${\mathcal{S}}_i,i=1,2$) and the design of Sch[2] (in Samples ${\mathcal{S}}_3$) are the optimum censoring plans compared to others.

Finally, it is clear that the optimum progressive censoring plans suggested in this section support the same findings reported in Section 4.

7. Concluding Remarks

This work considers the problem of statistical inference of new alpha power-inverted exponential parameters of life using generalized Type-II progressively hybrid censored data. Classically, the maximum likelihood and asymptotic confidence interval estimates of the model parameters and any related time function have been derived using Newton–Raphson optimization process via the “$\mathsf{maxLik}$” language. The joint posterior density has been derived in a nonlinear form because the formula of the likelihood function has a complex expression. Independent gamma priors, to derive the Bayes and HPD interval estimates, are considered. Metropolis–Hastings sampler via the “$\mathsf{coda}$” language is also recommended to simulate the MCMC samples of the same unknown parameters. Extensive simulation experiments, based on various options of n, m, $\mathbf{R}$, and $T_i,i=1,2$, have been conducted to judge the behavior of the offered estimates. These studies show that the MCMC methodology performs quite well compared to the maximum likelihood approach. An optimum progressive censoring has also been presented using several optimality criterion measurements. Two scenarios based on real-world data sets from the engineering and chemical sectors are examined to highlight the superiority of the proposed model and how the provided estimates can be performed in practice. These applications show that the derived estimators perform well in practical situations and that the proposed lifetime distribution is a good choice compared to several models in the literature, namely, the inverted exponential, inverted Lindley, inverted Weibull, inverted gamma, and inverted Nadarajah–Haghighi distributions. We also believe that the findings and methodology presented here will be useful to reliability technicians, statisticians, and/or other scientists.