Abstract
In this paper, we present meanings of K--bonvexity/K--pseudobonvexity and their generalization between the above-notice functions. We also construct various concrete non-trivial examples for existing these types of functions. We formulate K--Wolfe type multiobjective second-order symmetric duality model with cone objective as well as cone constraints and duality theorems have been established under these aforesaid conditions. Further, we have validates the weak duality theorem under those assumptions. Our results are more generalized than previous known results in the literature.
Keywords:
K-Gf-pseudobonvexity; second-order; K-Gf-Wolfe type; efficient solution; multiobjective programming; arbitrary cones; strong duality; generalized assumptions MSC:
90C26; 90C30; 90C32; 90C46
1. Introduction
The field of optimization theory has progressed far beyond anyone’s expectations. Due to its wide variety of uses, it has made its way into all disciplines of science and engineering. When approximations are utilized, one of the most important practical applications of duality is that it provides bounds on the value of the objective functions because there are more factors involved, second-order duality has a greater computational benefit than first-order duality. For intriguing applications and breakthroughs in multiobjective optimization, we refer to [1], and the references cited therein. Dorn [2] presented the primary symmetric duality definition for quadratic programming in 1965. Dantzig et al. [3] and Mond [4] proposed a pair of symmetric dual Duality plays a vital role in investigating nonlinear programming problem solutions. Several writers have proposed several duality models, such as Wolfe dual [5] and Mond-Weir dual [6]. Nanda and Das [7] introduced four different forms of duality models for the nonlinear programming problem with cone constraints. The work of Bazaraa and Goode [8] and Hanson and Mond [9] inspired these findings.
Mangasian [10] established the duality theorem in the context of a second-order dual problem in nonlinear programming, where none of the constraints imposed convexity restrictions on all functions. Mond [11] introduced second-order symmetric dual models and established second-order symmetric duality theorems under second-order convexity conditions for the first time. In mathematical programming, Hasnson [12] defined the second-order invexity of a differentiable function and studied it. In 1999, Mishra [13] proposed a pair of second-order vector symmetric dual multiobjective models for arbitrary cones based on the Wolfe and Mond-Weir types. In addition 2006, ref. [14] a couple of Mond–Weir type second-order symmetric duality multiobjective calculations for cone second-order pseudoinvex and emphatically cone second-order pseudoinvex algorithm were presented. A couple of Mond–Weir type second-order symmetric dual multiobjective projects over discretion cones is created under pseudoinvexity/-convexity assumptions by Gulati [15], which is as:
Primal(MP):
Dual(MD):
where,
- (i)
- are open sets,
- (ii)
- is a twice differentiable function of and , is a differentiable function of and ,
- (iii)
- ,
- (iv)
- for i = 1,2, is a closed convex cone with non-empty interior and is its positive polar cone.Aside from them, a number of other researchers are working in this field. For additional information, see [16,17,18,19,20].In this paper be start by defining in Section 2, K--bonvexity as well as pseduobonvexity and construct non-trivial numerical examples for clear understanding the concept introduced by authors. We identify several examples lying exclusively K--bonvex and not in the class of K-invex function with respect to same already exist in the literature. We illustrate an example which is K--pseudobonvex but not K--bonvex with respect to same . In the next section, we formulate a new pair of multiobjective symmetric second order K--primal-dual models over arbitrary cone and drive duality results under K--bonvex as well as K--pseudobonvex assumptions. We, also construct a non-trivial example for validate the weak duality theorem presented in the paper. we also introduced geometry figure for clear understanding the concept through figure.
2. Preliminaries and Definitions
In this paper, we used for n-dimensional Euclidean space and for semi-positive orthant. Also, here and used for closed convex cone and respectively, with non-void interiors. For a real-valued twice differentiable function described on an open set in , indicate by the gradient vector of g with respect to a at , the Hessian matrix with respect to an at
Throughout the paper , .
A differentiable function is range for . Also, K is used for pointed convex cone with non-void interiors in , for and we specify cone orders with respect to K as follows:
Let be a differentiable function defined on open set and be the range of .
Consider the following multiobjective programming problem with cone objective as well as constraints as:
(MP) K-min
subject to
where Q is a closed convex cone with a non-empty interior in .
Definition 1
([21]). is a weak efficient solution of (MP), such that
Definition 2
([21]). is an efficient solution of (MP), such that
Now, we consider the following multiobjective programming with cone objective and cone constraints as:
(GMP) min
subject to
Definition 3
([21]). is a weak efficient solution of (GMP), s.t.
Definition 4
([21]). is a efficient solution of (GMP), s.t.
Definition 5
([21]). The positive polar cone of (i=1,2) is defined as Suppose that and are open sets such that
A differentiable function and such that every component is strictly increasing on the range of .
Definition 6.
then f is K--bonvex at with respect to η.
If and η such that and , we have
Definition 7.
If ∃ and η such that and , we have
then f is K--boncave at with respect to η.
Generalized the above definitions on two variable, as follows,
Definition 8.
If ∃ and and such that and , we have
then, f is K--bonvex in the first variable at for fixed with ,
and
If ∃ such that and , we have
then, f is K--bonvex in the second variable at for fixed with .
Definition 9.
If ∃ and such that and , we have
then, f is K--boncave in the first variable at for fixed with respect to ,
and
If ∃ and such that and , we have
then function f is K--boncave in the second variable at for fixed with respect to .
Example 1.
Let us apply the following ansatz:
consider
The above expression breaks in and (say) as follows:
where
Let and . Consider be defined by
where,
Next, defined by
Let and be given by
Now, we have to claim that f is -bonvex, for this, we have driven that the following expression as
Let
Substituting the values of and η, we obtain
Now, we consider
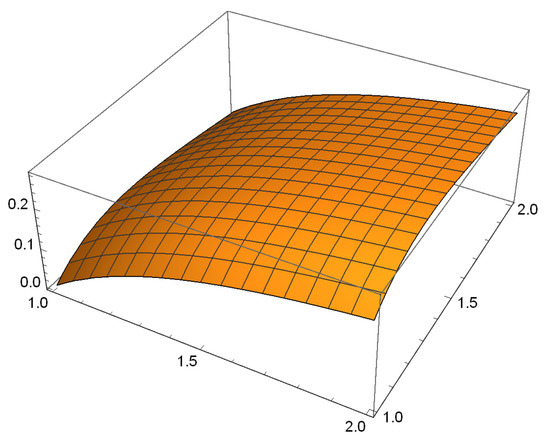
Figure 1.
.
It is clear from Figure 2, we obtain
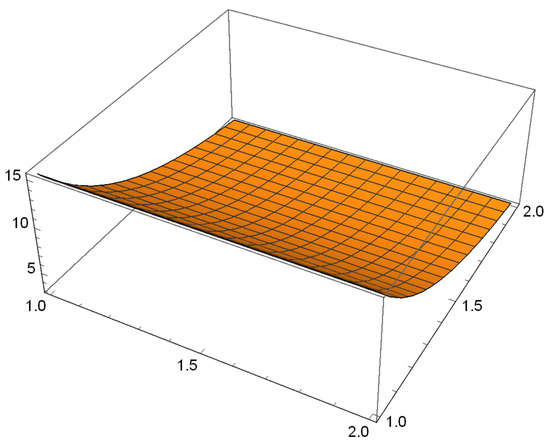
Figure 2.
.
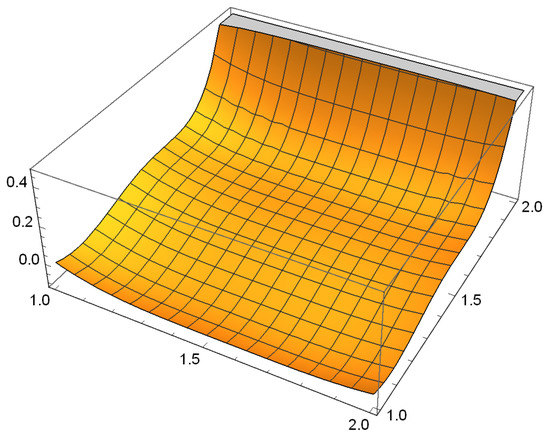
Figure 3.
.
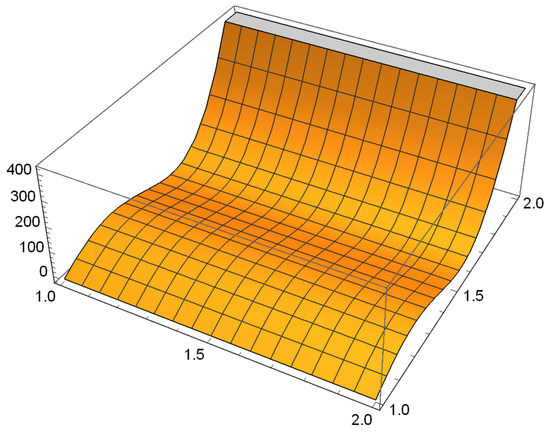
Figure 4.
.
Hence, and . This gives . Thus, we can find that
Hence, f is K--bonvex function at w.r.t. .
We will show that f is not invex. For this it is either
or
Since , is not as can be seen from Figure 5. Also, , is not as can be seen from Figure 6.
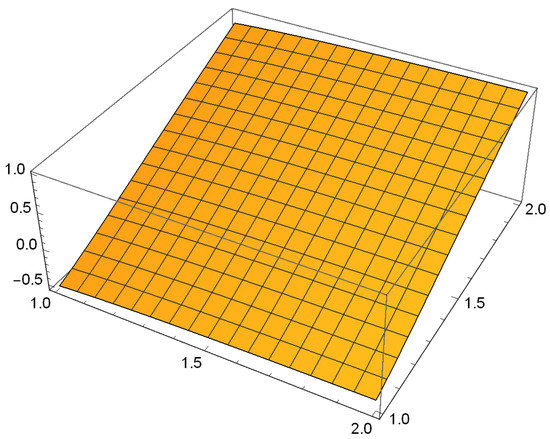
Figure 5.
.
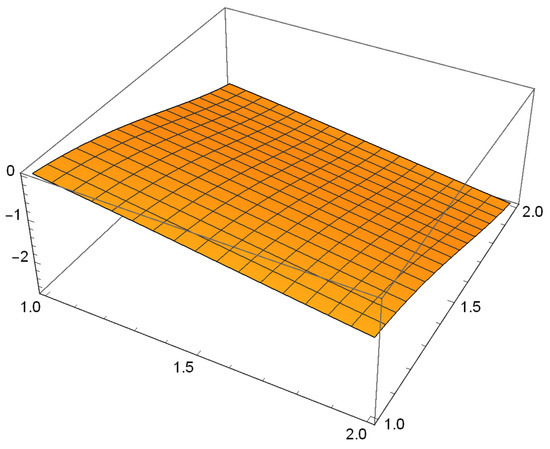
Figure 6.
.
Therefore, from the above example, it shows that f is K--bonvex, but it is not invex with respect to same .
Definition 10.
If ∃ and η such that and , we have
then, f is -pseudobonvex at with η.
Definition 11.
If ∃ and η such that and , we have
then f is -pseudoboncave at with respect to η.
We generalized the above definition as follows:
Definition 12.
If ∃ and such that and , we have
then f is K--bonvex in the first variable at for fixed with ,
and
if ∃ and such that and , we have
then f is K--bonvex in the second variable at for fixed with .
Definition 13.
If ∃ and such that and , we have
then f is K--bonvex in the first variable at for fixed with ,
and
If ∃ and such that and , we have
then f is K--boncave in the second variable at for fixed with respect to .
Remark 1.
If , then above definition reduces in -pseudo bonvex w.r.t. η,
Example 2.
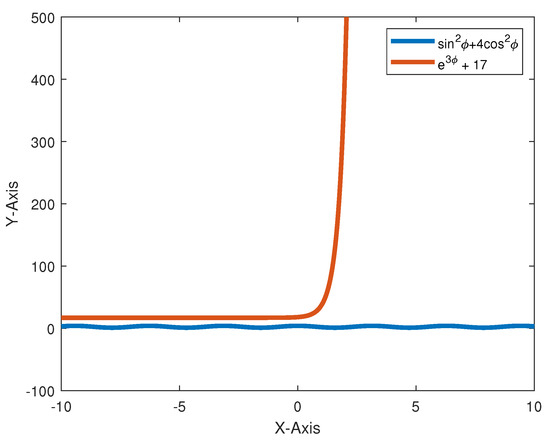
Let and . Consider the function defined by
where
Define given by
We have to claim that function f is K--pseudobonvex at point δ, i.e.,
Consider
Putting the values of and η, we have
At the point , the value of above expression becomes
Obviously,
Next, consider
Putting the values of and η, we have
The value of above expression at the point , we get
From the Figure 7. We can easily observe that the value of φ-coordinate always less than ϑ-coordinate in so

Figure 7.
.
Hence, f is K--pseudobonvex at the point with respect to
Next,
Let
Substituting the values of and η, we obtain
At the point , it follows that
Take particular point and we obtain,
Hence, f is K--pseudobonvex, but it is not K--bonvex at with respect to η.
In the following example, we showed that the function f is K--pseudobonvex, but it is not K--bonvex function with same .
Example 3.
Let and . Consider and given by
where
Define given by
Solution: In this example, we will try to derive that f is K--pseudobonvex i.e.,
Consider
Putting the values of and , we have
The value of above expression at the point , we get
Next, let
Putting the values of and , we have
After simplifying and the value at , it follows that
Hence, f is K--pseudobonvex at the point with respect to
Next,
Let
Substituting the values of and , we obtain
At the point , it follows that
Hence, f is K--pseudobonvex, but it is not K--bonvex at with respect to .
3. --Wolfe Type Second-Order Symmetric Primal-Dual Pair with Cones
The study of second-order duality is more significant due to computational advantage over first order duality as it provides tighter bounds for the objective functions, when approximation is used.
The motivated by [21,22,23,24,25,26,27] several researches in this area, we formulated a new type K--Wolfe type primal dual pair, with cone objectives as well as cone constraint as follows:
Primal Problem (GWPP):
K-minwhere
subject to
Dual Problem (GWDP):
K-max where
subject to
where, for
- is a differential function of and ,
- and are vectors in and , respectively and
Let and be the sets of feasible solutions of (GWPP) and (GWDP) respectively.
Theorem 1
(Weak duality). Let and . Let, for
- (i)
- be K--bonvex at δ w.r.t. ,
- (ii)
- be K--boncave in ϑ w.r.t. ,
- (iii)
- , ∀,
- (iv)
- , ∀,
Then,
Proof.
If possible, then suppose
or
Since , we get
By hypothesis and using , we get
Using feasibility of dual problem (GWDP) & using dual constraints with assumption , it yields
it implies that
Similarly, using hypotheses , feasible conditions of primal problem (GWPP), dual constraint and
Through following example, we validate the Weak duality theorem as:
Example 4.
Let n = m = 1, , , , , and
, Let and for be defined as
Further, let
Assume that
(GWPP)-minimize
Subject to constraints
(GWDP) K-maximize
Subject to constraints
(A1). is K--bonvex at w.r.t. ,∀, i.e.,
Consider
Putting the values of and at the point , and simplifying, we get
It is clear that
(A2). is K--boncave at w.r.t. , ,
Putting the values of at , we obtain
(A3)., .
(A4)., .
Validation: To validate Weak duality theorem it is enough to claim that any point such that , are feasible to . Also, the points such that , are feasible to . Now, at these feasible points,
and
Now, calculate the value at above feasible points, we have
In particular, the points and are feasible solutions for and , respectively. Also
Hence, this validate the results.
Remark 2.
Every pseudoconvex function is convex function. On the same pattern we can proof that K--pseudobonvex is K--bonvex with respect to same η. So, above proof of Weak duality 3.2 follows on same pattern as Theorem 1.
Theorem 2
(Weak duality). Let and . Let, For
- (i)
- be K--pseudobonvex at ℓ w.r.t. ,
- (ii)
- be K--pseudoboncave at ϑ, w.r.t. ,
- (iii)
- , ∀,
- (iv)
- , ∀,
Then,
Proof.
Proof follows on same lines as Weak Duality Theorem 1. □
Example 5.
For n = m = 1, ,,
Let be given as
Further, Let
Assume that
(GWPP)-minimize
Subject to constraints
(GWDP)-maximize
Subject to constraints
(A1). is K--pseudobonvex at with respect to , , so that
Let
Next, let
After simplification, substituting the value of and at , we get
(A2). is K--pseudoboncave at with respect to for fixed for all , i.e.,
Let
and
Substituting the value of and at the point and simplify, we get
(A3)., ∀.
(A4)., ∀.
Validation: To prove our result its enough to prove that any point such that , are feasible to . Also, the points such that , are feasible to . Now, at these feasible points,
and
Now at above feasible condition
In particular, the points and are
feasible for and respectively,
Now, calculate
Hence, this validate the Weak duality Theorem 2.
Theorem 3
(Strong duality). Let is an efficient solution of ; fix in such that
- (i)
- for all is nonsingular,
- (ii)
- the vector ∉span
- (iii)
- the set of vectors are linearly independent,
- (iv)
- and
- (v)
- K is closed convex pointed cone with
Then, and . Also, if the hypotheses of Theorem 1 or Theorem 2 are satisfied for all feasible solutions for and , then and is an efficient solution for and , respectively.
Proof.
Now, from hypothesis , it is given that ⇒
By hypothesis (ii), we get
Again, from hypothesis (iv), we have
From (39) implies
Using (42) and (43) in (37), we obtain
From hypothesis (iii), it yields
Using (43) and (44) in (30), we get
Using (40), (43), (44) and (46) in (30), we find that
Let Then, and inequality (47) gives that
Therefore,
Also, from (44), we obtain
Therefore, satisfies the constraint of (GWDP) and is therefore a feasible solution for the dual problem (GWDP).
Since is an efficient solution of , there exist and such that the following Fritz -John optimality condition stated by [28] are satisfied at
Obviously, because .
By hypothesis (33) gives
Suppose , then (39) yields . Further, from (38) gives . Now, we reach at contradiction (36). Hence, Further, implies
Now, we have to claim that Using (39) and (40) in (38), we get
Now, letting and in (47), we obtain
Further, from (34), (40), (43) and (44), we get
Therefore, using (43), (51) and (52), we obtain
This shows that the objective values are equal.
Finally, we have to claim that is an efficient solution of .
If possible, then suppose that is not an efficient solution of , then there exist is efficient solution of such that
As
which contradicts the Weak duality Theorem 1 or Theorem 2. Hence, completes the proof. □
Theorem 4
(Converse duality). Let is an efficient solution of ; fix in such that
- (i)
- for all is non singular,
- (ii)
- span
- (iii)
- the set of vectors are linearly independent,
- (iv)
- (v)
- K is closed convex pointed cone with
Then, is a feasible solution for and the objective values of and are equal. Furthermore, if the hypotheses of Theorem 1 or Theorem 2 are satisfied for all feasible solutions of and , then is an optimal solution of . Also, if the hypotheses of Theorem 1 or Theorem 2 are satisfied for all feasible solutions for and , then and is an efficient solution for and , respectively.
Proof.
It follows on the lines of Theorem 3. □
4. Conclusions
In this paper, we have presented a novel generalized group of definitions and illustrated various non-trivial numerical examples for existing such type of functions. Numerical examples have also been illustrated to justify the weak duality theorem. Furthermore, we have studied a new class of K--Wolfe type primal-dual model with cone objective as well as constraint and proved duality theorem under K--bonvexity and K--pseudobonvexity. This work can further be extended to higher order symmetric fractional programming problem and variational control problem over cones. This will be feature task for the researchers.
Author Contributions
All authors contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chinchuluun, A.; Pardalos, P.M. A survey of recent developments in multiobjective optimization. Ann. Oper. Res. 2007, 154, 29–50. [Google Scholar] [CrossRef]
- Dorn, W.S. A symmetric dual theorem for quadratic programming. J. Oper. Res. Soc. Jpn. 1960, 2, 93–97. [Google Scholar]
- Dantzig, G.B.; Eisenberg, E.; Cottle, R.W. Symmetric dual non-linear programs. Pac. J. Math. 1965, 15, 809–812. [Google Scholar] [CrossRef]
- Mond, B. A symmetric dual theorem for non-linear programs. Q. J. Appl. Math. 1965, 23, 265–269. [Google Scholar] [CrossRef]
- Mangasarian, O.L. Nonlinear Programming; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Mond, B.; Weir, T. Generalized concavity and duality. Gen. Concavity Optim. Econ. 1981, 263–279. [Google Scholar]
- Nanda, S.; Das, L.N. Pseudo-invexity and duality in nonlinear programming. Eur. J. Oper. Res. 1996, 88, 572–577. [Google Scholar] [CrossRef]
- Bazaraa, M.S.; Goode, J.J. On symmetric duality in nonlinear programming. Oper. Res. 1973, 21, 1–9. [Google Scholar] [CrossRef]
- Hanson, M.A.; Mond, B. Further generalization of convexity in mathematical programming. J. Inf. Optim. Sci. 1982, 3, 25–32. [Google Scholar] [CrossRef]
- Mangasarian, O.L. Second and higher order duality in non-linear programming. J. Math. Anal. Appl. 1975, 51, 607–620. [Google Scholar] [CrossRef]
- Mond, B. Second order duality for non-linear programs. Opsearch 1974, 11, 90–99. [Google Scholar]
- Hanson, M.A. Second order invexity and duality in mathematical programming. Opsearch 1993, 30, 313–320. [Google Scholar]
- Mishra, S.K. Multiobjective second order symmetric duality with cone constraints. Eur. J. Oper. Res. 2000, 126, 675–682. [Google Scholar] [CrossRef]
- Mishra, S.K.; Lai, K.K. Second order symmetric duality in multiobjective programming involving generalized cone-invex functions. Eur. J. Oper. Res. 2007, 178, 20–26. [Google Scholar] [CrossRef]
- Gulati, T.R. Mond-Weir type second-order symmetric duality in multiobjective programming over cones. Appl. Math. Lett. 2010, 23, 466–471. [Google Scholar] [CrossRef]
- Dhingra, V.; Kailey, N. Optimality and duality for second-order interval-valued variational problems. J. Appl. Math. Comput. 2021, 68, 3147–3162. [Google Scholar] [CrossRef]
- Dar, B.A.; Jayswal, A.; Singh, D. Optimality, duality and saddle point analysis for interval-valued nondifferentiable multiobjective fractional programming problems. Optimization 2021, 70, 1275–1305. [Google Scholar] [CrossRef]
- García-Alonso, C.R.; Pérez-Naranjo, L.M.; Fernández-Caballero, J.C. Multiobjective evolutionary algorithms to identify highly autocorrelated areas: The case of spatial distribution in financially compromised farms. Ann. Oper. Res. 2014, 219, 187–202. [Google Scholar] [CrossRef]
- Yang, X.M.; Yang, X.Q.; Teo, K.L.; Hou, S.H. Second order symmetric duality in non-differentiable multiobjective programming with F-convexity. Eur. J. Oper. Res. 2005, 164, 406–416. [Google Scholar] [CrossRef]
- Yang, X.M.; Yang, X.Q.; Teo, K.L.; Hou, S.H. Multiobjective second-order symmetric duality with F-convexity. Eur. J. Oper. Res. 2005, 165, 585–591. [Google Scholar] [CrossRef]
- Jayswal, A.; Prasad, A.K. Second order symmetric duality in nondifferentiable multiobjective fractional programming with cone convex functions. J. Appl. Math. Comput. 2014, 45, 15–33. [Google Scholar] [CrossRef]
- Chuong, T.D. Second-order cone programming relaxations for a class of multiobjective convex polynomial problems. Ann. Oper. Res. 2020, 311, 1017–1033. [Google Scholar] [CrossRef]
- Dubey, R.; Mishra, L.N.; Ali, R. Special class of second order nondifferentiable duality problems with (G,α)-pseudobonvexity assumptions. Mathematics 2019, 7, 763. [Google Scholar] [CrossRef]
- Dubey, R.; Mishra, V.N.; Tomar, P. Duality relations for second-order programming problem under (G,α)-bonvexity. Asian-Eur. J. Math. 2020, 13, 2050044. [Google Scholar] [CrossRef]
- Dubey, R.; Mishra, V.N.; Karateke, S. A class of second order nondifferentiable symmetric duality relations under generalized assumptions. J. Math. Comput. Sci. 2020, 21, 120–126. [Google Scholar] [CrossRef]
- Jayswal, A.; Jha, S. Second order symmetric duality in fractional variational problems over cone constraints. Yugosl. J. Oper. Res. 2018, 28, 39–57. [Google Scholar]
- Kapoor, M. Vector optimization over cones involving support functions using generalized (ϕ,ρ)-convexity. Opsearch 2017, 54, 351–364. [Google Scholar] [CrossRef]
- Kaur, A.; Sharma, M.K. Higher order symmetric duality for multiobjective fractional programming problems over cones. Yugosl. J. Oper. Res. 2021, 32, 29–44. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).