Theoretical Validation of New Two-Dimensional One-Variable-Power Copulas

Abstract

One of the most effective ways to illustrate the relationship between two quantitative variables is to describe the corresponding two-dimensional copula. This approach is acknowledged as practical, nonredundant, and computationally manageable in the context of data analysis. Modern data, however, contain a wide variety of dependent structures, and the copulas now in use may not provide the best model for all of them. As a result, researchers seek to innovate by building novel copulas with appealing properties that are also based on original methodologies. The foundations are theoretical; for a copula to be validated, it must meet specific requirements, which frequently dictate the constraints that must be placed on the relevant parameters. In this article, we make a contribution to the understudied field of one-variable-power copulas. We first identify the specific assumptions that, in theory, validate copulas of such nature. Some other general copulas and inequalities are discussed. Our general results are illustrated with numerous examples depending on two or three parameters. We also prove that strong connections exist between our assumptions and well-established distributions. To highlight the importance of our findings, we emphasize a particular two-parameter, one-variable-power copula that unifies the definition of some other copulas. We reveal its versatile shapes, related functions, various symmetry, Archimedean nature, geometric invariance, copula ordering, quadrant dependence, tail dependence, correlations, and distribution generation. Numerical tables and graphics are produced to support some of these properties. The estimation of the parameters based on data is discussed. As a complementary contribution, two new, intriguing one-variable-power copulas beyond the considered general form are finally presented and studied.

1. Introduction

It is ideal to assume two-dimensional normality when trying to explain the dependence of two quantitative variables. In this case, the theory has been around for a while, and well-mastered practical tools exist. However, a straightforward data analysis can typically disprove the non-normality assumption. Furthermore, the relationship between the two variables can have a complex structure beyond the standard schemes. The copula method suggests a workable resolution. Before going further, let us briefly define what a copula is from a mathematical viewpoint. A cumulative distribution function (CDF) on ${[0,1]}^2$ whose unidimensional margin distributions are uniformly distributed is known as a two-dimensional copula. The well-known Sklar’s theorem has helped copulas gain a lot of attention (see [1,2]). It asserts that every two-dimensional CDF can be expressed using the proper copula and its marginal CDFs. In this sense, a copula can be viewed as a dependence-related function. It is also a helpful tool for creating two-dimensional distributions. We refer to [3,4,5] for a complete view of the copula theory and a few of its uses. In the last few decades, numerous techniques have been developed for creating new copulas as a result of the increasing significance of dependence analysis in various statistical scenarios. The aim is to produce more adaptable families of two-dimensional CDFs that have a variety of attractive characteristics, such as tail dependence properties, asymmetries, broad correlation ranges, and probability density functions with original and flexible shapes. On these aspects, recent developments can be found in [6,7,8,9,10,11,12,13,14,15,16,17]. More specifically, in [11], some modifications of the Farlie–Gumbel–Morgenstern copula are proposed; in [13], a family of positive quadrant-dependent two-dimensional copulas is elaborated; in [17], Baker–Lin–Huang-type two-dimensional copulas based on order statistics are developed; in [9], some copulas are constructed from the pairs of order statistics; in [14], a family of two-dimensional independent copula transformations is studied; in [12], new types of multidimensional trigonometric copulas are proposed; in [15], various original three- and two-dimensional ratio-power copulas are developed; in [6], a collection of new trigonometric and hyperbolic Farlie–Gumbel–Morgenstern-type copulas are established; in [7], two generalized two-dimensional Farlie–Gumbel–Morgenstern copulas and rank reduction are investigated; in [10], two-dimensional copulas based on the counter-monotonic shock method are given; in [16], a multidimensional extension of the Raftery copula is proposed; and in [8], an extension of the Gumbel–Barnett family of copulas is studied.

In particular, in [8,18], copulas of the following form are studied:

$$\begin{array}{c}\hfill C(x,y)=xy{e}^{\theta A\left(x\right)B\left(y\right)},(x,y)\in {[0,1]}^2,\end{array}$$

(1)

where $\theta$ is a tuning parameter and $A\left(x\right)$ and $B\left(x\right)$ are differentiable continuous functions. Of course, the admissible values for $\theta$ are directly connected to the definitions of $A\left(x\right)$ and $B\left(x\right)$. The form in Equation (1) is general. In particular, it includes the Gumbel–Barnett copula, obtained with $\theta \in [-1,0]$ and $A\left(x\right)=B\left(x\right)=log\left(x\right)$ (see [5]), and the Celebioglu–Cuadras copula, which appears by taking $\theta \in [-1,1]$ and $A\left(x\right)=B\left(x\right)=1-x$ (see [19,20,21]). Furthermore, in the very special case where $\theta \in [0,1]$, and $A\left(x\right)=1-x$ and $B\left(x\right)=log\left(x\right)$, we obtain

$$\begin{array}{c}\hfill C(x,y)=x{y}^{1+\theta (1-x)}(x,y)\in {[0,1]}^2,\end{array}$$

(2)

which has been proposed in ([18] Example 2.3) (see also ([8] Exemple 3)). This specific one-variable-power (OVP) copula form is inspirational; to the best of our knowledge, there is no in-depth study on copulas expressed as

$$C(x,y)=x{y}^{f\left(x\right)},(x,y)\in {[0,1]}^2,$$

where $f\left(x\right)$ denotes a function that is only dependent on x (not y). Some motivations for considering it are listed below. This form is less general (and more simple) than the one in Equation (1), and it allows us to reveal some admissible functions $f\left(x\right)$ with a high level of originality or complexity. In particular, as sketched in Equation (2), two- or three-parameter special functions for $f\left(x\right)$ are quite conceivable. This is not the case when dealing with two functions that are dependent on different variables, such as $A\left(x\right)$ and $B\left(y\right)$.

We thus open this new room of research with the following contributions:

 (i)

We determine the precise assumptions on $f\left(x\right)$ that allow the two-dimensional function in Equation (2) to be a valid copula.

 (ii)

By using the flipping and survival methods, we derive some new general copulas with similar OVP functionalities.

 (iii)

Based on our copula findings, we derive some new general OVP two-dimensional inequalities.

 (iv)

We illustrate our general results with some concrete functions $f\left(x\right)$ depending on two or three tuning parameters and exhibit some connections between the assumptions made on $f\left(x\right)$ and well-established truncated lifetime distributions.

 (v)

We thoroughly investigate a particular proposed copula, emphasizing its related functions, shapes, various symmetry, Archimedean nature, geometric invariance, copula ordering, quadrant dependence, tail dependence, correlations, and distribution generation.

 (vi)

A short statistical work is given to illustrate how the involved parameters of this particular copula can be estimated from data.

 (vii)

Two new OVP copulas beyond the form in Equation (2) are finally presented as an additional contribution; one of them can be viewed as an original modified OVP version of the so-called Ali–Mikhail–Haq copula.

Typically, the proposed copulas may be used to model various claim types, payment and incurred loss data, and cross-industry- and cross-breach-type structures for monthly cyber losses, as well as the mortality of some countries, in the spirit of [22,23,24] with existing exponential–logarithmic-type copulas.

The rest of the article is organized as follows: Our general results are given in Section 2, along with some examples. Section 3 is devoted to the in-depth study of the suggested copula. Section 4 provides additional contributions by validating intriguing OVP copulas. The conclusion is given in Section 5.

2. OVP Variable Copulas

2.1. General Results

To begin, let us recall the exact mathematical definition of an absolutely continuous two-dimensional copula.

Definition 1

(absolutely continuous two-dimensional copulas [5]). A two-dimensional function $C(x,y)$, $(x,y)\in {[0,1]}^2$ is said to be an absolutely continuous two-dimensional copula if and only if the following assumptions are met for any $(x,y)\in {[0,1]}^2$:

 (I)

$C(x,0)=0$ and $C(0,y)=0$;

 (II)

$C(x,1)=x$ and $C(1,y)=y$;

 (III)

${\displaystyle {\partial }_{x,y}C(x,y)\ge 0}$, where ${\partial }_{x,y}={\partial }^2/(\partial x\partial y)$ represents the standard (mixed-second-order) partial derivatives according to x and y.

This definition is at the heart of most of our proofs. In the rest of the paper, we omit the sentence “absolutely continuous two-dimensional” to lighten the text.

The following result presents the general assumptions made on $f\left(x\right)$ to make copulas of the form $x{y}^{f\left(x\right)}$ valid.

Theorem 1.

Let $f\left(x\right)$, $x\in [0,1]$ be a function satisfying the following assumptions:

 A1:

$f\left(1\right)=1$ (or ${lim}_{x\to 1}f\left(x\right)=1$);

 A2:

${lim}_{x\to 0}f\left(x\right)=\ell$ with $\ell \in [1,+\infty )\cup \{+\infty \}$;

 A3:

$f\left(x\right)$ differentiable for $x\in [0,1]$ with $f^{\prime }\left(x\right)\le 0$ (so that $f\left(x\right)$ is non-increasing);

 A4:

$x{f}^{\prime }\left(x\right)+f\left(x\right)\ge 0$.

Then, the following two-dimensional OVP function is a copula:

$$\begin{array}{c}\hfill C(x,y)=x{y}^{f\left(x\right)},(x,y)\in {[0,1]}^2,\end{array}$$

(3)

with the usual convention that $0^0$ exists, i.e., equal to a finite value.

Proof. 

The proof consists in demonstrating that $C(x,y)$ satisfies the points (I), (II) and (III) of Definition 1.

 Proof

for (I) To begin, let us consider $C(x,0)$. For any $x\in [0,1]$, since $f\left(x\right)$ is non-increasing by A3 and $f\left(1\right)=1$ (or ${lim}_{x\to 1}f\left(x\right)=1$) by A1, we have $f\left(x\right)\ge f\left(1\right)=1>0$. Therefore, we obtain

$$C(x,0)=x\times 0^{f\left(x\right)}=0.$$

(For the case $x=0$, owing to A2, the case $\ell <+\infty$ is included, and if $\ell =+\infty$, we use the fact that $0^{+\infty }=0$).

Let us now consider $C(0,y)$ by distinguishing $\ell <+\infty$ and $\ell =+\infty$ based on A2. For the case $\ell <+\infty$, for any $y\in [0,1]$, we have

$$C(0,y)=0\times y^{\ell }=0.$$

For the case $\ell =+\infty$, we can remark that $y^{f\left(x\right)}=e^{f\left(x\right)log\left(y\right)},$ with $log\left(y\right)<0$ for $y\in [0,1)$, implying that ${lim}_{x\to 0}{y}^{f\left(x\right)}(=e^{\ell log\left(y\right)})=0$. Therefore, we obtain

$$C(0,y)=\underset{x\to 0}{lim}x\times e^{f\left(x\right)log\left(y\right)}=0\times 0=0.$$

Note that, for the case $y=0$, with the convention that $0^0$ exists, we have used $C(0,0)=0\times 0^0=0$. On the other hand, it is clear that $C(0,1)=0$. This ends this portion of the proof.

 Proof

for (II) For any $x\in [0,1]$, we have

$$C(x,1)=x\times 1^{f\left(x\right)}=x.$$

Similarly, for any $y\in [0,1]$, since $f\left(1\right)=1$ (or ${lim}_{x\to 1}f\left(x\right)=1$) by A1, it is immediate that

$$C(1,y)=1\times y^{f\left(1\right)}=y.$$

This ends this portion of the proof.

 Proof

for (III) After differentiation with the usual power-exponential rules and several simplifications and factorizations, for any $(x,y)\in {[0,1]}^2$, we find

$$\begin{array}{c}\hfill {\displaystyle {\partial }_{x,y}C(x,y)=y^{f\left(x\right)-1}\left[xf\left(x\right)log\left(y\right)f^{\prime }\left(x\right)+x{f}^{\prime }\left(x\right)+f\left(x\right)\right].}\end{array}$$

Since $(x,y)\in {[0,1]}^2$, it is clear that $y^{f\left(x\right)-1}\ge 0$. Furthermore, since $log\left(y\right)\le 0$, $f^{\prime }\left(x\right)\le 0$ by A3, and $f\left(x\right)\ge f\left(1\right)=1>0$ by A1, we have $xf\left(x\right)log\left(y\right)f^{\prime }\left(x\right)\ge 0$. These results and the inequality $x{f}^{\prime }\left(x\right)+f\left(x\right)\ge 0$ by A4 imply that ${\partial }_{x,y}C(x,y)\ge 0$.

This ends this portion of the proof.

The proof of Theorem 1 ends. □

The copula described in Equation (3) is thus modulated by a one-dimensional function $f\left(x\right)$ that only affects the power of y. The interest of Theorem 1 is that the assumptions A1, A2, A3, and A4 on $f\left(x\right)$ are fulfilled by functions of various nature. The most immediate example is $f\left(x\right)=1$, for which the copula in Equation (3) becomes the independence copula, i.e., $C(x,y)=xy$. Another simple example is $f\left(x\right)=1/x$, for which the copula in Equation (3) becomes $C(x,y)=x{y}^{1/x}$. This intriguing copula seems poorly referenced in the literature. More sophisticated functions with several parameters are presented in Section 2.2. This opens the door to the construction of new dependence models that can be used efficiently in diverse statistical scenarios. This claim is illustrated in Section 3 with the complete study of a special OVP copula that unified the independence copula and the intriguing $C(x,y)=x{y}^{1/x}$.

Of course, Theorem 1 and all the coming results can be applied to the copulas of the following form:

$$\begin{array}{c}\hfill C(x,y)=y{x}^{f\left(y\right)},(x,y)\in {[0,1]}^2,\end{array}$$

the roles of x and y being exchanged in comparison with Equation (3), but the required assumptions on $f\left(x\right)$ hold.

As one of the main important copula functions, the copula density related to the copula in Equation (3) is given as

$$\begin{array}{c}\hfill c(x,y)={\partial }_{x,y}C(x,y)=y^{f\left(x\right)-1}\left[xf\left(x\right)log\left(y\right)f^{\prime }\left(x\right)+x{f}^{\prime }\left(x\right)+f\left(x\right)\right],(x,y)\in {[0,1]}^2,\end{array}$$

in such a way that $C(x,y)={\int }_0^x{\int }_0^{y}c(s,t)dsdt$, $(x,y)\in {[0,1]}^2$. It has the advantage of being simple and quite manageable provided a moderate complexity in the definition of $f\left(x\right)$.

The next result shows how new OVP copulas can be immediately derived from Theorem 1 from the flipping (x-flipping and y-flipping) and survival approaches.

Proposition 1.

Let $f\left(x\right)$, $x\in [0,1]$ be a function satisfying the assumptions A1, A2, A3, and A4 of Theorem 1. Then, the following two-dimensional OVP functions are copulas:

 1.

$\overline{C}(x,y)=y-(1-x)y^{f(1-x)}$, $(x,y)\in {[0,1]}^2$;

 2.

$\tilde{C}(x,y)=x\left[1-{(1-y)}^{f\left(x\right)}\right]$, $(x,y)\in {[0,1]}^2$;

 3.

$\widehat{C}(x,y)=x+y-1+(1-x){(1-y)}^{f(1-x)}$, $(x,y)\in {[0,1]}^2$.

Proof. 

According to [5,25], the x-flipping, y-flipping, and survival copulas of a given copula are valid copulas. By denoting the baseline copula as $C(x,y)$, they are defined by

$$\begin{array}{c}\hfill \overline{C}(x,y)=y-C(1-x,y),\tilde{C}(x,y)=x-C(x,1-y)\end{array}$$

and

$$\begin{array}{c}\hfill \widehat{C}(x,y)=x+y-1+C(1-x,1-y),\end{array}$$

respectively. By considering Theorem 1 and the copula defined in Equation (3), i.e., $C(x,y)=x{y}^{f\left(x\right)}$, we obtain the desired results. The proof of Proposition 1 ends. □

To the best of our knowledge, Proposition 1 is the first result describing such OVP copulas, along with the precise theoretical assumptions behind them.

The next result presents some new two-dimensional inequalities that are of separate interest.

Proposition 2.

Let $f\left(x\right)$, $x\in [0,1]$ be a function satisfying the assumptions A1, A2, A3, and A4 of Theorem 1. Then, for any $(x,y)\in {[0,1]}^2$, the following two-dimensional OVP inequalities holds:

 1.

$max(x+y-1,0)\le x{y}^{f\left(x\right)}\le min(x,y);$

 2.

$max(x+y-1,0)\le y-(1-x)y^{f(1-x)}\le min(x,y)$;

 3.

$max(x+y-1,0)\le x\left[1-{(1-y)}^{f\left(x\right)}\right]\le min(x,y)$;

 4.

$max(x+y-1,0)\le x+y-1+(1-x){(1-y)}^{f(1-x)}\le min(x,y)$.

Proof. 

The proof follows immediately from the four copulas described in Theorem 1 and Proposition 1, and the Fréchet–Hoeffding theorem that is fulfilled for each of these copulas (as for any other copulas; see [5]). More precisely, this theorem states that for any copula $C(x,y)$, we have $max(x+y-1,0)\le C(x,y)\le min(x,y)$ for any $(x,y)\in {[0,1]}^2$. The proof of Proposition 2 ends. □

Proposition 2 can be picked up independently of the copula theory; new two-dimensional OVP inequalities are proved and can be used in various two-dimensional analysis settings.

The next results show how the proposed copulas and two baseline CDFs can be used to generate new two-dimensional distributions.

Proposition 3.

Let $f\left(x\right)$, $x\in [0,1]$ be a function satisfying the assumptions A1, A2, A3, and A4 of Theorem 1. Let $U\left(x\right)$ and $V\left(x\right)$ be two CDFs of absolutely continuous distributions. Then, for any $(x,y)\in {\mathbb{R}}^2$, the following two-dimensional OVP function are CDFs:

 1.

$F(x,y)=U\left(x\right)V{\left(y\right)}^{f\left[U\right(x\left)\right]}$;

 2.

$F(x,y)=V\left(y\right)-[1-U\left(x\right)]V{\left(y\right)}^{f[1-U(x\left)\right]}$;

 3.

$F(x,y)=U\left(x\right)\left\{1-{[1-V\left(y\right)]}^{f\left[U\right(x\left)\right]}\right\}$;

 4.

$F(x,y)=U\left(x\right)+V\left(y\right)-1+[1-U\left(x\right)]{[1-V\left(y\right)]}^{f[1-U(x\left)\right]}$.

Proof. 

The proof follows immediately from the four copulas described in Theorem 1 and Proposition 1, and the original definition of a copula (see Definition 1). This ends the proof of Proposition 3. □

Proposition 3 can be the starting point for various two-dimensional data analyses. For a panel of choices of lifetime baseline CDFs, we may suggest the overview in [26] and the references therein.

Theorem 1 opens the horizon for the creation of new copulas with an original definition beyond the OVP form. The following proposition illustrates this claim with a general ratio-form copula.

Proposition 4.

Let $f\left(x\right)$, $x\in [0,1]$ be a function satisfying the assumptions A1, A2, A3, and A4 of Theorem 1. Then, the following two-dimensional ratio-form function is a copula:

$$\begin{array}{c}\hfill C(x,y)=xy\frac{f\left(x\right)f\left(y\right)}{f\left(x\right)+f\left(y\right)-1},(x,y)\in {[0,1]}^2.\end{array}$$

(4)

Proof. 

The proof is based on the so-called copula product. For two-dimensional copulas, say $C_1(x,y)$ and $C_2(x,y)$, this product function is defined by

$$(C_1★C_2)(x,y)={\int }_0^1{\partial }_y{C}_1(x,t)\times {\partial }_x{C}_2(t,y)dt,(x,y)\in {[0,1]}^2.$$

A fundamental result is that $(C_1★C_2)(x,y)$ is a copula (see [5]). Let us apply it to $C_1(x,y)=x{y}^{f\left(x\right)}$ and $C_2(x,y)=y{x}^{f\left(y\right)}$, which are both copulas under the assumptions A1, A2, A3, and A4 of Theorem 1. We have ${\partial }_y{C}_1(x,y)=xf\left(x\right)y^{f\left(x\right)-1}$ and ${\partial }_x{C}_2(x,y)=yf\left(y\right)x^{f\left(y\right)-1}$. Hence, since $f\left(x\right)\ge f\left(1\right)=1$, we obtain

$$\begin{array}{cc}\hfill (C_1★C_2)(x,y)& ={\int }_0^{1}xf\left(x\right)t^{f\left(x\right)-1}\times yf\left(y\right)t^{f\left(y\right)-1}dt=xyf\left(x\right)f\left(y\right){\int }_0^1{t}^{f\left(x\right)+f\left(y\right)-2}dt\hfill \\ \hfill & =xyf\left(x\right)f\left(y\right){\left.\frac{t^{f\left(x\right)+f\left(y\right)-1}}{f\left(x\right)+f\left(y\right)-1}\right|}_{t=0}^{t=1}=xy\frac{f\left(x\right)f\left(y\right)}{f\left(x\right)+f\left(y\right)-1}.\hfill \end{array}$$

This ends the proof of Proposition 4. □

It is worth noting that the copula in Equation (4) is connected with the Ali–Mikhail–Haq copula (with parameter $\theta =1$). Indeed, by taking $f\left(x\right)=1/x$, we obtain

$$\begin{array}{c}\hfill C_{*}(x,y)=\frac{xy}{1-(1-x)(1-y)},(x,y)\in {[0,1]}^2,\end{array}$$

(5)

which is a special case of the Ali–Mikhail–Haq copula. Thus, Proposition 4 offers a new perspective on dependence ratio-copula models.

The following section includes numerous examples to illustrate the above theory.

2.2. Examples

We now aim to exemplify Theorem 1. More precisely, some examples of parametric functions $f\left(x\right)$ satisfying the main assumptions of this theorem and the related OVP copulas are described. The lemma below is the first result in this regard.

Lemma 1.

Let $(\alpha ,\beta ,\gamma )\in {\mathbb{R}}^3$. The following functions satisfy the assumptions A1, A2, A3, and A4 of Theorem 1:

 Function 1:

Power:

$$f\left(x\right)=1+\beta {(1-x^{\alpha })}^{\gamma },x\in [0,1],$$

for $\alpha >0$, $\gamma \ge 1$ and $\beta \in [0,1/(\alpha \gamma \left)\right]$.

 Function 2:

Exponential-power:

$$f\left(x\right)=e^{\beta (1-x^{\alpha })},x\in [0,1],$$

for $\alpha >0$ and $\beta \in [0,1/\alpha ]$.

 Function 3:

Sine

$$f\left(x\right)=1+\lambda sin\left[\beta (1-x^{\alpha })\right],x\in [0,1],$$

for $\beta \in [0,\pi /2]$, $\alpha >0$, and $\lambda \in [0,1/(\alpha \beta \left)\right]$.

 Function 4:

Logarithmic:

$$f\left(x\right)=1-\beta log\left(x\right),x\in [0,1],$$

for $\beta \in [0,1]$.

 Function 5:

Inverse-power:

$$f\left(x\right)=\beta (x^{-\alpha }-1)+1,x\in [0,1],$$

for $\alpha \in (0,1]$ and $\beta \in [0,1/\alpha ]$.

Proof. 

Let us prove that each of the proposed functions $f\left(x\right)$ satisfies the assumptions A1, A2, A3, and A4 of Theorem 1.

 Proof

for Function 1: We have the following:

• Since $\gamma \ge 1$, $f\left(1\right)=1+\beta {(1-1^{\alpha })}^{\gamma }=1$, A1 is satisfied;
• Since $\alpha >0$, ${lim}_{x\to 0}f\left(x\right)=1+\beta {(1-0^{\alpha })}^{\gamma }=1+\beta$ (so $\ell =1+\beta$), A2 is satisfied;
• Since $\alpha >0$, $\gamma \ge 1$ and $\beta \in [0,1/(\alpha \gamma \left)\right]$, $f^{\prime }\left(x\right)=-\alpha \beta \gamma x^{\alpha -1}{(1-x^{\alpha })}^{\gamma -1}\le 0$, A3 is satisfied;
• Since $\alpha >0$, $\gamma \ge 1$, $\beta \in [0,1/(\alpha \gamma \left)\right]$, $x^{\alpha }\le 1$ and ${(1-x^{\alpha })}^{\gamma -1}\le 1$ for $x\in [0,1]$,

  $$\begin{array}{cc}\hfill x{f}^{\prime }\left(x\right)+f\left(x\right)& =-\alpha \beta \gamma x^{\alpha }{(1-x^{\alpha })}^{\gamma -1}+1+\beta {(1-x^{\alpha })}^{\gamma }\hfill \\ \hfill & \ge 1-\alpha \beta \gamma x^{\alpha }{(1-x^{\alpha })}^{\gamma -1}\ge 1-\alpha \beta \gamma \ge 0,\hfill \end{array}$$

  so A4 is satisfied. Let us mentioned that the above inequality can be refined for values of $\alpha$, $\beta$, and $\gamma$ such that $\alpha \beta \gamma {sup}_{x\in [0,1]}{x}^{\alpha }{(1-x^{\alpha })}^{\gamma -1}\le 1$.

 Proof

for Function 2: We have the following:

• $f\left(1\right)=e^{\beta (1-1^{\alpha })}=e^0=1$, so A1 is satisfied;
• Since $\alpha >0$, ${lim}_{x\to 0}f\left(x\right)=e^{\beta (1-0^{\alpha })}=e^{\beta }$ (so $\ell =e^{\beta }$), A2 is satisfied;
• Since $\alpha >0$ and $\beta \in [0,1/\alpha ]$, $f^{\prime }\left(x\right)=-\alpha \beta x^{\alpha -1}{e}^{\beta (1-x^{\alpha })}\le 0$, A3 is satisfied;
• Since $\alpha >0$, $\beta \in [0,1/\alpha ]$ and $x^{\alpha }\le 1$ for $x\in [0,1]$,

  $$\begin{array}{cc}\hfill x{f}^{\prime }\left(x\right)+f\left(x\right)& =-\alpha \beta x^{\alpha }{e}^{\beta (1-x^{\alpha })}+e^{\beta (1-x^{\alpha })}=e^{\beta (1-x^{\alpha })}(1-\alpha \beta x^{\alpha })\hfill \\ \hfill & \ge 1-\alpha \beta \ge 0,\hfill \end{array}$$

  so A4 is satisfied.

 Proof

for Function 3: We have:

• $f\left(1\right)=1+\lambda sin\left[\beta (1-1^{\alpha })\right]=1+sin\left(0\right)=1$, so A1 is satisfied;
• Since $\beta \in [0,\pi /2]$, $\alpha >0$, and $\lambda \in [0,1/(\alpha \beta \left)\right]$,
  ${lim}_{x\to 0}f\left(x\right)=1+\lambda sin\left[\beta (1-0^{\alpha })\right]=1+\lambda sin\left(\beta \right)$ (so $\ell =1+\lambda sin\left(\beta \right)$), so A2 is satisfied;
• Since $\beta \in [0,\pi /2]$, $\alpha >0$, and $\lambda \in [0,1/(\alpha \beta \left)\right]$,
  $f^{\prime }\left(x\right)=-\lambda \alpha \beta x^{\alpha -1}cos\left[\beta (1-x^{\alpha })\right]\le 0$, A3 is satisfied;
• Using basic differentiation rules, we obtain

  $$\begin{array}{cc}\hfill x{f}^{\prime }\left(x\right)+f\left(x\right)& =-\lambda \alpha \beta x^{\alpha }cos\left[\beta (1-x^{\alpha })\right]+1+\lambda sin\left[\beta (1-x^{\alpha })\right]\hfill \\ \hfill & =\left\{1-\lambda \alpha \beta x^{\alpha }cos\left[\beta (1-x^{\alpha })\right]\right\}+\lambda sin\left[\beta (1-x^{\alpha })\right].\hfill \end{array}$$
  Since $\beta \in [0,\pi /2]$, $\alpha >0$, and $\lambda \in [0,1/(\alpha \beta \left)\right]$, $x^{\alpha }\le 1$ and $cos\left[\beta (1-x^{\alpha })\right]\le 1$ for $x\in [0,1]$,

  $$\lambda \alpha \beta x^{\alpha }cos\left[\beta (1-x^{\alpha })\right]\le \lambda \alpha \beta \le 1,$$

  and it is clear that $\lambda sin\left[\beta (1-x^{\alpha })\right]\ge 0$. Hence, $x{f}^{\prime }\left(x\right)+f\left(x\right)\ge 0$; so A4 is satisfied.

 Proof

for Function 4: We have:

• $f\left(1\right)=1-\beta log\left(1\right)=1$, so A1 is satisfied;
• ${lim}_{x\to 0}f\left(x\right)=1-\beta {lim}_{x\to 0}log\left(x\right)=+\infty$ (so $\ell =+\infty$), so A2 is satisfied;
• Since $\beta \in [0,1]$, $f^{\prime }\left(x\right)=-\beta x^{-1}\le 0$, A3 is satisfied;
• Since $\beta \in [0,1]$, and $-log\left(x\right)\ge 0$ for $x\in [0,1]$,

  $$\begin{array}{cc}\hfill x{f}^{\prime }\left(x\right)+f\left(x\right)& =-\beta +1-\beta log\left(x\right)\ge 1-\beta \ge 0,\hfill \end{array}$$

  so A4 is satisfied.

 Proof

for Function 5: We have:

• $f\left(1\right)=\beta (1^{-\alpha }-1)+1=1$, so A1 is satisfied;
• Since $\alpha \in (0,1]$, ${lim}_{x\to 0}f\left(x\right)=\beta ({lim}_{x\to 0}{x}^{-\alpha }-1)+1=+\infty$ (so $\ell =+\infty$), A2 is satisfied;
• Since $\alpha \in (0,1]$ and $\beta \in [0,1/\alpha ]$, $f^{\prime }\left(x\right)=-\alpha \beta x^{-\alpha -1}\le 0$, A3 is satisfied;
• Since $\alpha \in (0,1]$, $\beta \in [0,1/\alpha ]$, and $x^{-\alpha }\ge 1$ for $x\in [0,1]$,

  $$\begin{array}{cc}\hfill x{f}^{\prime }\left(x\right)+f\left(x\right)& =-\alpha \beta x^{-\alpha }+\beta (x^{-\alpha }-1)+1=1-\beta +x^{-\alpha }\beta (1-\alpha )\hfill \\ \hfill & \ge 1-\beta +\beta (1-\alpha )=1-\alpha \beta \ge 0,\hfill \end{array}$$

  so A4 is satisfied.

The proof of Lemma 1 comes to an end. □

Of course, Lemma 1 contains only a few examples, so much more can be found. This claim is illustrated in a coming result with the notion of CDF.

The functions in Lemma 1 combined with the result in Theorem 1 give the copulas collected in Table 1.

Table 1. Copulas derived from Theorem 1 and Lemma 1.

Name	Abbreviation	Copula C(x,y)	Conditions	New
Power	P	$x{y}^{1+\beta {(1-x^{\alpha })}^{\gamma }}$	$\alpha >0$, $\gamma \ge 1$, ${\displaystyle \beta \in \left[0,\frac{1}{\alpha \gamma }\right]}$	Yes
Exponential-power	EP	$x{y}^{e^{\beta (1-x^{\alpha })}}$	$\alpha >0$, ${\displaystyle \beta \in \left[0,\frac{1}{\alpha }\right]}$	Yes
Sine	S	$x{y}^{1+\lambda sin\left[\beta (1-x^{\alpha })\right]}$	${\displaystyle \beta \in \left[0,\frac{\pi }{2}\right]}$, $\alpha >0$, ${\displaystyle \lambda \in \left[0,\frac{1}{\alpha \beta }\right]}$	Yes
Logarithmic	L	$x{y}^{1-\beta log\left(x\right)}$	$\beta \in [0,1]$	No
Inverse-power	IP	$x{y}^{\beta (x^{-\alpha }-1)+1}$	$\alpha \in (0,1]$, ${\displaystyle \beta \in \left[0,\frac{1}{\alpha }\right]}$	Yes

By taking $\beta =0$, all of the suggested copulas are reduced to the independence copula. By taking $\alpha =\gamma =1$, the P copula is reduced to the copula in Equation (1), so exemplified in ([18] Example 2.3). The L copula as described in Table 1 is not new. Indeed, we can write

$$C(x,y)=x{y}^{1-\beta log\left(x\right)}=xy\times y^{-\beta log\left(x\right)}=xy{e}^{-\beta log\left(x\right)log\left(y\right)},$$

and we obtain the so-called Gumbel–Barnett copula (see [5]). To the best of our knowledge, the other copulas presented in the table are totally new and original. Because of its particular interest, the IP copula has a special treatment in Section 4 for reasons explained later.

In a similar manner, based on the specific functions of Lemma 1, we may express all the OVP copulas presented in Proposition 1; this is, however, omitted for space reasons. The same is true for the ratio copulas presented in Proposition 4, which are less relevant to the OVP copula topic but are of a certain interest.

The next result shows that the assumptions A1, A2, A3, and A4 of Theorem 1 may be connected with the notion of CDF; they are satisfied by a simple ratio transformation of a CDF under suitable assumptions.

Proposition 5.

Let $G\left(x\right)$ be a CDF of an absolutely continuous distribution with support $[0,1]$ and $g\left(x\right)$ be the corresponding probability density function. Suppose the following:

 B1:

${lim}_{x\to 0}xg\left(x\right)=0$;

 B2:

$g^{\prime }\left(x\right)\le 0$ (so that $g\left(x\right)$ is non-increasing).

Then, the following ratio CDF satisfies the assumptions A1, A2, A3, and A4 of Theorem 1:

$$f\left(x\right)=\frac{1}{G\left(x\right)},x\in [0,1].$$

Proof. 

Since $G\left(x\right)$ is the CDF of an absolutely continuous distribution with support $[0,1]$, we recall that $G\left(0\right)=0$, $G\left(1\right)=1$, $G\left(x\right)={\int }_0^{x}g\left(t\right)dt$ and $G^{\prime }\left(x\right)=g\left(x\right)\ge 0$. As a result:

• $f\left(1\right)=1/G\left(1\right)=1$, so A1 is satisfied;
• ${lim}_{x\to 0}f\left(x\right)=1/{lim}_{x\to 0}G\left(x\right)=+\infty$ (implying that $\ell =+\infty$), so A2 is satisfied;
• $f^{\prime }\left(x\right)=-g\left(x\right)/G{\left(x\right)}^2\le 0$, so A3 is satisfied;
• Since $G^{\prime }\left(x\right)=g\left(x\right)$, we have

  $$\begin{array}{cc}\hfill x{f}^{\prime }\left(x\right)+f\left(x\right)& =-\frac{xg\left(x\right)}{G{\left(x\right)}^2}+\frac{1}{G\left(x\right)}=\frac{1}{G{\left(x\right)}^2}\left[-xg\left(x\right)+G\left(x\right)\right].\hfill \end{array}$$
  It is clear that $1/G{\left(x\right)}^2\ge 0$. Let us now prove that $-xg\left(x\right)+G\left(x\right)\ge 0$. Using an integration by part, ${lim}_{x\to 0}xg\left(x\right)=0$ by B1, and $g^{\prime }\left(x\right)\le 0$ by B2, we obtain

  $$\begin{array}{cc}\hfill G\left(x\right)& ={\int }_0^{x}g\left(t\right)dt=tg\left(t\right){|}_{t=0}^{t=x}-{\int }_0^{x}t{g}^{\prime }\left(t\right)dt=xg\left(x\right)+{\int }_0^{x}t[-g^{\prime }\left(t\right)]dt\ge xg\left(x\right).\hfill \end{array}$$
  Hence, $-xg\left(x\right)+G\left(x\right)\ge 0$, implying that $x{f}^{\prime }\left(x\right)+f\left(x\right)\ge 0$, so A4 is satisfied.

The proof of Proposition 5 ends. □

Thus, based on Proposition 5, if $G\left(x\right)$ satisfies the assumptions B1 and B2, then the following two-dimensional OVP function is a valid copula:

$$C(x,y)=x{y}^{1/G\left(x\right)},(x,y)\in {[0,1]}^2.$$

Some examples of well-established parametric CDFs $G\left(x\right)$ satisfying the main assumptions in Proposition 5 are described in the lemma below. They are mainly based on truncated CDFs of recognized lifetime distributions (exponential distribution, Lomax distribution, etc.).

Lemma 2.

Let $(\alpha ,\beta )\in {\mathbb{R}}^2$. The following CDFs satisfy the assumptions B1 and B2 of Proposition 5:

 CDF 1:

Truncated exponential:

$$G\left(x\right)=\frac{1}{1-e^{-\alpha }}(1-e^{-\alpha x}),x\in [0,1],$$

for $\alpha >0$.

 CDF 2:

Truncated exponential-logarithmic:

$$G\left(x\right)=\frac{1}{1-log(1-(1-\beta )e^{-\alpha })/log\left(\beta \right)}\left[1-\frac{log(1-(1-\beta )e^{-\alpha x})}{log\left(\beta \right)}\right],x\in [0,1],$$

for $\alpha >0$ and $\beta \in (0,1)$.

 CDF 3:

Truncated Lomax:

$$G\left(x\right)=\frac{1}{\left[1-{(1+1/\beta )}^{-\alpha }\right]}\left[1-{\left(1+\frac{x}{\beta }\right)}^{-\alpha }\right],x\in [0,1],$$

for $\alpha >0$ and $\beta >0$.

 CDF 4:

Truncated half-normal:

$$G\left(x\right)=\frac{1}{erf(1/\sqrt{2}\beta )}erf\left(\frac{x}{\sqrt{2}\beta }\right),x\in [0,1],$$

where $erf\left(x\right)=(2/\sqrt{\pi }){\int }_0^x{e}^{-t^2}dt$ for $\beta >0$.

Proof. 

Let us prove that each of the proposed CDFs satisfies the assumptions B1 and B2 of Proposition 5.

 Proof

for CDF 1: We have the following:

• $$g\left(x\right)=G^{\prime }\left(x\right)=\frac{\alpha }{1-e^{-\alpha }}{e}^{-\alpha x},$$

  so it is immediate that ${lim}_{x\to 0}xg\left(x\right)=0$, so B1 is satisfied;
• For $\alpha >0$,

  $$g^{\prime }\left(x\right)=-\frac{{\alpha }^2}{1-e^{-\alpha }}{e}^{-\alpha x}\le 0,$$

  so B2 is satisfied.

 Proof

for CDF 2: We have the following:

• $$g\left(x\right)=G^{\prime }\left(x\right)=\frac{1}{1-log(1-(1-\beta )e^{-\alpha })/log\left(\beta \right)}\left(\frac{\alpha (1-\beta )}{-log\left(\beta \right)}\right)\frac{e^{-\alpha x}}{1-(1-\beta )e^{-\alpha x}},$$

  so it is clear that ${lim}_{x\to 0}xg\left(x\right)=0$, so B1 is satisfied;
• For $\alpha >0$ and $\beta \in (0,1)$,

  $$g^{\prime }\left(x\right)=-\frac{1}{1-log(1-(1-\beta )e^{-\alpha })/log\left(\beta \right)}\left(\frac{{\alpha }^2(1-\beta )}{-log\left(\beta \right)}\right)\frac{e^{-\alpha x}}{{\left[1-(1-\beta )e^{-\alpha x}\right]}^2}\le 0;$$

  all the main terms being positive, the minus in factor gives the final sign, so B2 is satisfied.

 Proof

for CDF 3: We have the following:

• $$g\left(x\right)=G^{\prime }\left(x\right)=\frac{1}{\left[1-{(1+1/\beta )}^{-\alpha }\right]}\frac{\alpha }{\beta }{\left(1+\frac{x}{\beta }\right)}^{-(\alpha +1)},$$

  so it is immediate that ${lim}_{x\to 0}xg\left(x\right)=0$, so B1 is satisfied;
• For $\alpha >0$ and $\beta >0$,

  $$g^{\prime }\left(x\right)=-\frac{\alpha +1}{\left[1-{(1+1/\beta )}^{-\alpha }\right]}\frac{\alpha }{{\beta }^2}{\left(1+\frac{x}{\beta }\right)}^{-(\alpha +2)}\le 0,$$

  so B2 is satisfied.

 Proof

for CDF 4: We have

• $$g\left(x\right)=G^{\prime }\left(x\right)=\frac{1}{erf(1/\sqrt{2}\beta )}\frac{1}{\beta }\sqrt{\frac{2}{\pi }}{e}^{-x^2/\left(2{\beta }^2\right)},$$

  so it is immediate that ${lim}_{x\to 0}xg\left(x\right)=0$, so B1 is satisfied;
• For $\beta >0$,

  $$g^{\prime }\left(x\right)=-\frac{1}{erf(1/\sqrt{2}\beta )}\frac{1}{{\beta }^3}\sqrt{\frac{2}{\pi }}x{e}^{-x^2/\left(2{\beta }^2\right)}\le 0,$$

  so B2 is satisfied.

The proof of Lemma 2 ends. □

The interest of the functions in Lemma 2 is that the assumptions on the parameters are relaxed; when $\alpha$ and $\beta$ are involved, they can be chosen independently. This aspect contrasts with the joint parameter restrictions imposed on the functions proposed in Lemma 1.

The functions in Lemma 2 combined with the result in Theorem 1 give the copulas collected in Table 2.

Table 2. Copulas derived from Theorem 1 and Lemma 2.

Name	Abbreviation	Copula $\mathit{C}(\mathit{x},\mathit{y})$	Conditions
Truncated exponential	TE	$x{y}^{(1-e^{-\alpha })/(1-e^{-\alpha x})}$	$\alpha >0$
Truncated exponential–logarithmic	TEL	$x{y}^{[1-log(1-(1-\beta )e^{-\alpha })/log\left(\beta \right)]/\left[1-log(1-(1-\beta )e^{-\alpha x})/log\left(\beta \right)\right]}$	$\alpha >0$, $\beta \in (0,1)$
Truncated Lomax	TL	$x{y}^{\left[1-{(1+1/\beta )}^{-\alpha }\right]/\left[1-{\left(1+x/\beta \right)}^{-\alpha }\right]}$	$\alpha >0$, $\beta >0$
Truncated half-normal	THN	$x{y}^{erf(1/\sqrt{2}\beta )/erf\left[x/\left(\sqrt{2}\beta \right)\right]}$	$\beta >0$

As a quick illustration of the findings, Figure 1 shows the TE copula for various values of the parameters $\alpha$.

Figure 1. Plots of the TE copula for $\alpha =1/2$ (left) and $\alpha =20$ (right).

This figure illustrates the mathematical validity of the TE copula, its flexibility in terms of shape deformations, and the ease of its implementation; all the graphical and numerical analyses of this article are realized by using the R software (see [27]).

3. Complete Study of the IP Copula

In this section, an emphasis is put on one of the more interesting proposed copulas: the IP copula (see Table 1).

3.1. Functions

To begin, we recall that the IP copula is defined by

$$C(x,y)=x{y}^{\beta (x^{-\alpha }-1)+1},(x,y)\in {[0,1]}^2,$$

where $\alpha \in (0,1]$ and $\beta \in [0,1/\alpha ]$. It is of particular interest because of the following reasons:

 (i)

It is simple, which aids in determining all related functions.

 (ii)

It is based on two tuning parameters with manageable ranges of values.

 (iii)

It is primarily nonexchangeable, i.e., we can find $(x,y)$ such that $C(x,y)\ne C(y,x)$ (except for $\beta =0$), which is a desired property when the symmetry in data is absent.

 (iv)

For $\beta =0$, it is reduced to the independence copula, i.e., $C(x,y)=xy$.

 (v)

For $\beta =1$ and $\alpha =1$, it becomes the simple power-variable copula: $C(x,y)=x{y}^{1/x}$, which has not received much attention in the literature despite a certain functional originality.

For illustrative purposes, Figure 2 and Figure 3 show some plots of the IP copula for selected admissible sets of parameter values.

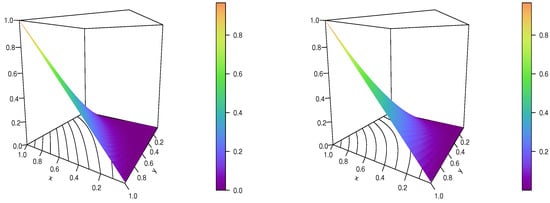
Figure 2. Plots of the IP copula for $\alpha =1/2$ and $\beta =2$ (left) and $\beta =1/2$ (right).

Figure 3. Plots of the IP copula for $\alpha =1$ and $\beta =1$ (left) and $\beta =1/2$ (right).

It is evident from these figures that the IP copula is correct mathematically for the considered values. Moreover, depending on the values of $\alpha$ and $\beta$, a variety of deformations of the colored plan shape can be seen. The contour plots make this adaptability especially clear.

The IP copula density is determined using the following formula:

$$\begin{array}{cc}\hfill & {\displaystyle c(x,y)={\partial }_{x,y}C(x,y)}\hfill \\ \hfill & =x^{-2\alpha }{y}^{\beta (x^{-\alpha }-1)}\{\alpha \beta log\left(y\right)[(\beta -1)x^{\alpha }-\beta ]-x^{\alpha }[(\alpha -1)\beta +(\beta -1)x^{\alpha }]\},(x,y)\in {[0,1]}^2.\hfill \end{array}$$

To comprehend the modeling capabilities of the IP copula, we may look at the shapes of its corresponding copula density. Thus, Figure 4 and Figure 5 display the IP copula density plots for various parameter values.

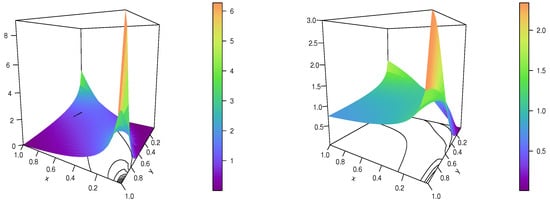
Figure 4. Plots of the IP copula density for $\alpha =1/2$ and $\beta =2$ (left) and $\beta =1/2$ (right).

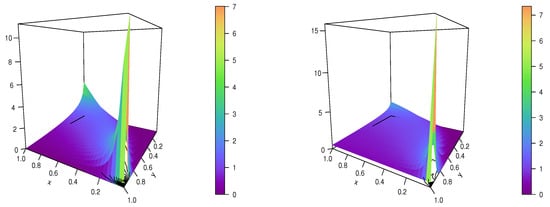
Figure 5. Plots of the IP copula density for $\alpha =1$ and $\beta =1$ (left) and $\beta =1/2$ (right).

These figures reveal entirely distinct overall forms for the IP copula density, with a degenerate point at $(0,1)$. Visually, the shapes are strongly influenced by $\alpha$ and $\beta$. The dependence flexibility is thus illustrated.

To end this portion, let us present some copulas that can be immediately derived from the IP copula. To begin, the x-flipping IP copula is specified as

$$\begin{array}{cc}\hfill \overline{C}(x,y)& =y-C(1-x,y)\hfill \\ \hfill & =y\left[1-(1-x)y^{\beta [{(1-x)}^{-\alpha }-1]}\right],(x,y)\in {[0,1]}^2.\hfill \end{array}$$

The y-flipping IP copula is indicated as

$$\begin{array}{cc}\hfill \tilde{C}(x,y)& =x-C(x,1-y)\hfill \\ \hfill & =x\left[1-{(1-y)}^{\beta (x^{-\alpha }-1)+1}\right],(x,y)\in {[0,1]}^2.\hfill \end{array}$$

Finally, the IP survival copula is given by

$$\begin{array}{cc}\hfill \widehat{C}(x,y)& =x+y-1+C(1-x,1-y)\hfill \\ \hfill & =x+y-1+(1-x){(1-y)}^{\beta [{(1-x)}^{-\alpha }-1]+1},(x,y)\in {[0,1]}^2.\hfill \end{array}$$

These copulas, which are new to the best of our knowledge, can be used as two-dimensional dependence models for data analysis. More information on the general formulas used for the flipping and survival approaches can be found in [5,25].

3.2. Fundamental Properties

In order to comprehend the modeling capability of the IP copula, this section establishes some fundamental properties of it. It is implicitly supposed that $\alpha \in (0,1]$ and $\beta \in [0,1/\alpha ]$. We recall that [3,4,5] contain most of the details about the upcoming concepts.

The exchangeability has already been mentioned; the IP copula is not exchangeable, except for $\beta =0$, which corresponds to the independence copula case.

The IP copula is not Archimedean; the associative property is not satisfied in particular; for $\alpha =\beta =1/2$, for instance, we have $C[1/4,C(1/2,1/3\left)\right]=0.01209179$ and $C\left[C\right(1/4,1/2),1/3]=0.008042948$, which differ.

The IP copula is not radially symmetric, except for $\beta =0$. Indeed, for $\beta \ne 0$, we can find $(x,y)$ such that $C(x,y)\ne \widehat{C}(x,y)$.

We can apply the Fréchet–Hoeffding theorem, which guarantees that for any $(x,y)\in {[0,1]}^2$, we have $max(x+y-1,0)\le C(x,y)\le min(x,y)$, which can also be expressed as

$$max(x+y-1,0)\le x{y}^{\beta (x^{-\alpha }-1)+1}\le min(x,y).$$

For purposes unrelated to copulas, these inequalities may be of independent interest.

Let us set $C(x,y;\beta )=C(x,y)$, with the parameter $\beta$ now being considered as a variable. Then, for any $\upsilon \in [0,1]$, and any ${\beta }_1$ and ${\beta }_2$, we have

$$\begin{array}{cc}\hfill C{(x,y;{\beta }_1)}^{\upsilon }C{(x,y;{\beta }_2)}^{1-\upsilon }& =x{y}^{[\upsilon {\beta }_1+(1-\upsilon ){\beta }_2](x^{-\alpha }-1)+1}\hfill \\ \hfill & =C(x,y;\upsilon {\beta }_1+(1-\upsilon ){\beta }_2).\hfill \end{array}$$

Thus, in this geometric mean sense, the IP copula is invariant. See [8] for more details on this invariance property.

Since, for any $(x,y)\in {[0,1]}^2$, $\beta (x^{-\alpha }-1)\ge 0$, we have $C(x,y)\ge xy$. Therefore, the IP copula is positively quadrant-dependent.

For any $(x,y)\in {[0,1]}^2$, we have

$${\partial }_{\alpha }C(x,y)=-\beta x^{1-\alpha }log\left(x\right)log\left(y\right)y^{\beta (x^{-\alpha }-1)+1}\le 0,$$

implying that $C(x,y)$ is non-increasing with respect to $\alpha$. By setting $C(x,y;\alpha )=C(x,y)$, the following copula ordering holds: for any ${\alpha }_1\le {\alpha }_2$, we have $C(x,y;{\alpha }_2)\le C(x,y;{\alpha }_1)$.

Furthermore, for any $(x,y)\in {[0,1]}^2$, we have

$${\partial }_{\beta }C(x,y)=x(x^{-\alpha }-1)log\left(y\right)y^{\beta (x^{-\alpha }-1)+1}\le 0,$$

implying that $C(x,y)$ is non-increasing with respect to $\beta$. By setting $C(x,y;\beta )=C(x,y)$, the following copula ordering holds: for any ${\beta }_1\le {\beta }_2$, we have $C(x,y;{\beta }_2)\le C(x,y;{\beta }_1)$.

Let us now study the tail dependence of the IP copula. We have

$$\begin{array}{cc}\hfill {\zeta }_{low}& =\underset{x\to 0}{lim}\frac{C(x,x)}{x}=\underset{x\to 0}{lim}{x}^{\beta (x^{-\alpha }-1)+1}=0.\hfill \end{array}$$

Furthermore, we have

$$\begin{array}{cc}\hfill {\zeta }_{up}& =\underset{x\to 1}{lim}\frac{1-2x+C(x,x)}{1-x}=\underset{x\to 1}{lim}\frac{1-2x+x^2-x^2(1-x^{\beta (x^{-\alpha }-1)})}{1-x}\hfill \\ \hfill & =\underset{x\to 1}{lim}\left(1-x+\alpha \beta (1-x)\right)=0.\hfill \end{array}$$

Due to the fact that ${\zeta }_{low}={\zeta }_{up}=0$, we draw the conclusion that the IP copula does not depend on the tail.

The medial correlation of the IP copula is calculated as

$$\mathcal{M}=4C\left(\frac{1}{2},\frac{1}{2}\right)-1=2^{-\beta (2^{\alpha }-1)}-1.$$

It is clearly negative.

Table 3 and Table 4 determine the numerical values of $\mathcal{M}$ under the following configurations: {$\alpha =1$ and $\beta \in [0,1]$} and {$\alpha =1/2$ and $\beta \in [0,2]$}, respectively.

Table 3. Numerical values of $\mathcal{M}$ for $\alpha =1$ and $\beta \in \{0,0.1,\dots ,0.9,1\}$.

$\mathit{\beta }$	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
$\mathcal{M}$	0	−0.067	−0.1294	−0.1877	−0.2421	−0.2929	−0.3402	−0.3844	−0.4257	−0.4641	−0.5

Table 4. Numerical values of $\mathcal{M}$ for $\alpha =1/2$ and $\beta \in \{0,0.2,\dots ,1.8,2\}$.

$\mathit{\beta }$	0	0.2	0.4	0.6	0.8	1.0	1.2	1.4	1.6	1.8	2.0
$\mathcal{M}$	0	−0.0558	−0.1085	−0.1582	$$-0.2052$$	−0.2496	−0.2914	−0.331	−0.3683	−0.4036	−0.4369

These tables show that for the particular configurations taken into account, we have $\mathcal{M}\in [-0.5,0]$. This range of values is quite good for this particular measure.

The Spearman rho of the IP copula is specified as

$$\rho =12{\int }_0^1{\int }_0^{1}C(x,y)dxdy-3=12{\int }_0^1{\int }_0^{1}x{y}^{\beta (x^{-\alpha }-1)+1}dxdy-3.$$

By integrating with respect to y, we obtain

$$\rho =12{\int }_0^1\frac{x^{\alpha +1}}{\beta +(2-\beta )x^{\alpha }}dx-3.$$

It can be expressed for very specific values of the parameters. For instance, for $\beta =2$ (so $\alpha \in (01/2]$), the denominator of the integrated term is equal to 2, and we have $\rho =6/(\alpha +2)-3$. However, in full generality, the functional complexity of the integrated term is too high; the Spearman rho does not have a closed-form expression in terms of $\alpha$ and $\beta$.

Table 5 and Table 6 determine the numerical values of $\rho$ under the following configurations: {$\alpha =1$ and $\beta \in [0,1]$} and {$\alpha =1/2$ and $\beta \in [0,2]$}, respectively.

Table 5. Numerical values of $\rho$ for $\alpha =1$ and $\beta \in \{0,0.1,\dots ,0.9,1\}$.

$\mathit{\beta }$	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
$\rho$	0	−0.1221	−0.2179	−0.2992	−0.3706	−0.4344	−0.4923	−0.5453	−0.5943	−0.6397	−0.6822

Table 6. Numerical values of $\rho$ for $\alpha =1/2$ and $\beta \in \{0,0.2,\dots ,1.8,2\}$.

$\mathit{\beta }$	0	0.2	0.4	0.6	0.8	1.0	1.2	1.4	1.6	1.8	2.0
$\rho$	0	−0.0918	−0.1713	−0.2421	−0.306	−0.3645	−0.4184	−0.4684	−0.5151	−0.5588	−0.6

These tables show that the IP copula can only model negative dependence and that for the considered configurations, we have $\rho \in [-0.6822,0]$. This range of values is relatively large, which validates the IP copula for weak-to-moderate negative dependence.

The IP copula can serve as a generator of two-dimensional distributions. Indeed, by considering two unidimensional CDFs, say $U\left(x\right)$ and $V\left(x\right)$, we define a new two-dimensional CDF as

$$\begin{array}{cc}\hfill F(x,y)& =C[U\left(x\right),V\left(y\right)]=U\left(x\right)V{\left(y\right)}^{\beta \left[U{\left(x\right)}^{-\alpha }-1\right]+1}(x,y)\in {\mathbb{R}}^2.\hfill \end{array}$$

In a two-dimensional lifetime data analysis scenario, one can consider lifetime baseline distributions. On this topic, we again refer to the survey in [26], and the references therein.

3.3. Statistical Study with Simulated Data

We now investigate the IP copula in a simulated data setting. Based on the available data, for the estimation of the parameters $\alpha$ and $\beta$, an efficient solution is the omnibus estimation method, as described in [28,29]. To present this method, let us consider observations drawn from a continuous random vector, such as $(X,Y)$. Thus, let n be the number of observations of this vector and $(x_1,y_1),\dots ,(x_n,y_n)$ be the observations representing the data. Then, the omnibus estimates (OEs) of $\alpha$ and $\beta$ are determined as

$$(\widehat{\alpha },\widehat{\beta })={argmax}_{(\alpha ,\beta )\in \Omega }\sum _{i=1}^{n}log\left\{c\left[\widehat{F}\left(x_i\right),\widehat{G}\left(y_i\right)\right]\right\},$$

where

$$\begin{array}{cc}\hfill & log\left[c(x,y)\right]=-2\alpha log\left(x\right)+\beta (x^{-\alpha }-1)log\left(y\right)\hfill \\ \hfill & +log\left\{\alpha \beta log\left(y\right)[(\beta -1)x^{\alpha }-\beta ]-x^{\alpha }[(\alpha -1)\beta +(\beta -1)x^{\alpha }]\right\},\hfill \end{array}$$

$\Omega =\{(\alpha ,\beta )\in {\mathbb{R}}^2;\alpha \in (0,1],\beta \in [0,1/\alpha ]\}$,

$$\widehat{F}\left(x\right)=\frac{1}{n}\sum _{j=1}^n\mathcal{I}\{x_j\le x\},\widehat{G}\left(y\right)=\frac{1}{n}\sum _{j=1}^n\mathcal{I}\{y_j\le y\},$$

and $\mathcal{I}\left\{A\right\}$ denotes the indicator function related to a set A. The accuracy of the omnibus estimation method is demonstrated in [28,29]. We now implement this method as an illustration.

For the first study, we generate $n=500$ pairs of data as follows: $(u_1,|cos\left(\pi u_1\right)|+v_1),\dots ,(u_n,|cos\left(\pi u_n\right)|+v_n)$, where, for any $i=1,\dots ,n$, $u_i$ and $v_i$ are the observations of two independent random variables U and V that follow the exponential distribution with parameter 1. Then, the obtained OEs are $\widehat{\alpha }=0.2178639$ and $\widehat{\beta }=0.3767299$, which are clearly admissible. Based on these estimates, we define the estimated IP copula density as

$$\begin{array}{cc}\hfill & \widehat{c}(x,y)=x^{-2\widehat{\alpha }}{y}^{\widehat{\beta }(x^{-\widehat{\alpha }}-1)}\{\widehat{\alpha }\widehat{\beta }log\left(y\right)[(\widehat{\beta }-1)x^{\widehat{\alpha }}-\widehat{\beta }]-x^{\widehat{\alpha }}[(\widehat{\alpha }-1)\widehat{\beta }+(\widehat{\beta }-1)x^{\widehat{\alpha }}]\}.\hfill \end{array}$$

Figure 6 displays the scatter plot of the data and the estimated function.

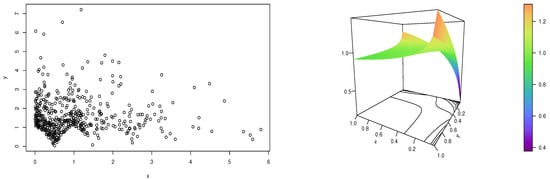
Figure 6. Scatter plot of the data (left) and plot of the estimated IP copula density (right).

This figure thus illustrates the functional print of the dependence structure behind the considered data.

A second simulated study is now performed with other kinds of data. We generate $n=500$ pairs of data as follows: $(u_1,exp(-u_1^2)+v_1),\dots ,(u_n,exp(-u_n^2)+v_n)$, where, for any $i=1,\dots ,n$, $u_i$ and $v_i$ are still the observations of two independent random variables U and V that follow the exponential distribution with parameter 1. In this experiment, the obtained OEs are $\widehat{\alpha }=0.00219458$ and $\widehat{\beta }=339.66025140$, which are clearly admissible. Based on these estimates, we consider the estimated IP copula density with the substitution technique as described above.

Figure 7 displays the scatter plot of the data and the estimated function.

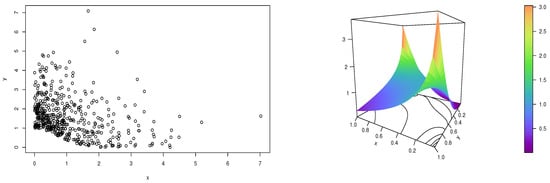
Figure 7. Scatter plot of the data (left) and plot of the estimated IP copula density (right).

This figure thus illustrates the functional print of the dependence structure behind the considered data. The differences in the OEs and in shapes in the estimated IP copula density prove the versatility of the IP copula and its ability to capture diverse structures of dependence.

This simulated work can be viewed as the first step for the application of the IP copula to real-data sets.

4. On Two Intriguing OVP Copulas

We complete this study with the presentation of two intriguing OVP copulas, completely different from those described above. They are intriguing because of their original definition, which is so far beyond the standard and has a certain degree of complexity from a mathematical viewpoint. As main features, the first proposed copula uses the term $(1-xy)$ in power $1/x$, which seems unique in the literature, and the second copula mixes various powers of x, including in the power of the main term. Some connections to the Ali–Mikhail–Haq copula are highlighted for this one. To the best of our knowledge, they are completely new.

4.1. Intriguing OVP Copula 1

The next result presents the first intriguing copula.

Proposition 6.

The following two-dimensional OVP function is a copula:

$$\begin{array}{c}\hfill C(x,y)=x\left[1+y{(1-x)}^{1/x}-{(1-xy)}^{1/x}\right],(x,y)\in {[0,1]}^2,\end{array}$$

(6)

(no parameters are involved).

Proof. 

The proof consists in demonstrating that $C(x,y)$ satisfies the points (I), (II), and (III) of Definition 1.

 Proof

for (I) For any $x\in [0,1]$, we have

$$C(x,0)=x\left[1+0\times {(1-x)}^{1/x}-{(1-x\times 0)}^{1/x}\right]=x(1-1)=0.$$

For any $y\in [0,1]$, with the use of limits, we obtain

$$\begin{array}{cc}\hfill C(0,y)& =\left(\underset{x\to 0}{lim}x\right)\times \left[1+y\underset{x\to 0}{lim}{(1-x)}^{1/x}-\underset{x\to 0}{lim}{(1-xy)}^{1/x}\right]\hfill \\ \hfill & =0\times \left[1+y{e}^{-1}-e^{-y}\right]=0.\hfill \end{array}$$

This ends this portion of the proof.

 Proof

for (II) For any $x\in [0,1]$, we have

$$\begin{array}{cc}\hfill C(x,1)& =x\left[1+1\times {(1-x)}^{1/x}-{(1-x\times 1)}^{1/x}\right]\hfill \\ \hfill & =x\left[1+{(1-x)}^{1/x}-{(1-x)}^{1/x}\right]=x.\hfill \end{array}$$

For any $y\in [0,1]$, we have

$$\begin{array}{cc}\hfill C(1,y)& =1\times \left[1+y{(1-1)}^{1/1}-{(1-1\times y)}^{1/1}\right]=1-1+y=y.\hfill \end{array}$$

This ends this portion of the proof.

 Proof

for (III) After differentiation with the usual rules and several simplifications and factorizations, for any $(x,y)\in {[0,1]}^2$, we find

$$\begin{array}{cc}\hfill & {\partial }_{x,y}C(x,y)=xy{(1-xy)}^{1/x-2}-y{(1-xy)}^{1/x-2}+{(1-xy)}^{1/x-1}\hfill \\ \hfill & -{(1-xy)}^{1/x-1}\frac{log(1-xy)}{x}-{(1-x)}^{1/x-1}+{(1-x)}^{1/x}-{(1-x)}^{1/x}\frac{log(1-x)}{x}.\hfill \end{array}$$

We aim to prove that this function is non-negative. For any $(x,y)\in {[0,1]}^2$, since ${(1-xy)}^{1/x-1}\ge 0$ and ${(1-x)}^{1/x}\ge 0$, owing to the following logarithmic inequality: $log(1-x)\le -x$ for $x\in [0,1)$, we have

$$\begin{array}{cc}\hfill {\partial }_{x,y}C(x,y)& \ge xy{(1-xy)}^{1/x-2}-y{(1-xy)}^{1/x-2}+{(1-xy)}^{1/x-1}\hfill \\ \hfill & +y{(1-xy)}^{1/x-1}-{(1-x)}^{1/x-1}+{(1-x)}^{1/x}+{(1-x)}^{1/x}\hfill \\ \hfill & =(1-x{y}^2){(1-xy)}^{1/x-2}+(1-2x){(1-x)}^{1/x-1}.\hfill \end{array}$$

Using $y^2\le y$, we get

$$\begin{array}{cc}\hfill {\partial }_{x,y}C(x,y)& \ge (1-xy){(1-xy)}^{1/x-2}+(1-2x){(1-x)}^{1/x-1}\hfill \\ \hfill & ={(1-xy)}^{1/x-1}+(1-2x){(1-x)}^{1/x-1}.\hfill \end{array}$$

Since $1/x-1\ge 0$ and $xy\le x$, we finally obtain

$$\begin{array}{c}\hfill {\partial }_{x,y}C(x,y)\ge {(1-x)}^{1/x-1}+(1-2x){(1-x)}^{1/x-1}=2{(1-x)}^{1/x}\ge 0.\end{array}$$

This ends this portion of the proof.

The proof of Proposition 6 ends. □

For the purpose of this study, the copula defined in Equation (6) is named the intriguing 1 (Int1) copula.

Some functions and properties related to the Int1 copula are listed below. To begin, the Int1 copula density is given by

$$\begin{array}{cc}\hfill & c(x,y)={\partial }_{x,y}C(x,y)=xy{(1-xy)}^{1/x-2}-y{(1-xy)}^{1/x-2}+{(1-xy)}^{1/x-1}\hfill \\ \hfill & -{(1-xy)}^{1/x-1}\frac{log(1-xy)}{x}-{(1-x)}^{1/x-1}+{(1-x)}^{1/x}-{(1-x)}^{1/x}\frac{log(1-x)}{x},\hfill \\ \hfill & (x,y)\in {[0,1]}^2.\hfill \end{array}$$

For a visual analysis, the Int1 copula and Int1 copula density are represented in Figure 8.

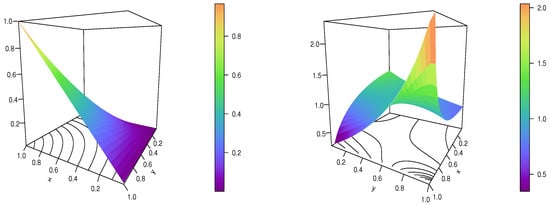
Figure 8. Plots of the Int1 copula (left) and the Int1 copula density (right).

This figure reveals some shapes of the Int1 copula and Int1 copula density, also illustrating their validity in the mathematical sense; it is clear that $C(x,y)\in [0,1]$, $c(x,y)\ge 0$, etc.

Among the new copulas that can be derived from the Int1 copula are the x-flipping Int1 copula, specified as

$$\begin{array}{cc}\hfill \overline{C}(x,y)& =y-C(1-x,y)\hfill \\ \hfill & =y-(1-x)\left\{1+y{x}^{1/(1-x)}-{[(1-x)(1-y)+x]}^{1/(1-x)}\right\},(x,y)\in {[0,1]}^2,\hfill \end{array}$$

the y-flipping Int1 copula indicated as

$$\begin{array}{cc}\hfill \tilde{C}(x,y)& =x-C(x,1-y)\hfill \\ \hfill & =x\left\{{[(1-x)(1-y)+y]}^{1/x}-(1-y){(1-x)}^{1/x}\right\},(x,y)\in {[0,1]}^2,\hfill \end{array}$$

and the Int1 survival copula given by

$$\begin{array}{cc}\hfill \widehat{C}(x,y)& =x+y-1+C(1-x,1-y)\hfill \\ \hfill & =y+(1-x)\left\{(1-y)x^{1/(1-x)}-{[1-(1-x)(1-y)]}^{1/(1-x)}\right\},(x,y)\in {[0,1]}^2.\hfill \end{array}$$

All these copulas can serve as two-dimensional dependence models in two-dimensional data analysis scenarios.

For the main properties, the Int1 copula is (obviously) free of parameters, not exchangeable, not radially symmetric, not Archimedean, its medial correlation is equal to $\mathcal{M}=4C(1/2,1/2)-1=1/8=0.125$, and its Spearman rho is equal to

$$\begin{array}{cc}\hfill \rho & =12{\int }_0^1{\int }_0^{1}C(x,y)dxdy-3\hfill \\ \hfill & =12{\int }_0^1{\int }_0^{1}x\left[1+y{(1-x)}^{1/x}-{(1-xy)}^{1/x}\right]dxdy-3\hfill \\ \hfill & =0.181836.\hfill \end{array}$$

As a last result, we may also mention the Fréchet–Hoeffding theorem that asserts that $max(x+y-1,0)\le C(x,y)\le min(x,y)$ for any $(x,y)\in {[0,1]}^2$, so

$$max(x+y-1,0)\le x\left[1+y{(1-x)}^{1/x}-{(1-xy)}^{1/x}\right]\le min(x,y).$$

This result innovates from a multidimensional (or multivariate) analysis viewpoint.

The Int1 copula is of mathematical interest because of its very original OVP definition. However, because there are no tuning parameters, it suffers from a lack of flexibility in a practical scenario. Several techniques to add parameters are possible, but we drop this aspect here.

The next part proposes another intriguing OVP copula that has the feature of depending on two tuning parameters, among others.

4.2. Intriguing OVP Copula 2

The next result presents the second intriguing copula.

Proposition 7.

Let $(\alpha ,\gamma )\in {\mathbb{R}}^2$. Then, for $(\alpha ,\gamma )\in {(0,1]}^2$ and $\gamma -\alpha \in [0,1]$, the following two-dimensional OVP function is a copula:

$$\begin{array}{c}\hfill C(x,y)=x{\left[1+x^{\alpha }\left(\frac{1}{y}-1\right)\right]}^{-x^{-\gamma }},(x,y)\in {[0,1]}^2.\end{array}$$

(7)

Proof. 

The proof consists in demonstrating that $C(x,y)$ satisfies the points (I), (II), and (III) of Definition 1.

 Proof

for (I) For any $x\in [0,1]$, since $\gamma >0$, $-x^{-\gamma }<0$ and ${lim}_{y\to 0}1/y=+\infty$, we have

$$C(x,0)=x{\left[1+x^{\alpha }\left(\underset{y\to 0}{lim}\frac{1}{y}-1\right)\right]}^{-x^{-\gamma }}=0.$$

For any $y\in [0,1]$ implying that $1/y-1\ge 0$, $(\alpha ,\gamma )\in {(0,1]}^2$, and $\gamma -\alpha \in [0,1]$, we have

$$\begin{array}{cc}\hfill C(0,y)& =\underset{x\to 0}{lim}x{\left[1+x^{\alpha }\left(\frac{1}{y}-1\right)\right]}^{-x^{-\gamma }}=\underset{x\to 0}{lim}x{e}^{-x^{\alpha -\gamma }(1/y-1)}=0.\hfill \end{array}$$

This ends this portion of the proof.

 Proof

for (II) For any $x\in [0,1]$, we have

$$C(x,1)=x{\left[1+x^{\alpha }\left(\frac{1}{1}-1\right)\right]}^{-x^{-\gamma }}=x{(1+0)}^{-x^{-\gamma }}=x.$$

For any $y\in [0,1]$, we have

$$C(1,y)=1\times {\left[1+1^{\alpha }\times \left(\frac{1}{y}-1\right)\right]}^{-1^{-\gamma }}={\left(\frac{1}{y}\right)}^{-1}=y.$$

 Proof

for (III) After differentiation with the standard rules and several simplifications and factorizations, for any $(x,y)\in {[0,1]}^2$, we find

$$\begin{array}{cc}\hfill & {\partial }_{x,y}C(x,y)=\frac{1}{y{[y-(y-1)x^{\alpha }]}^2}{x}^{\alpha -2\gamma }{\left[\left(\frac{1}{y}-1\right)x^{\alpha }+1\right]}^{-x^{-\gamma }}\times \hfill \\ \hfill & \{\gamma [y-(y-1)x^{\alpha }]log\left[1+\left(\frac{1}{y}-1\right)x^{\alpha }\right]\hfill \\ \hfill & +(\gamma -1)x^{\gamma }[(y-1)x^{\alpha }-y]+\alpha [(y-1)x^{\alpha }+y{x}^{\gamma }]\}.\hfill \end{array}$$

Since, for $(x,y)\in {[0,1]}^2$, it is clear that the main multiplicative term is non-negative, and we have $y-(y-1)x^{\alpha }=y(1-x^{\alpha })+x^{\alpha }\ge 0$. Owing to $\gamma \in [0,1]$ and the following logarithmic inequality: $log(1+u)\ge u/(1+u)$ for $u\ge 0$, we have

$$\begin{array}{cc}\hfill & {\partial }_{x,y}C(x,y)\ge \frac{1}{y{[y-(y-1)x^{\alpha }]}^2}{x}^{\alpha -2\gamma }{\left[\left(\frac{1}{y}-1\right)x^{\alpha }+1\right]}^{-x^{-\gamma }}\times \hfill \\ \hfill & \left\{\gamma [y-(y-1)x^{\alpha }]\frac{\left(1/y-1\right)x^{\alpha }}{1+\left(1/y-1\right)x^{\alpha }}+(\gamma -1)x^{\gamma }[(y-1)x^{\alpha }-y]+\alpha [(y-1)x^{\alpha }+y{x}^{\gamma }]\right\}\hfill \\ \hfill & =\frac{1}{y{[y-(y-1)x^{\alpha }]}^2}{x}^{\alpha -2\gamma }{\left[\left(\frac{1}{y}-1\right)x^{\alpha }+1\right]}^{-x^{-\gamma }}\times \hfill \\ \hfill & \left\{y(\alpha -\gamma +1)x^{\gamma }+(1-y)x^{\alpha }[\gamma -\alpha +(1-\gamma )x^{\gamma }]\right\}.\hfill \end{array}$$

Since $(\alpha ,\gamma )\in {(0,1]}^2$, $\gamma -\alpha \in [0,1]$, we have $\alpha -\gamma +1\ge 0$, $\gamma -\alpha \ge 0$ and $1-\gamma \ge 0$. Therefore, for any $(x,y)\in {[0,1]}^2$, the term in curly brackets is non-negative, and we finally have

$$\begin{array}{cc}\hfill & {\partial }_{x,y}C(x,y)\ge 0.\hfill \end{array}$$

The proof of Proposition 7 ends. □

For the purpose of this study, the copula defined in Equation (7) is named the intriguing 2 (Int2) copula. Our result excludes the case $\gamma =0$, since we focus on copulas of the OVP type, but we can prove that in this case, the Int2 copula is still valid for $\alpha \in [0,1]$; the case $\gamma =\alpha =0$ corresponds to the independence copula.

Furthermore, one can notice that for $\alpha =1$, it can be expressed as $C(x,y)=x{[C_{*}(x,y)/x]}^{x^{-\gamma }}$, where $C_{*}(x,y)$ is the Ali–Mikhail–Haq copula given by Equation (5).

Some functions and properties related to the Int2 copula are listed below. To begin, the Int2 copula density is given by

$$\begin{array}{cc}\hfill & c(x,y)={\partial }_{x,y}C(x,y)=\frac{1}{y{[y-(y-1)x^{\alpha }]}^2}{x}^{\alpha -2\gamma }{\left[\left(\frac{1}{y}-1\right)x^{\alpha }+1\right]}^{-x^{-\gamma }}\times \hfill \\ \hfill & \{\gamma [y-(y-1)x^{\alpha }]log\left[1+\left(\frac{1}{y}-1\right)x^{\alpha }\right]\hfill \\ \hfill & +(\gamma -1)x^{\gamma }[(y-1)x^{\alpha }-y]+\alpha [(y-1)x^{\alpha }+y{x}^{\gamma }]\},(x,y)\in {[0,1]}^2.\hfill \end{array}$$

For a visual analysis, the Int2 copula and Int2 copula density are represented in Figure 9 and Figure 10 for {$\alpha =\gamma =1$} and {$\alpha =1/3$ and $\gamma =2/3$}, respectively.

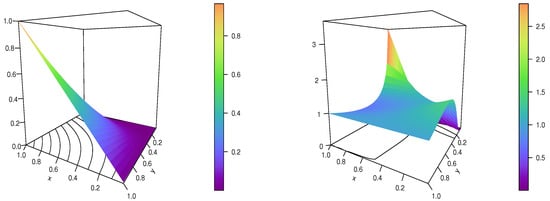
Figure 9. Plots of the Int2 copula (left) and the Int2 copula density (right) for $\alpha =\gamma =1$.

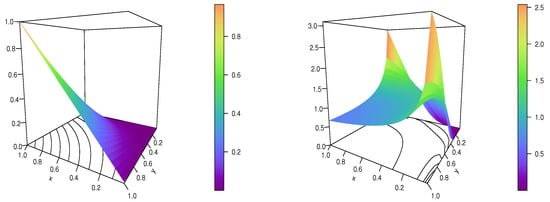
Figure 10. Plots of the Int2 copula (left) and the Int2 copula density (right) for $\alpha =1/3$ and $\gamma =2/3$.

These figures demonstrate the flexibility of the Int2 copula and Int2 copula density according to the values of $\alpha$ and $\gamma$.

Thanks to the flipping and survival approaches, the following copulas can be deduced: the x-flipping Int2 copula is given by

$$\begin{array}{cc}\hfill \overline{C}(x,y)& =y-C(1-x,y)\hfill \\ \hfill & =y-(1-x){\left[1+{(1-x)}^{\alpha }\left(\frac{1}{y}-1\right)\right]}^{-{(1-x)}^{-\gamma }},(x,y)\in {[0,1]}^2,\hfill \end{array}$$

the y-flipping Int2 copula is specified as

$$\begin{array}{cc}\hfill \tilde{C}(x,y)& =x-C(x,1-y)\hfill \\ \hfill & =x\left\{1-{\left[1+x^{\alpha }\left(\frac{1}{1-y}-1\right)\right]}^{-x^{-\gamma }}\right\},(x,y)\in {[0,1]}^2,\hfill \end{array}$$

and the Int2 survival copula is indicated as

$$\begin{array}{cc}\hfill \widehat{C}(x,y)& =x+y-1+C(1-x,1-y)\hfill \\ \hfill & =x+y-1+(1-x){\left[1+{(1-x)}^{\alpha }\left(\frac{1}{1-y}-1\right)\right]}^{-{(1-x)}^{-\gamma }},(x,y)\in {[0,1]}^2.\hfill \end{array}$$

All these copulas can serve as two-dimensional dependence models in various data analysis scenarios involving two quantitative variables.

For the main properties, we claim that the Int2 is not exchangeable, not radially symmetric, not Archimedean, and its medial correlation is equal to $\mathcal{M}=4C(1/2,1/2)-1=2{(1+2^{-\alpha })}^{-2^{\gamma }}-1$. The Spearman rho of the Int2 copula has the following complex integral form:

$$\begin{array}{cc}\hfill \rho & =12{\int }_0^1{\int }_0^{1}C(x,y)dxdy-3\hfill \\ \hfill & =12{\int }_0^1{\int }_0^{1}x{\left[1+x^{\alpha }\left(\frac{1}{y}-1\right)\right]}^{-x^{-\gamma }}dxdy-3.\hfill \end{array}$$

No closed-form expressions were found. In order to get an idea of its range of values, under the special configuration {$\alpha =\gamma /2$ with $\gamma \in [0,2]$}, Table 7 presents some of its values.

Table 7. Numerical values for $\rho$ with $\alpha =\gamma /2$ and $\gamma \in \{0,0.2,\dots ,1.8,2\}$.

$\mathit{\gamma }$	0	0.2	0.4	0.6	0.8	1.0	1.2	1.4	1.6	1.8	2.0
$\rho$	0	−0.0981	−0.1919	−0.281	−0.3654	−0.4453	−0.5209	−0.5926	−0.6605	−0.725	−0.7862

From this table, we see that the Int2 copula can model negative dependence with a wide range of values; for the considered configuration, which is certainly not optimal, we find $\rho \in [-0.7862,0]$. It is thus of interest to analyze the dependence of two quantitative variables that are compatible with such features.

As a last result, we may also mention the Fréchet–Hoeffding theorem that implies that $max(x+y-1,0)\le C(x,y)\le min(x,y)$ for any $(x,y)\in {[0,1]}^2$, so

$$max(x+y-1,0)\le x{\left[1+x^{\alpha }\left(\frac{1}{y}-1\right)\right]}^{-x^{-\gamma }}\le min(x,y).$$

To our knowledge, these inequalities are new, so they have potential interest.

5. Conclusions

This article focused on the full theory of underexplored copulas with one-variable power, i.e., of the form $x{y}^{f\left(x\right)}$, where $f\left(x\right)$ denotes a specific function. In the main result, we identified the precise assumptions required on $f\left(x\right)$ to validate such copulas. Based on the flipping and survival strategies, some additional general copulas were described. Numerous examples of function $f\left(x\right)$ depending on two or three parameters were given. In particular, we demonstrated that our assumptions and well-known truncated lifetime distributions have a close relationship. In order to emphasize the significance of our findings, we focused on a specific two-parameter, one-variable-power copula that combined the definition of the independence copula with the intriguing copula defined as $x{y}^{1/x}$. Its different shapes, associated functions, and various correlation features were revealed. The theory was rendered in numerical tables and graphics to make it less abstract. A short statistical work was given to show how the involved parameters can be estimated based on data. Two new intriguing one-variable-power copulas beyond the thought-of general form were finally presented and studied. A new one-variable-power extension of the so-called Ali–Mikhail–Haq copula can be seen in the second one. Additionally, they have appealing correlation properties that can be used in a variety of statistical contexts, such as the modeling of various claim types, payment and incurred loss data, cross-industry- and cross-breach-type structures for monthly cyber losses, the mortality of some countries, etc.

This article lays the theoretical groundwork for further exploration of one-variable-power copulas, including the extensions to a higher dimension and applications to the analysis of contemporary data in a two-dimensional setting. These aspects are postponed for future work.