Abstract
Chebyshev Wavelets of the third kind are proposed in this study to solve nonlinear systems of FDEs. The main goal of the method is to convert the nonlinear FDE into a nonlinear system of algebraic equations that can be easily solved using matrix methods. In order to achieve this, we first generate the operational matrices for the fractional integration using third kind Chebyshev Wavelets and block-pulse functions (BPF) for function approximation. Since the obtained operational matrices are sparse, the obtained numerical method is fast and computationally efficient. The original nonlinear FDE is transformed into a system of algebraic equations in a vector-matrix form using the obtained operational matrices. The collocation points are then used to solve the system of algebraic equations. Numerical results for various examples and comparisons are presented.
Keywords:
third kind Chebyshev Wavelets; systems of FDEs; operational matrix for fractional derivatives MSC:
34A08; 26A33; 65L99
1. Introduction
Fractional differential equations (FDEs) can use real-valued orders for derivatives and integrals. FDEs applied to the evolution of physical processes reveal behaviors that classical differential equations do not allow. On the other hand, because of the additional complexity brought on by arbitrary orders of derivation and integration, it is extremely difficult to derive analytical solutions to many sorts of such FDEs. Finding precise and efficient numerical solution methods for the FDEs is therefore crucial. Recent years have seen the use of specific numerical techniques for FDEs, including Adomian decomposition method [1,2], predictor–corrector methods [3,4], finite difference method [5], Adams-Bashforth-Moulton method [6,7], F-expansion method [8], B-spline collocation method [9], reproducing kernel method [10,11], the homotopy perturbation transform method [12,13], and the residual power series method [14,15].
Similar research is being conducted on several wavelet types for various computationally demanding problems. Data can be divided into numerous time-frequency components using wavelet analysis. These functions are produced by stretching and moving a so-called mother wavelet function. The obvious advantage of the wavelet basis is that it simplifies the FDE problem’s solution to the solution of a system of algebraic equations. The other benefits can be their orthogonality, compact support, and simultaneous representation of data in several resolutions. A wide variety of FDEs have been solved using numerous wavelet basis functions [16,17,18,19,20,21,22,23,24,25].
In this study, we attmpt to solve the system of FDEs in the form of:
where is the Caputo fractional differential operator. To this end, we obtain operational matrices for function integration by employing Chebyshev wavelets of the third kind. Chebyshev wavelets are constructed using Chebyshev polynomials. The set of Chebyshev polynomials form an orthonormal basis, thus, they can be used for function approximation by obtaining the corresponding Chebyshev series/expansion for the function. All identities and theorems of Fourier series have a corresponding Chebyshev counterpart because Chebyshev series can be converted to Fourier cosine series using a change of variables [26]. Some of their important advantages are forming a complete orthogonal system, converging to any piecewise smooth and continuous function (even this smoothness condition can be relaxed for many practical cases), converging to the average of the right and left limits of a discontinuity, etc.
This paper is organized as follows. In Section 2, we introduce the third kind Chebyshev wavelets and obtain the operational matrices for the numerical integration. We include several numerical examples in Section 3 to show the efficiency and accuracy of the method. The paper is concluded with the important results and prospects for future work In Section 4.
2. Operational Matrices of Fractional Integration for Third Kind Chebyshev Wavelets
2.1. Third Kind Chebyshev Wavelets
Wavelets consist of a localized wave-like main function and sub-functions can be obtained from this function with the properties of zero-average and finite-energy. The main function is called the mother wavelet. Then, the shifted and stretched versions of this mother wavelet is obtained using a dilation parameter (a) and a translation parameter (b). Using the shifted and stretched versions of the wavelet function provides information on both the frequency content of the analyzed signal and where in time this frequency component occurs. The family of continuous wavelets is defined by,
If parameters a and b are discrete as , , , the family of discrete wavelets are obtained as
where n and k are positive integers. Discrete Chebyshev Wavelets of the third kind can be defined on the interval [0, 1) as [25],
where k is a positive integer, , and t denotes the normalized time. are the Chebyshev polynomials of the third kind of the degree m, which are orthogonal with respect to the weight function on the interval [–1, 1] and satisfy the following recursive formula:
2.2. Function Approximation
A function defined over [0, 1) may be approximated by Chebyshev wavelets [16,17,18,19] as,
where, T denotes transposition, C and are vectors given as,
Now let us define . The third-kind Chebyshev wavelet matrix is defined as
where are collocation points chosen as , .
2.3. Block Pulse Functions
An set of Block Pulse Functions (BPFs) is defined as
where . The functions are disjoint and orthogonal. They have the following properties for
Any function defined in [0, 1) with the property of squarely integrable in the interval can be expanded into an set of BPFs as
where , and .
The third kind Chebyshev wavelet matrix can also be expanded to an set of BPFs as,
The block -pulse operational matrix for fractional integration is defined as [27]
where,
with .
Now we obtain the operational matrix of fractional integration for the third kind Chebyshev wavelet method (TKCWM):
where the matrix of size is called the TKCWM. Using (14) and (15) we obtain,
Employing (14), (15), (17) and (18) results in
The resulting operational matrix for TKCWM, denoted as yields
This method yields a fractional integration operational matrix with a large number of zero entries, which speeds up the simulation. The error estimation of the third kind Chebyshev Wavelets and the convergence analysis can be found in [25].
3. Numerical Examples
We present three numerical examples using TKCWM in this section. Matlab R2021a is used for the simulations.
3.1. Example 1
First, let us look at the system of FDE given below:
The initial values are , and the exact solution for is given as , .
As a result of using the proposed approach for fractional derivatives, we now obtain,
where, and are the unknown coefficients of size . Using the Caputo definition for fractional derivatives [28] and using (14), (17), (22), and the initial conditions we obtain,
where are also the vectors of size .
Finally, using (22) and (23) in (21) the following system of algebraic equations, which yields:
Here, the and vectors include the total of unknowns. Equation (24) is used to create a system of algebraic equations using collocation points and and are calculated by solving this system. Thus, the numerical solutions for and are also obtained as shown in (23).
The absolute errors obtained for TKCWM in and for several values () are given in Table 1 where the absolute errors in and are represented by and , respectively. The numerical solution results for fractional orders , are given in Table 2. Figure 1 shows the TKCWM result graphs and for with the exact solution, whereas Figure 2 displays the TKCWM result graphs and for the fractional orders , with the integer orders . The proposed method substantially approximates the exact solution for the integer-orders of , as shown in Table 1 and Figure 1. As increases, the absolute errors decrease. The calculated absolute errors are about 10−4 for , 10−4–10−5 for , and 10−5–10−6 for . The fractional orders can take any arbitrary value on the interval , they are chosen to be equal in Table 2 and Figure 2. As Table 2 and Figure 2 demonstrate, the solution approaches to the exact solution when approach 1. We provide a comparison using the Differential Transformation Method (DTM) [29] and Homotopy Perturbation Method (HPM) [30] for the fractional orders , in Table 3. Table demonstrates that the approximate solutions for these fractional orders are close to one another for all the methods. Table 1, Table 2 and Table 3 and Figure 1 and Figure 2 thus show that the suggested approach is a good approximation to the relevant system of FDE.

Table 1.
Example 1 ODE solution absolute errors and for several .

Table 2.
Example 1 FDE solutions for several .
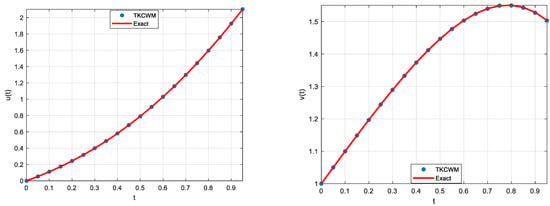
Figure 1.
Example 1 ODE solutions for ().
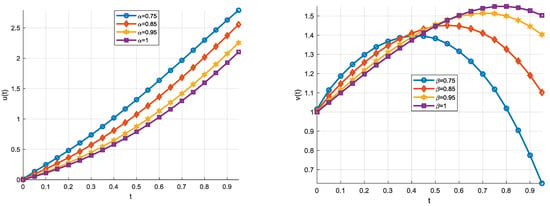
Figure 2.
Example 1 FDE solutions ().

Table 3.
Example 1 FDE solution comparisons for , .
3.2. Example 2
Now consider the system of FDE given as
with the initial values , , and the exact solution for is given as , , .
Employing the TKCWM method for this example, we obtain,
where, and are again the coefficients to be determined in the method. With the help of Caputo definition for fractional derivatives [28] and using (14), (17), and (26), together with the initial conditions, we obtain
where are also the vectors of size
Finally, substituting (26)–(28) in (25) results the following system of algebraic equations where and coefficients are the unknowns to be determined:
As before, the approximate solution of the proposed method is obtained by solving (29) for , and substituting those coefficients in (27).
The absolute errors obtained for TKCWM for and for several values () are given in Table 4 where the absolute errors in and are represented by and , respectively. As the table demonstrates, to increase the accuracy, should be increased. Table 5 demonstrates the results of the numerical method for fractional orders for several resolutions of . As can be seen from the table, the results approach the exact solution when fractional orders approach the integer values, which validates the results. Figure 3 shows the TKCWM result graphs and for with the exact solution, whereas Figure 4 displays the TKCWM result graphs and for the fractional orders , with the integer orders. As Figure 3 and Figure 4 demonstrate, the proposed TKCWM method substantially approximates the exact solution for the integer-orders and the approximate solution approaches to the exact solution of the approach 1 for fractional orders.

Table 4.
Example 2 ODE solution absolute errors and for several .

Table 5.
Example 2 FDE solutions for several .
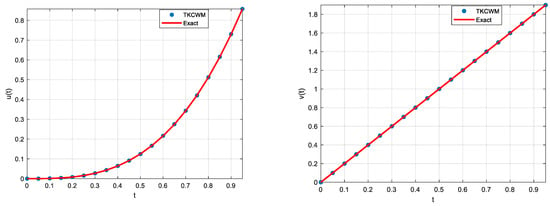
Figure 3.
Example 2 ODE solutions for ().
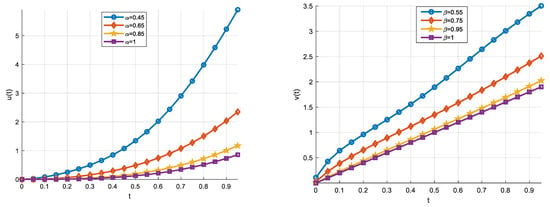
Figure 4.
Example 2 FDE solutions ().
3.3. Example 3
For our last example, we consider the following system of FDEs
with the initial conditions , , and the exact solution for is given as , , and , .
Let us now employ TKCWM for this example and obtain
Here, there are a total of coefficients to be determined, namely , and .
Employing (31)–(32) in (30) results in the following system of algebraic equations:
As before, the approximate solution is obtained by solving (33) for , and and substituting the coefficients in (32).
The absolute errors obtained for TKCWM in , , and for and () are summarized in Table 6 where , , and denote the absolute errors in , , and , respectively. We obtain the absolute errors around 10−3–10−4 for , and around 10−4–10−5 for . Again, for higher accuracy, should be increased. The solutions for fractional orders of for several resolutions is given in Table 7. When the orders approach 1, the TKCWM solution approaches the exact solution for integer orders, which is expected. Figure 5 shows the TKCWM result graphs of , , and for , whereas Figure 6 displays the TKCWM result graphs of , , and for the fractional orders with . As is the case with the previous examples, the solution approaches the exact solution when approach 1.

Table 6.
Example 3 ODE solution absolute errors , and for several .

Table 7.
Example 3 FDE solutions for several .
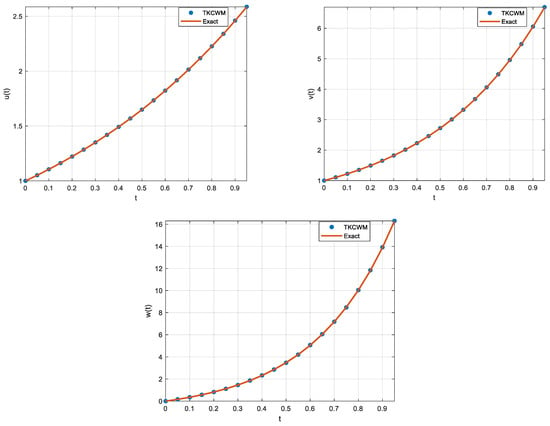
Figure 5.
Example 3 ODE solutions ().
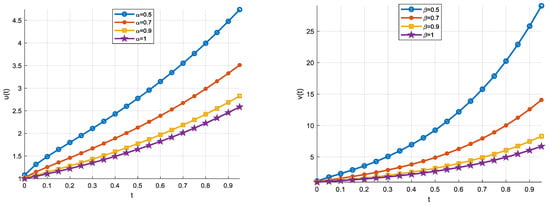
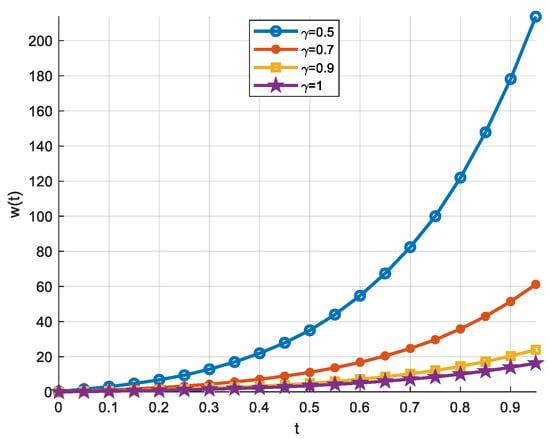
Figure 6.
Example 3 FDE solutions ().
4. Conclusions
We have developed a numerical solution approach for the systems of FDEs in this study. The operational matrices for the fractional integration are obtained using the suggested method, which makes use of discrete third kind Chebyshev Wavelets. We employ the block pulse functions and Chebyshev polynomials of the third kind in the method, which makes the operational matrices for fractional integration very sparse, which in turn is crucial for fast evaluation and reduced computational cost for the proposed method. Those sparse operational matrices are used to map fractional terms in FDEs into the discrete terms in the proposed method. The Newton-Raphson method is used to solve the algebraic equation system created from the system of FDEs in order to determine the unknown coefficients. As predicted, the accuracy of the suggested technique improves as the resolution is increased by larger collocation points. Table 1, Table 4 and Table 6 and Figure 1, Figure 3 and Figure 5 verify this claim. The maximum errors for the collocation points up to 128 are typically in the range of 10−4 to 10−6.
The main focus of this study is fractional orders, and the numerical solutions derived for these orders are consistent with those found for integer orders. Table 2, Table 3, Table 5 and Table 7 and Figure 2, Figure 4 and Figure 6 show how the method accurately solves fractional orders because when the fractional orders become close to integer values, the answer likewise become close to the exact solution found for integer orders.
Systems of variable-order FDEs, fractional partial differential equations, fractional integral equations, and fractional delay differential equation systems can all benefit from the advantages of the proposed method and are thus taken into consideration as potential future applications of this research.
Author Contributions
Methodology, A.T.D.; Software, S.N.T.P.; Formal analysis, A.T.D., original draft preparation, A.T.D. and S.N.T.P.; writing—review and editing, A.T.D. and S.N.T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Laoubi, M.; Odibat, Z.; Maayah, B. A Legendre-based approach of the optimized decomposition method for solving nonlinear Caputo-type fractional differential equations. Math. Methods Appl. Sci. 2022, 45, 7307–7321. [Google Scholar] [CrossRef]
- Fu, H.; Lei, T. Adomian Decomposition, Dynamic Analysis and Circuit Implementation of a 5D Fractional-Order Hyperchaotic System. Symmetry 2022, 14, 484. [Google Scholar] [CrossRef]
- Wu, G.-C.; Kong, H.; Luo, M.; Fu, H.; Huang, L.-L. Unified predictor–corrector method for fractional differential equations with general kernel functions. Fract. Calc. Appl. Anal. 2022, 25, 648–667. [Google Scholar] [CrossRef]
- Zeb, A.; Kumar, P.; Erturk, V.S.; Sitthiwirattham, T. A new study on two different vaccinated fractional-order COVID-19 models via numerical algorithms. J. King Saud Univ. Sci. 2022, 34, 101914. [Google Scholar] [CrossRef] [PubMed]
- Vargas, A.M. Finite difference method for solving fractional differential equations at irregular meshes. Math. Comput. Simul. 2021, 193, 204–216. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Agarwal, R.P.; Samet, B. A study of fractional Lotka-Volterra population model using Haar wavelet and Adams-Bashforth-Moulton methods. Math. Methods Appl. Sci. 2020, 43, 5564–5578. [Google Scholar] [CrossRef]
- Jeng, S.W.; Kilicman, A. Fractional Riccati Equation and Its Applications to Rough Heston Model Using Numerical Methods. Symmetry 2020, 12, 959. [Google Scholar] [CrossRef]
- Kaur, B.; Gupta, R.K. Dispersion analysis and improved F-expansion method for space–time fractional differential equations. Nonlinear Dyn. 2019, 96, 837–852. [Google Scholar] [CrossRef]
- Carpinteri, A.; Mainardi, F. (Eds.) Fractals and Fractional Calculus in Continuum Mechanics; Springer: Wien, NY, USA, 1997. [Google Scholar]
- Abu Arqub, O. Numerical simulation of time-fractional partial differential equations arising in fluid flows via reproducing Kernel method. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 4711–4733. [Google Scholar] [CrossRef]
- Jia, Y.-T.; Xu, M.-Q.; Lin, Y.-Z. A numerical solution for variable order fractional functional differential equation. Appl. Math. Lett. 2017, 64, 125–130. [Google Scholar] [CrossRef]
- Qin, Y.; Khan, A.; Ali, I.; Al Qurashi, M.; Khan, H.; Shah, R.; Baleanu, D. An Efficient Analytical Approach for the Solution of Certain Fractional-Order Dynamical Systems. Energies 2020, 13, 2725. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Alshorman, M.A.; Zamri, N.; Ali, M.; Albzeirat, A.K. New Implementation of Residual Power Series for Solving Fuzzy Fractional Riccati Equation. J. Model. Optim. 2018, 10, 81–87. [Google Scholar] [CrossRef]
- Bayrak, M.A.; Demir, A. A new approach for space-time fractional partial differential equations by residual power series method. Appl. Math. Comput. 2018, 336, 215–230. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, Q. The second kind Chebyshev wavelet method for solving fractional differential equations. Appl. Math. Comput. 2012, 218, 8592–8601. [Google Scholar] [CrossRef]
- Yi, M.; Huang, J. Wavelet operational matrix method for solving fractional differential equations with variable coefficients. Appl. Math. Comput. 2014, 230, 383–394. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Deshi, A.B. An efficient Haar wavelet collocation method for the numerical solution of multi-term fractional differential equations. Nonlinear Dyn. 2015, 83, 293–303. [Google Scholar] [CrossRef]
- Yuttanan, B.; Razzaghi, M. Legendre wavelets approach for numerical solutions of distributed order fractional differential equations. Appl. Math. Model. 2019, 70, 350–364. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y.; Lima, P. An improved composite collocation method for distributed-order fractional differential equations based on fractional Chelyshkov wavelets. Appl. Numer. Math. 2019, 145, 1–27. [Google Scholar] [CrossRef]
- Do, Q.H.; Ngo, H.T.; Razzaghi, M. A generalized fractional-order Chebyshev wavelet method for two-dimensional distributed-order fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 2020, 95, 105597. [Google Scholar] [CrossRef]
- Usman, M.; Hamid, M.; Haq, R.U.; Wang, W. An efficient algorithm based on Gegenbauer wavelets for the solutions of variable-order fractional differential equations. Eur. Phys. J. Plus 2018, 133, 327. [Google Scholar] [CrossRef]
- Dincel, A.T.; Polat, S.N.T. Fourth kind Chebyshev Wavelet Method for the solution of multi-term variable order fractional differential equations. Eng. Comput. 2021, 39, 1274–1287. [Google Scholar] [CrossRef]
- Saeed, U.; Idrees, S.; Javid, K.; Din, Q. Krawtchouk wavelets method for solving Caputo and Caputo–Hadamard fractional differential equations. Math. Methods Appl. Sci. 2022, 45, 11331–11354. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, X. The third kind Chebyshev wavelets collocation method for solving the time-fractional convection diffusion equations with variable coefficients. Appl. Math. Comput. 2016, 280, 11–29. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods, 2nd ed.; Courier Corporation: North Chelmsford, MA, USA, 2001. [Google Scholar]
- Kilicman, A.; Al Zhour, Z.A.A. Kronecker operational matrices for fractional calculus and some applications. Appl. Math. Comput. 2007, 187, 250–265. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Ertürk, V.S.; Momani, S. Solving systems of fractional differential equations using differential transform method. J. Comput. Appl. Math. 2007, 215, 142–151. [Google Scholar] [CrossRef]
- Abdulaziz, O.; Hashim, I.; Momani, S. Solving systems of fractional differential equations by homotopy-perturbation method. Phys. Lett. A 2008, 372, 451–459. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).