Dynamical Analysis and Misalignment Projection Synchronization of a Novel RLCM Fractional-Order Memristor Circuit System
Abstract
:1. Introduction
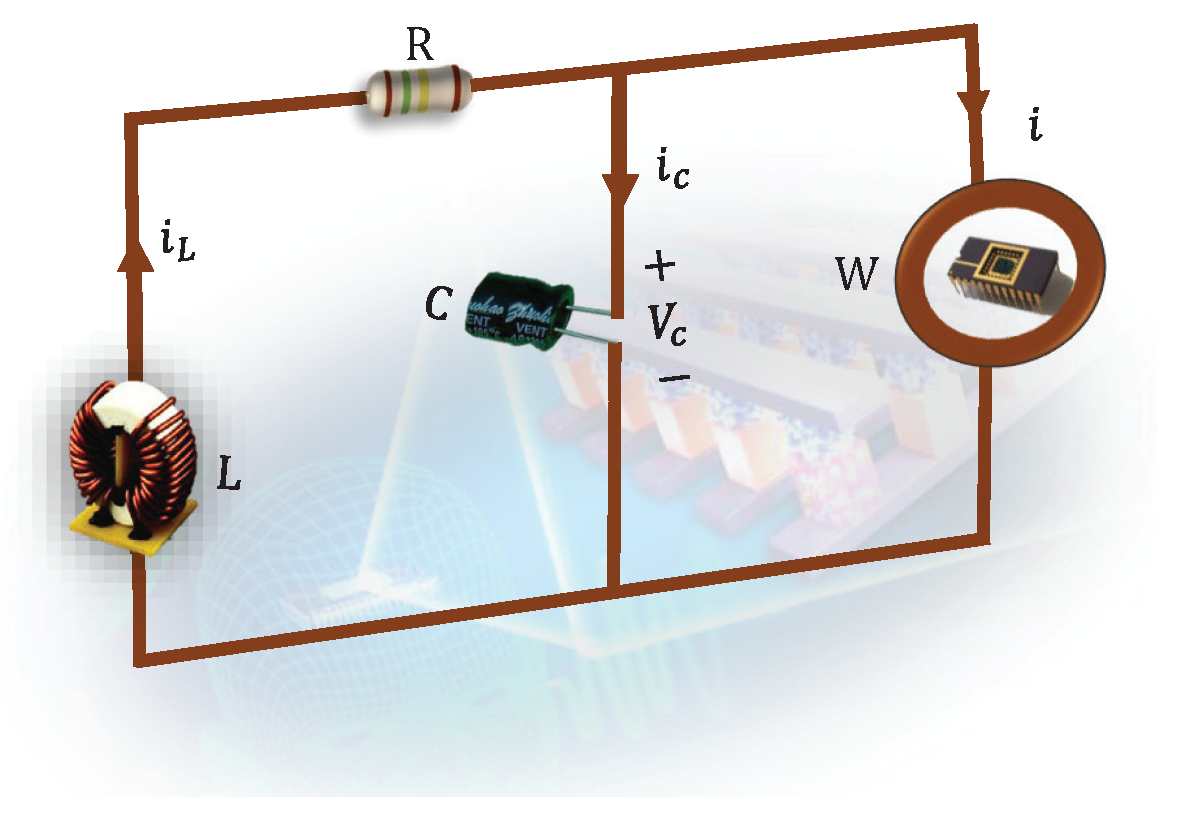
2. Fractional 3D Memristor Circuit System Model
2.1. Fractional Calculus Theory
2.2. A 3D Fractional-Order Flux-Controlled Memristor
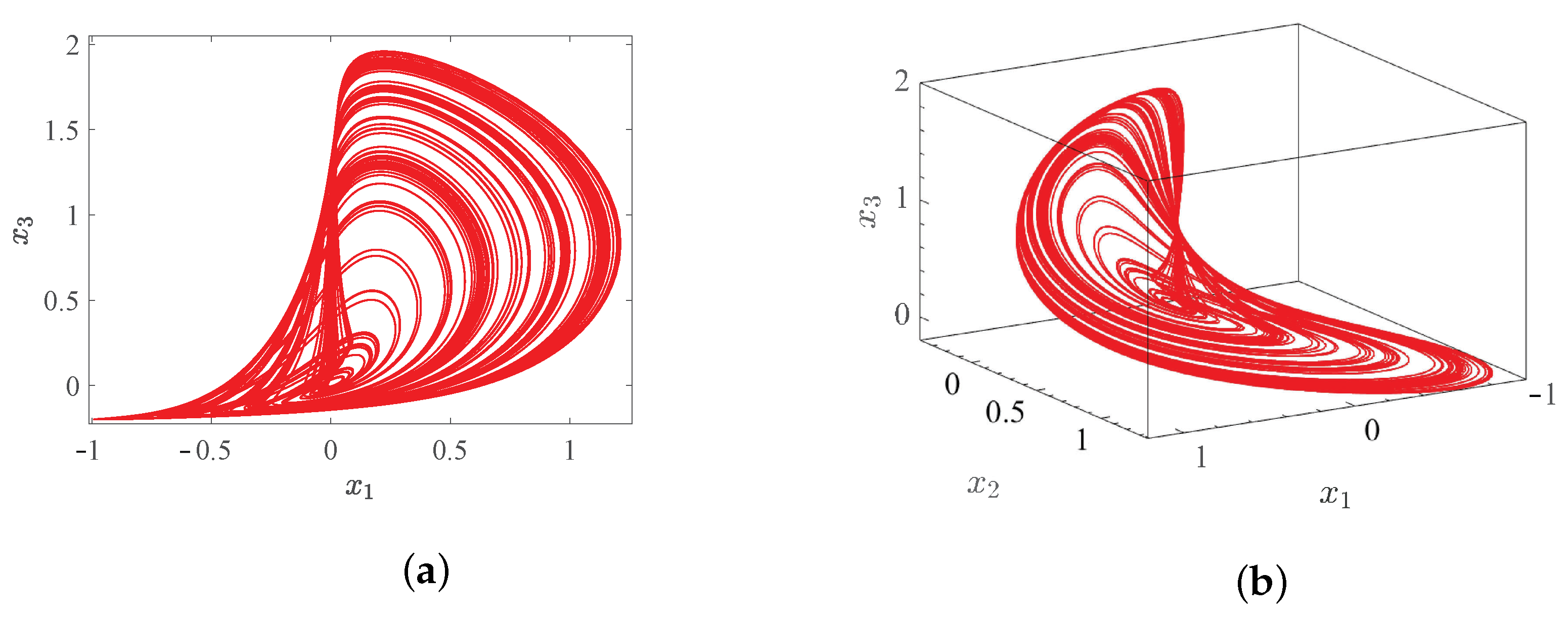
2.3. Fractional-Order System Description and Chaotic Description
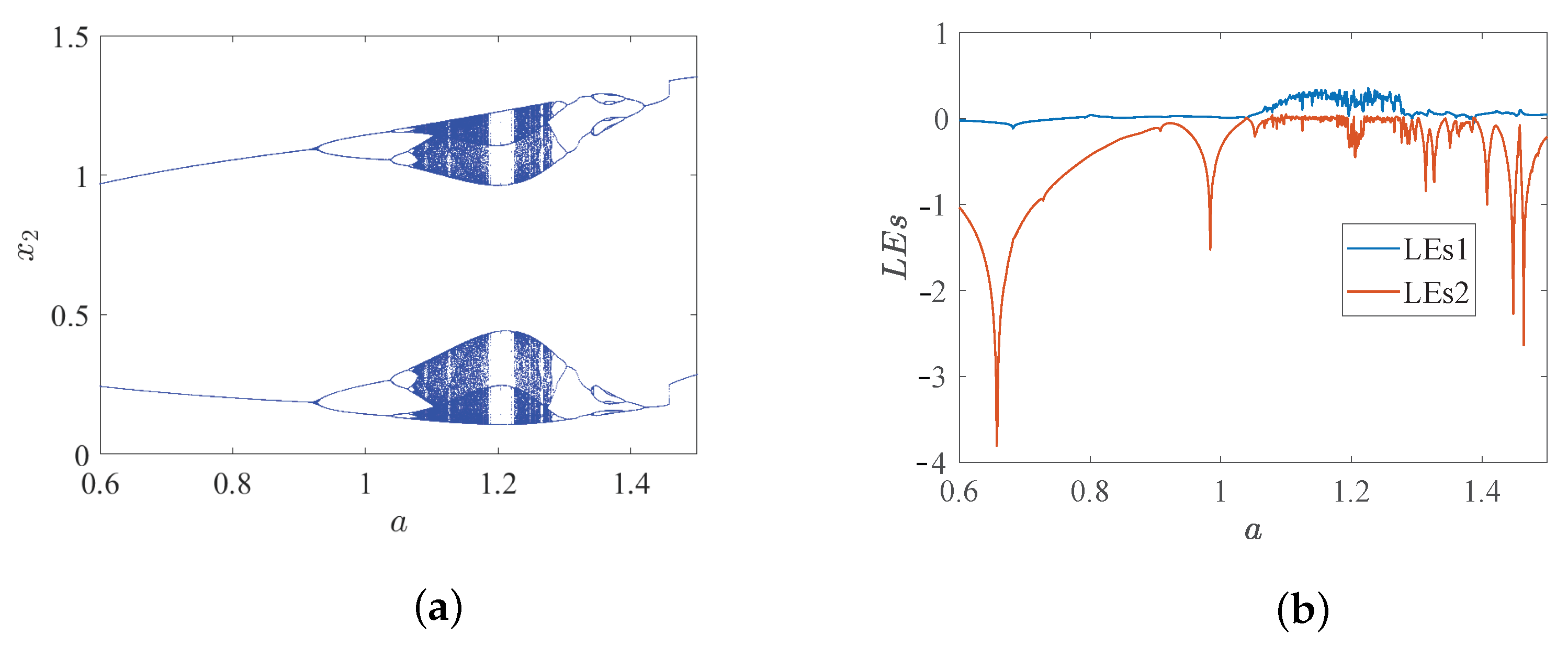
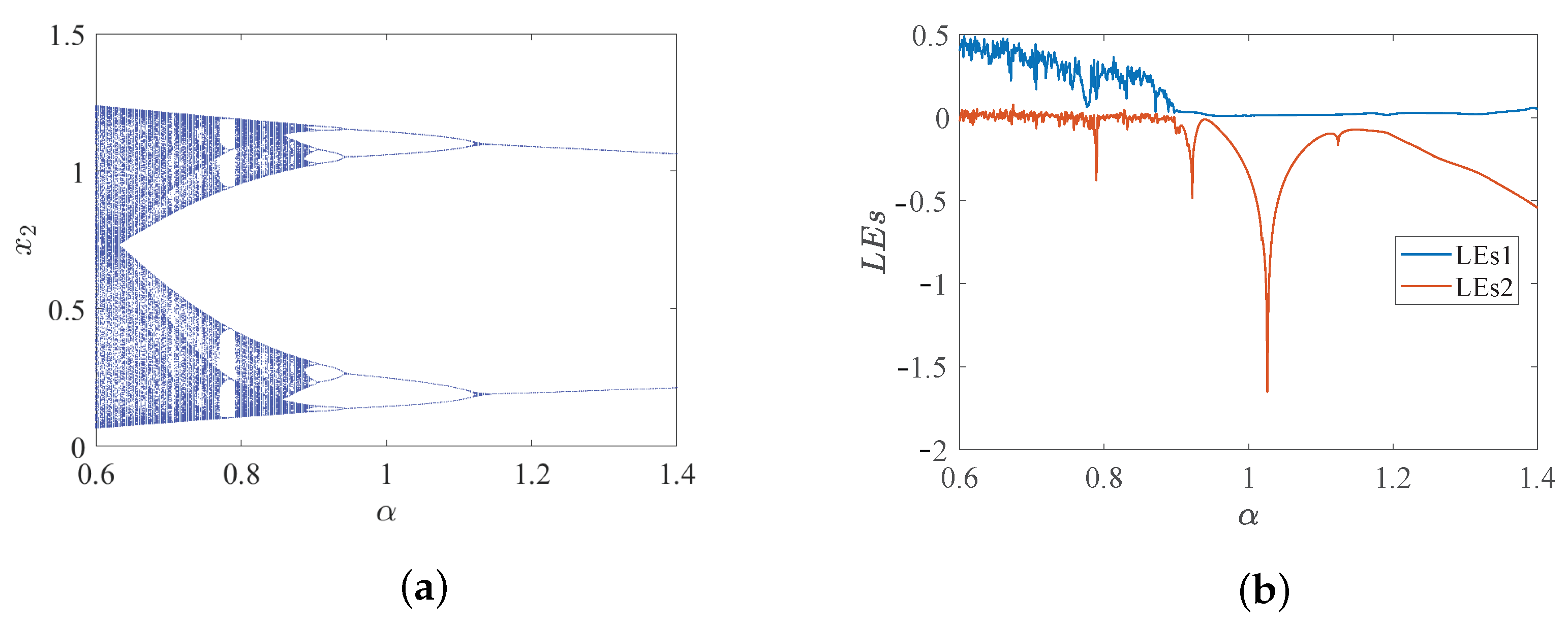
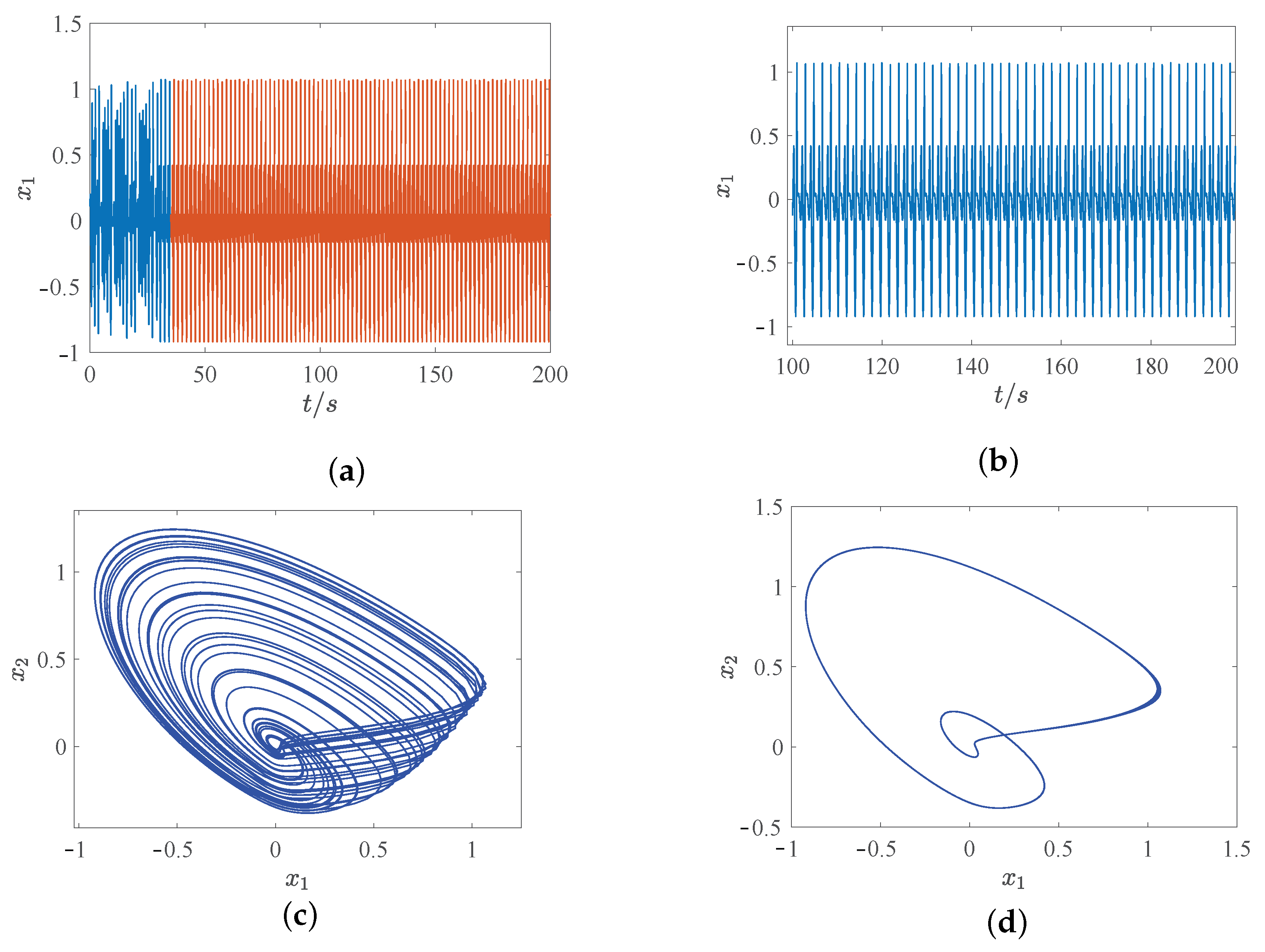
3. System Dynamics Behavior
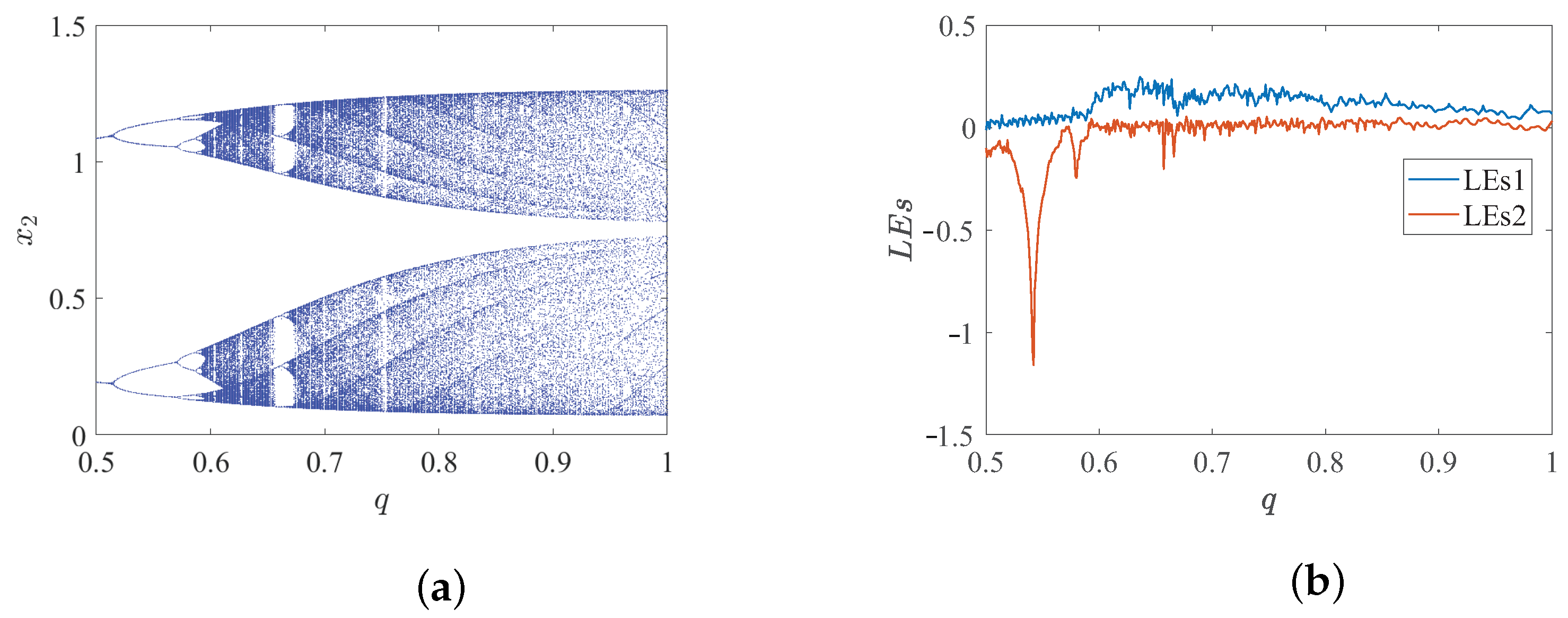
3.1. Special Bifurcation Phenomenon of the System
3.2. Chaotic Degradation Phenomenon of the System
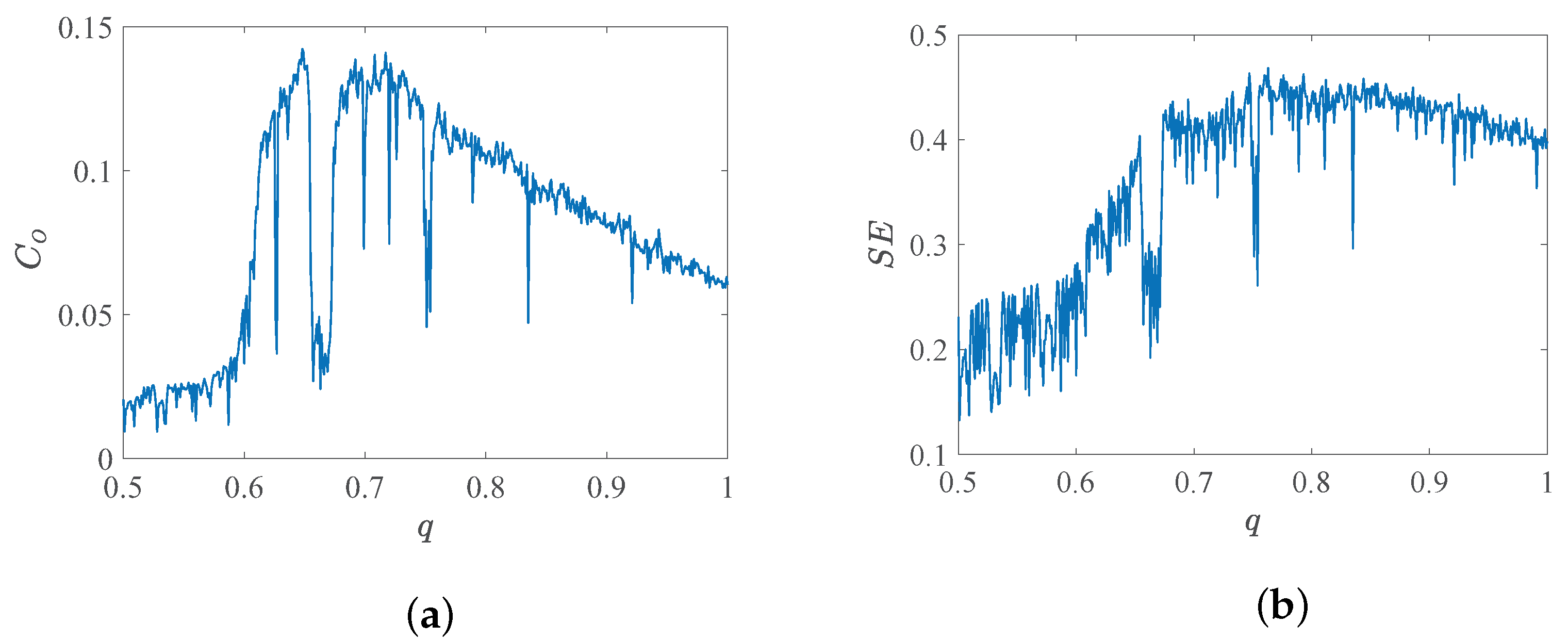
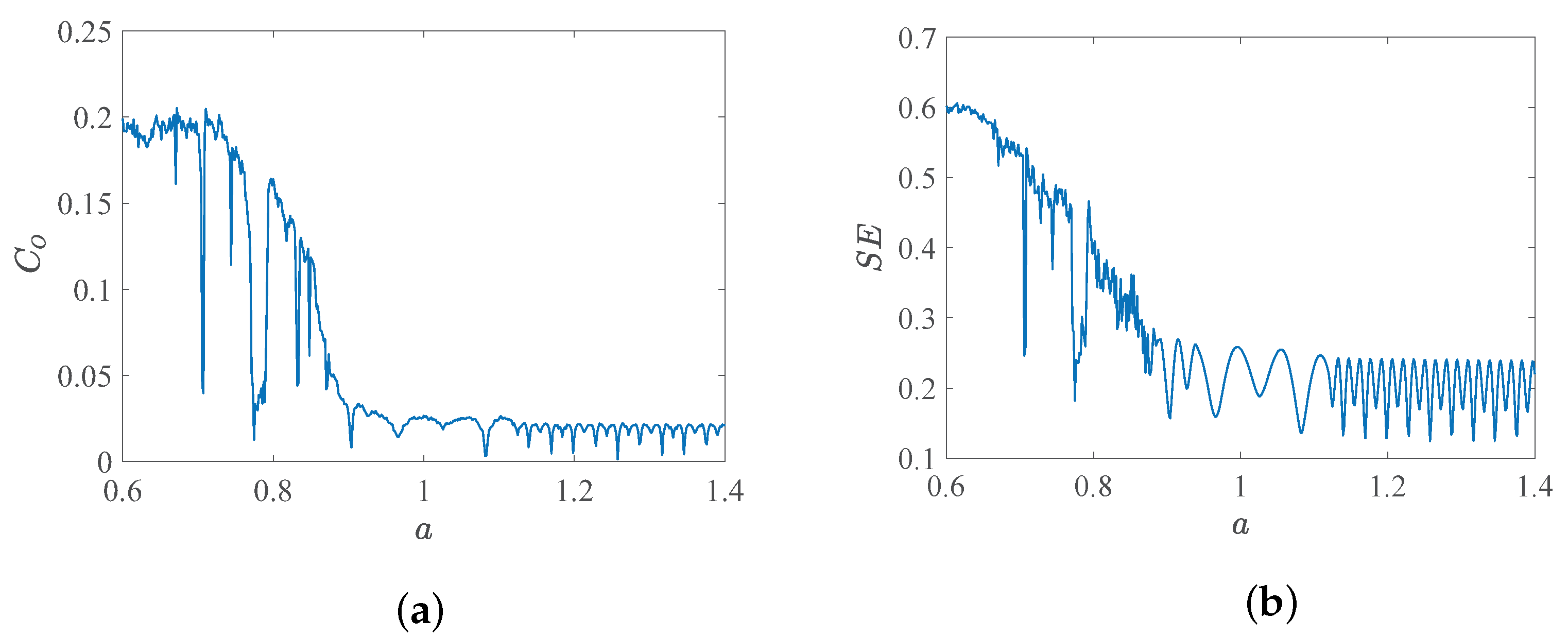
4. System Complexity Analysis
4.1. Characteristics of Complexity Variation with Order q
4.2. Characteristics of Complexity Variation with Internal Parameter of Memristor
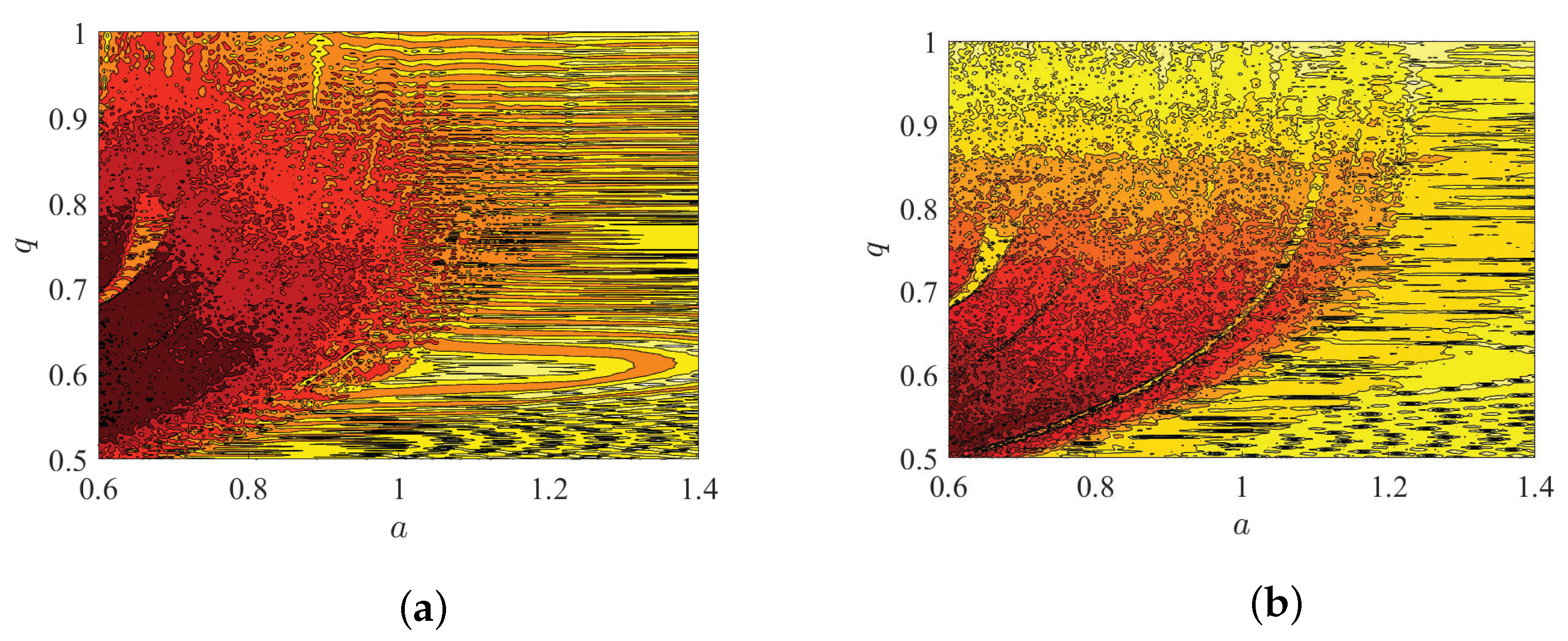
4.3. Chaotic Map of System Complexity
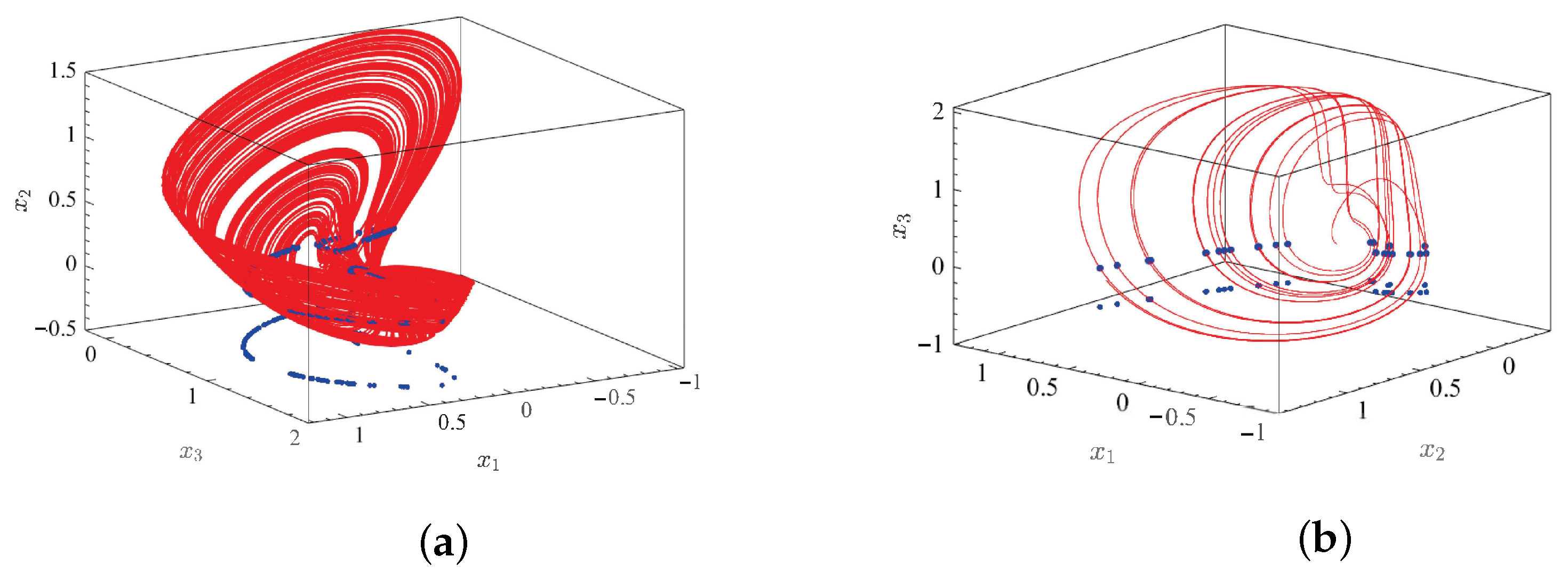
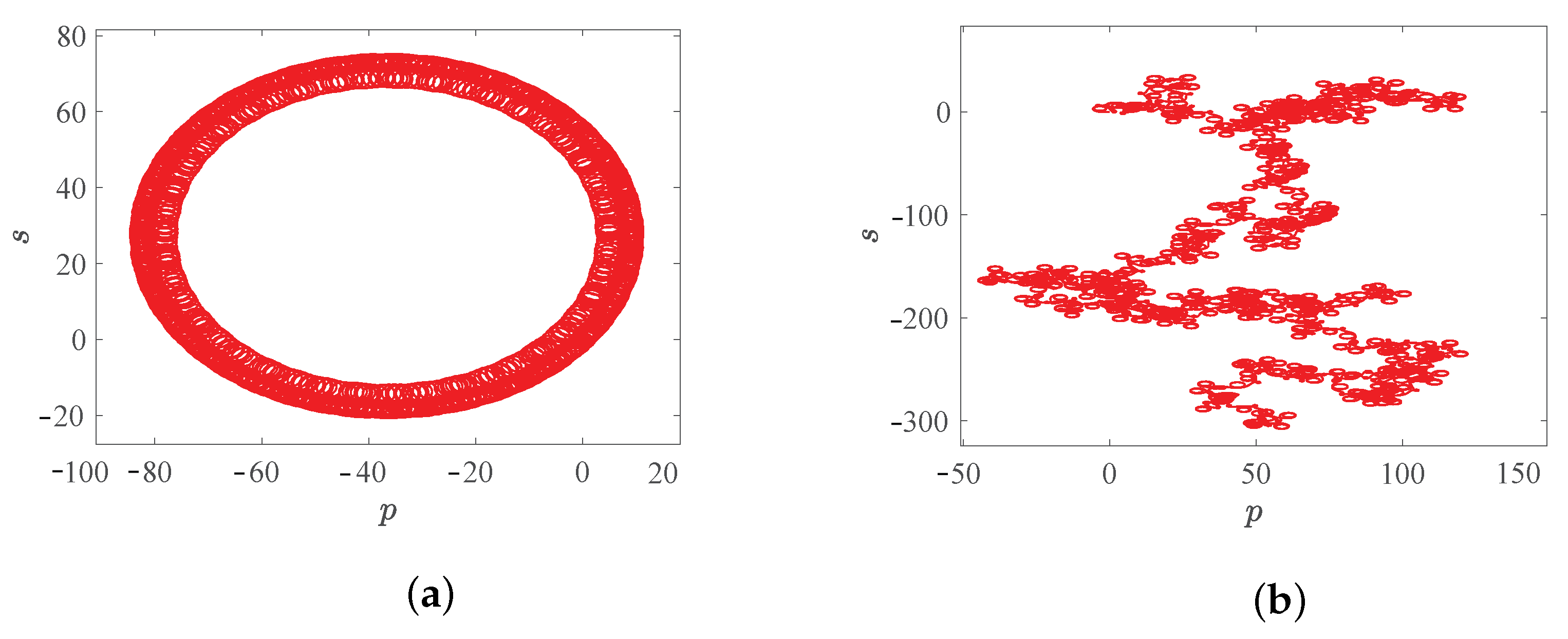
5. Misalignment Projection Synchronization of the System
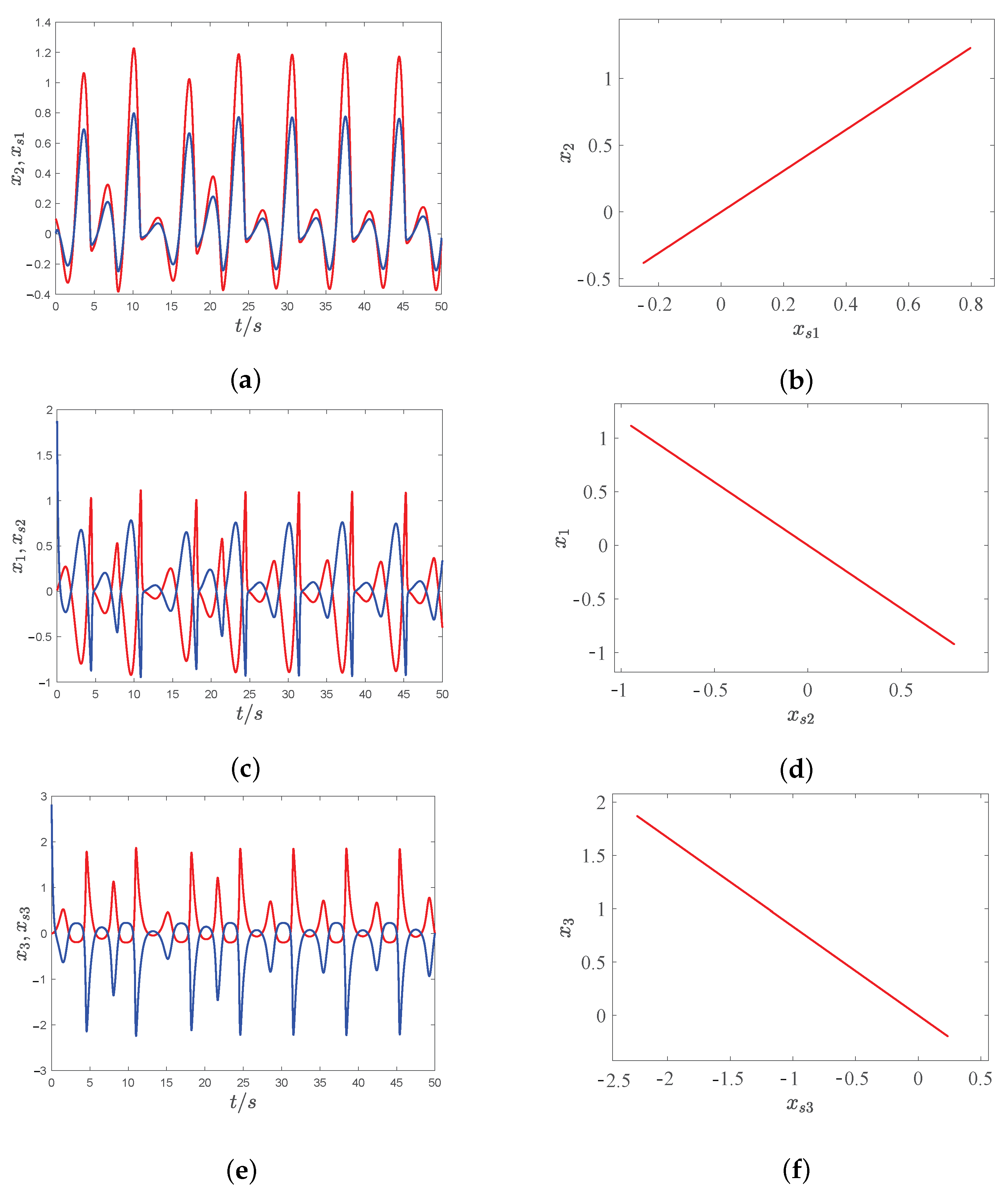
5.1. Theoretical Analysis of Misalignment Projection Synchronization
5.2. Numerical Simulation of Misalignment Projection Synchronization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.-Y.; Zhou, L.; Zhu, X.; Zhou, Y.; Han, S.-T. Photonic memristor for future computing: A perspective. Adv. Opt. Mater. 2019, 7, 1900766. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Riam, S.Z.; Ahmed, M.S.; Sundaravadivel, P. CMOS-Based Memristor Emulator Circuits for Low-Power Edge-Computing Applications. Electronics 2023, 12, 1654. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Yang, X.; Zi, X.; Xiao, F. A tristable locally active memristor and its application in Hopfield neural network. Nonlinear Dyn. 2022, 108, 1697–1717. [Google Scholar] [CrossRef]
- Cao, Z.; Sun, B.; Zhou, G.; Mao, S.; Zhu, S.; Zhang, J.; Ke, C.; Zhao, Y.; Shao, J. Memristor-based neural networks: A bridge from device to artificial intelligence. Nanoscale Horiz. 2023, 8, 716–745. [Google Scholar] [CrossRef]
- Danilin, S.N.; Shchanikov, S.A.; Galushkin, A.I. The research of memristor-based neural network components operation accuracy in control and communication systems. In Proceedings of the 2015 International Siberian Conference on Control and Communications (SIBCON), Omsk, Russia, 21–23 May 2015; pp. 1–6. [Google Scholar]
- Hasan, G. Real-time fuzzy-pid synchronization of memristor-based chaotic circuit using graphical coded algorithm in secure communication applications. Phys. Scr. 2022, 97, 055212. [Google Scholar]
- Luigi, F.; Arturo, B. Spiking neuron mathematical models: A compact overview. Bioengineering 2023, 10, 174. [Google Scholar]
- Mikhail, K.; Nikolay, N.; Iveta, N.; Irina, N.; Velika, K.; Marian, M. On a Mathematical Model of a General Autoimmune Disease. Axioms 2023, 12, 1021. [Google Scholar]
- Ella, G. TiO2-based memristors and ReRAM: Materials, mechanisms and models (a review). Semicond. Sci. Technol. 2014, 29, 104004. [Google Scholar]
- Mao, S.; Sun, B.; Ke, C.; Qin, J.; Yang, Y.; Guo, T.; Wu, Y.A.; Shao, J.; Zhao, Y. Evolution between CRS and NRS behaviors in MnO2@ TiO2 nanocomposite based memristor for multi-factors-regulated memory applications. Nano Energy 2023, 107, 108117. [Google Scholar] [CrossRef]
- Sun, K.; Chen, J.; Yan, X. The future of memristors: Materials engineering and neural networks. Adv. Funct. Mater. 2021, 31, 2006773. [Google Scholar] [CrossRef]
- Di Ventra, M.; Pershin, Y.V.; Chua, L.O. Circuit elements with memory: Memristors, memcapacitors, and meminductors. Proc. IEEE 2009, 97, 1717–1724. [Google Scholar] [CrossRef]
- Petráš, I.; Chen, Y.; Coopmans, C. Fractional-order memristive systems. In Proceedings of the 2009 IEEE Conference on Emerging Technologies & Factory Automation, Palma de Mallorca, Spain, 22–25 September 2009; pp. 1–8. [Google Scholar]
- Fouda, M.E.; Radwan, A.G. On the fractional-order memristor model. J. Fract. Calc. Appl. 2013, 4, 1–7. [Google Scholar]
- Fouda, M.E.; Radwan, A.G. Fractional-order memristor response under DC and periodic signals. Circuits Syst. Signal Process. 2015, 34, 961–970. [Google Scholar] [CrossRef]
- Ding, D.; Li, S.; Wang, N. Dynamics analysis of fractional-order memristive chaotic system. J. Harbin Inst. Technol. (New Ser.) 2020, 27, 65–74. [Google Scholar]
- Qin, C.; Sun, K.; He, S. Characteristic analysis of fractional-order memristor-based hypogenetic jerk system and its DSP implementation. Electronics 2021, 10, 841. [Google Scholar] [CrossRef]
- Tian, H.; Liu, J.; Wang, Z.; Xie, F.; Cao, Z. Characteristic analysis and circuit implementation of a novel fractional-order memristor-based clamping voltage drift. Fractal Fract. 2022, 7, 2. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Chen, M.; Zhang, P.; Yang, R.; Yang, B. Chaotic system dynamics analysis and synchronization circuit realization of fractional-order memristor. Eur. Phys. J. Spec. Top. 2022, 231, 3095–3107. [Google Scholar] [CrossRef]
- Akgül, A.; Rajagopal, K.; Durdu, A.; Pala, M.A.; Boyraz, Ö.F.; Yildiz, M.Z. A simple fractional-order chaotic system based on memristor and memcapacitor and its synchronization application. Chaos Solitons Fractals 2021, 152, 111306. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, H.; Krejcar, O.; Namazi, H. Synchronization in a network of map-based neurons with memristive synapse. Eur. Phys. J. Spec. Top. 2022, 231, 4057–4064. [Google Scholar] [CrossRef]
- Chang, H.; Li, Y.; Chen, G.; Yuan, F. Extreme multistability and complex dynamics of a memristor-based chaotic system. Int. J. Bifurc. Chaos 2020, 30, 2030019. [Google Scholar] [CrossRef]
- Chen, M.; Sun, M.; Bao, B.; Wu, H.; Xu, Q.; Wang, J. Controlling extreme multistability of memristor emulator-based dynamical circuit in flux–charge domain. Nonlinear Dyn. 2018, 91, 1395–1412. [Google Scholar] [CrossRef]
- Fatemeh, P.; Sajad, J.; Hamed, A. Traveling patterns in a network of memristor-based oscillators with extreme multistability. Eur. Phys. J. Spec. Top. 2019, 228, 2123–2131. [Google Scholar]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Chen, W.-H.; Wang, Z.; Lu, X. On sampled-data control for master-slave synchronization of chaotic Lur’e systems. IEEE Trans. Circuits Syst. II Express Briefs 2012, 59, 515–519. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Z.; Zhang, H.; Cao, Z.; Zhang, P. Dynamical analysis and fixed-time synchronization of a chaotic system with hidden attractor and a line equilibrium. Eur. Phys. J. Spec. Top. 2022, 231, 2455–2466. [Google Scholar] [CrossRef]
- Abarbanel, H.D.I.; Rulkov, N.F.; Sushchik, M.M. Generalized synchronization of chaos: The auxiliary system approach. Phys. Rev. E 1996, 53, 4528. [Google Scholar] [CrossRef]
- Bernd, B.; Lewi, S. Chaos and phase synchronization in ecological systems. Int. J. Bifurc. Chaos 2000, 10, 2361–2380. [Google Scholar]
- Min, F.; Wang, E. Misalignment projection synchronization of hyperchaotic Qi systems and its application in secure communication. Acta Phys. Sin. 2010, 59, 7657–7662. [Google Scholar]
- Sun, J.; Wang, Y.; Yao, L.; Shen, Y.; Cui, G. General hybrid projective complete dislocated synchronization between a class of chaotic real nonlinear systems and a class of chaotic complex nonlinear systems. Appl. Math. Model. 2015, 39, 6150–6164. [Google Scholar] [CrossRef]
- Li, D. Modified functional projective synchronization of the unidirectional and bidirectional hybrid connective star network with coupling time-delay. Wuhan Univ. J. Nat. Sci. 2019, 24, 321–328. [Google Scholar] [CrossRef]
- Li, C.-L.; Li, Z.-Y.; Feng, W.; Tong, Y.-N.; Du, J.-R.; Wei, D.-Q. Dynamical behavior and image encryption application of a memristor-based circuit system. AEU-Int. J. Electron. Commun. 2019, 110, 152861. [Google Scholar] [CrossRef]
- Ivo, P. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Marian, M.; Stoyan, Z. A note about stability of fractional retarded linear systems with distributed delays. Int. J. Pure Appl. Math. 2017, 115, 873–881. [Google Scholar]
- Hristo, K.; Mariyan, M.; Magdalena, V.; Andrey, Z. Continuous Dependence on the Initial Functions and Stability Properties in Hyers–Ulam–Rassias Sense for Neutral Fractional Systems with Distributed Delays. Fractal Fract. 2023, 7, 742. [Google Scholar]
- Cherruault, Y.; Adomian, G. Decomposition methods: A new proof of convergence. Math. Comput. Model. 1993, 18, 103–106. [Google Scholar] [CrossRef]
- Abdul-Majid, W. A new algorithm for calculating Adomian polynomials for nonlinear operators. Appl. Math. Comput. 2000, 111, 33–51. [Google Scholar]
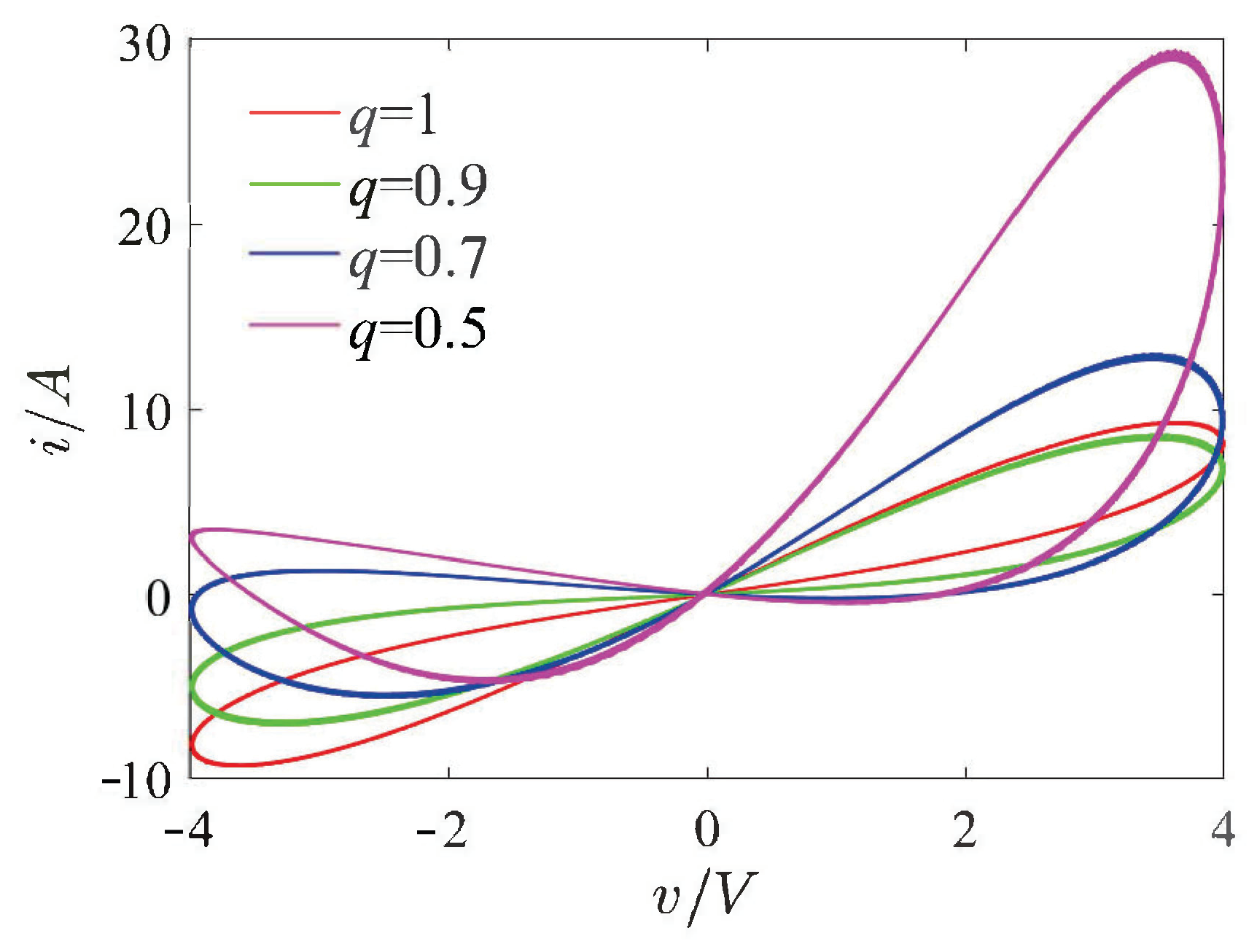
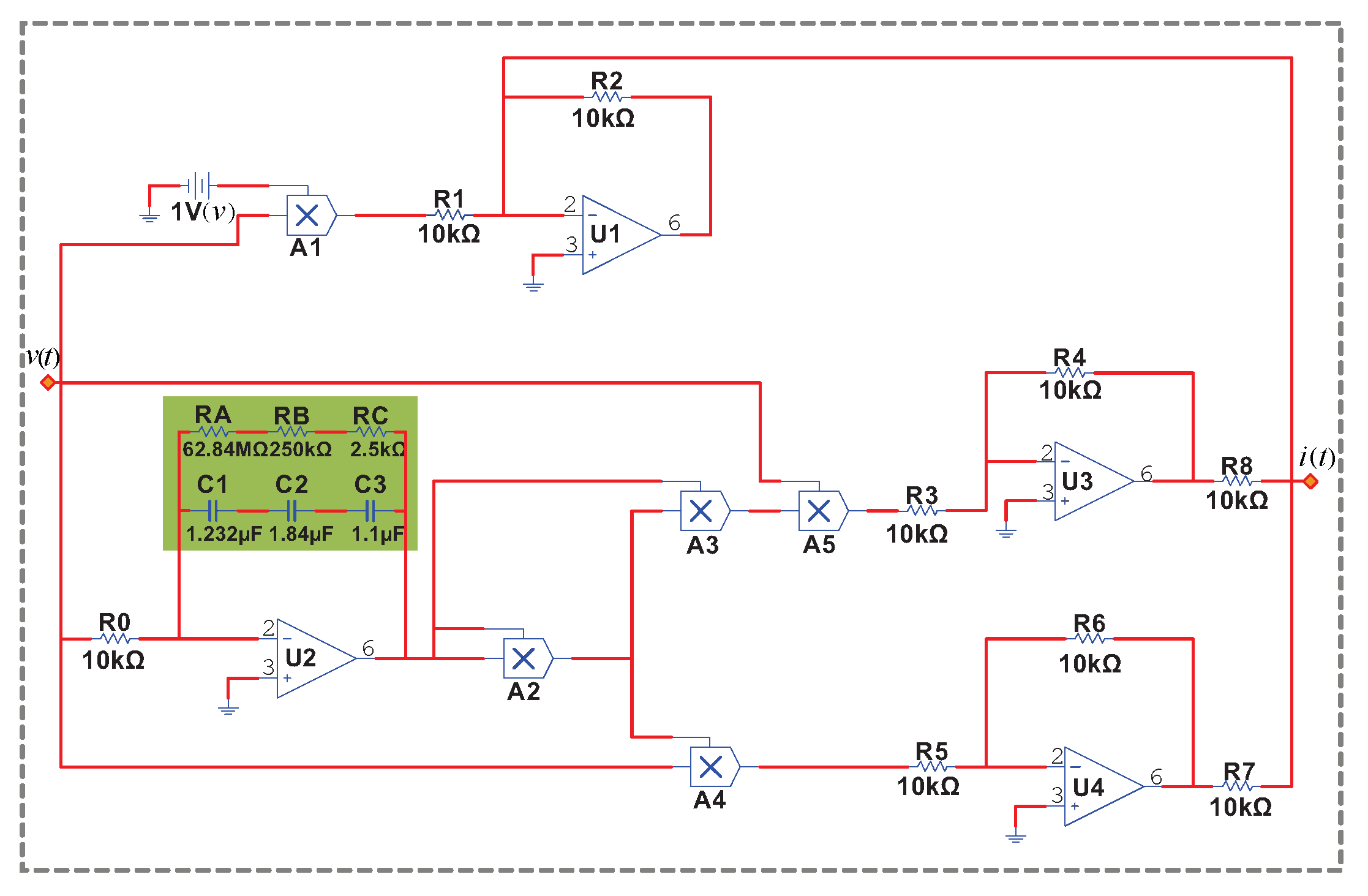
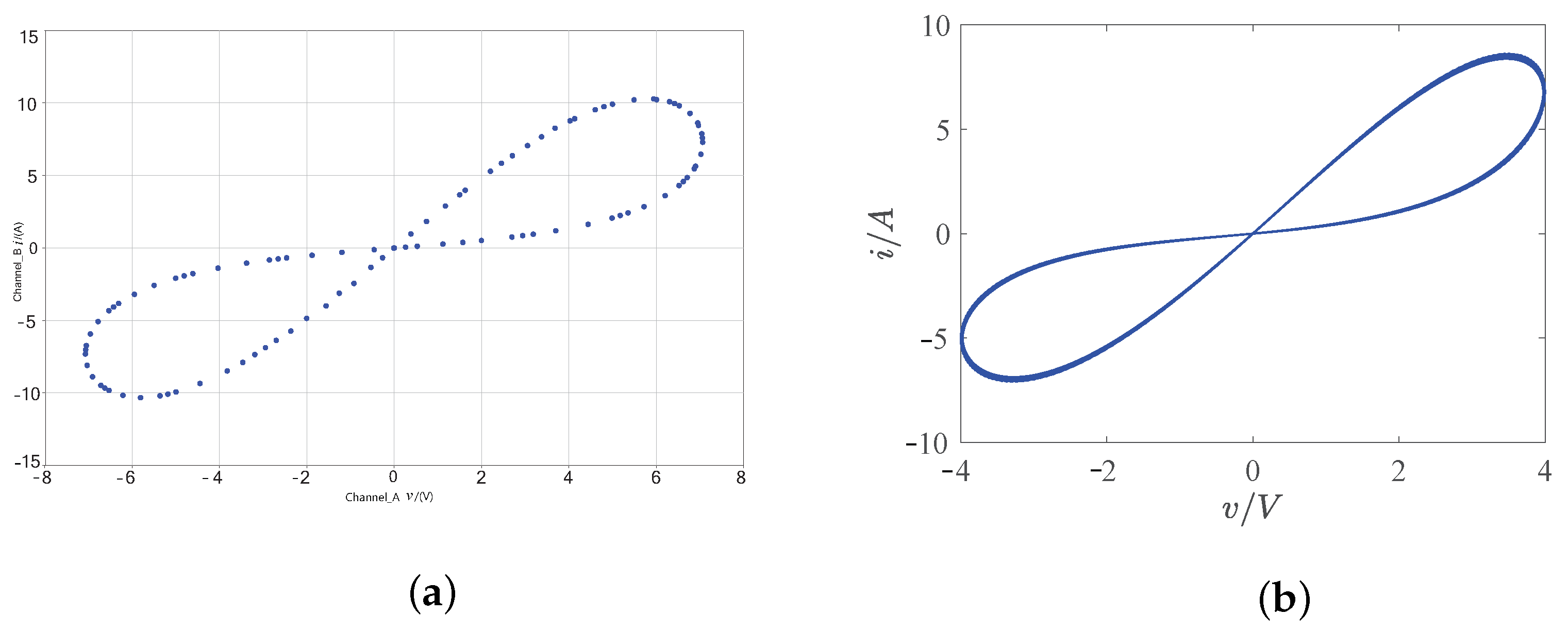
| Circuit Parameters | Physical Meaning | Parameter Value |
|---|---|---|
| C1 | Capacitance | 1.232 F |
| C2 | Capacitance | 1.84 F |
| C3 | Capacitance | 1.1 F |
| R0/R1/R2/R3/R4/R5/R6/R7/R8 | Resistance | 10 k |
| RA | Resistance | 62.84 M |
| RB | Resistance | 250 k |
| RC | Resistance | 2.5 k |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Tian, H.; Wang, Z.; Guan, Y.; Cao, Z. Dynamical Analysis and Misalignment Projection Synchronization of a Novel RLCM Fractional-Order Memristor Circuit System. Axioms 2023, 12, 1125. https://doi.org/10.3390/axioms12121125
Liu J, Tian H, Wang Z, Guan Y, Cao Z. Dynamical Analysis and Misalignment Projection Synchronization of a Novel RLCM Fractional-Order Memristor Circuit System. Axioms. 2023; 12(12):1125. https://doi.org/10.3390/axioms12121125
Chicago/Turabian StyleLiu, Jindong, Huaigu Tian, Zhen Wang, Yan Guan, and Zelin Cao. 2023. "Dynamical Analysis and Misalignment Projection Synchronization of a Novel RLCM Fractional-Order Memristor Circuit System" Axioms 12, no. 12: 1125. https://doi.org/10.3390/axioms12121125
APA StyleLiu, J., Tian, H., Wang, Z., Guan, Y., & Cao, Z. (2023). Dynamical Analysis and Misalignment Projection Synchronization of a Novel RLCM Fractional-Order Memristor Circuit System. Axioms, 12(12), 1125. https://doi.org/10.3390/axioms12121125









