Noninertial Proper Motions of the Minkowski Metric, the Sagnac Effect, and the Twin Paradox

Abstract

The Sagnac effect and related twin paradox with a rotating disc are analyzed. It may seem that the special theory of relativity gives an easy and exhaustive treatment here. However, such consideration is deceptive since the principles of special relativity are originally established only for the inertial frames of reference, whereas the Sagnac experiment and the twin paradox exist in a noninertial one. We introduce an additional group of motions related to the rotation with uniform angular speed and show that these transformations leave the Minkowski metric invariant. Thus, we can give a firm mathematical ground to a usual easy consideration of the Sagnac effect. It should be noted that the presented result is true for a special case of motions; general coordinate transformations into accelerating frames of reference do not preserve the metric.

1. Introduction

Along with the Michelson–Morley experiment, the Sagnac effect [1] is one of the most important fundamental experiments in relativity theory. One can recall that the essence of the Sagnac effect (SE) is as follows. Four mirrors are mounted at the corners of a square on a platform. The angles of their relative position are such that a beam of light emitted from a monochromatic source is reflected at the mirrors, and completes a closed cycle, returning to the source. By using a semitransparent plate it is possible to split the beam into two beams moving in the opposite directions of this closed cycle. Sagnac discovered that if the platform is made to rotate, then the beam that moves in the direction of platform rotation will arrive at the source later than the beam moving in the opposite direction. The delay gives rise to a shift of the interference pattern on the photographic plate.

The SE has been experimentally studied many times: for electromagnetic waves [1,2,3] and for massive particles [4,5,6] as well. It was observed with the help of the Earth’s rotation, i.e., using the entire Earth as a platform [7,8]. With the advent of laser and optical sensor technologies, the SE is harnessed in so-called laser or fiber-optic gyroscopes [9,10,11]. The theoretical consideration of the SE constitutes a broad variety of interpretations and explanations [12]. The explanation offered by Sagnac himself on the basis of the purely classical operation of addition and subtraction of the velocity of light and the linear velocity of rotation of the source yielded a discrepancy of about one per cent between theory and experiment.

The most widespread explanation (which is included in textbooks and can be called standard) is based on a special relativity statement of the constant light velocity, that immediately brings up the correct formula, see for instance [13]. However, this simplicity is an oversight of fundamental issues of the physics involved. A more elaborate treatment is applied with the help of a general frame of reference for a rotating observer [14]. Much effort has been paid to incorporating the SE into the frame of general relativity [15,16] including the generalization to Finsler coordinates [17]. The approach to the SE from a quantum point of view is given in [18]. One can also generalize the context to Born coordinates [19]. We consider that in the long run, such approaches somewhat obscure the simple physical meaning of the SE as a purely relativistic effect of special relativity. A more formal mathematical treatment by the means of group theory was given in [20,21].

It is worth mentioning that there were attempts to interpret the SE as a disproval or a possibility to introduce an alternative to some statements of the commonly accepted theory [22,23,24], which caused a rebuttal [25,26,27,28] and an ongoing discussion. Recently, an attempt was made to broaden the treatment of the SE so as to ascribe it to inertial frames. It is noticed that the time difference in ray arrival occurs for an observer moving inertially, i.e., along a straight line with a constant velocity, if the observer emits light beams directly forward and backward and the beams travel the same path [29]. However, that experimental setup has a completely different nature. In the original setup, all components (ray source, detector, mirrors) are in rest relative to each other. No linear inertial movement of this rigid installation is able to produce the effect; a noninertial or nonlinear one is necessary. The magnitude of the SE depends on the area enclosed into a light-beam loop and is independent of the loop length. Oppositely, in [29], the effect’s magnitude is independent from the area but depends on loop length. Here, we adopt the classical narrow interpretation of the SE as a substantially noninertial phenomenon in rotating frames.

Along with the SE, a uniform circular motion is involved in consideration of the so-called twin paradox, as formulated by Langevin [30]. As well as the explanation of the SE [13], the commonly accepted treatment of the twin paradox [31] is simple and is based on the constancy of light velocity. Analogously, it overlooks the fundamental physical issues of the space-time metric.

The present communication is aimed at showing that the Sagnac effect can be directly explained within the framework of the special relativity theory by the fact that there exists a group of motion of the Minkowski metric, i.e., a group of nonlinear transformations of the pseudo-Euclidean coordinates, which leaves the Minkowski metric invariant. It should be noted that such invariance is found in a special case of motions, and general coordinate transformations to accelerating frames do not leave the space-time invariant [32]. Additionally, we consider the application of this group to carry out a more mathematically correct analysis of the well-known twin paradox.

2. Formulation of the Problem

We discuss a somewhat modified version of the experiment [13], with the motion of a light beam in a light guide along a circular path. This modification leaves the physical meaning of the experiment unchanged.

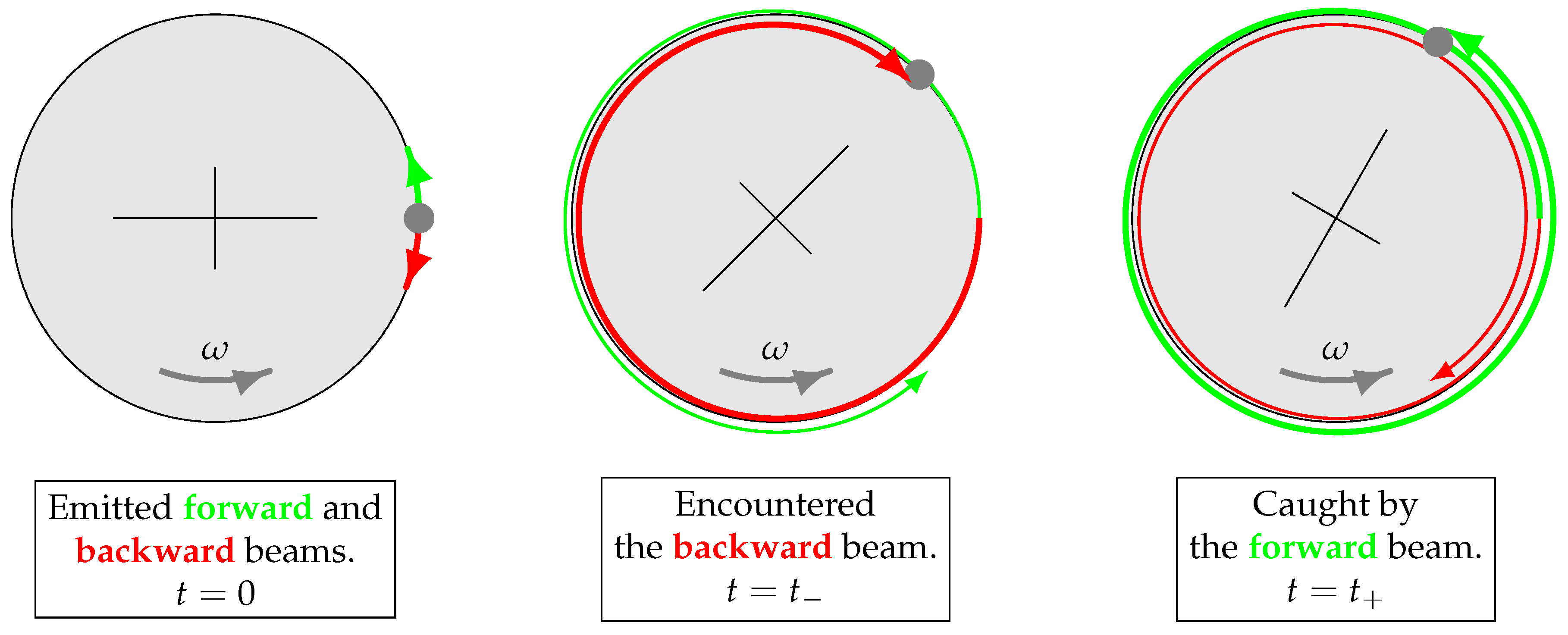
Thus, we have, in our experiment, a source which uniformly moves along a circular orbit and which simultaneously emits two light beams moving along the same circular orbit in the opposite directions, returning to the source at different moments in time, see Figure 1. The problem is to find the time interval between the beam arrivals at the moving source.

Before proceeding to solve the problem thus formulated, one should answer several questions of crucial importance.

1. Does the velocity of the light beam that travels along a circular orbit depend on the velocity at which the emitting source moves?

2. Will the form of the pseudo-Euclidean space change with the change-over from the inertial frame of reference to the one that moves uniformly along a circular orbit?

3. What is the relationship between the space-time coordinates of the source that moves relative to the frame of reference at rest and to the frame of reference uniformly moving along a circular orbit?

At first glance it would seem that the principles of the special theory of relativity (STR) enable one to give exhaustive answers to the questions posed above. However, such appearance is deceptive. The point is that all the principles of the STR are valid only in the inertial frame of reference, whereas the Sagnac experiment is done in a noninertial frame of reference. Therefore, in order to get correctly answers the above questions, one should construct a relativistic theory of uniformly rotating noninertial frames of reference. It turns out that such a theory completely rests, in all its essentials, upon the existence of the additional group of proper motions of the Minkowski metric.

3. Complete Group of Proper Motion in Space ${\mathbb{R}}_{\mathbf{1},\mathbf{2}}^{\mathbf{3}}$

The special theory of relativity is generally developed for the Minkowski space-time, which combines three-dimensional Euclidean $(x^1,x^2,x^3)\in {\mathbb{R}}^3$ spatial and one-dimensional temporal $x^0\in \mathbb{R}$ components into a four-vector $\overrightarrow{x}=(x^0,x^1,x^2,x^3)$. This space is equipped with the Minkowski metric, commonly written as

$$s^2={(x_1^0-x_2^0)}^2-{(x_1^1-x_2^1)}^2-{(x_1^2-x_2^2)}^2-{(x_1^3-x_2^3)}^2.$$

(1)

This is a case of a pseudo-Euclidean space ${\mathbb{R}}_{1,3}^4$ of signature $(1,3)$. To explain the relativistic effect discovered by Sagnac, it is sufficient to confine our consideration to the case of a pseudo-Euclidean space ${\mathbb{R}}_{1,2}^3$ by assigning $x^3\equiv 0$. Here, we denote the coordinates as $x^0$, $x^1$, and $x^2$ and consider $x^0$ as temporal and the other two as spatial ones, so we describe planar movements in time. The third spatial coordinate is omitted for simplicity. It is currently held [13,20] that the group of proper transformations of coordinates which leaves the pseudo-Euclidean space metric invariant is in fact the Lorentz group, i.e., the linear group of transformations performing transitions from one inertial frame of reference to another. It is now shown that along with the Lorentz linear group, there exists a group of proper transformations of the Minkowski metric which brings about transitions between noninertial frames of reference of a special kind. Proceeding from general considerations, this group, if it does exist, should represent a subgroup of group $SO(1,2)$, i.e., the group of all proper orthogonal and pseudo-orthogonal transformations in ${\mathbb{R}}_{1,2}^3$.

Any proper rotation in a three-dimensional pseudo-Euclidean space ${\mathbb{R}}_{1,2}^3$, i.e., any proper orthogonal or pseudo-orthogonal transformation which retains the coordinates’ origin, can be decomposed into three rotations in planes $\left\{x^1{x}^2\right\}$, $\left\{x^0{x}^1\right\}$, $\left\{x^0{x}^2\right\}$, and one rotation in the space ${\mathbb{R}}_{1,2}^3=\left\{x^0{x}^1{x}^2\right\}$ itself, which cannot be reduced to the previous ones. The first rotation modifies the space coordinates only and corresponds to the space rotations. The second and third rotations act in pseudo-Euclidean planes and correspond to the proper pseudo-orthogonal rotations or, which is the same, the Lorentz transformations of the form

$$\begin{array}{cc}\hfill d{x}^0& =\frac{d{x}^{0^{\prime }}+\frac{v}{c}d{x}^{i^{\prime }}}{\sqrt{1-{\left(\frac{v}{c}\right)}^2}},\hfill \\ \hfill d{x}^i& =\frac{d{x}^{i^{\prime }}+\frac{v}{c}d{x}^{0^{\prime }}}{\sqrt{1-{\left(\frac{v}{c}\right)}^2}},i=1,2.\hfill \end{array}$$

(2)

Now, we consider in detail the extra rotation in ${\mathbb{R}}_{1,2}^3$. The desired transformation should leave invariant the differential quadratic form

$$d{s}^2=d{x^0}^2-d{x^1}^2-d{x^2}^2.$$

(3)

Further calculations are better represented in a polar coordinate system. We denote $t=x^0$, $r=\sqrt{{x^1}^2+{x^2}^2}$, and $\phi =arctan(x^2/x^1)$, so $(t,r,\phi )$ are polar coordinates of a point s in the three-dimensional pseudo-Euclidean space $\left\{x^0{x}^1{x}^2\right\}$. It is required that the transformation from the desired group leave the radial coordinate r of the point s unchanged. Equation (3) in the polar coordinate system has the form

$$d{s}^2=d{x^0}^2-d{r}^2-r^{2}d{\phi }^2,$$

(4)

where $x_1=rcos\phi$, $x_2=rsin\phi$.

Let the differentials of coordinates t and $\phi$ of a point $s(t,r,\phi )$ be subjected to the linear transformation $a_{\omega }$: $(dt,d\phi )\to (d{t}^{\prime },d{\phi }^{\prime })$ of the form:

$$\begin{array}{cc}\hfill dt& =\frac{d{t}^{\prime }+\frac{r^2\omega }{c}d{\phi }^{\prime }}{\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}},\hfill \\ \hfill d\phi & =\frac{d{\phi }^{\prime }+\frac{\omega }{c}d{t}^{\prime }}{\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}},\hfill \end{array}$$

(5)

where $\omega$ is the angular velocity of a circle of radius r in the plane $\left\{x^1{x}^2\right\}$ relative to the origin of the coordinates, $\left|\omega \right|<\frac{c}{r}$. It is easy to see that the linear transformation (5) leaves the quadratic form (4) invariant, and is an element of some group $G_r$. Obviously, the element $a_0$ corresponds to unit I of the group $G_r$. The element $a_{-\omega }$ is identified as an element inverse to $a_{\omega }\in G_r$, i.e., ${\left(a_{\omega }\right)}^{-1}=a_{-\omega }$. If $a_{{\omega }_1},a_{{\omega }_2}\in G_r$, then their group product may be determined as

$$a_{{\omega }_1}·a_{{\omega }_2}=a_{\frac{{\omega }_1+{\omega }_2}{1+{\left(\frac{r}{c}\right)}^2{\omega }_1{\omega }_2}}.$$

(6)

If $|{\omega }_1|,|{\omega }_2|<\frac{c}{r}$, then it immediately follows from the group multiplication that

$$\left|\frac{{\omega }_1+{\omega }_2}{1+{\left(\frac{r}{c}\right)}^2{\omega }_1{\omega }_2}\right|<\frac{c}{r}.$$

(7)

The group $G_r$ can formally be supplemented by adding two elements $a_{-\frac{c}{r}}$, $a_{\frac{c}{r}}$. The replenished group is stationary relative to the associated elements $a_{-\frac{c}{r}}$, $a_{\frac{c}{r}}$. Indeed, for any $a_{\omega }\in G_r$, we have $a_{\omega }·a_{\pm \frac{c}{r}}=a_{\pm \frac{c}{r}}$.

In terms of special relativity theory, it means that the linear velocity of a circular motion cannot exceed the light speed c and that the light speed is the same in all steadily rotating noninertial reference systems.

If we compare the Lorentz transformations (2) with the pseudo-orthogonal transformations (5), it is not hard to notice their formal structural similarity. However, there is much difference between them.

The Lorentz transformation describes the transition between inertial reference systems which move uniformly and straight relative to each other, whereas the transformation (5) describes the transition between noninertial systems rotating uniformly in circles with different angular velocities. This difference becomes clear when we go back from the polar coordinate system to the pseudo-Euclidean one, and a considerably nonlinear character of the transformations emerges

$$\begin{array}{cc}\hfill d{x}^0& =\frac{1}{\sqrt{1-{\left(\frac{v}{c}\right)}^2}}d{x^0}^{\prime }-\frac{\omega }{c}\frac{{x^2}^{\prime }}{\sqrt{1-{\left(\frac{v}{c}\right)}^2}}{d{x}^1}^{\prime }+\frac{\omega }{c}\frac{{x^1}^{\prime }}{\sqrt{1-{\left(\frac{v}{c}\right)}^2}}d{x^2}^{\prime },\hfill \\ \hfill d{x}^1& =-\frac{v}{c}\frac{sin\phi }{\sqrt{1-{\left(\frac{v}{c}\right)}^2}}d{x^0}^{\prime }+\frac{\omega }{v}A{d{x}^1}^{\prime }+\frac{\omega }{v}Bd{x^2}^{\prime },\hfill \\ \hfill d{x}^2& =\frac{v}{c}\frac{cos\phi }{\sqrt{1-{\left(\frac{v}{c}\right)}^2}}d{x^0}^{\prime }+\frac{\omega }{v}C{d{x}^1}^{\prime }+\frac{\omega }{v}Dd{x^2}^{\prime },\hfill \end{array}$$

(8)

where

$$\begin{array}{cc}\hfill v=\omega r,& \phi =\frac{arccos\frac{{x^1}^{\prime }}{\sqrt{{{x^1}^{\prime }}^2+{{x^2}^{\prime }}^2}}+\frac{\omega }{c}{x^0}^{\prime }}{\sqrt{1-{\left(\frac{v}{c}\right)}^2}},\hfill \\ \hfill A={x^1}^{\prime }cos\phi +& \frac{{x^2}^{\prime }sin\phi }{\sqrt{1-{\left(\frac{v}{c}\right)}^2}},B={x^2}^{\prime }cos\phi -\frac{{x^1}^{\prime }sin\phi }{\sqrt{1-{\left(\frac{v}{c}\right)}^2}},\hfill \\ \hfill C={x^1}^{\prime }sin\phi -& \frac{{x^2}^{\prime }cos\phi }{\sqrt{1-{\left(\frac{v}{c}\right)}^2}},D={x^2}^{\prime }sin\phi +\frac{{x^1}^{\prime }cos\phi }{\sqrt{1-{\left(\frac{v}{c}\right)}^2}}.\hfill \end{array}$$

(9)

The whole group of all proper pseudo-orthogonal transformations $SO(1,2)$ in the space ${\mathbb{R}}_{1,2}^3$ is thus generated by elements from the Lorentz group (2) and by transformations of the form in (8) from the group $G_r$ into the pseudo-Euclidean coordinate system.

It is now appropriate to make one remark that proves useful in what follows. The transformations (5) are represented in differential form. However, because of their essentially linear character, nothing prevents us from representing them in the form

$$t=\frac{t^{\prime }+\frac{r^2\omega }{c}{\phi }^{\prime }}{\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}},\phi =\frac{{\phi }^{\prime }+\frac{\omega }{c}{t}^{\prime }}{\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}}.$$

(10)

4. An Explanation of the Sagnac Effect

Let us now show that the Sagnac effect is a trivial consequence of the existence of the nonlinear group of proper motions of the Minkowski metric.

Let index + denote the beam emitted from the moving source in the direction of its motion, and index −, the beam that moves in the opposite direction, see Figure 1. Let $t_{+(-)}$ be the time that has elapsed until the beam $+(-)$ arrives at the light source moving relative to a stationary frame of reference. Then, the following relations should hold:

$$c{t}_{+}=2\pi r+r\omega t_{+},c{t}_{-}=2\pi r-r\omega t_{-},$$

(11)

where r is the distance from the center of the disc upon which the source is mounted, $\omega$ being the angular velocity of rotation of the disc.

Hence, it follows that

$$t_{+}=\frac{2\pi r}{c-r\omega },t_{-}=\frac{2\pi r}{c+r\omega }.$$

(12)

The angular coordinates of the source, ${\phi }_{+}$ and ${\phi }_{-}$, at the moment of its meeting with the beams emitted, respectively, in the direction of the source motion and in the opposite direction relative to the stationary frame of reference, have the form:

$${\phi }_{+}=\omega t_{+},{\phi }_{-}=\omega t_{-}.$$

(13)

Let $t_{+(-)}^{\prime }$ be the time that has elapsed till the beam $+(-)$ meets with the moving light source relative to an observer who is directly connected with the source.

Then, proceeding from the first relation in (10), we obtain

$$t_{+}^{\prime }=\frac{t_{+}-\frac{r^2\omega }{c^2}{\phi }_{+}}{\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}},t_{-}^{\prime }=\frac{t_{-}-\frac{r^2\omega }{c^2}{\phi }_{-}}{\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}}.$$

(14)

Hence, it follows that the proper time interval $t_{+}^{\prime }$–$t_{-}^{\prime }$ between the arrival of the two beams at the source that moves relative to the observer directly connected with it has, according to (14), the following form

$$t_{+}^{\prime }-t_{-}^{\prime }=(t_{+}-t_{-})\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}.$$

(15)

Thus, according to formula (15), in a moving noninertial frame of reference, the interval between the arrivals of the beams to the source will be shorter than in the stationary one. Taking into account the relation (12), we finally arrive at the following result

$$t_{+}^{\prime }-t_{-}^{\prime }=\frac{4\pi \omega r^2}{c^2}\frac{1}{\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}}.$$

(16)

5. The Additional Group of Motions and the Twin Paradox

The meaning of the twin paradox is a follows: let there be two clocks, one of which moves along a closed path, returning to the original point where the other clock is at rest. If, at the initial moment of time, both clocks read the same, then at the moment of its return, the moving clock will be found to lag behind the one at rest. This conclusion is based on a nonrigorous heuristic reasoning [33], invoked by the properties of the Lorentz transformations and leading to the conclusion that a clock at rest always shows a longer time interval than the moving clock. The group of motions of the Minkowski metric constructed above enables one to carry out a more consistent analysis of this effect and cast some doubt on its plausibility.

At the initial moment of time, let there be two observers with clocks who are located at the same point and their clocks read the same time. Let the first observer be at rest, while the second uniformly moves along a circumference, e.g., a wheel’s rim where the wheel of radius r rotates with a constant angular velocity $\omega$. The question is: what will the readings of the clocks of both observers be at the moment of their second meeting?

In the frame of reference associated with the moving clock of the second observer, their clock is at rest. Due to the invariance of the metric relative to the transition of the rotating system to the immobile one, there holds the following relation

$$c^2{t}^{\prime }{}^2=c^2{t}^2-r^2{\phi }^2,$$

(17)

where $t^{\prime }$ is the time on the clock of the second observer and t is the time read by the clock of the first observer. Hence, it follows that

$$t^{\prime }=t\sqrt{1-{\left(\frac{\omega r}{c}\right)}^2},$$

(18)

i.e., just as one should expect, the clock of the second observer lags behind that of the first observer.

In the moving frame of reference associated with the second observer, let a segment of the wheel’s rim of length $r({\phi }_2^{\prime }-{\phi }_1^{\prime })$ be singled out. Let us find the length of this segment with respect to the frame of reference at rest associated with the first observer. To do so, it is necessary to find the angular coordinates ${\phi }_1$, ${\phi }_2$ of both ends of the segment of the rotating wheel at one and the same moment of time relative to the clock of the first observer. From (10), it follows that

$$r({\phi }_2-{\phi }_1)=r({\phi }_2^{\prime }-{\phi }_1^{\prime })\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2},$$

(19)

i.e., as should be expected, the length of the segment of the wheel is larger in the frame of reference where the wheel is at rest.

In particular, relative to the second observer associated with the rotating wheel, the length of the rim, and therefore the path it takes till its meeting with the first observer is $2\pi r$, whereas with respect to the first observer, the length of the rotating rim, and therefore the path the second observer travels till they meet the first one is, according to Formula (19), $2\pi r\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}$.

Since the second observer moves along the orbit with a constant velocity $v=r\omega$, the clock of the first observer reads a time interval between the two meetings with the second observer equal to

$$t=\frac{2\pi }{\omega }\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}.$$

(20)

Let us now see what the second observer’s clock reads at the moment of the meeting with the first observer. From the point of view of the second observer, till their meeting with the first observer, they travel a path of length $2\pi r$ with a constant linear velocity $v=r\omega$. The time taken to travel that path is, from the point of view of the first observer, equal to $t=\frac{2\pi }{\omega }$. However, then, the time read by the clock of the second observer at the moment of their meeting with the first one is, according to (18),

$$t^{\prime }=\frac{2\pi }{\omega }\sqrt{1-{\left(\frac{r\omega }{c}\right)}^2}.$$

(21)

Thus, the clocks of both the observers at the moment of their repeated meeting reads one and the same time.

Does this mean that the above analysis closes the question of whether the twin paradox exists? Certainly not, for to do so, it would be necessary to extend the result we have just obtained to any closed paths. This should involve quite an elaborate analysis, stemming from the basic properties of pseudo-orthogonal groups, as in [34].

6. Discussion and Conclusions

The Sagnac effect (SE) is the variance of the time a light beam takes while traversing the same path in opposite directions. The light source, the path, and the detector are rigidly fixed relative to each other. No linear inertial movement of this rigid installation is able to produce the effect; a noninertial or nonlinear motion is necessary. Thus, the SE is a substantially noninertial phenomenon in rotating frames. It may seem that the SE is easily explained with the help of the special theory of relativity (STR) and that the theoretical prediction perfectly matches experimental data. However, such consideration is deceptive since the principles of the STR were originally established only for the inertial frames of reference, whereas the SE exists in a noninertial one. In order to explain it consistently, one needs to extend the STR principles to the wider class of frames of reference including some noninertial ones. In the general case, it requires a nontrivial treatment. However, we show that a uniform circular motion corresponds to the group of nonlinear transformations of the pseudo-Euclidean coordinates, which leaves the Minkowski metric invariant. Hence, in this special case of a uniform circular motion, one can use Lorenz-like transformations as if it were a uniform straight motion with a constant velocity $v=r\omega$. It might be reasonable to test whether relativistically invariant theories (i.e., theories whose equations are covariant with respect to the Lorentz transformation) are also invariant with respect to the whole group $SO(1,3)$, which incorporates the group of nonlinear transformations of the metric.