Families of Orbits Produced by Three-Dimensional Central and Polynomial Potentials: An Application to the 3D Harmonic Oscillator

Abstract

We study three-dimensional potentials of the form $V=\mathcal{U}(x^p+y^p+z^p)$, where $\mathcal{U}$ is an arbitrary function of ${\mathcal{C}}^2$-class, and $p\in \mathbb{Z}$, which produces a preassigned two-parametric family of spatial regular orbits given in the solved form $f(x,y,z)$ = $c_1$, $g(x,y,z)$ = $c_2$ ($c_1$, $c_2$ = const). These potentials have to satisfy two linear PDEs, which are the basic equations of the 3D inverse problem of Newtonian dynamics. The functions f and g can be represented uniquely by the ”slope functions” $\alpha (x,y,z)$ and $\beta (x,y,z)$. The orbital functions $\alpha (x,y,z)$ and $\beta (x,y,z)$ have to satisfy three differential conditions according to the theory of the inverse problem. If these conditions are satisfied, then we can find such a potential analytically. We offer pertinent examples of potentials that are mainly used in physical problems. The values obtained for p lead to cases of well-known potentials, such as the Newtonian, cored, logarithmic, polynomial and quadratic ones. New families of orbits produced by the 3D harmonic oscillator are found. Pertinent examples are given and cover all cases. Two-dimensional potentials belong to a special category of potentials and are studied separately. The families of straight lines in 3D space are also examined.

1. Introduction

The three-dimensional inverse problem of dynamics seeks all potentials $V=V(x,y,z)$ that can produce, for adequate initial conditions, a two-parameter family of orbits traced by a material point of unit mass [1]. In the past, several authors studied three-dimensional versions of the inverse problem for a two-parametric family of orbits [2,3,4,5,6]. In [7], the researchers considered the case of two-parametric families of straight lines (FSL) created by three-dimensional potentials. The two energy-free PDEs of the three-dimensional inverse problem of dynamics were derived by [8,9] at the same time. Applications of the 3D inverse problem to homogeneous potentials and to axisymmetric ones were given by [9,10]. Other solvable cases of this problem were examined in [11] and in [12] for generalized Szebehely’s inverse problem of dynamics in three dimensions, which provided several examples of families of orbits. A three-dimensional inverse problem of geometrical optics was studied in [13]. Three-dimensional homogeneous potentials generating two-parametric families of orbits on the outside of a material concentration were studied in [14].

Central potentials are very useful in Celestial Mechanics problems. For instance, Ref. [15] studied the case of a satellite in a Manev gravitational potential under the influence of an atmospheric drag force that varies with the square of the velocity. Central potentials were also applied in Quantum Mechanics [16] and in high-energy physics [17]. On the other hand, polynomial potentials are used mainly in the study of the integrability of Hamiltonian systems with two or three degrees of freedom. In particular, Ref. [18] studied a family of two-dimensional dynamical systems and found integrals of motion quadratic in velocities. The same authors extended their work to third- and fourth-degree polynomial potentials [19]. In both cases, the weak-Pianlevé property was used as a criterion for integrability. Polynomial integrals of motion of degrees greater than 2 for planar systems were found in the review paper of [20]. Ref. [21] linearized integrable Hamiltonians with quartic potentials as well as the remaining integrable cubic potentials. In addition, Ref. [22] investigated 3D Hamiltonian systems with quartic potentials that are even in $x,y,z$ and found integrable cases. Furthermore, Ref. [23] gave a complete list of all integrable two-dimensional homogeneous polynomial potentials with a polynomial integral of order at most four in the momenta. We note here that polynomial potentials also have applications in astrophysics [24,25]. Polynomial potentials as solutions to the Schrödinger equation were also studied in [26] and for the confluent Heun equation in [27].

The harmonic oscillator is an essential tool that is widely used in many areas of physics in order to understand more realistic systems, from classical to quantum and relativistic regions. It was also used for the study of 3D perturbed Hamiltonian dynamical systems [28,29] and for the study of relativistic chaos [30].

In the present paper, we combine the theory of the inverse problem of dynamics with three-dimensional central and polynomial potentials. Our aim is to find new families of orbits compatible with these types of potentials and apply them to the case of the 3D harmonic oscillator. To our knowledge, there are not many papers in the literature related to this topic. More precisely, two-parametric families of orbits produced by cubic potentials were studied in [8]. Two-dimensional potentials that generate spatial families of orbits were found in [31]. This finding gave us the motivation to write the present article.

The structure of this paper is as follows: In Section 2, we give the basic facts of the inverse problem of Newtonian dynamics. In Section 3, we present our methodology in order to find solutions to this problem. Thus, we shall study potentials of the special form $V=\mathcal{U}(x^p+y^p+z^p)$, where $\mathcal{U}$ is an arbitrary function of ${\mathcal{C}}^2$-class, and $p\in \mathbb{Z}$. In Section 4, Section 5 and Section 6, we show our new results. By using this methodology, we can find homogeneous, polynomial and central potentials, which have many applications in physical problems (Section 4.1, Section 4.2 and Section 4.3). Polynomial potentials as solutions to Laplace’s equation are also found (Section 4.4). We can also obtain more general results (Section 5). Facing the direct problem of Newtonian dynamics, i.e., if the potential is given in advance, then find all the families of orbits that are generated by it, we can find new families of orbits produced by the 3D harmonic oscillator (Section 6). Two-dimensional potentials constitute a special category and are studied in Section 7. All the results are completely new and original. Families of straight lines are studied in Section 8. Finally, we make some concluding remarks in Section 9.

2. The Basic Equations

We consider the two-parametric family of regular orbits given in the solved form

$$f(x,y,z)=c_1,g(x,y,z)=c_2,$$

(1)

where $c_1,c_2=$ const., and the total energy is conserved. In a three-dimensional frame, we deal with two-parametric families of orbits written in the form of (1). As indicated by [8,9,31], the family of orbits (1) can be represented by two “slope functions”:

$$\alpha =\alpha (x,y,z)and\beta =\beta (x,y,z)$$

(2)

defined by

$$\alpha =\frac{{\delta }_2}{{\delta }_1},\beta =\frac{{\delta }_3}{{\delta }_1},$$

(3)

where

$${\delta }_1=f_y{g}_z-f_z{g}_y,{\delta }_2=f_z{g}_x-f_x{g}_z,{\delta }_3=f_x{g}_y-f_y{g}_x,$$

(4)

are the components of the vector $\overrightarrow{\delta }$ = $\nabla f\times \nabla g$. Furthermore, the indices “x, y, z” denote partial derivatives. There is a “one-to-one” correspondence between the slope functions (2) and the family of orbits (1). This means that if the pair of orbits $\alpha ,\beta$ is given in advance, then we can find the two-parametric family of orbits in the form of (1) by analytically solving the ODE system:

$$\frac{dy}{dx}=\alpha (x,y,z,),\frac{dz}{dx}=\beta (x,y,z)$$

(5)

The potential V = $V(x,y,z)$ has to satisfy two linear PDEs; the first one is of the first order, and the second one is of the second order. There exist two basic equations of the three-dimensional inverse problem of Newtonian dynamics, as was shown by [8,9,10]. Taking into account that ${\alpha }_0\ne$ 0, these equations are

$$l_1{V}_x+l_2{V}_y+l_3{V}_z=0,$$

(6)

where

$$l_1=\alpha {\beta }_0-\beta {\alpha }_0,l_2=-{\beta }_0,l_3={\alpha }_0.$$

(7)

and

$$m_{11}{V}_{xx}+m_{12}{V}_{xy}+m_{13}{V}_{xz}+m_{22}{V}_{yy}+m_{23}{V}_{yz}+m_{01}{V}_x+m_{02}{V}_y+m_{03}{V}_z=0,$$

(8)

where

$$\begin{array}{c}{m}_{11}=\alpha \mathsf{\Theta }{\alpha }_0,m_{12}=({\alpha }^2-1)\mathsf{\Theta }{\alpha }_0,m_{13}=\alpha \beta \mathsf{\Theta }{\alpha }_0,\hfill \\ m_{22}=-\alpha \mathsf{\Theta }{\alpha }_0,m_{23}=-\beta \mathsf{\Theta }{\alpha }_0,\hfill \\ m_{01}=(\mathsf{\Theta }+2){\alpha }_0^2+\alpha M,m_{02}=2\alpha {\alpha }_0^2-M,m_{03}=2\beta {\alpha }_0^2,\hfill \\ M=2(\alpha {\alpha }_0+\beta {\beta }_0){\alpha }_0-\mathsf{\Theta }({\alpha }_{0x}+\alpha {\alpha }_{0y}+\beta {\alpha }_{0z}).\hfill \end{array}$$

(9)

We can use the notation as follows:

$$\begin{array}{ccc}\hfill {\alpha }_0& =& \hfill {\alpha }_x+\alpha {\alpha }_y+\beta {\alpha }_z,{\beta }_0={\beta }_x+\alpha {\beta }_y+\beta {\beta }_z\hfill \\ \hfill \mathsf{\Theta }& =& 1+{\alpha }^2+{\beta }^2.\hfill \end{array}$$

(10)

The subscripts denote partial derivatives with respect to the variables $x,y,z$. We note here that if ${\alpha }_0=0,{\beta }_0\ne 0$, then we can use the second-order PDE, i.e., Equation (24), in [10]. This PDE reads

$$q_{11}{V}_{xx}+q_{12}{V}_{xy}+q_{13}{V}_{xz}+q_{23}{V}_{yz}+q_{33}{V}_{zz}+q_{01}{V}_x+q_{02}{V}_y+q_{03}{V}_z=0,$$

(11)

where

$$\begin{array}{ccc}\hfill q_{11}& =& \tilde{n}\beta ,q_{12}=\tilde{n}\alpha \beta ,q_{13}=\tilde{n}({\beta }^2-1),\hfill \\ \hfill q_{23}& =& -\tilde{n}\alpha ,q_{33}=-\tilde{n}\beta ,\hfill \\ \hfill q_{01}& =& \hfill 2+\beta {\tilde{n}}_0+\tilde{n}{\beta }_0,q_{02}=2\alpha ,q_{03}=2\beta -{\tilde{n}}_0\hfill \end{array}$$

(12)

and

$$\tilde{n}=\frac{\mathsf{\Theta }}{{\beta }_0},{\tilde{n}}_0={\tilde{n}}_x+\alpha {\tilde{n}}_y+\beta {\tilde{n}}_z$$

(13)

The energy of the family of orbits (1) is found to be [9]:

$$\mathcal{E}=\frac{\mathsf{\Theta }}{2{\alpha }_0}(\alpha V_x-V_y)+V.$$

(14)

From (14), we obtain $\mathcal{E}-V\ge$ 0. As was shown by [8] (p. 548), this requirement leads to the following:

$$A=\frac{\alpha V_x-V_y}{{\alpha }_0}\ge 0.$$

(15)

Inequality (15) defines the allowed region of the motion of a test particle in the family of orbits (1) in 3D space, which are traced by a particle of unit mass in the presence of a 3D potential $V=V(x,y,z)$. We note here that if both ${\alpha }_0={\beta }_0$ = 0, the family of orbits consists of straight lines [7], and this case will be studied in Section 9.

3. The Methodology

In this section, we shall find solutions of the form

$$V=\mathcal{U}\left(w\right),w=x^p+y^p+z^p,p\ne 0$$

(16)

for the above two Equations (6) and (8), where $\mathcal{U}$ is an arbitrary function of $C^2$-class.

Differential Conditions on the Slope Functions ($\alpha ,\beta$)

We suppose that $V=\mathcal{U}\left(w\right)$, and we find the derivatives of the first order of the potential function V with respect to $x,y,z$, i.e., $V_x={\mathcal{U}}^{\prime }{w}_x$, $V_y={\mathcal{U}}^{\prime }{w}_y$, $V_z={\mathcal{U}}^{\prime }{w}_z$, respectively, where ${\mathcal{U}}^{\prime }$ = $\frac{d\mathcal{U}}{dw}$. We insert them into (6) and obtain

$${\mathcal{U}}^{\prime }\left(w\right)(l_1{w}_x+l_2{w}_y+l_3{w}_z)=0$$

(17)

Setting ${\mathcal{U}}^{\prime }\left(w\right)\ne 0$, the first necessary differential condition on the orbital functions $(\alpha ,\beta )$ is

$$l_1{w}_x+l_2{w}_y+l_3{w}_z=0$$

(18)

Now, we will focus our interest on the second-order PDE (8). Firstly, we estimate the second-order derivatives of the potential function V with respect to $x,y,z$:

$$\begin{array}{ccc}\hfill V_{xx}& =& \hfill {\mathcal{U}}^{″}{w}_x^2+{\mathcal{U}}^{\prime }{w}_{xx},V_{xy}={\mathcal{U}}^{″}{w}_x{w}_y+{\mathcal{U}}^{\prime }{w}_{xy},V_{xz}={\mathcal{U}}^{″}{w}_x{w}_z+{\mathcal{U}}^{\prime }{w}_{xz},\hfill \\ \hfill V_{yy}& =& {\mathcal{U}}^{″}{w}_y^2+{\mathcal{U}}^{\prime }{w}_{yy},V_{yz}={\mathcal{U}}^{″}{w}_y{w}_z+{\mathcal{U}}^{\prime }{w}_{yz},\hfill \end{array}$$

(19)

and we insert them into Equation (8). Thus, we obtain the next relation,

$$r_2{\mathcal{U}}^{″}\left(w\right)+r_1{\mathcal{U}}^{\prime }\left(w\right)=0,$$

(20)

where

$$\begin{array}{ccc}\hfill r_2& =& \hfill m_{11}{w}_x^2+m_{12}{w}_x{w}_y+m_{13}{w}_x{w}_z+m_{22}{w}_y^2+m_{23}{w}_y{w}_z,\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill r_1& =& \hfill m_{11}{w}_{xx}+m_{12}{w}_{xy}+m_{13}{w}_{xz}+m_{22}{w}_{yy}+m_{23}{w}_{yz}+\hfill \\ & +& m_{01}{w}_x+m_{02}{w}_y+m_{03}{w}_z\hfill \end{array}$$

(22)

Putting $r_2\ne$ 0, from (20), we obtain

$$\frac{{\mathcal{U}}^{″}}{{\mathcal{U}}^{\prime }}=-\frac{r_1}{r_2}=\mathcal{R},$$

(23)

Now, we observe that $\frac{{\mathcal{U}}^{″}}{{\mathcal{U}}^{\prime }}$ is dependent only on the argument w. Consequently, the function $\mathcal{R}$ must depend on the same argument. Thus, we have

$$\mathcal{R}=\mathcal{R}\left(w\right)$$

(24)

or, equivalently,

$$\frac{{\mathcal{R}}_x}{w_x}=\frac{{\mathcal{R}}_y}{w_y}=\frac{{\mathcal{R}}_z}{w_z}.$$

(25)

This is true if and only if the following relations are verified for the given slope functions ($\alpha ,\beta$):

$$\left(i\right){\mathcal{R}}_x{w}_y-{\mathcal{R}}_y{w}_x=0,\left(ii\right){\mathcal{R}}_y{w}_z-{\mathcal{R}}_z{w}_y=0.$$

(26)

On the other hand, we consider that conditions (18) and ((26)i, ii) are satisfied by the functions $\alpha$ and $\beta$. In addition, $\mathcal{U}\left(w\right)\ne 0$. Then, we obtain $\mathcal{U}=\mathcal{U}\left(w\right)$, and we can find the function $\mathcal{U}$ by integrating relation (23) twice with respect to w. The result is

$$\mathcal{U}\left(w\right)=d_1\int e^{\int \mathcal{R}\left(w\right)dw}dw+d_2,d_1,d_2=const.$$

(27)

As a conclusion, by using solution (27), we can find the potential function V analytically. Now, we can formulate the following.

Proposition 1.

If $r_2\ne 0$ and $r_1\ne 0$ and the three conditions (18) and ((26)i, ii) are satisfied for the given functions α and β, then a potential of the form V = $\mathcal{U}\left(w\right)$ always exists, and it is determined uniquely from (27) up to two arbitrary constants.

We remark here that:

• Case I. If $r_2\ne$ 0 and $r_1$ = 0, then we obtain ${\mathcal{U}}^{″}\left(w\right)$ = 0 from (20). Thus, we have $\mathcal{U}\left(w\right)=d_{1}w+d_2,d_1,d_2=const.$
• Case II. If $r_2=$ 0 and $r_1$ = 0, then Equation (20) is identically zero. Thus, any function $V=\mathcal{U}\left(w\right)$ is a solution to our problem.
• Case III. If $r_2$ = 0 and $r_1\ne$ 0, then in this case, we obtain ${\mathcal{U}}^{\prime }\left(w\right)$ = 0 from (20). Thus, $\mathcal{U}\left(w\right)=const.$, and this case is excluded from our study.

4. Results

4.1. Central Potentials

In this section, we shall offer an example that covers the general theory ($r_1,r_2\ne$ 0).

Example 1 (The Newtonian potential).

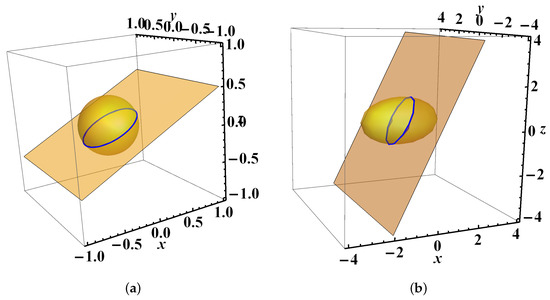
We consider the two-parametric family of orbits (see Figure 1a)

$$f(x,y,z)=5\sqrt{x^2+y^2+z^2}+2x=c_1,g(x,y,z)=\frac{z}{x}=c_2$$

(28)

which leads to the pair

$$\alpha =-\frac{5x^2+5z^2+2x\sqrt{x^2+y^2+z^2})}{5xy},\beta =\frac{z}{x}$$

(29)

and we check the first condition (18). It is satisfied only for p = 2, and then we proceed to the other conditions, i.e., Equation ((26)i, ii). They are also satisfied for p = 2, and we determine the function $\mathcal{R}\left(w\right)$ from (23). It is:

$$\mathcal{R}\left(w\right)=-\frac{3}{2w},w=x^2+y^2+z^2,$$

(30)

and, from (27), we find

$$\mathcal{U}\left(w\right)=-\frac{2d_1}{\sqrt{w}}+d_2,d_1,d_2=const.$$

(31)

Thus, we conclude that the family of orbits (28) is created by the potential

$$V(x,y,z)=-\frac{2d_1}{\sqrt{x^2+y^2+z^2}}+d_2.$$

(32)

For $d_1=\frac{1}{2}$ and $d_2=$ 0, we obtain the well-knownNewtonianpotential, which is the most basic spherical potential. It is homogeneous of degree $m=-$1 and axisymmetric. The energy of the family of orbits (28) is

$$\mathcal{E}=-\frac{21+25c_2^2}{10(1+c_2^2)c_1}=const.$$

(33)

and the allowed region is (15) $A=5\sqrt{x^2+y^2+z^2}+2x\ge$ 0.

4.2. Polynomial Potentials

In this section, we shall present results that belong to Case I ($r_2\ne 0,r_1=$ 0).

Example 2.

We consider the two-parametric family of elliptic orbits (see Figure 1b)

$$f(x,y,z)=x^2+4y^2+3z^2=c_1,g(x,y,z)=\frac{z}{x}=c_2$$

(34)

which leads to the pair

$$\alpha =-\frac{x^2+3z^2}{4xy},\beta =\frac{z}{x}$$

(35)

and we check the first condition (18). It is satisfied only for p = 2, and then we examine the other two conditions, i.e., Equation ((26)i, ii). In this case, we have $r_2\ne$ 0 and $r_1=$ 0. Conditions ((26)i, ii) are also satisfied for p = 2, and we determine the function $\mathcal{R}\left(w\right)$ from (23). It is $\mathcal{R}\left(w\right)$ = 0. Then, we find the function $\mathcal{U}\left(w\right)$ according to Case I. It is:

$$\mathcal{U}\left(w\right)=d_{1}w+d_2,w=x^2+y^2+z^2,d_1,d_2=const.$$

(36)

For $d_1=\frac{1}{2}$ and $d_2=$ 0, we obtain the well-knownharmonic oscillator

$$V(x,y,z)=\frac{1}{2}(x^2+y^2+z^2).$$

(37)

The energy of the family of orbits is found to be (14)

$$\mathcal{E}=\frac{c_1(5+7c_2^2)}{8(1+3c_2^2)}=const.$$

(38)

and the allowed region of the motion of the test particle is $A=\frac{4x^2{y}^2}{x^2+3z^2}\ge$ 0, which means that the test particle can move everywhere in 3D space.

Other pairs of orbits compatible with potential (37) are shown in

Table 1. Families of orbits compatible with potential (37).

Family of Orbits	Pair of Orbits $(\mathit{\alpha },\mathit{\beta })$	Energy ($\mathcal{E}$)
$f(x,y,z)=x^2+y^2-z^2=c_1$, $g(x,y,z)=\frac{z}{x}=c_2$	$\alpha =-\frac{(x-z)(x+z)}{xy},\beta =\frac{z}{x}$	$\frac{c_1}{1-c_2^2}$
$f(x,y,z)=x^2-y^2-z^2=c_1$, $g(x,y,z)=\frac{z}{x}=c_2$	$\alpha =\frac{(x-z)(x+z)}{xy},\beta =\frac{z}{x}$	$\frac{c_1{c}_2^2}{1-c_2^2}$
$f(x,y,z)=x^2+y^2=c_1$, $g(x,y,z)=\frac{y+z}{x}=c_2$	$\alpha =-\frac{x}{y},\beta =\frac{x^2+y^2+yz}{xy}$	$\frac{1}{2}{c}_1(3+c_2^2)$

One member of the family of orbits (No. 1 in Table 1) is presented at Figure 2a.

.

Example 3.

We shall study the two-parametric family of orbits

$$f(x,y,z)=\frac{x^2+y^2}{x^2{y}^2}=c_1,g(x,y,z)=\frac{x^2-z^2}{x^2{z}^2}=c_2$$

(39)

or, equivalently, given by the pair

$$\alpha =-\frac{y^3}{x^3},\beta =\frac{z^3}{x^3}$$

(40)

and we check the first condition (18). It is satisfied only for p = 6, and then we proceed to the other conditions, i.e., Equation ((26)i, ii). In this case, we obtain $r_1=$ 0 and $r_2\ne$ 0 again. Conditions ((26)i, ii) are also satisfied for p = 6, and we determine the function $\mathcal{U}\left(w\right)$ according to Case I. It is:

$$\mathcal{U}\left(w\right)=d_{1}w+d_2,w=x^6+y^6+z^6,d_1,d_2=const.$$

(41)

Thus, we obtain the separable potential

$$V(x,y,z)=d_1(x^6+y^6+z^6)+d_2.$$

(42)

The energy is found to be (14)

$$\mathcal{E}=0.$$

(43)

and the allowed region is (15) $A=-2d_1{x}^6\ge$ 0. This inequality is valid only for $d_1<$ 0.

Theorem 1.

Foranyvalues of s ($s\ne$ 0), the pair of slope functions $\alpha =-{\left(\frac{y}{x}\right)}^s,\beta ={\left(\frac{z}{x}\right)}^s$ is compatible with the potential $V(x,y,z)=d_1(x^p+y^p+z^p)d_2$ ($d_1,d_2=$const., $p\ne$ 0, 1), where $p=2s$. The allowed region is $A=-2d_1{x}^p\ge$ 0 ($d_1<$ 0).

Proof. 

For the pair of orbits $\alpha =-{\left(\frac{y}{x}\right)}^s,\beta ={\left(\frac{z}{x}\right)}^s$, we check the first condition (18). It is satisfied only for p = $2s$, and then we proceed to the other conditions, i.e., Equation ((26)i, ii). In this case, we have $r_2\ne$ 0 and $r_1=$ 0. Conditions ((26)i, ii) are also satisfied for p = $2s$, and we determine the function $\mathcal{U}\left(w\right)$ according to Case I. It is: □

$$\mathcal{U}\left(w\right)=d_{1}w+d_2,w=x^{2s}+y^{2s}+z^{2s},d_1,d_2=const.$$

(44)

4.3. Potentials Depending on the Distance r

In this section, we shall present results that belong to Case II, i.e., $r_2=r_1=$ 0. These potentials are compatible with the two-parametric family of orbits (45).

Example 4.

We consider the two-parametric family of orbits given by the pair (see Figure 2b)

$$f(x,y,z)=x^2+y^2+z^2=c_1,g(x,y,z)=\frac{x+y+z}{z}=c_2$$

(45)

or, equivalently, by the pair

$$\alpha =-\frac{x^2+xy+z^2}{xy+y^2+z^2},\beta =-\frac{(x-y)z}{xy+y^2+z^2}$$

(46)

and we check the first condition (18). It is satisfied only for p = 2. The value p = 2 leads to Case II of the general theory, i.e., $r_1=r_2=$ 0, and conditions ((26)i, ii) are identically zero. Thus, we can selectanyarbitrary function $V=\mathcal{U}\left(w\right)$, $w=x^2+y^2+z^2=r^2$, as a solution to our problem.

(1) 

The cored potential. This potential was studied by [32] for the planar problem. More precisely, the authors applied the averaging theory of the first order in the small parameter ε to compute periodic orbits of a perturbed differential system depending on the parameter ε. Now, we consider the potential

$$V(x,y,z)=\sqrt{1+r^2}=\sqrt{1+x^2+y^2+z^2}.$$

(47)

As was shown by [33], potential (47) is completely integrable with analytic first integrals. The allowed region of the motion of the test particle is everywhere in 3D space.

(2) 

The logarithmic potential.

The well-known logarithmic potential was studied by many researchers in the past. In particular, the phase space structure for the singular logarithmic potential in two-dimensional space was studied in [34] with the method of Poincaré surfaces of section, and a stability analysis for axial orbits was performed by the same authors. In [32], the potential was examined in a similar way, together with the cored potential.

$$V(x,y,z)=\frac{1}{2}log(1+r^2)=\frac{1}{2}log(1+x^2+y^2+z^2),$$

(48)

and the allowed region of the motion of the test particle is everywhere in 3D space.

4.4. Polynomial Potentials as Solutions to Laplace’s Equation

In this paragraph, we shall examine an interesting case of potentials that are solutions of Laplace’s equation.

Example 5.

We regard the two-parametric family of orbits

$$f(x,y,z)=\frac{x}{u_0}=c_1,g(x,y,z)=\frac{y}{u_0}=c_2$$

(49)

where

$$u_0=slog\left(z+\sqrt{z^2+4}\right),s=\frac{1}{\sqrt{2}}.$$

The family of orbits (49) leads to the pair

$$\alpha =-\frac{y}{x}{cot}^2\left(u_0\right),\beta =-\frac{2s\sqrt{4+z^2}}{x}cot\left(u_0\right)$$

(50)

We shall find solutions of the form

$$V=\mathcal{U}\left(w\right),w=k_1(x^p+y^p)+k_2{z}^p,p,k_1,k_2\ne 0,$$

(51)

for Equations (6) and (8), where $\mathcal{U}$ is an arbitrary function of $C^2$-class. First, we check the first condition (18). It is satisfied only for p = 2 and $k_2=-2k_1$. In this case, we have $r_2\ne$ 0 and $r_1=$ 0. Conditions ((26)i, ii) are also satisfied for the above values, and we determine the function $\mathcal{R}\left(w\right)$ from (23). It is $\mathcal{R}\left(w\right)$ = 0. Then, we find the function $\mathcal{U}\left(w\right)$ according to Case I. It is:

$$\mathcal{U}\left(w\right)=d_{1}w+d_2,w=k_1(x^2+y^2-2z^2),d_1,d_2=const.$$

(52)

For $k_1=$1, $d_1=\frac{1}{2}$ and $d_2=$ 0, we obtain the following result:

$$V(x,y,z)=\frac{1}{2}(x^2+y^2-2z^2).$$

(53)

and the allowed region of the motion of the test particle is $A=x^{2}tan\left(u_0\right)\ge$ 0, which means that the test particle can move everywhere in 3D space. We can easily check that potential (53) is homogeneous of degree m = 2 and satisfiesLaplace’sequation ${\nabla }^{2}V=$ 0.

5. Other Results

By using the above methodology, we can find many other potentials in addition to homogeneous and polynomial ones. We shall offer the following example.

Example 6.

We take into account the two-parametric family of orbits given by the pair

$$f(x,y,z)=(x+y+z+2)e^{-x}=c_1,g(x,y,z)=z-x=c_2$$

(54)

or, equivalently, by the pair

$$\alpha =x+y+z,\beta =1$$

(55)

and we check the first condition (18). It is satisfied for p = 1. In this case, conditions ((26)i, ii) are also verified for p = 1, and we obtain the function $\mathcal{R}\left(w\right)$ from (23). It is:

$$\mathcal{R}\left(w\right)=-\frac{7+2w}{(w-1)(w+2)},w=x+y+z,$$

(56)

and, from (27), we find

$$\mathcal{U}\left(w\right)=\frac{d_1(1+2w)}{2{(w-1)}^2}+d_2,d_1,d_2=const.$$

(57)

Setting $d_1=-$1 and $d_2$ = 0, we obtain the potential

$$V(x,y,z)=-\frac{1+2(x+y+z)}{2{(x+y+z-1)}^2}.$$

(58)

The energy of the family of orbits is found to be $\mathcal{E}=\frac{1}{2}$, and the allowed region of the motion of the test particle is $A=\frac{1}{{x+y+z-1)}^2}\ge$ 0, which means that the motion of the test particle can take place everywhere in 3D space except for the plane $x+y+z=$ 1.

6. The Direct Problem

The direct problem of Newtonian dynamics seeks all the two-parametric families of orbits that are produced by a three-dimensional potential $V=V(x,y,z)$ given in advance ([8]). As was shown by [8] (p. 550), we can rearrange the two basic Equations (6) and (8) and write two new linear PDEs for the families of orbits when the expression of the potential $V=V(x,y,z)$ is known. So, the totality of orbits is included in these two equations. Since the orbital functions $(\alpha ,\beta )$ appear in these equations, we can develop a methodology for searching for families of orbits in the form $(\alpha ,\beta )$.

1.

Plan $A_1$. We select a linear combination of the arguments $\psi =\frac{y}{x},\omega =\frac{z}{x},\tau =\frac{x}{z}$ for the orbital functions $(\alpha ,\beta )$, i.e.,

$$\alpha =k_1\psi +k_2\omega +k_3\tau ,\beta =k_4\psi +k_5\omega +k_6\tau ,$$

(59)

where $k_j,j=1,\dots ,6$ = const. We insert the expressions from (59) into Equations (18) and (26), and we look for suitable values of the constants $k_j,j=1,\dots ,6$ for which these conditions are satisfied. Then, by using system (5), we analytically find the two-parametric family of orbits (1).

2.

Plan $A_2$. We choose a linear combination of the arguments $\xi =\frac{z}{y},\omega =\frac{z}{x}$ for the orbital functions $(\alpha ,\beta )$, i.e.,

$$\alpha =k_1\xi +k_2\omega +k_3,\beta =k_4\xi +k_5\omega +k_6,$$

(60)

where $k_j,j=1,\dots ,6$. We insert the expressions from (60) into Equations (18) and (26), and we seek appropriate values of the constants $k_j,j=1,\dots ,6$ for which these conditions are satisfied. Then, by using system (5), we analytically find the two-parametric family of orbits (1).

6.1. New Families of Orbits Produced by the 3D Harmonic Oscillator

We set $p=$ 2 from the beginning, and we examine the potentials $V=\mathcal{U}(x^2+y^2+z^2)$.

1.

Following Plan $A_1$, we find one appropriate solution for the constants $k_j,j=1,\dots ,6$. This is

$$k_1=1,k_2=k_3=-1,k_4=k_5=0,k_6=-1,$$

(61)

Thus, we have the pair of orbits

$$\alpha =\frac{y}{x}-\frac{z}{x}-\frac{x}{z},\beta =-\frac{x}{z}$$

(62)

This set of orbits leads to Case I of the general theory ($r_1=0,r_2\ne$ 0). Thus, we have $\mathcal{R}\left(w\right)$ = 0. Now, we obtain the potential

$$V(x,y,z)=d_1(x^2+y^2+z^2)+d_2,d_1,d_2=const.$$

(63)

For $d_1=\frac{1}{2}$ and $d_2=$ 0, we have $V(x,y,z)=\frac{1}{2}(x^2+y^2+z^2)$. System (5) is written as follows:

$$\frac{dy}{dx}=\frac{y}{x}-\frac{z}{x}-\frac{x}{z},\frac{dz}{dx}=-\frac{x}{z}.$$

(64)

By analytically solving system (64), we obtain the two-parametric family of orbits (see Figure 3a)

$$f(x,y,z)=x^2+z^2=c_1,g(x,y,z)=\frac{y-z}{x}=c_2$$

(65)

and the allowed region is $A=2d_1{z}^2\ge$ 0. This inequality is valid only for $d_1>$ 0.

2.

According to Plan $A_2$, we find one appropriate solution for the constants $k_j,j=1,\dots ,6$. This is

$$k_1=-1,k_5=1,k_2=k_3=k_4=k_6=0$$

(66)

Thus, we have the pair of orbits

$$\alpha =-\frac{z}{y},\beta =\frac{z}{x}$$

(67)

This set of orbits leads to Case I of the general theory. Now, we obtain the potential

$$V(x,y,z)=d_1(x^2+y^2+z^2)+d_2,d_1,d_2=const.$$

(68)

System (5) is written as follows:

$$\frac{dy}{dx}=-\frac{z}{y},\frac{dz}{dx}=\frac{z}{x}.$$

(69)

By analytically solving system (69), we obtain the two-parametric family of orbits (see Figure 3b)

$$f(x,y,z)=y^2+xz=c_1,g(x,y,z)=\frac{z}{x}=c_2$$

(70)

and the allowed region is $A=\frac{x{y}^2}{z}\ge$ 0, or, equivalently, $xz\ge$ 0.

6.2. Families of Orbits Produced by the Perturbed Harmonic Oscillator

Now, we set $p=$ 2 from the beginning, and we study the potentials $V=\mathcal{U}\left(w\right)$, where $w=(x^2+y^2+z^2)+d_3{z}^m$ ($d_3=const$, $m\ne p$).

Example 7.

We consider the two-parametric family of orbits

$$f(x,y,z)=x^2+y^2+z^2=c_1,g(x,y,z)=\frac{y}{x}=c_2$$

(71)

or, equivalently, the pair

$$\alpha =\frac{y}{x},\beta =-\frac{x^2+y^2}{xz}$$

(72)

This pair of slope functions leads to the case ${\alpha }_0=$ 0 and ${\beta }_0\ne$ 0; so, we shall use Equations (6) and (11). Firstly, we check condition (18). It is satisfied for $m=0,2,-$2. The case for $m=$ 2 leads to the well-known known harmonic oscillator $V=\frac{1}{2}(x^2+y^2+z^2)$, and it is not taken into account. The case $m=$ 0 leads to the case $r_1=r_2=$ 0, and the function $\mathcal{R}=-\frac{r_1}{r_2}$ in (23) is not defined. Thus, according to Case II, we can consider thatanyfunction $V=\mathcal{U}(x^2+y^2+z^2)$, $\mathcal{U}$ is an arbitrary $C^2$-function, is a solution to our problem. We excluded this value from our study because we do not have a perturbation in the harmonic oscillator in this case. Thus, we are left only with the value $m=-$2.

For $m=-$2, we have $r_2\ne$ 0 and $r_1=$ 0, and we determine the function $\mathcal{R}\left(w\right)$ from (23). It is $\mathcal{R}\left(w\right)$ = 0. Then, we find the function $\mathcal{U}\left(w\right)$ according to Case I. It is:

$$\mathcal{U}\left(w\right)=d_{1}w+d_2,w=x^2+y^2+z^2+\frac{d_3}{z^2},d_1,d_2,d_3=const.$$

(73)

For $d_1=\frac{1}{2}$, $d_2=$ 0, we obtain theharmonic oscillatorwith a small perturbation. It is

$$V(x,y,z)=\frac{1}{2}(x^2+y^2+z^2)+\frac{d_3}{2z^2}.$$

(74)

The energy of the family of orbits is found to be (14)

$$\mathcal{E}=x^2+y^2+z^2=c_1.$$

(75)

Since ${\alpha }_0=$ 0 and ${\beta }_0\ne$ 0, the allowed region of the motion of the test particle is given by ([8], p. 550)

$$\tilde{B}=\frac{\beta V_x-V_z}{{\beta }_0}\ge 0.$$

(76)

So, the allowed region is (76) $\tilde{B}=z^2(x^2+y^2+z^2)\ge 2d_3$. For the planar problem, families of orbits related to an unharmonic oscillator for elliptical galaxies were studied by [35].

7. Two-Dimensional Potentials

An interesting class of potentials that produce two-parametric families of orbits in 3D space are those that depend on two variables, i.e., $V=V(x,z)$ or $V=V(y,z)$. These are two-dimensional potentials and were studied in detail by [31]. We set $p=$ 2, and we obtain $w=y^2+z^2$ in (16). Then, we select a combination for the orbital functions $(\alpha ,\beta )$ as follows:

1.

Plan $B_1$. We select a linear combination of the arguments $\psi =\frac{y}{x},\omega =\frac{z}{x}$ for the orbital functions $(\alpha ,\beta )$, i.e.,

$$\alpha =k_1\psi +k_2\omega ,\beta =k_3\psi +k_4\omega ,$$

(77)

where $k_j,j=1,\dots ,4$ = const. We insert the expressions from (77) into Equations (18) and (26), and we look for suitable values of the constants $k_j,j=1,\dots ,4$ for which these conditions are satisfied. Then, by using system (5), we analytically find the two-parametric family of orbits (1).

2.

Plan $B_2$. We consider the following pair of slope functions:

$$\alpha =k_1{x}^2+k_2{z}^2,\beta =k_3\left(\frac{y}{x}\right)+k_4\left(\frac{z}{x}\right),$$

(78)

where $k_j,j=1,\dots ,4$ = const. We insert the expressions from (78) into Equations (18) and (26), and we aim to find the correct values of the constants $k_j,j=1,\dots ,4$ for which these conditions are satisfied.

Examples

Now, we shall present two examples of 2D potentials.

1.

Following Plan $B_1$, we have found the set of values

$$k_1=k_4=-s\ne 0,k_2=k_3=0$$

(79)

This set of values of the constants $k_j,j=1,\dots ,4$ for the orbital functions $(\alpha ,\beta )$ leads to the case $r_2,r_1\ne$ 0. According to Proposition 1, there exists a potential that produces the above family of orbits, and it is found from (27). It is

$$V(y,z)=-\frac{{(y^2+z^2)}^q}{q},q=\frac{s+1}{s},s\ne 0.$$

(80)

Then, with the aid of system (5), we analytically find the two-parametric family of orbits (1). System (5) is written as

$$\frac{dy}{dx}=-\frac{sy}{x},\frac{dz}{dx}=-\frac{sz}{x}.$$

(81)

By analytically solving system (81), we obtain the two-parametric family of orbits

$$f(x,y,z)=y{x}^s=c_1,g(x,y,z)=z{x}^s=c_2,s\ne 0,-1$$

(82)

and the allowed region is $A=\frac{2x^2{(y^2+z^2)}^{1/s}}{s(s+1)}\ge$ 0.

2.

According to Plan $B_2$, an appropriate set of values is

$$k_1\ne 0,k_2\ne 0,k_3=0,k_4=1$$

(83)

This set of values of the constants $k_j,j=1,\dots ,4$ for the orbital functions $(\alpha ,\beta )$ leads to the general case $r_2,r_1\ne$ 0. According to Proposition 1, there exists a potential that produces the above family of orbits, and it is found from (27). It is

$$V(y,z)=-\frac{d_1}{2{(x^2+z^2)}^2}+d_2,d_1,d_2=const.$$

(84)

Then, by using system (5), we analytically find the two-parametric family of orbits (1). System (5) is written

$$\frac{dy}{dx}=k_1{x}^2+k_2{z}^2,\frac{dz}{dx}=\frac{z}{x}.$$

(85)

By analytically solving system (85), we obtain the two-parametric family of orbits

$$f(x,y,z)=3y-x(k_1{x}^2+k_2{z}^2)=c_1,g(x,y,z)=\frac{z}{x}$$

(86)

and the allowed region is $A=-\frac{xy}{(x^2+y^2){(y^2+z^2)}^3}\ge$ 0, which is valid only when $xy\le$ 0.

Remark 1.

The potential found in (84) istwo-dimensional, and we can easily ascertain that $V_y=0$. This means that the test particle of unit mass moving under the action of such a potential will follow a uniform motion, i.e., $\dot{y}=const.$ Thus, the orbits cannot be closed. Furthermore, the projection of this orbit on the level $xz$ is aregular curve, and it is determined by system (86).

8. Families of Straight Lines

If ${\alpha }_0$ = 0 and ${\beta }_0$ = 0, then we have to study a two-parameter family of straight lines (FSL) in 3D space. As was shown by [7], potentials that produce two-parametric families of straight lines in 3D space have to satisfy the following necessary and sufficient differential conditions:

$$\begin{array}{c}\hfill V_{xy}(V_x^2-V_y^2)-V_x{V}_y(V_{xx}-V_{yy})+V_z(V_x{V}_{yz}-V_y{V}_{xz})=0,\\ \hfill V_{xz}(V_x^2-V_z^2)-V_x{V}_z(V_{xx}-V_{zz})+V_y(V_x{V}_{yz}-V_z{V}_{xy})=0.\end{array}$$

(87)

We substitute (11) into (87), and we find that the equations in (87) are satisfied only for $p=1,2$. Thus, we have two solutions for the potential

$$V=\mathcal{U}(x+y+z)$$

(88)

and

$$V=\mathcal{U}(x^2+y^2+z^2)$$

(89)

The family of straight lines is

$$\alpha =\frac{V_y}{V_x},\beta =\frac{V_z}{V_x}$$

(90)

For the potential (88), we obtain

$$\alpha =1,\beta =1,$$

(91)

or, equivalently,

$$f(x,y,z)=y-x=c_1,g(x,y,z)=z-x=c_2.$$

(92)

For potential (89), we obtain

$$\alpha =\frac{y}{x},\beta =\frac{z}{x}$$

(93)

or, equivalently,

$$f(x,y,z)=\frac{y}{x}=c_1,g(x,y,z)=\frac{z}{x}=c_2.$$

(94)

This result was also found by [7] and verified by [12]. The potentials in (89) are of the form $V=\mathcal{U}\left(r\right)$. All the potentials of this form studied in previous sections belong to this case and produce the two-parametric family of straight lines (94) in 3D space.

9. Conclusions

The present paper gives a new idea to the reader of how we can find new solutions of the 3D inverse problem of dynamics by using the two basic equations. Here, we studied an interesting case of the 3D inverse problem of dynamics relating three-dimensional polynomial potentials of the form $V=U(x^p+y^p+z^p)$ to preassigned two-parametric families of spatial regular orbits $f(x,y,z)$ = $c_1$, $g(x,y,z)$ = $c_2$ ($c_1,c_2$ = const).

We used the two basic PDEs (6) and (8) that combine families of orbits and 3D potentials (Section 3), taking into account that at least one of $\{{\alpha }_0,{\beta }_0\}$ is different from zero. We imposed three differential conditions on the slope functions $\alpha ,\beta$ in order to obtain solutions to our problem. We focused our interest on central and polynomial potentials of the form $V(x,y,z)=\mathcal{U}(x^p+y^p+z^p)$ (p = integer). Our results were not restricted only to polynomial potentials, but we extended them to homogeneous potentials of degree m and to other known potentials from the literature. We did not obtain only mathematical results; we also found potentials with applications in many areas of physics, e.g., Galactic Dynamics. Such potentials are the following: the Newtonian and logarithmic potentials. Furthermore, an interesting case of potentials is the 3D harmonic oscillator, and many families of orbits that are compatible with it were found. Our aim was to find a suitable pair of orbits that are produced by these potentials. All the results are completely new and original.

In the present paper, we present families of orbits produced by the Newtonian potential, central and polynomial potentials and the three-dimensional harmonic oscillator. Polynomial potentials for solutions to Laplace’s equation were also studied. In each case, we determined the allowed area for the motion of the test particle. We focused our interest on the 3D harmonic oscillator, because it is widely used in many areas of physics. The two-dimensional potentials constitute a special case of potentials and were examined separately. We also studied the case of straight lines, which is a special category of orbits in 3D space.