Abstract
In this article, we introduce and study the behavior of the modules of the first two coefficients for the classes and of normalized holomorphic and bi-univalent functions that are connected with the prestarlike functions. We determine the upper bounds for the initial Taylor–Maclaurin coefficients and for the functions of each of these families, and we also point out some special cases and consequences of our main results. The study of these classes is closely connected with those of Ruscheweyh who in 1977 introduced the classes of prestarlike functions of order using a convolution operator and the proofs of our results are based on the well-known Carathédory’s inequality for the functions with real positive part in the open unit disk. Our results generalize a few of the earlier ones obtained by Li and Wang, Murugusundaramoorthy et al., Brannan and Taha, and could be useful for those that work with the geometric function theory of one-variable functions.
Keywords:
holomorphic functions; univalent functions; bi-univalent functions; convolution (Hadamard) product; prestarlike functions; coefficient estimates; Taylor–Maclaurin coefficients MSC:
30C45; 30C50
1. Introduction
We denote by the family of functions which are analytic in the open unit disk and with the following normalized form:
Let denote the subclass of of the functions that are univalent in . From the Koebe one-quarter theorem [1], all the functions have an inverse defined by
and
In addition, for every function , there exists an inverse function analytic in the domain , but it is not sure that . Therefore, if we denote by g the analytic continuation of to the unit disk , assuming that it exists, then
A function is called to be bi-univalent in if both f and are univalent in and denotes the class of normalized bi-univalent functions in . For the historical account and for many relevant examples of functions belonging to the class , see the pioneering work connected with this subject of Srivastava et al. [2], which has actually been of crucial importance for studies of bi-univalent functions in recent years. According to this article of Srivastava et al. [2], we would like to recall here some examples of functions belonging to the class , such as
Thus, the class is not empty, while the Koebe function does not belongs to .
In a large number of papers which appeared after the work of Srivastava et al. [2], the authors defined and studied the different families of the bi-univalent function class (as can be seen, for example, in [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]), but only non-sharp estimates on the initial coefficients and in the Taylor–Maclaurin expansion (1) were obtained in many of these recent papers. The problem of finding the upper bounds for the general coefficient of the power series expansion coefficients
for functions is still not completely solved for many subclasses of the bi-univalent function class (as can be seen, for example, in [11,14,15]).
For two analytic functions in , namely and , *” usually denotes the convolution (or Hadamard) product of these functions by
In [23], Ruscheweyh defined and investigated the family of prestarlike functions of order , that are the functions f with the property that is a starlike function of order in , where
Remark that the function could be written in the form
where
In addition, we note that is a decreasing function and satisfies the limit property
Next, we recall the following lemma that will be used as a main tool in the proofs of our two main results.
Lemma 1
([1,24]). (Carathéodory’s inequality) If , then
where is the class of all functions h analytic in , for which
with
2. Initial Coefficient Estimates for the Bi-Univalent Function Subclass
First, we will first define the new subclass of the bi-univalent function as follows:
Definition 1.
Remark 1.
The subclass generalizes some well-known families considered in earlier studies and which will be recalled below:
Remark 2.
We would like to emphasize that, for appropriate parameter choices, the classes are not empty. Thus, if we consider , then , and letting , it is easy to check that , and moreover, with .
A simple computation shows that the conditions (3) and (4) become
and
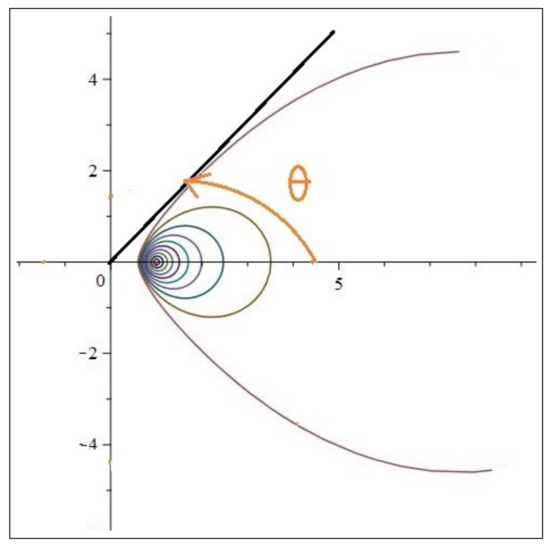
respectively. For the particular case , and , using the 2D plot of the MAPLE™ computer software, we obtain the image of the open unit disk by the function
which is the same with those by
and it is shown in Figure 1:

Figure 1.
The image of .
Since and similarly for Ψ, it follows that the domains are symmetric with respect to the real axe. Therefore, if θ is the positive argument of the tangent starting from the origin to the boundary of the domain that is , for (see also Figure 1), we obtain that the inequalities (5) and (6) are satisfied, and hence .
Concluding, for appropriate choices of the parameters γ, λ, δ, μ and α, the subclasses are not empty.
Our first main result is presented in the below theorem where we found upper bounds for the first two coefficients and of the power series expansion of the functions belonging to these classes.
Theorem 1.
Proof.
According to the conditions (3) and (4), we have
and
where , with the functions having the power series representations
and
Equating the corresponding coefficients of (8) and (9), we obtain that
and
Using (12) and (14), it follows that
and
and if we add (13) to (15), we obtain
where is given by (7).
Substituting the value of from (17) into the right-hand side of (18), a simple computation leads to
Taking the modules of both sides of (19) and using the Lemma 1 for the coefficients and , we obtain
In order to determine the upper bound of , subtracting (15) from (13), we have
Substituting the value of from (17) into (20) and using (16), we obtain
Taking the modules for both sides of (21) and once again using Lemma 1 for the coefficients , , and , it follows that
and the proof of our theorem is complete. □
Remark 3.
Note that Theorem 1 generalizes some earlier results obtained by different authors:
- (i)
- If, in this theorem, we choose , , and , then we have the following result of Li and Wang ([25] Theorem 2.2):
- (ii)
- For the special case , and , we obtain the result of Murugusundaramoorthy et al. ([27] Corollary 6), that is:Let f be given by (1) be in the class , . Then,
3. Initial Coefficient Estimates for the Bi-Univalent Function Subclass
In the next main result of the paper, we also found the upper bounds of the two initial coefficients of the power series. Thus, we define the subclass of the class of bi-univalent functions.
Definition 2.
Remark 4.
The subclass is a generalization of some well-known classes investigated previously, which we recall below:
Remark 5.
Considering the same values of the parameters γ, λ, δ, μ, and α as in the Remark 2, for the function , we obtain that the inequalities (22) and (23) become
respectively. As can be seen in Figure 1, there exists a positive value of such that the above two inequalities hold, hence
Consequently, for appropriate choices of the parameters γ, λ, δ, μ, and β, the subclasses are not empty.
Our second main result presented in the next theorem gives upper bounds for the two initial coefficients of the functions belonging to the class .
Theorem 2.
Proof.
From the relations (22) and (23), it follows that the functions exist such that
and
where , and the functions have the series expansions given by (10) and (11), respectively. Equating the corresponding coefficients of (24) and (25), we deduce
and
By adding (27) and (29), we obtain
where is given by (7). Consequently, we have
Applying the Lemma 1 for the coefficients and , it follows that
To obtain the upper bound of , by subtracting (29) from (27), we obtain
or equivalently,
Substituting the value of from (31) into (33), it follows that
Finally, applying once again the Lemma 1 for the coefficients , , , and , we obtain
Thus, we completed the proof of Theorem 2. □
Remark 6.
Theorem 2 also generalizes some previous results as follows:
- (i)
- If we choose, in this theorem, that , , and , then we obtain the result of Li and Wang ([25] Theorem 3.2) as follows:Let f be given by (1) in the class , , . Then
- (ii)
- For , and , we obtain the next result of Murugusundaramoorthy et al. ([27] Corollary 7):Let f be given by (1) in the class , , . Then
4. Conclusions
In this article, we defined two new subclasses of bi-univalent functions, that are and , with the aid of the arguments and real parts’ upper bounds, respectively. In these definitions, we used the convolution product with the function first defined in [23]. For some particular cases of parameters, the classes generalize those introduced by Li and Wang [25] and Brannan and Taha [26], while extends the classes of Li and Wang [25], and is defined as studied by Brannan and Taha [26].
The two main results give upper bounds for the first two coefficients of the power series for the functions that belong to these families. Our main results extend those of Li and Wang ([25] Theorem 2.2), Li and Wang ([25] Theorem 3.2), Murugusundaramoorthy et al. ([27] Corollary 6) and Murugusundaramoorthy et al. ([27] Corollary 7).
We would like to mention that neither of the main theorems give the best (i.e., the lowest) upper bounds for and for the functions that belong to the subclasses and . To find the best (that is the lowest, or so-called the sharp) upper bounds of these coefficients remains an interesting open question, and could motivate researchers to find other methods for this type of study.
Moreover, another open question is to find upper bounds for the general coefficients , for the functions of these new classes. Our attempts for the coefficient fail because of the very complicated expression of this coefficient, but still remains a challenging problem; maybe another approach could give a satisfactory result in this sense.
Author Contributions
Conceptualization, T.H., I.A.F., Y.A.A.-K., A.A.-H., A.K.W. and T.B.; methodology, T.H., I.A.F., Y.A.A.-K., A.A.-H., A.K.W. and T.B.; software, A.K.W. and T.B.; validation, T.H., I.A.F., Y.A.A.-K., A.A.-H., A.K.W. and T.B.; formal analysis, T.H., I.A.F., Y.A.A.-K., A.A.-H., A.K.W. and T.B.; investigation, T.H., I.A.F., Y.A.A.-K., A.A.-H., A.K.W. and T.B.; resources, T.H., I.A.F., Y.A.A.-K., A.A.-H., A.K.W. and T.B.; data curation, T.H., I.A.F., Y.A.A.-K., A.A.-H., A.K.W. and T.B.; writing—original draft preparation, A.K.W. and T.B.; writing—review and editing, A.K.W. and T.B.; visualization, A.K.W. and T.B.; supervision, T.H., I.A.F., Y.A.A.-K., A.A.-H., A.K.W. and T.B.; project administration, T.H., I.A.F., Y.A.A.-K., A.A.-H., A.K.W. and T.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Our manuscript has no associated data.
Acknowledgments
The authors are grateful to the reviewers of this article for providing valuable remarks, comments, and advice in order to improve the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Duren, P.L. Univalent Functions; Grundlehren der Mathematischen Wissenschaften, Band 259; Springer: New York, NY, USA; Berlin/Heidelberg, Germany; Tokyo, Japan, 1983. [Google Scholar]
- Srivastava, H.M.; Mishra, A.K.; Gochhayat, P. Certain subclasses of analytic and bi-univalent functions. Appl. Math. Lett. 2010, 23, 1188–1192. [Google Scholar] [CrossRef]
- Abirami, C.; Magesh, N.; Yamini, J. Initial bounds for certain classes of bi-univalent functions defined by Horadam polynomials. Abstr. Appl. Anal. 2020, 2020, 7391058. [Google Scholar] [CrossRef]
- Adegani, E.A.; Bulut, S.; Zireh, A.A. Coefficient estimates for a subclass of analytic bi-univalent functions. Bull. Korean Math. Soc. 2018, 55, 405–413. [Google Scholar]
- Güney, H.Ö.; Murugusundaramoorthy, G.; Sokół, J. Subclasses of bi-univalent functions related to shell-like curves connected with Fibonacci numbers. Acta Univ. Sapientiae Math. 2018, 10, 70–84. [Google Scholar] [CrossRef]
- Magesh, N.; Bulut, S. Chebyshev polynomial coefficient estimates for a class of analytic bi-univalent functions related to pseudo-starlike functions. Afr. Mat. 2018, 29, 203–209. [Google Scholar] [CrossRef]
- Páll-Szabó, Á.O.; Wanas, A.K. Coefficient estimates for some new classes of bi-Bazilevič functions of Ma-Minda type involving the Sălăgean integro-differential operator. Quaest. Math. 2021, 44, 495–502. [Google Scholar]
- Şeker, B. On a new subclass of bi-univalent functions defined by using Sălăgean operator. Turk. J. Math. 2018, 42, 2891–2896. [Google Scholar] [CrossRef]
- Srivastava, H.M. Operators of basic (or q-) calculus and fractional q-calculus and their applications in geometric function theory of complex analysis. Iran. J. Sci. Technol. Trans. A Sci. 2020, 44, 327–344. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Altınkaya, Ş.; Yalçin, S. Certain subclasses of bi-univalent functions associated with the Horadam polynomials. Iran. J. Sci. Technol. Trans. A Sci. 2019, 43, 1873–1879. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Eker, S.S.; Hamidi, S.G.; Jahangiri, J.M. Faber polynomial coefficient estimates for bi-univalent functions defined by the Tremblay fractional derivative operator. Bull. Iran. Math. Soc. 2018, 44, 149–157. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Gaboury, S.; Ghanim, F. Coefficient estimates for some general subclasses of analytic and bi-univalent functions. Afr. Mat. 2017, 28, 693–706. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Gaboury, S.; Ghanim, F. Coefficient estimates for a general subclass of analytic and bi-univalent functions of the Ma-Minda type. Rev. Real Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. (RACSAM) 2018, 112, 1157–1168. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Motamednezhad, A.; Adegani, E.A. Faber polynomial coefficient estimates for bi-univalent functions defined by using differential subordination and a certain fractional derivative operator. Mathematics 2020, 8, 172. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Sakar, F.M.; Güney, H.Ö. Some general coefficient estimates for a new class of analytic and bi-univalent functions defined by a linear combination. Filomat 2018, 32, 1313–1322. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Wanas, A.K.; Srivastava, R. Applications of the q-Srivastava-Attiya operator involving a certain family of bi-univalent functions associated with the Horadam polynomials. Symmetry 2021, 13, 1230. [Google Scholar] [CrossRef]
- Alshanti, W.G.; Alshanty, A.; Zraiqat, A.; Jebril, I.H.; Hammad, M.A.; Batiha, I.M. Cubature formula for double integrals based on Ostrowski type inequality. Int. J. Differ. Equ. 2022, 17, 379–387. [Google Scholar]
- Saadeh, R.; Al-Smadi, M.; Gumah, G.; Khalil, H.; Khan, R.A. Numerical investigation for solving two-point fuzzy boundary value problems by reproducing kernel approach. Appl. Math. Inf. Sci. 2016, 10, 2117–2129. [Google Scholar] [CrossRef]
- Wanas, A.K.; Cotîrlă, L.-I. Applications of (M-N)-Lucas polynomials on a certain family of bi-univalent functions. Mathematics 2022, 10, 595. [Google Scholar] [CrossRef]
- Juma, A.R.S.; Al-Fayadh, A.; Vijayalakshmi, S.P.; Sudharsan, T.V. Upper bound on the third hnkel determinant of the class of univalent functions using an operator. Afr. Mat. 2022, 33, 56. [Google Scholar] [CrossRef]
- Shahab, N.H.; Juma, A.R.S. Coefficient bounds for certain subclasses for meromorphic functions involving quasi subordination. AIP Conf. Proc. 2022, 2400, 030001. [Google Scholar]
- Amourah, A.; Alsoboh, A.; Ogilat, O.; Gharib, G.M.; Saadeh, R.; Al Soudi, M. A generalization of Gegenbauer polynomials and bi-univalent functions. Axioms 2023, 12, 128. [Google Scholar] [CrossRef]
- Ruscheweyh, S. Linear operators between classes of prestarlike functions. Comment. Math. Helv. 1977, 52, 497–509. [Google Scholar] [CrossRef]
- Carathéodory, C. Über den Variabilitätsbereich der Fourier’schen Konstanten von positiven harmonischen Funktionen. Rend. Circ. Mat. Palermo Ser. 2 1911, 32, 193–217. [Google Scholar] [CrossRef]
- Li, X.-F.; Wang, A.-P. Two new subclasses of bi-univalent functions. Int. Math. Forum 2012, 7, 1495–1504. [Google Scholar]
- Brannan, D.A.; Taha, T.S. On some classes of bi-univalent functions. Stud. Univ. Babeş-Bolyai Math. 1986, 31, 70–77. [Google Scholar]
- Murugusundaramoorthy, G.; Magesh, N.; Prameela, V. Coefficient bounds for certain subclasses of bi-univalent function. Abstr. Appl. Anal. 2013, 2013, 573017. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).