Isogeometric Schwarz Preconditioners with Generalized B-Splines for the Biharmonic Problem ^†

Abstract

We construct an overlapping additive Schwarz preconditioner for the biharmonic Dirichlet problems discretized by isogeometric analysis based on generalized B-splines (GB-splines) and analyze its optimal convergence rate bound that is cubic in the ratio between subdomains and overlap sizes. Our analysis is validated through a set of numerical experiments that illustrate good behavior of the proposed preconditioner with respect to the model parameters.

1. Introduction

Isogeometric analysis (IGA) is a novel numerical approach for solving partial differential equations (PDEs), introduced by Hughes et al. in [1], which forms a link between Computer-Aided Design (CAD) and Finite Element Analysis (FEA) technologies (see also the book [2] and the references therein). CAD systems widely employ Non-Uniform Rational B-Splines (NURBS) to define complex geometries [3]. In the IGA approach which follows an isoparametric paradigm, the NURBS basis functions that represent the CAD geometry are directly utilized in solving PDEs.

While NURBS are capable of exactly representing a wider class of geometries such as conic sections, transcendental curves such as cycloid or helices are excluded. In addition, the rational NURBS model has limits in exact differentiation and integration. To avoid these disadvantages, GB-splines describing both conic sections and transcendental geometries were introduced as a tool in the IGA framework and have further investigated in diverse fields (see, e.g., [4,5,6,7,8,9,10]).

In the present paper, our model problem is the following biharmonic Dirichlet problem, e.g., arising in the context of thin plate theories of elasticity and the Stokes problem in stream function and vorticity formulation [11,12]:

$${\Delta }^{2}u=f\mathrm{in}\Omega ,u=\frac{\partial u}{\partial \mathbf{n}}=0\mathrm{on}\partial \Omega ,$$

(1)

where $\Omega$ is a bounded and connected CAD domain in ${\mathbb{R}}^d$, $\mathbf{n}$ is the unit outward normal on the boundary $\partial \Omega$ (see [13] (Ch. 5.9) for a detailed description). For fourth-order problems, the conforming finite element space necessitates a finite-dimensional subspace of the Sobolev space $H^2(\Omega )$, implying that its basis functions belong to $C^1(\overline{\Omega })$. Due to the complexity of $C^1$-continuous piecewise polynomial elements, $H^2$-conforming elements are less used in practice for solving biharmonic equations. The nonconforming method circumvents the complicated construction of $C^1$ elements but its convergence depends on the elaborate design of the finite element space (see, for example, [13,14]). In the IGA setting, spline basis functions of degree p with high smoothness up to $C^{p-1}$ are useful when dealing with higher-order PDEs, e.g., the biharmonic equation that we consider. Additionally, thanks to [15], the biharmonic problem can be approximated using a mixed finite element method, which is beyond the scope of this paper. In this paper, particular attention is paid to the biharmonic primal formulation.

The linear systems arising from the biharmonic Dirichlet problem discretized with IGA GB-splines are highly ill-conditioned as the mesh size h decreases and polynomial degree p increases. Thus, the development of effective preconditioners for IGA GB-splines is a challenging issue (see [16], particularly for the scalar elliptic case). To our knowledge, overlapping additive Schwarz (OAS) preconditioners for IGA approximations of PDEs by GB-splines were first presented in [16]. The novelty of this paper is that in IGA methodology using GB-splines as the basis for analysis, overlapping Schwarz preconditioners can be extended to the discretization of the biharmonic equation. Theoretical analysis for our two-level overlapping preconditioner shows that the resulting preconditioned biharmonic operator satisfies a condition number bound that is scalable for an increasing number of subdomains N and is bounded by a $\left(1+\frac{H^3}{{\gamma }^3}\right)$-term, where H and $\gamma$, both of which will be defined later, are the characteristic subdomain size and an overlap parameter related to the size of the overlapping region between adjacent subdomains, respectively.

Previous works on overlapping domain decomposition methods (DDM) for IGA have concentrated on NURBS-based IGA discretizations such as overlapping additive Schwarz preconditioners (see, for instance, [17] for Galerkin IGA approximation of scalar elliptic problems, [18] for Galerkin IGA discretizations of linear elasticity systems, [19] for collocation IGA approximation of scalar elliptic equations and [20] for collocation IGA discretization of linear elasticity). Further works on NURBS-based IGA preconditioners are extended to BDDC [21,22,23,24], FETI-DP [25,26], BPX [27,28], IGA multigrid [29,30,31]. Fast solvers for NURBS-based IGA have also been studied in [32,33,34]. For the biharmonic problems, several NURBS-based IGA techniques are presented in [35,36] and NURBS-based IGA overlapping Schwarz preconditioners are analyzed in [37] (see also the references therein for DDM for finite element discretizations of biharmonic problems).

The present paper is organized as follows. In Section 2, we give a brief review of GB-splines and their fundamental properties. Section 3 introduces the proposed overlapping domain decomposition preconditioners. Several numerical results in two- and three-spatial dimensions are reported in Section 5. Finally Section 6 contains some conclusions and future directions of research.

We will adopt the following concise notation throughout the paper. Given two numbers $a,b$, we write $a\lesssim b$ when $a\le Cb$ for a generic constant C, which is independent of the knot vector $\Sigma$ and the mesh size h but depending on the spline degree p and the geometric map $\mathbf{F}$ (defined below), and we also write $a\approx b$ when $a\lesssim b$ and $b\lesssim a$.

2. GB-Splines: Definition and Basic Properties

2.1. Generalized Polynomial Spaces

In this section, we outline the definition of GB-splines and their fundamental properties, following [38] (Section 4). Throughout the paper, GB-splines are basis functions in IGA discretizations (see [7] for a detailed description).

Definition 1. 

Let $2\le p\in \mathbb{N}$ and Δ be a partition over the interval $[0,1]$,

$$\Delta :=\{0={\eta }_0<{\eta }_1<\cdots <{\eta }_{\ell +1}=1\},\ell \in \mathbb{N}.$$

(2)

A generalized polynomial space of degree p is defined as a space of the form

$${\mathbb{GP}}_p^{U,V}(\Delta ):=\langle 1,\zeta ,\cdots ,{\zeta }^{p-2},U(\zeta ),V(\zeta )\rangle ,\zeta \in [{\eta }_0,{\eta }_{\ell +1}]$$

(3)

where $U,V\in C^p[{\eta }_i,{\eta }_{i+1}]$ and $\langle D^{p-1}U,D^{p-1}V\rangle$ is an extended Tchebycheff space on $[{\eta }_i,{\eta }_{i+1}]$ for all $i=0,\dots ,\ell$.

In various kinds of spaces ${\mathbb{GP}}_p^{U,V}(\Delta )$ (see [38] for more details and also [39,40,41] for a complete description of Tchebycheff space), the popular choices for the functions $U,V$ on $[{\eta }_i,{\eta }_{i+1}]$ are

$${\mathbb{P}}_p([{\eta }_i,{\eta }_{i+1}]):=\langle 1,\zeta ,\dots ,{\zeta }^{p-2},{\zeta }^{p-1},{\zeta }^p\rangle ,$$

(4)

$${\mathbb{E}}_{p,{\alpha }_i}([{\eta }_i,{\eta }_{i+1}]):=\langle 1,\zeta ,\dots ,{\zeta }^{p-2},\exp ({\alpha }_i\zeta ),\exp (-{\alpha }_i\zeta )\rangle ,{\alpha }_i\in {\mathbb{R}}_{>0},$$

(5)

and

$${\mathbb{T}}_{p,{\alpha }_i}([{\eta }_i,{\eta }_{i+1}]):=\langle 1,\zeta ,\dots ,{\zeta }^{p-2},cos({\alpha }_i\zeta ),sin({\alpha }_i\zeta )\rangle ,0<{\alpha }_i({\eta }_{i+1}-{\eta }_i)<\pi .$$

(6)

2.2. Univariate GB-Splines

In order to follow the IGA paradigm, we consider $n,p\in \mathrm{I}\mathrm{N}$ with $p\ge 2$ and $\Sigma =\{{\xi }_1\le {\xi }_2\le \dots \le {\xi }_{n+p}\le {\xi }_{n+p+1}\}$ be a knot vector in the one-dimensional closed interval $[0,1]$ that is connected to the partition $\Delta$ defined in (2) as follows:

$$\Sigma =\{{\xi }_1,{\xi }_2,\dots ,{\xi }_{n+p+1}\}=\left(\stackrel{{\mu }_0}{\overbrace{{\eta }_0,\dots ,{\eta }_0}},\dots ,\stackrel{{\mu }_{\ell +1}}{\overbrace{{\eta }_{\ell +1},\dots ,{\eta }_{\ell +1}}}\right)$$

(7)

for some positive integers ${\mu }_0,\cdots ,{\mu }_{\ell +1}$ with ${\sum }_{i=0}^{\ell +1}{\mu }_i=n+p+1$. Moreover, in what follows, $\Sigma$ is assumed to be a p-open knot vector that interpolates at the ends of the one-dimensional parametric space $\widehat{I}:=(0,1)$, that is,

$$0={\xi }_1=\cdots ={\xi }_{p+1}<\cdots <{\xi }_{n+1}=\cdots ={\xi }_{n+p+1}=1.$$

Now, we are in a position to introduce GB-splines of degree p that are associated with a knot vector $\Sigma$ and a generalized polynomial space ${\mathbb{GP}}_p^{U,V}(\Delta )$. Both of these components are connecting to a partition $\Delta$ given in (2) (see [6,7,38,42] and references therein).

Definition 2. 

Given a partition Δ, let ${\mathbb{GP}}_p^{U,V}(\Delta )$ be a generalized polynomial space of degree $p\ge 2$, and let Σ be a knot vector that is connected to Δ as in (7). For any ${\xi }_j<{\xi }_{j+1}$, let $u_j,v_j$ be the unique functions in $\langle D^{p-1}U,D^{p-1}V\rangle$ on $[{\xi }_j,{\xi }_{j+1}]$ satisfying

$$u_j({\xi }_j)=1,u_j({\xi }_{j+1})=0,v_j({\xi }_j)=0,v_j({\xi }_{j+1})=1.$$

We set

$${\widehat{N}}_{i,1,\Sigma }^{U,V}(\zeta ):=\left\{\begin{array}{cc}{\displaystyle v_i(\zeta ),}\hfill & if{\xi }_i\le \zeta <{\xi }_{i+1},\hfill \\ {\displaystyle u_{i+1}(\zeta ),}\hfill & if{\xi }_{i+1}\le \zeta <{\xi }_{i+2},\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.,$$

(8)

and the j-th GB-spline ${\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta )$ of degree p over Σ is defined recursively using the formula

$${\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta ):={\int }_{{\xi }_j}^{\zeta }{\delta }_{j,p-1,\mathsf{\Sigma }}^{U,V}{\widehat{N}}_{j,p-1,\Sigma }^{U,V}(r)dr-{\int }_{{\xi }_{j+1}}^{\zeta }{\delta }_{j+1,p-1,\mathsf{\Sigma }}^{U,V}{\widehat{N}}_{j+1,p-1,\Sigma }^{U,V}(r)dr,$$

(9)

where

$${\delta }_{i,q,\Sigma }^{U,V}:={\left[{\int }_{{\xi }_i}^{{\xi }_{i+q+1}}{\widehat{N}}_{i,q,\Sigma }^{U,V}(r)dr\right]}^{-1},$$

(10)

and if ${\widehat{N}}_{i,q,\Sigma }^{U,V}(\zeta )=0$, then we set the following convention ${\int }_{{\xi }_i}^{\zeta }{\delta }_{i,q,\Sigma }^{U,V}{\widehat{N}}_{i,q,\Sigma }^{U,V}(r)dr:=\left\{\begin{array}{cc}1,\hfill & \zeta \ge {\xi }_{i+q+1},\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$

It is noteworthy that the recursive formula is referred to as the integral form of the Cox-de Boor algorithm, which is utilized for constructing polynomial B-splines of degree p (see [43] for a complete description). The GB-spline space is defined as the space spanned by GB-splines, namely,

$${\widehat{\mathcal{S}}}_h=\mathrm{span}\{{\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta ):1\le j\le n\}.$$

(11)

According to the definitions of U and V in (3), GB-splines ${\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta )$ with section spaces as given in (4)–(6) are commonly known as classical (polynomial) B-splines, exponential GB-splines and trigonometric GB-splines, respectively (see Figure 1 for some examples). The exponential GB-splines and trigonometric ones possess fundamental properties similar to those of the classical polynomial B-splines, see, e.g., [6,7,42] for their proofs.

Property 1. 

The GB-splines $\{{\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta ):j=1,\dots ,n\}$ of degree $p\ge 2$ over the knot vector Σ are characterized by the following properties:

1. 

Positivity:  ${\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta )>0,\zeta \in ({\xi }_j,{\xi }_{j+p+1})$.

2. 

Compact support:  if $\zeta \notin [{\xi }_j,{\xi }_{j+p+1}]$, ${\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta )=0$.

3. 

Local partition of unity:  ${\sum }_{j=m-p}^m{\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta )=1$, $\zeta \in [{\xi }_m,{\xi }_{m+1})$.

4. 

Local linear independence:  $\{{\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta ):j=m-p,\cdots ,m\}$ are linearly independent on $[{\xi }_m,{\xi }_{m+1}]$.

5. 

Smoothness:  each ${\widehat{N}}_{j,p,\Sigma }^{U,V}$ has a continuous derivative of order $p-m_i$ at the knot ${\xi }_i$, where $m_i$ is the multiplicity of ${\xi }_i$ in the knot vector $\{{\xi }_j,\dots ,{\xi }_{j+p+1}\}$.

6. 

Differentiation: The derivative of GB-splines is represented in terms of two consecutive GB-splines of a lower degree as

$$\frac{d}{d\zeta }{\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta )={\delta }_{j,p-1,\Sigma }^{U,V}{\widehat{N}}_{j,p-1,\Sigma }^{U,V}(\zeta )-{\delta }_{j+1,p-1,\Sigma }^{U,V}{\widehat{N}}_{j+1,p-1,\Sigma }^{U,V}(\zeta ).$$

Remark 1. 

A knot insertion procedure is available for GB-splines (see, e.g., [42,44,45] for more details) and thus, in an analogous way, the h-refinement obtained by knot insertion in NURBS-based IGA can be extended to IGA GB-splines. In the present paper, our theoretical work is only an h-analysis and does not cover the dependence of convergence rate on p.

It was demonstrated in [38] that GB-splines are regarded as a special instance of normalized Tchebycheff B-splines, ensuring that GB-splines possess all the properties as detailed in [46], Section 9. Of these, the most significant property for our h-analysis can be stated as follows:

Theorem 1. 

GB-splines are normalized Tchebycheffian B-splines.

Proof. 

The proof can be obtained in a similar way to ([38], Theorem 11). □

For the sake of completeness, we state some important lemmas from [46], without providing their proofs, which will play a fundamental role in demonstrating the approximation and stability of our proposed preconditioners (see Lemmas 1 and 2 below). We will make use of the dual functionals ${\lambda }_{i,p,\Sigma }^{U,V}$ (defined in ([46], Theorem 9.26)) that satisfy

$${\lambda }_{i,p,\Sigma }^{U,V}({\widehat{N}}_{j,p,\Sigma }^{U,V})={\delta }_{ij},1\le i,j\le n,$$

(12)

where ${\delta }_{ij}$ is the Kronecker delta. Furthermore, a projector on ${\widehat{\mathcal{S}}}_h$ is introduced in [46], Theorem 9.37, denoting with

$${\widehat{\Pi }}_{{\widehat{\mathcal{S}}}_h}v:=\sum _{j=1}^n({\lambda }_{j,p,\Sigma }^{U,V}v){\widehat{N}}_{j,p,\Sigma }^{U,V},\forall v\in L^2(0,1).$$

(13)

Now, we state a useful estimate of the functional ${\lambda }_{i,p,\Sigma }^{U,V}$,along with the stability and approximation properties of the quasi-interpolant ${\widehat{\Pi }}_{{\widehat{\mathcal{S}}}_h}$ (see ([46], Theorems 9.26 and 9.37) for their complete proofs).

Lemma 1. 

If $f\in L^q({\xi }_i,{\xi }_{i+p+1})$, with $1\le q\le +\infty$, then

$$|{\lambda }_{i,p,\Sigma }^{U,V}(f)|\lesssim |{\xi }_{i+p+1}-{\xi }_i{|}^{-1/q}{\parallel f\parallel }_{L^q({\xi }_i,{\xi }_{i+p+1})}.$$

(14)

Lemma 2. 

If the mesh on the parametric space $\widehat{I}$ satisfies the quasi-uniformity condition (defined later), then we have

$$\parallel \widehat{v}-{\widehat{\Pi }}_{{\widehat{\mathcal{S}}}_h}\widehat{v}{\parallel }_{L^2(\widehat{I})}+h|\widehat{v}-{\widehat{\Pi }}_{{\widehat{\mathcal{S}}}_h}\widehat{v}{|}_{H^1(\widehat{I})}+h^2|{\widehat{\Pi }}_{{\widehat{\mathcal{S}}}_h}\widehat{v}{|}_{H^2(\widehat{I})}\lesssim h^2{\left|\widehat{v}\right|}_{H^2(\widehat{I})},\forall \widehat{v}\in {\widehat{\mathcal{S}}}_h,$$

(15)

where h denotes the global mesh size of the mesh on the parametric space $\widehat{I}$.

2.3. Multivariate GB-Splines

Multidimensional GB-splines can be easily constructed using tensor products. For the sake of simplicity, we restrict our discussion to the bivariate case, noting that the construction in higher dimensions follows similarly.

Let $\widehat{\Omega }:=(0,1)\times (0,1)$ be the two-dimensional parametric space. With $d=1,2$, assuming $n_d,{\ell }_d\in \mathbb{N}$ and the degree $p_d\ge 2$, we consider the partitions ${\Delta }_d=\{0={\eta }_{d,0}<\cdots <{\eta }_{d,{\ell }_d+1}=1\}$ and their corresponding $p_d$-open knot vector ${\Sigma }_d=\{0={\xi }_{d,1},\dots ,{\xi }_{d,n_d+p_d+1}=1\}$. Additionally, section spaces ${\mathbb{GP}}_{p_d}^{U_d,V_d}$ can be appropriately selected according to PDEs problem of interest. We first introduce the set of multi-indices as follows:

• $\mathit{p}=(p_1,p_2)$;
• $\mathbf{\zeta }=({\zeta }_1,{\zeta }_2)$;
• $\mathsf{\Sigma }=\{{\Sigma }_1,{\Sigma }_2\}$;
• $\mathit{U}=\{U_1,U_2\}$ and $\mathit{V}=\{V_1,V_2\}$;
• $\mathit{J}=\{\mathit{j}=(j_1,j_2):1\le j_d\le n_d,d=1,2\}$.

Then, we introduce the set of bivariate GB-splines

$$\{{\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta }):={\widehat{N}}_{j_1,p_1,{\Sigma }_1}^{U_1,V_1}({\zeta }_1){\widehat{N}}_{j_2,p_2,{\Sigma }_2}^{U_2,V_2}({\zeta }_2),\forall \mathit{j}\in \mathit{J}\}.$$

The GB-spline space on $\widehat{\Omega }$ is defined as the space spanned by bivariate GB-splines

$${\widehat{\mathcal{S}}}_h:=\mathrm{span}\{{\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta }),\mathit{j}\in \mathit{J}\}.$$

In the context of IGA, the physical domain $\Omega$ can be described by means of a global geometric map $\mathbf{F}:\widehat{\Omega }\to \Omega$, which is given by

$$\mathbf{F}(\widehat{\mathit{x}})=\sum _{\mathit{j}\in \mathit{J}}{\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta }){\mathit{C}}_{\mathit{j}},{\mathit{C}}_{\mathit{j}}\in {\mathbb{R}}^d,\widehat{\mathit{x}}\in \widehat{\Omega }$$

where ${\mathit{C}}_{\mathit{j}}$ are the generalized control points. In accordance with the isoparametric concept, we define the space ${\widehat{V}}_h$ in the parameter domain $\widehat{\Omega }$ as follows:

$${\widehat{V}}_h:=\mathrm{span}\{{\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta }),\mathit{j}=(j_1,j_2)\in \mathit{J}\mathrm{with}3\le j_d\le n_d-2,d=1,2\},$$

(16)

and the space $V_h$ in the physical domain $\Omega$

$$V_h:=\mathrm{span}\{N_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta }):={\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta })\circ {\mathbf{F}}^{-1},\mathit{j}=(j_1,j_2)\in \mathit{J}\mathrm{with}3\le j_d\le n_d-2,d=1,2\}.$$

(17)

where the homogeneous Dirichlet boundary condition that we consider leads to the elimination of the first and last two functions in each coordinate. For simplicity in the presentation, we consider only the homogeneous Dirichlet boundary conditions throughout this paper. However, it is worth noting that a similar approach can be extended to accommodate different types of boundary conditions (see Section 6 for a explanation about handling various boundary conditions).

Observing that in multi-indices knot vector $\mathsf{\Sigma }$ defined above, two knot vectors ${\Sigma }_1=\{0={\xi }_{1,1},\dots ,{\xi }_{1,n_1+p_1+1}=1\}$ and ${\Sigma }_2=\{0={\xi }_{2,1},\dots ,{\xi }_{2,n_2+p_2+1}=1\}$ result in a mesh of rectangular elements in the parametric space, those mesh elements are mapped via the geometric map $\mathbf{F}$ to elements in the physical space. The physical mesh on $\Omega$ is therefore

$${\mathcal{T}}_h=\{\mathbf{F}(({\xi }_{1,i},{\xi }_{1,i+1})\times ({\xi }_{2,j},{\xi }_{2,j+1}),\mathrm{with}i=1,\dots ,n_1+p_1,j=1,\dots ,n_2+p_2\},$$

where the empty elements are excluded.

The discrete formulation of the model problem (1) becomes then:

• Find $u\in V_h$ such that

  $$a(u,v)={\int }_{\Omega }fvdx,\forall v\in V_h$$

  (18)

  with bilinear form $a(u,v):={\int }_{\Omega }\Delta u\Delta vdx$.

3. The Overlapping Schwarz Preconditioners

We now present overlapping additive Schwarz (OAS) preconditioners for the IGA discrete problem (18) by using GB-splines, following [16,17] and the notation therein.

3.1. Subdomains and Subspace Decomposition

The subdomains and subspace decomposition are first built for the IGA GB-splines space in one-dimensional parameter space and then are extended to the physical domain of interest through a geometrical mapping $\mathbf{F}$.

Given a partition $\Delta$ to which the knot vector $\Sigma =\{{\xi }_1=0,\dots ,{\xi }_{n+p+1}=1\}$ is connected (as described in the previous section), we can choose a subset $\{0={\xi }_{i_1}<{\xi }_{i_2}<\cdots <{\xi }_{i_N}<{\xi }_{i_{N+1}}=1\}$ consisting of interface knots in the closure of the parametric space $\overline{\left(\widehat{I}\right)}=[0,1]$. We can obtain a decomposition of $\overline{\left(\widehat{I}\right)}$ by selecting a suitable subset of interface knots, that is,

$$\overline{\left(\widehat{I}\right)}=[0,1]=\overline{\left(\bigcup _{k=1,..,N}{\widehat{I}}_k\right)},\mathrm{where}{\widehat{I}}_k=({\xi }_{i_k},{\xi }_{i_{k+1}}),$$

into N sub-intervals ${\widehat{I}}_k$ whose diameter $\mathrm{diam}({\widehat{I}}_k),1\le k\le N$, is assumed to have a similar characteristic diameter H. With each interface knot ${\xi }_{i_k},2\le k\le N$, we are able to associate an index $s_k\in \{3,4,\dots ,n-2\}$, which is strictly increasing with respect to k and satisfies the inequality $s_k<i_k<s_k+p+1$. From this choice of $s_k$ and Property 1, it follows that the GB-spline function ${\widehat{N}}_{s_k,p,\Sigma }^{U,V}$ has support that intersects both ${\widehat{I}}_{k-1}$ and ${\widehat{I}}_k$. Moreover, the construction of the basis function ${\widehat{N}}_{s_k,p,\Sigma }^{U,V}$ guarantees that there exists at least one such $s_k$, even if it is not unique.

An overlapping decomposition of $\widehat{I}$ can then be formulated as follows. The overlap index, denoted by $r\in \mathbb{N}$, represents the number of GB basis functions shared by adjacent subdomains that are defined as

$${\widehat{V}}_k:=\mathrm{span}\{{\widehat{N}}_{j,p,\Sigma }^{U,V}(\zeta ),s_k-r\le j\le s_{k+1}+r\}k=1,2,..,N,$$

(19)

with the exception that $3\le j\le s_2+r$ for the space ${\widehat{V}}_1$ and $s_N-r\le j\le n-2$ for the space ${\widehat{V}}_N$.

These subspaces constitute an overlapping decomposition of the GB-spline space ${\widehat{V}}_h$ on one-dimensional parameter domain $\widehat{I}$. For example, for the cubic degree case with maximum continuity $C^2$, $r=0$ represents the minimal overlap where only one common GB basis function is shared between adjacent subspaces, while more general $2r+1$ indicates the number of GB basis functions in common among neighboring local subspaces. Moreover, it is necessary to introduce the overlap parameter (that will be used in the following analysis)

$$\gamma :=h(2r+2),$$

(20)

which is connected to the width $\delta$ of the overlapping region in OAS approach for classical FEM. Additionally, the definitions of the extended subdomains ${\widehat{I}}_k^{\prime }$ and the further extended subdomains ${\widehat{I}}_k^{″}$ are provided as follows:

$${\widehat{I}}_k^{\prime }=\bigcup _{{\widehat{N}}_{j,p,\Sigma }^{U,V}\in {\widehat{V}}_k}\mathrm{supp}({\widehat{N}}_{j,p,\Sigma }^{U,V})=({\xi }_{s_k-r},{\xi }_{s_{k+1}+r+p+1}),$$

(21)

and

$${\widehat{I}}_k^{″}=\bigcup _{\mathrm{supp}({\widehat{N}}_{j,p,\Sigma }^{U,V})\cap {\widehat{I}}_k^{\prime }\ne \varnothing }\mathrm{supp}({\widehat{N}}_{j,p,\Sigma }^{U,V}),$$

(22)

respectively, except for ${\widehat{I}}_1^{\prime }$, ${\widehat{I}}_N^{\prime }$, ${\widehat{I}}_1^{″}$ and ${\widehat{I}}_N^{″}$.

To define a coarse space, we introduce a subpartition ${\Delta }_0$ of the partition $\Delta$ from Section 2.1 and a p-open coarse knot vector ${\Sigma }_0$ related to the subpartition ${\Delta }_0$, both of which satisfy the following:

$${\Delta }_0:=\{0={\eta }_0^0<\cdots <{\eta }_{{\ell }_0+1}^0=1\}\subset \Delta ,\mathrm{and}{\mathbb{GP}}_p^{U,V}({\Delta }_0)\subset {\mathbb{GP}}_p^{U,V}(\Delta ),$$

and

$${\Sigma }_0:=\{0={\xi }_1^0,\dots ,{\xi }_{N_c+p+1}^0=1\}=\{{\xi }_1,{\xi }_2,\dots ,{\xi }_p,{\xi }_{i_1},{\xi }_{i_2},{\xi }_{i_3},\dots ,{\xi }_{i_N},{\xi }_{i_N+1},{\xi }_{i_N+2}\dots ,{\xi }_{i_N+p+1}\}$$

corresponds to a coarse mesh determined by the subdomains ${\widehat{I}}_k=({\xi }_{i_k},{\xi }_{i_{k+1}})$.

Remark 2. 

For the following analysis, it is necessary for the coarse knot vector ${\Sigma }_0$ to satisfy Assumption 1, which is defined below. Therefore, we assume that the distance between neighboring distinct knots in ${\Sigma }_0$ is of characteristic order H, that is the characteristic diameter defined above.

We can now proceed to define the coarse spline space as

$${\widehat{V}}_0:={\widehat{\mathcal{S}}}_H=\mathrm{span}\{{\widehat{N}}_{j,p,{\Sigma }_0}^{U,V}(\zeta ),j=3,\dots ,N_c-2\},$$

which has the same degree p of ${\widehat{V}}_h$ so that it is a subspace of ${\widehat{V}}_h$. It is noted that the first and last two basis functions are excluded due to the boundary condition under consideration in this paper. Additionally, to obtain a smaller coarse space ${\widehat{V}}_0$, all the internal knots are repeated only once.

In the case of higher dimensions, we can extend the approach by using a tensor product. For instance, in the 2D case, we can define subdomains, overlapping subdomains, and extended supports as follows:

$$\begin{array}{cc}& {\widehat{I}}_{1,k}:=({\xi }_{1,i_k},{\xi }_{1,i_{k+1}}),{\widehat{I}}_{2,l}:=({\xi }_{2,j_l},{\xi }_{2,j_{l+1}}),\hfill \\ & {\widehat{\Omega }}_{kl}:={\widehat{I}}_{1,k}\times {\widehat{I}}_{2,l}{\widehat{\Omega }}_{kl}^{\prime }:={\widehat{I}}_{1,k}^{\prime }\times {\widehat{I}}_{2,l}^{\prime },{\widehat{\Omega }}_{kl}^{″}:={\widehat{I}}_{1,k}^{″}\times {\widehat{I}}_{2,l}^{″},\hfill \end{array}$$

for $1\le k\le N$ and $1\le l\le M$. Next, we derive the indices ${\{s_k\}}_{k=2}^N$ associated to ${\{{\xi }_{1,i_k}\}}_{k=2}^N$ and the indices ${\{{\overline{s}}_l\}}_{l=2}^M$ associated to ${\{{\xi }_{2,j_l}\}}_{l=2}^M$ in a similar manner to the univariate case. Then, to obtain the local and coarse subspaces, we follow the below procedure:

$$\begin{array}{ccc}\hfill {\widehat{V}}_{kl}& =& \mathrm{span}\{{\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta }),s_k-r\le j_1\le s_{k+1}+r,{\overline{s}}_l-r\le j_2\le {\overline{s}}_{l+1}+r\},\hfill \\ \hfill {\widehat{V}}_0& =& \mathrm{span}\{{\widehat{N}}_{{\mathit{j}}_0,\mathit{p},{\mathsf{\Sigma }}_{\mathbf{0}}}^{\mathit{U},\mathit{V}}(\mathbf{\zeta }):={\widehat{N}}_{j_{0,1},p_1,{\Sigma }_{0,1}}^{U_1,V_1}({\zeta }_1){\widehat{N}}_{j_{0,2},p_2,{\Sigma }_{0,2}}^{U_2,V_2}({\zeta }_2),{\mathit{j}}_0=(j_{0,1},j_{0,2}),\hfill \\ & & 3\le j_{0,1}\le N_c-2,3\le j_{0,2}\le M_c-2\},\hfill \end{array}$$

respectively except for boundary subdomains. Here, ${\widehat{N}}_{{\mathit{j}}_0,\mathit{p},{\mathsf{\Sigma }}_{\mathbf{0}}}^{\mathit{U},\mathit{V}}(\mathbf{\zeta })$ denote the coarse GB-spline functions that correspond to ${\mathbb{GP}}_p^{U,V}({\Delta }_0)$ and ${\mathsf{\Sigma }}_{\mathbf{0}}$ as previously defined. By the push-forward, these subspaces can be transformed to the GB-spline space $V_h$ in the physical domain $\Omega$ of interest. Therefore, except for the boundary subdomains, the local subspaces and the coarse space are expressed as follows:

$$\begin{array}{ccc}\hfill V_{kl}& =& \mathrm{span}\{{\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta })\circ {\mathbf{F}}^{-1},s_k-r\le j_1\le s_{k+1}+r,{\overline{s}}_l-r\le j_2\le {\overline{s}}_{l+1}+r\},\hfill \\ \hfill V_0& =& \mathrm{span}\{{\widehat{N}}_{{\mathit{j}}_0,\mathit{p},{\mathsf{\Sigma }}_{\mathbf{0}}}^{\mathit{U},\mathit{V}}(\mathbf{\zeta })\circ {\mathbf{F}}^{-1},j_{0,1}=3,\dots ,N_c-2,j_{0,2}=3,\dots ,M_c-2\}.\hfill \end{array}$$

The subdomains in physical space correspond to the images of the subdomains in parameter space:

$${\Omega }_{kl}=\mathbf{F}({\widehat{\Omega }}_{kl}),{\Omega }_{kl}^{\prime }=\mathbf{F}({\widehat{\Omega }}_{kl}^{\prime }),{\Omega }_{kl}^{″}=\mathbf{F}({\widehat{\Omega }}_{kl}^{″}).$$

In order to estimate the condition number, we require the following two assumptions concerning the mesh and subdivision:

Assumption 1. 

The parametric mesh in each extended subdomain ${\widehat{\Omega }}_{kl}^{″}$ has the property of quasi-uniformity, which implies that there exists a positive real number h such that $h\approx diam\left({\widehat{\Omega }}_{kl}^{″}\right)$ for all subdomains ${\widehat{\Omega }}_{kl}^{″}$.

Assumption 2. 

The overlap index r remains bounded, independently of both the mesh size and the polynomial degree.

It is worth noting that our analysis relies on the local quasi-uniformity assumption regarding the knot vector, which is a conventional assumption in both mathematical isogeometric literature (see, e.g., [17]) and finite element literature (see, e.g., [47]). Assumption 2 allows us to consider the case of practical significance, namely, when small overlap leads to optimal or close-to-optimal condition numbers, see, e.g., [48].

The discrete GB-spline space $V_h$ can be expressed as a sum of coarse and local spaces using the local and coarse embedding operators ${\mathbf{I}}_{kl}:V_{kl}\to V_h$, $k=1,..,N$, $l=1,..,M$ and ${\mathbf{I}}_0:V_0\to V_h$. Specifically, the decomposition is given by:

$$V_h={\mathbf{I}}_0{V}_0+\sum _{k,l}{\mathbf{I}}_{kl}{V}_{kl}.$$

Additionally, we define the local projections ${\tilde{\mathbf{T}}}_{kl}:V_h\to V_{kl}$ and the coarse projection ${\tilde{\mathbf{T}}}_0:V_h\to V_0$ as follows:

$$a({\tilde{\mathbf{T}}}_{kl}\mathit{u},\mathit{v})=a(\mathit{u},{\mathbf{I}}_{kl}\mathit{v})\forall \mathit{v}\in V_{kl},a({\tilde{\mathbf{T}}}_0\mathit{u},\mathit{v})=a(\mathit{u},{\mathbf{I}}_0\mathit{v})\forall \mathit{v}\in V_0,$$

and ${\mathbf{T}}_{kl}={\mathbf{I}}_{kl}{\tilde{\mathbf{T}}}_{kl}$ and ${\mathbf{T}}_0={\mathbf{I}}_0{\tilde{\mathbf{T}}}_0$. Then, our proposed OAS operator ${\mathbf{T}}_{OAS}$ can be viewed as either the one-level version with only local problems or the two-level version with both coarse and local problems:

$${\mathbf{T}}_{OAS}={\mathbf{T}}_{OAS(1)}:=\sum _{k=1}^N\sum _{l=1}^M{\mathbf{T}}_{kl},{\mathbf{T}}_{OAS}={\mathbf{T}}_{OAS(2)}:={\mathbf{T}}_0+\sum _{k=1}^N\sum _{l=1}^M{\mathbf{T}}_{kl}.$$

(23)

The matrix form of the OAS operator ${\mathbf{T}}_{OAS}$ can be written as

$${\mathbf{T}}_{OAS}={\mathbf{B}}_{OAS}\mathcal{A}$$

where $\mathcal{A}$ is the stiffness matrix associated with the discrete problem (18) and the respective OAS preconditioners ${\mathbf{B}}_{OAS}$ are

$$\begin{array}{cc}\hfill {\mathbf{B}}_{OAS}={\mathbf{B}}_{OAS(1)}& :=\sum _{k=1}^N\sum _{l=1}^M{R}_{kl}^T{A}_{kl}^{-1}{R}_{kl},\hfill \\ \hfill {\mathbf{B}}_{OAS}={\mathbf{B}}_{OAS(2)}& :=R_0^T{A}_0^{-1}{R}_0+\sum _{k=1}^N\sum _{l=1}^M{R}_{kl}^T{A}_{kl}^{-1}{R}_{kl}.\hfill \end{array}$$

(24)

Here, local restriction matrices $R_{kl}:V_h\to V_{kl}$ are defined as the transpose of the natural embedding matrices $R_{kl}^T:V_{kl}\to V_h$, $A_{kl}$ are the local stiffness matrices restricted to the subspace $V_{kl}$, the matrix $R_0^T$ corresponds to the interpolation from the coarse space $V_0$ to the GB-spline space $V_h$ and $A_0$ is the coarse stiffness matrix associated with the coarse space $V_0$.

In the iterative solution of the discrete system $\mathcal{A}\mathbf{u}=\mathbf{f}$, the preconditioner ${\mathbf{B}}_{OAS}$ can be interpreted as a technique for replacing the original system with a preconditioned system,

$${\mathbf{T}}_{OAS}\mathbf{u}=\mathbf{g},$$

which a Krylov subspace method with $\mathbf{g}={\mathbf{B}}_{OAS}\mathbf{f}$ can expedite.

4. A Condition Number Estimate

In the present work, our main contribution is the proof of a condition number bound for the resulting preconditioned system ${\mathbf{T}}_{OAS}$.

Theorem 2. 

If Assumptions 1 and 2 hold, then the condition number bound of the two-level additive Schwarz preconditioned operator ${\mathbf{T}}_{OAS(2)}$, defined in (23) for the isogeometric biharmonic operator, is given by

$${\kappa }_2({\mathbf{T}}_{OAS(2)})\le C\left(1+\frac{H^3}{{\gamma }^3}\right),$$

(25)

where $\gamma =h(2r+2)$ denotes the overlap parameter in (20) and C is a constant independent of $h,H,N,\gamma$ but dependent on $p,k$.

Proof. 

The proof is based on [37], following the identical approach as in ([37], Theorem 4.1) through the utilization of Lemmas 1 and 2 related to the dual functional (12) and the quasi-interpolant (13) on GB-splines. □

In the next section, numerical performance are investigated not only on the parametric space $\widehat{\Omega }$ but also on the physical space $\Omega$ where the geometrical map $\mathbf{F}$ is well-behaved.

5. Numerical Results

In this section, we provide numerical results to validate the convergence analysis of our 2-level overlapping Schwarz preconditioners (24) for solving the biharmonic Equation (1) over two-dimensional and three-dimensional domains.

Example 1. 

The first example involves the biharmonic problem in the 2D unit square:

$$\begin{array}{ccc}\hfill {\Delta }^{2}u& =& fin\widehat{\Omega }={(0,1)}^2,\hfill \\ \hfill u& =& 0on\partial \widehat{\Omega },\hfill \\ \hfill \frac{\partial u}{\partial \mathbf{n}}& =& 0on\partial \widehat{\Omega },\hfill \end{array}$$

where f is obtained from the exact solution $u(x,y)=100x^2{y}^2{(x-1)}^2{(y-1)}^2$. This first problem will be solved by using the GB-splines space ${\widehat{V}}_h=span\{{\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta })\}$ where the bivariate GB-spline ${\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta })$ is obtained from the exponential GB-splines ${\widehat{N}}_{j_d,p_d,{\Sigma }_d}^{U_d,V_d}({\zeta }_d),$$d=1,2$ of degree p associated with a knot vector ${\Sigma }_d$ and a generalized polynomial space ${\mathbb{E}}_{p,{\alpha }_i}([{\eta }_i,{\eta }_{i+1}])$ with ${\alpha }_i=10$.

Example 2. 

The second test problem in a quarter of an annulus is as follows:

$$\begin{array}{ccc}\hfill {\Delta }^{2}u& =& fin\Omega :=\{(x,y)|1<x^2+y^2<4,x>0,y>0\},\hfill \\ \hfill u& =& 0on\partial \Omega ,\hfill \\ \hfill \frac{\partial u}{\partial \mathbf{n}}& =& 0on\partial \Omega ,\hfill \end{array}$$

where f is determined by the exact solution $u=x^2{y}^2{(x^2+y^2-1)}^2{(x^2+y^2-4)}^2$. The second biharmonic problem on the deformed domain will be discretized by the GB-splines space $V_h=span\{{\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta })\circ {\mathbf{F}}^{-1}\}$ where the bivariate GB-spline ${\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta })$ is obtained from the trigonometric GB-splines ${\widehat{N}}_{j_d,p_d,{\Sigma }_d}^{U_d,V_d}({\zeta }_d),d=1,2$ of degree p associated with a knot vector ${\Sigma }_d$ and a generalized polynomial space ${\mathbb{T}}_{p,{\alpha }_i}([{\eta }_i,{\eta }_{i+1}])$ with ${\alpha }_i=\frac{\pi }{2}$.

Example 3. 

The 3D biharmonic problem in 3D cube under consideration reads as follows:

$$\begin{array}{ccc}\hfill {\Delta }^{2}u& =& fin\widehat{\Omega }={(0,1)}^3,\hfill \\ \hfill u& =& 0on\partial \widehat{\Omega },\hfill \\ \hfill \frac{\partial u}{\partial \mathbf{n}}& =& 0on\partial \widehat{\Omega },\hfill \end{array}$$

where f is obtained from the exact solution $u(x,y,z)=(1-cos(2\pi x))(1-cos(2\pi y))(1-cos(2\pi z))$. This 3D biharmonic problem is based on the GB-splines space ${\widehat{V}}_h=span\{{\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta })\}$ where the bivariate GB-spline ${\widehat{N}}_{\mathit{j},\mathit{p},\mathsf{\Sigma }}^{\mathit{U},\mathit{V}}(\mathbf{\zeta })$ is obtained from the exponential GB-splines ${\widehat{N}}_{j_d,p_d,{\Sigma }_d}^{U_d,V_d}({\zeta }_d),d=1,2,3$ of degree p associated with a knot vector ${\Sigma }_d$ and a generalized polynomial space ${\mathbb{E}}_{p,{\alpha }_i}([{\eta }_i,{\eta }_{i+1}])$ with ${\alpha }_i=10$.

Along with mesh size h, polynomial degree p, regularity k and the overlap index r, isogeometric GB-splines discretize these 2D and 3D biharmonic problems by using the MATLAB isogeometric library GeoPDEs [49,50] (see also [51] for a MATLAB library recently introduced for the construction of Tchebycheff B-splines). To run the tests, we used a Samsung Notebook 9 (900X3L) laptop with two Intel(R) Core(TM) i7-6500U @2.50GHz processors and 8.00GiB of RAM memory. As mentioned in Section 3.1, we recall that the geometrical domains $\widehat{\Omega }$ and $\Omega$ are decomposed into N overlapping subdomains of characteristic order H and overlap index r.

The biharmonic problem resulting from the IGA Galerkin discretization using GB-splines is tackled using the preconditioned conjugate gradient (PCG) technique with one-level (OAS(1)) and two-level (OAS(2)) overlapping additive Schwarz preconditioners (24), starting from an initial guess of zero and employing as stopping criterion a ${10}^{-6}$ reduction of the relative residual.

5.1. Two-Dimensional Tests: OAS(2) Scalability in N and Optimality in $H/\gamma$

The condition numbers ${\kappa }_2({\mathbf{T}}_{OAS})$ and the iteration counts it. of the proposed OAS(1) and OAS(2) preconditioners are reported in

Table 1. OAS preconditioners for biharmonic problems using IGA based on GB-splines: condition number ${\kappa }_2$ of the preconditioned operator and PCG iteration counts (it.) in brackets as a function of the number of subdomains N and mesh size $1/h$ for one-level (upper table) and two-level (lower table) OAS preconditioners.

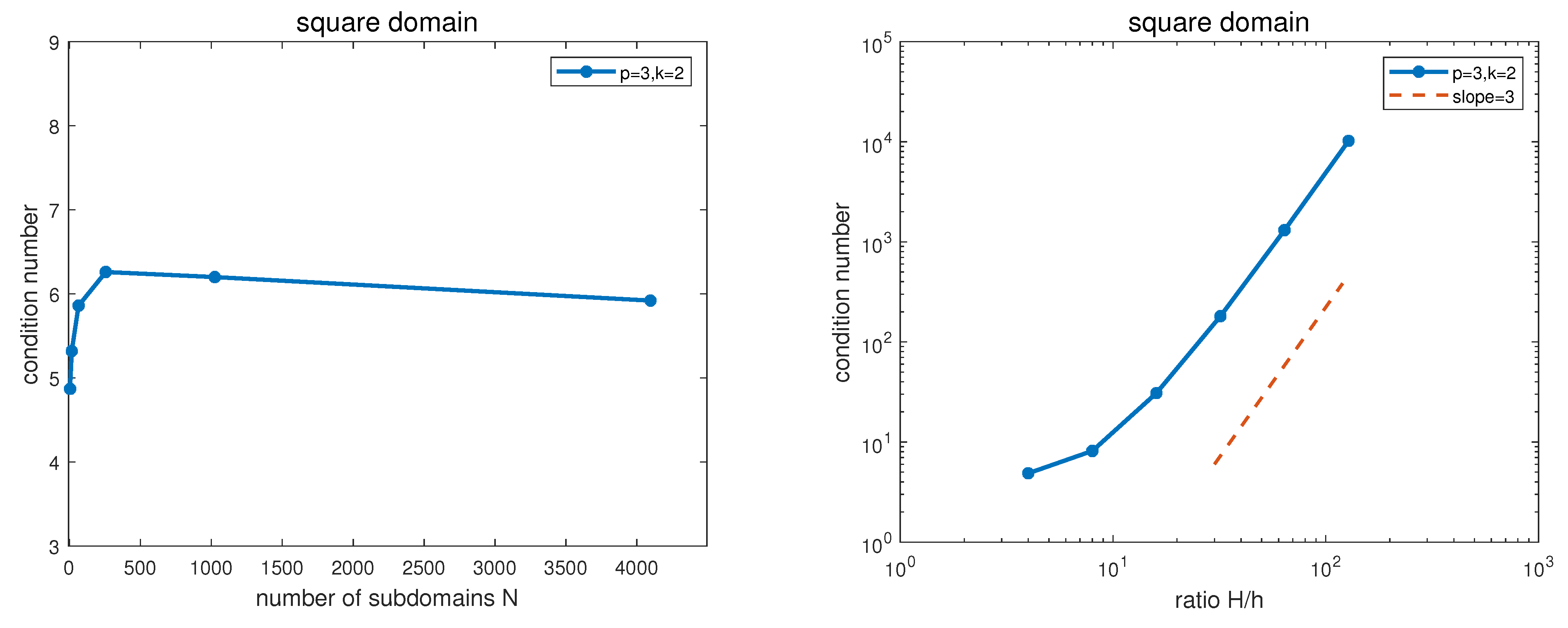
OAS(1) Preconditioners with $r=0$, $p=3,k=2$ GB-Splines, 2D Reference Square Domain
	$1/h$ = 8	$1/h$ = 16	$1/h$ = 32	$1/h$ = 64	$1/h$ = 128	$1/h$ = 256
N	${\kappa }_2$ (it.)	${\kappa }_2$ (it.)	${\kappa }_2$ (it.)	${\kappa }_2$ (it.)	${\kappa }_2$ (it.)	${\kappa }_2$ (it.)
$2\times 2$	1.21 $\times {10}^1$ (9)	5.86 $\times {10}^1$ (12)	3.80 $\times {10}^2$ (17)	2.84 $\times {10}^3$ (27)	2.23 $\times {10}^4$ (51)	1.78 $\times {10}^5$ (99)
$4\times 4$		8.50 $\times {10}^1$ (17)	5.88 $\times {10}^2$ (28)	4.46 $\times {10}^3$ (50)	3.51 $\times {10}^4$ (96)	2.79 $\times {10}^5$ (195)
$8\times 8$			1.16 $\times {10}^3$ (36)	8.86 $\times {10}^3$ (72)	6.97 $\times {10}^4$ (155)	5.55 $\times {10}^5$ (341)
$16\times 16$				1.78 $\times {10}^4$ (96)	1.40 $\times {10}^5$ (225)	1.11 $\times {10}^6$ (534)
$32\times 32$					2.82 $\times {10}^5$ (305)	2.23 $\times {10}^6$ (764)
$64\times 64$						4.51 $\times {10}^6$ (1077)
OAS(2) preconditioners with $r=0$, $p=3,k=2$ GB-splines, 2D reference square domain
	$1/h$ = 8	$1/h$ = 16	$1/h$ = 32	$1/h$ = 64	$1/h$ = 128	$1/h$ = 256
N	${\kappa }_2$ (it.)	${\kappa }_2$ (it.)	${\kappa }_2$ (it.)	${\kappa }_2$ (it.)	${\kappa }_2$ (it.)	${\kappa }_2$ (it.)
$2\times 2$	4.87 (8)	8.15 (12)	3.08 $\times {10}^1$ (16)	1.81 $\times {10}^2$ (25)	1.31 $\times {10}^3$ (47)	1.02 $\times {10}^4$ (93)
$4\times 4$		5.32 (14)	1.36 $\times {10}^1$ (20)	6.25 $\times {10}^1$ (36)	4.06 $\times {10}^2$ (75)	3.06 $\times {10}^3$ (163)
$8\times 8$			5.86 (16)	1.96 $\times {10}^1$ (26)	1.01 $\times {10}^2$ (53)	6.86 $\times {10}^2$ (138)
$16\times 16$				6.26 (17)	2.39 $\times {10}^1$ (29)	1.29 $\times {10}^2$ (66)
$32\times 32$					6.20 (16)	2.48 $\times {10}^1$ (30)
$64\times 64$						5.92 (15)

as a function of the number of subdomains N and the mesh size $1/h$. The numerical test is performed on the two-dimensional square domain with fixed spline parameters $p=3$ and $k=2$ and overlap index $r=0$. As indicated by the findings in the upper part of Table 1, the OAS(1) preconditioner, excluding the coarse problem, has condition numbers increasing with N along the diagonal. In other words, scalability can only be accomplished by including a coarse component.

Table 1,

Table 2. OAS preconditioner in 2D deformed and reference domains: condition number ${\kappa }_2(T_{OAS})$ and iteration counts it. as a function of the number of subdomains N and mesh size $1/h$, $r=0$ for non-preconditioned system and 2-level OAS preconditioner.

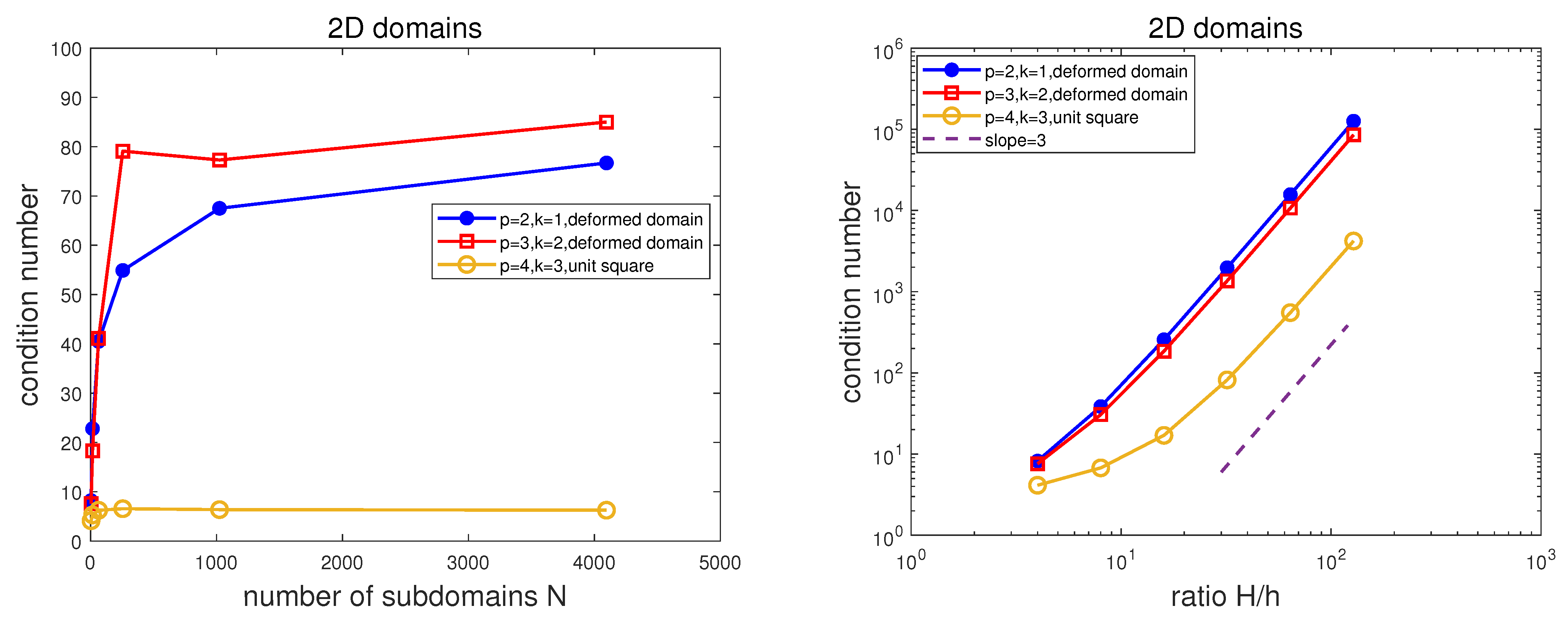
OAS prec. with $p=2,k=1,r=0$, 2D deformed domain
		$1/h$ = 8		$1/h$ = 16		$1/h$ = 32		$1/h$ = 64		$1/h$ = 128		$1/h$ = 256
	N	${\kappa }_2$	it.	${\kappa }_2$	it.	${\kappa }_2$	it.	${\kappa }_2$	it.	${\kappa }_2$	it.	${\kappa }_2$	it.
non-prec.		1.09 $\times {10}^2$	19	2.02 $\times {10}^3$	105	3.53 $\times {10}^4$	460	5.96 $\times {10}^5$	1950	9.86 $\times {10}^6$	8175	1.61 $\times {10}^8$	33,502
2-level OAS	$2\times 2$	8.21	11	3.85 $\times {10}^1$	18	2.56 $\times {10}^2$	33	1.97 $\times {10}^3$	62	1.57 $\times {10}^4$	125	1.26 $\times {10}^5$	257
	$4\times 4$			2.28 $\times {10}^1$	24	1.56 $\times {10}^2$	50	1.22 $\times {10}^3$	123	9.84 $\times {10}^3$	315	7.96 $\times {10}^4$	723
	$8\times 8$					4.05 $\times {10}^1$	33	2.97 $\times {10}^2$	79	2.41 $\times {10}^3$	228	1.97 $\times {10}^4$	645
	$16\times 16$							5.49 $\times {10}^1$	41	4.07 $\times {10}^2$	118	3.34 $\times {10}^3$	330
	$32\times 32$									6.75 $\times {10}^1$	48	5.02 $\times {10}^2$	133
	$64\times 64$											7.67 $\times {10}^1$	53
OAS prec. with $p=3,k=2,r=0$, 2D deformed domain
non-prec.		5.17 $\times {10}^1$	22	8.20 $\times {10}^2$	78	1.33 $\times {10}^4$	286	2.16 $\times {10}^5$	1159	3.49 $\times {10}^6$	4854	5.61 $\times {10}^7$	19,713
2-level OAS	$2\times 2$	7.59	13	3.06 $\times {10}^1$	18	1.85 $\times {10}^2$	33	1.36 $\times {10}^3$	65	1.07 $\times {10}^4$	138	8.54 $\times {10}^4$	313
	$4\times 4$			1.83 $\times {10}^1$	23	9.86 $\times {10}^1$	42	6.97 $\times {10}^2$	95	5.41 $\times {10}^3$	255	4.30 $\times {10}^4$	707
	$8\times 8$					4.11 $\times {10}^1$	32	2.49 $\times {10}^2$	69	1.95 $\times {10}^3$	177	1.54 $\times {10}^4$	509
	$16\times 16$							7.91 $\times {10}^1$	41	3.66 $\times {10}^2$	80	4.08 $\times {10}^3$	258
	$32\times 32$									7.73 $\times {10}^1$	42	5.15 $\times {10}^2$	91
	$64\times 64$											8.50 $\times {10}^1$	43
OAS prec. with $p=4,k=3,r=0$, 2D reference domain (unit square)
non-prec.		2.77 $\times {10}^1$	10	3.81 $\times {10}^2$	27	5.88 $\times {10}^3$	66	9.32 $\times {10}^4$	211	1.49 $\times {10}^6$	772	2.38 $\times {10}^7$	6202
2-level OAS	$2\times 2$	4.13	8	6.76	11	1.70 $\times {10}^1$	14	8.19 $\times {10}^1$	21	5.52 $\times {10}^2$	36	4.21 $\times {10}^3$	116
	$4\times 4$			5.30	16	1.05 $\times {10}^1$	18	3.62 $\times {10}^1$	28	2.02 $\times {10}^2$	49	1.45 $\times {10}^3$	123
	$8\times 8$					6.25	16	1.73 $\times {10}^1$	24	7.60 $\times {10}^1$	44	4.71 $\times {10}^2$	97
	$16\times 16$							6.56	16	2.27 $\times {10}^1$	26	1.18 $\times {10}^2$	55
	$32\times 32$									6.38	16	2.40 $\times {10}^1$	27
	$64\times 64$											6.26	18

and

Table 3. OAS preconditioner in 2D deformed domain: condition number ${\kappa }_2(T_{OAS})$ and iteration counts it. as a function of the number of subdomains N and mesh size $1/h$, $r=1$ for non-preconditioned system and 2-level OAS preconditioner.

OAS prec. with $p=2,k=1,r=1$, 2D deformed domain

$1/h$ = 8

$1/h$ = 16

$1/h$ = 32

$1/h$ = 64

$1/h$ = 128

$1/h$ = 256

N

${\kappa }_2$

it.

${\kappa }_2$

it.

${\kappa }_2$

it.

${\kappa }_2$

it.

${\kappa }_2$

it.

${\kappa }_2$

it.

non-prec.

1.09 $\times {10}^2$

19

2.02 $\times {10}^3$

105

3.53 $\times {10}^4$

460

5.96 $\times {10}^5$

1950

9.86 $\times {10}^6$

8175

1.61 $\times {10}^8$

33,502

2-level OAS

$2\times 2$

4.36

9

1.42 $\times {10}^1$

15

7.90 $\times {10}^1$

24

5.69 $\times {10}^2$

43

4.48 $\times {10}^3$

84

3.59 $\times {10}^4$

172

$4\times 4$

1.15 $\times {10}^1$

20

4.78 $\times {10}^1$

32

3.48 $\times {10}^2$

73

2.78 $\times {10}^3$

188

2.25 $\times {10}^4$

448

$8\times 8$

2.03 $\times {10}^1$

27

8.79 $\times {10}^1$

51

6.76 $\times {10}^2$

132

5.53 $\times {10}^3$

357

$16\times 16$

2.74 $\times {10}^1$

31

1.20 $\times {10}^2$

66

9.33 $\times {10}^2$

180

$32\times 32$

3.35 $\times {10}^1$

33

1.48 $\times {10}^2$

75

$64\times 64$

3.81 $\times {10}^1$

38

OAS prec. with $p=3,k=2,r=1$, 2D deformed domain

non-prec.

5.17 $\times {10}^1$

22

8.20 $\times {10}^2$

78

1.33 $\times {10}^4$

286

2.16 $\times {10}^5$

1159

3.49 $\times {10}^6$

4854

5.61 $\times {10}^7$

19,713

2-level OAS

$2\times 2$

5.04

11

1.08 $\times {10}^1$

15

4.98 $\times {10}^1$

23

3.30 $\times {10}^2$

43

2.52 $\times {10}^3$

84

2.00 $\times {10}^4$

180

$4\times 4$

7.85

17

2.81 $\times {10}^1$

28

1.73 $\times {10}^2$

55

1.28 $\times {10}^3$

137

1.01 $\times {10}^4$

361

$8\times 8$

1.58 $\times {10}^1$

23

6.76 $\times {10}^1$

42

4.61 $\times {10}^2$

94

3.63 $\times {10}^3$

263

$16\times 16$

3.01 $\times {10}^1$

30

1.34 $\times {10}^2$

54

9.65 $\times {10}^2$

133

$32\times 32$

3.51 $\times {10}^1$

32

1.32 $\times {10}^2$

56

$64\times 64$

3.44 $\times {10}^1$

32

present additional numerical findings for the physical (quarter ring) and reference (unit square) domains in two-dimensional space, featuring diverse polynomial degree p, maximal regularity $k=p-1$, and overlap $r=0$ (minimal) and $r=1$. They show that our proposed OAS(2) preconditioners are scalable, as it is indicated that the condition numbers remain bounded by a constant that is unaffected by N, as one moves along the diagonal of the tables. Furthermore, Figure 2 and Figure 3 provide stronger evidence for the scalability and quasi-optimality of our proposed OAS(2) preconditioners.

5.2. Two-Dimensional Tests: OAS Dependence on p and r

Although p dependency of OAS(2) preconditioners is not within the scope of our theory, it would be beneficial to assess the effectiveness of OAS biharmonic preconditioners as the polynomial degree p increases. The numerical tests are carried out on both the quarter ring and square domains, which are discretized with mesh size $h=1/64$ and subdivided into $N=2\times 2$ subdomains. The value of p in the experiments ranges from 2 to 4, and the overlap index r is symmetric and increases gradually from minimal $r=0$ to generous $r=p$. The condition numbers presented in

Table 4. Two-level OAS preconditioner on both the quarter ring domain and the reference unit square: condition number ${\kappa }_2(T_{OAS})$ as a function of the spline polynomial degree p for maximal regularity $k=p-1$ with different levels of overlap from symmetric minimal ($r=0$) to symmetric generous ($r=p$). Fixed $1/h=64$, $N=2\times 2$, $H/h=32$.

p	$\mathit{k}=\mathit{p}-1$, 2D Deformed Domain					$\mathit{k}=\mathit{p}-1$, Unit Square
	Non-Prec.	2-Level OAS				Non-Prec.	2-Level OAS
		$\mathit{r}=\mathbf{0}$	$\mathit{r}=\mathbf{2}$	$\mathit{r}=\mathbf{4}$	$\mathit{r}=\mathit{p}$		$\mathit{r}=\mathbf{0}$	$\mathit{r}=\mathbf{2}$	$\mathit{r}=\mathbf{4}$	$\mathit{r}=\mathit{p}$
2	5.96 $\times {10}^5$	1.97 $\times {10}^3$	2.43 $\times {10}^2$	7.70 $\times {10}^1$	2.43 $\times {10}^2$	2.07 $\times {10}^5$	1.70 $\times {10}^3$	2.18 $\times {10}^2$	7.14 $\times {10}^1$	2.18 $\times {10}^2$
3	2.16 $\times {10}^5$	1.36 $\times {10}^3$	1.34 $\times {10}^2$	4.22 $\times {10}^1$	6.95 $\times {10}^1$	7.08 $\times {10}^4$	1.81 $\times {10}^2$	2.34 $\times {10}^1$	9.83	1.41 $\times {10}^1$
4	2.88 $\times {10}^5$	5.03 $\times {10}^2$	8.58 $\times {10}^1$	3.22 $\times {10}^1$	3.22 $\times {10}^1$	9.32 $\times {10}^4$	8.19 $\times {10}^1$	1.91 $\times {10}^1$	1.00 $\times {10}^1$	1.00 $\times {10}^1$

demonstrate that OAS(2) biharmonic preconditioners exhibit favorable behavior, while the non-preconditioned systems display ill-conditioned behavior with increasing polynomial degree p. Moreover, the results indicate that OAS(2) preconditioners show good performance in case of generous overlap $(r=p)$.

5.3. Three-Dimensional Tests: OAS(2) Scalability in N

The condition numbers, extremal eigenvalues and iteration counts of our OAS(2) preconditioners are displayed in

Table 5. Two-level OAS preconditioners in the 3D cubic domain: condition number ${\kappa }_2(T_{OAS})$, extreme eigenvalues ${\lambda }_{\max },{\lambda }_{\min }$ and iteration counts it. as a function of the number of subdomains N. Fixed $H/h=4$, $p=2$, $k=1$ (top table), $p=3$, $k=2$ (bottom table).

Two-Level OAS, 3D Cubic Domain
		$\mathit{r}=\mathbf{0}$		$\mathit{r}=\mathbf{1}$
	$\mathit{N}$	${\mathbf{\kappa }}_{\mathbf{2}}={\mathbf{\lambda }}_{\max }/{\mathbf{\lambda }}_{\min }$	it.	${\mathbf{\kappa }}_{\mathbf{2}}={\mathbf{\lambda }}_{\max }/{\mathbf{\lambda }}_{\min }$	it.
	$2\times 2\times 2$	11.06 = 8.00/0.72	9	7.66 = 8.00/1.04	7
	$3\times 3\times 3$	22.30 = 8.10/0.36	18	9.43 = 9.43/1.00	18
$p=2$	$4\times 4\times 4$	25.86 = 8.09/0.31	22	14.28 = 11.52/0.81	22
$k=1$	$5\times 5\times 5$	24.54 = 8.08/0.33	26	17.08 = 11.25/0.66	23
	$6\times 6\times 6$	23.24 = 8.07/0.35	28	17.95 = 11.45/0.64	25
	$7\times 7\times 7$	22.52 = 8.07/0.36	29	17.28 = 11.38/0.66	26
	$2\times 2\times 2$	13.20 = 8.05/0.61	14	8.86 = 8.30/0.94	13
$p=3$	$3\times 3\times 3$	14.09 = 8.01/0.57	18	9.37 = 8.32/0.89	20
$k=2$	$4\times 4\times 4$	14.91 = 8.09/0.54	22	10.00 = 8.76/0.88	22
	$5\times 5\times 5$	15.85 = 8.03/0.51	23	10.08 = 8.77/0.87	23
	$6\times 6\times 6$	16.84 = 8.09/0.48	24	10.06 = 8.79/0.87	23

for the reference cubic domain as a function of the number of subdomains N. The numerical tests are performed with fixed subdomain size $H/h=4$, overlap index $r=0,1$ and $p=2,k=1$ and $p=3,k=2$ shown in upper part and bottom of the table, respectively. The three-dimensional test outcomes establish the scalability of OAS(2) preconditioners, since the condition numbers appear to be bounded above irrespective of N. In addition, the performance of OAS(2) preconditioners is enhanced as the overlap size is increased, in accordance with the bound of Theorem 2.

6. Conclusions

In this paper, we study overlapping additive Schwarz (OAS) preconditioners for the biharmonic problem, which fits very naturally in the context of IGA due to the $C^1$ continuity requirement associated to a conforming discrete space. More specifically, we consider the problem of solving the linear systems that arise from isogeometric discretization based on GB-splines of the biharmonic Dirichlet problem. We have developed a theoretical analysis on condition number bounds for the preconditioned system in terms of the involved mesh sizes and overlap parameter. A set of numerical tests have confirmed the theoretical predictions and investigated the performance of our preconditioners with respect to various discretization parameters.

In the current paper, we have focused only on the biharmonic problem with homogeneous Dirichlet boundary conditions on the reference patch. We believe that our preconditioning techniques can be applied to the biharmonic problems either with mixed Dirichlet and Neumann boundary conditions or with inhomogeneous Dirichlet boundary conditions, where the former would be resolved by determining the respective knot spans corresponding to ${\Gamma }_D$ and ${\Gamma }_N$ on $\partial \widehat{\Omega }$ and the latter would be resolved by interpolating for the approximation of the boundary data in terms of the basis functions.

A current research direction is the theoretical extension of our proposed OAS method to the biharmonic problem on multipatch domains, as well as to other higher-order differential equations. Another research direction is related to developing modified OAS preconditioners with various intergrid transfer operators from much coarser space to the entire GB-splines space, which would probably improve computational cost. Finally, we are devising alternative preconditioning techniques (e.g., multilevel Schwarz methods and two-level FETI methods) that may be more effective for solving the biharmonic problems discretized with IGA GB-splines.