Matrix Representations for a Class of Eigenparameter Dependent Sturm–Liouville Problems with Discontinuity

Abstract

Matrix representations for a class of Sturm–Liouville problems with eigenparameters contained in the boundary and interface conditions were studied. Given any matrix eigenvalue problem of a certain type and an eigenparameter-dependent condition, a class of Sturm–Liouville problems with this specified condition was constructed. It has been proven that each Sturm–Liouville problem is equivalent to the given matrix eigenvalue problem.

1. Introduction

Recently, Sturm–Liouville problems (SLPs) with discontinuity inside intervals have attracted significant attention from scholars due to their wide application in various fields. For example, one application involves a string loaded with point masses [1,2,3,4,5]. Generally speaking, the eigenparameter only appears in the equation, but in many actual phenomena, it is necessary for the eigenparameter to appear in the boundary conditions, such as heat conduction at the liquid–solid interface [6], and so on. Due to its physical significance, many scholars have studied the problem of boundary conditions containing a spectral parameter [7,8,9,10,11,12,13,14]. In recent decades, more researchers have studied eigenparameter-dependent SLPs with discontinuity, including the asymptotic behavior of eigenvalues, the inverse spectral theory, the finite spectrum, the oscillation of eigenfunctions, etc., see [9,10,15,16,17,18,19].

Regular SLPs have an infinite countable number of eigenvalues that are bounded below and unbounded above. However, Atkinson, in his well-celebrated book [20], stated that finite eigenvalues may exist under certain conditions. Kong and Zettl [18] solved this problem by constructing a class of regular SLPs, which has exactly $\mathfrak{N}$ eigenvalues for every positive integer $\mathfrak{N}$; they obtained the corresponding matrix representations in [19]. This special problem is called Atkinson-type SLPs (ASLPs). Ao et al. generalized this problem to various differential operators, for example, ASLPs with interface conditions, ASLPs with eigenparameters contained in boundary conditions, higher-order differential operators, etc. [21,22,23,24,25,26]. They discussed the existence of a finite spectrum and gave the corresponding matrix representation. In particular, Ao et al. proved that ASLPs with interface conditions have, at most, $\mathfrak{M}+\mathfrak{N}+2$ eigenvalues and gave the corresponding matrix representation in [23]. Moreover, the authors generalized the problem to eigenparameter-dependent ASLPs [24].

In recent years, SLPs with interface conditions dependent on parameters have also captured the attention of researchers, see [2,3,4] and references therein. In reference [2], the author obtained the operator–theoretic formulation. The asymptotic properties of eigenvalues were given for SLPs with interface conditions that were rationally dependent on the parameters in [3]. In work by Mukhtarov et al. [4], Green’s function was provided for eigenparameter-dependent SLPs with interface conditions.

In a recent paper, Ao et al. proved that SLPs with interface conditions dependent on the eigenparameter still have a finite spectrum [27]. Here, the following question arises: When the eigenparameter appears in both the boundary and interface conditions, does it affect the number in the spectrum? In this paper, we will solve this problem. We study an SLP in which an eigenparameter is contained in both the boundary and interface conditions, regardless of whether it is self-adjoint or non-self-adjoint. We prove that the problem has, at most, $\mathfrak{M}+\mathfrak{N}+5$ eigenvalues, which is different from the results in [27], where the number of eigenvalues is, at most, $\mathfrak{M}+\mathfrak{N}+4$. Moreover, we provide an example to illustrate our conclusion (as it turns out, it affects the number of eigenvalues). The basic method we used in this paper is a factorization of the characteristic function.

The rest of this paper is organized as follows: Some preliminaries are given in Section 2. In Section 3, we show that the number of eigenvalues of the considered problem is finite. In Section 4, the corresponding matrix representation is given, and for a given specific type of matrix eigenvalue problem, we construct a class of SLPs with the same boundary and interface conditions, ensuring that they have the same eigenvalues.

2. Preliminaries

In this work, we investigate the SL equation

$$-{\left(q\left(t\right)f^{\prime }\left(t\right)\right)}^{\prime }+p\left(t\right)f\left(t\right)=\mu w\left(t\right)f\left(t\right),t\in \mathfrak{I}=[c,\eta )\cup (\eta ,d],-\infty <c<d<\infty$$

(1)

with boundary conditions at the endpoints c and d, as follows

$${\xi }_{1}f\left(c\right)+{\xi }_2\left(q{f}^{\prime }\right)\left(c\right)+{\xi }_{3}f\left(d\right)+{\xi }_4\left(q{f}^{\prime }\right)\left(d\right)=\mu [{\xi }_1^{\prime }f\left(c\right)+{\xi }_2^{\prime }\left(q{f}^{\prime }\right)\left(c\right)+{\xi }_3^{\prime }f\left(d\right)+{\xi }_4^{\prime }\left(q{f}^{\prime }\right)\left(d\right)],$$

(2)

$${\tau }_{1}f\left(c\right)+{\tau }_2\left(q{f}^{\prime }\right)\left(c\right)+{\tau }_{3}f\left(d\right)+{\tau }_4\left(q{f}^{\prime }\right)\left(d\right)=\mu [{\tau }_1^{\prime }f\left(c\right)+{\tau }_2^{\prime }\left(q{f}^{\prime }\right)\left(c\right)+{\tau }_3^{\prime }f\left(d\right)+{\tau }_4^{\prime }\left(q{f}^{\prime }\right)\left(d\right)],$$

(3)

and interface conditions

$$f(\eta +0)=({\mathfrak{e}}_1\mu +{\mathfrak{e}}_1^{\prime })f(\eta -0)+({\mathfrak{e}}_2\mu +{\mathfrak{e}}_2^{\prime })\left(q{f}^{\prime }\right)(\eta -0),$$

(4)

$$\left(q{f}^{\prime }\right)(\eta +0)=({\mathfrak{e}}_3\mu +{\mathfrak{e}}_3^{\prime })f(\eta -0)+({\mathfrak{e}}_4\mu +{\mathfrak{e}}_4^{\prime })\left(q{f}^{\prime }\right)(\eta -0),$$

(5)

where $f(\eta +0)$ and $f(\eta -0)$ denote the right and left limits of $f\left(t\right)$ at $\eta$, respectively. $\mu \in \mathbb{C}$ is a spectral parameter; ${\xi }_{\mathfrak{i}},{\tau }_{\mathfrak{i}},{\mathfrak{e}}_{\mathfrak{i}},{\xi }_{\mathfrak{i}}^{\prime },{\tau }_{\mathfrak{i}}^{\prime },{\mathfrak{e}}_{\mathfrak{i}}^{\prime }\in \mathbb{R}$ ($\mathfrak{i}=\overline{1,4}$), and

$$\begin{gathered} \mathrm{rank}\left(\begin{array}{cccc}{\xi }_1& {\xi }_2& {\xi }_3& {\xi }_4\\ {\xi }_1^{\prime }& {\xi }_2^{\prime }& {\xi }_3^{\prime }& {\xi }_4^{\prime }\end{array}\right)=2,\mathrm{rank}\left(\begin{array}{cccc}{\tau }_1& {\tau }_2& {\tau }_3& {\tau }_4\\ {\tau }_1^{\prime }& {\tau }_2^{\prime }& {\tau }_3^{\prime }& {\tau }_4^{\prime }\end{array}\right)=2, \\ \mathrm{rank}\left(\begin{array}{cccc}{\xi }_1& {\xi }_2& {\xi }_3& {\xi }_4\\ {\tau }_1& {\tau }_2& {\tau }_3& {\tau }_4\end{array}\right)=2,\mathrm{rank}\left(\begin{array}{cccc}{\xi }_1^{\prime }& {\xi }_2^{\prime }& {\xi }_3^{\prime }& {\xi }_4^{\prime }\\ {\tau }_1^{\prime }& {\tau }_2^{\prime }& {\tau }_3^{\prime }& {\tau }_4^{\prime }\end{array}\right)=2. \end{gathered}$$

(6)

We assume that the coefficients satisfy the following conditions

$${\displaystyle \frac{1}{q\left(t\right)}},p\left(t\right),w\left(t\right)\in L^1(\mathfrak{I},\mathbb{R}),$$

(7)

where $L^1(\mathfrak{I},\mathbb{R})=\left\{f:\mathfrak{I}\to \mathbb{R}|{\int }_I\left|f\left(t\right)\right|dt<\infty \right\}$.

We suppose that $Rank\left[A_{\mu }\right|B_{\mu }]=2$ and $det\left({\Gamma }_{\mu }\right)\ne 0$, where

$$A_{\mu }=\left(\begin{array}{cc}{\xi }_1-\mu {\xi }_1^{\prime }& {\xi }_2-\mu {\xi }_2^{\prime }\\ {\tau }_1-\mu {\tau }_1^{\prime }& {\tau }_2-\mu {\tau }_2^{\prime }\end{array}\right),B_{\mu }=\left(\begin{array}{cc}{\xi }_3-\mu {\xi }_3^{\prime }& {\xi }_4-\mu {\xi }_4^{\prime }\\ {\tau }_3-\mu {\tau }_3^{\prime }& {\tau }_4-\mu {\tau }_4^{\prime }\end{array}\right),$$

(8)

$${\Gamma }_{\mu }=\left(\begin{array}{cc}{\mathfrak{e}}_1\mu +{\mathfrak{e}}_1^{\prime }& {\mathfrak{e}}_2\mu +{\mathfrak{e}}_2^{\prime }\\ {\mathfrak{e}}_3\mu +{\mathfrak{e}}_3^{\prime }& {\mathfrak{e}}_4\mu +{\mathfrak{e}}_4^{\prime }\end{array}\right),$$

(9)

then (2)–(5) turn into

$$A_{\mu }F\left(c\right)+B_{\mu }F\left(d\right)=0,F(\eta +0)={\Gamma }_{\mu }F(\eta -0),F=\left(\begin{array}{c}f\\ q{f}^{\prime }\end{array}\right).$$

Equation (1) can be represented as

$$\left\{\begin{array}{c}{u}^{\prime }=sv,\hfill \\ v^{\prime }=(p-\mu w)u.\hfill \end{array}\right.$$

(10)

by using $\left\{\begin{array}{c}u=f,\hfill \\ v=q{f}^{\prime }.\hfill \end{array}\right.$

Definition 1.

(Reference [18]) $f\left(t\right)$ is called a trivial solution of (1) if $f\left(t\right)\equiv q\left(t\right)f^{\prime }\left(t\right)\equiv 0,$$t\in \mathfrak{I}$.

Let $\Phi (t,\mu )=\left[{\varrho }_{kl}(t,\mu )\right](k,l=1,2)$ be the fundamental solution matrix of system (10), satisfying (4) and (5) as follows

$$\Phi (t,\mu )=\left\{\begin{array}{c}{\Phi }_1(t,\mu ),t\in [c,\eta ),\\ {\Phi }_2(t,\mu ),t\in (\eta ,d],\end{array}\right.$$

(11)

with the initial condition ${\Phi }_1(c,\mu )=I$.

Define $\Lambda \left(\mu \right):=det[A_{\mu }+B_{\mu }{\Phi }_2(d,\mu )]$. Let

$$H\left(\mu \right)=\left(\begin{array}{cc}{\mathfrak{h}}_{11}\left(\mu \right)& {\mathfrak{h}}_{12}\left(\mu \right)\\ {\mathfrak{h}}_{21}\left(\mu \right)& {\mathfrak{h}}_{22}\left(\mu \right)\end{array}\right),$$

where

$${\mathfrak{h}}_{11}\left(\mu \right)=({\xi }_3-\mu {\xi }_3^{\prime })({\tau }_2-\mu {\tau }_2^{\prime })-({\xi }_2-\mu {\xi }_2^{\prime })({\tau }_3-\mu {\tau }_3^{\prime }),$$

$${\mathfrak{h}}_{12}\left(\mu \right)=({\xi }_1-\mu {\xi }_1^{\prime })({\tau }_3-\mu {\tau }_3^{\prime })-({\xi }_3-\mu {\xi }_3^{\prime })({\tau }_1-\mu {\tau }_1^{\prime }),$$

$${\mathfrak{h}}_{21}\left(\mu \right)=({\xi }_4-\mu {\xi }_4^{\prime })({\tau }_2-\mu {\tau }_2^{\prime })-({\xi }_2-\mu {\xi }_2^{\prime })({\tau }_4-\mu {\tau }_4^{\prime }),$$

$${\mathfrak{h}}_{22}\left(\mu \right)=({\xi }_1-\mu {\xi }_1^{\prime })({\tau }_4-\mu {\tau }_4^{\prime })-({\xi }_4-\mu {\xi }_4^{\prime })({\tau }_1-\mu {\tau }_1^{\prime }).$$

By a direct calculation, we know

$$\begin{gathered} \begin{array}{c}\Lambda \left(\mu \right)=det[A_{\mu }+B_{\mu }{\Phi }_2(d,\mu )] \hfill \end{array} \\ =\left|\left(\begin{array}{cc}{\xi }_1-\mu {\xi }_1^{\prime }& {\xi }_2-\mu {\xi }_2^{\prime }\\ {\tau }_1-\mu {\tau }_1^{\prime }& {\tau }_2-\mu {\tau }_2^{\prime }\end{array}\right)+\left(\begin{array}{cc}{\xi }_3-\mu {\xi }_3^{\prime }& {\xi }_4-\mu {\xi }_4^{\prime }\\ {\tau }_3-\mu {\tau }_3^{\prime }& {\tau }_4-\mu {\tau }_4^{\prime }\end{array}\right)\left(\begin{array}{cc}{\varrho }_{11}(d,\mu )& {\varrho }_{12}(d,\mu )\\ {\varrho }_{21}(d,\mu )& {\varrho }_{22}(d,\mu )\end{array}\right)\right| \\ \begin{array}{cc}\hfill =& det\left(A_{\mu }\right)+det\left(B_{\mu }\right)-det\left(B_{\mu }\right)\hfill \\ \hfill & +[({\xi }_3-\mu {\xi }_3^{\prime })({\tau }_2-\mu {\tau }_2^{\prime })-({\xi }_2-\mu {\xi }_2^{\prime })({\tau }_3-\mu {\tau }_3^{\prime })]{\varrho }_{11}(d,\mu )\hfill \\ \hfill & +[({\xi }_1-\mu {\xi }_1^{\prime })({\tau }_3-\mu {\tau }_3^{\prime })-({\xi }_3-\mu {\xi }_3^{\prime })({\tau }_1-\mu {\tau }_1^{\prime })]{\varrho }_{12}(d,\mu )\hfill \\ \hfill & +[({\xi }_4-\mu {\xi }_4^{\prime })({\tau }_2-\mu {\tau }_2^{\prime })-({\xi }_2-\mu {\xi }_2^{\prime })({\tau }_4-\mu {\tau }_4^{\prime })]{\varrho }_{21}(d,\mu )\hfill \\ \hfill & +[({\xi }_1-\mu {\xi }_1^{\prime })({\tau }_4-\mu {\tau }_4^{\prime })-({\xi }_4-\mu {\xi }_4^{\prime })({\tau }_1-\mu {\tau }_1^{\prime })]{\varrho }_{22}(d,\mu )\hfill \\ \hfill & +({\xi }_3-\mu {\xi }_3^{\prime })({\tau }_4-\mu {\tau }_4^{\prime }){\varrho }_{22}(d,\mu ){\varrho }_{11}(d,\mu )+({\xi }_4-\mu {\xi }_4^{\prime })({\tau }_3-\mu {\tau }_3^{\prime }){\varrho }_{21}(d,\mu ){\varrho }_{12}(d,\mu )\hfill \\ \hfill & -({\xi }_4-\mu {\xi }_4^{\prime })({\tau }_3-\mu {\tau }_3^{\prime }){\varrho }_{22}(d,\mu ){\varrho }_{11}(d,\mu )+({\xi }_3-\mu {\xi }_3^{\prime })({\tau }_4-\mu {\tau }_4^{\prime }){\varrho }_{21}(d,\mu ){\varrho }_{12}(d,\mu )\hfill \\ \hfill =& det\left(A_{\mu }\right)+det\left(B_{\mu }\right)+{\mathfrak{h}}_{11}\left(\mu \right){\varrho }_{11}(d,\mu )+{\mathfrak{h}}_{12}\left(\mu \right){\varrho }_{12}(d,\mu )+{\mathfrak{h}}_{21}\left(\mu \right){\varrho }_{21}(d,\mu )\hfill \\ \hfill & +{\mathfrak{h}}_{22}\left(\mu \right){\varrho }_{22}(d,\mu )+[({\xi }_3-\mu {\xi }_3^{\prime })({\tau }_4-\mu {\tau }_4^{\prime })-({\xi }_4-\mu {\xi }_4^{\prime })({\tau }_3-\mu {\tau }_3^{\prime })]\times \hfill \\ \hfill & [{\varrho }_{11}(d,\mu ){\varrho }_{22}(d,\mu )-{\varrho }_{12}(d,\mu ){\varrho }_{21}(d,\mu )-1],\hfill \end{array} \end{gathered}$$

since $det\left({\Phi }_2(d,\mu )\right)=det\left({\Phi }_1(d,\mu )\right)=1$, so ${\varrho }_{11}(d,\mu ){\varrho }_{22}(d,\mu )-{\varrho }_{12}(d,\mu ){\varrho }_{21}(d,\mu )-1=0$, we have

$$\begin{array}{cc}\hfill \Lambda \left(\mu \right)=& det\left(A_{\mu }\right)+det\left(B_{\mu }\right)+{\mathfrak{h}}_{11}\left(\mu \right){\varrho }_{11}(d,\mu )+{\mathfrak{h}}_{12}\left(\mu \right){\varrho }_{12}(d,\mu )\hfill \\ \hfill & +{\mathfrak{h}}_{21}\left(\mu \right){\varrho }_{21}(d,\mu )+{\mathfrak{h}}_{22}\left(\mu \right){\varrho }_{22}(d,\mu ).\hfill \end{array}$$

(12)

Proposition 1.

$\Lambda \left(\mu \right)=0$⇔μ is an eigenvalue of (1)–(5).

Proof. 

We suppose $\Lambda \left(\mu \right)=0$, then the equation $[A_{\mu }+B_{\mu }{\Phi }_2(d,\mu )]C=0$ has non-zero solutions. We solve the initial value problem

$$F^{{}^{\prime }}=\left(\begin{array}{cc}0& s\\ p-\mu w& 0\end{array}\right)F,F=\left(\begin{array}{c}f\\ p{f}^{{}^{\prime }}\end{array}\right)\mathrm{on}J,F\left(c\right)=C,$$

then we have $F\left(d\right)={\Phi }_2(d,\mu )F\left(c\right)$ and $[A_{\mu }+B_{\mu }{\Phi }_2(d,\mu )]F\left(c\right)=0$, we can obtain $A_{\mu }F\left(c\right)+B_{\mu }F\left(d\right)=0$, so $\mu$ is an eigenvalue.

On the contrary, if $\mu$ is an eigenvalue and f is an eigenfunction, then $F=\left(\begin{array}{c}f\\ p{f}^{{}^{\prime }}\end{array}\right)$ satisfies $F\left(d\right)={\Phi }_2(d,\mu )F\left(c\right)$; thus, $[A_{\mu }+B_{\mu }{\Phi }_2(d,\mu )]F\left(c\right)=0$. If $F\left(c\right)=0$, then it is a trivial solution. This contradicts f being an eigenfunction, so we have $det[A_{\mu }+B_{\mu }{\Phi }_2(d,\mu )]=0$. □

3. The Finite Spectrum Problem of (1)–(5)

Problems (1)–(5) have finite eigenvalues in this section. In the sequel, we always suppose that (7) holds, and there is a partition of $\mathfrak{I}$

$$c=c_0<c_1<c_2<\cdots <c_{2\mathfrak{M}}<\eta <d_1<d_2<\cdots <d_{2\mathfrak{N}+1}=d,$$

(13)

for $\mathfrak{M},\mathfrak{N}\in {\mathbb{Z}}_{+}$, such that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{q\left(t\right)}}=0,t\in {\cup }_{\mathfrak{i}=0}^{\mathfrak{M}-1}[c_{2\mathfrak{i}},c_{2\mathfrak{i}+1}]\cup [c_{2\mathfrak{M}},\eta )\cup (\eta ,d_1]{\cup }_{\mathfrak{j}=1}^{\mathfrak{N}}[d_{2\mathfrak{j}},d_{2\mathfrak{j}+1}];\hfill \\ \hfill & p\left(t\right)=w\left(t\right)=0,t\in {\cup }_{\mathfrak{i}=0}^{\mathfrak{M}-1}[c_{2\mathfrak{i}+1},c_{2\mathfrak{i}+2}]{\cup }_{\mathfrak{j}=0}^{\mathfrak{N}-1}[d_{2\mathfrak{j}+1},d_{2\mathfrak{j}+2}];\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & {\int }_{c_{2\mathfrak{i}+1}}^{c_{2\mathfrak{i}+2}}{\displaystyle \frac{1}{q\left(t\right)}}dt\ne 0,\mathfrak{i}=\overline{0,\mathfrak{M}-1};{\int }_{d_{2\mathfrak{j}+1}}^{d_{2\mathfrak{j}+2}}{\displaystyle \frac{1}{q\left(t\right)}}dt\ne 0,\mathfrak{j}=\overline{0,\mathfrak{N}-1};\hfill \\ \hfill & {\int }_{c_{2\mathfrak{i}}}^{c_{2\mathfrak{i}+1}}w\left(t\right)dt\ne 0,\mathfrak{i}=\overline{0,\mathfrak{M}-1};{\int }_{d_{2\mathfrak{j}}}^{d_{2\mathfrak{j}+1}}w\left(t\right)dt\ne 0,\mathfrak{j}=\overline{1,\mathfrak{N}};\hfill \\ \hfill & {\int }_{\eta }^{d_1}w\left(t\right)dt\ne 0,{\int }_{2\mathfrak{M}}^{\eta }w\left(t\right)dt\ne 0.\hfill \end{array}$$

(15)

Definition 2.

(Reference [1]) If an SL Equation (1) satisfies (13)–(15), then Equation (1) is called an Atkinson type.

Definition 3.

(Reference [1]) If there exists an Equation (1) of the Atkinson type, then (1)–(5) is called an Atkinson type.

Definition 4.

Let (13)–(15) hold. We define the following notations.

$$\begin{array}{cc}\hfill & s_{\mathfrak{i}}:={\int }_{c_{2\mathfrak{i}-1}}^{c_{2\mathfrak{i}}}{\displaystyle \frac{1}{q\left(t\right)}}dt,\mathfrak{i}=1,2,\cdots ,\mathfrak{M};\hfill \\ \hfill & p_{\mathfrak{i}}:={\int }_{c_{2\mathfrak{i}}}^{c_{2\mathfrak{i}+1}}p\left(t\right)dt,w_{\mathfrak{i}}:={\int }_{c_{2\mathfrak{i}}}^{c_{2\mathfrak{i}+1}}w\left(t\right)dt,\mathfrak{i}=\overline{0,\mathfrak{M}-1};\hfill \\ \hfill & p_{\mathfrak{M}}:={\int }_{c_{2\mathfrak{M}}}^{\eta }p\left(t\right)dt,w_{\mathfrak{M}}:={\int }_{c_{2\mathfrak{M}}}^{\eta }w\left(t\right)dt;\hfill \\ \hfill & {\tilde{s}}_{\mathfrak{j}}:={\int }_{d_{2\mathfrak{j}-1}}^{d_{2\mathfrak{j}}}{\displaystyle \frac{1}{q\left(t\right)}}dt,\mathfrak{j}=1,2,\cdots ,\mathfrak{N};\hfill \\ \hfill & {\tilde{p}}_0:={\int }_{\eta }^{d_1}p\left(t\right)dt,{\tilde{p}}_{\mathfrak{j}}:={\int }_{d_{2\mathfrak{j}}}^{d_{2\mathfrak{j}+1}}p\left(t\right)dt,\mathfrak{j}=\overline{1,\mathfrak{N}};\hfill \\ \hfill & {\tilde{w}}_0:={\int }_{\eta }^{d_1}w\left(t\right)dt,{\tilde{w}}_{\mathfrak{j}}:={\int }_{d_{2\mathfrak{j}}}^{d_{2\mathfrak{j}+1}}w\left(t\right)dt,\mathfrak{j}=\overline{1,\mathfrak{N}}.\hfill \end{array}$$

(16)

Next, we give two fundamental solution matrices of system (10).

Lemma 1.

$\Phi (t,\mu )$ defined as (11), we have

$${\Phi }_1(c_1,\mu )=\left(\begin{array}{cc}1& 0\\ p_0-\mu w_0& 1\end{array}\right),$$

$${\Phi }_1(c_3,\mu )=\left(\begin{array}{cc}1+(p_0-\mu w_0)s_1& s_1\\ {\varrho }_{21}(c_3,\mu )& 1+(p_1-\mu w_1)s_1\end{array}\right),$$

where ${\varrho }_{21}(c_3,\mu )=(p_0-\mu w_0)+(p_1-\mu w_1)+(p_0-\mu w_0)(p_1-\mu w_1)s_1$.

In general, for $1\le \mathfrak{i}\le \mathfrak{M}-1$, we have

$${\Phi }_1(c_{2\mathfrak{i}+1},\mu )=\left(\begin{array}{cc}1& s_{\mathfrak{i}}\\ p_{\mathfrak{i}}-\mu w_{\mathfrak{i}}& 1+(p_{\mathfrak{i}}-\mu w_{\mathfrak{i}})s_{\mathfrak{i}}\end{array}\right){\Phi }_1(c_{2\mathfrak{i}-1},\mu ),$$

particularly,

$${\Phi }_1(\eta -0,\mu )=\left(\begin{array}{cc}1& s_{\mathfrak{M}}\\ p_{\mathfrak{M}}-\mu w_{\mathfrak{M}}& 1+(p_{\mathfrak{M}}-\mu w_{\mathfrak{M}})s_{\mathfrak{M}}\end{array}\right){\Phi }_1(c_{2\mathfrak{M}-1},\mu ).$$

Proof. 

From (14), we know that u is constant on ${\cup }_{\mathfrak{i}=0}^{\mathfrak{M}-1}[c_{2\mathfrak{i}},c_{2\mathfrak{i}+1}]\cup [c_{2\mathfrak{M}},\eta )$ by ${\displaystyle \frac{1}{q\left(t\right)}}=0$ and v is constant on ${\cup }_{\mathfrak{i}=0}^{\mathfrak{M}-1}[c_{2\mathfrak{i}+1},c_{2\mathfrak{i}+2}]$ by $p\left(t\right)=w\left(t\right)=0$. Thus, we can obtain the result by using the iterative method. □

 Using similar methods in Lemma 1, we have

Lemma 2.

For each $\mu \in \mathbb{C}$, we denote

$$\Theta (t,\mu )=\left[{\psi }_{kl}(t,\mu )\right](k,l=1,2)$$

(17)

a fundamental solution matrix of the system (10) with interface conditions (4) and (5), and satisfy the initial condition $\Theta (\eta +0,\mu )=I$. Then we have

$$\Theta (d_1,\mu )=\left(\begin{array}{cc}1& 0\\ {\tilde{p}}_0-\mu {\tilde{w}}_0& 1\end{array}\right).$$

Generally, for $1\le \mathfrak{j}\le \mathfrak{N}$,

$$\Theta (d_{2\mathfrak{j}+1},\mu )=\left(\begin{array}{cc}1& {\tilde{s}}_{\mathfrak{j}}\\ {\tilde{p}}_{\mathfrak{j}}-\mu {\tilde{w}}_{\mathfrak{j}}& 1+({\tilde{p}}_{\mathfrak{j}}-\mu {\tilde{w}}_{\mathfrak{j}}){\tilde{s}}_{\mathfrak{j}}\end{array}\right)\Theta (d_{2\mathfrak{j}-1},\mu ).$$

Lemma 3.

Let $\Phi (t,\mu )$ and $\Theta (t,\mu )$ be defined in (11) and (17), respectively. Then we have

$${\Phi }_2(d,\mu )=\Theta (d,\mu ){\Gamma }_{\mu }{\Phi }_1(\eta -0,\mu ),t\in (\eta ,d],$$

where ${\Gamma }_{\mu }$ is defined in (9).

Proof. 

From the two fundamental solutions, $\Theta (t,\mu )$ and $\Phi (t,\mu )$ of system (10), and the given initial value, we can obtain

$$\Theta (t,\mu )={\Phi }_2(t,\mu ){\Phi }_2^{-1}(\eta +0,\mu ),$$

from (4) and (5), we have

$${\Phi }_2(\eta +0,\mu )={\Gamma }_{\mu }{\Phi }_1(\eta -0,\mu ).$$

Particularly, let $t=d$, we obtain

$${\Phi }_2(d,\mu )=\Theta (d,\mu ){\Gamma }_{\mu }{\Phi }_1(\eta -0,\mu ).$$

□

In light of Lemmas 1–3, we can obtain the following theorem, and problems (1)–(5) have finite eigenvalues:

Theorem 1.

Let (14)–(16) hold, $H\left(\mu \right)$ is defined as above. Assume ${\mathfrak{e}}_2\ne 0$; thus,

Conditions	The number of eigenvalues
$\mathrm{If}{\xi }_4^{\prime }{\tau }_2^{\prime }-{\xi }_2^{\prime }{\tau }_4^{\prime }\ne 0;$	$\mathfrak{M}+\mathfrak{N}+5$
$\begin{array}{cc}\hfill \mathrm{If}& {\xi }_4^{\prime }{\tau }_2^{\prime }-{\xi }_2^{\prime }{\tau }_4^{\prime }=0;\hfill \\ & w_0{\tilde{w}}_{\mathfrak{N}}({\tau }_4{\xi }_2^{\prime }+{\xi }_2{\tau }_4^{\prime }-{\xi }_4{\tau }_2^{\prime }-{\tau }_2{\xi }_4^{\prime })\hfill \\ \hfill -& {\tilde{w}}_{\mathfrak{N}}\left({\xi }_1^{\prime }{\tau }_4^{\prime }-{\xi }_4^{\prime }{\tau }_1^{\prime }\right)-w_0\left({\tau }_2^{\prime }{\xi }_3^{\prime }-{\xi }_2^{\prime }{\tau }_3^{\prime }\right)\ne 0;\hfill \end{array}$	$\mathfrak{M}+\mathfrak{N}+4$
$\begin{array}{cc}\hfill \mathrm{If}& {\xi }_4^{\prime }{\tau }_2^{\prime }-{\xi }_2^{\prime }{\tau }_4^{\prime }={\xi }_3^{\prime }{\tau }_2^{\prime }-{\xi }_2^{\prime }{\tau }_3^{\prime }={\xi }_1^{\prime }{\tau }_4^{\prime }-{\xi }_4^{\prime }{\tau }_1^{\prime }\hfill \\ \hfill =& {\tau }_4{\xi }_2^{\prime }+{\xi }_2{\tau }_4^{\prime }-{\xi }_4{\tau }_2^{\prime }-{\tau }_2{\xi }_4^{\prime }=0;\hfill \\ & {\xi }_1^{\prime }{\tau }_3^{\prime }-{\xi }_3^{\prime }{\tau }_1^{\prime }+w_0{\tilde{w}}_{\mathfrak{N}}({\xi }_4{\tau }_2-{\xi }_2{\tau }_4)\hfill \\ \hfill -& w_0({\xi }_2{\tau }_3^{\prime }+{\xi }_2^{\prime }{\tau }_3-{\xi }_3{\tau }_2^{\prime }-{\xi }_3^{\prime }{\tau }_2)\hfill \\ \hfill -& {\tilde{w}}_{\mathfrak{N}}({\xi }_4{\tau }_1^{\prime }+{\xi }_4^{\prime }{\tau }_1-{\xi }_1{\tau }_4^{\prime }-{\xi }_1^{\prime }{\tau }_4)\ne 0;\hfill \end{array}$	$\mathfrak{M}+\mathfrak{N}+3$
$\begin{array}{cc}\hfill \mathrm{If}& {\xi }_4^{\prime }{\tau }_2^{\prime }-{\xi }_2^{\prime }{\tau }_4^{\prime }={\xi }_3^{\prime }{\tau }_2^{\prime }-{\xi }_2^{\prime }{\tau }_3^{\prime }={\xi }_1^{\prime }{\tau }_4^{\prime }-{\xi }_4^{\prime }{\tau }_1^{\prime }\hfill \\ \hfill =& {\xi }_4{\tau }_2-{\xi }_2{\tau }_4={\xi }_1^{\prime }{\tau }_3^{\prime }-{\xi }_3^{\prime }{\tau }_1^{\prime }={\tau }_4{\xi }_2^{\prime }+{\xi }_2{\tau }_4^{\prime }-{\xi }_4{\tau }_2^{\prime }-{\tau }_2{\xi }_4^{\prime }\hfill \\ \hfill =& {\xi }_2{\tau }_3^{\prime }+{\xi }_2^{\prime }{\tau }_3-{\xi }_3{\tau }_2^{\prime }-{\xi }_3^{\prime }{\tau }_2={\xi }_4{\tau }_1^{\prime }+{\xi }_4^{\prime }{\tau }_1-{\xi }_1{\tau }_4^{\prime }-{\xi }_1^{\prime }{\tau }_4=0;\hfill \\ & {\xi }_3{\tau }_1^{\prime }+{\xi }_3^{\prime }{\tau }_1-{\xi }_1{\tau }_3^{\prime }-{\xi }_1^{\prime }{\tau }_3\hfill \\ \hfill -& {\tilde{w}}_{\mathfrak{N}}({\xi }_1{\tau }_4-{\xi }_4{\tau }_1)-w_0({\xi }_3{\tau }_2-{\xi }_2{\tau }_3)\ne 0;\hfill \end{array}$	$\mathfrak{M}+\mathfrak{N}+2$
$\begin{array}{cc}\hfill \mathrm{If}& {\xi }_4^{\prime }{\tau }_2^{\prime }-{\xi }_2^{\prime }{\tau }_4^{\prime }={\xi }_3^{\prime }{\tau }_2^{\prime }-{\xi }_2^{\prime }{\tau }_3^{\prime }={\xi }_1^{\prime }{\tau }_4^{\prime }-{\xi }_4^{\prime }{\tau }_1^{\prime }={\xi }_4{\tau }_2-{\xi }_2{\tau }_4\hfill \\ \hfill =& {\xi }_1^{\prime }{\tau }_3^{\prime }-{\xi }_3^{\prime }{\tau }_1^{\prime }={\xi }_3{\tau }_2-{\xi }_2{\tau }_3={\xi }_1{\tau }_4-{\xi }_4{\tau }_1\hfill \\ \hfill =& {\tau }_4{\xi }_2^{\prime }+{\xi }_2{\tau }_4^{\prime }-{\xi }_4{\tau }_2^{\prime }-{\tau }_2{\xi }_4^{\prime }={\xi }_2{\tau }_3^{\prime }+{\xi }_2^{\prime }{\tau }_3-{\xi }_3{\tau }_2^{\prime }-{\xi }_3^{\prime }{\tau }_2\hfill \\ \hfill =& {\xi }_4{\tau }_1^{\prime }+{\xi }_4^{\prime }{\tau }_1-{\xi }_1{\tau }_4^{\prime }-{\xi }_1^{\prime }{\tau }_4={\xi }_3{\tau }_1^{\prime }+{\xi }_3^{\prime }{\tau }_1-{\xi }_1{\tau }_3^{\prime }-{\xi }_1^{\prime }{\tau }_3=0;\hfill \\ & {\xi }_1{\tau }_3-{\xi }_3{\tau }_1\ne 0;\hfill \end{array}$	$\mathfrak{M}+\mathfrak{N}+1$

 If none of the conditions in the table above are met, then (1)–(5) have ι eigenvalues for $\iota \in \{1,2,\cdots ,\mathfrak{M}+\mathfrak{N}\}$ or the system can be degenerate.

Proof. 

Firstly, by Lemma 3, we know that ${\Phi }_2(d,\mu )=\Theta (d,\mu ){\Gamma }_{\mu }{\Phi }_1(\eta -0,\mu )$; next, we can obtain the structure of ${\Phi }_2(d,\mu )$ by a direct calculation.

If ${\mathfrak{e}}_2\ne 0$, we can obtain the structure of ${\Phi }_2(d,\mu )$, as follows:

$$\begin{array}{cc}\hfill {\varrho }_{11}(d,\mu )=& {\rm Y}\widetilde{{\rm Y}}\left[({\mathfrak{e}}_2\mu +{\mathfrak{e}}_2^{\prime })(p_{\mathfrak{M}}-\mu w_{\mathfrak{M}})({\tilde{p}}_0-\mu {\tilde{w}}_0)+({\mathfrak{e}}_1\mu +{\mathfrak{e}}_1^{\prime })({\tilde{p}}_0-\mu {\tilde{w}}_0)+{\mathfrak{e}}_3\mu +{\mathfrak{e}}_3^{\prime }\right.\hfill \\ \hfill & \left.+({\mathfrak{e}}_4\mu +{\mathfrak{e}}_4^{\prime })(p_{\mathfrak{M}}-\mu w_{\mathfrak{M}})\right]\times \prod _{\mathfrak{i}=0}^{\mathfrak{M}-1}(p_{\mathfrak{i}}-\mu w_{\mathfrak{i}})\prod _{\mathfrak{j}=1}^{\mathfrak{N}-1}({\tilde{p}}_{\mathfrak{j}}-\mu {\tilde{w}}_{\mathfrak{j}})+{\tilde{\varrho }}_{11}\left(\mu \right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\varrho }_{12}(d,\mu )=& {\rm Y}\widetilde{{\rm Y}}\left[({\mathfrak{e}}_2\mu +{\mathfrak{e}}_2^{\prime })(p_{\mathfrak{M}}-\mu w_{\mathfrak{M}})({\tilde{p}}_0-\mu {\tilde{w}}_0)+({\mathfrak{e}}_1\mu +{\mathfrak{e}}_1^{\prime })({\tilde{p}}_0-\mu {\tilde{w}}_0)+{\mathfrak{e}}_3\mu +{\mathfrak{e}}_3^{\prime }\right.\hfill \\ \hfill & \left.+({\mathfrak{e}}_4\mu +{\mathfrak{e}}_4^{\prime })(p_{\mathfrak{M}}-\mu w_{\mathfrak{M}})\right]\times \prod _{\mathfrak{i}=1}^{\mathfrak{M}-1}(p_{\mathfrak{i}}-\mu w_{\mathfrak{i}})\prod _{\mathfrak{j}=1}^{\mathfrak{N}-1}({\tilde{p}}_{\mathfrak{j}}-\mu {\tilde{w}}_{\mathfrak{j}})+{\tilde{\varrho }}_{12}\left(\mu \right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\varrho }_{21}(d,\mu )=& {\rm Y}\widetilde{{\rm Y}}\left[({\mathfrak{e}}_2\mu +{\mathfrak{e}}_2^{\prime })(p_{\mathfrak{M}}-\mu w_{\mathfrak{M}})({\tilde{p}}_0-\mu {\tilde{w}}_0)+({\mathfrak{e}}_1\mu +{\mathfrak{e}}_1^{\prime })({\tilde{p}}_0-\mu {\tilde{w}}_0)+{\mathfrak{e}}_3\mu +{\mathfrak{e}}_3^{\prime }\right.\hfill \\ \hfill & \left.+({\mathfrak{e}}_4\mu +{\mathfrak{e}}_4^{\prime })(p_{\mathfrak{M}}-\mu w_{\mathfrak{M}})\right]\times \prod _{\mathfrak{i}=0}^{\mathfrak{M}-1}(p_{\mathfrak{i}}-\mu w_{\mathfrak{i}})\prod _{\mathfrak{j}=1}^{\mathfrak{N}}({\tilde{p}}_{\mathfrak{j}}-\mu {\tilde{w}}_{\mathfrak{j}})+{\tilde{\varrho }}_{21}\left(\mu \right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\varrho }_{22}(d,\mu )=& {\rm Y}\widetilde{{\rm Y}}\left[({\mathfrak{e}}_2\mu +{\mathfrak{e}}_2^{\prime })(p_{\mathfrak{M}}-\mu w_{\mathfrak{M}})({\tilde{p}}_0-\mu {\tilde{w}}_0)+({\mathfrak{e}}_1\mu +{\mathfrak{e}}_1^{\prime })({\tilde{p}}_0-\mu {\tilde{w}}_0)++{\mathfrak{e}}_3\mu +{\mathfrak{e}}_3^{\prime }\right.\hfill \\ \hfill & \left.({\mathfrak{e}}_4\mu +{\mathfrak{e}}_4^{\prime })(p_{\mathfrak{M}}-\mu w_{\mathfrak{M}})\right]\times \prod _{\mathfrak{i}=1}^{\mathfrak{M}-1}(p_{\mathfrak{i}}-\mu w_{\mathfrak{i}})\prod _{\mathfrak{j}=1}^{\mathfrak{N}}({\tilde{p}}_{\mathfrak{j}}-\mu {\tilde{w}}_{\mathfrak{j}})+{\tilde{\varrho }}_{22}\left(\mu \right),\hfill \end{array}$$

where ${\rm Y}={\prod }_{\mathfrak{i}=1}^{\mathfrak{M}}{s}_{\mathfrak{i}},\widetilde{{\rm Y}}={\prod }_{\mathfrak{j}=1}^{\mathfrak{N}}{\tilde{s}}_{\mathfrak{j}},$${\tilde{\varrho }}_{kl}\left(\mu \right)=o({\rm Y}\widetilde{{\rm Y}})$ when min $\{s_{\mathfrak{i}},{\tilde{s}}_{\mathfrak{j}}:\mathfrak{i}=\overline{1,\mathfrak{M}},\mathfrak{j}=\overline{1,\mathfrak{N}}\}\to \infty$, $k,l=1,2$.

So if ${\mathfrak{e}}_2\ne 0$, it follows that the degrees of ${\varrho }_{11}(d,\mu ),{\varrho }_{12}(d,\mu ),{\varrho }_{21}(d,\mu )$ and ${\varrho }_{22}(d,\mu )$ in $\mu$ are $\mathfrak{M}+\mathfrak{N}+2$, $\mathfrak{M}+\mathfrak{N}+1$, $\mathfrak{M}+\mathfrak{N}+3$, and $\mathfrak{M}+\mathfrak{N}+2$, respectively. According to (12) and Proposition 1, if ${\xi }_4^{\prime }{\tau }_2^{\prime }-{\xi }_2^{\prime }{\tau }_4^{\prime }\ne 0$ in ${\mathfrak{h}}_{21}\left(\mu \right)$, we can obtain the highest degree of $\mu$ in $\Lambda \left(\mu \right)$ is $\mathfrak{M}+\mathfrak{N}+5$; hence, $\Lambda \left(\mu \right)$ has $\mathfrak{M}+\mathfrak{N}+5$ roots. Moreover, other cases can be obtained by using similar methods.

□

Remark 1.

In Theorem 1, if ${\mathfrak{e}}_2=0$, but ${\mathfrak{e}}_2^{\prime }\ne 0$, we can obtain the same conclusions. In fact, the highest degree of μ in $\Lambda \left(\mu \right)$ is $\mathfrak{M}+\mathfrak{N}+4$. Thus, it has $\mathfrak{M}+\mathfrak{N}+4$, $\mathfrak{M}+\mathfrak{N}+3$, $\mathfrak{M}+\mathfrak{N}+2$, $\mathfrak{M}+\mathfrak{N}+1$, $\mathfrak{M}+\mathfrak{N}$ eigenvalues, respectively.

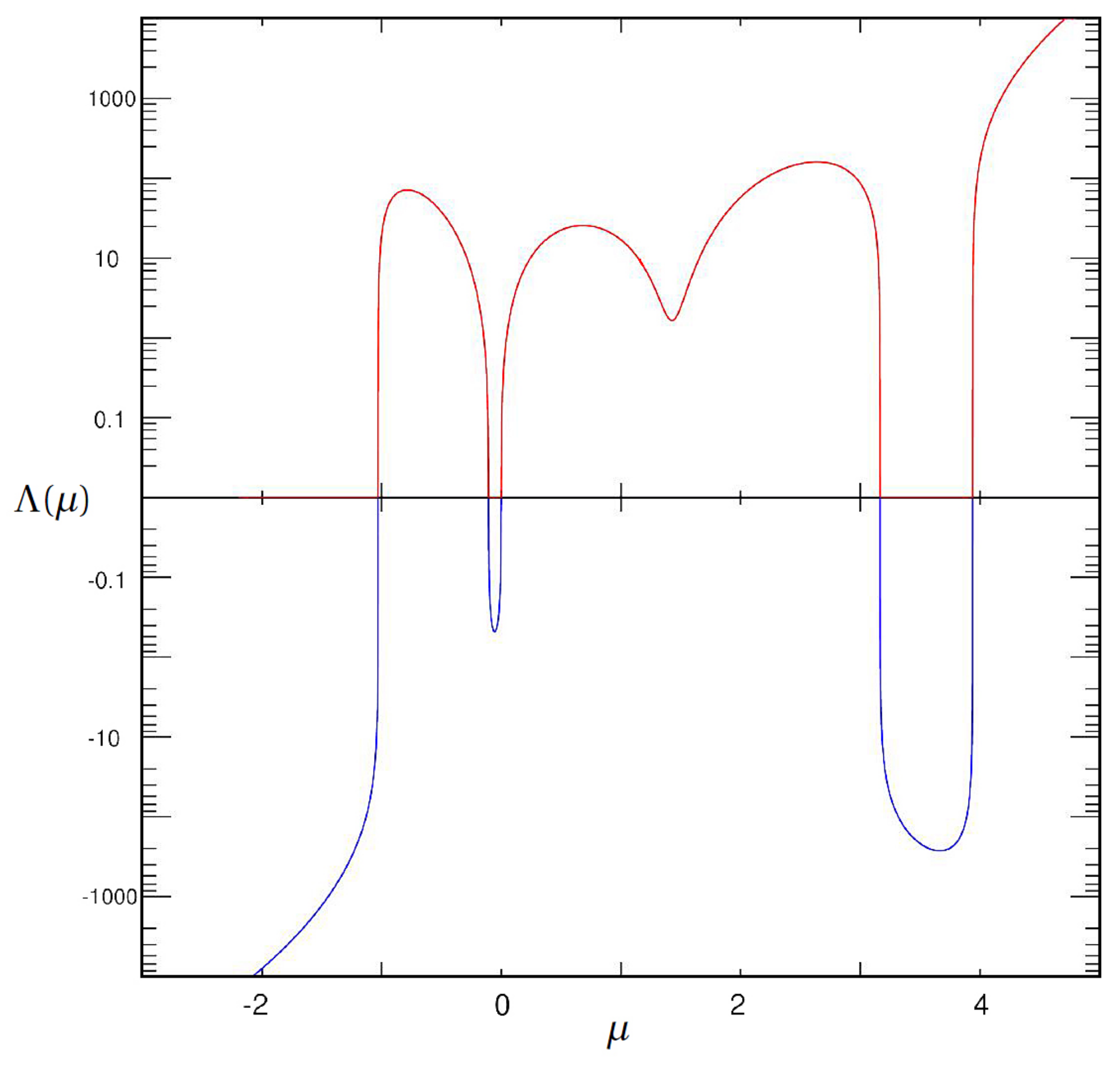
Example 1.

We study a specific SLP:

$$\left\{\begin{array}{c}-{\left(q\left(t\right)f^{\prime }\left(t\right)\right)}^{\prime }+p\left(t\right)f\left(t\right)=\mu w\left(t\right)f\left(t\right),t\in \mathfrak{I}=(-1,0)\cup (0,2).\hfill \\ A_{\mu }F(-1)+B_{\mu }F\left(2\right)=0,\hfill \\ F(0+)-{\Gamma }_{\mu }F(0-)=0,\hfill \end{array}\right.$$

where

$$A_{\mu }=\left(\begin{array}{cc}1& \mu \\ 0& 2\mu \end{array}\right),B_{\mu }=\left(\begin{array}{cc}1& 2\mu +1\\ 0& \mu \end{array}\right),{\Gamma }_{\mu }=\left(\begin{array}{cc}\mu & 2\mu \\ 1& 0\end{array}\right).$$

We choose $\mathfrak{M}=\mathfrak{N}=1$, and $q\left(t\right),p\left(t\right),w\left(t\right)$ are piece-wise constant functions:

$$q\left(t\right)=\left\{\begin{array}{c}\infty ,(-1,-\frac{2}{3})\hfill \\ \frac{1}{3},(-\frac{2}{3},-\frac{1}{3})\hfill \\ \infty ,(-\frac{1}{3},0)\hfill \\ \infty ,(0,\frac{1}{2})\hfill \\ \frac{1}{2},(\frac{1}{2},1)\hfill \\ \infty ,(1,2)\hfill \end{array},p\left(t\right)=\left\{\begin{array}{c}3,(-1,-\frac{2}{3})\hfill \\ 0,(-\frac{2}{3},-\frac{1}{3})\hfill \\ 6,(-\frac{1}{3},0)\hfill \\ 2,(0,\frac{1}{2})\hfill \\ 0,(\frac{1}{2},1)\hfill \\ 1,(1,2)\hfill \end{array},w\left(t\right)=\left\{\begin{array}{c}3,(-1,-\frac{2}{3})\hfill \\ 0,(-\frac{2}{3},-\frac{1}{3})\hfill \\ 3,(-\frac{1}{3},0)\hfill \\ 2,(0,\frac{1}{2})\hfill \\ 0,(\frac{1}{2},1)\hfill \\ 1,(1,2)\hfill \end{array}\right.\right.\right..$$

From the conditions, we know ${\mathfrak{e}}_2=2\ne 0$. By a direct calculation, we have

$$\Lambda \left(\mu \right)=6{\mu }^7-53{\mu }^6+142{\mu }^5-71{\mu }^4-166{\mu }^3+142{\mu }^2+17\mu .$$

Then the number of eigenvalues of this problem is 7.

$${\mu }_1\approx -1.0291,{\mu }_2\approx -0.1071,{\mu }_3=0,{\mu }_4\approx 1.4317+0.1083i,$$

$${\mu }_5\approx 1.4317-0.1083i,{\mu }_6\approx 3.1662,{\mu }_7\approx 3.9400.$$

Figure 1 shows the trace of $\Lambda \left(\mu \right)$. For clarity, we use a logarithmic scale for the vertical axis. We label trajectories above the horizontal axis in red and trajectories below the horizontal axis in blue. The alternating red and blue pattern represents the zero of the $\Lambda \left(\mu \right)$. By doing so, we can observe that the function has five real roots, meeting our desired outcome.

4. Matrix Presentations of (1)–(5)

In this section, we discuss the matrix representations of problems (1)–(5) with finite spectra.

Definition 5.

If the eigenvalues of SLPs of the Atkinson type coincide with matrix eigenvalue problems, then we call them equivalent.

For (1)–(5), we rebuild the matrix eigenvalue problems, which have the following form

$$BT=\mu FT,$$

whose eigenvalues coincide with the corresponding SLPs of the Atkinson type. Assume (16) holds, we have

$$\begin{array}{cc}\hfill & q_{\mathfrak{i}}={\left({\int }_{c_{2\mathfrak{i}-1}}^{c_{2\mathfrak{i}}}s\right)}^{-1},\mathfrak{i}=1,2,\cdots ,\mathfrak{M};\hfill \\ \hfill & {\tilde{q}}_{\mathfrak{j}}={\left({\int }_{d_{2\mathfrak{j}-1}}^{d_{2\mathfrak{j}}}s\right)}^{-1},\mathfrak{j}=1,2,\cdots ,\mathfrak{N}.\hfill \end{array}$$

(18)

In accordance with (14) and (15), we know $q_{\mathfrak{i}},w_{\mathfrak{i}},{\tilde{q}}_{\mathfrak{j}},{\tilde{w}}_{\mathfrak{j}}\in \mathbb{R}\backslash \left\{0\right\}$. In addition, by (14) and (15), for each solution $(u,v)$ of system (10), on the sub-intervals where $s\equiv 0$, we know that u is constant; regarding the sub-intervals where $p\equiv w\equiv 0$, we know that v is constant.

Let

$$\begin{array}{cc}\hfill & u\left(t\right)=\left\{\begin{array}{cc}{u}_{\mathfrak{i}},\hfill & t\in \left[c_{2\mathfrak{i}},c_{2\mathfrak{i}+1}\right],\mathfrak{i}=0,\cdots ,\mathfrak{M}-1,\hfill \\ u_{\mathfrak{M}},\hfill & t\in \left[c_{2\mathfrak{M}},\eta \right),\hfill \\ {\tilde{u}}_0,\hfill & t\in \left(\eta ,d_1\right],\hfill \\ {\tilde{u}}_{\mathfrak{j}},\hfill & t\in \left[d_{2\mathfrak{j}},d_{2\mathfrak{j}+1}\right],\mathfrak{j}=1,\cdots ,\mathfrak{N};\hfill \end{array}\right.\hfill \\ \hfill & v\left(t\right)=\left\{\begin{array}{cc}{v}_{\mathfrak{i}},\hfill & t\in \left[c_{2\mathfrak{i}},c_{2\mathfrak{i}+1}\right],\mathfrak{i}=0,\cdots ,\mathfrak{M}-1,\hfill \\ {\tilde{v}}_{\mathfrak{j}},\hfill & t\in \left[d_{2\mathfrak{j}},d_{2\mathfrak{j}+1}\right],\mathfrak{j}=1,\cdots ,\mathfrak{N};\hfill \end{array}\right.\hfill \end{array}$$

(19)

and

$$v_0=v\left(c_0\right)=v\left(c\right),{\tilde{v}}_{\mathfrak{N}+1}=v\left(d_{2\mathfrak{N}+1}\right)=v\left(d\right),v_{\mathfrak{M}+1}=v(\eta -0),{\tilde{v}}_0=v(\eta +0).$$

(20)

Lemma 4.

([23]) Suppose that Equation (1) is of the Atkinson type. Then for each solution $(u,v)$ of (10), we have

$$q_{\mathfrak{i}}\left(u_{\mathfrak{i}}-u_{\mathfrak{i}-1}\right)=v_{\mathfrak{i}},\mathfrak{i}=1,2,\cdots ,\mathfrak{M},$$

(21)

$$v_{\mathfrak{i}+1}-v_{\mathfrak{i}}=u_{\mathfrak{i}}\left(p_{\mathfrak{i}}-\mu w_{\mathfrak{i}}\right),\mathfrak{i}=0,1,\cdots ,\mathfrak{M},$$

(22)

$${\tilde{q}}_{\mathfrak{j}}\left({\tilde{u}}_{\mathfrak{j}}-{\tilde{u}}_{\mathfrak{j}-1}\right)={\tilde{v}}_{\mathfrak{j}},\mathfrak{j}=1,2,\cdots ,\mathfrak{N},$$

(23)

$${\tilde{v}}_{\mathfrak{j}+1}-{\tilde{v}}_{\mathfrak{j}}={\tilde{u}}_{\mathfrak{j}}\left({\tilde{p}}_{\mathfrak{j}}-\mu {\tilde{w}}_{\mathfrak{j}}\right),\mathfrak{j}=0,1,\cdots ,\mathfrak{N}.$$

(24)

On the contrary, for any solution, $u_{\mathfrak{i}}(\mathfrak{i}=\overline{0,\mathfrak{M}}),v_{\mathfrak{i}}(\mathfrak{i}=\overline{0,\mathfrak{M}+1}),{\tilde{u}}_{\mathfrak{j}}(\mathfrak{j}=\overline{0,\mathfrak{N}}),$ and ${\tilde{v}}_{\mathfrak{j}}(\mathfrak{j}=\overline{0,\mathfrak{N}+1})$ of systems (21)–(24), there exists a unique solution $(u,v)$ of system (10), such that (19) and (20) holds.

Theorem 2.

Suppose ${\xi }_{\mathfrak{i}},{\tau }_{\mathfrak{i}},{\mathfrak{e}}_{\mathfrak{i}},{\xi }_{\mathfrak{i}}^{\prime },{\tau }_{\mathfrak{i}}^{\prime },{\mathfrak{e}}_{\mathfrak{i}}^{\prime }\in \mathbb{R}(\mathfrak{i}=\overline{1,4})$ satisfy (6)–(9) and ${\mathfrak{e}}_2\ne 0$. Define an $(\mathfrak{M}+\mathfrak{N}+5)\times (\mathfrak{M}+\mathfrak{N}+5)$ matrix $\mathfrak{Q}$ as follows:

$$\left(\begin{array}{ccccccccccccc}{\xi }_2& {\xi }_1& & & & & & & & & & {\xi }_3& {\xi }_4\\ 1& q_1& -q_1& & & & & & & & & & \\ & -q_1& q_1+q_2& -q_2& & & & & & & & & \\ & & \ddots & \ddots & \ddots & & & & & & & & \\ & & & -q_{\mathfrak{M}-1}& q_{\mathfrak{M}-1}+q_{\mathfrak{M}}& -q_{\mathfrak{M}}& & & & & & & \\ & & & & -q_{\mathfrak{M}}& q_{\mathfrak{M}}& -1& & & & & & \\ & & & & & -{\mathfrak{e}}_1^{\prime }& -{\mathfrak{e}}_2^{\prime }& 1& & & & & \\ & & & & & {\mathfrak{e}}_3^{\prime }& {\mathfrak{e}}_4^{\prime }& {\tilde{q}}_1& -{\tilde{q}}_1& & & & \\ & & & & & & & -{\tilde{q}}_1& {\tilde{q}}_1+{\tilde{q}}_2& -{\tilde{q}}_2& & & \\ & & & & & & & & \ddots & \ddots & \ddots & & \\ & & & & & & & & & -{\tilde{q}}_{\mathfrak{N}-1}& {\tilde{q}}_{\mathfrak{N}-1}+{\tilde{q}}_{\mathfrak{N}}& -{\tilde{q}}_{\mathfrak{N}}& \\ & & & & & & & & & & -{\tilde{q}}_{\mathfrak{N}}& {\tilde{q}}_{\mathfrak{N}}& -1\\ {\tau }_2& {\tau }_1& & & & & & & & & & {\tau }_3& {\tau }_4\end{array}\right).$$

Let $\mathfrak{P}=\mathit{diag}(0,p_0,p_1,p_2,\cdots ,p_{\mathfrak{M}},0,{\tilde{p}}_0,{\tilde{p}}_1,{\tilde{p}}_2,\cdots ,{\tilde{p}}_{\mathfrak{N}-1},{\tilde{p}}_{\mathfrak{N}},0)$ and

$$\mathfrak{W}=\left(\begin{array}{ccccccccccccc}{\xi }_2^{\prime }& {\xi }_1^{\prime }& & & & & & & & & & {\xi }_3^{\prime }& {\xi }_4^{\prime }\\ & w_0& & & & & & & & & & & \\ & & w_1& & & & & & & & & & \\ & & & \ddots & & & & & & & & & \\ & & & & w_{\mathfrak{M}-1}& & & & & & & & \\ & & & & & w_{\mathfrak{M}}& & & & & & & \\ & & & & & {\mathfrak{e}}_1& {\mathfrak{e}}_2& & & & & & \\ & & & & & -{\mathfrak{e}}_3& -{\mathfrak{e}}_4& {\tilde{w}}_0& & & & & \\ & & & & & & & & {\tilde{w}}_1& & & & \\ & & & & & & & & & \ddots & & & \\ & & & & & & & & & & {\tilde{w}}_{\mathfrak{N}-1}& & \\ & & & & & & & & & & & {\tilde{w}}_{\mathfrak{N}}& \\ {\tau }_2^{\prime }& {\tau }_1^{\prime }& & & & & & & & & & {\tau }_3^{\prime }& {\tau }_4^{\prime }\end{array}\right).$$

Then SLPs (1)–(5) are equivalent to matrix eigenvalue problems

$$(\mathfrak{Q}+\mathfrak{P})U=\mu \mathfrak{W}U,$$

(25)

where $U={\left(v_0,u_0,u_1,\cdots ,u_{\mathfrak{M}},v_{\mathfrak{M}+1},{\tilde{u}}_0,{\tilde{u}}_1,\cdots ,{\tilde{u}}_{\mathfrak{N}},{\tilde{v}}_{\mathfrak{N}+1}\right)}^T$. Furthermore, (19) shows the relationship between the eigenfunction $u\left(x\right)$ of problems (1)–(5) and eigenvector U of (25), in terms of sharing the same eigenvalues.

Proof. 

Between the solutions of the following system:

$$q_1(u_1-u_0)-v_0=u_0(p_0-\mu w_0),$$

(26)

$$q_{\mathfrak{i}+1}(u_{\mathfrak{i}+1}-u_{\mathfrak{i}})-q_{\mathfrak{i}}(u_{\mathfrak{i}}-u_{\mathfrak{i}-1})=u_{\mathfrak{i}}(p_{\mathfrak{i}}-\mu w_{\mathfrak{i}}),\mathfrak{i}=1,2,\cdots ,\mathfrak{M}-1,$$

(27)

$$v_{\mathfrak{M}+1}-q_{\mathfrak{M}}(u_{\mathfrak{M}}-u_{\mathfrak{M}-1})=u_{\mathfrak{M}}(p_{\mathfrak{M}}-\mu w_{\mathfrak{M}}),$$

(28)

$${\tilde{q}}_1({\tilde{u}}_1-{\tilde{u}}_0)-{\tilde{v}}_0={\tilde{u}}_0({\tilde{p}}_o-\mu {\tilde{w}}_0),$$

(29)

$${\tilde{q}}_{\mathfrak{j}+1}({\tilde{u}}_{\mathfrak{j}+1}-{\tilde{u}}_{\mathfrak{j}})-{\tilde{q}}_{\mathfrak{j}}({\tilde{u}}_{\mathfrak{j}}-{\tilde{u}}_{\mathfrak{j}-1})={\tilde{u}}_{\mathfrak{j}}({\tilde{p}}_{\mathfrak{j}}-\mu {\tilde{w}}_{\mathfrak{j}}),\mathfrak{j}=1,2,\cdots ,\mathfrak{N}-1,$$

(30)

$${\tilde{v}}_{\mathfrak{N}+1}-{\tilde{q}}_{\mathfrak{N}}({\tilde{u}}_{\mathfrak{N}}-{\tilde{u}}_{\mathfrak{N}-1})={\tilde{u}}_{\mathfrak{N}}({\tilde{p}}_{\mathfrak{N}}-\mu {\tilde{w}}_{\mathfrak{N}}).$$

(31)

and those of (21)–(24), a one-to-one correspondence exists by the assumption.

Now, we suppose $u_{\mathfrak{i}}(\mathfrak{i}=\overline{0,\mathfrak{M}})$ and $v_{\mathfrak{i}}(\mathfrak{i}=\overline{0,\mathfrak{M}+1)}$ are solutions of systems (21) and (22). Then (26)–(28) follow from (21) to (22). Similarly, (29)–(31) follow from (23) to (24) by assuming that ${\tilde{u}}_{\mathfrak{j}}(\mathfrak{j}=\overline{0,\mathfrak{N}})$ and ${\tilde{v}}_{\mathfrak{j}}(\mathfrak{j}=\overline{0,\mathfrak{N}})$ are solutions of systems (23) and (24).

In other words, let $u_{\mathfrak{i}}(\mathfrak{i}=\overline{0,\mathfrak{M}})$ be a solution of (26)–(28); thus, $v_0$ and $v_{\mathfrak{M}+1}$ can be calculated by (26) and (28). Assume that $v_{\mathfrak{i}}(\mathfrak{i}=\overline{1,\mathfrak{M}})$ is defined in (21). Then, using (26), and utilizing induction on (27), (22) holds. Moreover, (23) and (24) can be similarly obtained.

Hence, according to Theorem 2, any solution of (10) is uniquely determined by solutions of (26)–(31). Note the first row of matrix (25)

$${\xi }_2{v}_0+{\xi }_1{u}_0+{\xi }_3{\tilde{u}}_{\mathfrak{N}}+{\xi }_4{\tilde{v}}_{\mathfrak{N}+1}=\mu ({\xi }_2^{\prime }{v}_0+{\xi }_1^{\prime }{u}_0+{\xi }_3^{\prime }{\tilde{u}}_{\mathfrak{N}}+{\xi }_4^{\prime }{\tilde{v}}_{\mathfrak{N}+1}),$$

(32)

and the last row of matrix (25)

$${\tau }_2{v}_0+{\tau }_1{u}_0+{\tau }_3{\tilde{u}}_{\mathfrak{N}}+{\tau }_4{\tilde{v}}_{\mathfrak{N}+1}=\mu ({\tau }_2^{\prime }{v}_0+{\tau }_1^{\prime }{u}_0+{\tau }_3^{\prime }{\tilde{u}}_{\mathfrak{N}}+{\tau }_4^{\prime }{\tilde{v}}_{\mathfrak{N}+1}),$$

(33)

substituting

$$u_0=u\left(c\right)=f\left(c\right),{\tilde{u}}_{\mathfrak{N}}=u\left(d\right)=f\left(d\right),v_0=v\left(c\right)=\left(q{f}^{\prime }\right)\left(c\right),{\tilde{v}}_{\mathfrak{N}+1}=v\left(d\right)=\left(q{f}^{\prime }\right)\left(d\right),$$

into (32) and (33), we obtain (2) and (3). From (4) to (5), we obtain

$${\tilde{u}}_0=({\mathfrak{e}}_1\mu +{\mathfrak{e}}_1^{\prime })u_{\mathfrak{M}}+({\mathfrak{e}}_2\mu +{\mathfrak{e}}_2^{\prime })v_{\mathfrak{M}+1},{\tilde{v}}_0=({\mathfrak{e}}_3\mu +{\mathfrak{e}}_3^{\prime })u_{\mathfrak{M}}+({\mathfrak{e}}_4\mu +{\mathfrak{e}}_4^{\prime })v_{\mathfrak{M}+1},$$

(34)

and let $U={\left(v_0,u_0,u_1,\cdots ,u_{\mathfrak{M}},v_{\mathfrak{M}+1},{\tilde{u}}_0,{\tilde{u}}_1,\cdots ,{\tilde{u}}_{\mathfrak{N}},{\tilde{v}}_{\mathfrak{N}+1}\right)}^T.$ Then the equivalence follows from (26) to (34). □

The following result shows that the SLP of the Atkinson type is equivalent to the SLP with piecewise constant coefficients in the sense that they have similar eigenvalues.

Theorem 3.

Suppose that (1) is of the Atkinson type and $q_{\mathfrak{i}}(\mathfrak{i}=\overline{1,\mathfrak{M}}),{\tilde{q}}_{\mathfrak{j}}(\mathfrak{j}=\overline{1,\mathfrak{N}}),p_{\mathfrak{i}},w_{\mathfrak{i}}(\mathfrak{i}=\overline{0,\mathfrak{M}}),{\tilde{p}}_{\mathfrak{j}},{\tilde{w}}_{\mathfrak{j}}(\mathfrak{j}=\overline{0,\mathfrak{N}})$ are defined in (16) and (18). Denote piecewise constant functions $\overline{q},\overline{p},\overline{w}$ on $\mathfrak{I}$ by

$$\overline{q}\left(t\right)=\left\{\begin{array}{c}{q}_{\mathfrak{i}}(c_{2\mathfrak{i}}-c_{2\mathfrak{i}-1}),t\in [c_{2\mathfrak{i}-1},c_{2\mathfrak{i}}],\mathfrak{i}=1,\cdots ,\mathfrak{M},\hfill \\ \infty ,t\in {\cup }_{\mathfrak{i}=1}^{\mathfrak{M}}[c_{2\mathfrak{i}-2},c_{2\mathfrak{i}-1}]\cup \left[c_{2\mathfrak{M}},\eta \right),\hfill \\ {\tilde{q}}_{\mathfrak{j}}(d_{2\mathfrak{j}}-d_{2\mathfrak{j}-1}),t\in [d_{2\mathfrak{j}-1},d_{2\mathfrak{j}}],\mathfrak{j}=1,\cdots ,\mathfrak{N},\hfill \\ \infty ,t\in {\cup }_{\mathfrak{j}=1}^{\mathfrak{N}}[d_{2\mathfrak{j}},d_{2\mathfrak{j}+1}]\cup (\eta ,d_1];\hfill \end{array}\right.$$

(35)

$$\overline{p}\left(t\right)=\left\{\begin{array}{c}\frac{p_{\mathfrak{i}}}{c_{2\mathfrak{i}+1}-c_{2\mathfrak{i}}},t\in [c_{2\mathfrak{i}},c_{2\mathfrak{i}+1}],\mathfrak{i}=0,\cdots ,\mathfrak{M}-1,\hfill \\ \frac{p_{\mathfrak{M}}}{\eta -c_{2\mathfrak{M}}},t\in [c_{2\mathfrak{M}},\eta ),\hfill \\ 0,t\in {\cup }_{\mathfrak{i}=1}^{\mathfrak{M}}[c_{2\mathfrak{i}-1},c_{2\mathfrak{i}}],\hfill \\ \frac{{\tilde{p}}_{\mathfrak{j}}}{d_{2\mathfrak{j}+1}-d_{2\mathfrak{j}}},t\in [d_{2\mathfrak{j}},d_{2\mathfrak{j}+1}],\mathfrak{j}=1,\cdots ,\mathfrak{N},\hfill \\ \frac{{\tilde{p}}_0}{d_1-\eta },t\in (\eta ,d_1],\hfill \\ 0,t\in {\cup }_{\mathfrak{j}=1}^{\mathfrak{N}}[d_{2\mathfrak{j}-1},d_{2\mathfrak{j}}];\hfill \end{array}\right.$$

(36)

$$\overline{w}\left(t\right)=\left\{\begin{array}{c}\frac{w_{\mathfrak{i}}}{c_{2\mathfrak{i}+1}-c_{2\mathfrak{i}}},t\in [c_{2\mathfrak{i}},c_{2\mathfrak{i}+1}],\mathfrak{i}=0,\cdots ,\mathfrak{M}-1,\hfill \\ \frac{w_{\mathfrak{M}}}{\eta -c_{2\mathfrak{M}}},t\in [c_{2\mathfrak{M}},\eta ),\hfill \\ 0,t\in {\cup }_{\mathfrak{i}=1}^{\mathfrak{M}}[c_{2\mathfrak{i}-1},c_{2\mathfrak{i}}],\hfill \\ \frac{{\tilde{w}}_{\mathfrak{j}}}{d_{2\mathfrak{j}+1}-d_{2\mathfrak{j}}},t\in [d_{2\mathfrak{j}},d_{2\mathfrak{j}+1}],\mathfrak{j}=1,\cdots ,\mathfrak{N},\hfill \\ \frac{{\tilde{w}}_0}{d_1-\eta },t\in (\eta ,d_1],\hfill \\ 0,t\in {\cup }_{\mathfrak{j}=1}^{\mathfrak{N}}[d_{2\mathfrak{j}-1},d_{2\mathfrak{j}}];\hfill \end{array}\right.$$

(37)

Suppose that (2)–(5) hold. Then the eigenvalues of SLPs (1)–(5) coincide with the eigenvalues of the SLP

$$-{\left(\overline{q}\left(t\right)f^{\prime }\left(t\right)\right)}^{\prime }+\overline{p}\left(t\right)f\left(t\right)=\mu \overline{w}\left(t\right)f\left(t\right),t\in \mathfrak{I}$$

(38)

with (2)–(5).

Proof. 

It is observed that SLPs (1)–(5) and (29), (2)–(5) determine the same

$$q_{\mathfrak{i}},\mathfrak{i}=1,2,\cdots ,\mathfrak{M},p_{\mathfrak{i}},w_{\mathfrak{i}},\mathfrak{i}=0,1,\cdots ,\mathfrak{M};$$

$${\tilde{q}}_{\mathfrak{j}},\mathfrak{j}=1,2,\cdots ,\mathfrak{N},{\tilde{p}}_{\mathfrak{j}},{\tilde{w}}_{\mathfrak{j}},\mathfrak{j}=0,1,\cdots ,\mathfrak{N}.$$

Thus, they are equivalent to the same matrix eigenvalue problem, based on Theorem 2. The results follow. □

In light of Theorem 3, we know that for a fixed set of Equations (2)–(5) on a given interval, there exists a family of SLPs of the Atkinson type, which have the same eigenvalues as SLPs (38), (2)–(5). We refer to this family as the equivalent family of SLPs (38), (2)–(5).

Next, we will illustrate that matrix eigenvalue problems in the following form:

$$AT=\mu FT$$

(39)

have representations as Atkinson-type SLPs.

Theorem 4.

Let $n\ge 7$, ${\mathfrak{e}}_{\mathfrak{i}},{\mathfrak{e}}_{\mathfrak{i}}^{\prime }(\mathfrak{i}=1,2,3,4)$ in (4) and (5) satisfy $det\left({\Gamma }_{\mu }\right)\ne 0$ (where ${\Gamma }_{\mu }$ is defined in (9)), assume ${\mathfrak{e}}_2\ne 0$. Assume that A is an $n\times n$ matrix as follows:

$$\left(\begin{array}{cccccccccccc}{a}_{11}& a_{12}& & & & & & & & & a_{1,n-1}& a_{1n}\\ 1& a_{22}& a_{23}& & & & & & & & & \\ & a_{23}& a_{33}& a_{34}& & & & & & & & \\ & & \ddots & \ddots & \ddots & & & & & & & \\ & & & a_{m,m+1}& a_{m+1,m+1}& a_{m+1,m+2}& & & & & & \\ & & & & a_{m+1,m+2}& a_{m+2,m+2}& -1& & & & & \\ & & & & & a_{m+3,m+2}& a_{m+3,m+3}& 1& & & & \\ & & & & & a_{m+4,m+2}& a_{m+4,m+3}& a_{m+4,m+4}& a_{m+4,m+5}& & & \\ & & & & & & & a_{m+4,m+5}& a_{m+5,m+5}& a_{m+5,m+6}& & \\ & & & & & & & \ddots & \ddots & \ddots & & \\ & & & & & & & & a_{n-2,n-3}& a_{n-2,n-2}& a_{n-2,n-1}& \\ & & & & & & & & & a_{n-2,n-1}& a_{n-1,n-1}& -1\\ a_{n1}& a_{n2}& & & & & & & & & a_{n,n-1}& a_{nn}\end{array}\right),$$

where $a_{\mathfrak{j},\mathfrak{j}+1}\ne 0(\mathfrak{j}=2,3,\cdots ,n-2),2\le m\le n-5,a_{\mathfrak{i}\mathfrak{j}}\in \mathbb{R}(1\le \mathfrak{i},\mathfrak{j}\le n),$$a_{21}=a_{m+3,m+4}=1,a_{m+2,m+3}=a_{n-1,n}=-1$. Let F be an $n\times n$ matrix of the following form:

$$\left(\begin{array}{ccccccccccccc}{f}_{11}& f_{12}& & & & & & & & & & f_{1,n-1}& f_{1n}\\ & f_{22}& & & & & & & & & & & \\ & & f_{33}& & & & & & & & & & \\ & & & \ddots & & & & & & & & & \\ & & & & f_{m+1,m+1}& & & & & & & & \\ & & & & & f_{m+2,m+2}& & & & & & & \\ & & & & & f_{m+3,m+2}& f_{m+3,m+3}& & & & & & \\ & & & & & f_{m+4,m+2}& f_{m+4,m+3}& f_{m+4,m+4}& & & & & \\ & & & & & & & & f_{m+5,m+5}& & & & \\ & & & & & & & & & \ddots & & & \\ & & & & & & & & & & f_{n-2,n-2}& & \\ & & & & & & & & & & & f_{n-1,n-1}& \\ f_{n1}& f_{n2}& & & & & & & & & & f_{n,n-1}& f_{nn}\end{array}\right),$$

where $f_{\mathfrak{j}\mathfrak{j}}\ne 0$, $f_{\mathfrak{j}\mathfrak{j}}\in \mathbb{R}(\mathfrak{j}=2,3,\cdots ,n-1)$, and

$$rank\left(\begin{array}{ccccc}& a_{11}& a_{12}& a_{1,n-1}& a_{1n}\\ & a_{n1}& a_{n2}& a_{n,n-1}& a_{nn}\end{array}\right)=2,rank\left(\begin{array}{ccccc}& f_{11}& f_{12}& f_{1,n-1}& f_{1n}\\ & f_{n1}& f_{n2}& f_{n,n-1}& f_{nn}\end{array}\right)=2,$$

$$rank\left(\begin{array}{ccccc}& a_{11}& a_{12}& a_{1,n-1}& a_{1n}\\ & f_{11}& f_{12}& f_{1,n-1}& f_{1n}\end{array}\right)=2,rank\left(\begin{array}{ccccc}& a_{n1}& a_{n2}& a_{n,n-1}& a_{nn}\\ & f_{n1}& f_{n2}& f_{n,n-1}& f_{nn}\end{array}\right)=2.$$

Then (39) represents an Atkinson-type SLP in the form of (1)–(5). Furthermore, SLPs (38), (2)–(5) have unique representations when a fixed partition (13) of $\mathfrak{I}$ is given, using the notations in (16) and (18). All SL representations of (39) are given by the corresponding equivalent families of SLPs (38), (2)–(5).

Proof. 

Let $\mathfrak{M}=m$, $\mathfrak{N}=n-m-5$, $\mathfrak{I}=[c,\eta )\cup (\eta ,d]$, $-\infty <c<d<\infty$. Firstly, one defines the parameters in (2) and (3), let

$${\xi }_2=a_{11},{\xi }_1=a_{12},{\xi }_3=a_{1,n-1},{\xi }_4=a_{1n};$$

$${\tau }_2=a_{n1},{\tau }_1=a_{n2},{\tau }_3=a_{n,n-1},{\tau }_4=a_{nn};$$

$${\xi }_2^{\prime }=f_{11},{\xi }_1^{\prime }=f_{12},{\xi }_3^{\prime }=a{f}_{1,n-1},{\xi }_4^{\prime }=f_{1n};$$

$${\tau }_2^{\prime }=f_{n1},{\tau }_1^{\prime }=f_{n2},{\tau }_3^{\prime }=f_{n,n-1},{\tau }_4^{\prime }=f_{nn};$$

and

$$-{\mathfrak{e}}_1^{\prime }=a_{m+3,m+2},-{\mathfrak{e}}_2^{\prime }=a_{m+3,m+3},{\mathfrak{e}}_3^{\prime }=a_{m+4,m+2},{\mathfrak{e}}_4^{\prime }=a_{m+4,m+3};$$

$${\mathfrak{e}}_1=f_{m+3,m+2},{\mathfrak{e}}_2=f_{m+3,m+3},-{\mathfrak{e}}_3=f_{m+4,m+2},-{\mathfrak{e}}_4=f_{m+4,m+3}.$$

For a given partition of $\mathfrak{I}$ by (13), one can define piecewise constant functions $\overline{q},\overline{p}$ and $\overline{w}$ on the interval $\mathfrak{I}$ that satisfies (7), (14) and (15), as follows:

$$q_{\mathfrak{i}}=-a_{\mathfrak{i}+1,\mathfrak{i}+2},\mathfrak{i}=\overline{1,\mathfrak{M}},{\tilde{q}}_{\mathfrak{j}}=-a_{\mathfrak{M}+\mathfrak{j}+3,\mathfrak{M}+\mathfrak{j}+4},\mathfrak{j}=\overline{1,\mathfrak{N}};$$

$$w_{\mathfrak{i}}=f_{\mathfrak{i}+2,\mathfrak{i}+2},\mathfrak{i}=\overline{0,\mathfrak{M}},{\tilde{w}}_{\mathfrak{j}}=f_{\mathfrak{M}+\mathfrak{j}+4,\mathfrak{M}+\mathfrak{j}+4},\mathfrak{j}=\overline{0,\mathfrak{N}};$$

and

$$\begin{array}{cc}& p_0=a_{22}-q_1,p_{\mathfrak{i}}=a_{\mathfrak{i}+2,\mathfrak{i}+2}-q_{\mathfrak{i}}-q_{\mathfrak{i}+1},\mathfrak{i}=\overline{1,\mathfrak{M}-1},\hfill \\ & p_{\mathfrak{M}}=a_{\mathfrak{M}+2,\mathfrak{M}+2}-q_{\mathfrak{M}};\hfill \\ & {\tilde{p}}_0=a_{\mathfrak{M}+4,\mathfrak{M}+4}-{\tilde{q}}_1,{\tilde{p}}_{\mathfrak{j}}=a_{\mathfrak{M}+\mathfrak{j}+4,\mathfrak{M}+\mathfrak{j}+4}-{\tilde{q}}_{\mathfrak{j}}-{\tilde{q}}_{\mathfrak{j}+1},\mathfrak{j}=\overline{1,\mathfrak{N}-1},\hfill \\ & {\tilde{p}}_n=a_{\mathfrak{M}+\mathfrak{N}+4,\mathfrak{M}+\mathfrak{N}+4}-{\tilde{q}}_{\mathfrak{N}}.\hfill \end{array}$$

Next, we define $\overline{q},\overline{p}$ and $\overline{w}$ by (35)–(37), respectively. Such piecewise constant functions, $\overline{q},\overline{p}$, and $\overline{w}$ on interval $\mathfrak{I}$, satisfying (7) and (14) and (15), are found; Equation (38) is of the Atkinson type, and (16) and (18) satisfy with $q,p$, and w replaced by $\overline{q},\overline{p}$, and $\overline{w}$, respectively. Obviously, Equation (39) is of the same form as Equation (25). Therefore, the problem (39) is equivalent to the SLPs (1)–(5) by Theorem 2. The last part is yielded by Theorem 3. □

Remark 2.

If ${\xi }_{\mathfrak{i}}^{\prime }={\tau }_{\mathfrak{i}}^{\prime }={\mathfrak{e}}_{\mathfrak{i}}=0$ ($\mathfrak{i}=\overline{1,4}$) in (2)–(5), then the problem under consideration degenerates to the case discussed in [22].

If ${\mathfrak{e}}_{\mathfrak{i}}=0$ ($\mathfrak{i}=\overline{1,4}$) in (4) and (5), then the problem under consideration degenerates to the case discussed in [26].