On Some Branched Continued Fraction Expansions for Horn’s Hypergeometric Function H₄(a,b;c,d;z₁,z₂) Ratios

Abstract

The paper deals with the problem of representation of Horn’s hypergeometric functions by branched continued fractions. The formal branched continued fraction expansions for three different Horn’s hypergeometric function $H_4$ ratios are constructed. The method employed is a two-dimensional generalization of the classical method of constructing of Gaussian continued fraction. It is proven that the branched continued fraction, which is an expansion of one of the ratios, uniformly converges to a holomorphic function of two variables on every compact subset of some domain $H,$$H\subset {\mathbb{C}}^2,$ and that this function is an analytic continuation of this ratio in the domain $H.$ The application to the approximation of functions of two variables associated with Horn’s double hypergeometric series $H_4$ is considered, and the expression of solutions of some systems of partial differential equations is indicated.

1. Introduction

It is well known that BCFs are a multidimensional generalization of continued fractions, which are one of the most intriguing sections of classical analysis.

BCFs have been used in various fields, in particular in numerical theory to express algebraic irrational numbers ([1], Chapter 3), in computational mathematics for the solution of systems of linear algebraic Equations ([2], Chapter 4), in applied mathematics for the solution of differential Equations ([1], Chapter 5), in the theory of probabilities for some problems related to Markov processes ([1], Chapter 4), in chemistry to calculate the Hosoya index (see, [3,4]), in analysis of approximating functions of one and several variables (see, ([1], Chapter 5), ([2], Chapter 3), and [5,6,7,8,9]). It should be noted that the last direction is the most developed. Furthermore, it is here that BCFs are considered special families of functions of several complex variables.

To represent a hypergeometric function of several complex variables in BCF form, we need to solve the following three problems:

(i)

To construct the BCFE;

(ii)

To prove the convergence of the constructed expansion;

(iii)

To prove the convergence of the BCF to the function of which it is an expansion.

The first problem is to obtain the simplest structure of a BCFE whose elements are simple polynomials. This can be achieved by setting and choosing certain recurrence relations. The methods employed here are generalizations of the classical method of constructing Gaussian continued fraction. Problem (ii) consists of improving the known and developing new methods of studying the convergence of BCFs. Truncation error analysis is also considered here. The last problem is more important and is related to the so-called ’principle of correspondence’ (see, [10,11] and also ([12], Section 2.2)).

BCFEs for Appell’s hypergeometric function $F_1$ were considered in ([1,13], pp. 244–252), and BCFEs of other structures in [14]. For $F_2$, the BCFEs were constructed in [15]. In [16], the problem of the boundedness of BCFs approximants for $F_2$ was investigated. However, the problems (ii) and (iii) remain open. For $F_4$, the BCFEs were obtained in [17]. The convergence of BCFE for one partial case of $F_4$ was studied in [18]. BCFEs of different structures for $F_3$ can be found in [19,20]. For some partial cases of BCFs, the problems (ii) and (iii) were considered in [20].

For Horn’s hypergeometric function $H_3,$ such expansions were investigated in [10,21]. For $H_6,$ BCFEs were studied in [22]. In this paper, we continue to study BCFEs for hypergeometric functions from the Horn’s list (see, [23,24,25] and also books ([26], Chapter 9), ([27], Section 5.7), and ([28], Chapter 2)).

The FBCFEs for three different Horn’s hypergeometric function $H_4$ ratios will be given in Section 2. It will be proved (Theorem 3) that the BCF, which is an expansion of one of the ratios of double hypergeometric series $H_4,$ uniformly converges to a holomorphic function on every compact subset of some domain H and that this function is analytic continuation of this ratio in the domain $H.$ The applications of expansions to some problems of approximation of functions of two variables associated with the Horn’s double hypergeometric series $H_4$ and to the expression of solutions of systems of partial differential equations will be shown in Section 4.

2. Expansions

Horn’s hypergeometric function $H_4$ is defined by DPS (see, [23])

$$\begin{array}{c}\hfill H_4(a,b;c,d;\mathbf{z})=\sum _{r,s=0}^{\infty }\frac{{\left(a\right)}_{2r+s}{\left(b\right)}_s}{{\left(c\right)}_r{\left(d\right)}_s}\frac{z_1^r}{r!}\frac{z_2^s}{s!},|z_1|<p,|z_2|<l,\end{array}$$

where $a,$b, and c are complex constants; c and d are not equal to a non-positive integer; p and l are positive numbers such that $4p={(l-1)}^2$; and $l\ne 1,$${(·)}_k$ is the Pochhammer symbol defined for any complex number $\alpha$ and non-negative integer n by ${\left(\alpha \right)}_0=1$ and ${\left(\alpha \right)}_n=\alpha (\alpha +1)\dots (\alpha +n-1),$ $\mathbf{z}=(z_1,z_2)\in {\mathbb{C}}^2.$

Let ${\left(ij\right)}_0=(i_0,j_0)$ be a double index and

$$\mathcal{I}=\left\{\right(1,1);(1,2);(2,2\left)\right\}$$

be a set of double indices. Then, for each pair $(i_0,j_0)\in \mathcal{I}$ we set

$$\begin{array}{c}\hfill R_{{\left(ij\right)}_0}(a,b;c,d;\mathbf{z})=\frac{H_4(a,b;c,d;\mathbf{z})}{H_4(a+{\delta }_{i_0}^1,b+{\delta }_{i_0}^2;c+{\delta }_{j_0}^1,d+{\delta }_{j_0}^2;\mathbf{z})},\end{array}$$

(1)

where ${\delta }_i^j$ is the Kronecker symbol. Now, let ${\left(ij\right)}_k=(i_1,j_1,i_2,j_2,\dots ,i_k,j_k)$ be a multiindex (see, [29]). Then, for each ${\left(ij\right)}_0\in \mathcal{I}$ we introduce the following sets of multiindices

$$\begin{array}{c}\hfill {\mathcal{I}}_k^{{\left(ij\right)}_0}=\{{\left(ij\right)}_k:1\le i_k\le 2-{\delta }_{i_{k-1}}^2,j_k=i_k+{\delta }_{i_{k-1}}^2\},k\ge 1,\end{array}$$

and also for each ${\left(ij\right)}_k\in {\mathcal{I}}_k^{{\left(ij\right)}_0},$$k\ge 1,$ we set

$$\begin{array}{c}\hfill a_{{\left(ij\right)}_k}^{{\left(ij\right)}_0}=a+\sum _{r=0}^{k-1}{\delta }_{i_r}^1,b_{{\left(ij\right)}_k}^{{\left(ij\right)}_0}=b+\sum _{r=0}^{k-1}{\delta }_{i_r}^2,c_{{\left(ij\right)}_k}^{{\left(ij\right)}_0}=c+\sum _{r=0}^{k-1}{\delta }_{j_r}^1,d_{{\left(ij\right)}_k}^{{\left(ij\right)}_0}=d+\sum _{r=0}^{k-1}{\delta }_{j_r}^2.\end{array}$$

(2)

Theorem 1.

For each pair $(i_0,j_0)\in \mathcal{I}$ the ratio (1) has a FBCFE of the form

$$\begin{array}{c}1-\sum _{\begin{array}{c}{i}_1=1\\ j_1=i_1+{\delta }_{i_0}^2\end{array}}^{2-{\delta }_{i_0}^2}\frac{h_{{\left(ij\right)}_1}^{{\left(ij\right)}_0}{z}_{j_1}}{1}\genfrac{}{}{0pt}{}{}{-}\sum _{\begin{array}{c}{i}_2=1\\ j_2=i_2+{\delta }_{i_1}^2\end{array}}^{2-{\delta }_{i_1}^2}\frac{h_{{\left(ij\right)}_2}^{{\left(ij\right)}_0}{z}_{j_2}}{1}\genfrac{}{}{0pt}{}{}{-}\sum _{\begin{array}{c}{i}_3=1\\ j_3=i_3+{\delta }_{i_2}^2\end{array}}^{2-{\delta }_{i_2}^2}\frac{h_{{\left(ij\right)}_3}^{{\left(ij\right)}_0}{z}_{j_3}}{1}\genfrac{}{}{0pt}{}{}{-}\dots ,\end{array}$$

(3)

where for ${\left(ij\right)}_k\in {\mathcal{I}}_k^{{\left(ij\right)}_0},$$k\ge 1,$ ${\left(ij\right)}_0\in \mathcal{I},$

$$h_{{\left(ij\right)}_k}^{{\left(ij\right)}_0}=\frac{(2c-a+{\sum }_{r=0}^{k-2}(2{\delta }_{j_r}^1-{\delta }_{i_r}^1))(a+1+{\sum }_{r=0}^{k-2}{\delta }_{i_r}^1)}{(c+{\sum }_{r=0}^{k-2}{\delta }_{j_r}^1)(c+1+{\sum }_{r=0}^{k-2}{\delta }_{j_r}^1)},$$

(4)

if $i_{k-1}=j_{k-1}=i_k=j_k=1,$

$$h_{{\left(ij\right)}_k}^{{\left(ij\right)}_0}=\frac{b+{\sum }_{r=0}^{k-2}{\delta }_{i_r}^2}{d+{\sum }_{r=0}^{k-2}{\delta }_{j_r}^2},$$

(5)

if $i_{k-1}=j_{k-1}=1,$ $i_k=j_k=2,$

$$h_{{\left(ij\right)}_k}^{{\left(ij\right)}_0}=\frac{2(a+1+{\sum }_{r=0}^{k-2}{\delta }_{i_r}^1)}{c+{\sum }_{r=0}^{k-2}{\delta }_{j_r}^1},$$

(6)

if $j_{k-1}=2,$ $i_{k-1}=i_k=j_k=1,$

$$h_{{\left(ij\right)}_k}^{{\left(ij\right)}_0}=\frac{(b+{\sum }_{r=0}^{k-2}{\delta }_{i_r}^2)(d-a+{\sum }_{r=0}^{k-2}({\delta }_{j_r}^2-{\delta }_{i_r}^1))}{(d+{\sum }_{r=0}^{k-2}{\delta }_{j_r}^2)(d+1+{\sum }_{r=0}^{k-2}{\delta }_{j_r}^2)},$$

(7)

if $i_{k-1}=1,$ $j_{k-1}=i_k=j_k=2,$

$$h_{{\left(ij\right)}_k}^{{\left(ij\right)}_0}=\frac{(a+{\sum }_{r=0}^{k-2}{\delta }_{i_r}^1)(d-b+{\sum }_{r=0}^{k-2}({\delta }_{j_r}^2-{\delta }_{i_r}^2))}{(d+{\sum }_{r=0}^{k-2}{\delta }_{j_r}^2)(d+1+{\sum }_{r=0}^{k-2}{\delta }_{j_r}^2)},$$

(8)

if $j_{k-1}=i_{k-1}=j_k=2,$$i_k=1.$

Proof. 

In [30], the formal recurrence relations of Horn’s hypergeometric functions $H_4$

$$\begin{array}{c}{H}_4(a,b;c,d;\mathbf{z})\hfill \\ \hspace{1em}=H_4(a+1,b;c+1,d;\mathbf{z})-\frac{(2c-a)(a+1)}{c(c+1)}{z}_1{H}_4(a+2,b;c+2,d;\mathbf{z})\hfill \\ \hspace{1em}\hspace{1em}-\frac{b}{d}{z}_2{H}_4(a+1,b+1;c+1,d+1;\mathbf{z}),\hfill \end{array}$$

(9)

$$\begin{array}{c}{H}_4(a,b;c,d;\mathbf{z})\hfill \\ \hspace{1em}=H_4(a+1,b;c,d+1;\mathbf{z})-\frac{2(a+1)}{c}{z}_1{H}_4(a+2,b;c+1,d+1;\mathbf{z})\hfill \\ \hspace{1em}\hspace{1em}-\frac{b(d-a)}{d(d+1)}{z}_2{H}_4(a+1,b+1;c,d+2;\mathbf{z}),\hfill \end{array}$$

(10)

$$\begin{array}{c}{H}_4(a,b;c,d;\mathbf{z})\hfill \\ \hspace{1em}=H_4(a,b+1;c,d+1;\mathbf{z})-\frac{a(d-b)}{d(d+1)}{z}_2{H}_4(a+1,b+1;c,d+2;\mathbf{z})\hfill \end{array}$$

(11)

are proved. Dividing (9) by $H_4(a+1,b;c+1,d;\mathbf{z}),$ (10) by $H_4(a+1,b;c,d+1;\mathbf{z}),$ and (11) by $H_4(a,b+1;c,d+1;\mathbf{z}),$ we obtain

$$\begin{array}{cc}\hfill R_{1,1}(a,b;c,d;\mathbf{z})& =1-\frac{{\displaystyle \frac{(2c-a)(a+1)}{c(c+1)}}{z}_1}{R_{1,1}(a+1,b;c+1,d;\mathbf{z})}-\frac{{\displaystyle \frac{b}{d}}{z}_2}{R_{2,2}(a+1,b;c+1,d;\mathbf{z})},\hfill \\ \hfill R_{1,2}(a,b;c,d;\mathbf{z})& =1-\frac{{\displaystyle \frac{2(a+1)}{c}}{z}_1}{R_{1,1}(a+1,b;c,d+1;\mathbf{z})}-\frac{{\displaystyle \frac{b(d-a)}{d(d+1)}}{z}_2}{R_{2,2}(a+1,b;c,d+1;\mathbf{z})},\hfill \\ \hfill R_{2,2}(a,b;c,d;\mathbf{z})& =1-\frac{{\displaystyle \frac{a(d-b)}{d(d+1)}}{z}_2}{R_{1,2}(a,b+1;c,d+1;\mathbf{z})}.\hfill \end{array}$$

Hence, for any ${\left(ij\right)}_0\in \mathcal{I}$ it follows

$$\begin{array}{cc}\hfill R_{i_0,j_0}& (a,b;c,d;\mathbf{z})=1-\sum _{\begin{array}{c}{i}_1=1\\ j_1=i_1+{\delta }_{i_0}^2\end{array}}^{2-{\delta }_{i_0}^2}\frac{h_{{\left(ij\right)}_1}^{{\left(ij\right)}_0}{z}_{j_1}}{R_{i_1,j_1}(a+{\delta }_{i_0}^1,b+{\delta }_{i_0}^2;c+{\delta }_{j_0}^1,d+{\delta }_{j_0}^2;\mathbf{z})},\hfill \end{array}$$

(12)

where $h_{{\left(ij\right)}_1}^{{\left(ij\right)}_0},$${\left(ij\right)}_1\in {\mathcal{I}}_1^{{\left(ij\right)}_0},$ ${\left(ij\right)}_0\in \mathcal{I},$ are defined by (4)–(8). Furthermore, this is the first step to constructing branched continued fraction expansions.

By analogy, it is clear that for all ${\left(ij\right)}_{k-1}\in {\mathcal{I}}_{k-1}^{{\left(ij\right)}_0},$$k\ge 2,$ ${\left(ij\right)}_0\in \mathcal{I},$ the following relation holds

$$\begin{array}{cc}\hfill R_{i_{k-1},j_{k-1}}& (a_{{\left(ij\right)}_{k-1}}^{{\left(ij\right)}_0},b_{{\left(ij\right)}_{k-1}}^{{\left(ij\right)}_0};c_{{\left(ij\right)}_{k-1}}^{{\left(ij\right)}_0},d_{{\left(ij\right)}_{k-1}}^{{\left(ij\right)}_0};\mathbf{z})\hfill \\ \hfill & =1-\sum _{\begin{array}{c}{i}_k=1\\ j_k=i_k+{\delta }_{i_{k-1}}^2\end{array}}^{2-{\delta }_{i_{k-1}}^2}\frac{h_{{\left(ij\right)}_k}^{{\left(ij\right)}_0}{z}_{j_k}}{R_{i_k,j_k}(a_{{\left(ij\right)}_k}^{{\left(ij\right)}_0},b_{{\left(ij\right)}_k}^{{\left(ij\right)}_0};c_{{\left(ij\right)}_k}^{{\left(ij\right)}_0},d_{{\left(ij\right)}_k}^{{\left(ij\right)}_0};\mathbf{z})},\hfill \end{array}$$

(13)

where $h_{{\left(ij\right)}_k}^{{\left(ij\right)}_0},$${\left(ij\right)}_k\in {\mathcal{I}}_k^{{\left(ij\right)}_0},$ $k\ge 2,$${\left(ij\right)}_0\in \mathcal{I},$ are defined by (4)–(8), $a_{{\left(ij\right)}_k}^{{\left(ij\right)}_0},$ $b_{{\left(ij\right)}_k}^{{\left(ij\right)}_0},$$c_{{\left(ij\right)}_k}^{{\left(ij\right)}_0},$ $d_{{\left(ij\right)}_k}^{{\left(ij\right)}_0},$${\left(ij\right)}_k\in {\mathcal{I}}_k^{{\left(ij\right)}_0},$$k\ge 1,$ ${\left(ij\right)}_0\in \mathcal{I},$ are defined by (2).

Substituting relation (13) at $k=2$ in formula (12) on the second step for any ${\left(ij\right)}_0\in \mathcal{I}$ we obtain

$$\begin{array}{c}\hfill R_{i_0,j_0}(a,b;c,d;\mathbf{z})=1-\sum _{\begin{array}{c}{i}_1=1\\ j_1=i_1+{\delta }_{i_0}^2\end{array}}^{2-{\delta }_{i_0}^2}\frac{h_{{\left(ij\right)}_1}^{{\left(ij\right)}_0}{z}_{j_1}}{{\displaystyle 1-\sum _{\begin{array}{c}{i}_2=1\\ j_2=i_2+{\delta }_{i_1}^2\end{array}}^{2-{\delta }_{i_1}^2}\frac{h_{{\left(ij\right)}_2}^{{\left(ij\right)}_0}{z}_{j_2}}{R_{i_2,j_2}(a_{{\left(ij\right)}_2}^{{\left(ij\right)}_0},b_{{\left(ij\right)}_2}^{{\left(ij\right)}_0};c_{{\left(ij\right)}_2}^{{\left(ij\right)}_0},d_{{\left(ij\right)}_2}^{{\left(ij\right)}_0};\mathbf{z})}}}.\end{array}$$

Next, applying recurrence relation (13) after n steps, we obtain

$$\begin{array}{cc}\hfill R_{i_0,j_0}(a,b;c,d;\mathbf{z})& =1-\sum _{\begin{array}{c}{i}_1=1\\ j_1=i_1+{\delta }_{i_0}^2\end{array}}^{2-{\delta }_{i_0}^2}\frac{h_{{\left(ij\right)}_1}^{{\left(ij\right)}_0}{z}_{j_1}}{1}\genfrac{}{}{0pt}{}{}{-}\dots \genfrac{}{}{0pt}{}{}{-}\sum _{\begin{array}{c}{i}_{n-1}=1\\ j_{n-1}=i_{n-1}+{\delta }_{i_{n-2}}^2\end{array}}^{2-{\delta }_{i_{n-2}}^2}\frac{h_{{\left(ij\right)}_{n-1}}^{{\left(ij\right)}_0}{z}_{j_{n-1}}}{1}\hfill \end{array}$$

$$\begin{array}{c}\hfill \genfrac{}{}{0pt}{}{}{-}\sum _{\begin{array}{c}{i}_n=1\\ j_n=i_n+{\delta }_{i_{n-1}}^2\end{array}}^{2-{\delta }_{i_{n-1}}^2}\frac{h_{{\left(ij\right)}_n}^{{\left(ij\right)}_0}{z}_{j_n}}{R_{i_n,j_n}(a_{{\left(ij\right)}_n}^{{\left(ij\right)}_0},b_{{\left(ij\right)}_n}^{{\left(ij\right)}_0};c_{{\left(ij\right)}_n}^{{\left(ij\right)}_0},d_{{\left(ij\right)}_n}^{{\left(ij\right)}_0};\mathbf{z})},\end{array}$$

(14)

where $h_{{\left(ij\right)}_k}^{{\left(ij\right)}_0},$${\left(ij\right)}_k\in {\mathcal{I}}_k^{{\left(ij\right)}_0},$ $1\le k\le n,$${\left(ij\right)}_0\in \mathcal{I},$ are defined by (4)–(8), $a_{{\left(ij\right)}_n}^{{\left(ij\right)}_0},$ $b_{{\left(ij\right)}_n}^{{\left(ij\right)}_0},$$c_{{\left(ij\right)}_n}^{{\left(ij\right)}_0},$ $d_{{\left(ij\right)}_n}^{{\left(ij\right)}_0},$${\left(ij\right)}_n\in {\mathcal{I}}_n^{{\left(ij\right)}_0},$ ${\left(ij\right)}_0\in \mathcal{I},$ are defined by (2).

Finally, by (13), one obtains the FBCFE (3) for ratio (1) for each ${\left(ij\right)}_0\in \mathcal{I}.$ □

Note that there are three different FBCFE in (3). For example, for $R_{1,1}(a,b;c,d;\mathbf{z})$ we have

$$\begin{array}{cc}\hfill 1& -{\displaystyle \frac{c_{1,1}^{1,1}{z}_1}{1-{\displaystyle \frac{c_{1,1,1,1}^{1,1}{z}_1}{1-{\displaystyle \frac{c_{1,1,1,1,1,1}^{1,1}{z}_1}{1-{}_{\ddots }}}-{\displaystyle \frac{c_{1,1,1,1,2,2}^{1,1}{z}_2}{1-{}_{\ddots }}}}}-{\displaystyle \frac{c_{1,1,2,2}^{1,1}{z}_2}{1-{\displaystyle \frac{c_{1,1,2,2,1,2}^{1,1}{z}_2}{1-{}_{\ddots }}}}}}}\hfill \\ \hfill & -{\displaystyle \frac{c_{2,2}^{1,1}{z}_2}{1-{\displaystyle \frac{c_{2,2,1,2}^{1,1}{z}_2}{1-{\displaystyle \frac{c_{2,2,1,2,1,1}^{1,1}{z}_1}{1-{}_{\ddots }}}-{\displaystyle \frac{c_{2,2,1,2,2,2}^{1,1}{z}_2}{1-{}_{\ddots }}}}}}}.\hfill \end{array}$$

In case $b=d$ and ${\left(ij\right)}_0=(1,1),$ from the theorem the following result follows.

Corollary 1.

The ratio

$$\begin{array}{c}\hfill R_{1,1}(a,b;c,b;\mathbf{z})=\frac{H_4(a,b;c,b;\mathbf{z})}{H_4(a+1,b;c+1,b;\mathbf{z})}\end{array}$$

(15)

has a FBCFE of the form

$$\begin{array}{c}\hfill 1-z_2-\frac{{\displaystyle \frac{(2c-a)(a+1)}{c(c+1)}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{(2c-a+1)(a+2)}{(c+1)(c+2)}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{(2c-a+2)(a+3)}{(c+2)(c+3)}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\dots .\end{array}$$

(16)

Note that the BCF (16) is a continued fraction by its form. The peculiarity here is that their nth approximants are defined differently (see, ([31], pp. 17–18) and ([32], pp. 15–17)). Namely, the sequence of approximants of the continued fraction for the BCF is a sequence of so-called ’figured approximants’ (see, ([32], p. 18)). Convergence studies related to various figured approximations can be found for two-dimensional continued fractions in [33,34], for BCFs of the special form [35,36,37], for BCFs with independent variables in [38,39], and for BCFs of a general form in [40].

3. Convergence of BCFE for $R_{\mathbf{1},\mathbf{1}}(a,b;c,b;\mathbf{z})$

We refer the reader to the paper [10] and the books [12,31,32,41] to learn more on the concepts and notations that will be used in this section.

The following result about the convergence of a confluent two-dimensional S-fraction with independent variables

$$\begin{array}{c}\hfill s_{1,0}{z}_1+\frac{s_{0,1}{z}_2}{1+s_{1,1}{z}_1}\genfrac{}{}{0pt}{}{}{+}\frac{s_{0,2}{z}_2}{1+s_{1,2}{z}_1}\genfrac{}{}{0pt}{}{}{+}\frac{s_{0,3}{z}_2}{1}\genfrac{}{}{0pt}{}{}{+}\dots ,\end{array}$$

(17)

where $s_{1,k-1}>0$ and $s_{0,k}>0,$ $k\ge 1,$ follows directly from ([42], Theorem 2).

Theorem 2.

Let (17) be a confluent two-dimensional S-fraction with independent variables whose coefficients $s_{1,k-1}$ and $s_{0,k},$$k\ge 1,$ satisfy the conditions

$$\begin{array}{c}\hfill s_{1,k-1}+s_{0,k}\le rforallk\ge 1,\end{array}$$

(18)

where r is a positive number. Then the confluent two-dimensional S-fraction with independent variables (17) converges to a holomorphic function in the domain

$$\begin{array}{c}\hfill D=\left\{\mathbf{z}\in {\mathbb{C}}^2:\left|arg\left(\frac{1}{4r}+z_k\right)\right|<\pi ,k=1,2\right\}.\end{array}$$

The convergence is uniform on every compact subset of $D.$

Now we prove the following theorem.

Theorem 3.

Let a and c be real constants such that

$$\begin{array}{c}\hfill 0<{\displaystyle \frac{(2c-a+k-1)(a+k)}{(c+k-1)(c+k)}}\le rforallk\ge 1,\end{array}$$

where r is a positive number. Then:

(A) 

The BCF (16) converges uniformly on every compact subset of

$$\begin{array}{c}\hfill H=\left\{\mathbf{z}\in {\mathbb{C}}^2:\left|arg\left(\frac{1}{4(1+r)}-z_k\right)\right|<\pi ,k=1,2\right\}\end{array}$$

(19)

to a function $f\left(\mathbf{z}\right)$ holomorphic in $H;$

(B) 

The function $f\left(\mathbf{z}\right)$ is an analytic continuation of (15) in the domain (19).

Proof. 

It is clear that we can consider (16) as a confluent two-dimensional S-fraction with independent variables $-z_1$ and $-z_2.$ Then, the conditions (18) one can write as

$$1+{\displaystyle \frac{(2c-a+k-1)(a+k)}{(c+k-1)(c+k)}}\le 1+r.$$

Therefore, by Theorem 2 the part (A) follows.

We will prove the second part of this theorem similarly as in ([10], Theorem 2).

Let

$$\begin{array}{c}\hfill G_n^{\left(n\right)}\left(\mathbf{z}\right)=1,F_n^{\left(n\right)}\left(\mathbf{z}\right)=R_{1,1}(a+n,b;c+n,b;\mathbf{z}),n\ge 1,\end{array}$$

(20)

where from (13) it follows that for all $n\ge 1$

$$\begin{array}{c}\hfill R_{1,1}(a+n,b;c+n,b;\mathbf{z})=1-z_2-\frac{{\displaystyle \frac{(2c-a+n)(a+n+1)}{(c+n)(c+n+1)}}{z}_1}{R_{1,1}(a+n+1,b;c+n+1,b;\mathbf{z})},\end{array}$$

and let

$$\begin{array}{cc}\hfill G_k^{\left(n\right)}\left(\mathbf{z}\right)& =1-z_2-\frac{{\displaystyle \frac{(2c-a+k)(a+k+1)}{(c+k)(c+k+1)}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\dots \genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{(2c-a+n-1)(a+n)}{(c+n-1)(c+n)}}{z}_1}{G_n^{\left(n\right)}\left(\mathbf{z}\right)},\hfill \\ \hfill F_k^{\left(n\right)}\left(\mathbf{z}\right)& =1-z_2-\frac{{\displaystyle \frac{(2c-a+k)(a+k+1)}{(c+k)(c+k+1)}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\dots \genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{(2c-a+n-1)(a+n)}{(c+n-1)(c+n)}}{z}_1}{F_n^{\left(n\right)}\left(\mathbf{z}\right)},\hfill \end{array}$$

where $1\le k\le n-1,$ $n\ge 2.$ Then it is easily seen that

$$\begin{array}{cc}\hfill G_k^{\left(n\right)}\left(\mathbf{z}\right)& =1-z_2-\frac{{\displaystyle \frac{(2c-a+k)(a+k+1)}{(c+k)(c+k+1)}}{z}_1}{G_{k+1}^{\left(n\right)}\left(\mathbf{z}\right)},\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill F_k^{\left(n\right)}\left(\mathbf{z}\right)& =1-z_2-\frac{{\displaystyle \frac{(2c-a+k)(a+k+1)}{(c+k)(c+k+1)}}{z}_1}{F_{k+1}^{\left(n\right)}\left(\mathbf{z}\right)},\hfill \end{array}$$

(22)

where $1\le k\le n-1,$ $n\ge 2.$

From (13), (14), (20), and (22) it follows that for each $n\ge 1$

$$\begin{array}{cc}\hfill R_{1,1}(a,b;c,b;\mathbf{z})& =1-z_2-\frac{{\displaystyle \frac{(2c-a)(a+1)}{c(c+1)}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{(2c-a+1)(a+2)}{(c+1)(c+2)}}{z}_1}{1-z_2}\hfill \\ & \genfrac{}{}{0pt}{}{}{-}\dots \genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{(2c-a+n-1)(a+n)}{(c+n-1)(c+n)}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{(2c-a+n)(a+n+1)}{(c+n)(c+n+1)}}{z}_1}{F_n^{(n+1)}\left(\mathbf{z}\right)}\hfill \\ & =1-z_2-\frac{{\displaystyle \frac{(2c-a)(a+1)}{c(c+1)}}{z}_1}{F_1^{(n+1)}\left(\mathbf{z}\right)}.\hfill \end{array}$$

Moreover, taking into account (20) and (21), for each $n\ge 1$ the nth approximant of (16) we write as

$$f_n\left(\mathbf{z}\right)=1-z_2-\frac{{\displaystyle \frac{(2c-a)(a+1)}{c(c+1)}}{z}_1}{G_1^{\left(n\right)}\left(\mathbf{z}\right)}.$$

Since $F_k^{\left(r\right)}\left(\mathbf{0}\right)=1$ and $G_k^{\left(r\right)}\left(\mathbf{0}\right)=1$ for any $1\le k\le r$ and $r\ge 1,$ then for each $1\le k\le r$ and $r\ge 1$ there exist $\Lambda (1/F_k^{\left(r\right)})$ and $\Lambda (1/G_k^{\left(r\right)}),$ where $\Lambda (·)$ is the Taylor expansion of a function holomorphic in some neighborhood of the origin. In addition, it is clear that $F_k^{\left(r\right)}\left(\mathbf{z}\right)\not\equiv 0$ and $G_k^{\left(r\right)}\left(\mathbf{z}\right)\not\equiv 0$ for all indices.

Applying the method suggested in ([32], p. 28) and recurrence relations (21), (22), for any $n\ge 1$ on the first step we obtain

$$\begin{array}{cc}\hfill R_{1,1}(a,b;c,b;\mathbf{z})-f_n\left(\mathbf{z}\right)& =1-z_2-\frac{{\displaystyle \frac{(2c-a)(a+1)}{c(c+1)}}{z}_1}{F_1^{(n+1)}\left(\mathbf{z}\right)}-\left(1-z_2-\frac{{\displaystyle \frac{(2c-a)(a+1)}{c(c+1)}}{z}_1}{G_1^{\left(n\right)}\left(\mathbf{z}\right)}\right)\hfill \\ & =\frac{{\displaystyle \frac{(2c-a)(a+1)}{c(c+1)}}{z}_1}{F_1^{(n+1)}\left(\mathbf{z}\right)G_1^{\left(n\right)}\left(\mathbf{z}\right)}(F_1^{(n+1)}\left(\mathbf{z}\right)-G_1^{\left(n\right)}\left(\mathbf{z}\right)).\hfill \end{array}$$

Let k be an arbitrary integer number such that $1\le k\le n$, $n\ge 1.$ Then we have

$$\begin{array}{cc}\hfill F_k^{(n+1)}\left(\mathbf{z}\right)& -G_k^{\left(n\right)}\left(\mathbf{z}\right)\hfill \\ \hfill & =1-z_2-\frac{{\displaystyle \frac{(2c-a+k)(a+k+1)}{(c+k)(c+k+1)}}{z}_1}{F_{k+1}^{(n+1)}\left(\mathbf{z}\right)}-\left(1-z_2-\frac{{\displaystyle \frac{(2c-a+k)(a+k+1)}{(c+k)(c+k+1)}}{z}_1}{G_{k+1}^{\left(n\right)}\left(\mathbf{z}\right)}\right)\hfill \\ \hfill & =\frac{{\displaystyle \frac{(2c-a+k)(a+k+1)}{(c+k)(c+k+1)}}{z}_1}{F_{k+1}^{(n+1)}\left(\mathbf{z}\right)G_{k+1}^{\left(n\right)}\left(\mathbf{z}\right)}(F_{k+1}^{(n+1)}\left(\mathbf{z}\right)-G_{k+1}^{\left(n\right)}\left(\mathbf{z}\right)).\hfill \end{array}$$

(23)

Next, applying recurrence relations (23) and taking into account that

$$\begin{array}{cc}\hfill F_n^{(n+1)}\left(\mathbf{z}\right)-G_n^{\left(n\right)}\left(\mathbf{z}\right)& =1-z_2-\frac{{\displaystyle \frac{(2c-a+n)(a+n+1)}{(c+n)(c+n+1)}}{z}_1}{F_{n+1}^{(n+1)}\left(\mathbf{z}\right)}-1\hfill \\ & =-z_2-\frac{{\displaystyle \frac{(2c-a+n)(a+n+1)}{(c+n)(c+n+1)}}{z}_1}{F_{n+1}^{(n+1)}\left(\mathbf{z}\right)}\hfill \end{array}$$

for any $n\ge 1$ one obtains

$$\begin{array}{cc}\hfill R_{1,1}(a,b;c,b;\mathbf{z})& -f_n\left(\mathbf{z}\right)\hfill \\ & =-\prod _{r=1}^n\frac{{\displaystyle \frac{(2c-a+r-1)(a+r)}{(c+r-1)(c+r)}}{z}_1}{F_r^{(n+1)}\left(\mathbf{z}\right)G_r^{\left(n\right)}\left(\mathbf{z}\right)}\left(z_2+\frac{{\displaystyle \frac{(2c-a+n)(a+n+1)}{(c+n)(c+n+1)}}{z}_1}{F_{n+1}^{(n+1)}\left(\mathbf{z}\right)}\right).\hfill \end{array}$$

It follows that in a neighborhood of zero for any $n\ge 1$ we have

$$\begin{array}{c}\hfill \Lambda \left(R_{1,1}\right)-\Lambda \left(f_n\right)=\sum _{\begin{array}{c}r+s\ge n+1\\ r\ge 0,s\ge 0\end{array}}{\alpha }_{r,s}^{\left(n\right)}{z}_1^r{z}_2^s,\end{array}$$

(24)

where ${\alpha }_{r,s}^{\left(n\right)},$$r\ge 0,$$s\ge 0,$$r+s\ge n+1,$ are some coefficients.

Recall that the sequence $\left\{F_n\left(\mathbf{z}\right)\right\}$ of functions holomorphic at the origin is corresponding (at $\mathbf{z}=\mathbf{0}$) to a FDPS $L\left(\mathbf{z}\right)$ if

$$\underset{n\to \infty }{lim}\lambda \left(L-\Lambda \left(F_n\right)\right)=\infty ,$$

where $\lambda (·)$ is the function defined as follows: if $L\left(\mathbf{z}\right)\equiv 0$ then $\lambda \left(L\right)=\infty ;$ if $L\left(\mathbf{z}\right)\not\equiv 0$ then $\lambda \left(L\right)=m,$ where m is the smallest degree of homogeneous terms for which at least one coefficient is different from zero. The BCF (16) is corresponding (at $\mathbf{z}=\mathbf{0}$) to a FDPS $L\left(\mathbf{z}\right)$ if each approximant $f_n\left(\mathbf{z}\right)$ is a holomorphic function of $\mathbf{z}$ at the origin and if $\left\{f_n\left(\mathbf{z}\right)\right\}$ corresponds to $L\left(\mathbf{z}\right)$ (see, [10] and also ([31], Section 5.1)).

From (24) it follows that

$$\lambda \left(\Lambda \left(R_{1,1}\right)-\Lambda \left(f_n\right)\right)=n+1$$

tends monotonically to ∞ as $n\to \infty$, i.e., the BCF (16) corresponds (at $\mathbf{z}=\mathbf{0}$) to a FDPS $\Lambda \left(R_{1,1}\right).$

Let D be the neighborhood of the origin which contained in (19) and in which

$$\Lambda \left(R_{1,1}\right)=\sum _{r,s=0}^{\infty }{\alpha }_{r,s}{z}_1^r{z}_2^s.$$

Then, from part (A) it follows that the sequence $\left\{f_n\left(\mathbf{z}\right)\right\}$ converges uniformly on every compact subset of D to a function $f\left(\mathbf{z}\right)$ holomorphic in $D.$ By Weierstrass’s theorem ([43], p. 288) for arbitrary $r+s,r\ge 0,s\ge 0,$ we have

$$\frac{{\partial }^{r+s}{f}_n\left(\mathbf{z}\right)}{\partial z_1^r\partial z_2^s}\to \frac{{\partial }^{r+s}f\left(\mathbf{z}\right)}{\partial z_1^r\partial z_2^s}\mathrm{as}n\to \infty$$

on each compact subset of the domain $D.$ Furthermore, according to the above, for each $n\ge 1$ the $\Lambda \left(f_n\right)$ and $\Lambda \left(R_{1,1}\right)$ agree for all homogeneous terms up to and including degree $n.$

Thus, for any $r+s,$ $r\ge 0,$ $s\ge 0,$ one obtains

$$\underset{n\to \infty }{lim}\left(\frac{{\partial }^{r+s}{f}_n}{\partial z_1^r\partial z_2^s}\left(\mathbf{0}\right)\right)=\frac{{\partial }^{r+s}f}{\partial z_1^r\partial z_2^s}\left(\mathbf{0}\right)=r!s!{\alpha }_{r,s}.$$

Hence, for all $\mathbf{z}\in D,$

$$f\left(\mathbf{z}\right)=\sum _{r,s=0}^{\infty }\left(\frac{{\partial }^{r+s}f}{\partial z_1^r\partial z_2^s}\left(\mathbf{0}\right)\right)\frac{z_1^r}{r!}\frac{z_2^s}{s!}=\sum _{r,s=0}^{\infty }{\alpha }_{r,s}{z}_1^r{z}_2^s.$$

Finally, by the principle of analytic continuation ([44], p. 53) part (B) follows. □

Setting $a=0$ and replacing c by $c-1$ in Theorem 3, we obtain the following result.

Corollary 2.

Let c be a positive constant such that

$$\begin{array}{c}\hfill \frac{2}{c}\le r<4\mathrm{and}{\displaystyle \frac{k(2c+k-3)}{(c+k-2)(c+k-1)}}\le rforallk\ge 2,\end{array}$$

(25)

where r is a positive number. Then:

(A) 

The BCF

$$\begin{array}{cc}\hfill \frac{1}{1-z_2}& \genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{2}{c}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{2(2c-1)}{c(c+1)}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\dots \genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{k(2c+k-3)}{(c+k-2)(c+k-1)}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\dots \hfill \end{array}$$

(26)

converges uniformly on every compact subset of (19) to a function $f\left(\mathbf{z}\right)$ holomorphic in $H;$

(B) 

The function $f\left(\mathbf{z}\right)$ is an analytic continuation of $H_4(1,b;c,b;\mathbf{z})$ in the domain (19).

Note that other convergence criteria of two-dimensional S-fractions with independent variables can be found in [45,46,47] and truncation error bounds in [46,48,49]. The results of these works can be applied to the branched continued fractions (16) and (26).

Furthermore, note that (26) as a continued fraction is equivalent to the Gaussian continued function

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\displaystyle \frac{1}{1-z_2}}}{1}}& \genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{1}{2c}}{\displaystyle \frac{4z_1}{{(1-z_2)}^2}}}{1}\genfrac{}{}{0pt}{}{}{-}\dots \genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{k(2c+k-3)}{4(c+k-2)(c+k-1)}}{\displaystyle \frac{4z_1}{{(1-z_2)}^2}}}{1}\genfrac{}{}{0pt}{}{}{-}\dots .\hfill \end{array}$$

(27)

In [50], in particular, the formal identity

$$\begin{array}{c}\hfill H_4(1,b;c,b;\mathbf{z})=\frac{1}{1-z_2}{}_2{F}_1\left(\frac{1}{2},1;c;\frac{4z_1}{{(1-z_2)}^2}\right)\end{array}$$

(28)

is given. However, it follows from the proof of ([31], Theorem 6.1) that ([31], Corollary 6.2) can not be applied to the continued fraction (27) and the function on the right-hand side of (28).

Thus, in general, the problems of proving the convergence of constructed expansions (3), and, more importantly, proving the convergence of BCFs (3) to the corresponding ratios (1), are open.

New results to solve these problems will be made in next paper.

4. Numerical Experiments

It is well known [23] (see also ([27], p. 235)) that the solution of the system of partial differential equations

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{z}_1(1-4z_1){\displaystyle \frac{{\partial }^{2}u}{\partial z_1^2}}-4z_1{z}_2{\displaystyle \frac{{\partial }^{2}u}{\partial z_1\partial z_2}}-z_2^2{\displaystyle \frac{{\partial }^{2}u}{\partial z_2^2}}+(c-8z_1){\displaystyle \frac{\partial u}{\partial z_1}}-5z_2{\displaystyle \frac{\partial u}{\partial z_2}}-2u=0,\hfill \\ -2z_1{z}_2{\displaystyle \frac{{\partial }^{2}u}{\partial z_1\partial z_2}}+z_2(1-z_2){\displaystyle \frac{{\partial }^{2}u}{\partial z_2^2}}-2b{z}_1{\displaystyle \frac{\partial u}{\partial z_1}}+(b-(1+b)z_2){\displaystyle \frac{\partial u}{\partial z_2}}-bu=0,\hfill \end{array}\right.\end{array}$$

(29)

where $u=u\left(\mathbf{z}\right)$ is an unknown function, are expressed by means of Horn’s hypergeometric function $H_4(1,b;c,b;\mathbf{z}).$

Let c be a real constant satisfying the inequalities (25), and let b is complex constant, which is not equal to a non-positive integer. Then, by Corollary 2 it follows that the BCF (26) satisfies (29) for all $\mathbf{z}\in H,$ where H is defined by (19).

As an example, by Corollary 2 we obtain

$$\begin{array}{cc}\hfill {({(1-z_2)}^2-4z_1)}^{-1/2}& =H_4(1,b;1,b;\mathbf{z})\hfill \\ \hfill & =\frac{1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{2z_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{z_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{z_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\dots .\hfill \end{array}$$

(30)

The BCF in (30) converges and represents a single-valued branch of the analytic function of two variables

$$\begin{array}{c}\hfill {({(1-z_2)}^2-4z_1)}^{-1/2}\end{array}$$

(31)

in the domain (19) with $r=1.$ If $f_n\left(\mathbf{z}\right)$ denotes the nth approximant of (30), then for every negative real $\mathbf{z}={\mathbf{z}}^0,$ the so-called ‘fork property’ (see, ([32], p. 29))

$$f_{2k-2}\left({\mathbf{z}}^0\right)<f_{2k}\left({\mathbf{z}}^0\right)<f_{2k+1}\left({\mathbf{z}}^0\right)<f_{2k-1}\left({\mathbf{z}}^0\right),k\ge 1,$$

holds (here $f_0\left({\mathbf{z}}^0\right)=0$).

The numerical illustration of DPS

$$\begin{array}{c}\hfill {({(1-z_2)}^2-4z_1)}^{-1/2}=H_4(1,b;1,b;\mathbf{z})=\sum _{r,s=0}^{\infty }\frac{{\left(1\right)}_{2r+s}}{{\left(1\right)}_r}\frac{z_1^r}{r!}\frac{z_2^s}{s!}\end{array}$$

(32)

and BCF (30) is given in Table 1. Numerical experiments also show that to compute $1/\sqrt{2}={({(1+1/4)}^2+4(7/64))}^{-1/2}$ with an error not exceeding ${10}^{-5}$ by the DPS (32), one would need to take 57th partial sum, and that $1/\sqrt{2}$ can be computed with an error less than ${10}^{-5}$ by using the 5th approximant of the BCF (30).

Table 1. Relative error of 10th partial sum and 10th approximants for ${({(1-z_2)}^2-4z_1)}^{-1/2}$.

z	(31)	(32)	(30)
$(-1/8,1/10)$	0.873704	$6.62333\times {10}^{-8}$	$1.98945\times {10}^{-10}$
$(1/10,-1/16)$	1.17129	$7.23624\times {10}^{-8}$	$2.01913\times {10}^{-10}$
$(-1/10,-1/100)$	0.839152	$1.01955\times {10}^{-5}$	$3.27995\times {10}^{-11}$
$(-1/10,-1/10)$	1.56174	$6.56397\times {10}^{-4}$	$5.81362\times {10}^{-8}$
$(-1/5,-1/5)$	0.668153	$6.5287\times {10}^{-1}$	$1.43181\times {10}^{-9}$
$(-1/8,-1)$	0.471405	$2.92301\times {10}^{+02}$	$3.32075\times {10}^{-14}$
$(-2,-1/4)$	0.323381	$9.46661\times {10}^{+08}$	$5.42958\times {10}^{-4}$
$(-3,-4)$	0.164399	$6.95343\times {10}^{+12}$	$4.77831\times {10}^{-9}$
$(-10,-20)$	0.045596	$2.12733\times {10}^{+19}$	$2.98276\times {10}^{-14}$
$(-100,-100)$	0.0097124	$8.3222\times {10}^{+28}$	$1.78609\times {10}^{-16}$

In Figure 1a–d, we can see the plots, where the 20th approximants of (30) guarantees certain truncation error bounds for function of two variables (31).

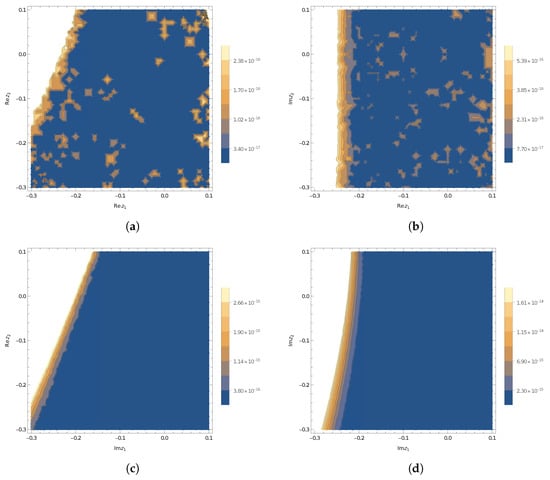
Figure 1. The plots where the approximant $f_{20}\left(\mathbf{z}\right)$ of BCF (30) guarantees certain truncation error bounds for function ${({(1-z_2)}^2-4z_1)}^{-1/2}$.

One more example, by Corollary 2 we obtain

$$\begin{array}{cc}\hfill arctan\frac{2\sqrt{-z_1}}{1-z_2}& =2\sqrt{-z_1}{H}_4(1,b;3/2,b;\mathbf{z})\hfill \\ \hfill & =\frac{2\sqrt{-z_1}}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{4}{3}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{16}{15}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\dots \genfrac{}{}{0pt}{}{}{-}\frac{{\displaystyle \frac{k^2}{k^2-1/4}}{z}_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\dots ,\hfill \end{array}$$

(33)

where the BCF converges and represents a single-valued branch of the analytic function of two variables

$$\begin{array}{c}\hfill arctan\frac{2\sqrt{-z_1}}{1-z_2}\end{array}$$

(34)

in the domain (19) with $r=4/3.$

In Table 2, we can see that the 10th approximant of (33) is eventually a better approximation to (34) than the corresponding 10th partial sum of the DPS

$$\begin{array}{c}\hfill arctan\frac{2\sqrt{-z_1}}{1-z_2}=2\sqrt{-z_1}{H}_4(1,b;3/2,b;\mathbf{z})=2\sqrt{-z_1}\sum _{r,s=0}^{\infty }\frac{{\left(1\right)}_{2r+s}}{{(3/2)}_r}\frac{z_1^r}{r!}\frac{z_2^s}{s!}.\end{array}$$

(35)

Table 2. Relative error of 10th partial sum and 10th approximants for $arctan(2\sqrt{-z_1}/(1-z_2))$.

z	(34)	(35)	(33)
$(-1/50,1/10)$	0.304496	$9.2228\times {10}^{-13}$	$3.6461\times {10}^{-16}$
$(-1/8,1/10)$	0.665944	$1.06644\times {10}^{-8}$	$1.60922\times {10}^{-10}$
$(-1/10,-1/100)$	0.559457	$2.59086\times {10}^{-6}$	$2.59205\times {10}^{-11}$
$(-1/5,1/50)$	0.739777	$1.46368\times {10}^{-3}$	$8.30048\times {10}^{-9}$
$(-1/5,-1/5)$	0.640522	$1.91315\times {10}^{-1}$	$1.14109\times {10}^{-9}$
$(-1/8,-1)$	0.339837	$1.30864\times {10}^{+02}$	$2.56454\times {10}^{-14}$
$(-4,-1)$	1.10715	$5.94092\times {10}^{+11}$	$2.99918\times {10}^{-4}$
$(-3,-4)$	0.605891	$2.17485\times {10}^{+12}$	$3.78678\times {10}^{-9}$
$(-10,-20)$	0.292529	$7.43863\times {10}^{+18}$	$2.27715\times {10}^{-14}$
$(-100,-100)$	0.195491	$2.65535\times {10}^{+28}$	$2.83958\times {10}^{-16}$

The graphical illustrations of the function of two variables (34) and the BCF (33) are given in Figure 2a,b and Figure 3a–d. In particular, in Figure 2a,b we can see the plots of the values of even (odd) approximations of approaches from below (above) to the plot of the function of two variables (34).

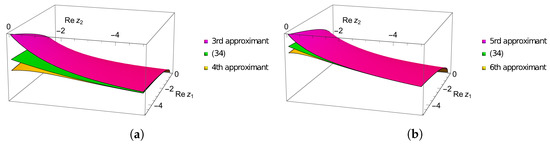
Figure 2. The plots of values of the nth approximants of (33).

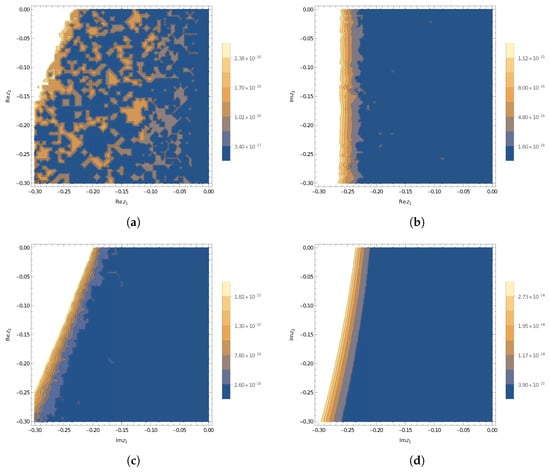
Figure 3. The plots where the approximant $f_{20}\left(\mathbf{z}\right)$ of BCF (33) guarantees certain truncation error bounds for function $arctan(2\sqrt{-z_1}/(1-z_2))$.

In the last example, by Theorem 3 we have

$$\begin{array}{cc}\hfill \frac{1-z_2+\sqrt{{(1-z_2)}^2-4z_1}}{2}& =\frac{H_4(-1/2,b;1/2,b;\mathbf{z})}{H_4(1/2,b;3/2,b;\mathbf{z})}\hfill \\ \hfill & =1-z_2-\frac{z_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{z_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\frac{z_1}{1-z_2}\genfrac{}{}{0pt}{}{}{-}\dots .\hfill \end{array}$$

(36)

Here the BCF converges and represents a single-valued branch of the analytic function of two variables

$$\begin{array}{c}\hfill \frac{1-z_2+\sqrt{{(1-z_2)}^2-4z_1}}{2}\end{array}$$

(37)

in the domain (19) with $r=1.$

Figure 4a–d shows the plots, where the 20th approximants of (36) guarantees certain truncation error bounds for function of two variables (37).

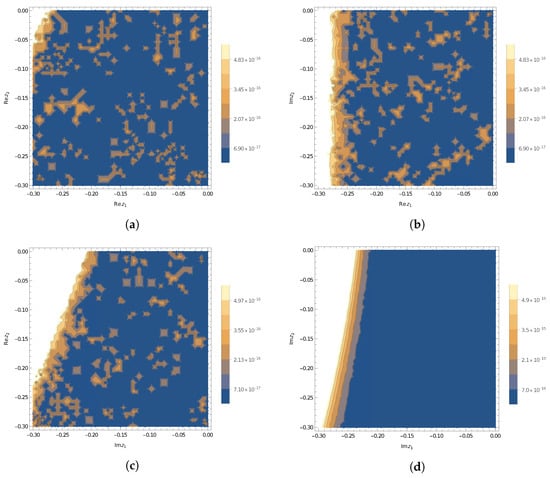
Figure 4. The plots where the approximant $f_{20}\left(\mathbf{z}\right)$ of BCF (36) guarantees certain truncation error bounds for function $(1-z_2+\sqrt{{(1-z_2)}^2-4z_1})/2$.

Given all the above, the expediency and effectiveness of using BCFs as an approximation tool, in particular, of the functions of two variables, is confirmed by numerical experiments. Calculations and plots were performed using Wolfram Mathematica software.

5. Discussion

The paper considers the problem of representing the Horn’s hypergeometric function by BCFs. Three different FBCFEs are derived for three different ratios of Horn’s hypergeometric function $H_4.$ However, the problem of constructing and studying FBCFs of other structures (perhaps simpler) remains open. It is proved that the BCF converges to the ratio of the hypergeometric series, whose expansion it is. Still, the conditions of their convergence impose additional restrictions on the parameters of the function. Numerical experiments confirm the expediency and effectiveness of using BCFs as an approximation tool. Nevertheless, the problems of improving and developing new methods of studying the convergence of such and similar BCFs are open.