Abstract
The present study is concerned with studying the dynamical behavior of two space-dimensional nonlinear time-fractional models governing the unsteady-flow of polytropic-gas (in brief, pGas) that occurred in cosmology and astronomy. For this purpose, two efficient hybrid methods so-called optimal homotopy analysis -transform method (HATM) and -variational iteration transform method (-VITM) have been adopted. The OHATM is the hybrid method, where optimal-homotopy analysis method (HAM) is utilized after implementing the properties of -transform (T), and in -VITM is the -transform-based variational iteration method. Banach’s fixed point approach is adopted to analyze the convergence of these methods. It is demonstrated that -VITM is -stable, and the evaluated dynamics of pGas are described in terms of Mittag–Leffler functions. The proposed evaluation confirms that the implemented methods perform better for the referred model equation of pGas. In addition, for a given iteration, the proposed behavior via HATM performs better in producing more accurate behavior in comparison to -VITM and the methods introduced recently.
Keywords:
caputo derivative; polytropic gas; MSC:
35R11; 65F10; 26A33
1. Introduction
Fractional calculus (FC) is one of the growing/youthful branches of applied mathematics that is a generalized concept of differential equations from an integer order to positive fractional order. It is a preferred selection in modeling complicated physical realistic situations marked by hereditary/memory behaviors. It is because of the nonlocal nature of these operators [1,2]. FC is a useful tool for showcasing the transition of highly complicated nonlinear dynamics with long-term memory effects. In contrast to ordinary derivatives, identifying fractional order derivatives of a function requires its entire history [3]. This nonlocal property, referred as the memory consequence, allows it even more convenient to characterize real-world physical systems using differential equations with fractional derivatives. In recent decades, investigating the evolution of fractional order systems, such as chaos, complexity, stability, bifurcation, and synchronization has emerged as an exciting area of research in areas of research and development [4,5,6,7], and the fractional partial differential equations (FPDEs) are more appropriate for modeling numerous realistic situations such as in optics, earthquake propagation, population growth, volcanic eruption, signal processing, the process of reaction/diffusion, in electrical networking, control theory, hydrology, astrophysics, and in biological systems [8,9,10,11,12,13].
To know about the behavior of a model, one must know about its solution behaviors, and many physical phenomena can be represented by a suitable model in terms of the nonlinear fractional partial differential equations (NFPDEs), and the evaluation of the solution behaviors of such type of model is quite difficult, and so the study of these NFPDEs is of vital importance. In the last three decades, various rigorous new techniques are investigated to elucidate a system of NFPDEs. In consequence, Liao [14] developed a rigorous technique so-called homotopy analysis method for studying many types of nonlinear partial differential equations (NPDEs) like differential-integral/algebraic equations/partial differential equations/ordinary differential equations and associated coupled systems or the fractional models of the above-mentioned types equations. Differ from all the perturbation/nonperturbation approaches for nonlinear differential equations (NDEs), HAM generates an effective/easy technique to assure the convergent solutions by suitable selection of different base functions (see [9,13,15] and inside articles for more details).
In this article, the fractional order model of gas-dynamic equations administering the development of the two-space dimensional unsteady flow of an ideal gas has been studied. Write , where energy density, total energy of the gas, container volume, polytropic index, and a constant. In the sequel, degenerate electron gas and adiabatic gas are two instances of such types of gases. The investigation of polytropic gases identified an essential job in cosmology and astronomy [16], and its behavior is found dark energy-like [11], and the special case of the pGas model has been utilized in astrophysics in stellar wind and accretion problems. In recent years, the researchers generalized the model of gas-dynamic equations governing the advancement of unsteady progression of an ideal-gas of fraction order [17,18]. We need both evolution equations for and P due to the energy density and and polytropic index. The value of in the below system (1) is due to the dynamics of a strongly nonlocal reaction–diffusion population model [19]. The fractional model of equations of a pGas [15,20] given below in (1) via two hybrid techniques, namely - HATM and -VITM
with initial condition
where and velocity components, is the density, pressure and ratio of specific heat and refers adiabatic index. is the Caputo-fractional differential operator (C-FDO) as defined below:
Definition 1
([1,2]). The C-FDO
of order of a function is defined by and
In addition, letis the αth order Riemann–Liouville fractional integral operator (RLFIO) on φ. Then
- and
The readers are referred to [1,2,21,22] for more details on fractional calculus. The researchers have beendeveloped/ implemented various rigorous methods for studying behaviors of various models occurred in terms of NFPDEs (see [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]). The behavior of the integer order system of the referred model equations was analyzed using distinct techniques like Adomian decomposition method (ADM) [38], variational iteration technique (VIT) [17], and HAM [18]. Recently, numerical simulation and behavior of fractional order system have been investigated by fractional natural decomposition method (NDM) [20] and q-homotopy analysis transform method (q-HATM) [15]. In the present work, the novel integral transform called -transform is implemented in combination with two efficient techniques, namely oHAM and VIM to investigate the nonlinear time-fractional model governing unsteady flow of polytropic. The main strategy of our work in considering the -transform is that it is the generalized form of the Laplace transform and the Elzaki transform. Also, in case of the -transform, we will get the two-dimensional frequency domain, which will give us more degree of freedom to analyze the respective solutions. The proposed fractional model interprets the most realistic behavior for considered fractional orders and which states the originality of the paper. The relative error solutions are presented in terms of logarithmic plots for different fractional orders. We have achieved the faster rate of convergence of the obtained series solution to the exact solution with the help of optimal value of the convergence control parameter.
The rest part of the work is structured as follows: Section 2 reports some basic literature to complete understanding of the work. In Section 3, we report the basic procedure for -VITM and its stability/convergence analysis. In Section 4, we report the basic procedure for HATM and its convergence analysis. Validity/effectiveness/efficiency of the aforesaid methods is tested in Section 5 by considering test examples of the fractional model equation of pGas. At last, concluding remark is reported in Section 6.
2. Basic Concepts
Banach’s fixed point approach and T-based basics are revisited to understand the rest part of the study. Let us denote as a metric space.
Definition 2
([39]). Let be a contraction on metric space Π; this is a map that satisfies the following condition
for some positive real less than unity, i.e., , where be set of positive reals.
Theorem 1
(Banach’s Fixed-Point Theorem [39]). A contraction over complete space Π always has a unique fixed point.
In the sequel, if is a iterative sequence formulated via the iterative procedure with (arbitrary) such that approaches the unique fixed point y as , the error estimates are evaluated as follows
- (prior-etimate), and
- and
- (posterior-estimate).
Theorem 2
([40,41]). A self-map defined over Π (Banach space) is termed as Picard T-stable if the condition holds true for some non-negative real κ, and γ with .
-Transform and Its Properties
The transformation
is referred to as -transform of (provided it exists), are transformed variables, and is the set functions of exponential order satisfying the following conditions
The properties of T are listed is the following
Lemma 1
(Properties of T, [42]).Let and are T of , respectively. Then
- (a)
- (b)
- (c)
- (d)
- , whereis the convolution of g and ψ.
The properties of T for fractional calculus [31] that we use to study the behavior of referred model equation is mentioned below
Lemma 2.
If is the -transform of, then
- (i)
- (ii)
where , denote C-FDO and Riemann–Liouville FIO of ψ of order α.
Proof.
The proof is reported in [31]. □
3. Procedure of Variational Iteration Technique (VIT)
The variational theory-based technique so-called VIT is an efficient technique introduced by He [43] for the study of various models that occurred in terms of classical differential equations. After He’s seminal work, VIT and its modified forms has been introduced for studying various types of nonlinear problems of integer orders [44,45,46,47] and fractional order [47,48,49,50,51].
Consider time-fractional nonlinear partial differential equation (TF-NPDE).
where be space-variable of 2-dimensions, is Caputo FDO [23,24,25], nonlinear differential operator involving linear operators and nonhomogeneous/source term as well, and .
The basic procedure of VIT for TF-NPDE, the correction functional of (4) in mVIT [47], is given via
where refers to Lagrange multiplier to be determine, is th-iteration solution, and is the restricted variation [52]. The evaluation of the Lagrange multiplier is a tedious task in studying the behavior of TF-NPDE. On imposing optimality criteria to the functional as in (5), we have
The evaluation of the Lagrange multiplier in the above equation is tough for fraction case [51]. The implementation of the properties of an integral transform with variational theory [53,54] makes the evaluation procedure for finding the optimal value of the Lagrange multiplier easily.
3.1. Procedure of -VITM for NFPDEs
The -VITM is a hybrid method that is based on properties of T and variational theory (see [31]) that we implemented for studying nonlinear fractional partial differential equations (NFPDEs).
Impose T to NFPDEs (4) and adopt the property of T from Theorem 2(ii), we have
In sequel to modified variational iteration technique, correction functional for (6) constructed as
where and restricted variations, i.e., and .
The variational operator to (7) with the above-mentioned property leads to
The optimality condition: for (7) in (8) leads to the optimal value of the Lagrange multiplier . Thus, (7) reduces to
The inverse T operator with (9) leads to
where
- and
3.2. Convergence and Stability Analysis of -VITM
The analysis of convergence and stability for the aforesaid -VITM is provided in the following theorem. For sake of convenience, we read in place of throughout this section
Theorem 3
(Stability analysis). Let a self-map , where is the Banach space; then, the iterative results via iteration formula (10) are: is Picard stable if for which the following axioms hold true for every τ.
- (a)
- (b)
- .
Proof.
Let .Then,
as at each iteration holds from the initial condition. Imposing norm to both sides of (12) with condition (a) leads to
and this can be expressed in the following form
which confirms that the proposed -VITM is Picard stable whever (see Theorem 2). □
Theorem 4
(Convergence analysis). In a Banach space , let be a sequence from the iteration procedure (10): , where be associated self-map on . Then
- (a)
- with (initial value) is convergent.
- (b)
- A unique fixed point exist for in .
- (c)
- In κth order iterative results, the error bounds as derived as
- (Prior-estimate of error),
- and
- (posterior-error estimate)
Proof.
For the complete proof please visit [31]. □
4. Basic Procedure of HATM
The basic solution procedure of HATM for NFPDEs (4) is derived in [31], is reported in the following. On operating T to NFPDEs (4) with the help of the property of T to get (6) that can be expressed as
Set nonlinear operator as
where is the real-valued map of ; standard embedded-parameter.
The following zeroth-order deformation equation as in [12,14] is
where is the auxiliary function/parameter, and is the initial guess of . Remark that HATM have a merit in selecting auxiliary things in procedure.
- For ,
- and ,
and it signifies that when ℵ moving from 0 to 1, the solution moves simultaneously from initial approximation: to the exact solution behavior: .
Expand via Taylor’s formula in the powers of ℵ as:
where on selecting suitable value of ℏ improves convergence region to the solution as in (15). Convergence of result (15) at can be secured via selecting appropriate values of and the initial guess, and so
Set
In the squel, th order deformation equation is evaluated as
where if and 1 otherwise.
On evaluation , . We can calculate Mth-order series behavior of (4) is evaluated as:
which converges to , the exact behavior of the Equation (4) accurately for sufficiently large M (see the following).
Theorem 5
(Convergence & Error Estimates in HATM). If ∃ θ with , for which the condition holds true, then
- (a)
- (b)
- the maximum absolute error in is
- (c)
Proof.
The assumption leads to
In consequence, and so, for with , we get
Moreover, as , and so, the above inequality reduces to
implying that is Cauchy sequence, and so, it is convergent.
Part (b) is obtained direct by taking in (21) as follows
(c) In special case, when Then, from Equation (21), we get
Since
Use condition and in (18) with property to get
Evaluation of Optimal Value of the Convergence Control Parameter (ℏ)
The efficiency/validity of HATM is confirmed by measuring the or residual-errors. The square residual error [12,14] in the Mth-order solution behavior as in (19)
where is refer to residual error in the solution behavior of order M as , and controlling parameter ℏ appeared in solution (19) have a significant role and that receive faster convergence rate on suitable adjustment of ℏ. Precisely, the optimal value for ℏ is values of ℏ within the ℏ-region correspond to that is minimized, and so ℏ correspond for which To CPU time under consideration, following formula in place of (23) is preferred.
where , and . We set
5. Validation of Technique
To validate the efficiency and accuracy of the proposed techniques, we consider the fractional order system of equations of governing unsteady flow of a polytropic gas.
Take the fractional order system as described in Equation (1) subject to the initial conditions:
where is a real constant.
5.1. Validation of -VITM
By implementing the iteration formula Equation (10) of -VITM on the system of Equation (1) with ICs (25), we obtain the following recurrence relation
On solving the recurrence (26), we get
At first iteration:
At second iteration:
At third iteration:
In similar fashion, th order iterative results for are given computed as
and
This concludes that general th order iterative solutions is of the form
In consequence, th order iterative solutions converges to the exact solutions as :
In special case, when the above results converges to the exact solutions:
5.2. Validation of HATM
Formulate nonlinear operator as follows:
Utilizing (31) in (18) to obtain the recursive formula
where
with the aid of Mathematica software, solve recurrence relation (30).
At first iteration:
At second iteration:
At third iteration:
In sequel, the terms corresponding to for the system of equation can be computed from (30). The 6th order approximate results for the system is
5.3. Result and Discussion
Throughout computation fixed . The comparison in absolute errors th order results for / and via -VITM and HATM in are reported in Table 1 and Table 2, respectively. In consequence, Table 3 reports the comparison of exact results with 10th order results for and computed via HATM with optimal value of ℏ for at different time levels . The computation is carried out by taking and (optimal value). One can see that, we can achieve faster convergence rate with the help of optimal value of the convergence control parameter (ℏ). The obtained error solutions witness the efficacy of the projected schemes.

Table 1.
Comparison of absolute errors th order results for / via -VITM and HATM for at different time levels .

Table 2.
Comparison of absolute errors th order results for via -VITM and HATM for at different time levels .

Table 3.
Comparison of 10th order results for and via HATM with optimal value of ℏ for at different time levels with exact results.
For : Figure 1a,b depict 2D and 3D behavior of 10th-order computed results for different . There is a significant variation in the obtained solutions for different fractional order . For the accuracy of the projected schemes, we can consider plots for where the secured solutions are in best match with the exact solutions of the problem under consideration. Figure 1c,d depicts logarithmic plots of relative errors in th iterative results via HATM for , respectively, while Figure 1e,f depicts logarithmic plots of relative errors in th iterative results via -VITM for , respectively. The value of the relative error for the obtained solution is decreases as we increase the iterations. In the 10th-order iteration, we have achieved the better solutions as compare to the previous iterations.
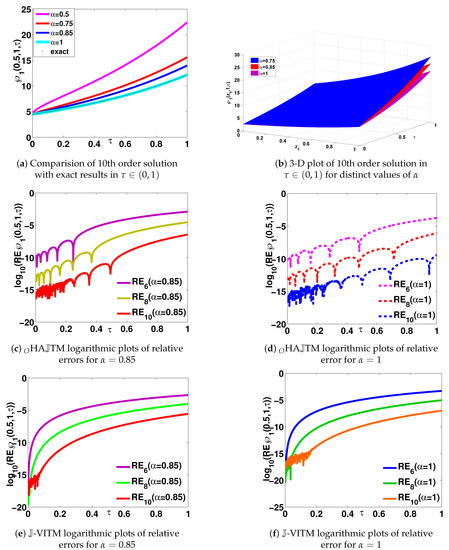
Figure 1.
Solutions for . (a) Behavior of computed results from HATM at 10th iteration with exact results; (b) logarithmic plots of relative errors in th iterative results for (c,e) , (d,f) ; at and optimal value of ℏ, for obtained from HATM (c,d), -VITM (e,f) respectively.
For : Figure 2a,b, depict 2D and 3D behavior of 10th-order computed results for different . The velocity decreases with increase in time variable . curve matches exactly with the exact solution of the considered problem. The velocity drops faster for the decreasing fractional order . The 3D view of variation of the solution for different fractional order is presented to analyze the influence of fractional parameter . Figure 2c,d depicts logarithmic plots of relative errors in th iterative results via HATM for , respectively while Figure 2e,f depicts logarithmic plots of relative errors in th iterative results via -VITM for respectively. As we increase the number of iterations, we are getting the better approximate solution for both projected algorithms. These plots gives an explaination about how large the absolute error is in comparision with the exact numerical value of the solution.
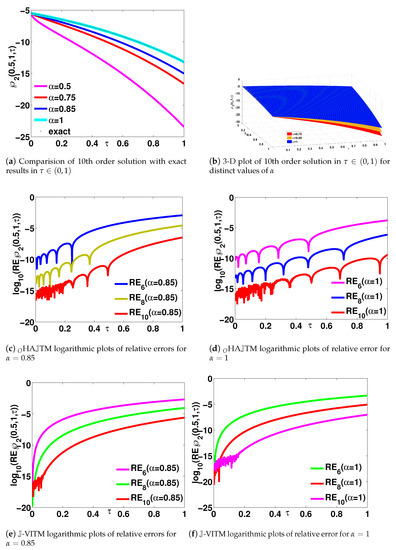
Figure 2.
Solutions for . (a) Behavior of computed results from HATM at 10th iteration with exact results; (b) logarithmic plots of relative errors in th iterative results for (c,e) , (d,f) ; at and optimal value of ℏ, for obtained from HATM (c,d), -VITM (e,f) respectively.
For : Figure 3a,b depict 2D and 3D behavior of 10th-order computed results for different . We can see that the density increases with increase in time . The density distribution over the space with coordinates is presented in Figure 3b. Figure 3c,d depicts logarithmic plots of relative errors in th iterative results via HATM for , respectively, while Figure 3e,f depicts logarithmic plots of relative errors in th iterative results via -VITM for , respectively. Table 3 cites that we have achieved the solution which is in best match with the exact solution of the considered problem. We can observe the same in Figure 3.
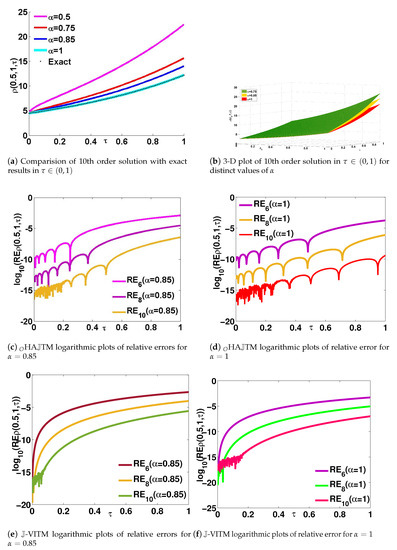
Figure 3.
Solutions for . (a) Behavior of computed results from HATM at 10th iteration with exact results; (b) logarithmic plots of relative errors in th iterative results for (c,e) , (d,f) ; at and optimal value of ℏ, for obtained from HATM (c,d), -VITM (e,f), respectively.
It is easy to demonstrate numerically from Figure 1c–f Figure 2c–f and Figure 3c–f and Table 1 and Table 2 that for a given order of approximation, HATM with optimal ℏ are of high accuracy but requires larger CPU time as compared to -VITM. In addition both of the proposed hybrid methods converges, that is, HATM with optimal ℏ converges faster than -VITM. For , the rate of convergence of HATM is the same as that of -VITM while -VITM requires less computational timethan HATM.
6. Conclusions
In that present work studied, two space-dimensional time-fractional models governing the unsteady flow of pGas via two new efficient techniques so-called HATM and -VITM. Both techniques are shown convergent with help of the Banach’s fixed point approach, and -VITM is shown -stable.
For an arbitrary fractional order , the evaluated solution behavior of the referred model equation is expressed in the form of well known Mittag–Leffler function. The effectiveness/validity of the evaluated new approximations is demonstrated via a numerical test example of a two space-dimensional time-fractional model governing the unsteady flow of a pGas by computing the absolute-errors/relative-error.
The numerical evaluation demonstrates that both of the developed techniques are convergent and perform better for the considered time-fractional model governing the unsteady flow of pGas. In addition, for given iteration new results by HATM with optimal convergence control parameter (ℏ) are of high accuracy but require larger CPU time as compared to -VITM, that is, HATM with optimal ℏ converges faster than -VITM. It is remarkably mentioned that for , both methods converge to the exact results with the same rate of convergence while -VITM requires less computational time than HATM. The motivation of this work is to explore the fractional behaviour of the considered model. We have observed the significant variations in the solutions for different fractional orders, which may lead to various physical consequences for the future work.
Author Contributions
Methodology, B.K.S.; Formal analysis, N.S.; Supervision, H.M.B.; Project administration, M.G. and D.G.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors want to declare that there are no competing interests.
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Srivastava, H.M.; Trujillo, J.J.; Kilbas, A.A. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Atangana, A. Blind in a commutative world: Simple illustrations with functions and chaotic attractors. Chaos Solitons Fractals 2018, 114, 347–363. [Google Scholar] [CrossRef]
- Atangana, A. Fractle-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Altizer, S.M.; Oberhauser, K.S. Effects of the protozoan parasite ophryocystis elektroscirrha on the fitness of monarch butterflies (danaus plexippus). J. Invertebr. Pathol. 1999, 74, 76–88. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Al-Mdallal, Q.M.; Khan, H.; Shah, K.; Khan, A. Fractional order mathematical modelling of covid-19 transmission. Chaos Solitons Fractals 2020, 139, 396–406. [Google Scholar] [CrossRef]
- Gupta, S. Numerical simulation of time-fractional black-scholes equation using fractional variational iteration method. J. Comput. Math. Sci. 2019, 9, 1101–1110. [Google Scholar] [CrossRef]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Song, L.; Xu, S.; Yang, J. Dynamical models of happiness with fractional order. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 616–628. [Google Scholar] [CrossRef]
- Moradpour, H.; Abri, A. Thermodynamic behavior and stability of polytropic gas. Int. J. Mod. Phys. D 2016, 12, 1650014. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to Homotopy Analysis Method; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Liao, S. An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun Nonlinear Sci Numer Simulat. 2010, 15, 2003–2016. [Google Scholar] [CrossRef]
- Liao, S. The Proposed Homotopy Analysis Techniques for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Prakasha, D.G.; Veeresha, P.; Baskonus, H.M. An efficient technique for a fractional-order system of equations describing the unsteady flow of a polytropic gas. Pramana J. Phys. 2019, 93, 75. [Google Scholar]
- Dalsgard, J.C. Lecture Notes on Stellar Structure and Evolution; Aarhus University Press: Aarhus, Denmark, 2004. [Google Scholar]
- Matinfar, M.; Nodeh, S.J. Application of he’s variational iteration method for solving the equation governing the unsteady flow of a polytropic gas. J. Math. Ext. 2009, 3, 61–67. [Google Scholar]
- Matinfar, M.; Saeidy, M. Homotopy analysis method for solving the equation governing the unsteady flow of a polytropic gas. World Appl. Sci. J. 2010, 9, 980–983. [Google Scholar]
- Billingham, J. Dynamics of a strongly nonlocal reaction-diffusion population model. Nonlinearity 2003, 17, 313. [Google Scholar] [CrossRef]
- Cherif, M.A.; Ziane, D.; Belghaba, K. Fractional natural decomposition method for solving fractional system of nonlinear equations of unsteady flow of a polytropic gas. Nonlinear Std. 2018, 25, 753–764. [Google Scholar]
- Adel, W.; Srinivasa, K. A new clique polynomial approach for fractional differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2022. [Google Scholar] [CrossRef]
- Yadav, L.K.; Agarwal, G.; Suthar, D.L.; Purohit, S.D. Time-fractional partial differential equations: A novel technique for analytical and numerical solutions. Arab. J. Basic Appl. Sci. 2022, 29, 86–98. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Kumam, P.; Arif, M. An analytical system to solve the system of nonlinear fractional differential equations. Mathematics 2019, 7, 505. [Google Scholar] [CrossRef]
- Srivastava, V.K.; Singh, B.K. Approximate series solution of multi-dimensional, time fractional-order (heat-like) diffusion equations using frdtm. R. Soc. Open Sci. 2015, 2, 140511. [Google Scholar]
- Saleh, R.; Kassem, M.; Mabrauk, S.M. Exact solutions of nonlinear fractional order partial differential equations via singular manifold method. Chin. J. Phys. 2019, 61, 290–300. [Google Scholar] [CrossRef]
- Weiguo, R. Comments on whether nonlinear fractional partila differential equations have soliton solutions. Partial. Differ. Equ. Appl. Math. 2022, 5, 100396. [Google Scholar]
- Ali, H.M.; Ahmad, H.; Askar, S.; Ameen, I.G. Efficient apporaches for solving system of nonlinear time-fractional partial differential equations. Fractal Fract. 2022, 6, 32. [Google Scholar] [CrossRef]
- Shakeel, M.; Shah, N.A.; Chung, J.D. Novel analytical technique to find closed form solutions of time fractional partial differential equations. Fractal Fract. 2022, 6, 24. [Google Scholar] [CrossRef]
- Hosseini, V.R.; Zou, W. The peridynamic differential opertaor for solving time-fractional partial differential equations. Nonlinear Dyn. 2022, 109, 1823–1850. [Google Scholar] [CrossRef]
- Malagi, N.S.; Prakasha, D.G.; Veeresha, P.; Prasannakumara, B.C. Fractional Reaction-Diffusion Model: An Efficient Computational Technique for Nonlinear Time-Fractional Schnackenberg Model; Springer: Singapore, 2022. [Google Scholar]
- Joujehi, A.S.; Derakhshan, M.H.; Marasi, H.R. An efficient hybrid numerical method for multi-term time fractional partial differential equations in fluid mechanics with convergence and error analysis. Commun. Nonlinear Sci. Numer. Simul. 2022, 114, 106620. [Google Scholar] [CrossRef]
- Alesemi, M.; Shahrani, J.S.A.; Iqbal, N.; Shah, R.; Nonlapon, K. Analysis and numerical simulation of system of fractional partial differential equations with non-singular kernel operators. Symmetry 2023, 15, 233. [Google Scholar] [CrossRef]
- Laoubi, M.; Odibat, Z.; Maayah, B. Effective optimized decomposition algorithms for solving nonlinear fractional differential equations. J. Comput. Nonlinear Dyn. 2023, 18, 021001. [Google Scholar] [CrossRef]
- Elshenhab, A.M.; Wang, X.T.; Mofarreh, F.; Bazighifan, O. Exact solutions and finite time stability of linear conformable fractional systems with pure delay. Comput. Model. Eng. Sci. 2023, 134, 927–940. [Google Scholar] [CrossRef]
- Wang, S.; Luo, X.; Riaz, S.; Zaman, H.; Zhou, C.; Hao, P. A fractional order fast repetitive control paradigm ofvienna rectifier for power quality improvement. Cmes-Comput. Model. Eng. Sci. 2023, 135, 259–273. [Google Scholar]
- Khan, H.; Kumam, P.; Nawaz, A.; Khan, Q.; Khan, S. The fractional investigation of fornberg-whitham equation using an efficient technique. Cmes-Comput. Model. Eng. Sci. 2023, 134, 1159–1176. [Google Scholar] [CrossRef]
- Veeresha, P.; Ilhan, E.; Prakasha, D.G.; Baskonus, H.M.; Gao, W. Regarding on the fractional mathematical model of tumor invasion and metastasis. Cmes-Comput. Model. Eng. Sci. 2021, 127, 1013–1036. [Google Scholar]
- Mohamed, M.A. Adomian decomposition method for solving the equation governing the unsteady flow of a polytropic gas. Appl. Appl. Math. 2009, 4, 52–61. [Google Scholar]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley and Sons: New York, NY, USA, 1978. [Google Scholar]
- Qing, Y.; Rhoades, B.E. T-Stability of Picard iteration in metric spaces. Fixed Point Theory Appl. 2008, 2008, 418971. [Google Scholar] [CrossRef]
- Khan, H.; Khan, A.; Chen, W.; Shah, K. Stability analysis and a numerical scheme for fractional Klein-Gordon equations. Math. Meth. Appl. Sci. 2019, 42, 723–732. [Google Scholar] [CrossRef]
- Maitama, S.; Zhao, W. Beyond sumudu transform and natural transform: j-transform properties and applications. J. Appl. Anal. Comput. 2020, 10, 1223–1241. [Google Scholar]
- He, J.H. Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput. Methods Appl. Mech. Eng. 1998, 167, 57–68. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method—A kind of non-linear analytical technique: Some examples. Int. J. -Non-Linear Mech. 1999, 167, 57–68. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method-Some recent results and new interpretations. J. Comput. Appl. Math. 2007, 207, 3–17. [Google Scholar] [CrossRef]
- Odibat, Z.M. A study on the convergence of variational iteration method. Math. Comput. Model. 2010, 51, 1181–1192. [Google Scholar] [CrossRef]
- Abassy, T.A.; El-Tawil, M.A.; El-Zoheiry, H. Modified variational iteration method for Boussinesq equation. Comput. Math. Appl. 2007, 54, 955–965. [Google Scholar] [CrossRef]
- Singh, B.K.; Kumar, P. Fractional variational iteration method for solving fractional partial differential equations with proportional delay. Int. J. Differ. Equ. 2017, 88, 1–11. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z.M. The variational iteration method: An efficient scheme for handling fractional partial differential equation in fluid mechanics. Comput. Math. Appl. 2009, 58, 2199–2208. [Google Scholar]
- Jafari, H.; Alipoor, A. A new method for calculating general Lagrange multiplier in the variational iteration method. Numer. Methods Partial. Differ. Equ. 2011, 27, 996–1001. [Google Scholar] [CrossRef]
- Goswami, P.; Alqahtani, R. Solutions of fractional differential equations by sumudu transform and variational iteration method. J. Nonlinear Sci. Appl. 2016, 9, 1944–1951. [Google Scholar] [CrossRef]
- Finlayson, B.A. The Method of Weighted Residuals and Variational Principles; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Khuri, S.A.; Sayfy, A. A laplace variational iteration strategy for the solution of differential equations. Appl. Math. Lett. 2012, 25, 2298–2305. [Google Scholar] [CrossRef]
- Li, F.; Nadeem, H.A.M. Modified laplace variational iteration method for solving fourth-order parabolic partial differential equation with variable coefficients. Comput. Math. Appl. 2020, 78, 2052–2062. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).