Aristotelian Diagrams for the Proportional Quantifier ‘Most’

Abstract

In this paper, we study the interaction between the square of opposition for the Aristotelian quantifiers (‘all’, ‘some’, ‘no’, and ‘not all’) and the square of opposition generated by the proportional quantifier ‘most’ (in its standard generalized quantifier theory reading of ‘more than half’). In a first step, we provide an analysis in terms of bitstring semantics for the two squares independently. The classical square for ‘most’ involves a tripartition of logical space, whereas the degenerate square for ‘all’ in first-order logic ($\mathsf{FOL}$) involves a quadripartition, due to $\mathsf{FOL}$’s lack of existential import. In a second move, we combine these two squares into an octagon of opposition, which was hitherto unattested in logical geometry, while the meet of the original tri- and quadripartitions yields a hexapartition for this octagon. In a final step, we switch from $\mathsf{FOL}$ to a logical system, which does assume existential import. This yields an octagon of the well known Lenzen type, and its bitstring semantics is reduced to a pentapartition.

1. Introduction

In the framework of logical geometry [1,2], a central object of investigation is the so-called ‘Aristotelian square’ or ‘square of opposition’, visualising Aristotelian relations, i.e., logical relations of opposition and implication. Two propositions $\alpha$ and $\beta$ are said to be

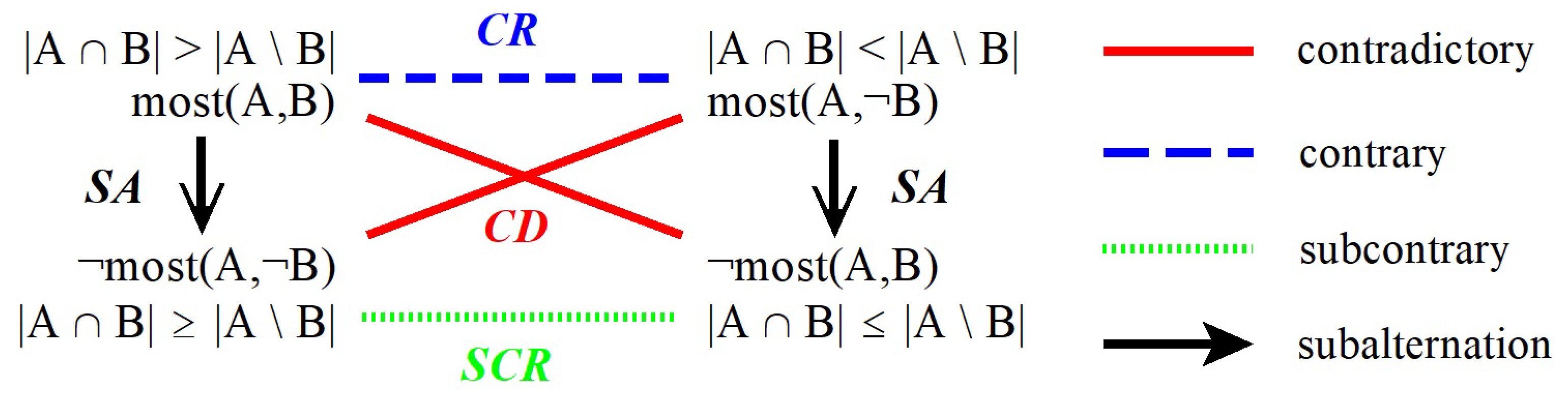
a.	contradictory	$\mathit{CD}(\alpha$,$\beta )$	iff	$\alpha$ and $\beta$ cannot be true together and
				$\alpha$ and $\beta$ cannot be false together,
b.	contrary	$\mathit{CR}(\alpha$,$\beta )$	iff	$\alpha$ and $\beta$ cannot be true together but
				$\alpha$ and $\beta$ can be false together,
c.	subcontrary	$\mathit{SCR}(\alpha$,$\beta )$	iff	$\alpha$ and $\beta$ can be true together but
				$\alpha$ and $\beta$ cannot be false together,
d.	in subalternation	$\mathit{SA}(\alpha$,$\beta )$	iff	$\alpha$ entails $\beta$ but $\beta$ does not entail $\alpha$.

An Aristotelian diagram (AD, for short) consists of a fragment $\mathcal{F}$ of a language $\mathcal{L}$, i.e., a subset of formulas of that language, and a logical system $\mathsf{S}$. The formulas in $\mathcal{F}$ are typically assumed to be $\mathsf{S}$-contingent and pairwise non-$\mathsf{S}$-equivalent, and the fragment is standardly also assumed to be closed under negation: if a formula $\alpha$ belongs to $\mathcal{F}$, then its negation $\neg \alpha$ also belongs to $\mathcal{F}$. More concretely, an Aristotelian diagram for $\mathcal{F}$ relative to $\mathsf{S}$ visualises a vertex- and edge-labeled graph G. The vertices of G are labeled by the elements of $\mathcal{F}$, whereas the edges of G are labeled by all the Aristotelian relations holding between those elements in $\mathsf{S}$.

The central aim of this paper is to study the interaction between two four-formula fragments that independently yield an AD. The first fragment—${\mathcal{F}}_{most}$—is generated on the basis of the formula most(A,B). On its standard reading in generalized quantifier theory [3,4], the proportional quantifier most is taken to be equivalent to more than half. In other words, the sentence most A are B is true iff the number of As that are B is strictly greater than the number of As that are not B. Starting from this basic formula most(A,B), we can then negate either the complete formula, or the predicate B, or both. This yields the fragment ${\mathcal{F}}_{most}$, which is listed here, together with the formulas’ denotations in the standard set-theoretical notation format of GQT:

${\mathcal{F}}_{most}$	$:=$	{	most(A,B),		$|A\cap B|>|A\setminus B|$
			¬most(A,B),		$|A\cap B|\le |A\setminus B|$
			most(A,¬B),		$|A\cap B|<|A\setminus B|$
			¬most(A,¬B)	}	$|A\cap B|\ge |A\setminus B|$

Completely analogously, the second fragment—${\mathcal{F}}_{all}$ — contains the four Aristotelian quantifiers [5], which are listed below, together with their denotations in GQT format and with equivalent formulations that clearly exhibit how this fragment is generated on the basis of all(A,B):

${\mathcal{F}}_{all}$	$:=$	{	all(A,B),		$|A\setminus B|=0$		all(A,B)
			not all(A,B),		$|A\setminus B|>0$		¬all(A,B)
			no(A,B),		$|A\cap B|=0$		all(A,¬B)
			some(A,B),	}	$|A\cap B|>0$		¬all(A,¬B)

In the past, authors such as Peterson [6,7], Brown [8], Veloso and Veloso [9], and Murinová and Novák [10,11] have already proposed Aristotelian diagrams for most (and other modulated/intermediate/generalized quantifiers). However, in the present paper, we will study these diagrams from the specific perspective of logical geometry, focusing (inter alia) on the partitions of logical space that are induced by such diagrams.

The paper is organised as follows. In a first major step, the two fragments ${\mathcal{F}}_{most}$ and ${\mathcal{F}}_{all}$ are analysed independently of one another by distinguishing the two radically different ADs that they give rise to in first-order logic ($\mathsf{FOL}$), i.c., a classical square for ‘most’ versus a degenerate square for ‘all’ (Section 2.1), and by computing the corresponding bitstring semantics in terms of a tripartition versus a quadripartition of logical space (Section 2.2). Notice that, by analysing ${\mathcal{F}}_{most}$ in $\mathsf{FOL}$, we do not mean to suggest that most(A,B) is first-order definable—which it famously is not [3]—but, merely, wish to emphasise that we are working in a logical system without existential import, in which the predicates A and B are thus allowed to have empty extensions. In a second move, the two fragments ${\mathcal{F}}_{most}$ and ${\mathcal{F}}_{all}$ are combined into the eight-formula fragment ${\mathcal{F}}_{allmost}$. The AD for ${\mathcal{F}}_{allmost}$ relative to $\mathsf{FOL}$ is an octagon hitherto unattested in logical geometry (Section 3.1), with bitstring semantics involving a hexapartition of logical space (Section 3.2). In a final step, we switch from $\mathsf{FOL}$—which does not assume existential import—to a new logical system, $\mathsf{SYL}$ (from ‘syllogistics’)—which does assume existential import. The AD for ${\mathcal{F}}_{allmost}$ relative to $\mathsf{SYL}$ is another octagon, this time of the familiar Lenzen type (Section 4.1), with a pentapartition for its bitstring semantics (Section 4.2). We finish off with some concluding remarks and issues for further research (Section 5).

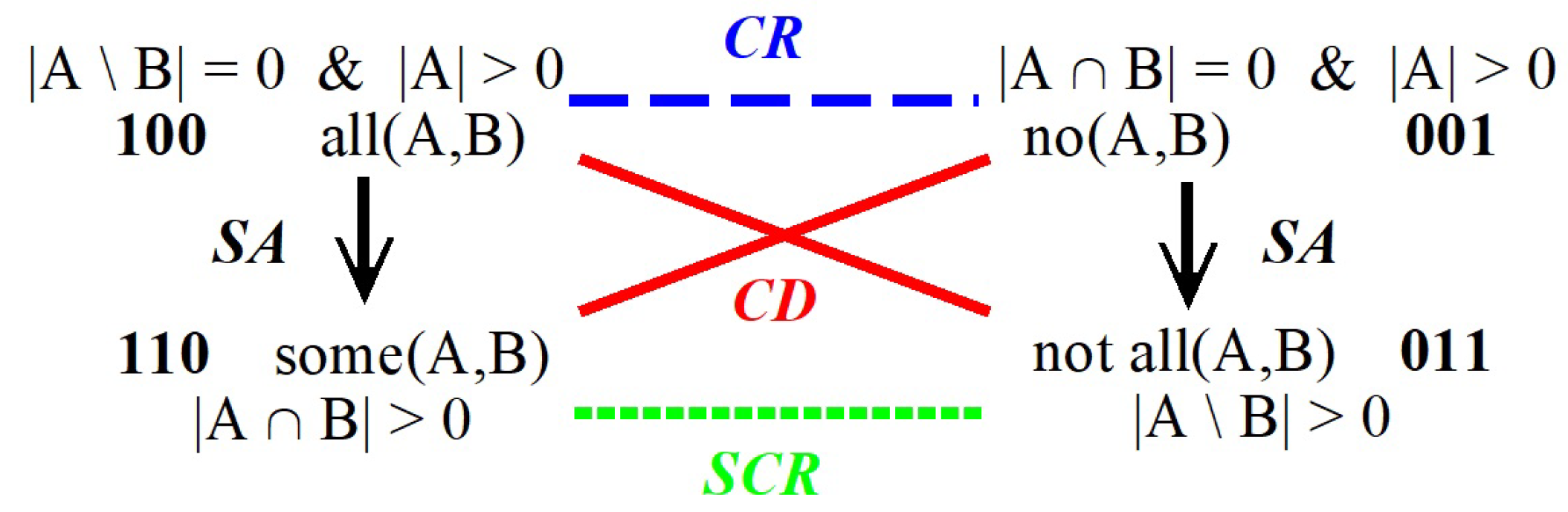
2. Aristotelian Squares for ‘Most’ versus ‘All’

2.1. Aristotelian Relations for ‘Most’ versus ‘All’

The definitions of the Aristotelian relations and the characterisation of the fragment ${\mathcal{F}}_{most}$ in Section 1 give rise to the so-called classical Aristotelian square in Figure 1, which uses the by now standard graphical conventions: two contradiction (CD) relations on the diagonals, two subalternation (SA) relations on the vertical edges, and one contrariety (CR) and one subcontrariety (SCR) relation on the horizontal edges. Note, furthermore, that (positive occurrences of) the proportional quantifier most always have existential import: even in $\mathsf{FOL}$, most A are B entails that there is at least one A (semantically: $|A\cap B|>|A\setminus B|$ entails $|A\cap B|>0$, and hence $\left|A\right|>0$). (However, the negated quantifier not most lacks existential import: not most A are B is true in case there are no A’s, i.e., if $\left|A\right|=0$ then $|A\cap B|=0\le 0=|A\setminus B|$.) The Aristotelian quantifiers all and no, by contrast, lack existential import in $\mathsf{FOL}$: neither all A are B nor no A are B entails in $\mathsf{FOL}$ that there is at least one A. The resulting constellation is the so-called degenerate Aristotelian square for ${\mathcal{F}}_{\mathit{all}}$ in Figure 2, sometimes also referred to as an ‘X of opposition’ [12].

In such a degenerate square, only the two contradiction (CD) relations on the diagonals remain, i.e., there is no contrariety (C) between all and no, no subcontrariety (SC) between some and not all, and no subalternation (SA) from all to some, nor from no to not all. The four pairs of formulas on the outer edge of the square are said to be unconnected, i.e., they stand in no Aristotelian relation whatsoever.

Finally, it bears emphasising that the squares for ${\mathcal{F}}_{\mathit{most}}$ and ${\mathcal{F}}_{\mathit{all}}$ are both duality squares, as well. For example, in Figure 1, we observe that most(A,B) and ¬most(A,¬B) are dual to each other, just like all(A,B) and some(A,B) = ¬all(A,¬B) are dual to each other in Figure 2. The fact that a classical and a degenerate Aristotelian square are both duality squares clearly illustrates the conceptual independence between the Aristotelian relations on the one hand, and the duality relations on the other. This issue has been studied extensively in logical geometry [13,14,15]. However, we will not pursue it further in this paper, but focus exclusively on the Aristotelian relations that hold among the formulas of ${\mathcal{F}}_{\mathit{most}}$ and ${\mathcal{F}}_{\mathit{all}}$.

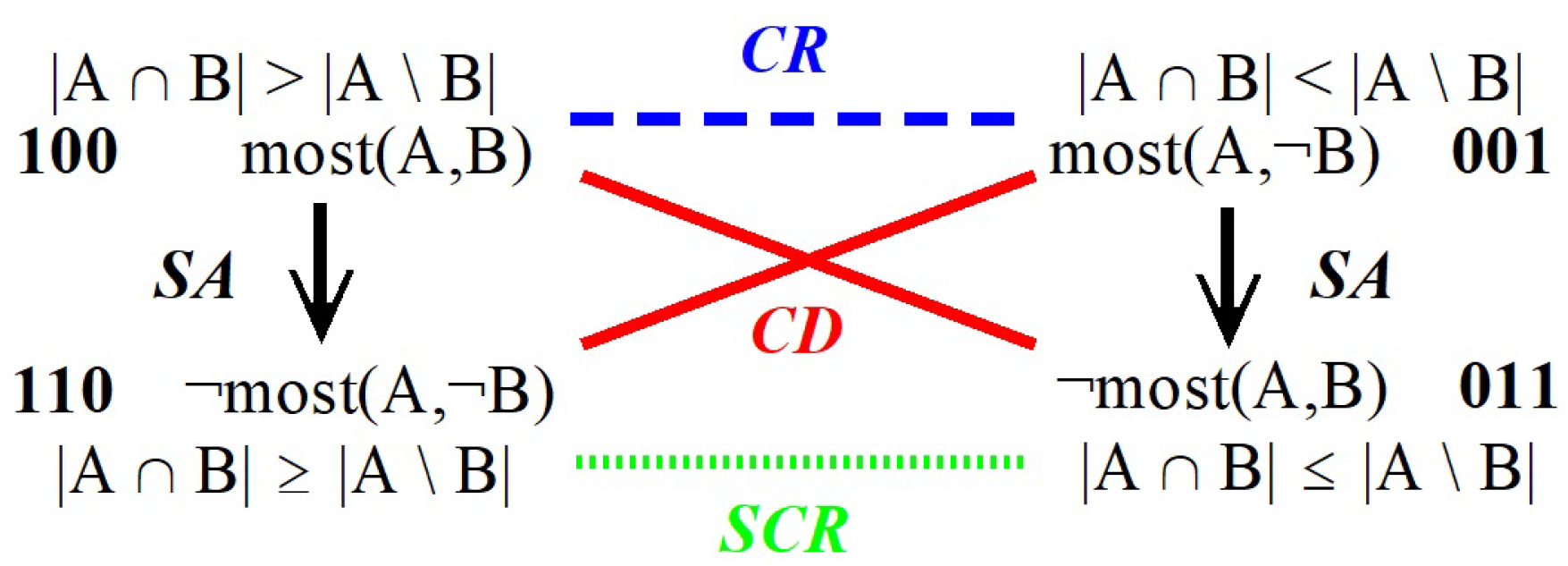
2.2. Bitstring Semantics for ‘Most’ versus ‘All’

Bitstring semantics is a technique developed within the research framework of logical geometry [1,16,17,18], which allows us to systematically compute combinatorial representations of a given number of propositions, thus providing a concrete grip on their logical behavior. Given a logical system $\mathsf{S}$ and fragment $\mathcal{F}$, we first compute the partition induced by $\mathcal{F}$ in $\mathsf{S}$, denoted ${\mathsf{\Pi }}_{\mathsf{S}}\left(\mathcal{F}\right)$, as follows:

$${\mathsf{\Pi }}_{\mathsf{S}}\left(\mathcal{F}\right):=\{\underset{\phi \in \mathcal{F}}{\bigwedge }\pm \phi \mid \underset{\phi \in \mathcal{F}}{\bigwedge }\pm \phi \mathrm{is}\mathsf{S}-\mathrm{consistent}\},$$

where $+\phi =\phi$ and $-\phi =\neg \phi$. The fragment ${\mathcal{F}}_{most}$ defined in Section 1 can be shown to induce the following partition in $\mathsf{FOL}$:

${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right)$	=	{	${\alpha }_1$: more than half (A,B),		$|A\cap B|>|A\setminus B|$
			${\alpha }_2$: exactly half (A,B),		$|A\cap B|=|A\setminus B|$
			${\alpha }_3$: less than half (A,B)	}	$|A\cap B|<|A\setminus B|$

The elements of a partition, which are called anchor formulas, are (i) jointly exhaustive, that is, ${\vDash }_{\mathsf{S}}\bigvee {\mathsf{\Pi }}_{\mathsf{S}}\left(\mathcal{F}\right)$, and (ii) mutually exclusive, that is, ${\vDash }_{\mathsf{S}}\neg (\alpha \wedge \beta )$ for distinct $\alpha ,\beta \in {\mathsf{\Pi }}_{\mathsf{S}}\left(\mathcal{F}\right)$; for example, the tripartition of logical space ${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right)$ consists of the three anchor formulas ${\alpha }_1\equiv$most(A,B)∧¬most(A,¬B), ${\alpha }_2\equiv$¬most(A,B)∧¬most(A,¬B), and ${\alpha }_3\equiv$most(A,¬B)∧¬most(A,B), the remaining three conjunctions—most(A,B)∧most(A,¬B), most(A,B)∧¬most(A,B), and most(A,¬B)∧¬most(A,¬B)—being inconsistent. Finally, note that ${\alpha }_1$ and ${\alpha }_3$ both entail $\left|A\right|>0$, whereas ${\alpha }_2$ holds even in case $\left|A\right|=0$.

In a second step, the bitstring semantics is defined, not just for the fragment $\mathcal{F}$ itself, but rather for its entire Boolean closure in $\mathsf{S}$, denoted ${\mathbb{B}}_{\mathsf{S}}\left(\mathcal{F}\right)$ and defined as the smallest set $C\subseteq {\mathcal{L}}_{\mathsf{S}}$, such that (i) $\mathcal{F}\subseteq C$ and (ii) C is closed under the Boolean operations (up to logical equivalence), i.e., for all $\phi ,\psi \in C$, there exist $\alpha ,\beta \in C$ such that $\alpha {\equiv }_{\mathsf{S}}\phi \wedge \psi$ and $\beta {\equiv }_{\mathsf{S}}\neg \phi$. The bitstring semantics ${\beta }_{\mathsf{S}}^{\mathcal{F}}:{\mathbb{B}}_{\mathsf{S}}\left(\mathcal{F}\right)\to {\{0,1\}}^{|{\mathsf{\Pi }}_{\mathsf{S}}\left(\mathcal{F}\right)|}$ maps every formula $\phi \in {\mathbb{B}}_{\mathsf{S}}\left(\mathcal{F}\right)$ onto its bitstring representation ${\beta }_{\mathsf{S}}^{\mathcal{F}}\left(\phi \right)$, which is a sequence of $|{\mathsf{\Pi }}_{\mathsf{S}}\left(\mathcal{F}\right)|$ bits that will have the value 1 in its $i^{\mathrm{th}}$ bit position iff ${\vDash }_{\mathsf{S}}{\alpha }_i\to \phi$. Given that $|{\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right)|=3$, the bitstring semantics${\beta }_{\mathsf{FOL}}^{most}$ for ${\mathbb{B}}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right)$ is defined in terms of bitstrings of length three. In particular, the resulting bitstrings for the formulas of ${\mathcal{F}}_{most}$ are:

${\beta }_{\mathsf{FOL}}^{most}\left(most(A,B)\right)$	=	100		$|A\cap B|>|A\setminus B|$
${\beta }_{\mathsf{FOL}}^{most}(\neg most(A,B))$	=	011		$|A\cap B|\le |A\setminus B|$
${\beta }_{\mathsf{FOL}}^{most}\left(most(A,\neg B)\right)$	=	001		$|A\cap B|<|A\setminus B|$
${\beta }_{\mathsf{FOL}}^{most}(\neg most(A,\neg B))$	=	110		$|A\cap B|\ge |A\setminus B|$

Let us now turn to the partition induced by the second fragment that was introduced in Section 1, namely, ${\mathcal{F}}_{all}$:

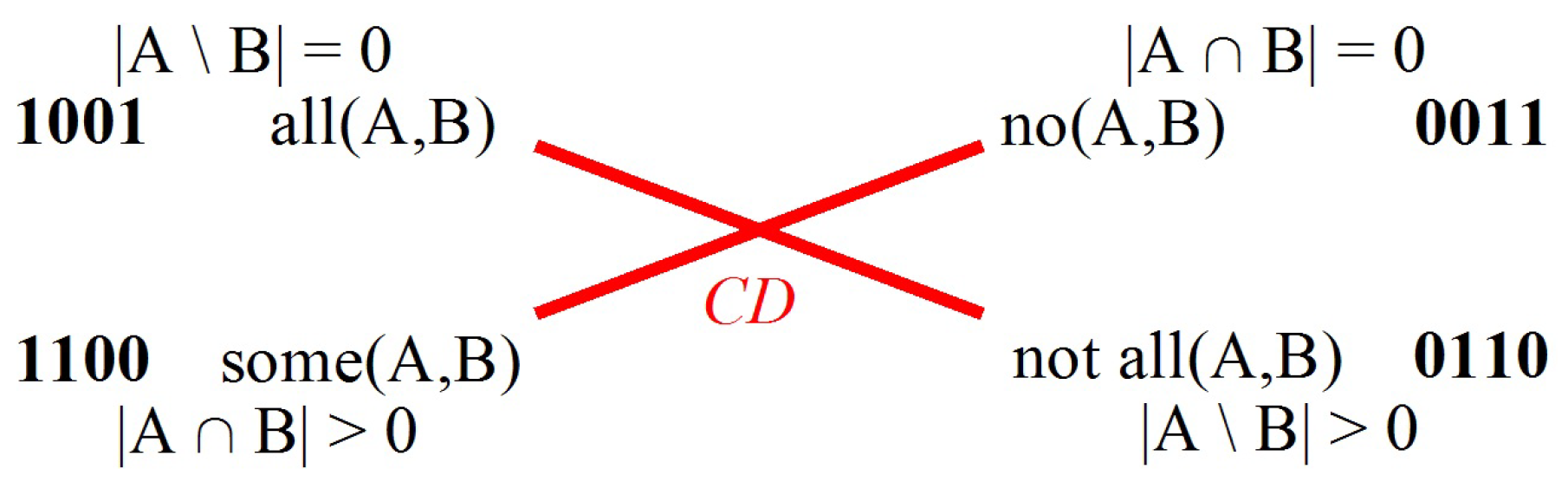
${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{all}\right)$	=	{	${\alpha }_1^{\prime }$: all A are B & there are A’s,		$|A\setminus B|=0\&\left|A\right|>0$
			${\alpha }_2^{\prime }$: some but not all A are B,		$|A\setminus B|>0\&|A\cap B|>0$
			${\alpha }_3^{\prime }$: no A are B & there are A’s,		$|A\cap B|=0\&\left|A\right|>0$
			${\alpha }_4^{\prime }$: there are no A’s	}	$\left|A\right|=0$

In contrast to the tripartition ${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right)$ above, the quadripartition of logical space ${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{all}\right)$ consists of the four anchor formulas ${\alpha }_1^{\prime }$, ${\alpha }_2^{\prime }$, ${\alpha }_3^{\prime }$ and ${\alpha }_4^{\prime }$. Crucially, the fourth anchor formula ${\alpha }_4^{\prime }$ takes care of the lack of existential import with the Aristotelian quantifiers in $\mathsf{FOL}$: both the formulas all A are B and no A are B make perfect sense—they are true in fact—if there are no As. As a consequence, the bitstring semantics ${\beta }_{\mathsf{FOL}}^{all}$ for ${\mathbb{B}}_{\mathsf{FOL}}\left({\mathcal{F}}_{all}\right)$ is defined in terms of bitstrings of length four. In particular, the resulting bitstrings for the formulas of ${\mathcal{F}}_{all}$ are as follows:

${\beta }_{\mathsf{FOL}}^{all}\left(all(A,B)\right)$	=	1001		$|A\setminus B|=0$
${\beta }_{\mathsf{FOL}}^{all}\left(notall(A,B)\right)$	=	0110		$|A\setminus B|>0$
${\beta }_{\mathsf{FOL}}^{all}\left(no(A,B)\right)$	=	0011		$|A\cap B|=0$
${\beta }_{\mathsf{FOL}}^{all}\left(some(A,B)\right)$	=	1100		$|A\cap B|>0$

Observe that the ${\beta }_{\mathsf{FOL}}^{all}$-bitstrings for both all(A,B) and no(A,B) have a value 1 in their fourth bit position—these formulas are true if there are no As, i.e., they do not have existential import in $\mathsf{FOL}$—whereas those for not all(A,B) and some(A,B) have a value 0 in their fourth bit position—these formulas are false if there are no As, i.e., they do have existential import. The two ADs in Figure 3 and Figure 4—which are the respective counterparts of Figure 1 and Figure 2, but with the bitstring representations added—nicely reflect the standard result from logical geometry that a classical square only requires bitstrings of length 3, whereas a degenerate square requires bitstrings of length 4 [1].

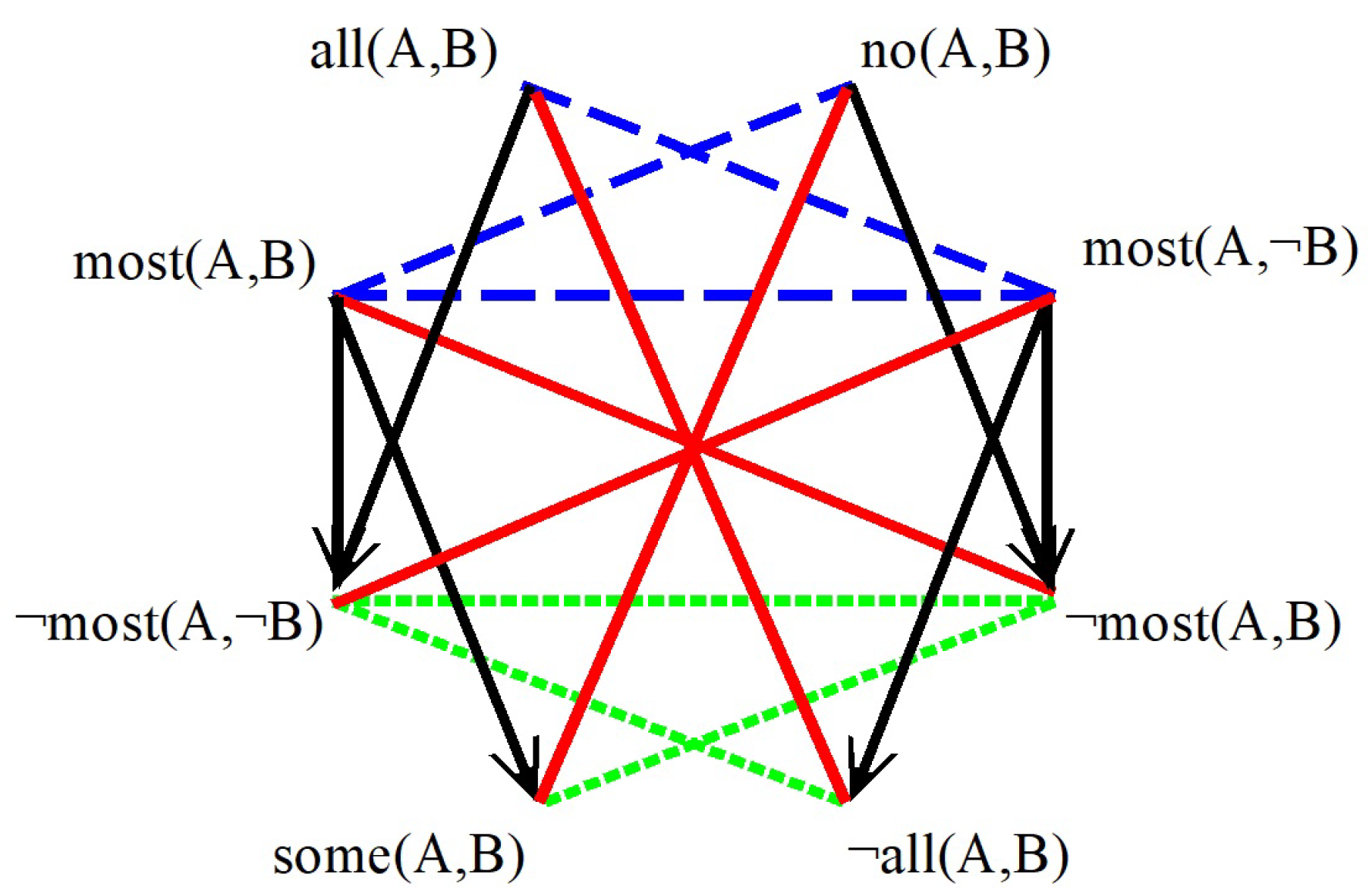
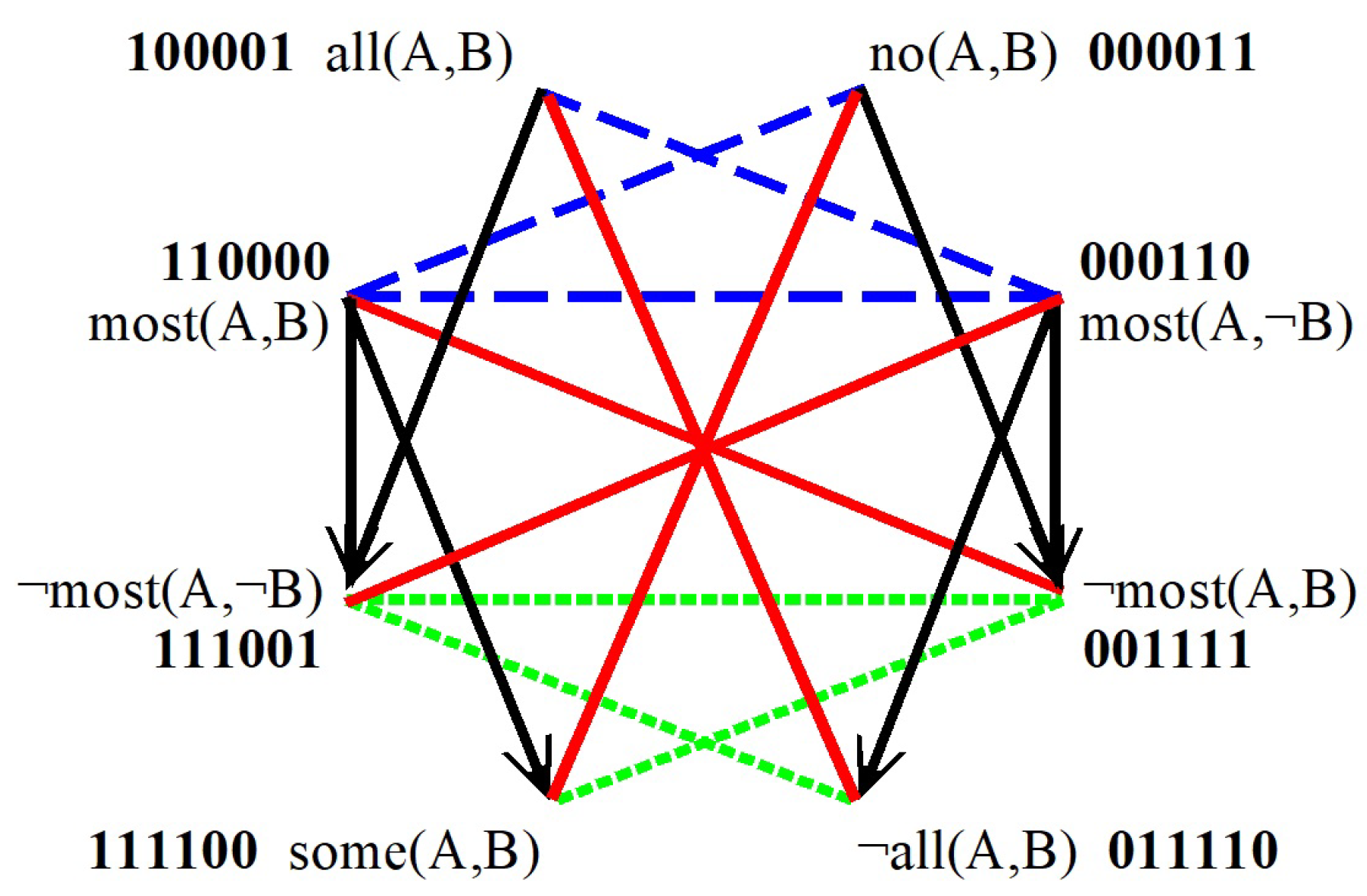
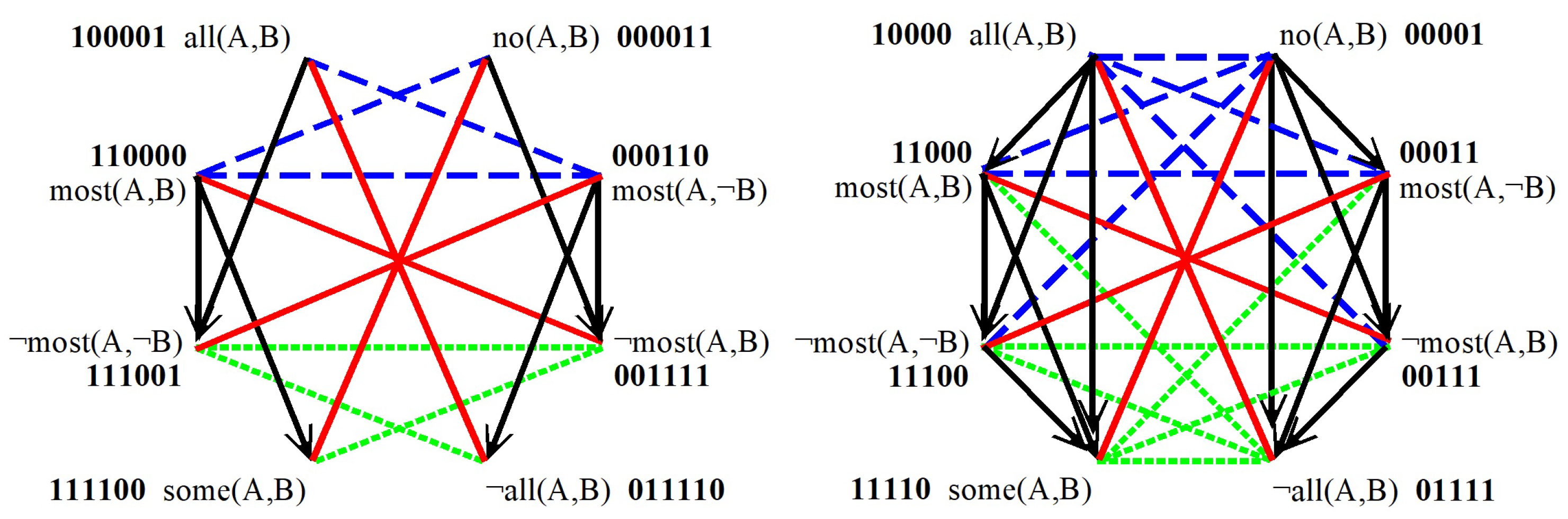
3. A First Aristotelian Octagon for ‘Most’ and ‘All’

Having provided the ADs and the bitstring semantics for the two four-formula fragments ${\mathcal{F}}_{most}$ and ${\mathcal{F}}_{all}$ independently in the previous section, we now continue working in $\mathsf{FOL}$, and combine these two fragments into one large eight-formula fragment ${\mathcal{F}}_{allmost}:={\mathcal{F}}_{all}\cup {\mathcal{F}}_{most}$, whose formulas are listed again below, together with their denotations in GQT format:

${\mathcal{F}}_{allmost}$	=	{	all(A,B),		$|A\setminus B|=0$
			no(A,B),		$|A\cap B|=0$
			most(A,B),		$|A\cap B|>|A\setminus B|$
			most(A,¬B),		$|A\cap B|<|A\setminus B|$
			¬most(A,¬B),		$|A\cap B|\ge |A\setminus B|$
			¬most(A,B),		$|A\cap B|\le |A\setminus B|$
			some(A,B),		$|A\cap B|>0$
			¬all(A,B)	}	$|A\setminus B|>0$

In Section 3.1 we will first of all look at the Aristotelian relations holding among the eight formulas of this new fragment ${\mathcal{F}}_{allmost}$ and the octagonal AD that these relations give rise to in $\mathsf{FOL}$. In Section 3.2, we will then compute the partition induced by ${\mathcal{F}}_{allmost}$ in $\mathsf{FOL}$ and consider the resulting bitstring semantics in full detail.

3.1. Aristotelian Relations in the First Octagon

The first, and perhaps the most obvious type of additional Aristotelian relations that show up in ${\mathcal{F}}_{allmost}$ are relations of subalternation between one formula from the classical square and one formula from the degenerate square. The first two SA relations given below go from a formula in ${\mathcal{F}}_{most}$ to a formula in ${\mathcal{F}}_{all}$, whereas the last two SA relations go from ${\mathcal{F}}_{all}$ to ${\mathcal{F}}_{most}$. Next to each subalternation, we have also added its semantic justification in GQT format.

SA[	most(A,B),	some(A,B)	]		if $|A\cap B|>|A\setminus B|$	then $|A\cap B|>0$
SA[	most(A,¬B),	¬all(A,B)	]		if $|A\cap B|<|A\setminus B|$	then $|A\setminus B|>0$
SA[	all(A,B),	¬most(A,¬B)	]		if $|A\setminus B|=0$	then $|A\cap B|\ge |A\setminus B|$
SA[	no(A,B),	¬most(A,B)	]		if $|A\cap B|=0$	then $|A\cap B|\le |A\setminus B|$

These four SA relations allow us to interlock the two squares from Figure 1 and Figure 2 into the octagonal AD in Figure 5. This octagon furthermore yields two additional contrariety relations (CR) and two additional subcontrariety relations (SCR) between a formula from ${\mathcal{F}}_{most}$ and a formula from ${\mathcal{F}}_{all}$, namely:

CR[	all(A,B),	most(A,¬B)	]	CR[	most(A,B),	no(A,B)	]
SCR[	¬most(A,¬B),	¬all(A,B)	]	SCR[	some(A,B),	¬most(A,B)	]

Hence, in addition to the original classical square for ${\mathcal{F}}_{most}$, the octagonal AD in Figure 5 also contains two further classical squares. We will refer to these two as mixed squares, since they consist of two formulas from ${\mathcal{F}}_{most}$ and two formulas from ${\mathcal{F}}_{all}$. The three classical squares embedded in Figure 5 visualise the following three subfragments of ${\mathcal{F}}_{allmost}$:

${\mathcal{F}}_{allmost-square1}$	$:=$		${\mathcal{F}}_{most}$
${\mathcal{F}}_{allmost-square2}$	$:=$	{	all(A,B),	most(A,¬B),	¬most(A,¬B),	¬all(A,B)	}
${\mathcal{F}}_{allmost-square3}$	$:=$	{	most(A,B),	no(A,B),	some(A,B),	¬most(A,B)	}

The original classical square for ${\mathcal{F}}_{allmost-square1}$ sits horizontally stretched inside the octagon in Figure 5. The mixed classical square for ${\mathcal{F}}_{allmost-square2}$ is tilted 22.5${}^{\circ }$ clockwise in Figure 5; it comprises the second and third additional SA relations mentioned above, together with the additional (S)CR relations on the left. Finally, the mixed classical square for ${\mathcal{F}}_{allmost-square3}$ is tilted 22.5${}^{\circ }$ counterclockwise in Figure 5, and comprises the first and fourth additional SA relations and the additional (S)CR relations on the right.

Completely analogously, we now observe that, in addition to the original degenerate square for ${\mathcal{F}}_{all}$, the octagonal AD in Figure 5 also contains two further mixed degenerate squares. These three degenerate squares embedded in Figure 5 visualise the following subfragments of ${\mathcal{F}}_{allmost}$:

${\mathcal{F}}_{allmost-square4}$	$:=$		${\mathcal{F}}_{all}$
${\mathcal{F}}_{allmost-square5}$	$:=$	{	most(A,B),	all(A,B),	¬all(A,B),	¬most(A,B)	}
${\mathcal{F}}_{allmost-square6}$	$:=$	{	no(A,B),	most(A,¬B),	¬most(A,¬B),	some(A,B)	}

The original degenerate square ${\mathcal{F}}_{allmost-square4}$ sits vertically stretched inside the octagon in Figure 5, whereas the two mixed squares—${\mathcal{F}}_{allmost-square5}$ and ${\mathcal{F}}_{allmost-square6}$—are again tilted 45${}^{\circ }$ counterclockwise and clockwise, respectively.

It is important to stress that, although this type of Aristotelian octagon—containing three classical and three degenerate squares—was known in theory as one of the 18 families of Aristotelian octagons, the AD in Figure 5 can be considered the first ‘non-artificial’ instance of this family. (In a completely different application context, Frijters [19] has recently found another instance of this family.) Furthermore, this AD naturally fits into a series of families of octagons in which the number of degenerate squares increases from zero (with the families of Moretti and Lenzen octagons [20,21]) over one (with the families of Béziau and Buridan octagons [22,23,24]) and two (with the family of Keynes-Johnson octagons [25,26]) to three (with the family to which ${\mathcal{F}}_{allmost}$ in Figure 5 belongs).

3.2. Bitstring Semantics for the First Octagon

In order to compute the bitstring semantics for ${\mathcal{F}}_{allmost}$ in $\mathsf{FOL}$, we start from the two basic partitions computed in Section 2.2 for ${\mathcal{F}}_{most}$ and ${\mathcal{F}}_{all}$, which are repeated here for the sake of convenience:

${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right)$	=	{	${\alpha }_1$: more than half (A,B),		$|A\cap B|>|A\setminus B|$
			${\alpha }_2$: exactly half (A,B),		$|A\cap B|=|A\setminus B|$
			${\alpha }_3$: less than half (A,B)	}	$|A\cap B|<|A\setminus B|$
${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{all}\right)$	=	{	${\alpha }_1^{\prime }$: all A are B & there are A’s,		$|A\setminus B|=0\&\left|A\right|>0$
			${\alpha }_2^{\prime }$: some but not all A are B,		$|A\setminus B|>0\&|A\cap B|>0$
			${\alpha }_3^{\prime }$: no A are B & there are A’s,		$|A\cap B|=0\&\left|A\right|>0$
			${\alpha }_4^{\prime }$: there are no A’s	}	$\left|A\right|=0$

We now compute ${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{allmost}\right)$ by taking the meet of these two original partitions, i.e., ${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{allmost}\right):={\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right){\wedge }_{\mathsf{FOL}}{\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{all}\right)$, which consists of all $\mathsf{FOL}$-consistent conjunctions ${\alpha }_i\wedge {\alpha }_j^{\prime }$ of an anchor formula ${\alpha }_i\in {\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right)$ and an anchor formula ${\alpha }_j^{\prime }\in {\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{all}\right)$ (for more details, see [1]). This initially yields $|{\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right)|\times |{\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{all}\right)|=3\times 4=12$ conjunctions. After elimination of the $\mathsf{FOL}$-inconsistent conjunctions—such as ${\alpha }_3\wedge {\alpha }_1^{\prime }$, where $|A\setminus B|$ cannot simultaneously be equal to and strictly greater that zero—we obtain the following hexapartition:

${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{allmost}\right)=$	{	${\alpha }_1^{\prime \prime }$: all A are B and there are A’s,		$|A\cap B|>|A\setminus B|=0$
		${\alpha }_2^{\prime \prime }$: most but not all A’s are B,		$|A\cap B|>|A\setminus B|>0$
		${\alpha }_3^{\prime \prime }$: exactly half the A’s are B,		$|A\cap B|=|A\setminus B|>0$
		${\alpha }_4^{\prime \prime }$: most but not all A’s are not B,		$0<|A\cap B|<|A\setminus B|$
		${\alpha }_5^{\prime \prime }$: no A’s are B, but there are A’s,		$0=|A\cap B|<|A\setminus B|$
		${\alpha }_6^{\prime \prime }$: there are no A’s	}	$0=|A\cap B|=|A\setminus B|$

Given this partition, the bitstring semantics ${\beta }_{\mathsf{FOL}}^{allmost}$ for ${\mathbb{B}}_{\mathsf{FOL}}\left({\mathcal{F}}_{allmost}\right)$ is defined in terms of bitstrings of length six. In particular, the resulting bitstrings for the formulas of ${\mathcal{F}}_{allmost}$ are as follows:

${\beta }_{\mathsf{FOL}}^{allmost}\left(all(A,B)\right)$	=	100001		$|A\setminus B|=0$
${\beta }_{\mathsf{FOL}}^{allmost}\left(no(A,B)\right)$	=	000011		$|A\cap B|=0$
${\beta }_{\mathsf{FOL}}^{allmost}\left(most(A,B)\right)$	=	110000		$|A\cap B|>|A\setminus B|$
${\beta }_{\mathsf{FOL}}^{allmost}\left(most(A,\neg B)\right)$	=	000110		$|A\cap B|<|A\setminus B|$
${\beta }_{\mathsf{FOL}}^{allmost}(\neg most(A,\neg B))$	=	111001		$|A\cap B|\ge |A\setminus B|$
${\beta }_{\mathsf{FOL}}^{allmost}(\neg most(A,B))$	=	001111		$|A\cap B|\le |A\setminus B|$
${\beta }_{\mathsf{FOL}}^{allmost}\left(some(A,B)\right)$	=	111100		$|A\cap B|>0$
${\beta }_{\mathsf{FOL}}^{allmost}\left(notall(A,B)\right)$	=	011110		$|A\setminus B|>0$

Observe, once again, that the ${\beta }_{\mathsf{FOL}}^{allmost}$-bitstrings for all(A,B) and no(A,B) have a value 1 in their sixth bit position—these formulas are true if there are no A’s, i.e., they do not have existential import in $\mathsf{FOL}$. Finally, the AD in Figure 6 is the counterpart of Figure 5, with the bitstring representations added to it.

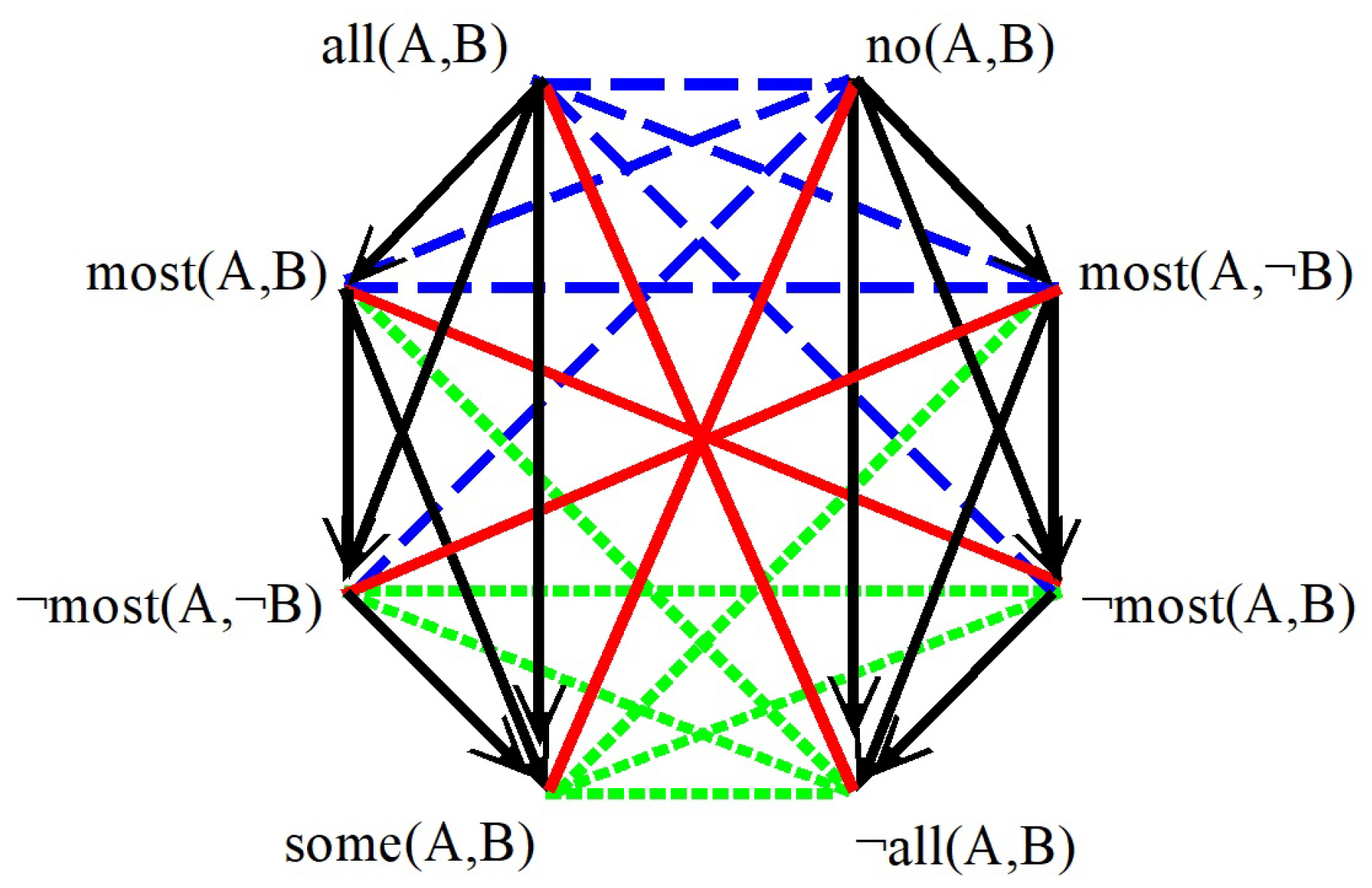
4. A Second Aristotelian Octagon for ‘Most’ and ‘All’

At this point, we want to switch from $\mathsf{FOL}$—which does not assume existential import—to a new logical system, $\mathsf{SYL}$—which does assume existential import, i.e., it only assigns non-empty sets as extensions of unary predicates. This switch does not fundamentally affect the semantics of ${\mathcal{F}}_{most}$, and hence the classical square from Figure 3 and the induced partition remain unchanged—i.e., ${\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{most}\right)={\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right)$. (Note, however, that the interpretation of the anchor formula ${\alpha }_2$ changes slightly upon moving from $\mathsf{FOL}$ to $\mathsf{SYL}$: relative to $\mathsf{FOL}$, situations in which $\left|A\right|=0$ are taken into consideration, and ${\alpha }_2$ is said to be true in them; however, relative to $\mathsf{SYL}$, such situations are no longer considered to begin with.) By contrast, the semantics of ${\mathcal{F}}_{all}$ is quite different from before; relative to $\mathsf{SYL}$, it now looks as follows (in GQT format):

${\mathcal{F}}_{all}$	=	{	all(A,B),		$|A\setminus B|=0\&\left|A\right|>0$
			¬all(A,B),		$|A\setminus B|>0$
			no(A,B),		$|A\cap B|=0\&\left|A\right|>0$
			some(A,B)	}	$|A\cap B|>0$

This fragment induces the following partition in $\mathsf{SYL}$:

${\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{all}\right)$	=	{	${\alpha }_1^{\prime }$: all A are B & there are A’s,		$|A\setminus B|=0\&\left|A\right|>0$
			${\alpha }_2^{\prime }$: some but not all A are B,		$|A\setminus B|>0\&|A\cap B|>0$
			${\alpha }_3^{\prime }$: no A are B & there are A’s	}	$|A\cap B|=0\&\left|A\right|>0$

When we compare ${\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{all}\right)$ with ${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{all}\right)$ from before, we note that the anchor formulas ${\alpha }_1^{\prime }$, ${\alpha }_2^{\prime }$ and ${\alpha }_3^{\prime }$ have remained the same, whereas ${\alpha }_4^{\prime }$ is no longer present, because it has gone from $\mathsf{FOL}$-consistent to $\mathsf{SYL}$-inconsistent. As a consequence, the bitstring semantics ${\beta }_{\mathsf{SYL}}^{all}$ for ${\mathbb{B}}_{\mathsf{SYL}}\left({\mathcal{F}}_{all}\right)$ is defined in terms of bitstrings of length three, since the fourth bit position from the ${\beta }_{\mathsf{FOL}}^{all}$-bitstrings has been deleted. In particular, the resulting bitstrings for the formulas of ${\mathcal{F}}_{all}$ are given as follows:

${\beta }_{\mathsf{SYL}}^{all}\left(all(A,B)\right)$	=	100		$|A\setminus B|=0\&\left|A\right|>0$
${\beta }_{\mathsf{SYL}}^{all}(\neg all(A,B))$	=	011		$|A\setminus B|>0$
${\beta }_{\mathsf{SYL}}^{all}\left(no(A,B)\right)$	=	001		$|A\cap B|=0\&\left|A\right|>0$
${\beta }_{\mathsf{SYL}}^{all}\left(some(A,B)\right)$	=	110		$|A\cap B|>0$

This move from the quadripartition ${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{all}\right)$ to the tripartition ${\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{all}\right)$ has important consequences for the Aristotelian relations in ${\mathcal{F}}_{all}$. In particular, in addition to the two contradiction relations on the diagonals in Figure 7, ${\mathcal{F}}_{all}$ also has the vertical subalternation arrows from all to some and from no to not all, as well as the horizontal contrariety between all and no and the horizontal subcontrariety between some and not all. In other words, we move from the degenerate square for ${\mathcal{F}}_{all}$ relative to $\mathsf{FOL}$ in Figure 4—with bitstrings of length 4—to the classical square for ${\mathcal{F}}_{all}$ relative to $\mathsf{SYL}$ in Figure 7—with bitstrings of length 3. This contrast between a degenerate and a classical square is the standard example of the logic-sensitivity of Aristotelian diagrams, which is a well known phenomenon in logical geometry [1,27,28]: although we are dealing with one and the same fragment ${\mathcal{F}}_{all}$, this fragment gives rise to very different ADs relative to different logical systems ($\mathsf{FOL}$ versus $\mathsf{SYL}$).

In Section 3 we combined ${\mathcal{F}}_{most}$ and ${\mathcal{F}}_{all}$ into the eight-formula fragment ${\mathcal{F}}_{allmost}$, and studied it relative to $\mathsf{FOL}$. We now return to ${\mathcal{F}}_{allmost}$, and study it relative to $\mathsf{SYL}$. As expected, the semantics (in GQT format) looks different from before:

${\mathcal{F}}_{allmost}$	=	{	all(A,B),		$|A\setminus B|=0\&\left|A\right|>0$
			no(A,B),		$|A\cap B|=0\&\left|A\right|>0$
			most(A,B),		$|A\cap B|>|A\setminus B|$
			most(A,¬B),		$|A\cap B|<|A\setminus B|$
			¬most(A,¬B),		$|A\cap B|\ge |A\setminus B|$
			¬most(A,B),		$|A\cap B|\le |A\setminus B|$
			some(A,B),		$|A\cap B|>0$
			¬all(A,B)	}	$|A\setminus B|>0$

In Section 4.1, we will first of all look at the Aristotelian relations holding among the eight formulas of the fragment ${\mathcal{F}}_{allmost}$ and the octagonal AD that these relations give rise to in $\mathsf{SYL}$. In Section 4.2, we will compute the partition induced by ${\mathcal{F}}_{allmost}$ in $\mathsf{SYL}$ and consider the resulting bitstring semantics in full detail.

4.1. Aristotelian Relations in the Second Octagon

When we interlock the two classical squares for ${\mathcal{F}}_{most}$ and ${\mathcal{F}}_{all}$ from Figure 3 and Figure 7, we obtain the octagonal AD in Figure 8. Comparing this octagon for ${\mathcal{F}}_{allmost}$ in $\mathsf{SYL}$ to the octagon for ${\mathcal{F}}_{allmost}$ in $\mathsf{FOL}$ given in Figure 5, we observe that the former contains six additional subalternation relations. Two of them, of course, come from ${\mathcal{F}}_{all}$ being a classical square in $\mathsf{SYL}$ instead of a degenerate one. The remaining four resemble the ones given at the beginning of Section 3.1, in that they hold between one formula from ${\mathcal{F}}_{most}$ and one formula from ${\mathcal{F}}_{all}$:

SA[	all(A,B),	most(A,B)	]	SA[	¬most(A,B),	¬all(A,B)	]
SA[	no(A,B),	most(A,¬B)	]	SA[	¬most(A,¬B),	some(A,B)	]

Moving from ${\mathcal{F}}_{allmost}$ in $\mathsf{FOL}$ (Figure 5) to ${\mathcal{F}}_{allmost}$ in $\mathsf{SYL}$ (Figure 8), we also get three additional contrariety relations and three additional subcontrariety relations. Again, one of each is due to ${\mathcal{F}}_{all}$ being a classical square in $\mathsf{SYL}$, whereas the remaining two pairs hold between one formula from ${\mathcal{F}}_{most}$ and one formula from ${\mathcal{F}}_{all}$:

CR[	all(A,B),	¬most(A,B)	]	CR[	¬most(A,¬B),	no(A,B)	]
SCR[	most(A,B),	¬all(A,B)	]	SCR[	some(A,B),	most(A,¬B)	]

The fundamental differences in overall Aristotelian constellations between the two octagonal ADs can be summarised as follows:

relations in ${\mathcal{F}}_{allmost}$	...relative to $\mathsf{FOL}$	...relative to $\mathsf{SYL}$
contradiction	4	4
contrariety	3	6
subcontrariety	3	6
subalternation	6	12
unconnectedness	12	0
total ($\frac{8\times 7}{2}$)	28	28

All twelve pairs of formulas which are unconnected—i.e., stand in no Aristotelian relation whatsoever—in $\mathsf{FOL}$ and which thus characterise the three degenerate squares embedded in the octagon in Figure 6, turn out to stand in a (proper) relation of (sub)contrariety or subalternation in $\mathsf{SYL}$. In other words, the octagonal AD in Figure 8 no longer contains any degenerate squares, and instead consists of six classical squares, which visualise the six subfragments of ${\mathcal{F}}_{allmost}$ that we already encountered before:

${\mathcal{F}}_{allmost-square1}$	=		${\mathcal{F}}_{most}$
${\mathcal{F}}_{allmost-square2}$	=	{	all(A,B),	most(A,¬B),	¬most(A,¬B),	¬all(A,B)	}
${\mathcal{F}}_{allmost-square3}$	=	{	most(A,B),	no(A,B),	some(A,B),	¬most(A,B)	}
${\mathcal{F}}_{allmost-square4}$	=		${\mathcal{F}}_{all}$
${\mathcal{F}}_{allmost-square5}$	=	{	most(A,B),	all(A,B),	¬all(A,B),	¬most(A,B)	}
${\mathcal{F}}_{allmost-square6}$	=	{	no(A,B),	most(A,¬B),	¬most(A,¬B),	some(A,B)	}

The first two mixed squares (i.e., consisting of two formulas from ${\mathcal{F}}_{most}$ and two formulas from ${\mathcal{F}}_{all}$), namely, ${\mathcal{F}}_{allmost-square2}$ and ${\mathcal{F}}_{allmost-square3}$, are identical relative to $\mathsf{FOL}$ and to $\mathsf{SYL}$: in both systems they are classical squares. (In this sense, they also resemble ${\mathcal{F}}_{allmost-square1}={\mathcal{F}}_{most}$.) By contrast, the last two mixed squares, namely, ${\mathcal{F}}_{allmost-square5}$ and ${\mathcal{F}}_{allmost-square6}$, are degenerate squares relative to $\mathsf{FOL}$, but classical squares relative to $\mathsf{SYL}$. (In this sense, they also resemble ${\mathcal{F}}_{allmost-square4}={\mathcal{F}}_{all}$.)

Notice that with the octagonal AD in Figure 8—consisting of six interlocking classical squares, but no degenerate squares—we return to a well documented family of octagons, namely, the so-called Lenzen octagon [20]. Furthermore, this contrast between the two families of octagons (Figure 5 versus Figure 8) constitutes a more complex and rich illustration of the logic sensitivity of Aristotelian diagrams: once again, we are dealing with a single fragment, ${\mathcal{F}}_{allmost}$, which gives rise to very different ADs relative to different logical systems ($\mathsf{FOL}$ versus $\mathsf{SYL}$).

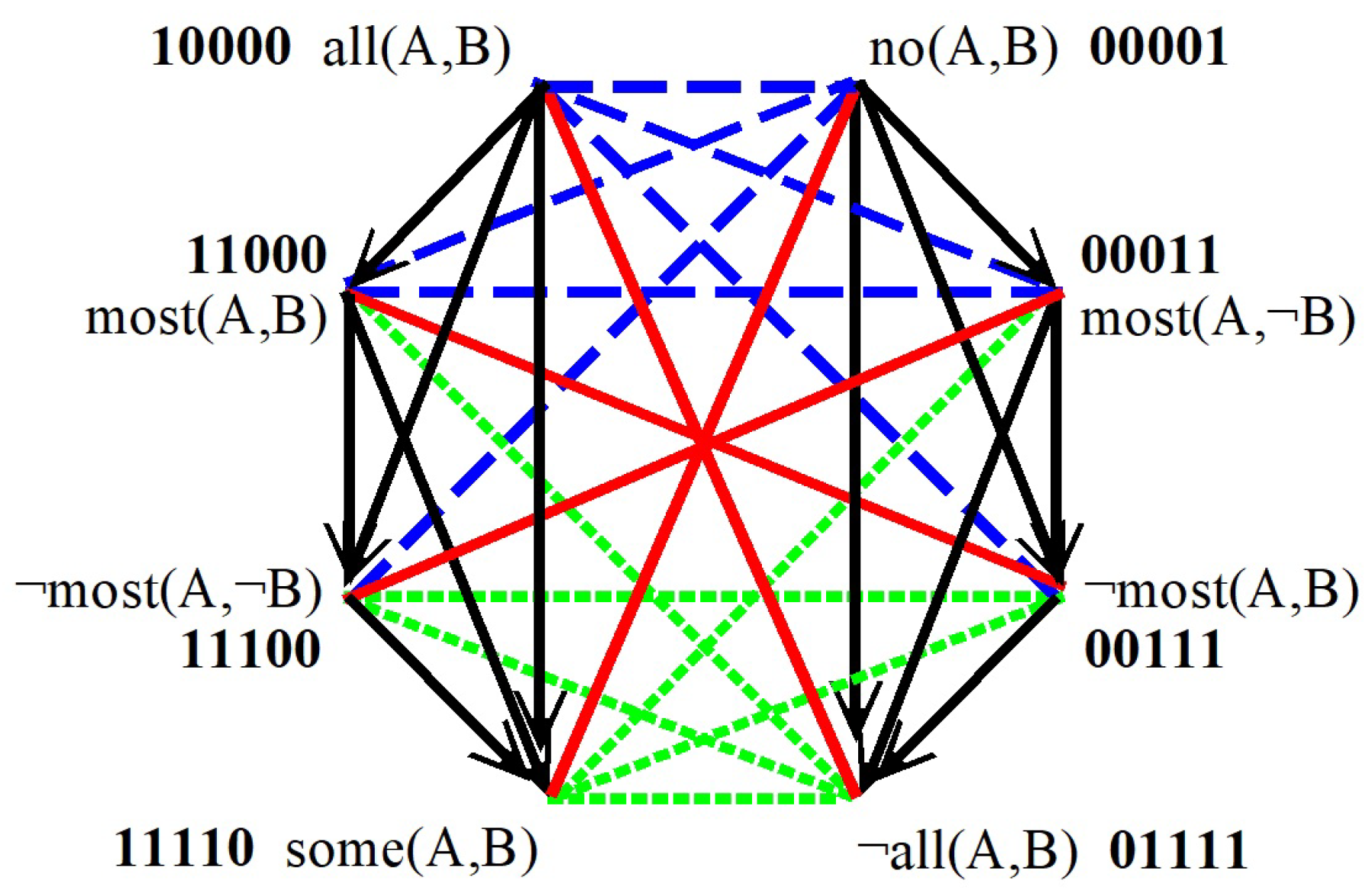
4.2. Bitstring Semantics for the Second Octagon

In order to compute the bitstring semantics for ${\mathcal{F}}_{allmost}$ in $\mathsf{SYL}$, we start from the two tripartitions that we calculated for ${\mathcal{F}}_{most}$ and ${\mathcal{F}}_{all}$ in $\mathsf{SYL}$, which we repeat here for the sake of convenience:

${\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{most}\right)$	=	{	${\alpha }_1$: more than half (A,B),		$|A\cap B|>|A\setminus B|$
			${\alpha }_2$: exactly half (A,B),		$|A\cap B|=|A\setminus B|$
			${\alpha }_3$: less than half (A,B)	}	$|A\cap B|<|A\setminus B|$
${\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{all}\right)$	=	{	${\alpha }_1^{\prime }$: all A are B & there are A’s,		$|A\setminus B|=0\&\left|A\right|>0$
			${\alpha }_2^{\prime }$: some but not all A are B,		$|A\setminus B|>0\&|A\cap B|>0$
			${\alpha }_3^{\prime }$: no A are B & there are A’s,	}	$|A\cap B|=0\&\left|A\right|>0$

We now take the meet of these two partitions, i.e., ${\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{allmost}\right):={\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{most}\right){\wedge }_{\mathsf{SYL}}{\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{all}\right)$, which results in the following pentapartition:

${\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{allmost}\right)=$	{	${\alpha }_1^{\prime \prime }$: All A are B and there are A’s,		$|A\cap B|>|A\setminus B|=0$
		${\alpha }_2^{\prime \prime }$: Most but not all A’s are B,		$|A\cap B|>|A\setminus B|>0$
		${\alpha }_3^{\prime \prime }$: Exactly half the A’s are B,		$|A\cap B|=|A\setminus B|>0$
		${\alpha }_4^{\prime \prime }$: Most but not all A’s are not B,		$0<|A\cap B|<|A\setminus B|$
		${\alpha }_5^{\prime \prime }$: No A’s are B, but there are A’s,	}	$0=|A\cap B|<|A\setminus B|$

Note that in comparison to ${\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{allmost}\right)$, the anchor formula ${\alpha }_6^{\prime \prime }$ is no longer present, because it has gone from $\mathsf{FOL}$-consistent to $\mathsf{SYL}$-inconsistent. As a consequence, the bitstring semantics ${\beta }_{\mathsf{SYL}}^{allmost}$ for ${\mathbb{B}}_{\mathsf{SYL}}\left({\mathcal{F}}_{allmost}\right)$ is defined in terms of bitstrings of length five, since the sixth bit position from the ${\beta }_{\mathsf{FOL}}^{allmost}$-bitstrings has been deleted. In particular, the resulting bitstrings for the formulas of ${\mathcal{F}}_{allmost}$ are given as follows:

${\beta }_{\mathsf{SYL}}^{allmost}\left(all(A,B)\right)$	=	10000		$|A\setminus B|=0\&\left|A\right|>0$
${\beta }_{\mathsf{SYL}}^{allmost}\left(no(A,B)\right)$	=	00001		$|A\cap B|=0\&\left|A\right|>0$
${\beta }_{\mathsf{SYL}}^{allmost}\left(most(A,B)\right)$	=	11000		$|A\cap B|>|A\setminus B|$
${\beta }_{\mathsf{SYL}}^{allmost}\left(most(A,\neg B)\right)$	=	00011		$|A\cap B|<|A\setminus B|$
${\beta }_{\mathsf{SYL}}^{allmost}(\neg most(A,\neg B))$	=	11100		$|A\cap B|\ge |A\setminus B|$
${\beta }_{\mathsf{SYL}}^{allmost}(\neg most(A,B))$	=	00111		$|A\cap B|\le |A\setminus B|$
${\beta }_{\mathsf{SYL}}^{allmost}\left(some(A,B)\right)$	=	11110		$|A\cap B|>0$
${\beta }_{\mathsf{SYL}}^{allmost}\left(notall(A,B)\right)$	=	01111		$|A\setminus B|>0$

The AD in Figure 9 is the counterpart of Figure 8, with the bitstring representations added to it.

5. Conclusions

In

Table 1. Overview of fragments, logics, partitions and Aristotelian diagrams.

$\mathcal{F}$	$\left|\mathcal{F}\right|$	$\mathsf{S}$	$|{\mathbf{\Pi }}_{\mathsf{S}}\left(\mathcal{F}\right)|$	Aristotelian Diagram
${\mathcal{F}}_{most}$	4	$\mathsf{FOL}$	3	classical square
${\mathcal{F}}_{most}$	4	$\mathsf{SYL}$	3	classical square
${\mathcal{F}}_{all}$	4	$\mathsf{FOL}$	4	degenerate square
${\mathcal{F}}_{all}$	4	$\mathsf{SYL}$	3	classical square
${\mathcal{F}}_{allmost}$	8	$\mathsf{FOL}$	6	new type of octagon
${\mathcal{F}}_{allmost}$	8	$\mathsf{SYL}$	5	Lenzen octagon

, we provide an overview of the fragments, logics, partitions and Aristotelian diagrams discussed in this paper. The starting point of our analysis are two four-formula fragments, namely, ${\mathcal{F}}_{most}$ for the proportional quantifiers (generated on the basis of ‘most’), and ${\mathcal{F}}_{all}$ for the standard Aristotelian quantifiers (generated on the basis of ‘all’). Relative to $\mathsf{FOL}$ as well as to $\mathsf{SYL}$, the fragment ${\mathcal{F}}_{most}$ induces a tripartition of logical space—i.e., $|{\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{most}\right)|=3=|{\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{most}\right)|$—and yields a classical square with bitstrings of length three. By contrast, the fragment ${\mathcal{F}}_{all}$ induces a quadripartition relative to $\mathsf{FOL}$—i.e., $|{\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{all}\right)|=4$—and yields a degenerate square with bitstrings of length four, but this same fragment induces a tripartition relative to $\mathsf{SYL}$—i.e., $|{\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{all}\right)|=3$—and yields a classical square with bitstrings of length three. The difference between these two ADs for (and partitions induced by) the fragment ${\mathcal{F}}_{all}$ relative to $\mathsf{FOL}$ and to $\mathsf{SYL}$ is the standard example of the well known logic sensitivity of Aristotelian diagrams.

Combining ${\mathcal{F}}_{most}$ with ${\mathcal{F}}_{all}$, we obtained the eight-formula fragment ${\mathcal{F}}_{allmost}$. Relative to $\mathsf{FOL}$, this fragment induces a hexapartition—i.e., $|{\mathsf{\Pi }}_{\mathsf{FOL}}\left({\mathcal{F}}_{allmost}\right)|=6$—and bitstrings of length six, but relative to $\mathsf{SYL}$, this same fragment induces a pentapartition—i.e., $|{\mathsf{\Pi }}_{\mathsf{SYL}}\left({\mathcal{F}}_{allmost}\right)|=5$—and bitstrings of length five. In Figure 10 the two resulting octagonal ADs are juxtaposed. The AD for ${\mathcal{F}}_{allmost}$ in $\mathsf{FOL}$ is an octagon—of a type hitherto only known ‘in theory’ in logical geometry—in which three classical and three degenerate squares are embedded. By contrast, the AD for ${\mathcal{F}}_{allmost}$ in $\mathsf{SYL}$ is a standard Lenzen octagon, with six embedded classical squares. The difference between these two ADs for (and partitions induced by) the fragment ${\mathcal{F}}_{allmost}$ relative to $\mathsf{FOL}$ and to $\mathsf{SYL}$ constitutes a more complex and rich illustration of the logic-sensitivity of Aristotelian diagrams.

In future research, we intend to consider alternative interpretations for the fragment ${\mathcal{F}}_{most}$ available in the formal semantics literature on proportional quantification [29,30] and investigate their interaction with the fragment ${\mathcal{F}}_{all}$ from the point of view of logic-sensitivity. In addition, we continue our search for natural instances of the 18 families of octagonal ADs, many of which are known to exist in theory, but have not been attested in the literature so far.