1. Introduction
Bell’s polynomials were initially introduced to represent successive derivatives of composite functions [
1]. However, as it has been pointed out in [
2], such polynomials, being related to partitions of integers [
3], find immediate applications in combinatorial mathematics [
4]. They also intervene in formulas for representing symmetric functions of the zeros of analytic functions, thus generalizing the classical Newton–Girard formulas. Using these results, the reduction formulas of the orthogonal invariants of a strictly positive compact operator were expressed. In this way, Robert’s formulas [
5] and other expressions related to those can be derived.
Generalized classes of Bell’s polynomials have been proposed in the literature, e.g., by Fujiwara [
6], Kim [
7], and Rai, Singh [
8]. Further generalizations, including the multidimensional case, can be found in papers by Bernardini, Natalini, Ricci and Natalini, and Ricci (see [
9], and the references therein).
There are many areas in which the adoption of Bell’s polynomials has allowed useful approximations to be obtained in applied mathematics, such as those concerning the Laplace transform of composite analytic functions (see [
10], and the references therein).
In this paper, we discuss another application to the probability theory [
11] by deriving some formulas useful to calculate the moments of generalized Gaussian distributions. To this end, judicious use is made of the extensions of Bell’s polynomials presented in previous papers.
This article is organized as follows: In
Section 2, Bell’s polynomials and their main properties are briefly recalled. In
Section 3, Bell’s polynomials are used to approximate the primitives of composite exponential functions. Finally, after recalling, in
Section 4, the generalization of Bell’s polynomials to the case of multi-nested functions, the moments of generalized Gaussian distributions are approximated in
Section 5. Some examples illustrated using version 13.2 of the computer algebra software Mathematic
are shown in
Section 6.
2. Recalling the Bell’S Polynomials
Consider the composite function , where and are differentiable functions (up to a sufficiently large order), defined in suitable intervals of the real axis so that can be differentiated n times with respect to t by using the chain rule.
Here, and in what follows, we use the following notation:
Then, the
n-th derivative of
is represented by
where
denotes the general Bell’s polynomial, and the coefficients
for all
are homogeneous polynomials of the variables
of degree
k and
isobaric of weight
n (i.e., they are a linear combination of monomials
having the same degree
).
Bell’s polynomials satisfy the recurrence relation
and they can be expressed explicitly using the Faà di Bruno’s formula [
12,
13]
where the sum runs over all the partitions
of the integer
n,
denotes the number of parts of size
i, and
denotes the number of parts of the considered partition [
2].
The coefficients
in Equation (
1) depend only on the values
, and satisfy the recursion
In the particular case where
, that is equivalent to considering the composite function
, and upon assuming that
, we obtain the following simplified expression for the right-hand side of (
1):
where the
are the
complete Bell’s polynomials. It results in
, and the first few values of
, for
are given by
The values of the complete Bell’s polynomials for particular choices of the parameter can be found in [
14].
The complete Bell’s polynomials satisfy the identity (see e.g., [
15])
3. Primitives of Exponential Functions
Let
be a composite function that is analytic in a neighborhood of the origin. The relevant Taylor’s expansion is given by
where
and
Then, the primitive of the composite function
writes
Remark 1. Note that here and in what follows we avoid adding a constant to indefinite integrals, based on the assumption that the relevant primitives vanish at the origin.
In the case of exponential functions, Equation (
11) becomes
where we have assumed, for convenience,
.
Then, in particular, it results
As a consequence, we find
4. An Extension of Bell’s Polynomials
We consider the second-order Bell’s polynomials, , defined by the n-th derivative of the composite function .
Consider the functions , , , and suppose that , , and are n times differentiable with respect to their variables, so that the composite function can be differentiated n times with respect to t, by using the chain rule.
Similarly to the previous section, we use the following notation:
Then, the
n-th derivative of
can be represented by
where
denotes the general second-order Bell’s polynomial.
The first few polynomials are given by
A more extended table can be found in [
10].
The connection between
and the ordinary Bell’s polynomials is discussed below. In [
16], the following theorem has been proven.
Theorem 1. For every integer n, the polynomials are represented in terms of the ordinary Bell’s polynomials by the following equation: From here, it has been shown that the second-order Bell’s polynomials can be computed recursively, avoiding the use of computationally cumbersome expressions such as the Faà di Bruno formula, on the basis of the following theorem.
Theorem 2. The second-order Bell’s polynomials verify the recursion The proof of this result is provided in [
16].
Primitives of Nested Functions
Considering the second-order nested functions of the type
, the preceding Equation (11) writes
and in the case of a nested exponential function, with
,
5. Moments of Generalized Gaussian Distributions
Consider the analytic monotonically increasing function and consider the nested exponential function .
The normalization constant of the generalized Gaussian distribution writes
the mean value is
and the second moment
so that we find the variance
Note that, thanks to the rapid decay of the exponential function, the integrals in (
21)–(
23) can be estimated with a pretty negligible numerical error using a suitable Gaussian quadrature rule on a bounded interval of the real axis.
Then, assuming
, the
nth moment is given by
and using the second order Bell’s polynomials (
17), and assuming
, we find
6. Particular Examples
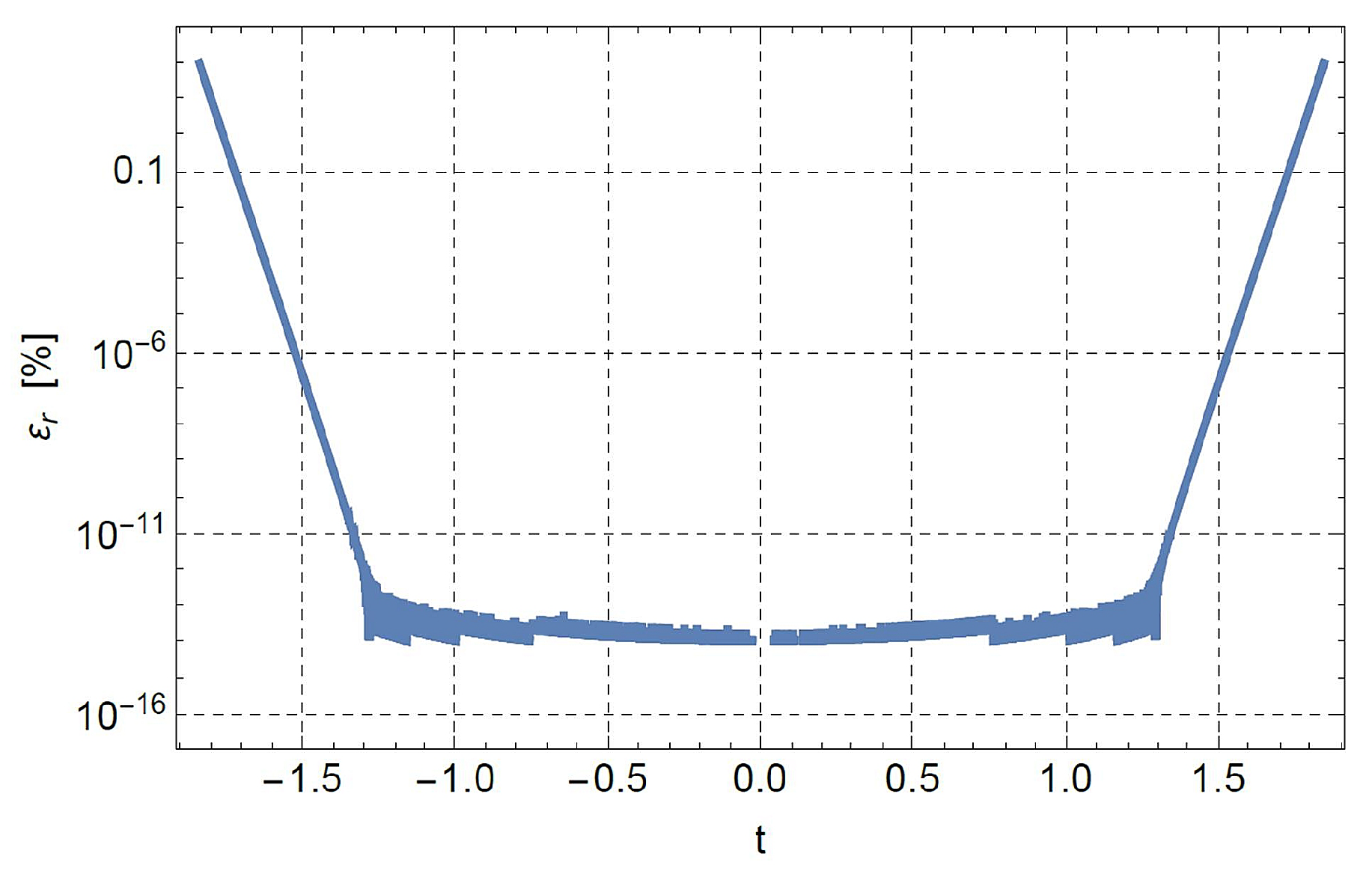
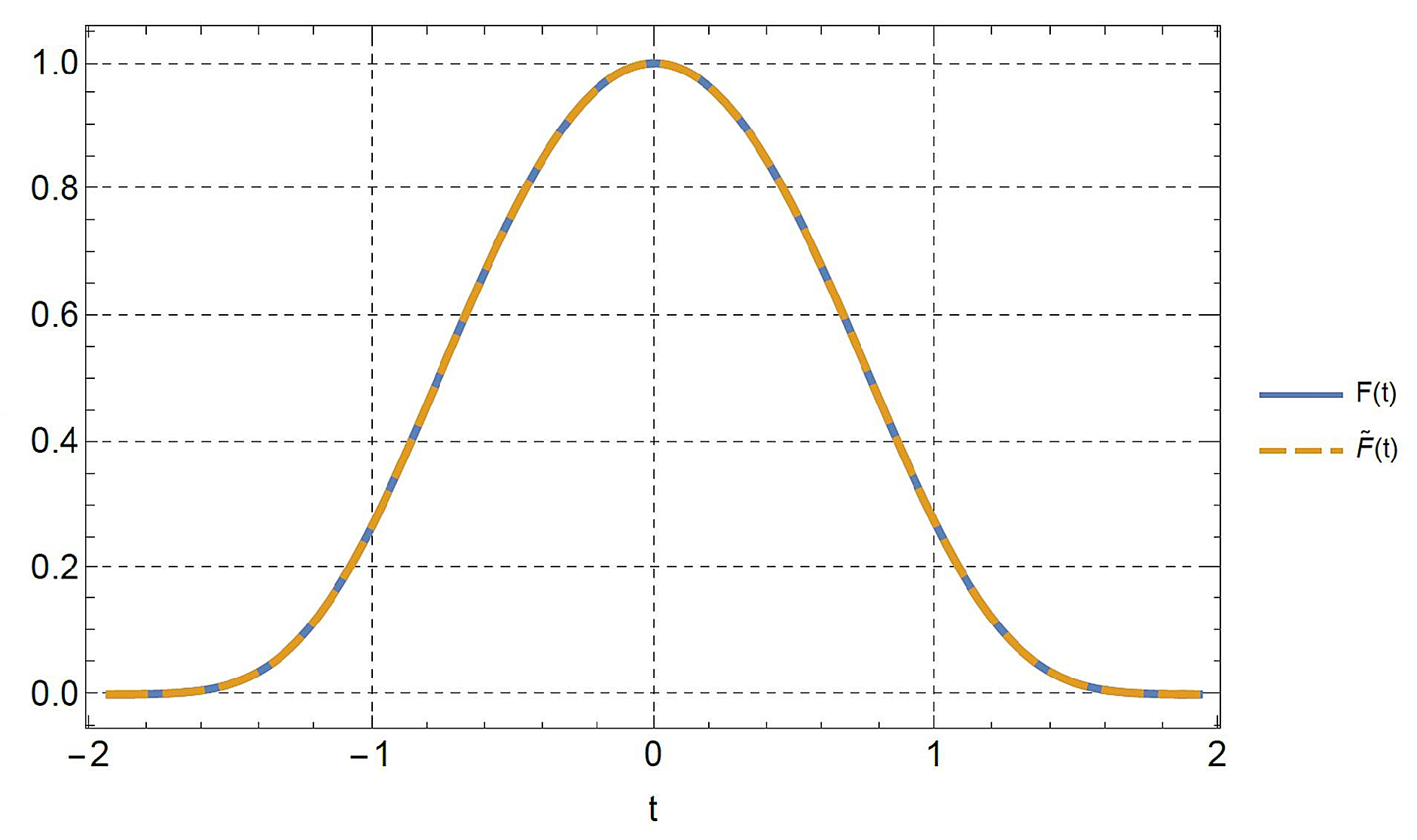
6.1. Example 1
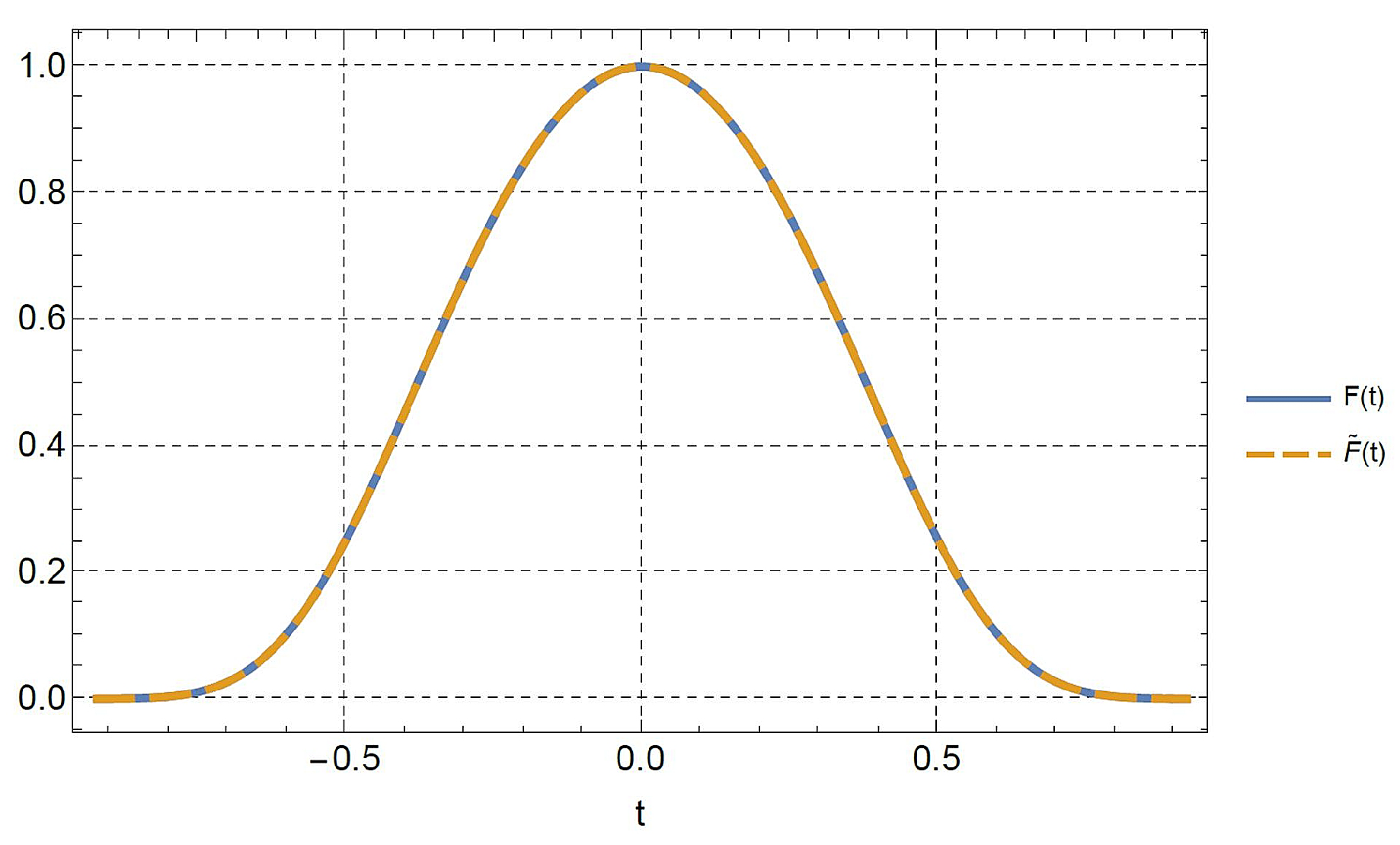
Consider the generalized Gaussian distribution defined by the function
We find and .
The percentage deviation between
and the relevant expansion
in terms of Bell’s polynomials is shown in
Figure 2. As can be seen,
is nicely approximated by
in the domain where
does not assume negligibly small values.
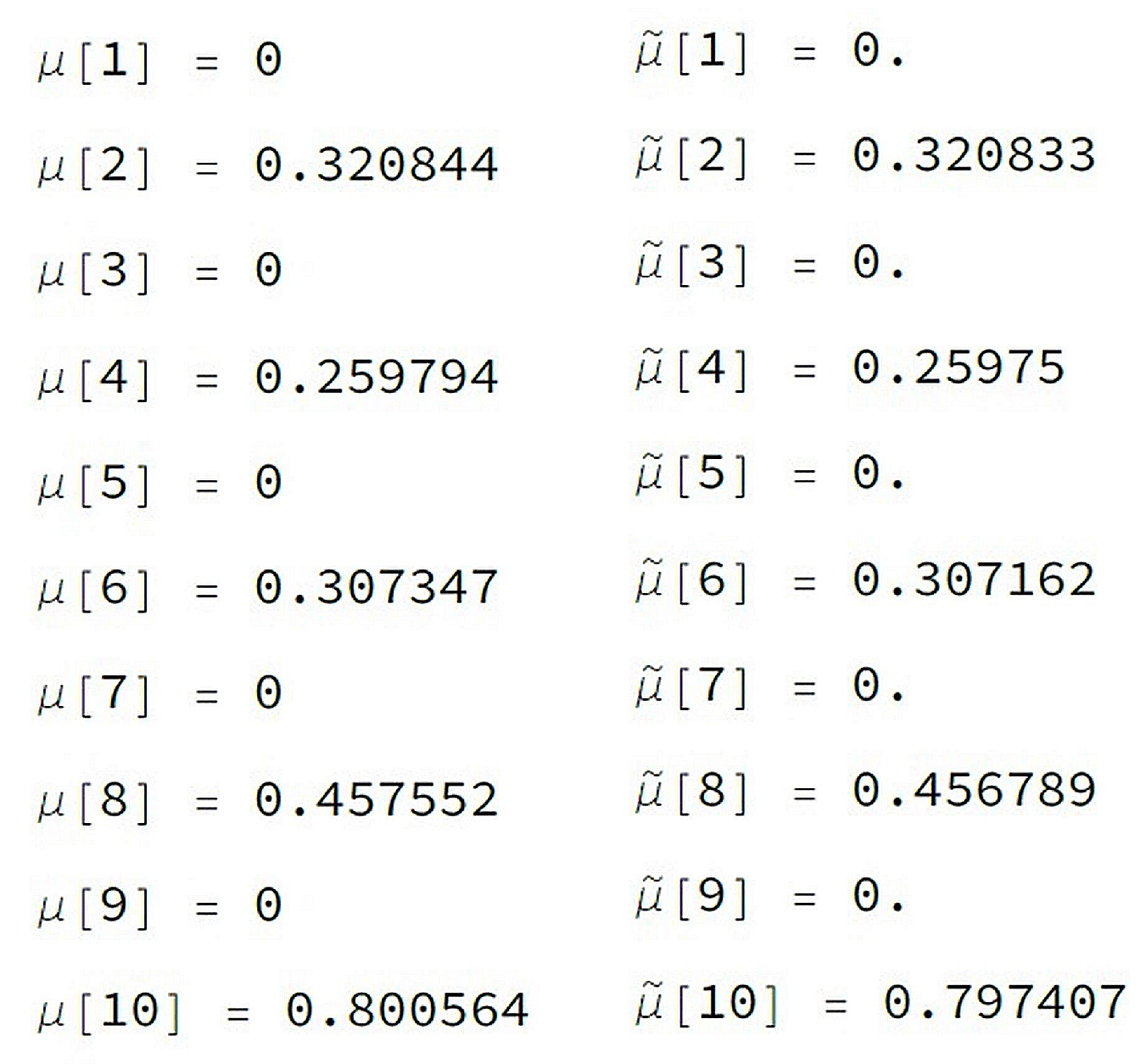
The table containing the first few moments of the considered function
, as computed using the Gauss–Kronrod quadrature rule (G-KQR),
, and the proposed Bell’s method,
, is reported in
Figure 3.
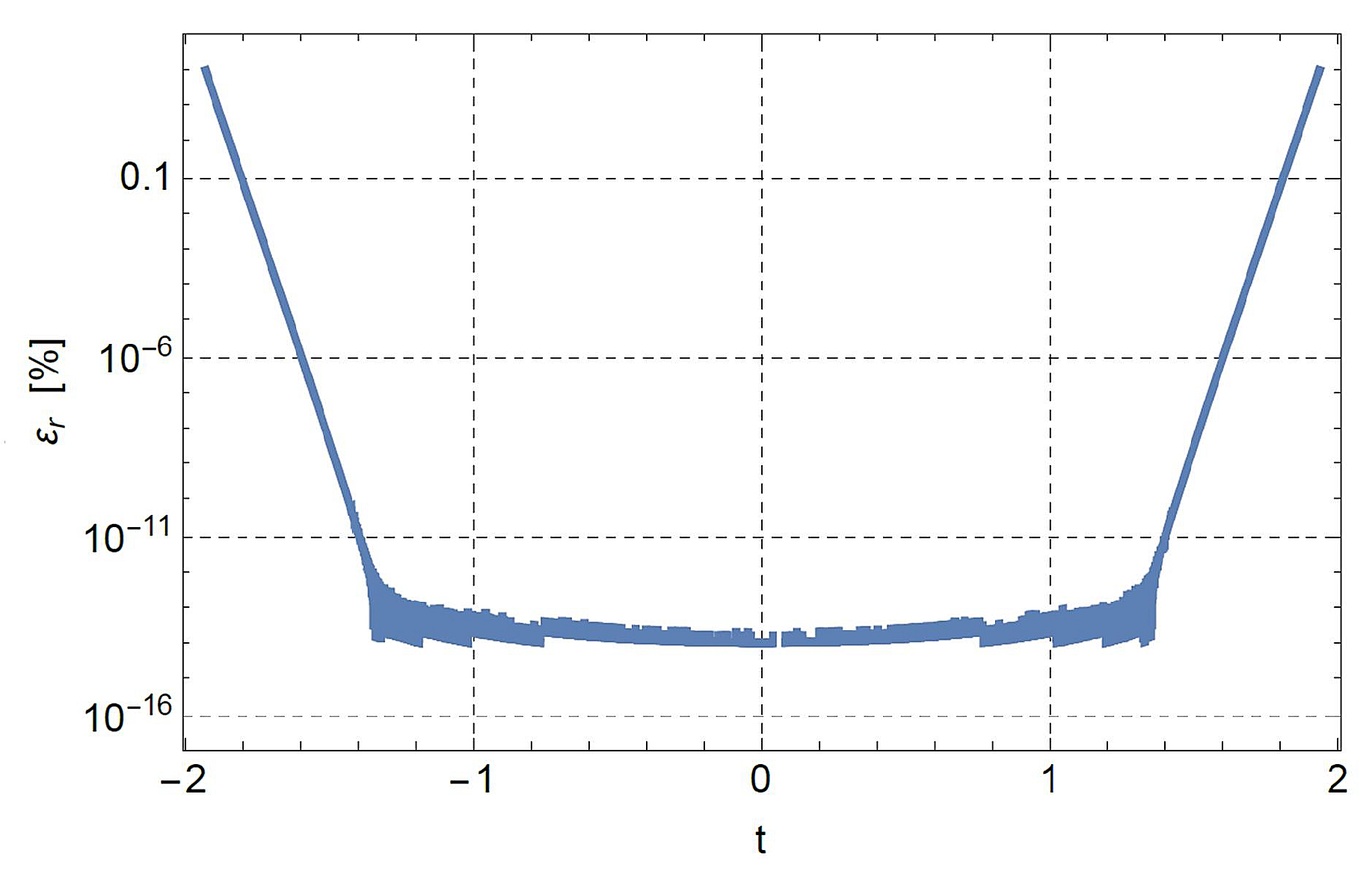
6.2. Example 2
Consider the generalized Gaussian distribution defined by the function
We find and .
The percentage deviation between
and the relevant expansion
in terms of Bell’s polynomials is shown in
Figure 5. As can be seen,
is nicely approximated by
in the domain where
does not assume negligibly small values.
The table containing the first few moments of the considered function
, as computed using the Gauss–Kronrod quadrature rule (G-KQR),
, and the proposed Bell’s method,
, is reported in
Figure 6.
6.3. Example 3
Consider the generalized Gaussian distribution defined by the function
We find and .
The percentage deviation between
and the relevant expansion
in terms of Bell’s polynomials is shown in
Figure 8. As can be seen,
is nicely approximated by
in the domain where
does not assume negligibly small values.
The table containing the first few moments of the considered function
, as computed using the Gauss–Kronrod quadrature rule (G-KQR),
, and the proposed Bell’s method,
, is reported in
Figure 9.
6.4. Example 4
Consider the generalized Gaussian distribution defined by the function
We find and .
The percentage deviation between
and the relevant expansion
in terms of Bell’s polynomials is shown in
Figure 11. As can be seen,
is nicely approximated by
in the domain where
does not assume negligibly small values.
The table containing the first few moments of the considered function
, as computed using the Gauss–Kronrod quadrature rule (G-KQR),
, and the proposed Bell’s method,
, is reported in
Figure 12.
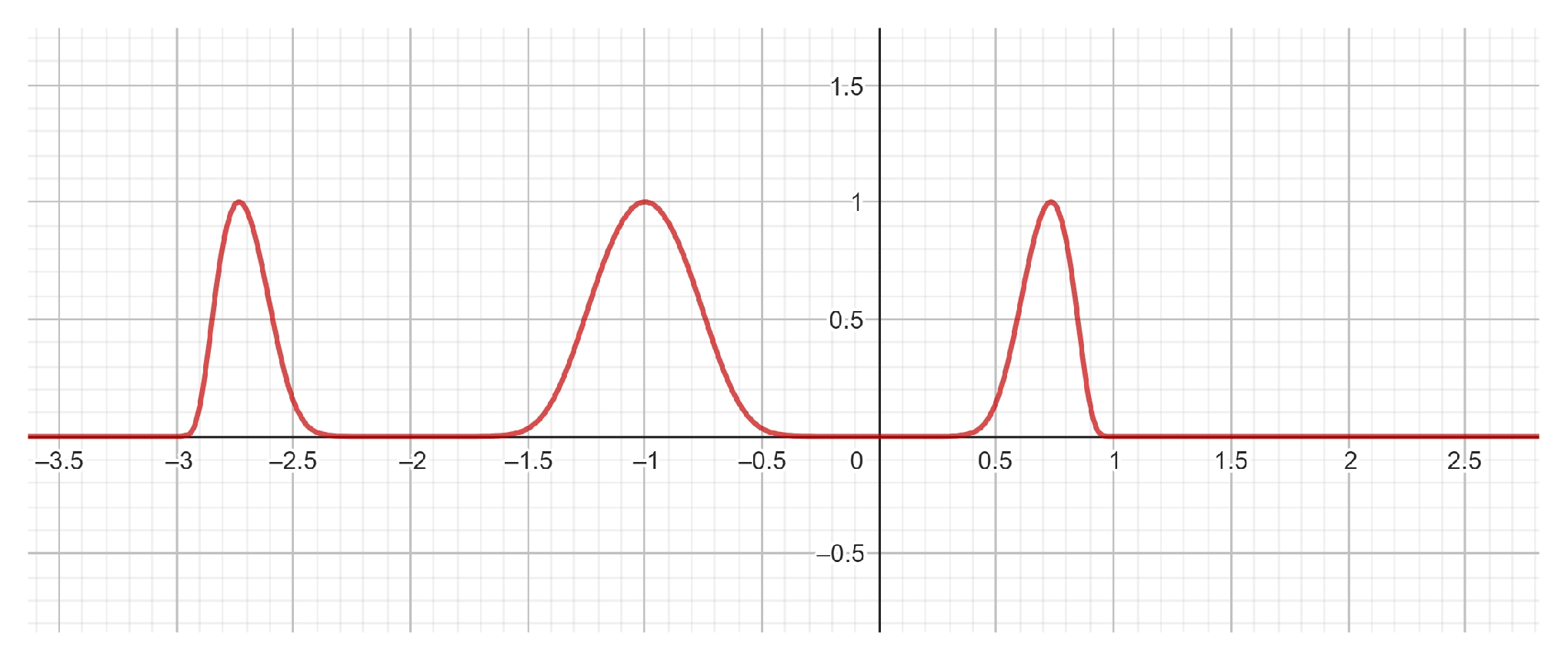
Different generalized Gaussian distributions can be evaluated using the approach illustrated in
Section 5. The same applies to the multimodal distributions considered hereafter.
Assuming
, we find the graph in
Figure 13.
Figure 13.
Graph of the function .
Figure 13.
Graph of the function .
Assuming
, we find the graph in
Figure 14.
Figure 14.
Graph of the function .
Figure 14.
Graph of the function .
In the next example, we evaluate the moments of a bi-modal distribution. In this and other similar cases, one can verify that achieving the desired precision requires a drastic increase in the number of expansion terms, thus affecting the overall computational times.
6.5. Example 5
Consider the generalized Gaussian distribution defined by the function
We find and .
The percentage deviation between
and the relevant expansion
in terms of Bell’s polynomials is shown in
Figure 16. As can be seen,
is nicely approximated by
in the domain where
does not assume negligibly small values.
The table containing the first few moments of the considered function
, as computed using the Gauss–Kronrod quadrature rule (G-KQR),
, and the proposed Bell’s method,
, is reported in
Figure 17.
7. Conclusions
We have shown how Bell’s polynomials can be adopted to evaluate the moments of generalized Gaussian distributions originated by the composition of the classical Gauss exponential. The possibility of computing integrals of composite and higher-order nested analytic functions by means of Bell’s polynomials allows for tackling the considered application in a very effective way.
By using the generalization of the Gaussian distribution, as proposed in this research study and illustrated with several examples, one can define a wide variety of curves starting from arbitrary coefficients of series expansions. Different bell-shaped functions can thus be obtained that can be adapted to represent the most diverse probabilistic distributions.
Numerical calculations using the computer algebra program Mathematica have shown that our approach for approximating moments is accurate and efficient.
Author Contributions
Conceptualization, P.E.R., D.C. and R.S.; Data curation, R.S.; Investigation, P.E.R. and D.C.; Methodology, P.E.R.; Software, D.C.; Supervision, R.S.; Validation, D.C.; Writing—original draft, P.E.R. and D.C.. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bell, E.T. Exponential polynomials. Ann. Math. 1934, 35, 258–277. [Google Scholar] [CrossRef]
- Riordan, J. An Introduction to Combinatorial Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1958. [Google Scholar]
- Faà di Bruno, F. Théorie des Formes Binaires; Brero: Turin, Italy, 1876. [Google Scholar]
- Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions; Springer: Berlin, Germany, 1974. [Google Scholar]
- Robert, D. Invariants orthogonaux pour certaines classes d’operateurs. Annales Mathém. Pures Appl. 1973, 52, 81–114. [Google Scholar]
- Fujiwara, D. Generalized Bell’s polynomials. Sugaku 1990, 42, 89–90. [Google Scholar]
- Kim, H.K. Fully degenerate Bell polynomials associated with degenerate Poisson random variables. Open Math. 2021, 19, 284–296. [Google Scholar] [CrossRef]
- Rai, P.N.; Singh, S.N. Generalization of Bell polynomials and related operatorial formula (in Hindi). Vijnana Parishad Anusandhan Patrika 1982, 25, 251–258. [Google Scholar]
- Natalini, P.; Ricci, P.E. Higher order Bell polynomials and the relevant integer sequences. Appl. Anal. Discrete Math. 2017, 11, 327–339. [Google Scholar] [CrossRef]
- Caratelli, D.; Srivastava, R.; Ricci, P.E. The Laplace Transform of composite functions and Bivariate Bell’s polynomials. Axioms 2022, 11, 591. [Google Scholar] [CrossRef]
- Duran, U.; Acikgoz, M. A new approach to the Poisson distribution. J. Ineq. Special Func. 2020, 11, 1–11. [Google Scholar]
- Roman, S.M.; Rota, G.C. The umbral calculus. Adv. Math. 1978, 27, 95–188. [Google Scholar] [CrossRef]
- Roman, S.M. The Faà di Bruno Formula. Amer. Math. Monthly 1980, 87, 805–809. [Google Scholar] [CrossRef]
- Qi, F.; Niu, D.-W.; Lim, D.; Yao, Y.-H. Special values of the Bell’s polynomials of the second kind for some sequences and functions. J. Math. Anal. Appl. 2020, 491, 124382. [Google Scholar] [CrossRef]
- Orozco López, R. Solution of the Differential Equation y(k)=eay, Special Values of Bell’s polynomials, and (k,a)-Autonomous Coefficients. J. Integer Seq. 2021, 24, 21.8.6. [Google Scholar]
- Natalini, P.; Ricci, P.E. An Extension of the Bell’s polynomials. Comput. Math. Appl. 2004, 47, 719–725. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).