Numerical Computation of Hybrid Morphologies of Nanoparticles on the Dynamic of Nanofluid: The Case of Blood-Based Fluid
Abstract
1. Introduction
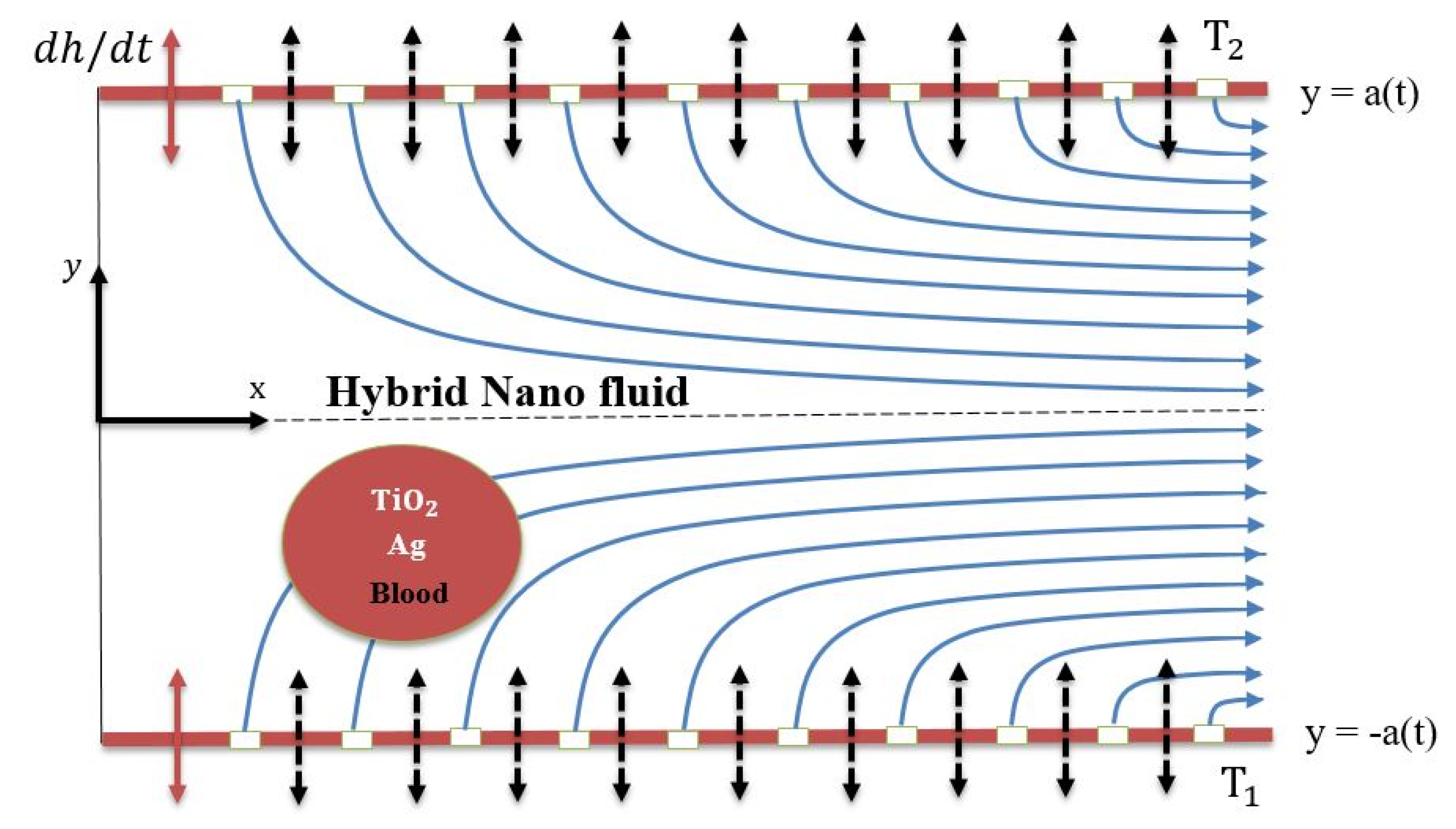
2. Mathematical Formulation
2.1. Numerical Procedure
2.2. Engineering Interest Quantities
2.2.1. Skin Friction Coefficients
2.2.2. Nusselt Numbers
3. Result and Discussion
4. Conclusions/Final Result
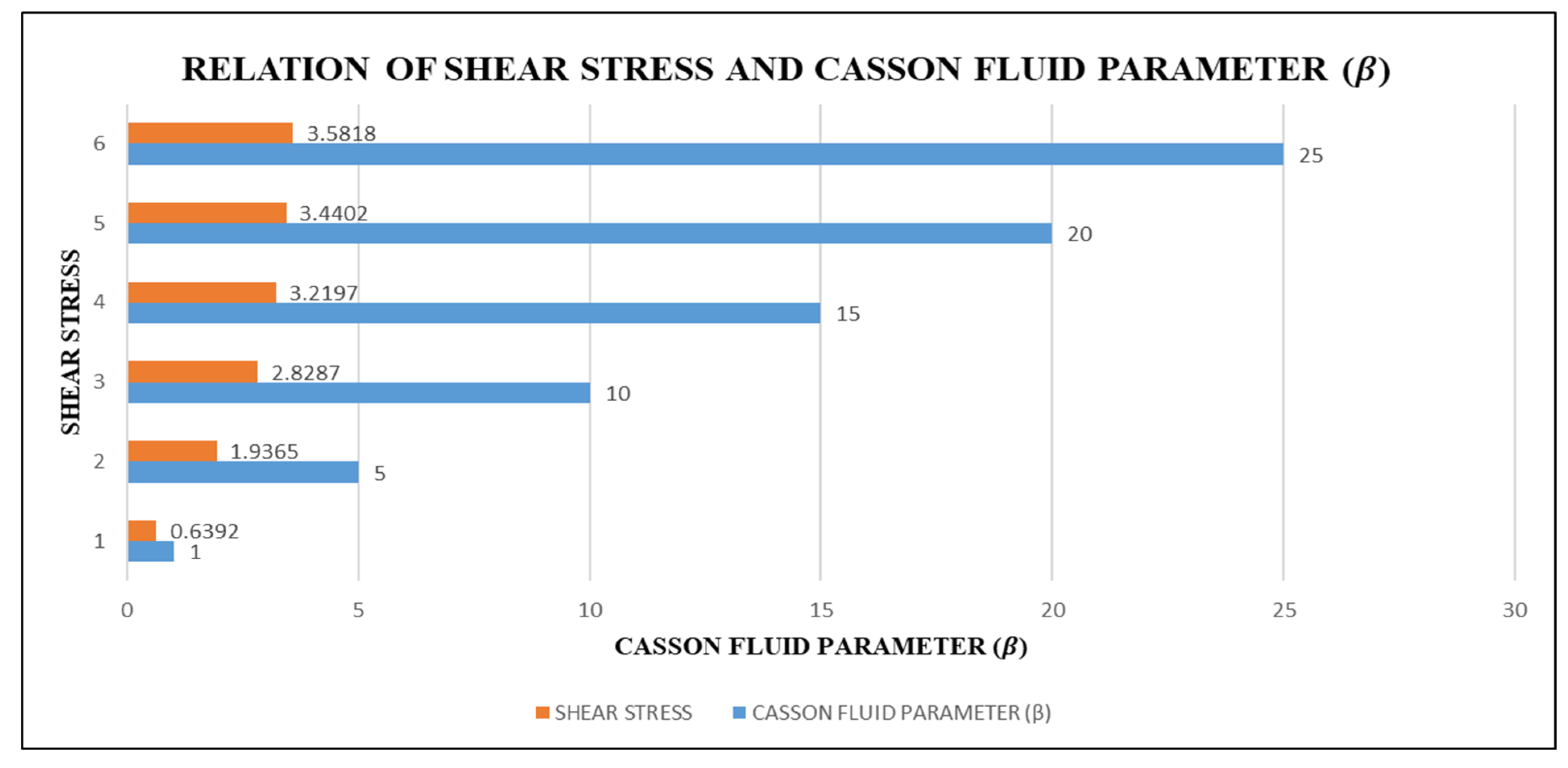
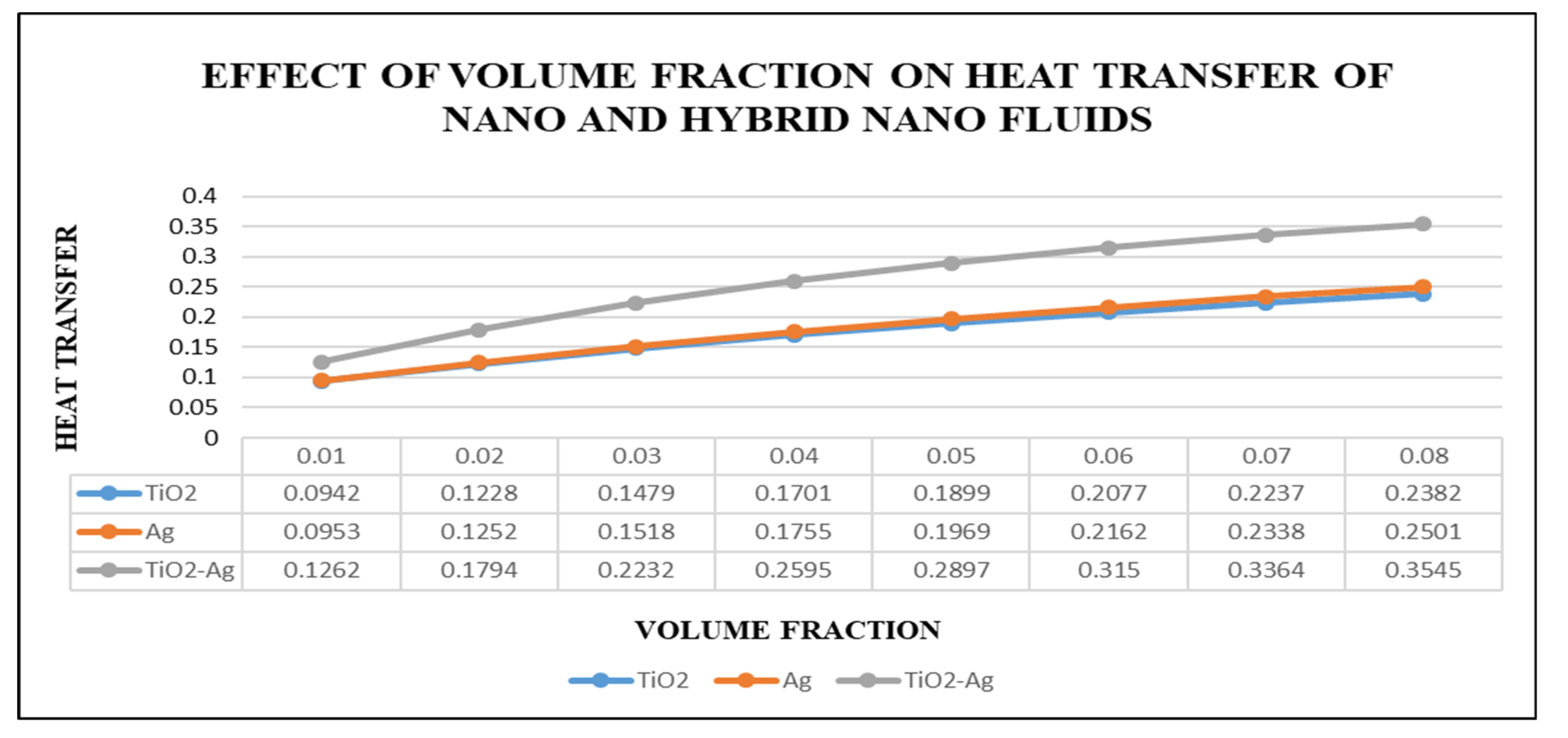
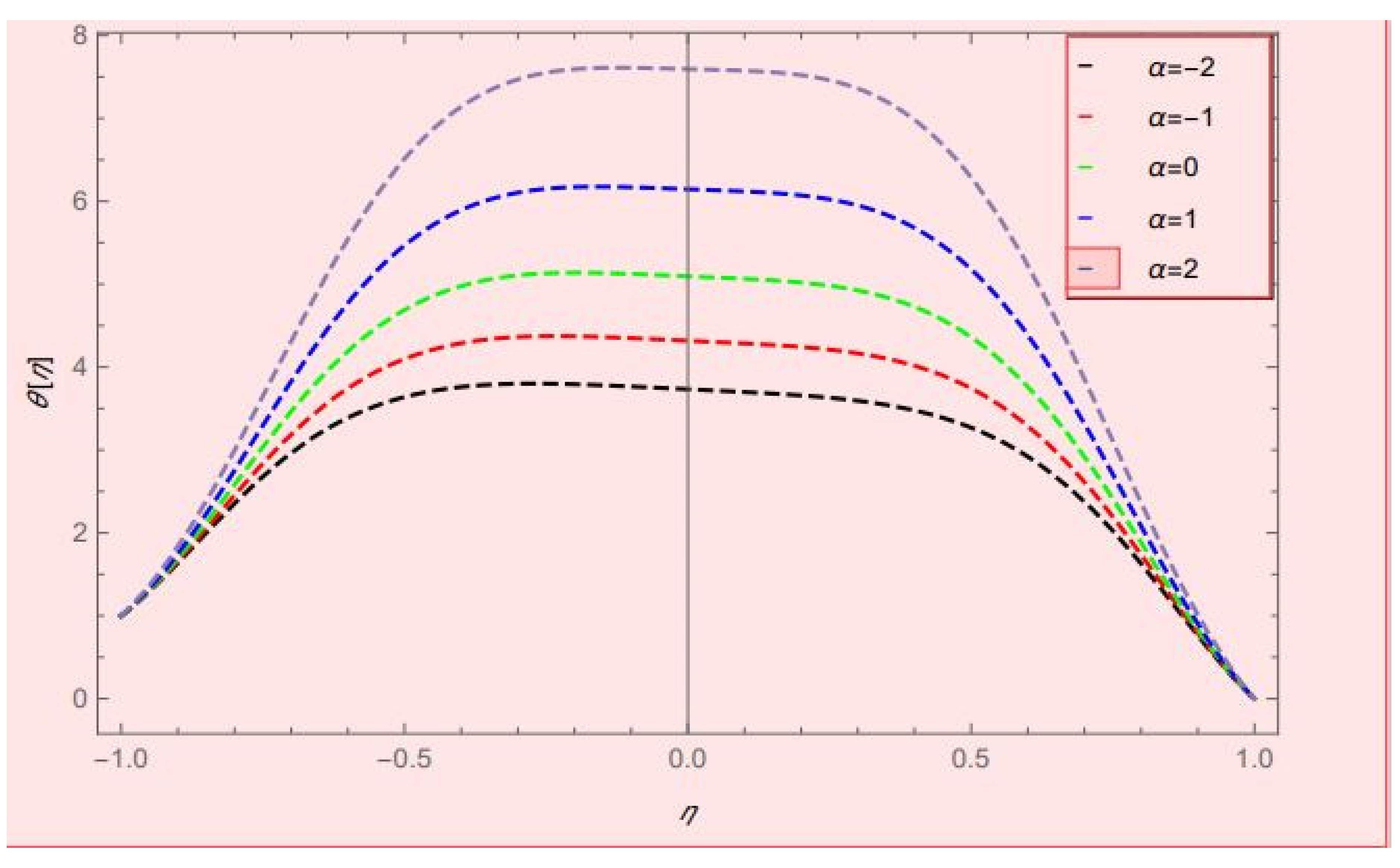
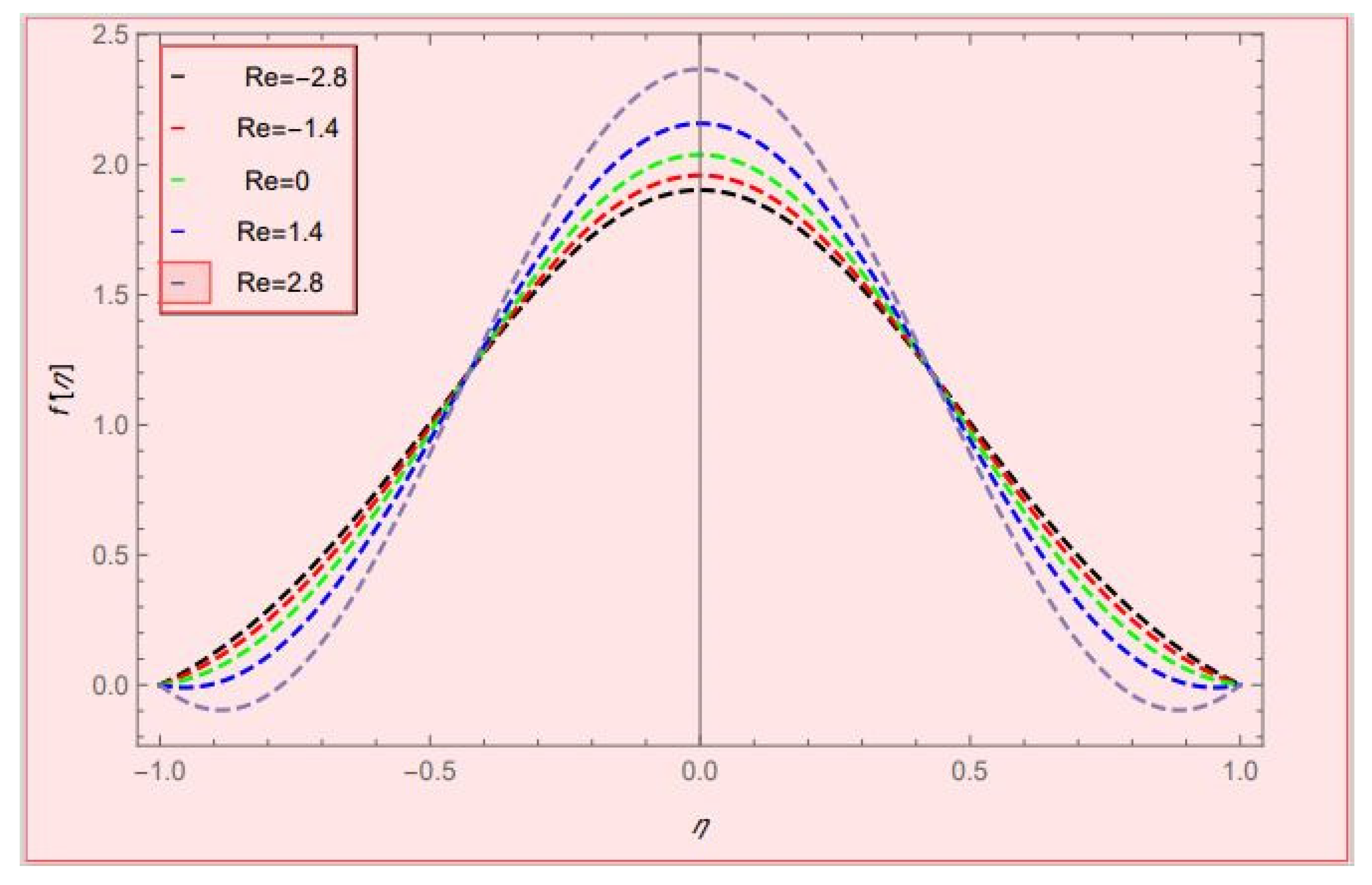
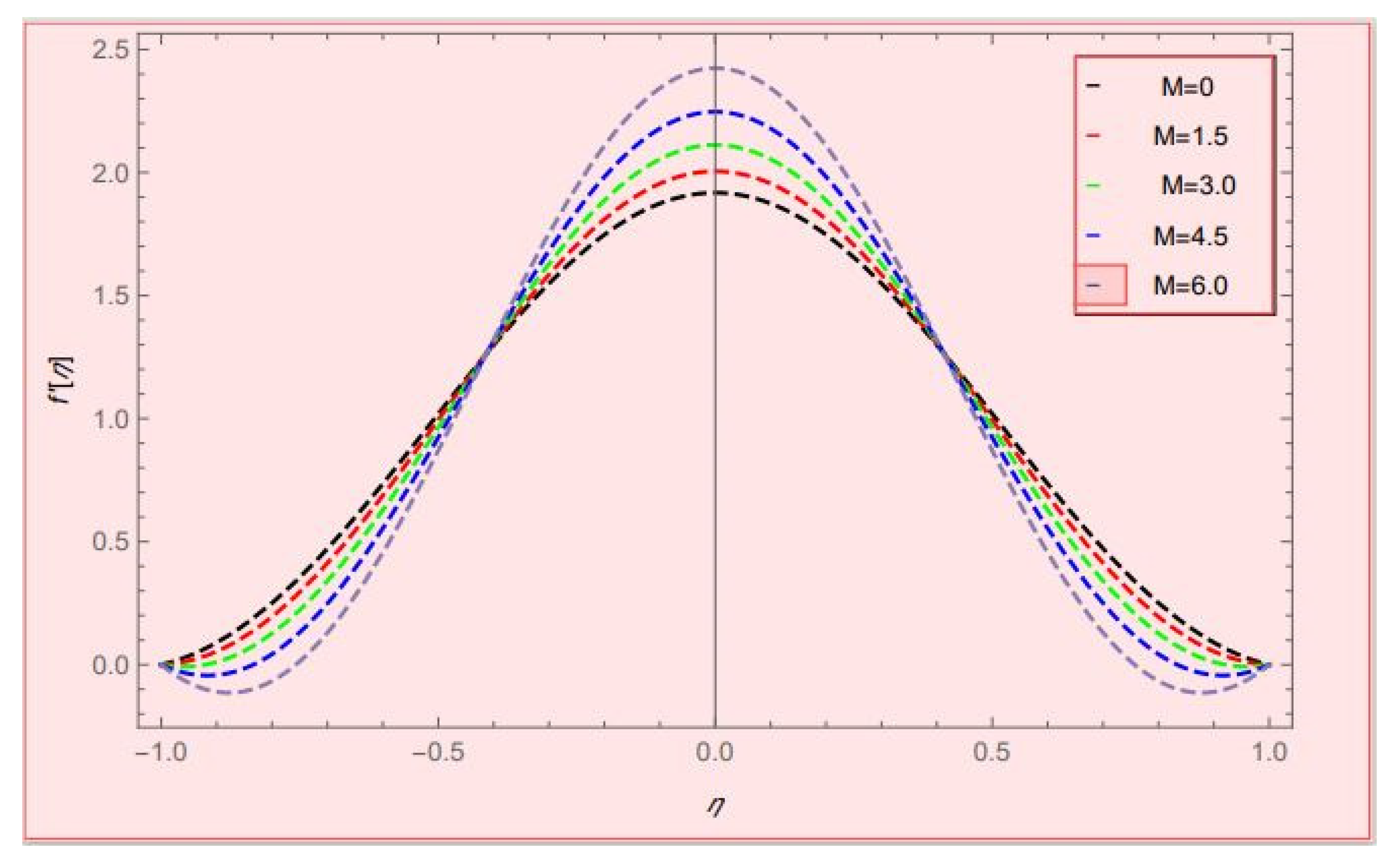
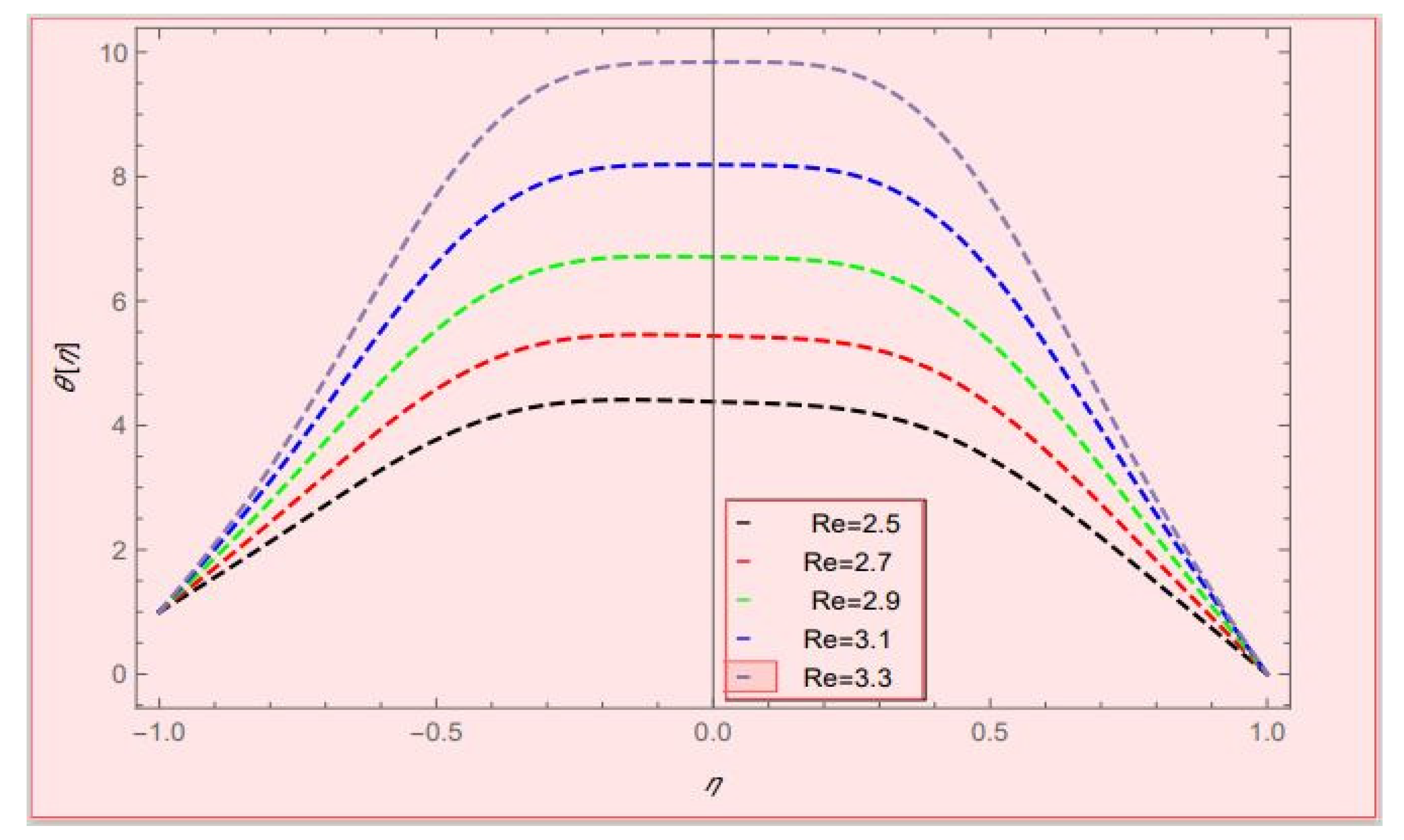
- By increasing the values of , the comparison of nanofluid and hybrid nanofluids gave much better results for hybrid nanofluids.
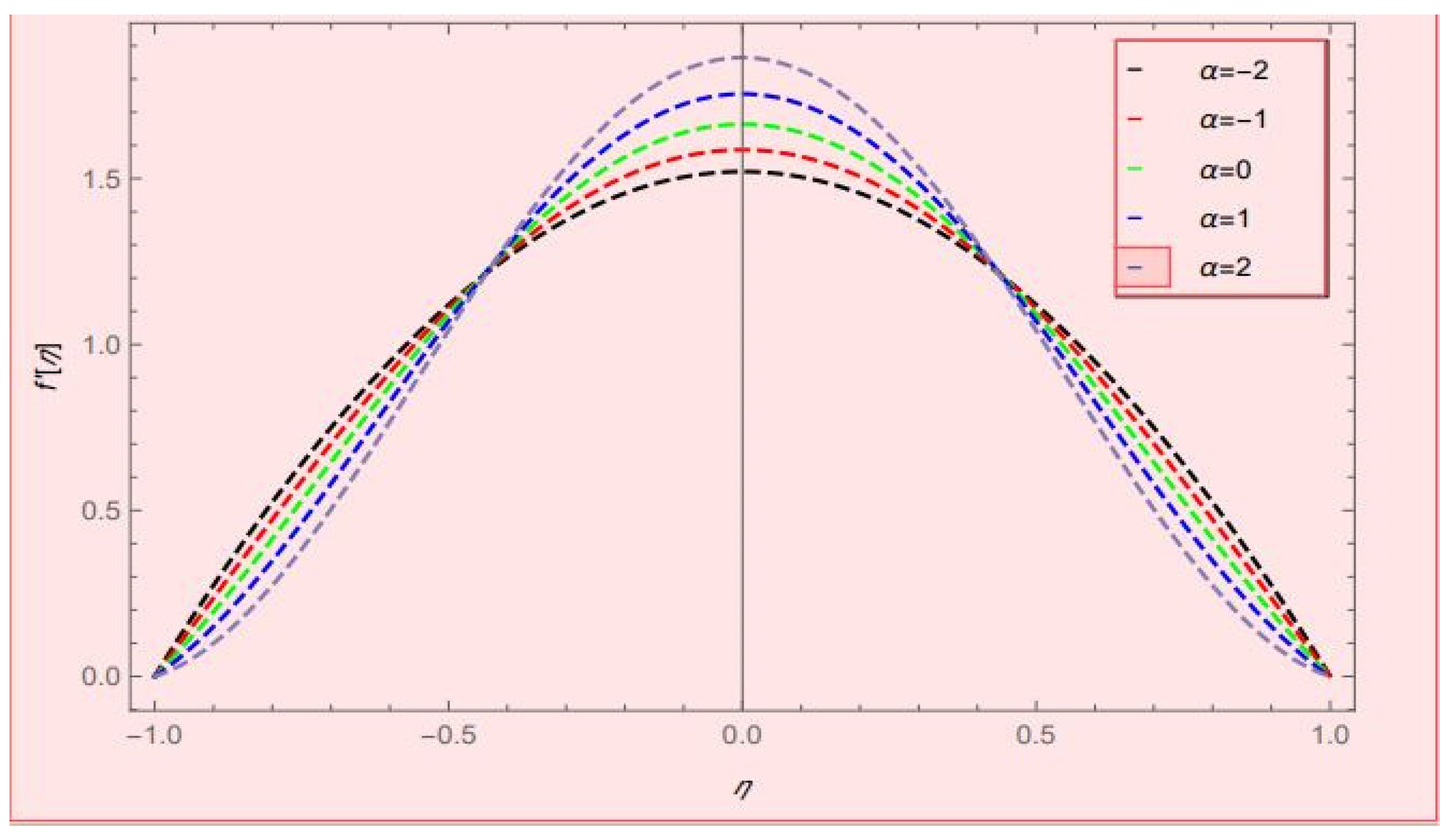
- Taking > 0, the momentum profile decreased on both upper and lower walls and increased at the center of the channel.
- Taking h > 0 and r > 0, the thermal conductivity of hybrid nanofluids was vice versa.
- By enhancing the values of Nt and Nb, the flow of heat transfer rate gradually increased on the upper wall and decreased on the lower wall of the channel.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| velocity components along the x and y-axis | |
| T | temperature |
| P | pressure |
| magnetic strength | |
| A | permeability component |
| specific heat at constant pressure | |
| electrical conductivity | |
| kinematic viscosity | |
| Casson fluid parameter | |
| contraction/expansion parameter | |
| fluid density | |
| Brownian diffusion constant | |
| thermophoresis diffusion coefficient | |
| thermal diffusivity of hybrid nanofluids | |
| θ | temperature profile |
| h | momentum layer thickness |
| r | radius of the particle |
| η | boundary layer condition |
| volume fraction | |
| Brickman number | |
| Peclet number | |
| thermal conductivity of hybrid nanofluid | |
| thermal conductivity of the base fluid | |
| thermal conductivity of 1st particle | |
| thermal conductivity of 2nd particle | |
| kinematic viscosity of hybrid nanofluid | |
| kinematic viscosity of the base fluid | |
| density of hybrid nanofluid | |
| density of the base fluid | |
| viscosity of hybrid nanofluid | |
| viscosity of the base fluid | |
| heat capacitance of hybrid nanofluid | |
| heat capacitance of base fluid | |
| HNfl | hybrid nanofluid |
| Prandtl number | |
| Reynolds number | |
| magnetic parameter | |
| Eckert number | |
| = | Brownian motion parameter. |
| = | thermophoresis motion parameter |
References
- Majdalani, J.; Zhou, C.; Dawson, C. Two-dimensional viscous flow between slowly expanding or contracting walls with weak permeability. J. Biomech. 2002, 35, 1399–1403. [Google Scholar] [CrossRef]
- Umavathi, J.; Chamkha, A.; Mateen, A.; Al-Mudhaf, A. Unsteady oscillatory flow and heat transfer in a horizontal composite porous medium channel. Nonlinear Anal. Model. Control. 2009, 14, 397–415. [Google Scholar] [CrossRef]
- Choi, S. Enhancing thermal conductivity of fluids with nanoparticles. ASME-Publications-Fed. 1995, 231, 99–106. [Google Scholar]
- Ali, N.; Teixeira, J.; Addali, A. A Review on Nanofluids: Fabrication, Stability, and Thermophysical Properties. J. Nanomater. 2018, 2018, 1–33. [Google Scholar] [CrossRef]
- Sundar, L.; Sharma, K.V.; Singh, M.; Sousa, A. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor—A review. Renew. Sustain. Energy Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Suganthi, K.; Rajan, K. Metal oxide nanofluids: Review of formulation, thermo-physical properties, mechanisms, and heat transfer performance. Renew. Sustain. Energy Rev. 2017, 76, 226–255. [Google Scholar] [CrossRef]
- Elsaid, K.; Olabi, A.; Wilberforce, T.; Abdelkareem, M.; Sayed, E. Environmental impacts of nanofluids: A review. Sci. Total Environ. 2020, 763, 144202. [Google Scholar] [CrossRef] [PubMed]
- Wole-osho, I.; Okonkwo, E.; Abbasoglu, S.; Kavaz, D. Nanofluids in Solar Thermal Collectors: Review and Limitations. Int. J. Thermophys. 2020, 41, 1–74. [Google Scholar] [CrossRef]
- Le Ba, T.; Mahian, O.; Wongwises, S.; Szilágyi, I. Review on the recent progress in the preparation and stability of graphene-based nanofluids. J. Therm. Anal. Calorim. 2020, 142, 1145–1172. [Google Scholar] [CrossRef]
- Yu, W.; Xie, H. A review on nanofluids: Preparation, stability mechanisms, and applications. J. Nanomater. 2011, 2012, 1–17. [Google Scholar] [CrossRef]
- He, Y.; Jin, Y.; Chen, H.; Ding, Y.; Cang, D.; Lu, H. Heat transfer and flow behaviour of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe. Int. J. Heat Mass Transf. 2007, 50, 2272–2281. [Google Scholar] [CrossRef]
- Li, J. Computational Analysis of Nanofluid Flow in Microchannels with Applications to Micro-Heat Sinks and Bio-MEMS; NC State University: Raleigh, NC, USA, 2008. [Google Scholar]
- Mishra, A.; Ram, S.; Ghosh, G. Dynamic Light Scattering and Optical Absorption in Biological Nanofluids of Gold Nanoparticles in Poly(vinyl pyrrolidone) Molecules. J. Phys. Chem. C 2009, 113, 6976–6982. [Google Scholar] [CrossRef]
- Ebrahimnia-Bajestan, E.; Moghadam, M.C.; Niazmand, H.; Daungthongsuk, W.; Wongwises, S. Experimental and numerical investigation of nanofluids heat transfer characteristics for application in solar heat exchangers. Int. J. Heat Mass Transf. 2016, 92, 1041–1052. [Google Scholar] [CrossRef]
- Ali, H.; Babar, H.; Shah, T.; Sajid, M.; Qasim, M.; Javed, S. Preparation Techniques of TiO2 Nanofluids and Challenges: A Review. Appl. Sci. 2018, 8, 587. [Google Scholar] [CrossRef]
- Dakshayani, S.S.; Marulasiddeshwara, M.B.; Kumar, S.; Golla, R.; Devaraja, S.R.H.K.; Hosamani, R. Antimicrobial, anticoagulant and antiplatelet activities of green synthesized silver nanoparticles using Selaginella (Sanjeevini) plant extract. Int. J. Biol. Macromol. 2019, 131, 787–797. [Google Scholar] [CrossRef]
- Brzóska, K.; Golba, A.; Kuczak, M.; Mrozek-Wilczkiewicz, A.; Boncel, S.; Dzida, M. Bio-Based Nanofluids of Extraordinary Stability and Enhanced Thermal Conductivity as Sustainable Green Heat Transfer Media. ACS Sustain. Chem. Eng. 2021, 9, 7369–7378. [Google Scholar] [CrossRef]
- Jana, S.; Salehi-Khojin, A.; Zhong, W.-H. Enhancement of fluid thermal conductivity by the addition of single and hybrid nano-additives. Thermochim. Acta 2007, 462, 45–55. [Google Scholar] [CrossRef]
- Jha, N.; Ramaprabhu, S. Synthesis and Thermal Conductivity of Copper Nanoparticle Decorated Multiwalled Carbon Nanotubes Based Nanofluids. J. Phys. Chem. C 2008, 112, 9315–9319. [Google Scholar] [CrossRef]
- Madhesh, D.; Parameshwaran, R.; Kalaiselvam, S. Experimental investigation on convective heat transfer and rheological characteristics of Cu–TiO2 hybrid nanofluids. Exp. Therm. Fluid Sci. 2014, 52, 104–115. [Google Scholar] [CrossRef]
- Sundar, L.; Singh, M.; Sousa, A. Enhanced heat transfer and friction factor of MWCNT–Fe3O4/water hybrid nanofluids. Int. Commun. Heat Mass Transf. 2014, 52, 73–83. [Google Scholar] [CrossRef]
- Dinarvand, S.; Rostami, M.N.; Dinarvand, R.; Pop, I. Improvement of drug delivery micro-circulatory system with a novel pattern of CuO-Cu/blood hybrid nanofluid flow towards a porous stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4408–4429. [Google Scholar] [CrossRef]
- Chahregh, H.S.; Dinarvand, S. TiO2-Ag/blood hybrid nanofluid flow through an artery with applications of drug delivery and blood circulation in the respiratory system. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 4775–4796. [Google Scholar] [CrossRef]
- Ramadhan, A.; Azmi, W.; Mamat, R.; Hamid, K. Experimental and numerical study of heat transfer and friction factor of plain tube with hybrid nanofluids, Case Stud. Therm. Eng. 2020, 22, 100782. [Google Scholar] [CrossRef]
- Kim, T.; Li, Q.Z.J.; Jokerst, L.Z.J.V. A Gold/Silver Hybrid Nanoparticle for Treatment and Photoacoustic Imaging of Bacterial Infection. ACS Nano 2018, 12, 5615–5625. [Google Scholar] [CrossRef]
- Rathore, N. A modified thermal flux model to examine the enhanced heat transmission in hybrid blood flow through artery: A comparison between Maxwell and Oldroyd-B models. Proc. Inst. Mech. Eng. Part E J. Proc. Mech. Eng. 2022, 09544089221128367. [Google Scholar] [CrossRef]
- Sandeep, N.; Samrat, S.; Ashwinkumar, G. Flow and heat transfer in radiative MHD dusty-hybrid ferrofluids. Waves Random Complex Media 2022, 1–4. [Google Scholar] [CrossRef]
- Rathore, N. Darcy–Forchheimer and Ohmic heating effects on GO-TiO2 suspended cross nanofluid flow through stenosis artery. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 09544062221105166. [Google Scholar] [CrossRef]
- Riahi, M.K.; Ali, M.; Addad, Y.; Abu-Nada, E. Combined Newton–Raphson and Streamlines-Upwind Petrov–Galerkin iterations for nanoparticles transport in buoyancy-driven flow. J. Eng. Math. 2022, 132, 1–26. [Google Scholar] [CrossRef]
- Durgaprasad, P.; Varma, S.V.; Hoque, M.M.; Raju, C.S. Combined effects of Brownian motion and thermophoresis parameters on three-dimensional (3D) Casson nanofluid flow across the porous layers slendering sheet in a suspension of graphene nanoparticles. Neural Comput. Appl. 2019, 31, 6275–6286. [Google Scholar] [CrossRef]
- Wakif, A.; Animasaun, I.L.; Narayana, P.S.; Sarojamma, G. Meta-analysis on thermo-migration of tiny/nano-sized particles in the motion of various fluids. Chin. J. Phys. 2020, 68, 293–307. [Google Scholar] [CrossRef]
- Amidu, M.A.; Addad, Y.; Riahi, M.K.; Abu-Nada, E. Numerical investigation of nanoparticles slip mechanisms impact on the natural convection heat transfer characteristics of nanofluids in an enclosure. Sci. Rep. 2021, 11, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Ijaz, S.; Iqbal, Z.; Maraj, E.; Nadeem, S. Investigation of Cu-CuO/blood mediated transportation in stenosed artery with unique features for theoretical outcomes of hemodynamics. J. Mol. Liq. 2018, 254, 421–432. [Google Scholar] [CrossRef]
- Qureshi, M.Z.; Ali, K.; Iqbal, M.; Ashraf, M.; Ahmad, S. Heat and mass transfer enhancement of nanofluids flow in the presence of metallic/metallic-oxides spherical nanoparticles. Eur. Phys. J. Plus 2017, 132, 1–2. [Google Scholar] [CrossRef]
- Sadiq, M.; Bahaidarah, H. Numerical Study on Generalized Heat and Mass in Casson Fluid with Hybrid Nanostructures. Nanomaterials 2021, 11, 2675. [Google Scholar] [CrossRef]
- Alghamdi, W.; Alsubie, A.; Kumam, P.; Saeed, A.; Gul, T. MHD hybrid nanofluid flow comprising the medication through a blood artery. Sci. Rep. 2021, 11, 11621. [Google Scholar] [CrossRef]
- Qureshi, M.Z.; Raza, Q.; Ramzan, A.; Faisal, M.; Ali, B.; Shah, N.A.; Weera, W. Activation Energy Performance through Magnetized Hybrid Fe3O4–PP Nanofluids Flow with Impact of the Cluster Interfacial Nanolayer. Mathematics 2022, 9, 3277. [Google Scholar] [CrossRef]
- Rathore, N.; Sandeep, N. A relative study on blood-based cross ferrofluid flow over a stenosis artery. Waves Random Complex Media 2022, 14, 1–20. [Google Scholar] [CrossRef]
- Maxwell, J. A Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1873; Volume 1. [Google Scholar]
- Hamilton, R.; Crosser, O. Thermal conductivity of heterogeneous two-component systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Qureshi, M.Z.; Bilal, S.; Chu, Y.M.; Farooq, A.B. Physical impact of nano-layer on nano-fluid flow due to dispersion of magnetized carbon nano-materials through an absorbent channel with thermal analysis. J. Mol. Liq. 2021, 325, 115211. [Google Scholar] [CrossRef]


| Nanoparticles and Base Fluid | Molecular Formula | Density, ⍴ | Specific Heat, Cp (J/kg·K) | Thermal Conductivity, k (W/m·k) |
|---|---|---|---|---|
| Titanium dioxide (titania) | 4250 | 686.2 | 8.954 | |
| Silver | Ag | 10,500 | 235 | 429 |
| Blood | - | 1063 | 3594 | 0.492 |
| Hybrid Nanofluids | |
|---|---|
| Density | |
| Viscosity | |
| Heat capacity | |
| Thermal conductivity of Nano-layer | = = |
| 2 | 1.8 | 0.01 = 1% | |
| 4 | |||
| 6 | |||
| 8 | |||
| 10 | |||
| 2 | 1.9 | ||
| 2.0 | |||
| 2.1 | |||
| 2.2 | |||
| 1.8 | 0.02 = 2% | ||
| 0.03 = 3% | |||
| 0.04 = 4% | |||
| 0.05 = 5% |
| 0.01 = 1% | −0.5 | 1 | ||||||||
| 0.02 = 2% | ||||||||||
| 0.03 = 3% | ||||||||||
| 0.04 = 4% | ||||||||||
| 0.01 = 1% | −1 | |||||||||
| −1.5 | ||||||||||
| −2.0 | ||||||||||
| −0.5 | 2 | |||||||||
| 3 | ||||||||||
| 4 | ||||||||||
| 0.01 = 1% | 0.01 = 1% | −0.5 | 1 | ||||
| 0.02 = 2% | |||||||
| 0.03 = 3% | |||||||
| 0.04 = 4% | |||||||
| 0.01 = 1% | 0.02 = 2% | ||||||
| 0.03 = 3% | |||||||
| 0.04 = 5% | |||||||
| 0.01 = 1% | −1 | ||||||
| −1.5 | |||||||
| −2.0 | |||||||
| −0.5 | 2 | ||||||
| 3 | |||||||
| 4 | |||||||
| 0.1 | 0.5 | ||
| 0.6 | |||
| 1.2 | |||
| 1.8 | |||
| 2.4 | |||
| 0.8 | |||
| 1.1 | |||
| 1.4 | |||
| 1.7 | |||
| 0.5 | 0.05 | 2 | 1.5 | ||
| 0.6 | |||||
| 0.7 | |||||
| 0.8 | |||||
| 0.5 | 0.10 | ||||
| 0.15 | |||||
| 0.20 | |||||
| 0.05 | 4 | ||||
| 6 | |||||
| 8 | |||||
| 1.6 | |||||
| 1.7 | |||||
| 1.8 | |||||
| Qureshi et al. [30] | Present Results | |||
|---|---|---|---|---|
| −1 | 4.19168 | −0.36988 | 4.19169 | −0.36989 |
| −0.5 | 4.40338 | −0.968884 | 4.40339 | −0.968885 |
| 0 | 4.64876 | −1.98464 | 4.64878 | −1.98465 |
| 0.5 | 4.93215 | −3.26874 | 4.93216 | −3.26875 |
| 1 | 5.25781 | −4.63023 | 5.25782 | −4.63024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alanazi, M.M.; Hendi, A.A.; Raza, Q.; Rehman, M.A.; Qureshi, M.Z.A.; Ali, B.; Shah, N.A. Numerical Computation of Hybrid Morphologies of Nanoparticles on the Dynamic of Nanofluid: The Case of Blood-Based Fluid. Axioms 2023, 12, 163. https://doi.org/10.3390/axioms12020163
Alanazi MM, Hendi AA, Raza Q, Rehman MA, Qureshi MZA, Ali B, Shah NA. Numerical Computation of Hybrid Morphologies of Nanoparticles on the Dynamic of Nanofluid: The Case of Blood-Based Fluid. Axioms. 2023; 12(2):163. https://doi.org/10.3390/axioms12020163
Chicago/Turabian StyleAlanazi, Meznah M., Awatif A. Hendi, Qadeer Raza, Muhammad Abdul Rehman, Muhammad Zubair Akbar Qureshi, Bagh Ali, and Nehad Ali Shah. 2023. "Numerical Computation of Hybrid Morphologies of Nanoparticles on the Dynamic of Nanofluid: The Case of Blood-Based Fluid" Axioms 12, no. 2: 163. https://doi.org/10.3390/axioms12020163
APA StyleAlanazi, M. M., Hendi, A. A., Raza, Q., Rehman, M. A., Qureshi, M. Z. A., Ali, B., & Shah, N. A. (2023). Numerical Computation of Hybrid Morphologies of Nanoparticles on the Dynamic of Nanofluid: The Case of Blood-Based Fluid. Axioms, 12(2), 163. https://doi.org/10.3390/axioms12020163








