1. Introduction
Bridged structures are very popular for solving connecting problems. Such structures may be different in type, and their quality depends on the purposes addressed. In this paper, we analyze the structure consisting of two Kirchhoff–Love elastic plates and a junction (bridge) that is in contact with the plates. To describe the behavior of the bridge, we use the Euler–Bernoulli beam model. The junction has the displacement coinciding with the displacement of the plates at two fixed points. Moreover, an inequality-type restriction is assumed to be imposed for the solution to provide a mutual non-penetration between the plates and the bridge. This approach implies that the problem is formulated as a free boundary one.
During the last years, boundary-value problems in elasticity with inequality-type boundary conditions have been under active study. We can refer the reader to the books [
1,
2] containing results for crack models with the non-penetration boundary conditions for a wide class of elasticity problems. There are many papers related to thin inclusions incorporated into elastic bodies. In the case of delamination of the surrounding elastic body from the inclusion, one more difficulty appears since we obtain an interfacial crack. We pay attention to the paper [
3] where an equilibrium problem for two elastic plates is analyzed in the case of thin incorporated inclusion and Neumann type boundary conditions for the plate. Different properties of solutions in equilibrium problems for elastic bodies with thin rigid, semi-rigid, and elastic inclusions and cracks are analyzed in [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13] and many other papers. In [
14,
15,
16], one can find models for the analysis of non-homogeneous elastic bodies. Note that a derivation of models for elastic bodies with thin inclusions usually takes into account changing physical and geometrical parameters [
17,
18,
19]. Contact problems for elastic plates with thin elastic structures were analyzed in [
20,
21]. We can also mention a number of applied studies related to thin inclusions of different nature in elastic bodies [
22,
23,
24,
25,
26,
27,
28,
29]. An application of the finite element method for planar mechanical elastic systems can be found in [
30]. As for inverse problems in elasticity, the literature in this field is very vast. We will only mention the articles [
31,
32] and the links in them.
The structure of the paper is as follows.
Section 2 addresses variational and differential formulations of the equilibrium problem. Passages to limits, as a rigidity parameter of the bridge tends to infinity and to zero, are investigated in
Section 3 and
Section 4. We provide a justification of the limit procedure and analyze the limit models.
Section 5 is concerned with the analysis of the inverse problem.
2. Setting the Problem
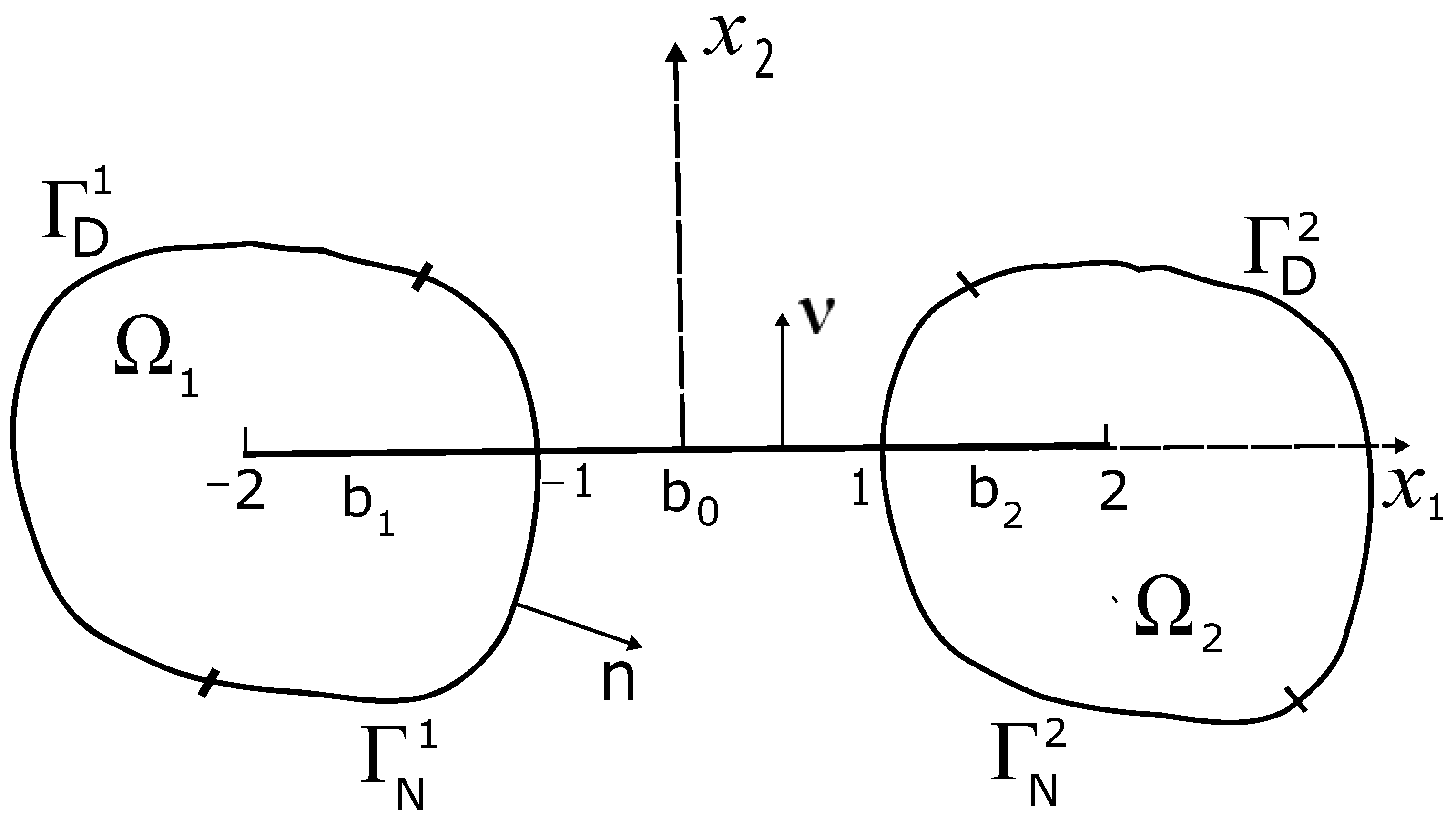
Let
be bounded domains with Lipschitz boundaries
respectively, such that
Assume that
is divided into two smooth parts
and
We set
Moreover, we assume that
and
b crosses
see
Figure 1. Denote by
unit normal vectors to
, respectively, and set
The set corresponds to two elastic plates, and b fits to a thin elastic crossing bridge between two plates. We describe b in the frame of the Euler–Bernoulli beam model. In what follows, the crossing bridge b will be characterized by a rigidity parameter At the first step, this parameter is fixed being equal to 1, and in the sequel we analyze passages to the limit as goes to infinity and to zero.
Let w be a scalar-valued function. We use the notations If then We also put Summation convention over repeated indices is used; all functions with two lower indices are assumed to be symmetric in those indices.
In the domains
, elasticity tensors
are considered with the usual properties of symmetry and positive definiteness,
Similar properties are fulfilled for the tensor B on
We introduce notations for a bending moment
and a transverse force
on the boundaries of the plates,
In this case, for smooth functions
the following Green’s formula holds, see [
2], Section 1.2.3,
Since the domain
with the cut
is a union of the domains
and
, the above Green’s formula allows us to write Green’s formula for
where
is a jump of a function
h on
are the traces of
h on the crack faces
. The signs ± fit to positive and negative directions of
the values
with the normal vector
are defined on
b similar to (
2).
In view of the above notations, an equilibrium problem for the plates
and the crossing bridge
b is formulated as follows. Given external forces
acting on the plates and the crossing bridge, respectively, we have to find a displacement of the plates
; a moment tensor
defined in
respectively; and a crossing bridge displacement
v defined on
b such that
Here, The tensor E is equal to in respectively. Functions defined on b we identify with functions of the variable
Relations (
4) and (
5) are the equilibrium equations for the Kirchhoff–Love elastic plates
and the constitutive law; (
6) is the Euler–Bernoulli equilibrium equations for the crossing bridge parts
, see [
1,
2]. The right-hand side
in (
6) describes forces acting on
from the elastic plates. The first inequality in (
9) provides a non-penetration between the plates and the bridge. Relation (
11) provides glue conditions at the points where the bridge
b crosses the external boundaries of the elastic plates. Note that, by (
9), the contact set between the plates and the bridge is unknown.
We can provide a variational formulation of the problem (
4)–(
11). Introduce the space
with the norm
where
are the usual Sobolev spaces,
and consider the energy functional
Denote by
S the set of admissible displacements,
and consider the problem:
This minimization problem has a unique solution since the functional
is weakly lower semicontinuous and coercive. The coercivity of the functional
follows from the Dirichlet boundary conditions on the sets
for the function
w and conditions
. The set
S is weakly closed. The solution of the problem satisfies the following variational inequality
Theorem 1. Problem formulations (4)–(13) are equivalent for smooth solutions. Proof. Assume that (
12) and (
13) hold. We can substitute in (
13) test functions of the form
This provides the equilibrium Equation (
4) fulfilled in the distributional sense. Next, test functions of the form
can be substituted in (
13), where
on
Taking into account the equilibrium Equation (
4) and Green Formula (
3), we obtain
Now, test functions of the form
are substituted in (
13),
This gives
Consequently, by using the Green Formula (
3), in view of (
4), (
14), we derive
Choosing the above inequality
on
, the following equation
is derived. To proceed, take test functions of the form
in (
3),
The following relation is obtained:
Now, we are aiming to derive the last relation of (
9). Assume that the inequality
holds at a point
In this case, we can take
as a test function in (
13), where the support of
belongs to a small neighborhood of
the support of
belongs to a small neighborhood of the point
, and
is small. This implies
By (
3), (
4), and (
14), we obtain the relation
In particular, this provides
This means that
The next step of our reasoning is to derive boundary conditions for
v at the points
and the last condition of (7). To this end, we take test function in (
13) of the form
on
It provides the equality
Applying the Green Formula (
3), this relation implies
From here, it follows that
Taking into account (
4), (
14)–(
16), from (
17) we obtain
Hence, we derived all relations (
4)–(
11) from (
12) and (
13).
Let us prove the converse. Assume that (
4)–(
11) are fulfilled. Then, we have for all
Integrating by parts in the second and the third integrals of (
20) and using the Formula (
3), it follows that
We can change the integration over
by integration over
in the first two integrals of (
21) and use boundary conditions for
. To derive the variational inequality (
12) and (
13) from (
21), it suffices to check that
However, the inequality (
22) easily follows from (
6)–(
11). Hence, we proved that (
4)–(
11) imply (
12) and (
13). Theorem 1 is proved. □
3. Convergence of Rigidity Parameter to Infinity
In this section, we introduce a positive bridge rigidity parameter
into the model (
12) and (
13) and analyze a passage to the limit as
. Our aim is to justify this passage to the limit and investigate the limit model. Instead of (
12) and (
13), for any
, consider the following problem
The solution
of this problem is supplied with the index
Note that we can write an equivalent differential formulation of the problem (
23) and (
24) similar to (
4)–(
11). In this case, instead of (
6) we have the following equations for the crossing bridge
In what follows, we justify a passage to the limit as
in (
23) and (
24). At the first step, a priori estimates of the solutions are derived.
From (
23) and (
24), the following relation is obtained:
From (
25), we derive the estimate being uniform in
moreover, the relation (
25) implies
By estimates (
26) and (
27), we can assume that as
On the other hand, since consequently, v = 0 on b.
Then introduce the set of admissible displacements for the limit problem,
We take any element
. Then,
Substitute this function in (
24). By (
28) and (
29), it is possible to pass to the limit in (
23) and (
24) as
The limit relations are of the form
Thus, we have shown the following result.
Theorem 2. As , the solutions of the problem (23) and (24) converge in the sense (28) and (29) to the solution of (30) and (31). To conclude this section, we provide a differential formulation of the problem (
30) and (
31): find functions
defined in
respectively, such that
The following statement takes place providing a connection between problems (
30)–(
36).
Theorem 3. Problem formulations (30)–(36) are equivalent provided that the solutions are smooth. Proof. Let (
32)–(
36) be fulfilled. Then, we have
From this relation, by (
3), it follows that
In so doing, we changed the integration domain
by
since
on
. Thus, to obtain (
30) and (
31) from (
37) it suffices to check that
However, the inequality (
38) easily follows from (
35).
Conversely, assume that (
30) and (
31) hold. We take a test function of the form
and substitute it in (
31). This implies the equilibrium Equation (
32). The other arguments are reminiscent of those used in the proof of Theorem 1, and we omit them. Theorem 3 is proved. □
4. Convergence of Rigidity Parameter of to Zero
In this section, we assume that on A convergence to zero of the rigidity parameter will be analyzed when assuming that a change of this parameter happens at . In this case, the rigidity parameter at is fixed and is equal to 1.
We first provide a formulation of the equilibrium problem such as (
4)–(
11) for this case: find functions
defined in
respectively, and functions
defined on
b such that
In relations (
46) and (
47), we should simultaneously take upper or lower signs.
The problem (
39)–(
47) can be formulated in a variational form. Indeed, consider the energy functional
Then, the problem
has a solution satisfying the variational inequality
In what follows, we aim to justify a passage to the limit in (
48) and (
49) as
From (
48) and (
49), the following relation is obtained:
This relation provides the following estimate being uniform in
moreover, the relation (
50) implies
By estimates (
51) and (
52), we can assume that, as
From (
51) it follows that uniformly in
Here, and in (
55) below, we should take upper or below signs simultaneously. Taking into account the conditions
we obtain for small
that
Consequently, relations (
52), (
55) imply for small
that
Thus, we can assume that as
Now, introduce the set of admissible displacements for the limit problem
Take
and extend the function
to
assuming that the extension belongs to the space
In this case
and we can substitute
in (
48) and (
49) as a test function. Passing to the limit as
by (
53), (
56), the following variational inequality is obtained:
Thus, the following statement is proved.
Theorem 4. As , the solutions of the problem (48) and (49) converge in the sense (53) to the solution of (57) and (58). To conclude the section, we provide a differential formulation of the problem (
57) and (
58): find a displacement of the elastic plates
a moment tensor
defined in
respectively, and a function
v defined on
such that
The following statement is valid.
Theorem 5. Problem formulations (57)–(59) and (66) are equivalent provided that the solutions are smooth. We omit the proof of this theorem since it is reminiscent of that of Theorem 1. The only step we have to take is to provide a proof that from (
57) and (
58) the boundary conditions (
66) follow. Indeed, take in (
57) and (
58) test functions of the form
on
This gives
Since
we can integrate by parts in the third term of (
67) and use Green’s Formula (
3). This implies
Since the equilibrium equations (
59), (
61) hold, and since
, the relation (
68) implies boundary conditions (
66) and the second group of boundary conditions (
62).
Theorem 5 is proved.
To conclude this section, we note that the problems (
59) and (
66) describe an equilibrium state for two plates occupying the domains
. In fact, we have two independent problems (for each plate) since there is no connection between the plates.
5. Analysis of Inverse Problem
In this section, we analyze an inverse problem related to the equilibrium problem (
12) and (
13). Elasticity tensors
are assumed to be constant. The inverse problem consists in finding displacement fields of the plates and the bridge together with an elasticity tensor
A when assuming that additional data are provided by measurement. More precisely, it is assumed that for a given continuous function
a value
is known, where
is the displacement of the plate at a given point
,
In particular, we can assume that
Note that from a practical standpoint, it is no problem to provide measurements for finding a displacement
of the point
; consequently,
We first introduce the 6D space with the Euclidean metric,
Let
be a bounded domain with a smooth boundary whose elements satisfy the inequality (
1). Then, for any
and the fixed tensor
B it is possible to find a solution of the variational inequality
where
with the given tensor
Now, we assume that the elasticity tensor
A is unknown in the problems (
69) and (
70). On the other hand, the plate displacement of the point
is known. Namely,
is known from a measurement. Then, the precise formulation of the inverse problem is as follows. Let
be given. We have to find
such that
Below, we prove the existence of a solution of the inverse problem (
71)–(
73).
Theorem 6. exist such that for any fixed the inverse problem (71)–(73) has a solution. Proof. We introduce a function
L defined on the closed set
where
is the solution of the direct problem (
69) and (
70) with the given elasticity tensor
A. In what follows, we prove that this function is continuous on the set
Indeed, let
where we use the convergence in the Euclidean norm
. For any
we can find the unique solution of the problem
where
fits the elasticity tensor
The variational inequality (
76) and (
77) implies
From (
78), by the uniformity of this estimate in
p, it follows that
Choosing a subsequence, if necessary, we can assume that as
,
By (
75), (
80), a passage to the limit in (
76) and (
77), as
is possible, and the limit relation reads as follows:
Consequently, we have
Moreover, by (
80), we can assume that
as
; consequently,
We proved, therefore, that the function
L is continuous on the compact set
By the Weierstrass extreme value theorem, this means that we can find
Taking into account the intermediate value theorem for continuous functions, we conclude that for any
exists such that
This implies that the inverse problems (
71) and (
73) have a solution. Theorem 6 is proved. □
Note that similar arguments can be used for proving a solution existence to an inverse boundary problem with a different additional information compared to (
73). In particular, instead of (
73), we can consider
where
is a given point, and
is the displacement of the bridge.