Coincidence Theory of a Nonlinear Periodic Sturm–Liouville System and Its Applications
Abstract
1. Introduction
2. Preliminaries and Coincidence Theory of System (1)
- (i)
- every solution of possesses ,
- (ii)
- ,
- (iii)
- .
- then has a solution in .
3. Existence of Periodic Solution
- Assume that , , , and is a constant. Moreover, α, β, , and are ϖ-periodic functions.
- , , and .
- Assume that , , , and α, β, , and are ϖ-periodic functions.
- , .
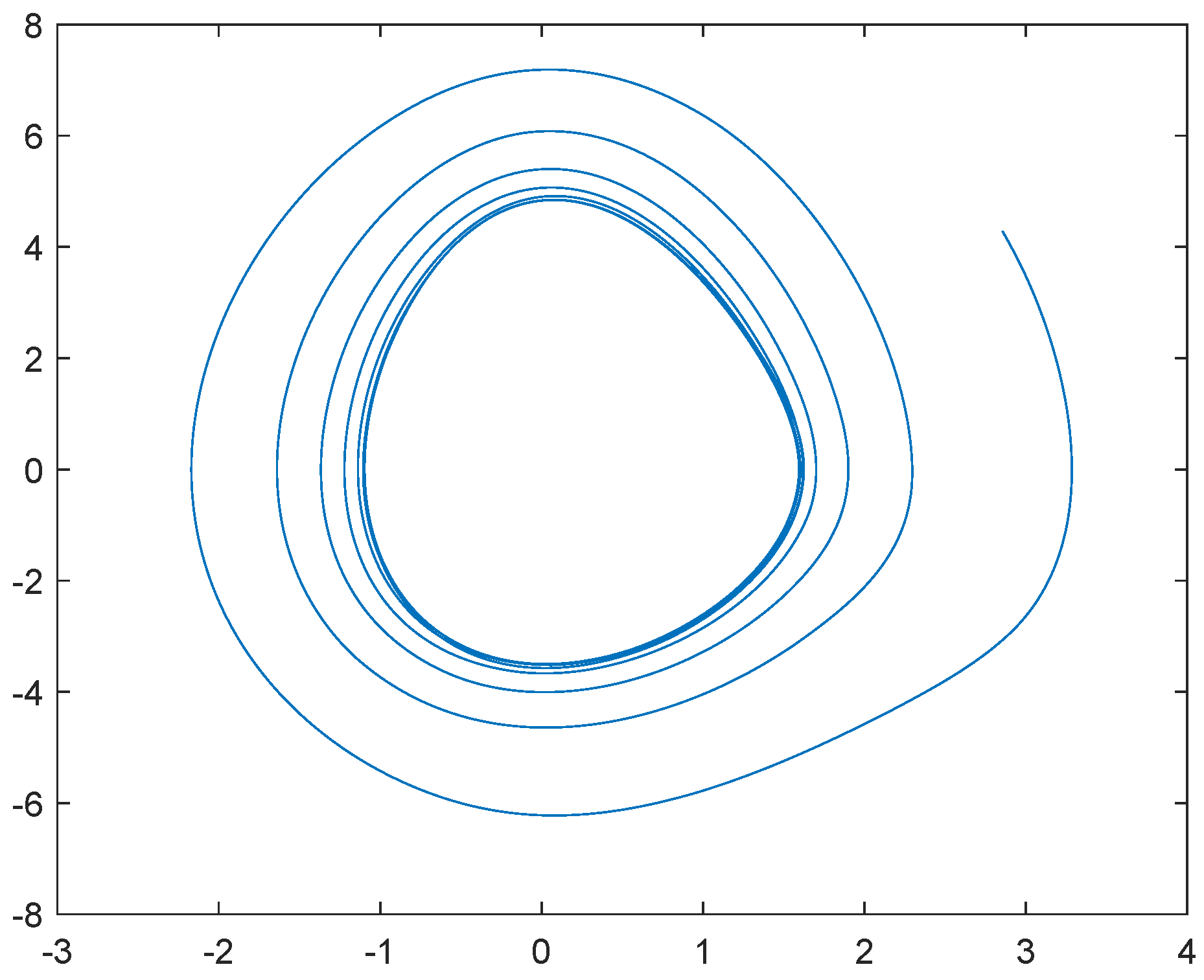
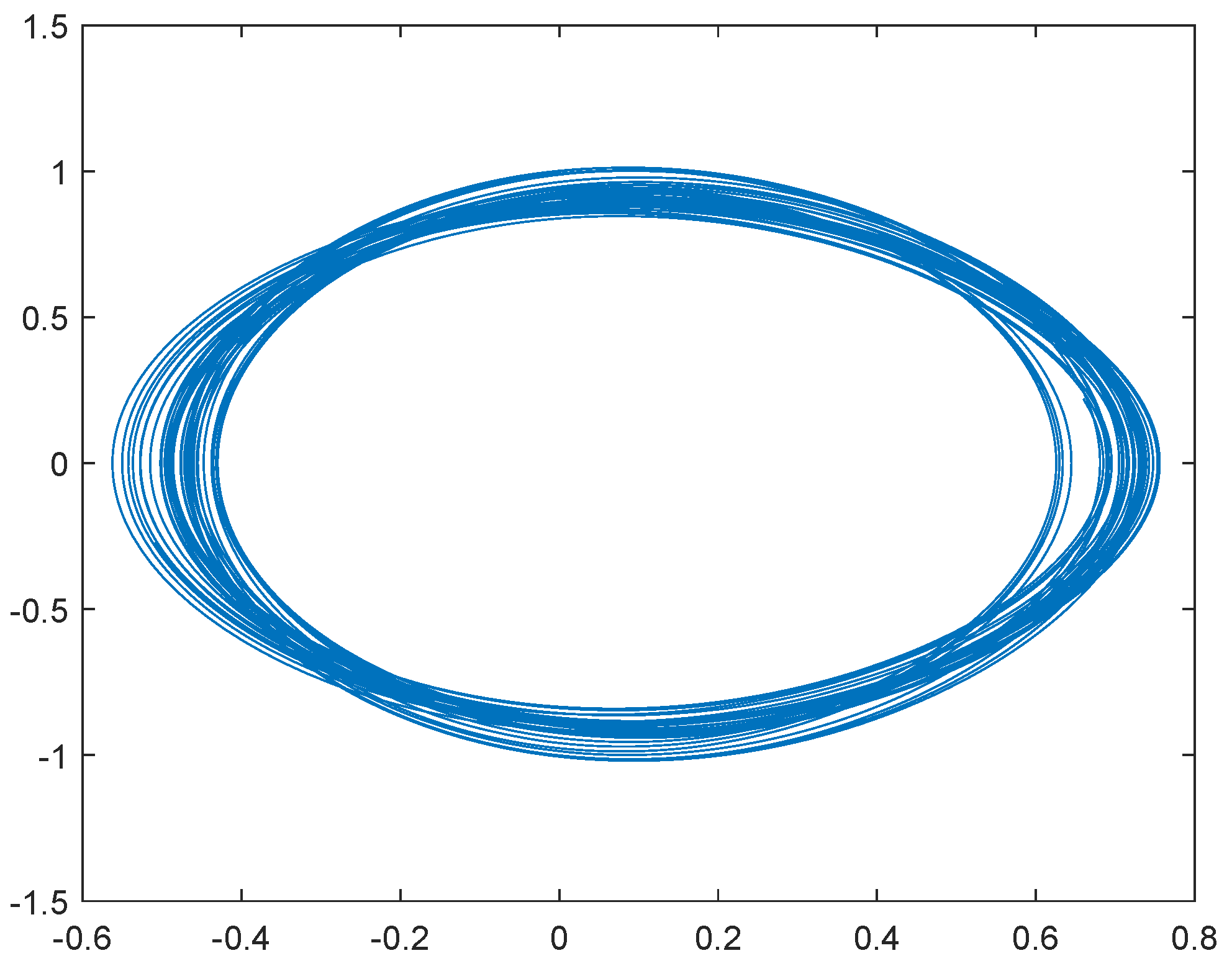
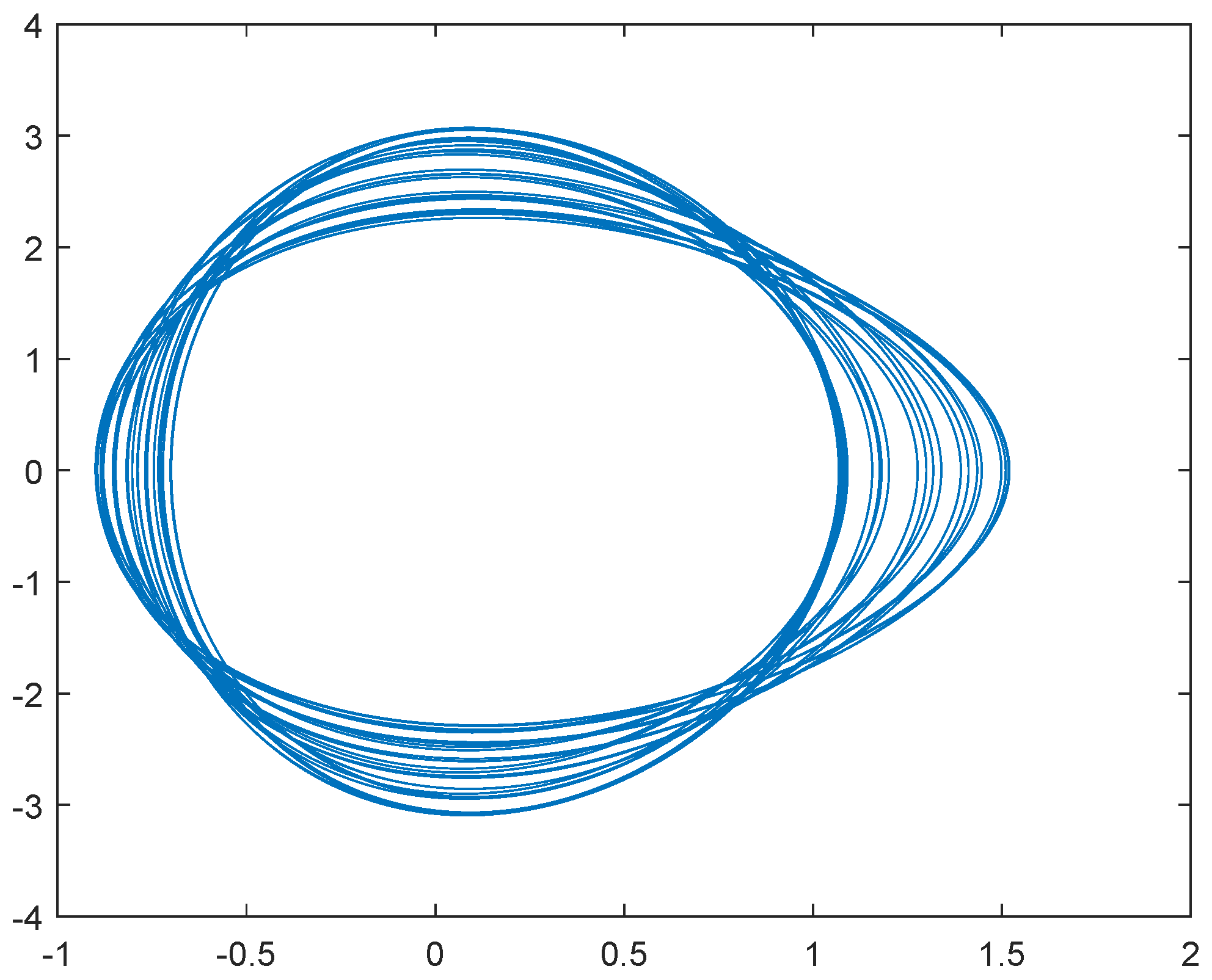
4. Illustrative Examples and Simulations
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Li, B. Reconstructing a second–order Sturm–Liouville operator by an energetic boundary function iterative method. Appl. Math. Lett. 2017, 73, 49–55. [Google Scholar] [CrossRef]
- Bondarenko, N. Finite-difference approximation of the inverse Sturm–Liouville problem with frozen argument. Appl. Math. Comput. 2022, 413, 126653. [Google Scholar] [CrossRef]
- Kravchenko, V. On a method for solving the inverse Sturm–Liouville problem. J. Inverse Ill-Pose. P. 2019, 27, 401–407. [Google Scholar] [CrossRef]
- Kravchenko, V.; Torba, S. A direct method for solving inverse Sturm–Liouville problems. Inverse Probl. 2021, 37, 015015. [Google Scholar] [CrossRef]
- Kravchenko, V.; Torba, S. A practical method for recovering Sturm–Liouville problems from the Weyl function. Inverse Probl. 2021, 37, 065011. [Google Scholar] [CrossRef]
- Yang, C.; Bondarenko, N.; Xu, X. An inverse problem for the Sturm–Liouville pencil with arbitrary entire functions in the boundary condition. Inverse Probl. Imaging 2020, 14, 153–169. [Google Scholar] [CrossRef]
- Yang, C.; Wang, F.; Huang, Z. Ambarzumyan theorems for Dirac operators. Acta Math. Appl. Sin.-E 2021, 37, 287–298. [Google Scholar] [CrossRef]
- Sadovnichii, V.; Sultanaev, Y.; Valeev, N. Reconstruction of nonsplitting boundary conditions of the Sturm–Liouville operator from a minimal set of eigenvalues. Differ. Equ. 2020, 56, 1290–1297. [Google Scholar] [CrossRef]
- Dalvand, Z.; Hajarian, M. Solving generalized inverse eigenvalue problems via L–BFGS–B method. Inverse Probl. Sci. Eng. 2020, 28, 1719–1746. [Google Scholar] [CrossRef]
- Delgado, B.; Khmelnytskaya, K.; Kravchenko, V. The transmutation operator method for efficient solution of the inverse Sturm–Liouville problem on a half–line. Math. Method Appl. Sci. 2019, 42, 7359–7366. [Google Scholar] [CrossRef]
- Bason, G. Inverse method identification of thermophysical properties based on solotone effect analysis for discontinuous Sturm–Liouville systems. Inverse Probl. Sci. Eng. 2019, 27, 1718–1739. [Google Scholar] [CrossRef]
- Yang, C.; Bondarenko, N. Local solvability and stability of inverse problems for Sturm–Liouville operators with a discontinuity. J. Differ. Equ. 2020, 268, 6173–6188. [Google Scholar] [CrossRef]
- Ali, M.; Aziz, S.; Malik, S. Inverse problem for a space–time fractional diffusion equation: Application of fractional Sturm–Liouville operator. Math. Method Appl. Sci. 2018, 40, 2733–2747. [Google Scholar] [CrossRef]
- Ali, M.; Aziz, S.; Malik, S. Inverse problem for a multi–parameters space–time fractional diffusion equation with nonlocal boundary conditions: Operational calculus approach. J. Pseudo–Differ. Oper. 2022, 13, 3. [Google Scholar] [CrossRef]
- Sa’idu, A.; Koyunbakan, H. Inverse fractional Sturm–Liouville problem with eigenparameter in the boundary conditions. Math. Method Appl. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Djennadi, S.; Shawagfeh, N.; Abu Arqub, O. A fractional Tikhonov regularization method for an inverse backward and source problems in the time–space fractional diffusion equations. Chaos Solitons Fract. 2021, 150, 111127. [Google Scholar] [CrossRef]
- Geng, X.; Cheng, H.; Fan, W. A note on analytical solution for the time–fractional telegraph equation by the method of separating variables. J. Math. Anal. Appl. 2022, 512, 126144. [Google Scholar] [CrossRef]
- Batiha, I.; Ouannas, A.; Albadarneh, R.; Al-Nana, A.A.; Momani, S. Existence and uniqueness of solutions for generalized Sturm–Liouville and Langevin equations via Caputo-Hadamard fractional–order operator. Eng. Comput. 2022, 39, 2581–2603. [Google Scholar] [CrossRef]
- Moutamal, M.; Joseph, C. Optimal control of fractional Sturm–Liouville wave equations on a star graph. Optimization 2022, in press. [Google Scholar] [CrossRef]
- Javed, S.; Malik, S. Some inverse problems for fractional integro–differential equation involving two arbitrary kernels. Z. Angew. Math. Phys. 2022, 73, 40. [Google Scholar] [CrossRef]
- Heydarpour, Z.; Izadi, J.; George, R.; Ghaderi, M.; Rezapour, S. On a partial fractional hybrid version of generalized Sturm–Liouville–Langevin equation. Fractal Fract. 2022, 6, 269. [Google Scholar] [CrossRef]
- Klimek, M.; Ciesielski, M.; Blaszczyk, T. Exact and numerical solution of the fractional Sturm–Liouville problem with Neumann boundary conditions. Entropy 2022, 24, 143. [Google Scholar] [CrossRef] [PubMed]
- Min, D.; Chen, F. Variational Methods to the p–Laplacian type nonlinear fractional impulsive differential equations with Sturm-Liouville boundary value problems. Fract. Calc. Appl. Anal. 2021, 24, 1069–1093. [Google Scholar] [CrossRef]
- Paknazar, M.; De La Sen, M. Fractional coupled hybrid Sturm–Liouville differential equation with multi–point boundary coupled hybrid condition. Axioms 2021, 10, 65. [Google Scholar] [CrossRef]
- Koyunbakan, H. Reconstruction of potential in discrete Sturm–Liouville problem. Qual. Theory Dyn. Syst. 2022, 21, 13. [Google Scholar] [CrossRef]
- Allahverdiev, B.; Tuna, H. Conformable fractional Sturm–Liouville problems on time scales. Math. Method Appl. Sci. 2022, 45, 2299–2314. [Google Scholar] [CrossRef]
- Kuznetsova, M. On recovering the Sturm–Liouville differential operators on time scales. Math. Notes 2021, 109, 74–88. [Google Scholar] [CrossRef]
- Adalar, I.; Ozkan, A. An interior inverse Sturm–Liouville problem on a time scale. Anal. Math. Phys. 2020, 10, 58. [Google Scholar] [CrossRef]
- Heidarkhani, S.; Moradi, S.; Caristi, G. Existence results for a dynamic Sturm–Liouville boundary value problem on time scales. Optim. Lett. 2020, 15, 2497–2514. [Google Scholar] [CrossRef]
- Kuznetsova, M. A uniqueness theorem on inverse spectral problems for the Sturm–Liouville differential operators on time scales. Results Math. 2020, 75, 44. [Google Scholar] [CrossRef]
- Ozkan, A.; Adalar, I. Half–inverse Sturm-Liouville problem on a time scale. Inverse Probl. 2020, 36, 025015. [Google Scholar] [CrossRef]
- Ao, J.; Wang, J. Eigenvalues of Sturm–Liouville problems with distribution potentials on time scales. Quaest. Math. 2019, 42, 1185–1197. [Google Scholar] [CrossRef]
- Ao, J.; Wang, J. Finite spectrum of Sturm–Liouville problems with eigenparameter–dependent boundary conditions on time scales. Filomat 2019, 33, 1747–1757. [Google Scholar] [CrossRef]
- Barilla, D.; Bohner, M.; Heidarkhani, S.; Moradi, S. Existence results for dynamic Sturm–Liouville boundary value problems via variational methods. Appl. Math. Comput. 2021, 409, 125614. [Google Scholar] [CrossRef]
- Ishkin, K.; Davletova, L. Regularized trace of a Sturm–Liouville operator on a curve with a regular singularity on the chord. Differ. Equ. 2020, 56, 1257–1269. [Google Scholar] [CrossRef]
- Hu, X.; Liu, L.; Wu, L.; Zhu, H. Singularity of the n–th eigenvalue of high dimensional Sturm–Liouville problems. J. Differ. Equ. 2019, 266, 4106–4136. [Google Scholar] [CrossRef]
- Bondarenko, N. Inverse problems for the matrix Sturm–Liouville equation with a Bessel–type singularity. Appl. Anal. 2018, 97, 1209–1222. [Google Scholar] [CrossRef]
- Chen, L. A sub–density theorem of Sturm–Liouville eigenvalue problem with finitely many singularities. J. Contemp. Math. Anal. 2018, 53, 1–5. [Google Scholar] [CrossRef]
- Gaines, R.; Mawhin, J. Coincidence Degree and Nonlinear Differetial Equitions; Lecture Notes in Mathematics Series; Springer: Berlin/Heidelberg, Germany, 1977; Volume 568. [Google Scholar]
- Zhao, K. Local exponential stability of four almost–periodic positive solutions for a classic Ayala–Gilpin competitive ecosystem provided with varying–lags and control terms. Int. J. Control 2022, in press. [Google Scholar] [CrossRef]
- Zhao, K. Local exponential stability of several almost periodic positive solutions for a classical controlled GA–predation ecosystem possessed distributed delays. Appl. Math. Comput. 2023, 437, 127540. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y. Exponential Euler scheme of multi–delay Caputo–Fabrizio fractional–order differential equations. Appl. Math. Lett. 2022, 124, 107709. [Google Scholar] [CrossRef]
- Zhang, T.; Xiong, L. Periodic motion for impulsive fractional functional differential equations with piecewise Caputo derivative. Appl. Math. Lett. 2020, 101, 106072. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y. Global exponential stability of discrete–time almost automorphic Caputo–Fabrizio BAM fuzzy neural networks via exponential Euler technique. Knowl.–Based Syst. 2022, 246, 108675. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, J.; Liao, Y. Exponentially stable periodic oscillation and Mittag–Leffler stabilization for fractional-order impulsive control neural networks with piecewise Caputo derivatives. IEEE Trans. Cybern. 2022, 52, 9670–9683. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K. Stability of a nonlinear fractional Langevin system with nonsingular exponential kernel and delay control. Discret. Dyn. Nat. Soc. 2022, 2022, 9169185. [Google Scholar] [CrossRef]
- Zhao, K. Existence, stability and simulation of a class of nonlinear fractional Langevin equations involving nonsingular Mittag–Leffler kernel. Fractal Fract. 2022, 6, 469. [Google Scholar] [CrossRef]
- Zhao, K. Stability of a nonlinear ML–nonsingular kernel fractional Langevin system with distributed lags and integral control. Axioms 2022, 11, 350. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, K.; Liu, X. On solvability of BVP for a coupled Hadamard fractional systems involving fractional derivative impulses. AIMS Math. 2022, 7, 19221–19236. [Google Scholar] [CrossRef]
- Zhao, K. Stability of a nonlinear Langevin system of ML–type fractional derivative affected by time–varying delays and differential feedback control. Fractal Fract. 2022, 6, 725. [Google Scholar] [CrossRef]
- Zhao, K. Global stability of a novel nonlinear diffusion online game addiction model with unsustainable control. AIMS Math. 2022, 7, 20752–20766. [Google Scholar] [CrossRef]
- Zhao, K. Probing the oscillatory behavior of internet game addiction via diffusion PDE model. Axioms 2022, 11, 649. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, K. Coincidence Theory of a Nonlinear Periodic Sturm–Liouville System and Its Applications. Axioms 2022, 11, 726. https://doi.org/10.3390/axioms11120726
Zhao K. Coincidence Theory of a Nonlinear Periodic Sturm–Liouville System and Its Applications. Axioms. 2022; 11(12):726. https://doi.org/10.3390/axioms11120726
Chicago/Turabian StyleZhao, Kaihong. 2022. "Coincidence Theory of a Nonlinear Periodic Sturm–Liouville System and Its Applications" Axioms 11, no. 12: 726. https://doi.org/10.3390/axioms11120726
APA StyleZhao, K. (2022). Coincidence Theory of a Nonlinear Periodic Sturm–Liouville System and Its Applications. Axioms, 11(12), 726. https://doi.org/10.3390/axioms11120726





