Abstract
In this study, we utilize the properties of the Sumudu transform (SuT) and combine it with the homotopy perturbation method to address the time fractional Navier-Stokes equation. We introduce a new technique called the homotopy perturbation Sumudu transform Strategy (HPSuTS), which combines the SuT with the homotopy perturbation method using He’s polynomials. This approach proves to be powerful and practical for solving various linear and nonlinear fractional partial differential equations (FPDEs) in scientific and engineering fields. We demonstrate the efficiency and simplicity of this method through examples, showcasing its ability to approximate solutions for FPDEs. Additionally, we compare the numerical results obtained using this technique for different values of alpha, showing that as the value moves from a fractional order to an integer order, the solution becomes increasingly similar to the exact solution. Furthermore, we provide the tabular representations of the solution for each example.
Keywords:
homotopy perturbation strategy; Sumudu transform; approximate solution; fractional Caputo derivatives MSC:
44A20; 34A08; 34A12; 34C60
1. Introduction
Fractional calculus (Fc), an extension of traditional integer-order calculus, has gained significant attention across various scientific and engineering disciplines due to its capability to model complex phenomena with long-range memory and anomalous diffusion. This mathematical discipline dates back to the 17th century, with pioneers like L’Hôpital and Leibniz exploring the idea of Fractional derivative (Fd). However, it was Liouville and Riemann in the late 19th century who laid the rigorous foundations of Fc [1,2]. Fc finds applications in various scientific and engineering fields, including physics, engineering, finance, biology, and signal processing. It allows the modeling of complex phenomena with long-range memory and anomalous diffusion, which cannot be adequately captured by traditional integer-order calculus [1,3,4,5]. Fc has emerged as a robust mathematical framework that extends the conventional integer-order calculus to accommodate derivatives and integrals of non-integer orders. This extension allows for the description and analysis of complex dynamical systems and processes that exhibit behaviors beyond the scope of traditional calculus. Over the past few decades, Fc has found applications in various scientific and engineering disciplines, such as physics, biology, economics, and engineering, enabling researchers to model intricate phenomena with long-range memory and anomalous diffusion [3,6,7,8].
The study of FPDEs has gained significant attention in recent years. These equations are frequently encountered in various fields such as fluid mechanics, viscoelasticity, biology, engineering, and physics [9,10]. However, most of these equations do not have exact analytical solutions, necessitating the use of approximation and numerical techniques. Several numerical methods have been developed to tackle these equations, including the Adomain decomposition method [11], Homotopy analysis method [12], Variational iteration method [13], and Homotopy perturbation method [14,15,16,17]. The homotopy perturbation method [18] proposed by He, has proven to be a useful tool for obtaining exact and approximate solutions for both linear and nonlinear FPDEs.
One of the main advantages of the homotopy perturbation method is that it does not require a small parameter or linearization. The solution procedure is straightforward and only a few iterations are needed to achieve highly accurate solutions that are valid for the entire solution domain. Moreover, the solution is expressed as the summation of an infinite series, which is expected to converge to the exact solution. The Sumudu transform (SuT) introduced by Watugala in 1994, has emerged as a valuable mathematical tool for transforming a wide range of integral and DEs into algebraic equations and thus simplifying their solution process [19]. This transform has proven particularly useful in the context of Fc, where it enables the conversion of FDEs into algebraic forms, facilitating the application of various solution methods. The SuT has gained prominence recently due to its versatility and effectiveness in handling complex mathematical problems across different scientific and engineering disciplines. The SuT, known for its scale and unit-preserving properties, eliminates the need for introducing a new frequency domain. It has been demonstrated that the SuT maintains the units of the original problem, making it a valuable tool for solving problems without relying on the frequency domain [20]. One of the notable strengths of the SuT is its applicability to problems involving physical dimensions. This transform, being linear in nature, possesses the ability to preserve linear functions, thereby ensuring that units remain unchanged. This characteristic is particularly advantageous when solving problems that involve physical dimensions [19,21]. When integrated with the HPS, the resulting HPSuTS offers a comprehensive approach for solving FDEs. The SuT aids in simplifying the Fc operations, and the HPS provides an iterative framework for obtaining accurate approximate solutions. This combination of the SuT and the HPS has gained recognition for its ability to handle complex problems involving Fc, enabling researchers to explore a wide range of scientific and engineering applications [19].
In [22], Hamed, Yousif, and Arbab presented a novel approach for solving Schrödinger space-time fractional equations through the integration of the HPS with the SuT. The researchers aimed to obtain both analytic and approximate solutions for these complex equations. The proposed method demonstrated its efficacy in providing accurate solutions, highlighting its potential in handling the challenges posed by Schrödinger space-time fractional equations. In his work, Khader explored the application of the HPSuTS to solve nonlinear heat-like fractional equations. The study aimed to address the challenges posed by these intricate equations by combining the HPS with the SuT technique. By doing so, the researcher sought to derive approximate solutions that capture the nonlinear dynamics of the equations [23]. By exploring the domain of mathematical challenges, recent studies have showcased innovative approaches to overthrow the complexities of nonlinear FPDEs. Many researchers have solved different equations with the help of HPSuTS, such as heat and wave-like equations [24], Black-Scholes European option pricing equations [25] and references therein.
Recently, El-Shahed and Salem generalized the traditional Navier-Stokes equations by introducing a fractional derivative of order in place of the classical time derivative. They utilized Laplace transform, Fourier sine transform, and finite Hankel transforms to derive approximate solutions for three specific cases [26]. The most important advantage of using fractional differential equations in these and other applications is their non-local property. It is well known that the integer order differential operator is a local operator but the fractional order differential operator is non-local. This means that the next state of a system depends not only upon its current state but also upon all of its historical states. This is more realistic and it is one of the main reason why fractional calculus has become more and more popular. However, due to the nonlinearity of the Navier-Stokes Time-Fractional Equation (NS-TFEs), there is currently no universally known method for analytically solving this equations. Obtaining an exact solution for this equations is rare and typically requires assumptions about the fluid’s state and consideration of a simple flow pattern configuration. Subsequently, various numerical methods have been employed to study this equation, such as the Adomian decomposition method [27], Homotopy analysis method [28], and Modified Laplace decomposition method [29].
In this paper, we will focus on the unsteady flow of a viscous fluid in a tube. The main objective of this research is to expand the applications of the HPS in combination with the SuT to investigate the approximate solution of NS-TFEs in cylindrical frame of reference. Additionally, to demonstrate the accuracy of this suggested technique, we have compared our results with already established results. The results indicates that as the values of approaches to 1, the solution becomes more similar to exact solution. Moreover, we have provided the tabular representation of the approximate solution for various fractional order.
The structured of this study is as follows. A comprehensive discussion of the essential concepts of Fc is provided in Section 2. The model formulation and applicability are addressed in detail in Section 3. The implementation of the suggested technique and its numerical solution is discussed in Section 4. Finally, concluding remarks are given in Section 5.
2. Revealing Fundamental Notions
Fc, a branch of mathematics extending traditional calculus to non-integer orders, has gained prominence for its ability to model complex phenomena with long-range memory and anomalous diffusion. This section explores the concept of fractional Caputo derivatives (FCd), introduces the SuT as a powerful mathematical tool, and discusses their interplay with related properties.
2.1. Definition
A mathematical function known as the “Gamma function” generalizes the factorial sense to real and complex numbers. It is denoted by , where z is a complex number. The gamma function is defined as an integral over the positive real numbers [1,2,30]:
where the real part of z must be greater than zero for the integral to converge.
2.2. Definition
The Riemann–Liouville (R–L) integral operator of fractional order is a mathematical operation that extends the concept of integration to non-integer orders. Given a real function and a parameter , the R–L integral operator of fractional order is defined as follows [2,30,31]:
where is the gamma function, and the integral is taken from to .
2.2.1. Properties of Riemann–Liouville Fractional Integral Operator
2.2.2. Linearity: [20,30,31]
For any real constants a and b, and functions and , we have
2.2.3. Scaling Property: [20,30,31]
2.2.4. Connection with Derivatives
If has n continuous derivatives on and continuous derivatives at , then is the nth derivative of the nth R–L integral of fractional order of [1,2,30].
2.2.5. Inverse Property
The R–L integral of fractional order is invertible, and its inverse is given by [1,2,30],
2.2.6. Composition Rule: [2,30]
If , then
The R–L integral of fractional order is a fundamental tool in Fc, allowing the extension of traditional calculus concepts to non-integer orders and enabling the study of various complex systems and phenomena.
2.3. Definition
The FCd is a mathematical notion that extends the concept of classical derivative to fractional orders. It is often used in Fc to describe the behavior of functions involving Fd. The FCd of a function of order , denoted by , is defined as follows [2,30]:
where n is the smallest integer greater than , a is a lower limit of integration, and represents the gamma function. The FCd has an important relation to ordinary derivatives. When we take as a positive integer, i.e., . In this case, the FCd reduces to the nth ordinary derivative:
However, for non-integer values of , the FCd involves both the fractional order and an integral of the ordinary derivatives. This integral term accounts for the “memory” of the function , capturing the effect of past values of the function up to -th order in the fractional differentiation process.
2.4. Definition
The Mittag-Leffler function (M-LF) is a special function that arises in various areas of mathematics, including Fc, complex analysis, and probability theory. It is represented as and is defined by the following infinite series [2,30]:
where z is a complex number, and are real or complex parameters, and is the gamma function. The M-LF generalizes the exponential function and is closely related to Fc. It exhibits behavior that interpolates between exponential decay and algebraic decay, making it suitable for modeling processes with memory or anomalous diffusion.
2.5. Some Properties of the Mittag-Leffler Function
2.5.1. Fractional Derivatives: [2,30]
The M-LF is often used to represent Fd in Fc. Specifically, , where represents a Fd of order .
2.5.2. Series Convergence: [2,30]
The M-LF converges for all complex z and such that and .
2.5.3. Special Cases: [2,30]
When and , the M-LF reduces to the ordinary exponential function, .
2.6. Definition
The SuT [19,22,32] of a function defined for is denoted as . It involves integrating multiplied by an exponential term over the entire non-negative time domain:
This transform provides insight into the function’s behavior in a new parameter -domain, aiding in the solution of various mathematical problems, including integral and differential equations, with applications across diverse fields. Now, let us recall some interesting special properties of the Sumudu Transform that are necessary in the further development of this study.
2.6.1. Constant Function
The SuT of the constant function is equal to 1 [33,34]:
2.6.2. Exponential Function: [33,34]
For positive n, the SuT of the function is given by:
2.6.3. Exponential Decay: [33,34]
The SuT of the exponential decay function is given by:
2.6.4. Linearity: [25,33,34]
The SuT obeys the linearity property:
For further properties and details about the SuT, see [20,31] and references therein. These properties are useful tools in applying the SuT to various mathematical problems and functions.
2.6.5. Sumudu Transform and Fractional Caputo Derivative
The SuT of the FCd , where is within the range , is denoted as and is calculated as follows [33,34]:
Here, is the SuT of the function , represents the m-th derivative of evaluated at . This SuT of the FCd aids in analyzing and solving FDEs involving the FCd, providing insights into the transformed function’s properties and contributing to the mathematical solutions of various problems.
In the subsequent section, we will provide a comprehensive explanation of how the SuT and the HPS can be utilized to address FDEs in detail.
3. Homotopy Perturbation Sumudu Transform Strategy
In this section, we present a comprehensive formulation of a novel approach termed “Homotopy Perturbation Sumudu Transform Strategy” (HPSuTS). This approach is applied to address complex FDEs, which have significant applications in various scientific and engineering domains.
The problem at hand is represented by the following equation:
with the initial condition (I.C):
where represents a function of two variables, denotes a FCd of order , ℜ signifies the second part of a linear operator, represents a non-linear operator, and is a non-homogeneous term. Applying the linearity of the SuT, the equation can be rewritten as:
Alternatively, the equation can be expressed as:
By applying definition (Section 2.6.5), the following expression is derived:
Incorporating the initial condition, the equation becomes:
Finally, by applying the inverse SuT, we obtained the above expression as:
where represents the contribution from the source term and I.C. To effectively address the problem, the HPSuTS introduces a novel technique for decomposing the solution into an infinite series of components:
Similarly, the non-linear term is decomposed as:
Here, the He’s polynomials [18], denoted by , are defined as follows:
With the utilization of the previously presented equations, the HPSuTS transforms the problem into a series of iterative equations for . Utilizing Equations (16) and (17), we elegantly transform Equation (15) to yield the following insightful expressions:
Through a series of consecutive iterations and evaluation of well-established components of p, we uncover the following pattern:
Consequently, the solution to the intricate FDEs emerges as the sum of these terms:
This method adeptly harnesses the concept of successive iterations and mathematical scrutiny to unveil a holistic solution for the complex FDEs, effectively showcasing the skills of mathematical techniques in tackling intricate equations.
In the forthcoming sections, we will explore the practical implementation of the HPSuTS and assess its efficacy in resolving NS-TFEs.
4. Implementation of the Proposed Technique
Let us consider the NS-TFEs in general form as [29,35]:
where , p denotes the pressure, the kinematics viscosity, and is the density of a viscous fluid of unsteady flow. When , the Equation (22) becomes the classical NSEs.
4.1. Case: 1
Let us first consider the NS-TFEs (22) [35] as:
with I.C:
By applying SuT on both sides of (23), the equation can be rewritten as:
By applying definition Section 2.6.5, the following expression is derived:
Incorporating the I.C, the above equation becomes:
Finally, by taking the inverse SuT, we obtain:
By implementing the HPS to the above equation we get:
The coefficients of the powers are equated as follows:
and so on. By substituting the above values into the equation, we have:
When the solution becomes,
which is the required solution as in [29,35]. The approximate solutions for different values of under two distinct scenarios i.e., for and are shown in the Figure 1a and Figure 1b respectively. Moreover, the 3D representation of the solution is provided in Figure 2. Also, the tabular representation of the solution for various fractional order is provided in Table 1 and Table 2 for the parameter and respectively.
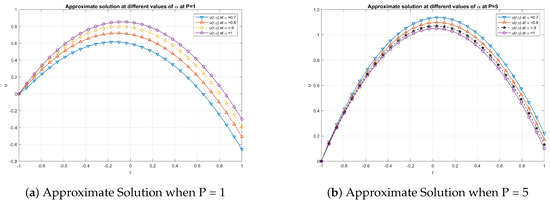
Figure 1.
Numerical Comparison of solution.
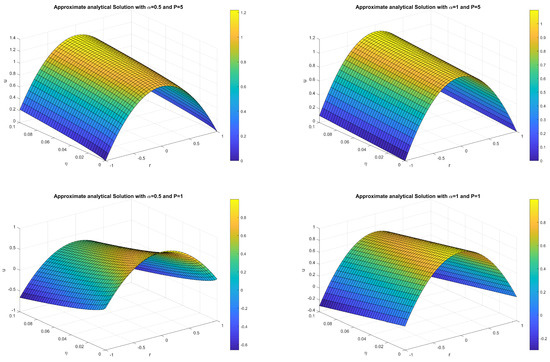
Figure 2.
Approximate analytical solution.

Table 1.
Approximate solution of (23) at .

Table 2.
Approximate solution of (23) at .
4.2. Case: 2
Let us consider the NS-TFEs (22) [35] as:
with I.C:
By taking SuT on both sides of the above equations, the equations becomes:
By applying definition Section 2.6.5, the following expression is derived:
Incorporating the I.C, the equation becomes:
Finally, by using the inverse SuT, we obtain:
By implementing the HPS to the above equation we get:
The coefficients of the powers are equated as follows:
and so on. By substituting the above values into the equation, we have:
When the solution becomes,
which is the required solution as in [29,35]. The approximate solutions for different values of are shown in the Figure 3 and Figure 4. Moreover, tabular representation of solution is provided in Table 3.
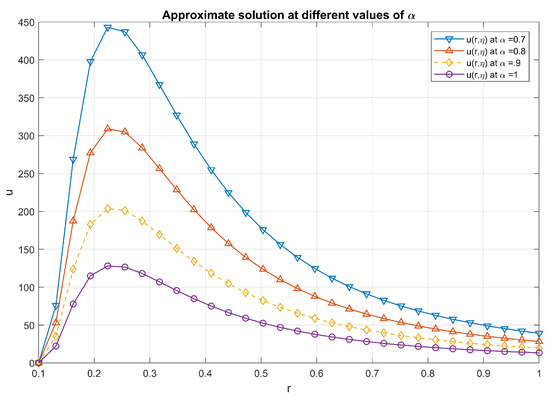
Figure 3.
Numerical Comparison of Solution.

Figure 4.
Approximate analytical solution.

Table 3.
Approximate solution of (30).
5. Conclusions
This study introduces the HPSuT method, which is a semi-analytical technique used to solve NS-TFEs. By combining the SuT and HPS techniques, we were able to successfully solved the NS-TFEs and obtained an approximate solution. The proposed solution is supported by graphical results in both 2D and 3D, which depict the solution for different values of . Furthermore, numerical results obtained using the suggested technique for various values of are compared, demonstrating that as the value transitions from a fractional order to an integer order, the solution becomes increasingly similar to the exact solution. The results presented in Table 1, Table 2 and Table 3 also indicate that the series solution rapidly converges to the exact solution as the non-integer order approaches an integer order.
The HPSuT method offers several advantages that contribute to its effectiveness and interactivity. Firstly, it provides series solutions that converge quickly and exhibit a high degree of accuracy, enabling reliable numerical results to be efficiently obtained. Additionally, this method significantly reduces the computational workload compared to other traditional methods, which is particularly beneficial for complex problems and large datasets. Moreover, the HPSuT method is not limited to specific types of FDEs, as it can be applied to both linear and non-linear FDEs. This versatility makes it a valuable tool applicable in various scientific and engineering fields.
To summarize, the HPSuT method has been demonstrated to be an interactive and efficient approach for solving NS-TFEs. Its accuracy, computational efficiency, and applicability to different types of FDEs make it a valuable tool for researchers and practitioners in various domains.
Author Contributions
Conceptualization, S.I. and F.M.; methodology, S.I.; software, S.I.; validation, S.I. and F.M.; formal analysis, S.I. and F.M.; investigation, S.I. and F.M.; writing—original draft preparation, S.I.; writing—review and editing, S.I. and F.M.; visualization, S.I and F.M.; supervision, S.I. and F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Podlubnv, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA; Boston, MA, USA, 1999; Volume 6. [Google Scholar]
- Chen, W. Time-space fabric underlying anomalous diffusion. Chaos Solitons Fractals 2006, 28, 923–929. [Google Scholar] [CrossRef]
- Iqbal, S.; Wei, Y. Recovery of the time-dependent implied volatility of time fractional Black–Scholes equation using linearization technique. J. Inverse Ill-Posed Probl. 2021, 29, 599–610. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; El-Morshedy, M. Solitary Wave Solution of a Generalized Fractional–Stochastic Nonlinear Wave Equation for a Liquid with Gas Bubbles. Mathematics 2023, 11, 1692. [Google Scholar] [CrossRef]
- Sene, N. Stokes’ first problem for heated flat plate with Atangana-Baleanu fractional derivative. Chaos Solitons Fractals 2018, 117, 68–75. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A.; Baleanu, D. Analysis of the fractional tumour-immune-vitamins model with Mittag-Leffler kernel. Results Phys. 2020, 19, 103559. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Shaikh, A.A.; Inc, M.; Baleanu, D. Mathematical modeling for adsorption process of dye removal nonlinear equation using power law and exponentially decaying kernels. Chaos 2020, 30, 043106. [Google Scholar] [CrossRef]
- Schneider, W.R.; Wyss, W. Fractional diffusion and wave equation. J. Math. Phys. 1989, 30, 134–144. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Numerical comparison of methods for solving linear differential equations of fractional order. Chaos Solitons Fractals 2007, 31, 1248–1255. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. Numerical methods for nonlinear partial differential equations of fractional order. Appl. Math. Model. 2008, 32, 28–39. [Google Scholar] [CrossRef]
- Jafari, H.; Seifi, S. Homotopy analysis method for solving linear and nonlinear fractional diffusion-wave equation. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2006–2012. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. The variational iteration method: An efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput. Math. Appl. 2009, 58, 2199–2208. [Google Scholar] [CrossRef]
- Maitama, S.; Zhao, W. Homotopy Perturbation Shehu Transform Method for Solving Fractional Models Arising in Applied Sciences. J. Appl. Math. Comput. Mech. 2021, 20, 71–82. [Google Scholar] [CrossRef]
- Akinyemi, L.; Enol, M.; Huseen, S.N. Modified homotopy methods for generalized fractional perturbed Zakharov–Kuznetsov equation in dusty plasma. Adv. Differ. Equ. 2021, 2021, 1–27. [Google Scholar] [CrossRef]
- Iqbal, S.; Kaabar, M.K.A.; Martinez, F. A Novel Homotopy Perturbation Algorithm Using Laplace Transform for Conformable Partial Differential Equations. Math. Probl. Eng. Theory Methods Appl. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Iqbal, S.; Martínez, F.; Kaabar, M.K.A.; Samei, M.E. A novel Elzaki transform homotopy perturbation method for solving time-fractional non-linear partial differential equations. Bound. Value Probl. 2022, 2022, 1–23. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Watugala, G.K. Sumudu transform: A new integral transform to solve differential equations and control engineering problems. Integr. Educ. 1993, 24, 35–43. [Google Scholar] [CrossRef]
- Belgacem, F.B.M.; Karaballi, A.A. Sumudu transform fundamental properties investigations and applications. Int. J. Stoch. Anal. 2006, 2006, 91083. [Google Scholar] [CrossRef]
- Muhammed, B.F.B.; Abdullatif, K.A.; Kalla, S.L. Analytical investigations of the Sumudu transform and applications to integral production equations. Math. Probl. Eng. 2003, 2003, 103–118. [Google Scholar]
- Hamed, S.H.M.; Yousif, E.A.; Arbab, A.I. Analytic and Approximate Solutions of the Space-Time Fractional Schrdinger Equations by Homotopy Perturbation Sumudu Transform Method. Abstr. Appl. Anal. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Khader, M.M. Application of homotopy perturbation Sumudu transform method for solving nonlinear fractional heat-like equations. Sci. Iran. 2017, 24, 648–655. [Google Scholar] [CrossRef]
- Jassim, H.K.; Kadmim, H. Fractional Sumudu decomposition method for solving PDEs of fractional order. J. Appl. Comput. Mech. 2021, 7, 302–311. [Google Scholar]
- Ouafoudi, M.; Gao, F. Exact solution of fractional Black-Scholes European option pricing equations. Appl. Math. 2018, 9, 86–100. [Google Scholar] [CrossRef]
- El-Shahed, M.; Salem, A. On the Generalized Navier-Stokes Equations. Appl. Math. Comput. 2003, 156, 287–293. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. The Analytical solution of a time-fractional Navier–Stokes equation by Adomian decomposition method. Appl. Math. Comput. 2006, 177, 488–494. [Google Scholar] [CrossRef]
- Ragab, A.A.; Hemida, K.M.; Mohamed, M.S.; Salam, M.A.A.E. Solution of Time-Fractional Navier-Stokes Equation by Using Homotopy Analysis Method. Gen 2013, 13, 13–21. [Google Scholar]
- Kumar, S.; Kumar, D.; Abbasbandy, S.; Rashidi, M. Analytical solution of fractional Navier–Stokes equation by using modified Laplace decomposition method. Ain Shams Eng. J. 2014, 5, 569–574. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integral Transform. Spec. Funct. 2004, 15, 31–49. [Google Scholar] [CrossRef]
- Wang, K.; Liu, S. A new Sumudu transform iterative method for time-fractional Cauchy reaction–diffusion equation. SpringerPlus 2016, 5, 1–20. [Google Scholar] [CrossRef]
- Alomari, A.; Syam, M.I.; Anakira, N.; Jameel, A. Homotopy Sumudu transform method for solving applications in physics. Results Phys. 2020, 18, 103265. [Google Scholar] [CrossRef]
- Atangana, A.; Kılıçman, A. The use of Sumudu transform for solving certain nonlinear fractional heat-like equations. In Abstract and Applied Analysis; Hindawi: London, UK, 2013; Volume 2013. [Google Scholar]
- Ragab, A.; Hemida, K.; Mohamed, M.; Abd El Salam, M. Solution of time-fractional Navier–Stokes equation by using homotopy analysis method. Gen. Math. Notes 2012, 13, 13–21. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).