1. Introduction
The concept of a cozero-divisor graph on commutative rings was introduced in [
1]. In [
2], the Laplacian eigenvalues of this type of graph is computed. Some applications of this research could be in the following areas: quantum chemistry, the topological theory of aromaticity, counts of random walks, structure-resonance theory, and eigenvector–eigenvalue problems.
Throughout this article, unless otherwise stated, R will denote a commutative ring with identity . denotes the ideal generated by an element w in R and it is defined as . is the set of all non-unit and non-zero elements of ring R.
We denote the graph
, where
V is the vertex set and
E denotes the edge set of graph
G. The symbol
indicates that
is adjacent to
in a graph
G, where
and
are distinct vertices of
G. The complete graph is denoted by
with
m vertices and the set of
G vertices that are adjacent to vertex
y is known as the vertex’s neighbourhood, and it is represented by the symbol
. The number of edges incident with
is represented by
, which is the
of vertex
y, and
y is referred to as an
vertex if
. For each vertex
y if
, then
G is
. Now, let
be the distinct eigenvalues of a square matrix
B with multiplicities
, respectively, then
denotes the
of
B and is defined by
The square matrix
of
G is the
matrix of
G and is given by
The
Laplacian matrix
of a graph
G is defined as
Let
be the diagonal matrix of vertex degrees given by
, where
. The Laplacian matrix of a graph
G is defined as
and the
signless Laplacian matrix of a graph
G is defined as
If all the signless Laplacian eigenvalues of a graph
G are integers, then
G is said to be a signless Laplacian
. The spectrum of signless Laplacian matrix and Laplacian matrix is known as the signless Laplacian spectrum and the Laplacian spectrum of the graph
G, respectively. The details of adjacency and the signless Laplacian spectrum can be found in [
3,
4,
5,
6].
On commutative rings, Afkhami et al. [
1] introduced the concept of a cozero-divisor graph.
denotes the cozero-divisor graph of
R, which is an undirected graph with a vertex set
,
, and
if and only if two distinct vertices
w and
z are adjacent. For more details on the cozero-divisor graph see, for example, [
1,
7,
8] where further references can be found.
Parveen et al. [
2] calculated the Laplacian eigenvalues of the graph
for
, where
are distinct primes and
. In this article, we find the signless Laplacian eigenvalues of the graphs
for different values of
n. In
Section 2, we recall several basic notions that are used to prove our main conclusions. In
Section 3, we look at the signless Laplacian eigenvalues of
, where
.
2. Preliminaries
We begin our discussions with the definition of a generalized join graph and some known results that are used to prove the main results.
Definition 1. Let be the vertex set of graph of order m and let be the order of the disjoint graphs , . The graphs formed the generalized join graph and whenever i and j are adjacent in G, joined each vertex of to every vertex of .
We write
x ![Axioms 12 00957 i001 Axioms 12 00957 i001]()
to denote that
x does not divide
n and
denotes the gcd of
x and
n. For a positive integer
n, the number of positive divisors of
n is given by
. An integer
x divides
n for
if and only if
x is a proper divisor of
n. Euler’s
. The
of
n is
, where
are positive integers and
are distinct primes.
Let the proper divisors of
n be
. For
, consider the sets
Moreover, we see that
, when
. This implies that the sets
are pairwise disjoints and partition the vertex set of
as
The next lemma shows the cardinality of .
Lemma 1 ([
6], Proposition 2.1)
. Let be the divisor of n. Then, , . Lemma 2 ([
2], Lemma 3.3)
. Let , where . Then, in if and only if ![Axioms 12 00957 i001 Axioms 12 00957 i001]() and
and ![Axioms 12 00957 i001 Axioms 12 00957 i001]() .
. Let
be the distinct proper divisors of
n and let
be the simple graph with vertex set
. Two distinct vertices
and
of graph
are adjacent if and only if
![Axioms 12 00957 i001 Axioms 12 00957 i001]()
and
![Axioms 12 00957 i001 Axioms 12 00957 i001]()
. If
is a prime decomposition of
n, then the order of graph
is given by
Lemma 3 ([
2], Corollary 3.4)
. Let be the proper divisor of the positive integer n. Then, the following holds:- (i)
For , the induced subgraph of on the vertex set is isomorphic to .
- (ii)
For with , a vertex of is adjacent to either all or none of the vertices of in .
The above lemma shows that the induced subgraph of is an empty graph. The next lemma says that is a generalized join of complements of complete graphs.
Lemma 4 ([
2], Lemma 3.6)
. Let be the induced subgraph of on the vertex set for . Then, . The following result gives the signless Laplacian spectrum of the generalized join graph.
Theorem 1 ([
9], Theorem 2.1)
. Let K be a graph with and ’s be -regular graphs of order with signless Laplacian eigenvalues , where . If , then the signless Laplacian spectrum of G can be computed as follows:whereandThe number and the matrix are only dependent on the graph K. Let
W be a weighted graph by assigning
to the vertex
of graph
W and let
s vary from 1 to
n. Consider the matrix
, where
The vertex-weighted signless Laplacian matrix of
W is
. It can be seen that the matrices
and
are similar, and hence
.
3. Main Results
In the result section, we shall prove the main results of this paper. Let
be the proper divisors of
n. For
, we assign the weight
to the vertex
of the graph
. Define the integer
Then, the vertex-weighted signless Laplacian matrix
of
is given by
Our main result gives the signless Laplacian spectrum of the cozero-divisor graph of
.
Theorem 2. Let the proper divisors of n be . Then, the signless Laplacian spectrum of can be calculated aswhere are regular graphs and represents that is added to each element of the multiset . Proof. In view of Lemma 4, we have
Thus, by using the relation
and consequence of Theorem 1, the result holds. □
By Lemma 3, is isomorphic to for . Thus, by Theorem 2, signless Laplacian eigenvalues of exists, out of which are known. The remaining k signless Laplacian eigenvalues of are the roots of the characteristic polynomial of the matrix given in (2).
Proposition 1. The signless Laplacian spectrum of , where and are distinct primes, is given by Proof. Let
, where
and
are distinct primes. Here, we see that
and
are the proper divisors of
n. So,
and by Lemma 4, we have
In view of Lemma 3, we have
Moreover,
and
. So, by the consequence of Theorem 2, the signless Laplacian spectrum of
is given by
Now, from (2), the matrix
is given by
which has characteristic polynomial
and eigenvalues 0 and
. □
Proposition 2. The signless Laplacian spectrum of , where are distinct primes, consists of the eigenvaluesThe other signless Laplacian eigenvalues of are the roots of the characteristic polynomial of the matrix (3). Proof. Let
, where
and
are distinct primes. The proper divisors of
m are
, and
. So,
and by Lemma 4, we have
In view of result Lemma 3, we have
Moreover, the values of
are as follows
In view of Theorem 2, the signless Laplacian spectrum of
is given by
Now, from (2), the matrix
is given by
□
Example 1. The signless Laplacian spectrum of the cozero-divisor graph consists of the eigenvalues Proof. In this example we find the signless Laplacian spectrum of the cozero-divisor graph of
. Here
is of the form
i.e.,
and
. So, by Proposition 2 we can easily verify the spectrum of the cozero-divisor graph of
. On the other hand, the approximate eigenvalues
are calculated from the matrix (
4), as follows
□
Now, we calculate the signless Laplacian eigenvalues of , which are the second main results of this paper.
Theorem 3. The signless Laplacian spectrum of , where are distinct primes and m is a positive integer, consists of the eigenvalues The roots of the characteristic polynomial of the matrix (5) are the other signless Laplacian eigenvalues of . Proof. Let , where are distinct primes and m is a positive integer. The proper divisors of n are
We have the following adjacency relations by the definition of
,
By using Lemma 4, we have
By applying Lemma 3, we can write as
It also follows that
By the consequence of Theorem 2, the signless Laplacian spectrum of
is given by
The roots of the characteristic polynomial of the matrix
given in (5) are the remaining
signless Laplacian eigenvalues of
□
For distinct primes and , our last result gives the signless Laplacian spectrum of , where
Theorem 4. The signless Laplacian spectrum of for distinct primes and are positive integers consisting of eigenvalueswith multiplicitiesrespectively, and the zeros of the characteristic polynomial of the matrix given in (2) are the signless Laplacian eigenvalues of . Proof. Let
, where
and
are distinct primes. The proper divisor of
n are
. We have the following adjacency relations by the definition of
,
Apply Lemma 4, we have
In view of Lemmas 1 and 3 we obtain
Moreover, the values of
are as follows
Thus, by Theorem 2, the signless Laplacian spectrum of
is given by
The remaining
eigenvalues are the roots of the characteristic polynomial of the matrix
given in (2). □
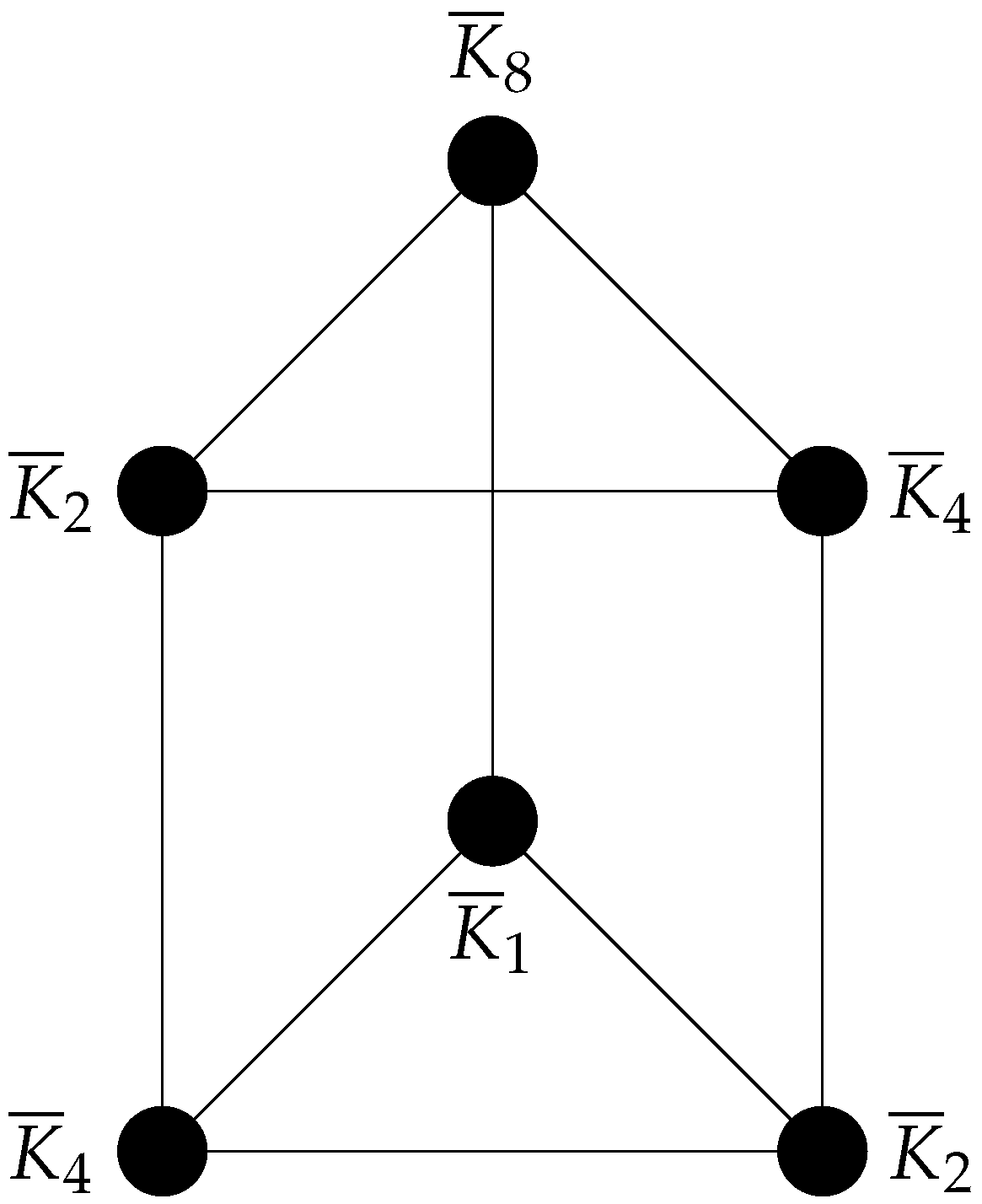
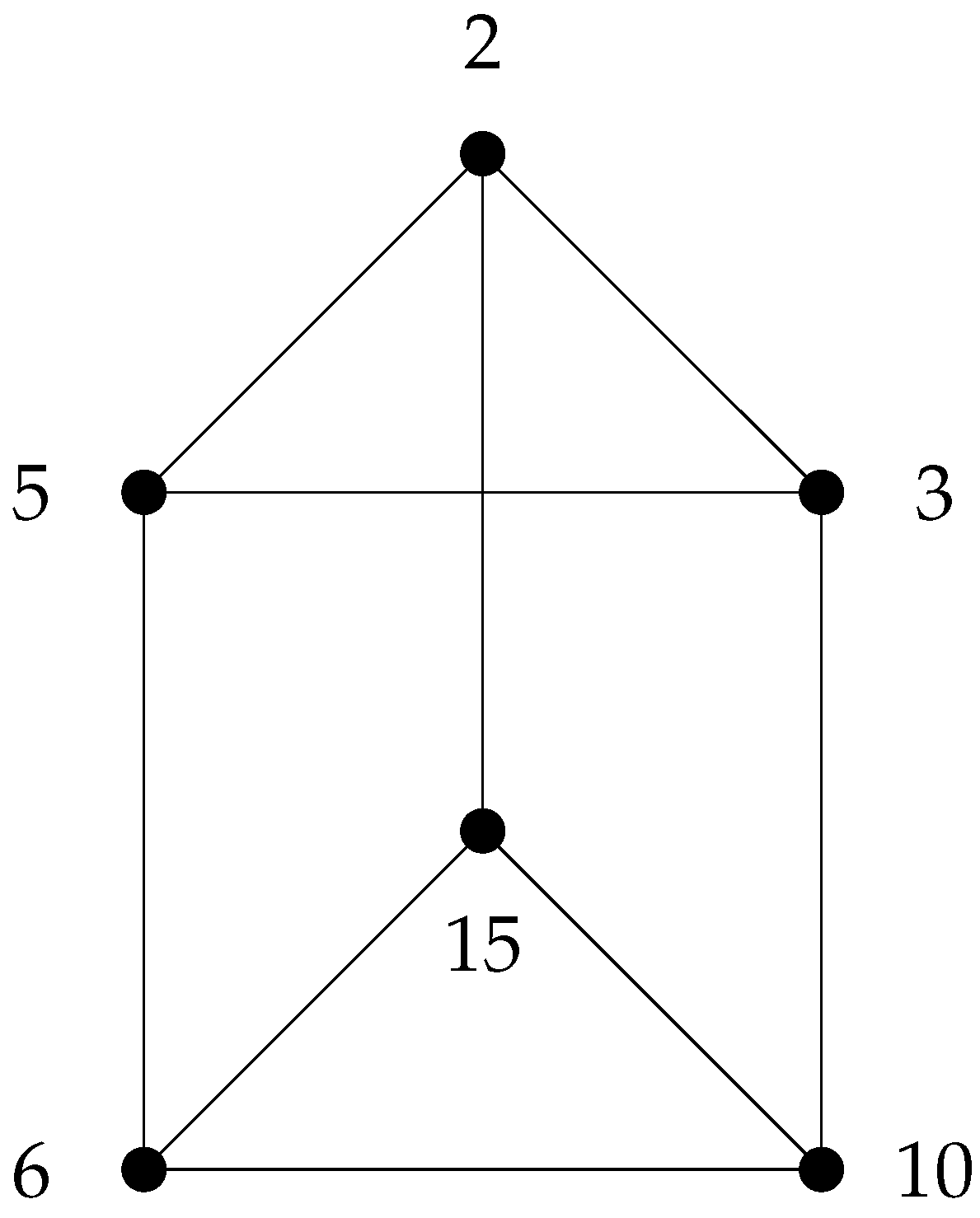
Example 2. The signless Laplacian spectrum of the cozero-divisor graph of shown in Figure 1 is Proof. Let
. The proper divisors of 30 are
, and
,
,
Now, increasing the divisor sequence to order the vertices and using Lemma 4,
where the simple graph
is shown in
Figure 2. Using Lemma 3, we have
The values of
are given by
Thus, by Theorem 2 the signless Laplacian spectrum of
consists of eigenvalues
together with the eigenvalues of the matrix
given below
The characteristic polynomial of matrix
is given by
or
and approximated eigenvalues of matrix
given in (6) are
The nodes of the graph of the cozero-divisor graph
shown in
Figure 1 are the complement of the complete graph, i.e., a node in
Figure 1 itself an empty graph, whereas the nodes of the graph of the proper divisor graph
shown in
Figure 2 are simply the proper divisors of 30. □
4. Conclusions and Further Work
The characteristic polynomial in
of degree
n, where
n is the number of atoms, finds its uses in quantum chemistry, the topological theory of aromaticity, counts of random walks, structure-resonance theory, and eigenvector–eigenvalue problems (for more details see [
10] and references therein). Our result gives the signless Laplacain spectrum of the cozero-divisor graph of integer modulo
n for different values of
n by using the generalize join graph of induced subgraphs. One may generalized these results and find the signless Laplacian spectrum when
for positive integers
, and
P and
, where
p,
q,
r are distinct primes.
Author Contributions
All authors made equal contribution. All authors have read and agreed to the published version of the manuscript.
Funding
Princess Nourah bint Abdulrahman University researchers supporting project No. PNURSP2023R231, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Data Availability Statement
Data sharing is not applicable as no datasets were generated or analyzed during the current study.
Acknowledgments
The authors are thankful to the anonymous referees for their valuable comments and suggestions which have improved the manuscript immensely. Moreover, fourth author is supported by DST-SERB MATRICS project file number: MTR/2022/000153.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Afkhami, M.; Khashyarmanesh, K. The cozero-divisor graph of a commutative ring. Southeast Asian Bull. Math. 2011, 35, 753–762. [Google Scholar] [CrossRef]
- Mathil, P.; Baloda, B.; Kumar, J. On the cozero-divisor graphs associated to rings. AKCE Int. J. Graphs Comb. 2022, 19, 238–248. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Patra, K.L.; Sahoo, B.K. Laplacian eigenvalues of the zero-divisor graph of the ring . Linear Algebra Appl. 2020, 584, 267–286. [Google Scholar] [CrossRef]
- Pirzada, S.; Rather, B.A.; Shaban, R.U.; Merajuddin, S. On signless Laplacian spectrum of zero divisor graphs of the ring . Korean J. Math. 2021, 29, 13–24. [Google Scholar] [CrossRef]
- Rather, B.A.; Pirzada, S.; Naikoo, T.A.; Shang, Y. On Laplacian eigenvalues of the zero-divisor graph associated to the ring of integers modulo n. Mathematics 2021, 9, 482. [Google Scholar] [CrossRef]
- Young, M. Adjacency matrices of zero divisor graphs of integer modulo n. Involve 2015, 8, 753–761. [Google Scholar] [CrossRef]
- Afkhami, M.; Khashyarmanesh, K. On the cozero-divisor graphs of commutative rings and their complements. Bull. Malays. Math. Sci. Soc. 2012, 35, 935–944. [Google Scholar]
- Akbari, S.; Alizadeh, F.; Khojasteh, S. Some results on cozero-divisor graph of a commutative ring. J. Algebra Appl. 2014, 13, 1350113. [Google Scholar] [CrossRef]
- Wu, B.F.; Lou, Y.Y.; He, C.X. Signless Laplacian and normalized Laplacian on the H-join operation of graphs. Discrete Math. Algorithms Appl. 2014, 6, 1450046. [Google Scholar] [CrossRef]
- Joita, D.M.; Jäntschi, L. Extending the characteristic Polynomial for characterization of C20 Fullerene Congeners. Mathematics 2017, 5, 84. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
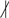 to denote that x does not divide n and denotes the gcd of x and n. For a positive integer n, the number of positive divisors of n is given by . An integer x divides n for if and only if x is a proper divisor of n. Euler’s . The of n is , where are positive integers and are distinct primes.
to denote that x does not divide n and denotes the gcd of x and n. For a positive integer n, the number of positive divisors of n is given by . An integer x divides n for if and only if x is a proper divisor of n. Euler’s . The of n is , where are positive integers and are distinct primes.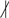 and
and  .
. and
and  . If is a prime decomposition of n, then the order of graph is given by
. If is a prime decomposition of n, then the order of graph is given by