1. Introduction
A harmonic wave propagating in the acoustic medium causes several remarkable effects. The periodic acoustic pressure and constant component of sound radiation are among them. The latter one is usually referred to as acoustic radiation pressure and is averaged over the incident wave period and over the surface of an object placed in the medium results in the acoustic radiation force (ARF) (see, for example [
1,
2,
3]). From a mechanical point of view, the ARF is generated if an average impulse transferred by the wave over the correspondent period of oscillation varies in some volume of medium due to the presence of a foreign body located there.
The phenomenon mentioned is of great interest for technological applications either already developed or potentially valuable. This has resulted in a large number of studies in the field (see, for instance [
3,
4,
5]). It is worth mentioning here that the researchers applied several techniques to estimate the ARF. The range of methods comprise the exact analytical solution and its approximations (see, for instance [
3,
6,
7]) as well as a vast variety of numerical simulations (see [
8,
9,
10]).
Various aspects of the ARF phenomenon were addressed in the scientific works over the decades: type of wave, properties of bearing medium, geometry and properties of submerged body, and the boundedness of the region filled with the acoustic medium, to name a few. For instance, generation of the acoustic radiation force by the plane traveling wave, plane standing wave, double orthogonal standing waves, acoustic beams with arbitrary wavefronts, and Bessel helicoidal beam were studied in several publications [
5,
7,
9,
10,
11]. Due to practical applications, the ideal and viscous fluids were usually considered as the acoustic bearing medium [
4,
5]. Obviously, the complex geometry of the submerged body (solid, liquid, or gaseous), complicated functions describing viscous properties, effects of acoustic streaming, etc., demand the application of sophisticated numerical techniques to attack the problem (see [
8,
9,
10,
12] for details). Nevertheless, usage of analytical approaches has significant advantage when investigating cylindrical and spherical bodies located in the infinite medium and has proved to be applicable to study ARF even for the bodies placed in the vicinity of a flat wall or free boundary [
6].
As well as being of theoretical interest, the effect of the acoustic radiation force acting upon the body in the acoustic field finds its industrially valuable application in various technologies [
1,
2,
13]. Remote manipulation and control (or suspension) of the rigid particle, drop of liquid, or bubble of gas placed in the acoustic medium, non-crucible glass fusing, multi-components casting, preserving the cloud of the object at the targeted location and acoustic levitation, facilitation of coagulation and degassing processes of the liquids, ultrasonic cleaning, as well as crystal growing, etc., are among both well-established and prospective fields of ARF application [
13].
Another level of complexity for the problem under consideration is introduced by the oscillatory and wave processes that occur in the liquid containing foreign solid, liquid, or gaseous inclusions [
14,
15]. The interactions of particles, drops of liquid, and gas bubbles in the acoustic field, acoustic levitation, numerous cavitation effects in fuel pipelines and various propulsion systems, as well as bubble generation in a liquid by fast moving solids, are among them. The special significance of the ARF study is obvious for the medicine industry and health care. Being injected into the circulatory system of the living organisms, the microscopic solid particles, liquid drops, or gaseous bubbles provide great opportunities for morphology investigation and for visualization of a variety of processes in the organs. This approach can also be used for drug delivery applications to ensure the prescribed drug doses with specific localization at the targeted organ [
16].
As mentioned above, the ARF affecting an object submerged in a liquid is determined as a time-averaged value of the acoustic pressure over the object surface. Thus, the Lagrange reference frame is more suitable to derive the problem statement for this case. To apply this approach, the acoustic pressure in the vicinity of the object considered has to be calculated with accuracy up to the second order of magnitude. It means the deviation of the acoustic pressure from the harmonic law has to be accounted for in the region around the object [
1,
2,
3]. It is obvious that the linear approximation of the pressure results in the zero value of the ARF. It is caused by the fact the pressure is a periodic function of time, and being averaged over the wave period yields zero. For details, see [
17], for example. Therefore, the second order terms have to be preserved in the wave equation to provide a reliable estimation of the ARF. In other words, the second order approximation has to be used. Fortunately, as was shown by L.V.King in his pioneering work [
3], to address the issue, the velocity field potential derived as the solution of a linear problem of an incident wave scattering on an object placed in an acoustic medium can be made use of. The remarkable result of [
3] allows one to evaluate the acoustic pressure with accuracy to the quadratic terms, providing that the velocity field potential obtained from a linear diffraction problem is used in the present paper as well.
The acoustic radiation force can be used as a quantity to estimate the level of interaction between the wave and the object placed in the acoustic field. As mentioned above, to characterize this interaction qualitatively, the sound pressure averaged over the field oscillation period and over the object surface has to be evaluated. Theoretical examination of the ARF effect on the system of solid particles, liquid drops, or gaseous bubble is a complicated problem [
18,
19]. It is necessary to account for a set of instances to attack it properly: the shape of the object, its nature (solid, liquid, or gaseous), its size with regard to the wave length, the properties of a bearing liquid (or gaseous) medium, wave scattering on the other particles, and their mutual effect (if system of solids, drops, or bubbles are under investigation), etc. Some of these aspects were already addressed in the publications devoted to the estimation on ARF for a case of solitary rigid, liquid, or gaseous particles located in an infinite liquid space or in the vicinity of the plane boundary of a liquid (see papers [
5,
6,
16]).
In the present paper, the case of two spherical liquid drops placed in an ideal compressible liquid is under investigation. The plane acoustic wave propagates along the line passing through the centers of the spherical drops. The purpose of the work is to study the interaction regularities between liquid spherical particles and to estimate the ARF induced by the acoustic wave irradiation of the system of the drops. The technique of the problem solution is elaborated. It comprises two basic steps according to the version of approach developed in the paper by Guz and Zhuk [
5]. At the first step, solution to the problem of the incident wave scattering on the system of two liquid particles (drops) is addressed. Once the problem is solved and the velocity field potential is derived, the main features of the two-drop system and acoustic wave can be studied. At the second step, the hydrodynamic forces experienced by each of the particles are calculated. Then, the ARFs are obtained by the time-averaging over the period of the primary wave oscillation. The results of the ARF case studies for the variety of liquid media and spheres’ liquid properties, as well as for different geometrical parameters of the system are presented. Conclusions on the main regularities for ARF affecting both liquid spherical particles are drawn.
2. The Problem of the Velocity Potential Determination
To clarify the problem statement even further, it is worth mentioning here that the velocity of the translational movement of each spherical particle is supposed to be negligibly small in comparison to the velocity of the incident acoustic wave. Therefore, the particle displacement is considered to be quite small. In fact, the solution of the problem is derived from a system of two immobile suspended liquid spherical drops in the present paper (see
Figure 1). Accounting for the translational motion of the target results in the non-linear problem formulation and essentially complicates the solution procedure. The linear problem formulation chosen provides a relatively straightforward way to derive the exact analytical solution for the velocity potential determination while accounting for the incident wave scattering on the spheres. As such, the boundary conditions on both spherical surfaces are satisfied exactly.
The linear approximation problem statement for the first step mentioned above, i.e., the problem of determination of the fluid velocity potential field in a tube is described below. The procedure adopted for this aim corresponds to the approach developed in other papers [
5,
15]. It is assumed that an ideal compressible fluid of density
fills the outer space continuously. The velocity of the plane sound wave propagating in the liquid is
. Two spherical drops of another ideal liquid are placed in the medium. The distance between the drops’ centers is denoted with
. Furthermore, the number 1 is always assigned to the sphere which is placed first on the way of propagating acoustic wave, while number 2 is assigned to the second drop in a row (see
Figure 1). Let us denote the density of the liquid of the first and second drop as
and
, respectively. Notations
and
are used for the speed of sound in the liquid of the first and second drops, respectively, while
and
are the drop radii, respectively. The main coordinate system is chosen to be the rectangular Cartesian coordinate system
with the origin located in the middle between the drop centers. Two other Cartesian rectangular
and spherical
,
coordinate systems attached to the spherical drops are introduced in such a manner that their origins
coincide with the drop centers and the axis
runs along the line that passing through the sphere centers (see
Figure 1). Let us apply the model of compressible barotropic liquid to describe the response of both the liquid medium and the drops. Conditions of a potential flow are assumed to be valid to determine the medium’s effect on the drops.
In this configuration, the steady wave process is under consideration. The incident plane harmonic wave propagating in a positive direction of the
axis is governed by a potential
. Let us denote the potentials of the waves scattered on the spherical drops as
. The general potential of the velocity field
is, therefore, the combination of the abovementioned potentials. Then, the pressure
in the bearing liquid (medium) can be determined by making use of the potential
, with accuracy up to the squares of the Mach number according to the following formula [
3,
5]:
where potential
is the solution of the following wave equation:
Then, determination of the ARF acting upon the target in the liquid is reduced to the time-averaging of the hydrodynamic force, as follows:
where
is a vector of a unit normal to the external surface
of the target.
The linearity of the Equation (2) allows one to apply the superposition principle for the determination of the velocity field in the case of the system of objects placed in the liquid and, therefore, to determine the solution to the problem of the interaction of the bodies.
Let the incident wave potential (the solution of the Equation (2)) be as follows:
where
is the amplitude;
is the wave number;
is the angular frequency;
is the time. An incident wave with potential
propagates along the positive direction of the
axis.
As mentioned above, the wave field in the bearing liquid (medium) is formed by the interference of the incident wave (4) and waves scattered on the spherical drops, as follows:
Furthermore, index (either subscript or superscript) is used to denote the quantity related to the drop with number .
From the mathematical point of view, determination of the potentials (5) of the stationary wave field in a liquid is reduced to the solution of a linear problem of incident wave (4) scattering on the liquid spherical drops over the multiply connected region, i.e., the problem is reduced to finding solution to the linear differential Equation (2) that meets the boundary conditions on the surfaces of spherical drops.
The boundary conditions demand continuity of the radial components of velocity in the outer and internal liquids on the drop surfaces, as well as continuity of pressure through the surfaces. They can be written in the following form:
Let us emphasize here that potentials of the waves scattered on the spherical drops have to meet the Sommerfeld radiation condition for infinitely distant points. Furthermore, the drop surface tension is not taken into account in boundary condition formulations. It is also assumed the amplitude of the drop surface oscillations is small enough to consider the drop radius to be constant. In Equation (6), the bar over a symbol denotes the quantities characterizing the state of the liquid inside the corresponding drop.
3. Wave Field Potential Construction: Determination of the Acoustic Pressure
As mentioned above, the ARF affecting an object submerged in a liquid is determined as a time-averaged value of the acoustic pressure over the object surface. Thus, the Lagrange reference frame is more suitable to derive the problem statement for this case. To apply this approach, the acoustic pressure in the vicinity of the object considered has to be calculated with accuracy up to the second order of magnitude. It means that the deviation of the acoustic pressure from the harmonic law has to be accounted for in the region around the object [
1,
2,
3]. Let us emphasize once again that a linear approximation of the radiation pressure in the vicinity of the object yields zero ARF, which contradicts the experimental data. Therefore, preservation of the quadratic terms in the wave equation is needed to avoid occurrence of the zero ARFs. Evaluating the acoustic pressure with accuracy to the quadratic terms, thus, providing the velocity field potential, is achieved by using a linear diffraction problem in the present paper.
To construct the solution to the problem (2), let us apply the variable separation method with respect to the local spherical coordinate systems associated with the corresponding drop. The potential of the incident wave (1) with respect to the spherical coordinate system
,
is as follows:
where
are the spherical Bessel functions of the first kind, and
are the orthonormalized Legendre polynomials.
The potential of the wave scattered on the
th drop,
, (i.e., the solution of Equation (2) satisfying the radiation condition for infinitely distant points) is represented by the generalized Fourier series expansion over the spherical wave functions, as follows:
where
is the spherical Hankel function of the first kind.
The potential
,
, of the wave field in the liquid inside the corresponding spherical drop (which is solution of Equation (2) that meet the boundedness condition) can be written as follows:
To find the expansion coefficients
and
,
, in expressions (8) and (9), the boundary conditions (6) on the spherical surfaces are used. Therefore, the potential (5) of the acoustic field in the outer liquid should be rewritten with respect to each local spherical coordinate system. The addition theorems for spherical wave functions have to be implemented to realize it. As a result, the following expression can be derived:
where multiplier
is omitted.
The following notations are used in (10):
Here are spherical coordinates of the pole located at the sphere center with respect to th local spherical coordinate system, i.e., they are coordinates of the center (pole) with respect to the center (pole) and vice versa. Thus, the relations are true for the particular geometry under consideration.
At the first stage of the ARF determination (i.e., to solve the linear problem of the incident wave scattering on the spherical drops), the following formulae are used to calculate the pressure and disturbance of liquid inside the drops:
Making use of the boundary conditions on the drop surfaces and taking into account the expressions for the potentials (9), (10), along with the formulae for pressure and velocity of liquid, yields an infinite system of algebraic equations with respect to the unknown coefficients
and
,
of the generalized Fourier series expansions for the potentials
and
, as follows:
Let us emphasize there is no need to use the bar over symbols and in (12).
The infinite system of algebraic Equation (12) has a unique solution , that can be found by the truncation method. Calculation of the coefficients and , of truncated system (12) of the algebraic equations formally completes the procedure of determination of the velocity field potentials for both the outer liquid and the liquids inside the drops. The accuracy needed is achieved by the comparison of calculation results for a consecutively growing number of equations.
4. Determination of the Acoustic Radiation Forces Acting upon Liquid Drops
The acoustic radiation force affecting two spherical drop submerged in a liquid is equal to the hydrodynamic force acting on each spherical particle averaged over the period of an incident wave and is, in fact, the constant component of this force. In the system configuration under study, the hydrodynamic forces acting on each drop are directed along the
axis because the liquid velocity field is symmetrical with respect to this axis. This force can be calculated as an integral of the pressure
over the correspondent drop surface [
20], as follows:
where pressure
is calculated by making use of Expression (1) where the real part of the complex potential (10) has to be used. As a result, the formula can be derived as follows:
Here, the following notations are used:
For the sake of brevity, the symbol denoting the real part of the potential will be omitted.
The contribution of the first term in the righthand side of Expression (1) is zero because it varies sinusoidally over time [
5,
6]. This term will, therefore, not be taken into consideration for ARF calculation any further. Finally, taking account of the reasoning concerning Equation (1), as mentioned, the expression for the pressure
takes the following form:
Let us emphasize here that the pressure is calculated on the surface of the spherical drop (i.e., ).
Let us determine the contribution to the hydrodynamic force (13) (and, therefore, to ARF) of each additive from Formula (15) for the pressure.
The contribution of the first term to the force
,
is governed by an integral, as follows:
Taking into account (14) and the following condition:
where
, integration of (16) yields the expression for the contribution of the first term from (15) to the total value of the hydrodynamic force
, as follows:
The terms resulting in nonzero values being averaged over the period are preserved in Expression (18) only. Time-averaging of (18) over the period of the incident wave yields the contribution of the first term from the expression for pressure (15) to the total value of the acoustic radiation force, as follows:
The contribution of second term from (15) is governed by an integral, as follows:
Making use of Expression (14) and Condition (17), the integration of (20) yields the following formula for the estimation of the second term contribution to the force
:
In Formula (21), the derivatives are taken with respect to
at
. The terms resulting in zero values being averaged over the period are not taken into account in (21). Time-averaging of (21) over the period of the incident wave yields the contribution of the second term from the expression for pressure (15) to the total value of the ARF, as follows:
The contribution of the third term from (15) is, in turn, determined by an integral, as follows:
Taking account for (14) and the following condition:
integration of (23) yields the expression for the contribution of the third term from (15) to the total value of the hydrodynamic force
, as follows:
The terms resulting in zero values being averaged over the period are not taken into account in (24). Time-averaging of (21) over the period of the incident wave yields the contribution of the third term from the expression for pressure (15) to the total value of the ARF, as follows:
Summation of the expressions (19), (22), and (25) gives the final formula for the acoustic radiation force affecting each of the two spherical liquid drops placed in the outer liquid (bearing acoustic medium), provided that the acoustic wave propagates along the line passing through the centers of the drops, as follows:
The formulae obtained through the mathematical manipulations above show that the expressions for the ARF are of the same form as the ones derived in [
20]. Nevertheless, let us emphasize here that the expressions are similar only in appearance. In fact, they predict absolutely different responses of the system depending on the nature of acoustic medium, constituents, and the region under investigation.
5. Numerical Results of ARF Calculation and Discussion
As an example of the developed theory application, investigation of the acoustic radiation force influencing a system consisting of the two liquid spherical drops placed in the liquid medium in the acoustic field is carried out. Calculations are performed numerically, making use of Equation (15) for pressure and (26) for the ARF itself. It is worth mentioning here that ARF is of primary interest due to the technological applications mentioned in the Introduction section. With this idea in mind, several types of bearing outer liquid (liquid medium) and liquids filling the drops were considered. The parameters of the incident sound wave were chosen to correspond to moderate radiated power. Dimensionless amplitude in Expression (4) is chosen to be equal to 0.918 × 10–4 for the case under consideration.
The calculation algorithm is organized as a two-stage procedure. At the first stage, the determination of the velocity field potential according to Expression (5) is carried out. For this aim, calculation of the coefficients and , , from the truncated system of the algebraic Equation (12) with account of the Expression (10), is carried out with the preset accuracy of 10–6, which is secured by comparison of the evaluation results for the sequentially increasing number of the equations in the truncated system. As soon as the and are found, the absolute value of the linear hydrodynamic acoustic pressure is calculated with making use of the expressions (8), (9), and (10).
In the second stage, the ARF itself is calculated, making use of (26).
As mentioned in the Introduction, estimation of the ARF is of interest for the technological applications listed above. The approach proposed and expressions derived allow one to characterize the ARF without direct determination of the acoustic pressure field, which is not of primary interest in the present paper.
In the present study, water is considered as a bearing liquid (liquid medium) for the system of two drops. The following characteristics of the water are used: sound velocity is 1500 m/sand density is 1000 kg/m3. The properties of the drop liquids and geometrical parameters of the system will be individually indicated for each particular case.
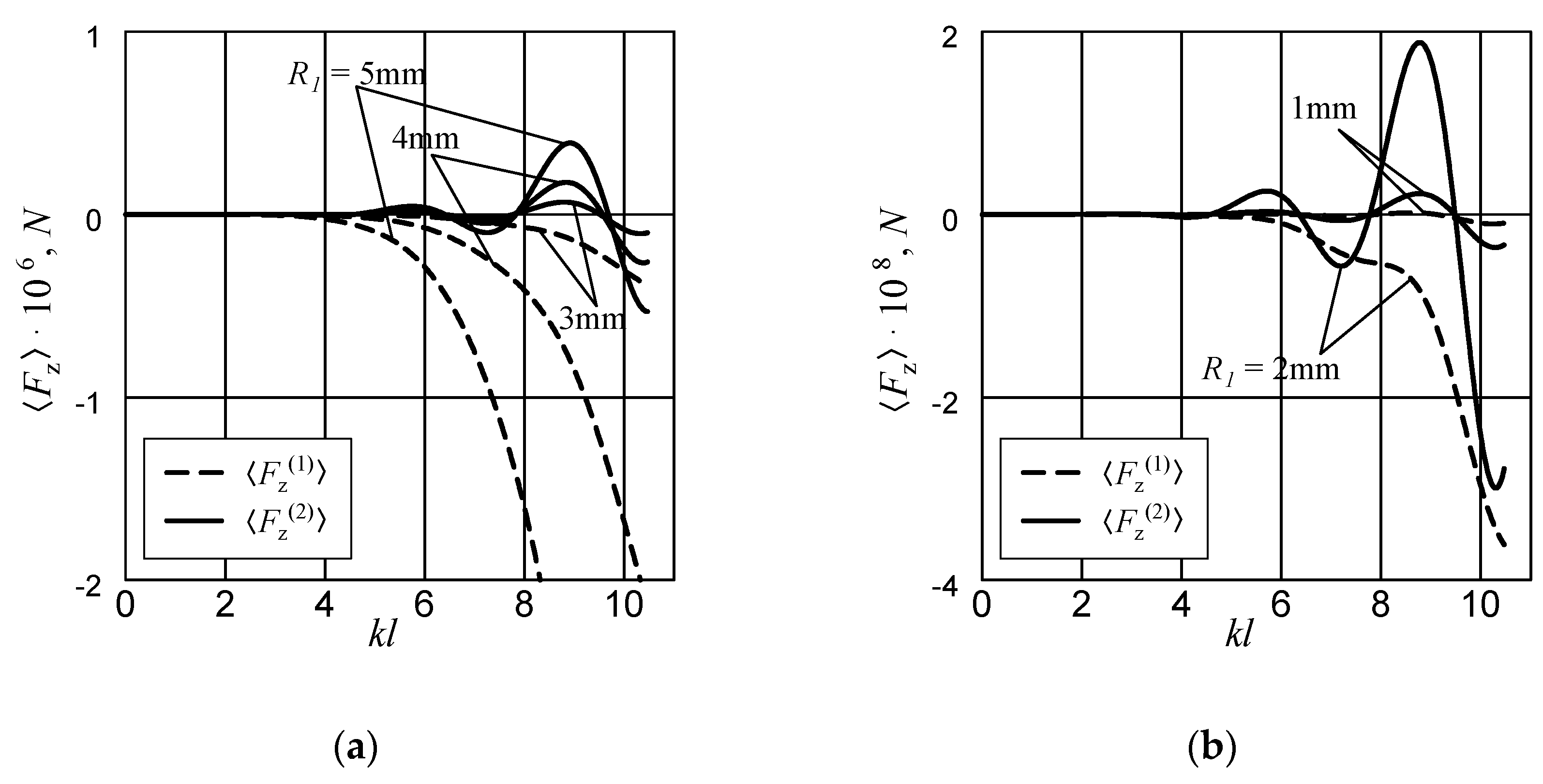
To study the influence of the drop radii on the ARF behavior, dependencies of the ARF on the incident wave frequency are shown in
Figure 2 for two carbon tetrachloride drops placed in water on the distance
50 mm between drop centers. The sound velocity and density of the carbon tetrachloride are chosen to be equal to
926 m/s and
1594 kg/m
3, respectively. The radius of the first drop,
, is always equal to 5 mm, while the radius of the second drop,
, varies in
Figure 2 (values are shown at the corresponding curve). The ARF acting upon the first drop,
, is shown with dashed line, while the same quantity for the second drop,
, is depicted with a solid line elsewhere in the paper. Let us reiterate here that we agreed that the acoustic wave propagates in the direction from the first drop to the second one.
Figure 2a shows that ARF acting upon the first drop is independent of the radius of the second drop (the dashed lines coincide to the drawing accuracy). It always remains negative for the case studies within the radius range of interest. This means that the direction of
is always opposite to the direction of incident wave propagation. Therefore, ARF causes the start of drop motion towards the direction of sound wave propagation. These results corresponds to the data obtained in [
5,
20].
The values and direction of
vary depending on the incident wave frequency. Details are shown by the solid lines in
Figure 2b. Here again, the radii of the second drop are written at the corresponding lines. It is obvious there are frequency intervals where the direction of the
is opposite to the
leading to the divergence of drops (they drift out of each other). In the other intervals where the directions are the same, the drops start to drift unidirectionally.
Figure 2 illustrates one more remarkable situation. There are frequency values at which the ARF acting upon the second drop is equal to zero, meaning that it remains immobile.
In contrast to
Figure 2, where
,
Figure 3 contains curves that illustrate the same dependencies but for the system where the second drop radius is larger than the one of the first drop, i.e.,
. The behavior of the curves for the ARF acting upon the first drop,
, is quite different from the one depicted in
Figure 2.
The value of this ARF decreases as the drop radius becomes smaller. It can be explained by the general reduction in the drop surface and, therefore, integration over the smaller surface leads to the lower ARF value. Nevertheless
remains negative for all values of geometrical parameters and frequencies investigated. The behavior of the acoustic radiation force acting upon the second drop,
, is qualitatively the same as in
Figure 2. Therefore, one can again control the drop’s movement by varying the frequency of the incident wave.
The next geometrical parameter that significantly influences the ARF response is the distance,
, between the drop centers. In
Figure 4, the dependencies of
and
on the
are shown for several different frequencies of the incident wave for the same system of two carbon tetrachloride drops of equal radii
5 mm placed in water. The wave frequency is written by the correspondent curve. Analysis of the figure evidently shows that the closer drops are located, the higher values of ARF observed. An increase in the distance
leads to a decrease in the interaction between drops.
The following features of the ARF behavior can be noted: at all frequencies investigated, the value of ARF acting upon the first drop remains negative, causing the start of the drop shift in the direction which is opposite to the direction of incident wave propagation (see
Figure 4a). The direction of the
varies depending on the distance between the drop centers. Once again, it can be directed either towards the first drop or away from it, and there are specific values of the frequency providing zero values of the
. This means that the second drop remains immobile and doesn0t start to move under the conditions mentioned.
Figure 5 illustrates the influence of the physical characteristics of the liquids involved (both the outer liquid medium and the liquid inside the drops) on the acoustic radiation forces. Here, typical results for the system under investigation are shown. The outer liquid is always water, while drops are considered to be ones of the same liquid (carbon tetrachloride, benzene, or mercury) possessing the range of densities and speeds of sound in them.
In
Figure 5a,
dependencies of the ARF on the incident wave frequency are shown for two drops
of carbon tetrachloride, benzene (
a = 1298
m/s and
870 kg/m
3), and mercury (
1450 m/s and
13593 kg/m
3). The drops are of the same radii, i.e.,
5 mm. The distance between centers is
30 mm. The liquid of the drops is labeled by the corresponding curve.
It can be seen that the density of the inner liquid affects ARF, acting on the first drop significantly. A denser liquid (mercury) causes changes even in the ARF direction. This corresponds to the case of a rigid particle placed in an ideal compressible liquid [
5]. The
force changes its sign in comparison to the cases of benzene and carbon tetrachloride as well. The ARF acting on the second drop is of variable direction depending on the incident wave frequency, as was mentioned for
Figure 2. The frequencies providing zero value
0 occurred as well.
The same tendency for more dense liquids is preserved for the ARF dependencies on the distance between drop centers presented in
Figure 5b for the same system as in
Figure 5a for incident wave frequency 40 kHz. The values of the ARF are of the opposite sign and are much higher than for the less dense liquids. In all the cases, the behavior is also influenced by the speed of sound in the liquid. The variations in the direction of the ARF acting upon the second drop are also observed.
6. Conclusions
The case of two immobile spherical liquid drops placed in an ideal compressible fluid in the field of an acoustic wave propagating along the line passing through the drop centers is under investigation. The approach to estimate the acoustic radiation force induced due to acoustic pressure imposed onto the drops and the interaction between them is elaborated.
The calculation algorithm is organized as a two-stage procedure. At the first stage, the determination of the velocity field potential is carried out. The problem is solved by the variable separation method. To satisfy the boundary conditions on spherical surfaces, the expansion of the incident and reflected wave potentials over the spherical wave functions are used. Required constants in the solution are calculated from an infinite system of algebraic equations, which is solved by a truncation method.
At the second stage, encompassing the determination of hydrodynamic forces acting on the liquid spheres with their subsequent averaging over the suitable time interval, the ARF itself is calculated making use of the expression derived.
The main regularities of the interaction between liquid spherical particles as well as ARF induced by the acoustic wave irradiation of the system of the drops are studied with the application of the proposed approach. It was found the behavior of the ARF depends significantly on the geometrical parameters of the system, properties of the liquids involved, and frequency of the incident wave. The possibility of controlling the drops’ movement by varying the frequency of the incident wave for a particular setup of the system is defined.