Kinematic Geometry of a Timelike Line Trajectory in Hyperbolic Locomotions

Abstract

This study utilizes the axodes invariants to derive novel hyperbolic proofs of the Euler–Savary and Disteli formulae. The inflection circle, which is widely recognized, is situated on the hyperbolic dual unit sphere, in accordance with the principles of the kinematic theory of spherical locomotions. Subsequently, a timelike line congruence is defined and its spatial equivalence is thoroughly studied. The formulated assertions degenerate into a quadratic form, which facilitates a comprehensive understanding of the geometric features of the inflection line congruence.

1. Introduction

Line geometry has an alliance with spatial locomotions and has thus found implementations in mechanism layout and robot kinematics. In locomotion, it is interested in inspecting the essential characteristics of the line path from the connotations of ruled surface. It is well known in spatial locomotions that the instantaneous screw axis $(\mathbb{ISA}$) of a movable body traces a couple of ruled surfaces, named the mobile and immobile axodes, with $\mathbb{ISA}$ as its tracing line in the movable space and in the steady space, respectively. Through locomotion, the axodes slide and roll relative to each other in a specific path such that the contact amidst the axodes is permanently maintained on the length of the two matting rulings (one being in all axodes), which define the $\mathbb{ISA}$ at any instant. It is essential that not only does an assured locomotion confer a rise to a unique set of axodes but the converse furthermore stratifies. This shows that, should the axodes of any locomotion be renowned, the evident locomotion can be reconstructed without knowledge of the physical features of the mechanism, their explications, given dimensions, or the manners by which they are united. There exists major literature on the topic including sundry monographs [1,2,3,4,5].

On the other hand, dual numbers have been employed to study the locomotion of a line space; and they may even serve as more effective tools for this purpose. According to the E. Study map in the theory of dual numbers, it may be concluded that there exists a bijection between the set of the dual points on dual unit sphere ($\mathcal{DUS}$) in the dual 3-space ${\mathbb{D}}^3$ and the set of all directed lines in Euclidean 3-space ${\mathbb{E}}^3$. By use of this map, a one-parameter set of points (a dual curve ) on $\mathcal{DUS}$ can be associated with a one-parameter set of directed lines (ruled surface) in ${\mathbb{E}}^3$ [6,7,8,9,10,11,12]. In the Minkowski three-space ${\mathbb{E}}_1^3$, since the Lorentzian metric can be positive, negative or zero. Conversely, in the Euclidean three-space ${\mathbb{E}}^3$, the metric is exclusively positive definite. Therefore, the kinematic and geometrical clarifications hold significant importance in ${\mathbb{E}}_1^3$ [13,14,15,16,17,18,19].

In this paper, we utilized the E. Study map for investigating the kinematic-geometry of a timelike ($\mathbb{T}-like$) line trajectory in one-parameter hyperbolic spatial locomotions. Then, we gained new dual versions of Euler–Savary formula ($\mathbb{ES}$), resulting in distinct statements that are based on the axode invariants. Lastly, we explored a theoretical narration of the infliction circle of planar locomotions.

2. Preliminaries

In this section, we list notations of dual Lorentzian vectors and E. Study map (See [13,14,15,16,17,18,19]): A non-null oriented line L in Minkowski 3-space ${\mathbb{E}}_1^3$ can be appointed by a point $\mathbf{q}\in L$ and a normalized vector $\mathbf{u}$ of L, that is, ${∥\mathbf{u}∥}^2=\pm 1$. To have coordinates for L, one must have the moment vector ${\mathbf{u}}^{*}=\mathbf{q}\times \mathbf{u}$ in ${\mathbb{E}}_1^3$. If $\mathbf{q}$ is reciprocal by any point $\mathbf{p}=\mathbf{q}+t\mathbf{u}$,$t\in \mathbb{R}$ on L, this offers that ${\mathbf{u}}^{*}$ is independent of $\mathbf{q}$ on L. The two non-null vectors $\mathbf{u}$ and ${\mathbf{u}}^{*}$ satisfy that

$$⟨\mathbf{u},\mathbf{u}⟩=\pm 1,⟨{\mathbf{u}}^{*},\mathbf{u}⟩=0.$$

(1)

The 6-component $u_i,u_i^{*}(i=1,2,3)$ of $\mathbf{u}$ and ${\mathbf{u}}^{*}$ are the normalized Plűcker coordinates of L [1,2,3,4].

A dual number $\widehat{u}$ is a number $u+\epsilon u^{*}$, where $(u,$$u^{*})\in \mathbb{R}\times \mathbb{R}$, $\epsilon$ is a dual unit with $\epsilon \ne 0$, and ${\epsilon }^2=0$. Thus, the set

$${\mathbb{D}}^3=\{\widehat{\mathbf{u}}:=\mathbf{u}+\epsilon {\mathbf{u}}^{*}=({\widehat{u}}_1,{\widehat{u}}_2,{\widehat{u}}_3)\},$$

(2)

with the Lorentzian scalar product

$$⟨\widehat{\mathbf{u}},\widehat{\mathbf{u}}⟩=-{\widehat{u}}_1^2+{\widehat{u}}_2^2+{\widehat{u}}_3^2,$$

(3)

explain dual Lorentzian three-space ${\mathbb{D}}_1^3$. Then, a point $\widehat{u}={({\widehat{u}}_1,{\widehat{u}}_2,{\widehat{u}}_3)}^t$ has dual coordinates ${\widehat{u}}_i=(u_i+\epsilon u_i^{*})\in \mathbb{D}$. If $\mathbf{u}\ne \mathbf{0}$, the norm $∥\widehat{\mathbf{u}}∥$ of $\widehat{\mathbf{u}}=\mathbf{u}+\epsilon {\mathbf{u}}^{*}$ is

$$∥\widehat{\mathbf{u}}∥=\sqrt{\left|⟨\widehat{\mathbf{u}},\widehat{\mathbf{u}}⟩\right|}=∥\mathbf{u}∥(1+\epsilon \frac{⟨\mathbf{u},{\mathbf{u}}^{*}⟩}{{∥\mathbf{u}∥}^2}).$$

(4)

So, if ${∥\widehat{\mathbf{u}}∥}^2=-1$ (${∥\widehat{\mathbf{u}}∥}^2=1$), the vector $\widehat{\mathbf{u}}$ is a $\mathbb{T}-like$ (spacelike ($\mathbb{S}-like$)) dual unit vector. Then,

$${∥\widehat{\mathbf{u}}∥}^2=\pm 1⟺{∥\mathbf{u}∥}^2=\pm 1,⟨\mathbf{u},{\mathbf{u}}^{*}⟩=0.$$

(5)

The dual hyperbolic, and Lorentzian (de Sitter space) unit spheres with the center $\widehat{\mathbf{0}}$, respectively, are [13,14,15,16,17,18,19]:

$${\mathbb{H}}_{+}^2=\left\{\widehat{\mathbf{u}}\in {\mathbb{D}}_1^3\mid -{\widehat{u}}_1^2+{\widehat{u}}_2^2+{\widehat{u}}_3^2=-1\right\},$$

(6)

and

$${\mathbb{S}}_1^2=\left\{\widehat{\mathbf{u}}\in {\mathbb{D}}_1^3\mid -{\widehat{u}}_1^2+{\widehat{u}}_2^2+{\widehat{u}}_3^2=1\right\}.$$

(7)

Therefore, presented here is the map provided by E. Study: the ring-shaped hyperboloid may be bijectively mapped to the set of $\mathbb{S}-like$ lines. Similarly, the common asymptotic cone can be bijectively mapped to the set of null-lines. Lastly, the oval-shaped hyperboloid can be bijectively mapped to the set of $\mathbb{T}-like$ lines (see Figure 1). Then, a regular curve on ${\mathbb{H}}_{+}^2$ matches a $\mathbb{T}-like$ ruled surface in ${\mathbb{E}}_1^3$. Also, a regular curve on ${\mathbb{S}}_1^2$ matches a $\mathbb{S}-like$ or $\mathbb{T}-like$ ruled surface in ${\mathbb{E}}_1^3$ [13,14,15,16,17,18,19].

Figure 1. The dual hyperbolic and dual Lorentzian unit spheres.

Hyperbolic Dual Spherical Locomotions

Let us address that ${\mathbb{H}}_{+m}^2$ and ${\mathbb{H}}_{+f}^2$ are two hyperbolic $\mathcal{DUS}$ centered at the origin $\widehat{\mathbf{0}}$ in ${\mathbb{D}}_1^3$. Let $\left\{\widehat{\mathbf{u}}\right\}$ = {$\widehat{\mathbf{0}}$;${\widehat{\mathbf{u}}}_1$($\mathbb{T}-like$)$,{\widehat{\mathbf{u}}}_2,{\widehat{\mathbf{u}}}_3$}, and $\left\{\widehat{\mathsf{\zeta }}\right\}=\{\widehat{\mathbf{0}}$;${\widehat{\mathsf{\zeta }}}_1$($\mathbb{T}-like$),${\widehat{\mathsf{\zeta }}}_2$,${\widehat{\mathsf{\zeta }}}_3$} be two orthonormal dual frames of ${\mathbb{H}}_{+m}^2$ and ${\mathbb{H}}_{+f}^2$, respectively. If we say $\left\{\widehat{\mathsf{\zeta }}\right\}$ is stationary, whereas the elements of $\left\{\widehat{\mathbf{u}}\right\}$ are functions of a real parameter $t\in \mathbb{R}$ (say the time). Then, we say that ${\mathbb{H}}_{+m}^2$ moves on ${\mathbb{H}}_{+f}^2.$ This is a one-parameter Lorentzian dual spherical ($\mathcal{DS}$) locomotion and will signalize by ${\mathbb{H}}_{+m}^2/{\mathbb{H}}_{+f}^2$. Via the E. Study map, the hyperbolic $\mathcal{DUS}$ ${\mathbb{H}}_{+m}^2$ and ${\mathbb{H}}_{+f}^2$ matches the hyperbolic line spaces $\mathbb{L}$${}_m$(mobile) and $\mathbb{L}$${}_f$ (immobile), respectively. Therefore, ${\mathbb{L}}_m/{\mathbb{L}}_f$ is the mobile hyperbolic line space against the hyperbolic immobile space ${\mathbb{L}}_f$, because at any instant the instantaneous screw axis ($\mathbb{ISA}$) of ${\mathbb{L}}_m/{\mathbb{L}}_f$ creates a mobile $\mathbb{T}-like$ axode ${\pi }_m$ in ${\mathbb{L}}_m$, and immobile $\mathbb{T}-like$ axode ${\pi }_f$ in ${\mathbb{L}}_f$. Therefore, we insert an orthonormal dual frame $\left\{\widehat{\mathbf{r}}\right\}=\{\widehat{\mathbf{0}}$;${\widehat{\mathbf{r}}}_1$($\mathbb{T}-like$),${\widehat{\mathbf{r}}}_2$,${\widehat{\mathbf{r}}}_3$}, which is specified as follows: we set ${\widehat{\mathbf{r}}}_1\left(t\right)={\mathbf{r}}_1\left(t\right)+\epsilon {\mathbf{r}}_1^{*}\left(t\right)$, as the $\mathbb{ISA}$ and ${\widehat{\mathbf{r}}}_2\left(t\right):={\mathbf{r}}_2\left(t\right)+\epsilon {\mathbf{r}}_2^{*}\left(t\right)=\frac{d{\widehat{\mathbf{r}}}_1}{dt}{∥\frac{d{\widehat{\mathbf{r}}}_1}{dt}∥}^{-1}$ as the joint central normal of two disjoint screw axes. A third dual unit vector is designated as ${\widehat{\mathbf{r}}}_3\left(t\right)={\widehat{\mathbf{r}}}_1\times {\widehat{\mathbf{r}}}_2$. Then,

$$\left.\begin{array}{c}{\widehat{\mathbf{r}}}_1\times {\widehat{\mathbf{r}}}_2={\widehat{\mathbf{r}}}_3,{\widehat{\mathbf{r}}}_1\times {\widehat{\mathbf{r}}}_3=-{\widehat{\mathbf{r}}}_2,{\widehat{\mathbf{r}}}_2\times {\widehat{\mathbf{r}}}_3=-{\widehat{\mathbf{r}}}_1,\hfill \\ -⟨{\widehat{\mathbf{r}}}_1,{\widehat{\mathbf{r}}}_1⟩=⟨{\widehat{\mathbf{r}}}_2,{\widehat{\mathbf{r}}}_2⟩=⟨{\widehat{\mathbf{r}}}_3,{\widehat{\mathbf{r}}}_3⟩=1.\hfill \end{array}\right\}$$

(8)

The set $\left\{\widehat{\mathbf{r}}\right\}$ is the relative Blaschke frame, and ${\widehat{\mathbf{r}}}_1,$${\widehat{\mathbf{r}}}_2,$ and ${\widehat{\mathbf{r}}}_3$ are intersected at the joint striction (central) point $\mathbf{s}\left(t\right)$ of the $\mathbb{T}-like$ axodes ${\pi }_i$$(i=m,$$f)$. The dual arc length $d{\widehat{s}}_i=d{s}_i+\epsilon d{s}_i^{*}$ of ${\widehat{\mathbf{r}}}_1\left(t\right)$ is

$$d{\widehat{s}}_i=∥\frac{d{\widehat{\mathbf{r}}}_1}{dt}∥dt=\widehat{\sigma }\left(t\right)dt.$$

(9)

$\widehat{\sigma }\left(t\right)=\sigma \left(t\right)+\epsilon {\sigma }^{*}\left(t\right)$ is the first order asset of the locomotions ${\mathbb{H}}_{+m}^2/{\mathbb{H}}_{+f}^2$. We set $d\widehat{s}=ds+\epsilon d{s}^{*}$ to represent $d{\widehat{s}}_i$, since they are equal to each other. Then,

$$\mu \left(s\right):=\frac{{\sigma }^{*}}{\sigma }=\frac{d{s}^{*}}{ds},$$

(10)

is the distribution parameter ($\mathcal{D}-par$) of the $\mathbb{T}-like$ axodes. Via the E. Study map: for the locomotion the $\mathbb{T}-like$ axodes have the $\mathbb{ISA}$ in mutual; that is the mobile axode osculating with the immobile axode along the $\mathbb{ISA}$ in the first order (compared with [1,2,3]). For the Blaschke formulae with respect to ${\mathbb{H}}_{+i}^2(i=m,$$f)$, we find

$${\mathbb{H}}_{+r}^2/{\mathbb{H}}_{+i}^2:\left(\begin{array}{c}{\widehat{\mathbf{r}}}_1^{{}^{\prime }}\hfill \\ {\widehat{\mathbf{r}}}_2^{{}^{\prime }}\hfill \\ {\widehat{\mathbf{r}}}_3^{{}^{\prime }}\hfill \end{array}\right)={\widehat{\mathsf{\varrho }}}_i\times \left(\begin{array}{c}{\widehat{\mathbf{r}}}_1\hfill \\ {\widehat{\mathbf{r}}}_2\hfill \\ {\widehat{\mathbf{r}}}_3\hfill \end{array}\right),(\prime =\frac{d}{d\widehat{s}}).$$

(11)

where ${\widehat{\mathsf{\varrho }}}_i:={\mathsf{\varrho }}_i+\epsilon {\mathsf{\varrho }}_i^{*}={\widehat{\beta }}_i{\widehat{\mathbf{r}}}_1-{\widehat{\mathbf{r}}}_3$ is the Darboux vector, and

$${\widehat{\beta }}_i={\beta }_i+\epsilon ({\mathsf{\Omega }}_i+\lambda {\beta }_i)=det({\widehat{\mathbf{r}}}_1,{\widehat{\mathbf{r}}}_1^{{}^{\prime }},{\widehat{\mathbf{r}}}_1^{{}^{″}}),$$

(12)

is the radii of curvature of the $\mathbb{T}-like$ axodes ${\pi }_i$. ${\beta }_i\left(s\right)$, ${\mathsf{\Omega }}_i\left(s\right)$ and $\lambda \left(s\right)$ are the curvature (construction) functions of the $\mathbb{T}-like$ axodes. By setting $\left|{\widehat{\beta }}_i\right|<1$, the $\mathbb{S}-like$ Disteli-axes ($\mathbb{DA}$) of the $\mathbb{T}-like$ axodes is

$${\widehat{\mathbf{b}}}_i\left(\widehat{s}\right)=\frac{{\widehat{\mathsf{\varrho }}}_i}{∥{\widehat{\mathsf{\varrho }}}_i∥}=\frac{{\widehat{\beta }}_i{\widehat{\mathbf{r}}}_1-{\widehat{\mathbf{r}}}_3}{\sqrt{1-{\widehat{\beta }}_i^2}}=sinh{\widehat{\varphi }}_i{\widehat{\mathbf{r}}}_1-cosh\widehat{\varphi }{\widehat{\mathbf{r}}}_3,$$

(13)

where ${\widehat{\phi }}_i\left(\widehat{s}\right)={\phi }_i+\epsilon {\phi }_i^{*}$ is a Lorentzian $\mathbb{T}-like$ dual angle (radius of curvature) among ${\widehat{\mathbf{r}}}_1$ and ${\widehat{\mathbf{b}}}_i$. Then,

$${\widehat{\beta }}_f-{\widehat{\beta }}_m=tanh{\widehat{\phi }}_f-tanh{\widehat{\phi }}_m.$$

(14)

Equation (14) is a novel dual hyperbolic version of the $\mathbb{ES}$ formula (Compared with [1,2,3]). Via the real and the dual parts, respectively, we attain

$$tanh{\phi }_f-tanh{\phi }_m={\beta }_f-{\beta }_m,$$

(15)

and

$$\frac{{\phi }_f^{*}}{{cosh}^2{\vartheta }_f}-\frac{{\phi }_m^{*}}{{cosh}^2{\vartheta }_m}+\lambda \left({\beta }_f-{\beta }_m\right)={\mathsf{\Omega }}_m-{\mathsf{\Omega }}_f.$$

(16)

Equation (15) in conjuction with (16) are new Disteli formulae ($\mathbb{DF}$) for the $\mathbb{T}-like$ axodes of the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$.

Now let us assume that $\left\{\widehat{\mathbf{r}}\right\}$ is stabilized in ${\mathbb{H}}_{+m}^2$. Then,

$${\mathbb{H}}_{+m}^2/{\mathbb{H}}_{+f}^2:\left(\begin{array}{c}{\widehat{\mathbf{r}}}_1^{{}^{\prime }}\hfill \\ {\widehat{\mathbf{r}}}_2^{{}^{\prime }}\hfill \\ {\widehat{\mathbf{r}}}_3^{{}^{\prime }}\hfill \end{array}\right)=\widehat{\mathsf{\varrho }}\times \left(\begin{array}{c}{\widehat{\mathbf{r}}}_1\hfill \\ {\widehat{\mathbf{r}}}_2\hfill \\ {\widehat{\mathbf{r}}}_3\hfill \end{array}\right),$$

(17)

where

$$\widehat{\mathsf{\varrho }}:={\widehat{\mathsf{\varrho }}}_f-{\widehat{\mathsf{\varrho }}}_m=\widehat{\varrho }{\widehat{\mathbf{r}}}_1,$$

(18)

is the relative Darboux vector. $∥\widehat{\mathsf{\varrho }}∥=\widehat{\varrho }=\widehat{\varrho }+\epsilon {\widehat{\varrho }}^{*}={\beta }_r+\epsilon \left({\mathsf{\Omega }}_r+\lambda {\beta }_r\right)$ is the relative radii of curvature; $\varrho ={\beta }_f-{\beta }_m$, and ${\varrho }^{*}={\mathsf{\Omega }}_f-{\mathsf{\Omega }}_m-\lambda \left({\beta }_f-{\beta }_m\right)$ are the rotational angular speed and translational angular speed of the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, as well they are both invariants in kinematics, respectively. As a result, the following corollary can be stated:

Corollary 1. 

For the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, at any instant $t\in \mathbb{R}$, the pitch is

$$h\left(s\right):=\frac{{\varrho }^{*}}{\varrho }=\frac{{\mathsf{\Omega }}_f-{\mathsf{\Omega }}_m}{{\beta }_f-{\beta }_m}-\lambda .$$

(19)

In this study, we deviate from the exclusive use of translational locomotion, namely when ${\varrho }^{*}\ne 0$. Moreover, we impose the condition of excluding zero divisors, denoted by $\varrho =0$. Consequently, our investigation will solely focus on non-torsional locomotions, ensuring that the axodes associated with these motions are non-developable $\mathbb{T}-like$ ruled surfaces, characterized by $\lambda \ne 0$.

3. Timelike Line with Particular Trajectories

Through the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, any fixed $\mathbb{T}-like$ line $\widehat{\mathbf{x}}$ connected with the mobile space ${\mathbb{L}}_m$-space, normally, creates a $\mathbb{T}-like$ ruled surface ($\widehat{x}$) in the immobile ${\mathbb{L}}_f$-space. Then,

$$\widehat{\mathbf{x}}\left(\widehat{s}\right)={\widehat{x}}^t\widehat{\mathbf{r}},\widehat{x}=\left(\begin{array}{c}{\widehat{x}}_1\hfill \\ {\widehat{x}}_2\hfill \\ {\widehat{x}}_3\hfill \end{array}\right)=\left(\begin{array}{c}{x}_1+\epsilon x_1^{*}\hfill \\ x_2+\epsilon x_2^{*}\hfill \\ x_3+\epsilon x_3^{*}\hfill \end{array}\right),\widehat{\mathbf{r}}=\left(\begin{array}{c}{\widehat{\mathbf{r}}}_1\hfill \\ {\widehat{\mathbf{r}}}_2\hfill \\ {\widehat{\mathbf{r}}}_3\hfill \end{array}\right),$$

(20)

where

$$\begin{array}{c}-x_1^2+x_2^2+x_3^2=-1,\\ -x_1{x}_1^{*}+x_2{x}_2^{*}+x_3{x}_3^{*}=0.\end{array}$$

(21)

The velocity and the acceleration vectors of $\widehat{\mathbf{x}}\in {\mathbb{H}}_{+m}^2$, respectively, are

$${\widehat{\mathbf{x}}}^{{}^{\prime }}=\widehat{\mathsf{\varrho }}\times \widehat{\mathbf{x}}=\widehat{\varrho }\left(-{\widehat{x}}_3{\widehat{\mathbf{r}}}_2+{\widehat{x}}_2{\widehat{\mathbf{r}}}_3\right),$$

(22)

and

$${\widehat{\mathbf{x}}}^{{}^{″}}=-{\widehat{x}}_3\widehat{\varrho }{\widehat{\mathbf{r}}}_1-({\widehat{x}}_2{\widehat{\varrho }}^2+{\widehat{x}}_3{\widehat{\varrho }}^{{}^{\prime }}){\widehat{\mathbf{r}}}_2+({\widehat{x}}_2{\widehat{\varrho }}^{{}^{\prime }}-{\widehat{x}}_1\widehat{\varrho }-{\widehat{x}}_3{\widehat{\varrho }}^2){\widehat{\mathbf{r}}}_3.$$

(23)

So, we have

$${\widehat{\mathbf{x}}}^{{}^{\prime }}\times {\widehat{\mathbf{x}}}^{{}^{″}}=-{\widehat{\varrho }}^2\left[({\widehat{x}}_1^2-1)\widehat{\varrho }{\widehat{\mathbf{r}}}_1+{\widehat{x}}_3\widehat{\mathbf{x}}\right].$$

(24)

The dual arc-length of the dual curve $\widehat{\mathbf{x}}\left(\widehat{s}\right)$ is

$$d\widehat{w}:=dw+\epsilon d{w}^{*}=∥{\widehat{\mathbf{x}}}^{{}^{\prime }}∥d\widehat{s}=\widehat{\varrho }\sqrt{{\widehat{x}}_1^2-1}d\widehat{s},\mathrm{with}\left|{\widehat{x}}_1\right|>1.$$

(25)

Then, the $\mathcal{D}-par$ of $\left(\widehat{x}\right)$ is

$$\mu \left(w\right):=\frac{d{w}^{*}}{dw}=h-\frac{x_1{x}_1^{*}}{x_1^2-1}.$$

(26)

Moreover, the Balschke frame is

$$\widehat{\mathbf{x}}=\widehat{\mathbf{x}}\left(\widehat{s}\right),\widehat{\mathbf{t}}\left(\widehat{s}\right)={\widehat{\mathbf{x}}}^{{}^{\prime }}{∥{\widehat{\mathbf{x}}}^{{}^{\prime }}∥}^{-1},\widehat{\mathbf{g}}\left(\widehat{s}\right)=\widehat{\mathbf{x}}\times \widehat{\mathbf{t}},$$

(27)

where

$$\left.\begin{array}{c}\widehat{\mathbf{x}}\times \widehat{\mathbf{t}}=\widehat{\mathbf{g}},\widehat{\mathbf{x}}\times \widehat{\mathbf{g}}=-\widehat{\mathbf{t}},\widehat{\mathbf{t}}\times \widehat{\mathbf{g}}=\widehat{\mathbf{x}},\hfill \\ \\ -⟨\widehat{\mathbf{x}},\widehat{\mathbf{x}}⟩=⟨\widehat{\mathbf{t}},\widehat{\mathbf{t}}⟩=⟨\widehat{\mathbf{g}},\widehat{\mathbf{g}}⟩=1.\hfill \end{array}\right\}$$

(28)

The dual unit vectors $\widehat{\mathbf{x}}$, $\widehat{\mathbf{t}}$, and $\widehat{\mathbf{g}}$ are three simultaneous alternately orthogonal lines in Minkowski three-space ${\mathbb{E}}_1^3$. Their joint point is the central point $\mathbf{c}$ on the ruling $\widehat{\mathbf{x}}$. $\widehat{\mathbf{g}}\left(\widehat{s}\right)$ is the mutual orthogonal to $\widehat{\mathbf{x}}\left(\widehat{w}\right)$ and $\widehat{\mathbf{x}}(\widehat{w}+d\widehat{w})$, and it is named the central tangent of ($\widehat{\mathbf{x}}$) at the central point. The trace of $\mathbf{c}$ is the striction curve. The line $\widehat{\mathbf{t}}$ is the central normal of $\left(\widehat{\mathbf{x}}\right)$ at $\mathbf{c}$. So, the Blaschke formulae are

$$\frac{d}{d\widehat{w}}\left(\begin{array}{c}\widehat{\mathbf{x}}\hfill \\ \widehat{\mathbf{t}}\hfill \\ \widehat{\mathbf{g}}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & 1\hfill & 0\hfill \\ 1\hfill & 0\hfill & \widehat{\beta }\hfill \\ 0\hfill & -\widehat{\beta }\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}\widehat{\mathbf{x}}\hfill \\ \widehat{\mathbf{t}}\hfill \\ \widehat{\mathbf{g}}\hfill \end{array}\right)=\widehat{\mathsf{\eta }}\left(\widehat{w}\right)\times \left(\begin{array}{c}\widehat{\mathbf{x}}\hfill \\ \widehat{\mathbf{t}}\hfill \\ \widehat{\mathbf{g}}\hfill \end{array}\right),$$

(29)

where $\widehat{\mathsf{\eta }}=\mathsf{\eta }+\epsilon {\mathsf{\eta }}^{*}=\widehat{\beta }\widehat{\mathbf{x}}-\widehat{\mathbf{g}}$ is the Darboux vector, and

$$\widehat{\beta }\left(\widehat{w}\right)=\beta +\epsilon (\mathsf{\Omega }+\mu \beta )=det(\widehat{\mathbf{x}},\frac{d\widehat{\mathbf{x}}}{d\widehat{w}},\frac{d^2\widehat{\mathbf{x}}}{d{\widehat{w}}^2})=\frac{{\widehat{x}}_1\widehat{\varrho }({\widehat{x}}_1^2-1)+{\widehat{x}}_3}{\widehat{\varrho }{({\widehat{x}}_1^2-1)}^{\frac{3}{2}}},$$

(30)

is the radii of curvature of $\widehat{\mathbf{x}}\left(\widehat{w}\right)$. The tangent vector of $\mathbf{c}\left(w\right)$ is

$$\frac{d\mathbf{c}}{dw}=-\mathsf{\Omega }\mathbf{x}+\mu \mathbf{g},$$

(31)

which is a $\mathbf{S}like$ (a $\mathbf{T}like$) curve if $\left|\mu \right|>\left|\mathsf{\Omega }\right|$ ($\left|\mu \right|<\left|\mathsf{\Omega }\right|$). $\beta \left(w\right)$, $\mathsf{\Omega }\left(w\right)$ and $\mu \left(w\right)$ are construction parameters of the $\mathbb{T}-like$ ruled surface $\left(\widehat{x}\right)$. Under the hypothesis that $\left|\widehat{\beta }\right|<1$, we specify the $\mathbb{S}-like$$\mathbb{DA}$ as follows:

$$\widehat{\mathbf{b}}\left(\widehat{w}\right)=\frac{\widehat{\overline{\mathsf{\varrho }}}}{∥\widehat{\overline{\mathsf{\varrho }}}∥}=\frac{\widehat{\beta }\widehat{\mathbf{x}}-\widehat{\mathbf{g}}}{\sqrt{1-{\widehat{\beta }}^2}}=sinh\widehat{\vartheta }\widehat{\mathbf{x}}-cosh\widehat{\vartheta }\widehat{\mathbf{g}},$$

(32)

where $\widehat{\vartheta }\left(\widehat{w}\right)=\vartheta +\epsilon {\vartheta }^{*}$ is radii of curvature through $\widehat{\mathbf{x}}$ and $\widehat{\mathbf{b}}$. Then,

$$tanh\widehat{\vartheta }=\frac{{\widehat{x}}_1\widehat{\varrho }({\widehat{x}}_1^2-1)+{\widehat{x}}_3}{\widehat{\varrho }{({\widehat{x}}_1^2-1)}^{\frac{3}{2}}}=\widehat{\beta }\left(\widehat{w}\right).$$

(33)

Further, we may have

$$\left.\begin{array}{c}\widehat{\kappa }\left(\widehat{w}\right)=\kappa +\epsilon {\kappa }^{*}=\sqrt{1-{\widehat{\beta }}^2}=\frac{1}{cosh\widehat{\vartheta }},\hfill \\ \\ \widehat{\tau }\left(\widehat{w}\right)=\tau +\epsilon {\tau }^{*}=\pm \frac{d\widehat{\vartheta }}{d\widehat{w}}=\pm \frac{1}{1-{\widehat{\beta }}^2}\frac{d\widehat{\beta }}{d\widehat{w}},\hfill \end{array}\right\}$$

(34)

where $\widehat{\kappa }\left(\widehat{w}\right)$ is the dual curvature, and $\widehat{\tau }\left(\widehat{w}\right)$ is the dual torsion of the dual curve $\widehat{\mathbf{x}}\left(\widehat{w}\right)$. Via Equations (26) and (31), $\left(\widehat{x}\right)$ is a $\mathbb{T}-like$ tangential developable surface if and only if $\frac{d\mathbf{c}}{dw}\Vert \mathbf{x}$, that is,

$$\mu =0\iff h(x_1^2-1)-x_1{x}_1^{*}=0,$$

(35)

which represents that the developable conditions of a $\mathbb{T}-like$ line trajectory are only founded on $x_1$, $x_1^{*}$ and h.

Theorem 1. 

For the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, the $\mathbb{T}-like$ line trajectory has torsional rulings at those instants at which it belongs to the quadratic $\mathbb{T}-like$ line complex pointed out by Equation (35).

In any quadratic $\mathbb{T}-like$ line complex the lines of this complex passing through a point mostly form a quadratic $\mathbb{T}-like$ cone. Primarily, for some points, this $\mathbb{T}-like$ cone reduces to a couple of $\mathbb{T}-like$ planes. Such points are the singular points of the $\mathbb{T}-like$ line complex. Thus, when $\left(\widehat{x}\right)$ is a $\mathbb{T}-like$ cone, the conditions are $\mu =0$, and $\mathsf{\Omega }=0$ define a quadratic $\mathbb{T}-like$ line congruence given by the mutual lines of the two quadratic $\mathbb{T}-like$ line complexes ($\mu =0$, and $\mathsf{\Omega }=0$).

Theorem 2. 

For the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$, the set of $\mathbb{T}-like$ lines correlated with the mobile $\mathbb{T}-like$ axode are rulings of a quadratic $\mathbb{T}-like$ cone in ${\mathbb{L}}_f$. Moreover, this family of $\mathbb{T}-like$ lines belong to a quadratic $\mathbb{T}-like$ line congruence.

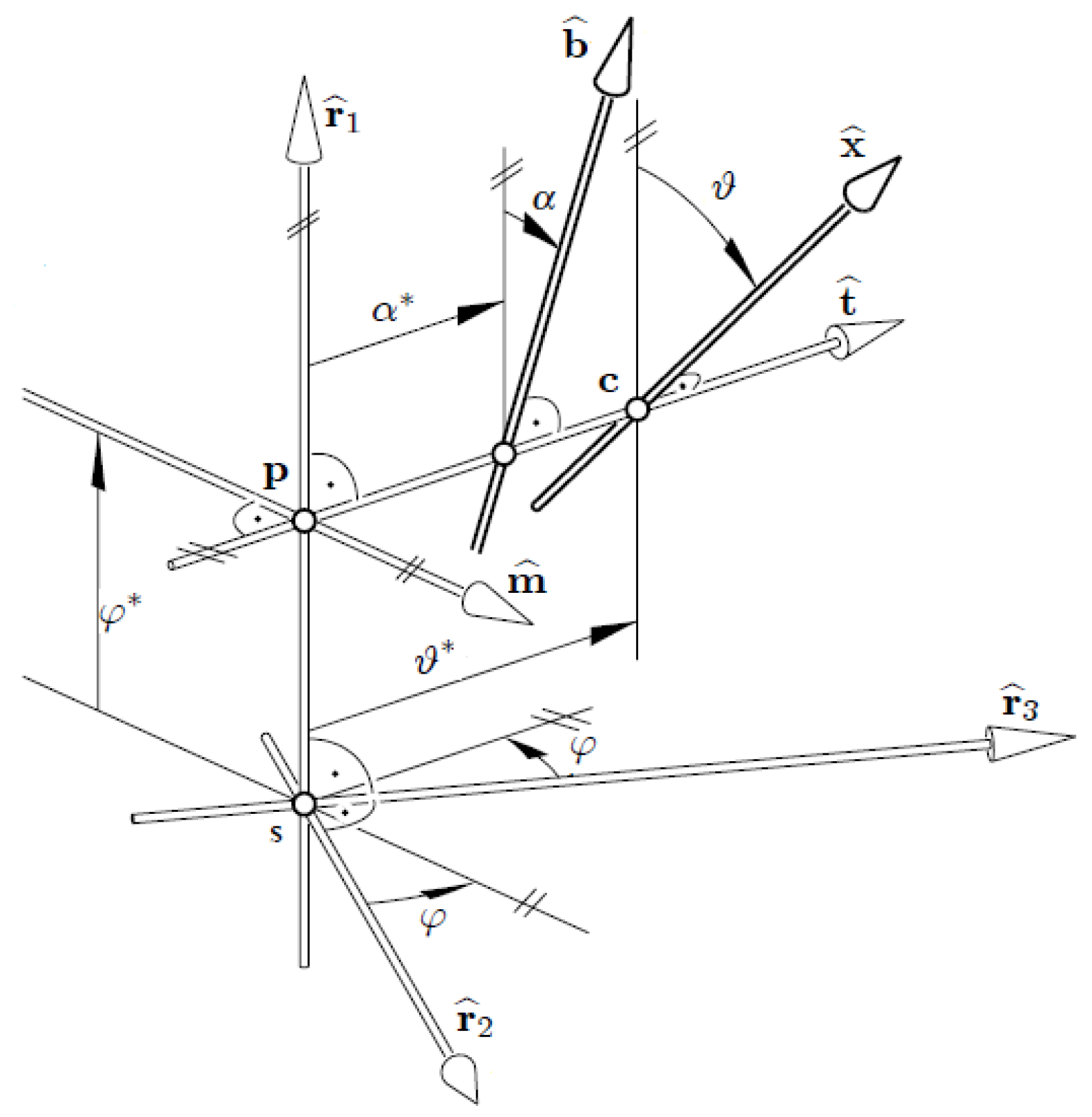
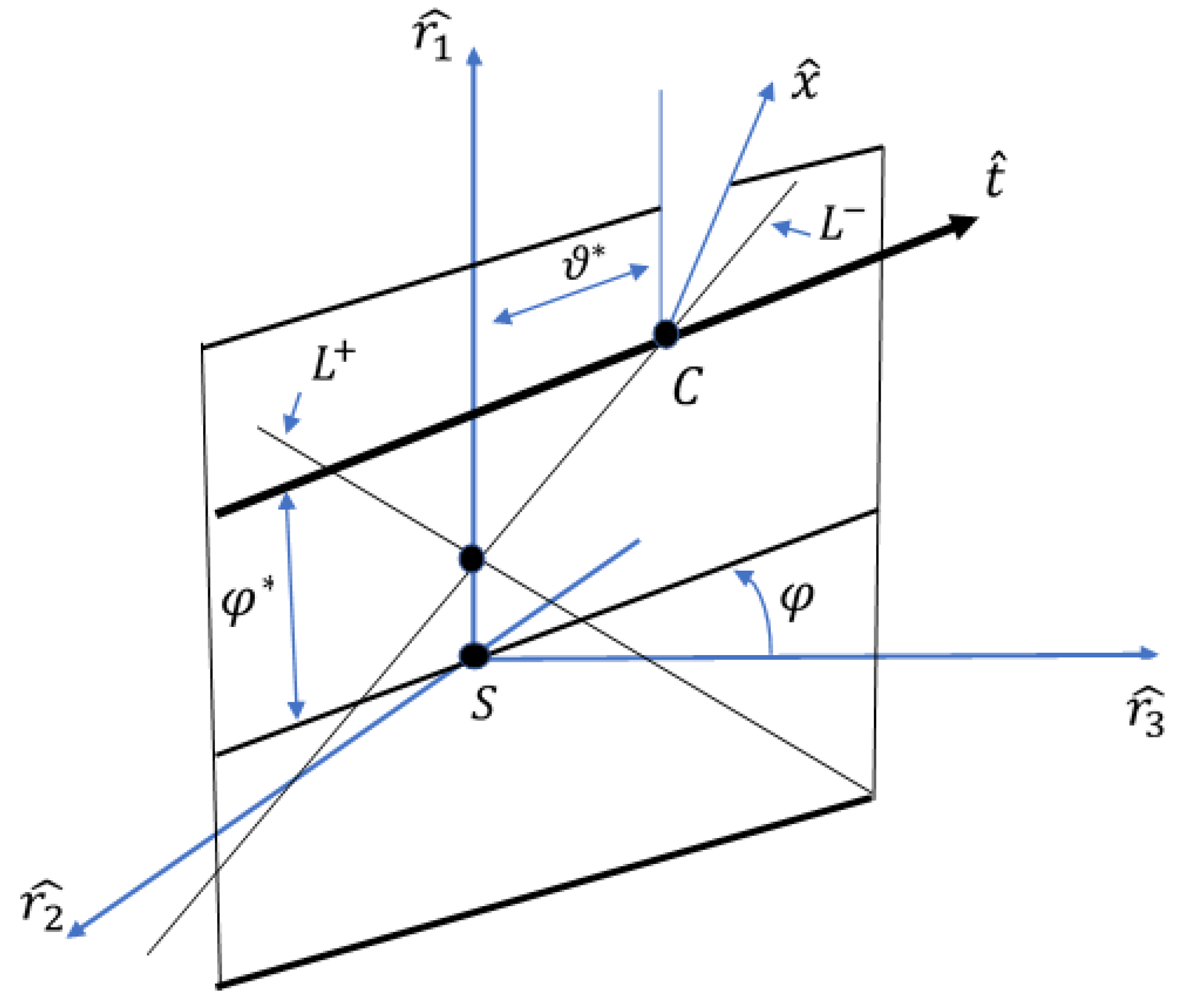
3.1. The Euler–Savary and Disteli Formulae

In the context of planar locomotions, the $\mathbb{ES}$ formula associates the locus of a point to its curvature center and is the main ingredient for a graphical structure producing one assigned the other [1,2,3]. In 1914, Disteli [20] assigned a curvature axis for the ruling of a ruled surface and extended the planar $\mathbb{ES}$ formula to spatial locomotions. However, the $\mathbb{DF}$ of a line trajectory had been acquired in [4,5,6,7,8,21], around inscription should be refind as follows: we shall define a new manner to have $\mathbb{DF}$ by dual function approximations. Thus, we request the $\mathbb{T}-like$ line $\widehat{\mathbf{x}}\in {\mathbb{L}}_m$, which at a steady dual angle from a steady $\mathbb{S}-like$ line $\widehat{\mathbf{y}}\in {\mathbb{L}}_f$. So, if $\widehat{\psi }=\psi +\epsilon {\psi }^{*}$ is the dual angle of $\widehat{\mathbf{x}}$( $\mathbb{T}-like$), and $\widehat{\mathbf{y}}$ ($\mathbb{S}-like$), then

$$\widehat{\psi }={sinh}^{-1}\left(⟨\widehat{\mathbf{x}},\widehat{\mathbf{y}}⟩\right).$$

(36)

For $\widehat{\psi }$ is steady up to the 2nd order at $\widehat{w}={\widehat{w}}_0$, we have

$${\widehat{\psi }}_{\mid \widehat{w}={\widehat{w}}_0}^{{}^{\prime }}=0,{\widehat{\mathbf{x}}}_{\mid \widehat{w}={\widehat{w}}_0}^{{}^{\prime }}=\mathbf{0},$$

(37)

and

$${\widehat{\psi }}_{\mid \widehat{w}={\widehat{w}}_0}^{{}^{″}}=0,{\widehat{\mathbf{x}}}_{\mid \widehat{w}={\widehat{w}}_0}^{{}^{{}^{″}}}=\mathbf{0}.$$

(38)

Hence, for the 1st order $⟨{\widehat{\mathbf{x}}}^{{}^{\prime }},\widehat{\mathbf{y}}⟩=0$, and for the 2nd order $⟨{\widehat{\mathbf{x}}}^{{}^{{}^{″}}},\widehat{\mathbf{y}}⟩=0$. Therefore, $\widehat{\psi }$ will be steady in the 2nd approximation if and only if $\widehat{\mathbf{y}}$ is the $\mathbb{S}-like$ $\mathbb{DA}$$\widehat{\mathbf{b}}$ of ($\widehat{x}$), that is,

$${\widehat{\psi }}^{{}^{\prime }}={\widehat{\psi }}^{{}^{″}}=0\iff \pm \widehat{\mathbf{y}}=\frac{{\widehat{\mathbf{x}}}^{{}^{\prime }}\times {\widehat{\mathbf{x}}}^{{}^{{}^{″}}}}{∥{\widehat{\mathbf{x}}}^{{}^{\prime }}\times {\widehat{\mathbf{x}}}^{{}^{{}^{″}}}∥}=\widehat{\mathbf{b}}.$$

(39)

Hence, from Equations (32) and (39), the following corollary can be given.

Corollary 2. 

($\widehat{x}$) is a steady-$\mathbb{DA}$$\mathbb{T}-like$ ruled surface if and only if ${\widehat{\vartheta }}^{{}^{\prime }}=0$.

Via this corollary, and based on Equation (34), it can be concluded that the rulings of ($\widehat{x}$) are the constant dual angle $\widehat{\vartheta }$ with respect to the $\mathbb{S}-like$$\mathbb{DA}$ if and only if ${\widehat{\beta }}^{{}^{\prime }}=0$. Therefore, the $\mathbb{T}-like$ ruled surface ($\widehat{x}$) is generated locally by a one-parameter hyperbolic spatial locomotion with pitch $h\left(s\right)$ along the steady $\mathbb{DA}$$\widehat{\mathbf{b}}$, This locomotion is performed by the $\mathbb{T}-like$ line $\widehat{\mathbf{x}}$, which is positioned at a constant hyperbolic distance ${\vartheta }^{*}$ and a constant angle $\vartheta$ relative to $\widehat{\mathbf{b}}$. This indicates that the striction curve of ($\widehat{x}$) can be classified as either a $\mathbb{S}-like$ or $\mathbb{T}-like$ cylindrical helix. The corollary shown below can be used to identify the circumstances of steady $\mathbb{DA}$.

Corollary 3. 

($\widehat{x}$) is a steady $\mathbb{DA}$$\mathbb{T}-like$ ruled surface if and only if

$${\widehat{\beta }}^{{}^{\prime }}=0\iff \frac{d\beta }{dw}=0,\mathit{and}\frac{d\mathsf{\Omega }}{dw}+\beta \frac{d\mu }{dw}=0.$$

(40)

Furthermore, from Equations (32) and (39), we find that

$$\widehat{\vartheta }={sinh}^{-1}(⟨\widehat{\mathbf{x}},\widehat{\mathbf{b}}⟩),⟨{\widehat{\mathbf{x}}}^{{}^{\prime }},\widehat{\mathbf{b}}⟩=0,⟨{\widehat{\mathbf{x}}}^{{}^{″}},\widehat{\mathbf{b}}⟩=0.$$

(41)

So, $\widehat{\mathbf{b}}$ is the osculating circle of $\widehat{\mathbf{x}}\left(\widehat{u}\right)\in {\mathbb{H}}_{+f}^2$. Further, it can be seen from Equations (22), (27) and (32) that

$$⟨\widehat{\mathbf{t}},{\widehat{\mathbf{r}}}_1⟩=⟨\widehat{\mathbf{t}},\widehat{\mathbf{x}}⟩=⟨\widehat{\mathbf{t}},\widehat{\mathbf{b}}⟩=0,$$

(42)

Then, all ${\widehat{\mathbf{r}}}_1$, $\widehat{\mathbf{x}}$ and $\widehat{\mathbf{b}}$ belong to a $\mathbb{T}-like$ line congruence whose focus line is the $\mathbb{S}-like$ line $\widehat{\mathbf{t}}$. This can be realized as follows: we set $\widehat{\mathbf{t}}$ with respect to the set $\left\{\widehat{\mathbf{r}}\right\}$ by its intercept distance ${\phi }^{*}$, control on the $\mathbb{ISA}$ and the angle $\phi$, control with respect to ${\widehat{\mathbf{r}}}_2$. We set the dual angle $\widehat{\alpha }=\alpha +\epsilon {\alpha }^{*}$, which realizes the attitude of $\widehat{\mathbf{b}}$ over $\widehat{\mathbf{t}}$. These dual angles are all estimated relative to the $\mathbb{ISA}$ (see Figure 2). The following governs the signals: $(\vartheta ,$${\vartheta }^{*})$ and $(\alpha ,$${\alpha }^{*})$ are via the right-hand screw rule with the thumb pointing on $\widehat{\mathbf{t}}$; the sense of $\widehat{\mathbf{t}}$ is such that $\widehat{\vartheta }=\vartheta +\epsilon {\vartheta }^{*}\ge 0$, and $0\le \phi \le 2\pi$, ${\phi }^{*}\in \mathbb{R}$ are explained with the thumb in the direction of the $\mathbb{ISA}$. Since $\widehat{\mathbf{x}}$ is a $\mathbb{T}-like$ dual unit vector, we can write out the components of $\widehat{\mathbf{x}}$ in the following form:

$$\widehat{\mathbf{x}}=cosh\widehat{\vartheta }{\widehat{\mathbf{r}}}_1+sinh\widehat{\vartheta }\widehat{\mathbf{m}},\mathrm{with}\widehat{\mathbf{m}}=cos\widehat{\phi }{\widehat{\mathbf{r}}}_2+sin\widehat{\phi }{\widehat{\mathbf{r}}}_3.$$

(43)

Therefore, the Blaschke frame of $\widehat{\mathbf{x}}=\widehat{\mathbf{x}}\left(\widehat{w}\right)$ can be written as

$$\left(\begin{array}{c}\widehat{\mathbf{x}}\hfill \\ \widehat{\mathbf{t}}\hfill \\ \widehat{\mathbf{g}}\hfill \end{array}\right)=\left(\begin{array}{ccc}cosh\widehat{\vartheta }\hfill & sinh\widehat{\vartheta }cos\widehat{\phi }\hfill & sinh\widehat{\vartheta }sin\widehat{\phi }\hfill \\ 0\hfill & -sin\widehat{\phi }\hfill & cos\widehat{\phi }\hfill \\ -sinh\widehat{\vartheta }\hfill & -cosh\widehat{\vartheta }cos\widehat{\phi }\hfill & -cosh\widehat{\vartheta }sin\widehat{\phi }\hfill \end{array}\right)\left(\begin{array}{c}{\widehat{\mathbf{r}}}_1\hfill \\ {\widehat{\mathbf{r}}}_2\hfill \\ {\widehat{\mathbf{r}}}_3\hfill \end{array}\right).$$

(44)

Comparably, the $\mathbb{S}-like$$\mathbb{DA}$ is

$$\widehat{\mathbf{b}}=sinh\widehat{\alpha }{\widehat{\mathbf{r}}}_1+cosh\widehat{\alpha }\widehat{\mathbf{m}},\mathrm{with}\widehat{\alpha }=\alpha +\epsilon {\alpha }^{*}\ge 0.$$

(45)

Substituting from Equations (23) and (45) into the third term of Equation (38) yields

$$\widehat{\varrho }{\widehat{x}}_{3}tanh\widehat{\alpha }-({\widehat{x}}_2^2\widehat{\varrho }+{\widehat{x}}_3{\widehat{\varrho }}^{{}^{\prime }})cos\widehat{\phi }+(-{\widehat{x}}_1\widehat{\varrho }+{\widehat{x}}_2{\widehat{\varrho }}^{{}^{\prime }}-{\widehat{x}}_3^2\widehat{\varrho })sin\widehat{\phi }=0.$$

(46)

Into Equation (46) we substitute from Equation (43) to obtain

$$coth\widehat{\alpha }-coth\widehat{\vartheta }=\frac{\widehat{\varrho }}{sin\widehat{\phi }}.$$

(47)

Equation (47) is a new hyperbolic $\mathbb{ES}$ formula that fastens a $\mathbb{T}-like$ ruled surface and its osculating circle in terms of the dual angle $\widehat{\phi }$ as well as the second order invariant $\widehat{\varrho }$. Via the real and the dual parts, respectively, we obtain

$$coth\alpha -coth\vartheta =\frac{\varrho }{sin\phi },$$

(48)

and

$${\phi }^{*}=\frac{1}{\varrho }\left[(\frac{{\alpha }^{*}}{{sinh}^2\alpha }-\frac{{\vartheta }^{*}}{{sinh}^2\vartheta })sin\phi +\frac{\varrho }{sin\phi }\left(h-\mu \right)\right]tan\phi .$$

(49)

Equation (48) with (49) are novel $\mathbb{DF}$ in the context of one-parameter hyperbolic spatial locomotions. The former equation establishes a relationship between the positions of the $\mathbb{T}-like$ line in the space ${\mathbb{L}}_m$ and the $\mathbb{S}-like$$\mathbb{DA}$ denoted as $\widehat{\mathbf{b}}$. Based on the information provided in Figure 2, the presence of the signal ${\alpha }^{*}$ (+ or −) in Equation (49) indicates whether the positions of the $\mathbb{DA}$$\widehat{\mathbf{b}}$ are located on the positive or negative direction of the mutual central normal $\widehat{\mathbf{t}}$.

Figure 2. Position relation of $\widehat{\mathbf{x}}$ and $\widehat{\mathbf{b}}$.

However, we can derive the Equation (47) as follows: the hyperbolic radii of curvature $\widehat{\psi }$ can be written as (see Figure 2):

$$\widehat{\psi }=\widehat{\vartheta }-\widehat{\alpha }\iff \psi =\vartheta -\alpha ,{\psi }^{*}={\vartheta }^{*}-{\alpha }^{*}.$$

(50)

Then, we have

$$\widehat{\beta }\left(\widehat{u}\right):=tanh\widehat{\psi }=tanh\left(\widehat{\vartheta }-\widehat{\alpha }\right).$$

(51)

Substituting Equation (51), into Equation (33), with awareness of (43), we obtain

$$tanh(\widehat{\vartheta }-\widehat{\alpha })=\frac{sin\widehat{\phi }}{\widehat{\varrho }{sinh}^2\widehat{\vartheta }},$$

(52)

After some algebraic manipulations, we find

$$coth\widehat{\alpha }-coth\widehat{\vartheta }=\frac{\widehat{\varrho }}{sin\widehat{\phi }}.$$

(53)

as asserted. Moreover, in the case of axodes, it is possible to derive a second dual formulation of the $\mathbb{ES}$ formulae in the following manner: from Equations (22) and (43), one finds facilely

$$d\widehat{s}=\widehat{\varrho }sinh\widehat{\vartheta }dt.$$

(54)

Moreover, from Equation (44) we have

$${\widehat{\mathbf{r}}}_1=cosh\widehat{\vartheta }\widehat{\mathbf{x}}+sinh\widehat{\vartheta }\widehat{\mathbf{g}}.$$

(55)

A simple computation offers that

$${\widehat{\mathbf{r}}}_1^{{}^{\prime }}:=(\frac{dt}{d\widehat{s}})\frac{d{\widehat{\mathbf{r}}}_1}{dt}=(\sinh \widehat{\vartheta }\widehat{\mathbf{x}}+cosh\widehat{\vartheta }\widehat{\mathbf{g}}){\widehat{\vartheta }}^{{}^{\prime }}+(cosh\widehat{\vartheta }-\widehat{\gamma }sinh\widehat{\vartheta })\widehat{\mathbf{t}},$$

(56)

and

$${\widehat{\mathbf{r}}}_1^{{}^{\prime }}=\left(\frac{1}{\widehat{\varrho }sinh\widehat{\vartheta }}\right){\widehat{\mathbf{r}}}_2.$$

(57)

The amalgamation of Equations (44) and (57) leads to

$${\widehat{\mathbf{r}}}_1^{{}^{\prime }}=\frac{1}{\widehat{\varrho }sinh\widehat{\vartheta }}(-sinh\widehat{\vartheta }cos\widehat{\phi }\widehat{\mathbf{x}}-sin\widehat{\phi }\widehat{\mathbf{t}}-cosh\widehat{\vartheta }cos\widehat{\phi }\widehat{\mathbf{g}}).$$

(58)

Then, by equating the coefficients of $\widehat{\mathbf{x}},$ $\widehat{\mathbf{t}}$, and $\widehat{\mathbf{g}}$ in Equations (56) and (58), we have

$${\widehat{\vartheta }}^{{}^{\prime }}sinh\widehat{\vartheta }+\frac{1}{\widehat{\varrho }}cos\widehat{\phi }=0,$$

(59)

and

$$cosh\widehat{\vartheta }-\widehat{\beta }sinh\widehat{\vartheta }=-\frac{sin\widehat{\phi }}{\widehat{\varrho }sinh\widehat{\vartheta }}.$$

(60)

Substituting this into the left hand side of Equation (53), one finds

$$cosh\widehat{\vartheta }-\widehat{\beta }sinh\widehat{\vartheta }=-\frac{1}{sinh\widehat{\vartheta }}\left(\frac{1}{coth\widehat{\alpha }-coth\widehat{\vartheta }}\right).$$

(61)

Finally, by substituting $\widehat{\varrho }:={\widehat{\beta }}_f-{\widehat{\beta }}_m=tanh{\widehat{\phi }}_f-tanh{\widehat{\phi }}_m$ into Equation (59), one obtains

$$tanh{\widehat{\phi }}_m-tanh{\widehat{\phi }}_f=\frac{cos\widehat{\phi }}{{\widehat{\vartheta }}^{{}^{\prime }}sinh\widehat{\vartheta }}.$$

(62)

Equation (62) presents a novel hyperbolic dual variant of the widely recognized $\mathbb{ES}$ formula in the context of conventional spherical kinematics, as discussed in References [1,2,3,4,5,6,7,8,9,21]. This narrative provides a link between the two $\mathbb{T}-like$ axodes in the locomotion of ${\mathbb{L}}_m/{\mathbb{L}}_f$. It should be noted that the striction point is the origin of the relative Blaschke frame, denoted as $\mathbf{s}=\mathbf{0}$, see Figure 2.

3.2. A Timelike Line Congruence

We present a method for locating a $\mathbb{T}-like$ line congruence. Therefore, from the real and the dual parts of $\widehat{\mathbf{x}}$ in Equation (43), respectively, we obtain

$$\mathbf{x}(\vartheta ,\phi )=\left(\cosh \vartheta ,sinh\vartheta cos\phi ,sinh\vartheta sin\phi \right),$$

(63)

and

$${\mathbf{x}}^{*}(\vartheta ,\phi ,{\vartheta }^{*},{\phi }^{*})=\left(\begin{array}{c}{\vartheta }^{*}sinh\vartheta \hfill \\ {\vartheta }^{*}cosh\vartheta cos\phi -{\phi }^{*}sinh\vartheta sin\phi \hfill \\ {\vartheta }^{*}cosh\vartheta sin\phi +{\phi }^{*}sinh\vartheta cos\phi \hfill \end{array}\right).$$

(64)

Since ${\mathbf{x}}^{*}=$$ϵ$$\times \mathbf{x}$, we possess the system of linear equations in ${ϵ}_i$ (i = 1, 2, 3):

$$\left.\begin{array}{c}\hfill c-{ϵ}_{2}sinh\vartheta sin\phi +{ϵ}_{3}sinh\vartheta cos\phi =x_1^{*},\hfill \\ \hfill -{ϵ}_{1}sinh\vartheta sin\phi +{ϵ}_{3}cosh\vartheta =x_2^{*},\hfill \\ \hfill {ϵ}_{1}sinh\vartheta cos\phi -{ϵ}_{2}cosh\vartheta =x_3^{*}.\hfill \end{array}\right\}$$

(65)

The coefficient matrix of unknowns ${ϵ}_i$(i = 1, 2, 3) is the skew-adjoint matrix

$$\left(\begin{array}{ccc}0\hfill & -sinh\vartheta sin\phi \hfill & sinh\vartheta cos\phi \hfill \\ -sinh\vartheta sin\phi \hfill & 0\hfill & cosh\vartheta \hfill \\ sinh\vartheta cos\phi \hfill & -cosh\vartheta \hfill & 0\hfill \end{array}\right),$$

(66)

and thus its rank is 2 with $\vartheta \ne 0$, and $\phi \ne 2\pi k$ (k is an integer). The rank of the augmented matrix

$$\left(\begin{array}{cccc}0\hfill & -sinh\vartheta sin\phi \hfill & sinh\vartheta cos\phi \hfill & x_1^{*}\\ -sinh\vartheta sin\phi \hfill & 0\hfill & cosh\vartheta \hfill & x_2^{*}\\ sinh\vartheta cos\phi \hfill & -cosh\vartheta \hfill & 0\hfill & x_3^{*}\end{array}\right),$$

(67)

is also 2. Hence, this system possesses an infinite number of solutions that are specified by

$$\begin{array}{c}\hfill {ϵ}_2=({ϵ}_1-{\phi }^{*})tanh\vartheta cos\phi -{\vartheta }^{*}sin\phi ,\hfill \\ \hfill {ϵ}_3=({ϵ}_1-{\phi }^{*})tanh\vartheta sin\phi +{\vartheta }^{*}cos\phi ,\hfill \\ \hfill {ϵ}_1={ϵ}_1(\vartheta ,\phi ).\hfill \end{array}$$

(68)

Since ${ϵ}_1$ can be arbitrary, we may then put ${ϵ}_1={\phi }^{*}$. In this affair, we have

$$ϵ(\phi ,{\phi }^{*})=({\phi }^{*},-{\vartheta }^{*}sin\phi ,{\vartheta }^{*}cos\phi ),$$

(69)

which is the base (director) surface of the $\mathbb{T}-like$ line congruence. Let $\mathsf{\xi }({\xi }_1,{\xi }_2,{\xi }_3)$ be a point on the directed $\mathbb{T}-like$ line $\widehat{\mathbf{x}}$. We can write that

$$\left(\widehat{x}\right):\left.\begin{array}{c}{\xi }_1(\phi ,{\phi }^{*},\rho )={\phi }^{*}+\rho cosh\vartheta ,\hfill \\ {\xi }_2(\phi ,{\phi }^{*},\rho )=-{\vartheta }^{*}sin\phi +\rho sinh\vartheta cos\phi ,\hfill \\ {\xi }_3(\phi ,{\phi }^{*},\rho )={\vartheta }^{*}cos\phi +sinh\vartheta sin\phi ,\hfill \end{array}\right\}$$

(70)

where $\rho \in \mathbb{R}$. Given that $\phi$ and ${\phi }^{*}$ are two independent variables, it may be said that $\widehat{x}$ is a $\mathbb{T}-like$ line congruence in ${\mathbb{L}}_f$-space in general. If we define ${\phi }^{*}=h\phi$ and $\phi$ as the parameter for locomotion, then $\left(\widehat{x}\right)$ can be considered as a $\mathbb{T}-like$ ruled in ${\mathbb{L}}_f$-space. As a result, the director surface represented by Equation (69) is constrained by the striction curve on ($\widehat{x}$), which implies that

$$\mathbf{c}\left(\phi \right)=(h\phi ,-{\vartheta }^{*}sin\phi ,{\vartheta }^{*}cos\phi ).$$

(71)

The curvature ${\kappa }_c\left(\phi \right)$ and torsion ${\tau }_c\left(\phi \right)$ can be given by

$${\kappa }_c\left(\phi \right)=\frac{{\vartheta }^{*}}{{\vartheta }^{*2}-h^2},{\tau }_c\left(\phi \right)=\frac{h}{{\vartheta }^{*2}-h^2}.$$

(72)

Then, $\mathbf{c}\left(\phi \right)$ is a $\mathbb{S}-like$ ($\left|{\vartheta }^{*}\right|>\left|h\right|$) or $\mathbb{T}-like$ ($\left|{\vartheta }^{*}\right|<\left|h\right|$) cylindrical helix with the $\mathbb{ISA}$ as its axis. Further, the $\mathbb{T}-like$ ruled surface is

$$\left(\widehat{x}\right):\left.\begin{array}{c}{\xi }_1(\phi ,\rho )=h\phi +\rho cosh\vartheta ,\hfill \\ {\xi }_2(\phi ,\rho )=-{\vartheta }^{*}sin\phi +\rho sinh\vartheta cos\phi ,\hfill \\ {\xi }_3(\phi ,\rho )={\vartheta }^{*}cos\phi +sinh\vartheta sin\phi .\hfill \end{array}\right\}$$

(73)

The constants h, $\vartheta$ and ${\vartheta }^{*}$ can control the shape of $\left(\widehat{x}\right)$. In the case of $0\le \phi \le 2\pi$, and ${\vartheta }^{*}\ne 0$, we attain

$$\left(\widehat{x}\right):-\frac{{\mathsf{\Psi }}_1^2}{{\varpi }^2}+\frac{{\xi }_2^2}{{\vartheta }^{*2}}+\frac{{\xi }_3^2}{{\vartheta }^{*2}}=1,$$

(74)

where $\varpi ={\vartheta }^{*}tanh\vartheta$, and ${\mathsf{\Psi }}_1={\xi }_1-h\phi$. So, $\left(\widehat{x}\right)$ is a two-parameter family of one-sheeted hyperboloids. The intersection of each hyperboloid and the $\mathbb{S}-like$ plane ${\xi }_1=h\phi$ is a one-parameter family of Lorentzian cylinder $\left(c\right)$: ${\xi }_2^2+{\xi }_3^2={\vartheta }^{*2}$ which is the envelope of $\left(\widehat{x}\right)$. The $\mathbb{T}-like$ ruled surface $\left(\widehat{x}\right)$ can be classified into 4-kinds via their striction curves:

(a)

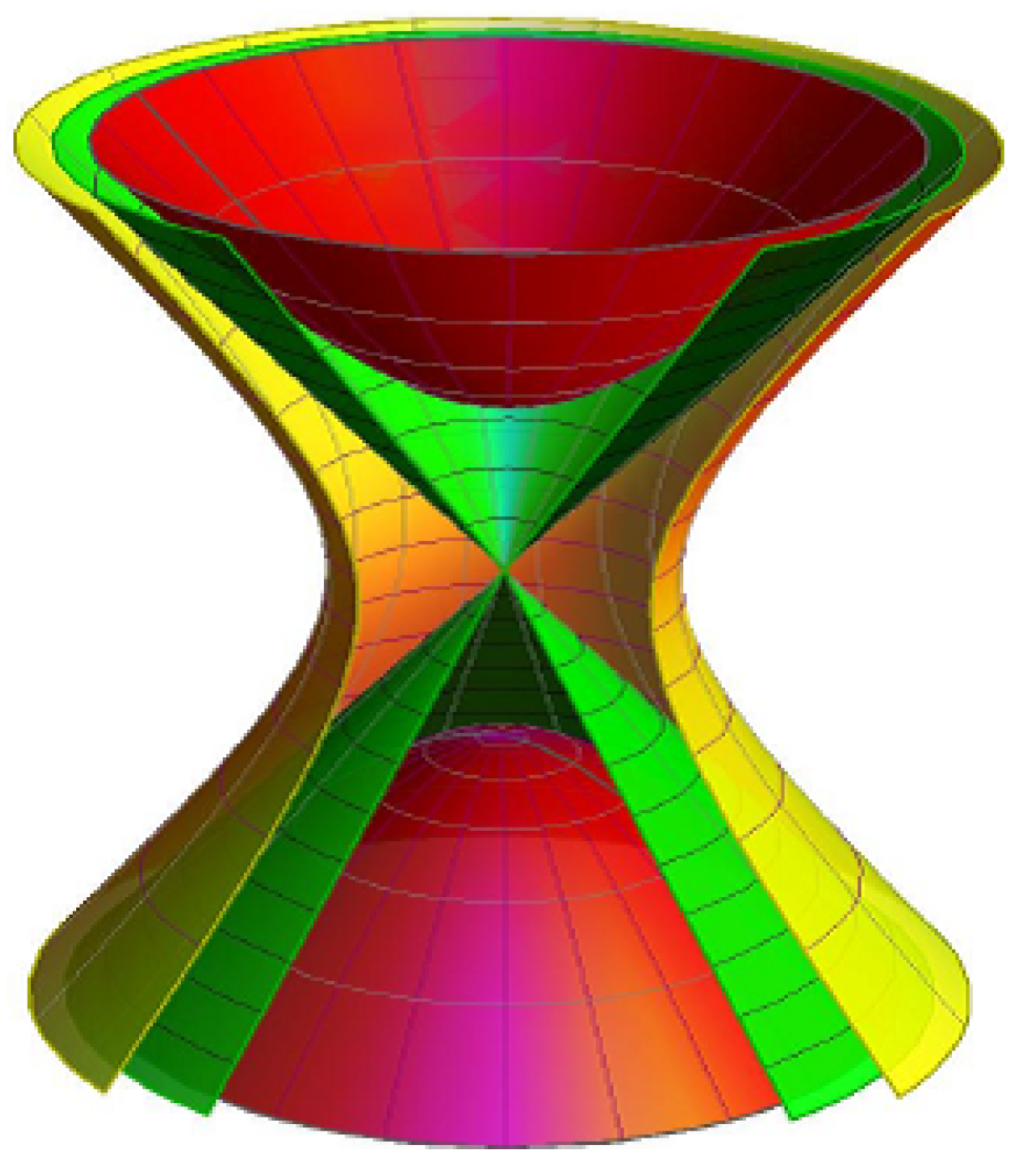
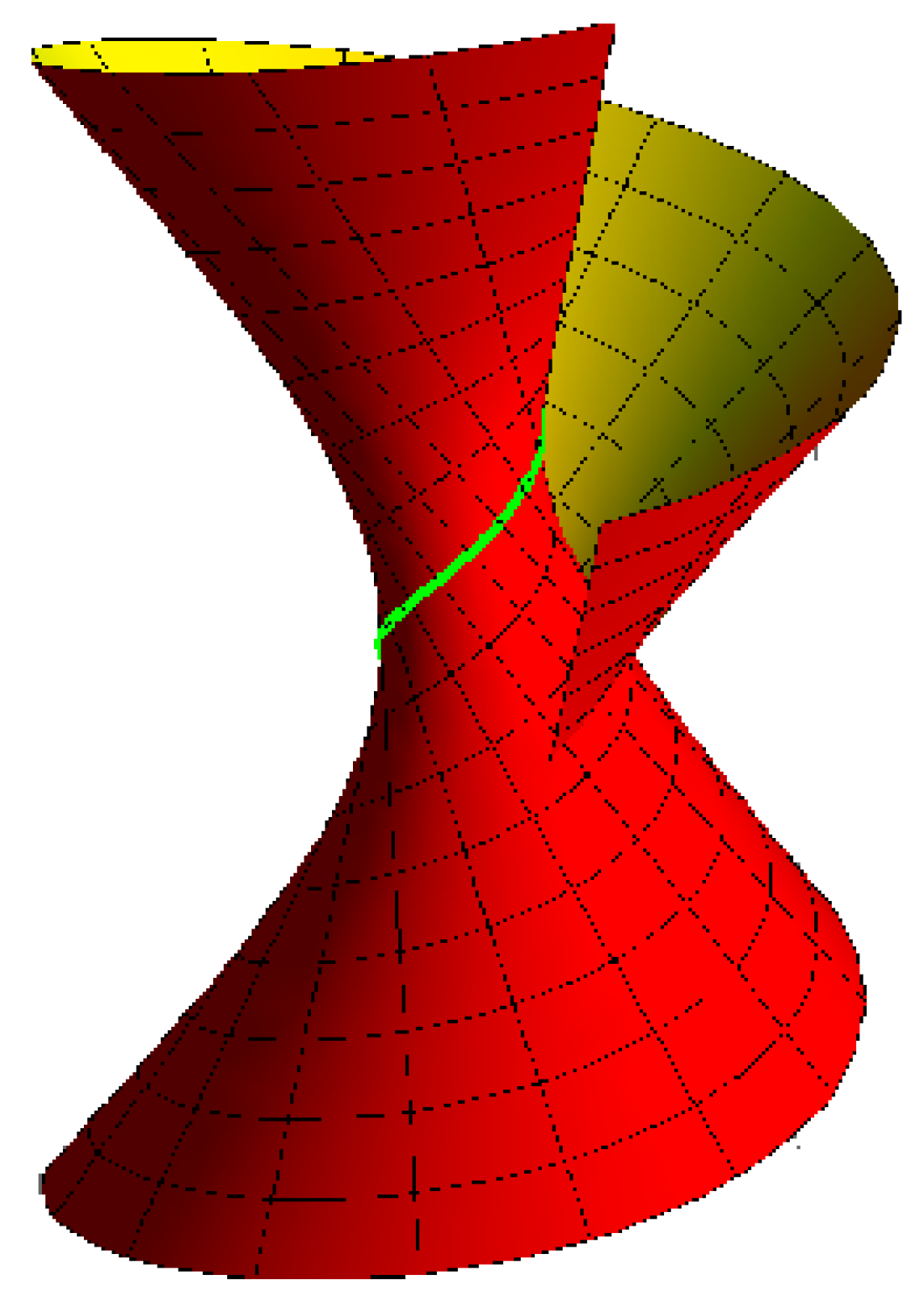
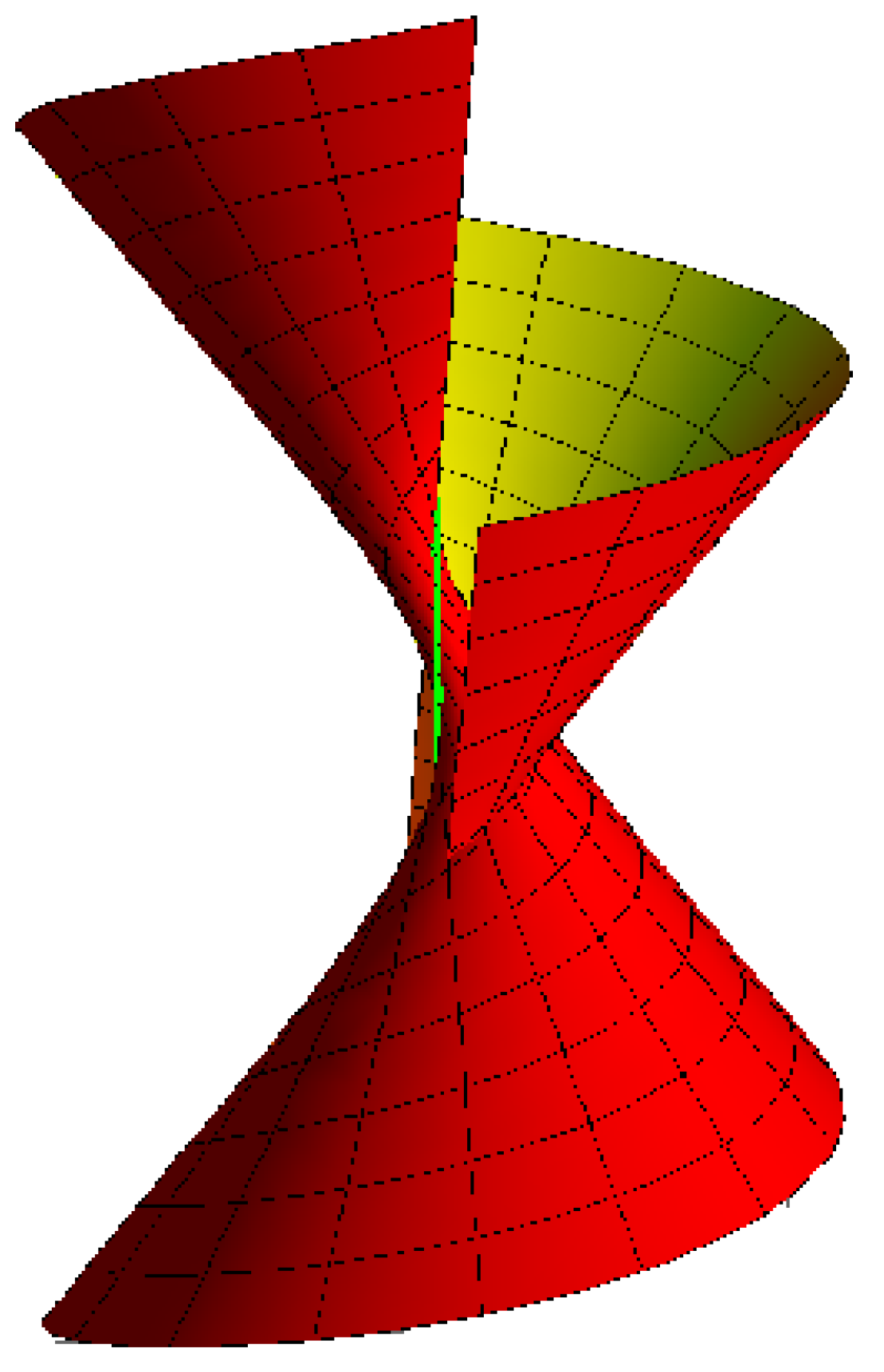
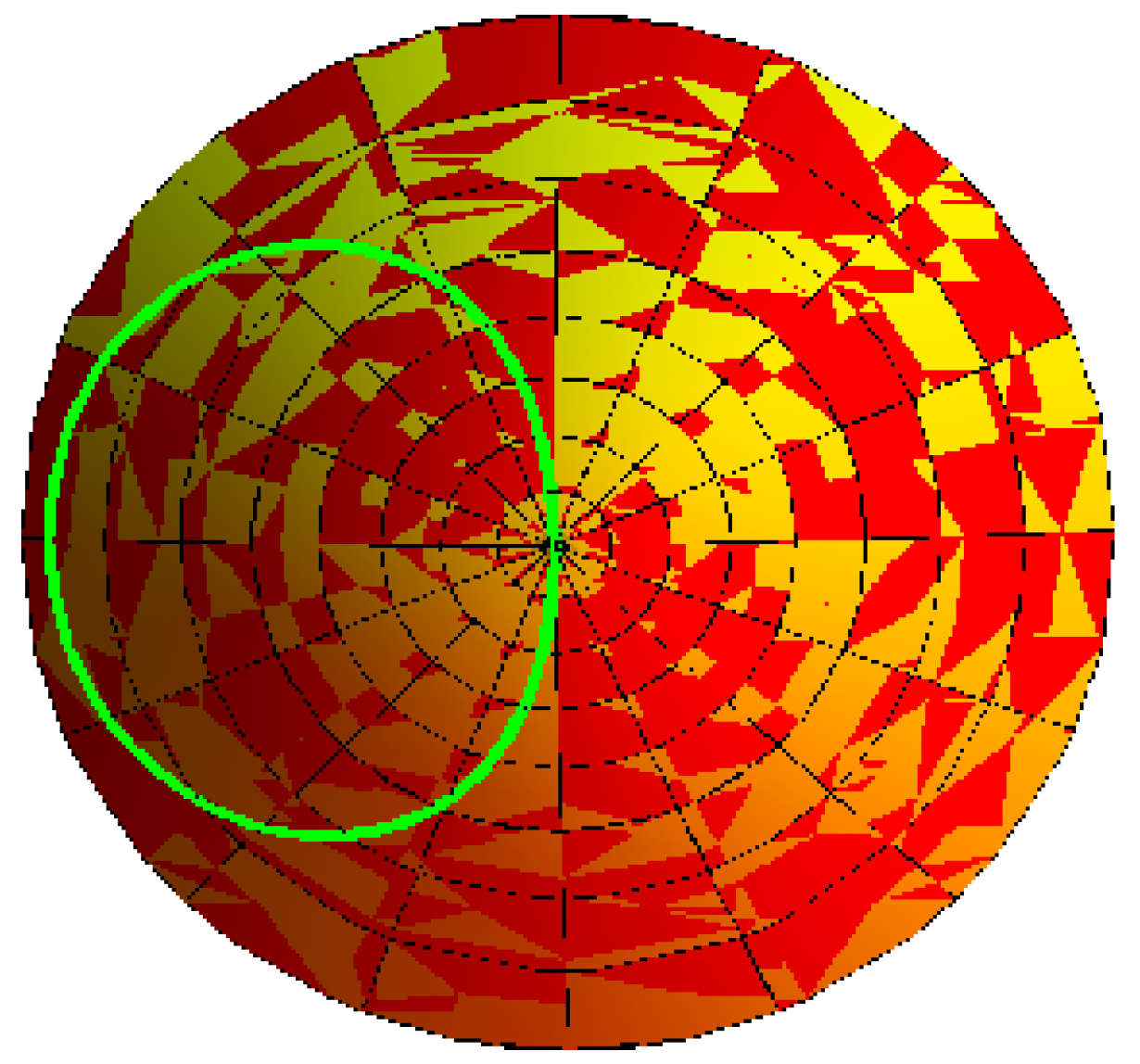
$\mathbb{T}-like$ Archimedes with its striction curve is a $\mathbb{T}-like$ cylindrical helix for $h={\vartheta }^{*}=1$, $\vartheta =1.1$, $-4\le v\le 4$, and $0\le \phi \le 2\pi$ (Figure 3).

Figure 3. $\mathbb{T}-like$ Archimedes.

(b)

Lorentzian sphere with its striction curve is a $\mathbb{S}-like$ circle for $h=0,$${\vartheta }^{*}=1$, $\vartheta =1.1$, $-4\le v\le 4$, and $0\le \phi \le 2\pi$ (Figure 4).

Figure 4. Lorentzian sphere.

(c)

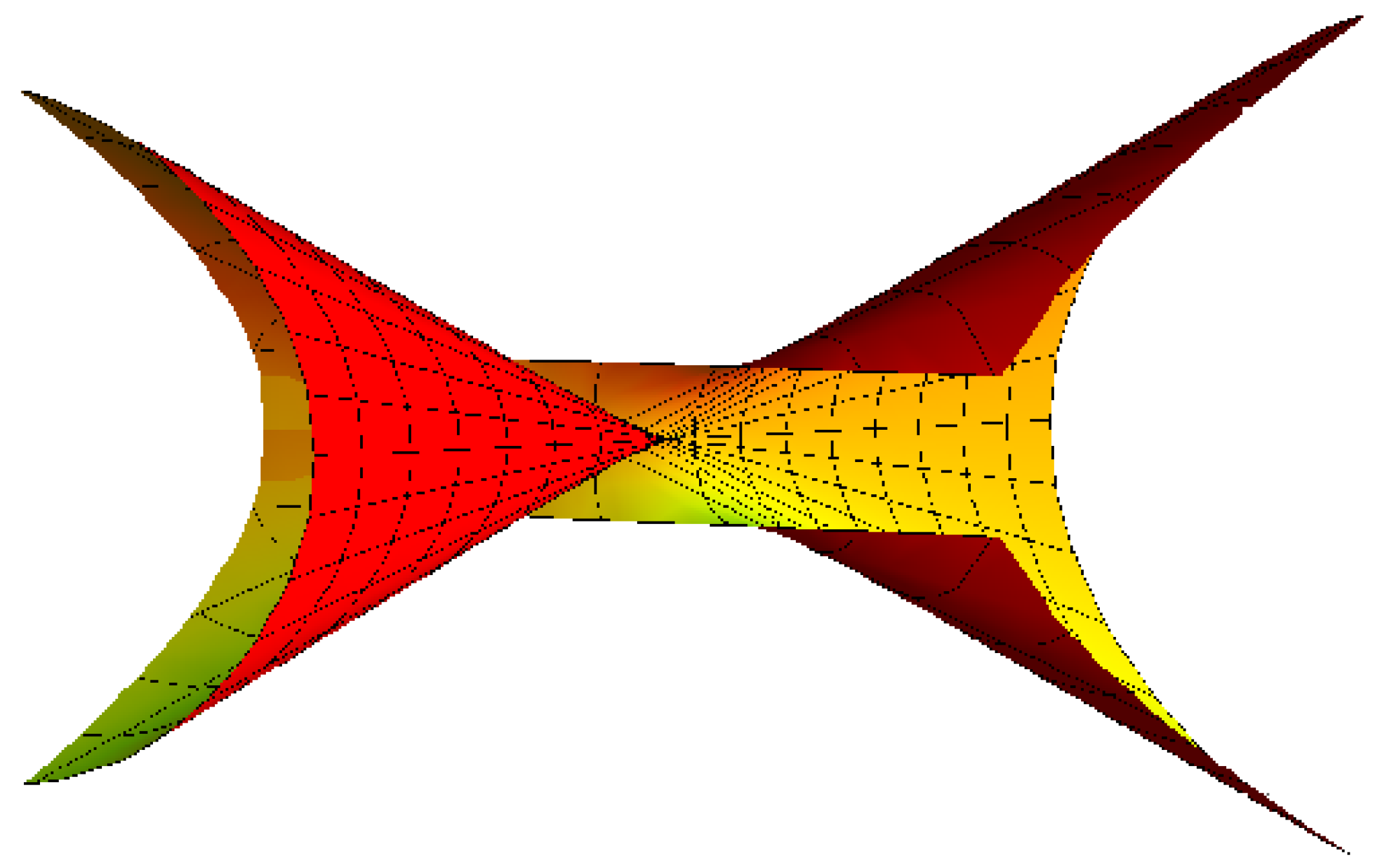
$\mathbb{T}-like$ helicoid with its striction curve is a $\mathbb{T}-like$ line for $h=1$, ${\vartheta }^{*}=0$, $\vartheta =1.1$, $-4\le v\le 4$, and $0\le \phi \le 2\pi$ (Figure 5).

Figure 5. $\mathbb{T}-like$ helicoid.

(d)

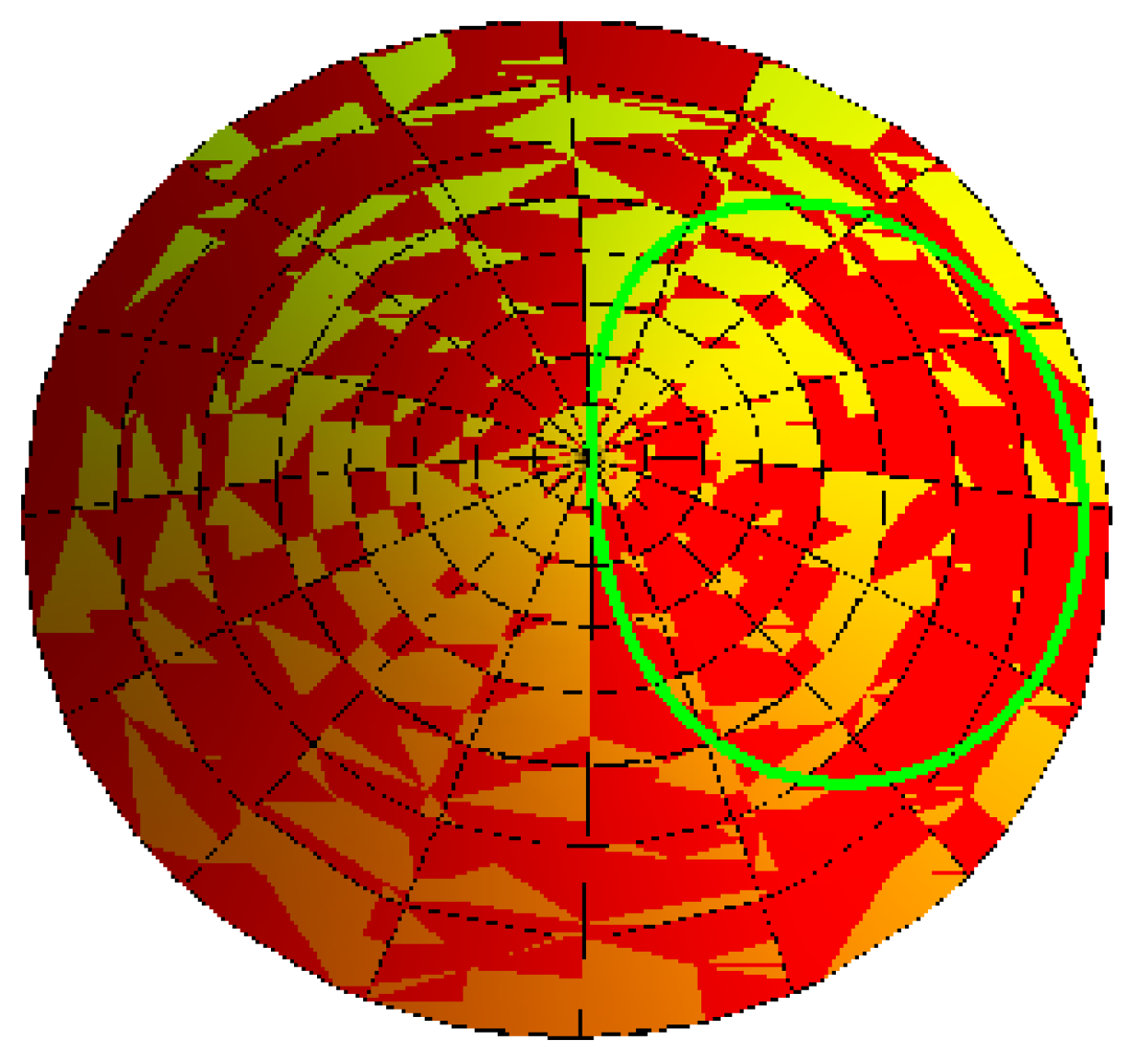
$\mathbb{T}-like$ cone with its striction curve is a stationary point for $h={\vartheta }^{*}=0$, $\vartheta =1.1$, $-4\le v\le 4$, and $0\le \phi \le 2\pi$ (Figure 6).

Figure 6. $\mathbb{T}-like$ cone.

4. Inflection Timelike Line Congruence

This section demonstrates how a line congruence, which we refer to as an inflection $\mathbb{T}-like$ line congruence, is the spatial equivalent of the inflection circle of planar kinematics. Hence, we establish that the locus comprising the entire set of lines exhibiting a dual geodesic curvature of zero corresponds to the spatial equivalent of the circle of inflection for planar locomotios. Then, from Equation (34), we have

$$\widehat{\beta }\left(\widehat{w}\right)=0\iff \widehat{\kappa }\left(\widehat{w}\right)=1.$$

(75)

Furthermore, from Equations (30) and (33), we can see that

$$\widehat{\beta }\left(\widehat{w}\right)=0\iff tanh\widehat{\psi }=0\iff \psi ={\psi }^{*}=0\iff \beta =0,\mathrm{and}\mathsf{\Omega }=0.$$

(76)

In this particular case, the lines denoted as $\widehat{\mathbf{x}}$, $\widehat{\mathbf{t}}$, and $\widehat{\mathbf{b}}$ represent the Blaschke frame. These lines intersect at the striction point of the $\mathbb{T}-like$ ruled surface denoted as $\left(\widehat{x}\right)$. Based on the Equations (31) and (76), it may be inferred that the striction curve is a $\mathbb{S}-like$ curve, that is, $\frac{d\mathbf{c}}{dw}\Vert \mathbf{g}$. Given that $\widehat{\beta }\left(\widehat{w}\right)=0$, we can derive the ODE $\frac{d^2\widehat{\mathbf{t}}}{d{\widehat{w}}^2}-\widehat{\mathbf{t}}=\mathbf{0}$ from Equation (29). Furthermore, by setting $\widehat{\mathbf{t}}\left(0\right)=(0,1,0)$, the solution of the ODE is obtained as follows:

Since $\widehat{\beta }\left(\widehat{w}\right)=0$, from Equation (29) we have the ODE, $\frac{d^2\widehat{\mathbf{t}}}{d{\widehat{w}}^2}-\widehat{\mathbf{t}}=\mathbf{0}$. Moreover, we may write $\widehat{\mathbf{t}}\left(0\right)=(0,1,0)$, and the solution of the ODE becomes

$$\widehat{\mathbf{t}}\left(\widehat{w}\right)=\left({\widehat{b}}_{1}sinh\widehat{w},cosh\widehat{w}+{\widehat{b}}_{2}sinh\widehat{w},{\widehat{b}}_{3}sinh\widehat{w}\right),$$

(77)

for dual constants ${\widehat{b}}_1$, ${\widehat{b}}_2$, and ${\widehat{b}}_3$. Since ${∥\widehat{\mathbf{t}}∥}^2=1$, we obtain ${\widehat{b}}_2=0$, and ${\widehat{b}}_1^2-{\widehat{b}}_3^2=1$, it shows that $\widehat{\mathbf{x}}\left(\widehat{w}\right)$ can be specified by

$$x\left(\widehat{w}\right)=\left({\widehat{b}}_{1}cosh\widehat{w}+{\widehat{d}}_1,sinh\widehat{w},{\widehat{b}}_{3}cosh\widehat{w}+{\widehat{d}}_3\right),$$

(78)

for dual constants ${\widehat{d}}_2$, and ${\widehat{d}}_3$ satisfying ${\widehat{b}}_1{\widehat{d}}_1-{\widehat{b}}_3{\widehat{d}}_3=0$. We make change the coordinates by

$$\left(\begin{array}{c}{\tilde{x}}_1\hfill \\ {\tilde{x}}_2\hfill \\ {\tilde{x}}_3\hfill \end{array}\right)=\left(\begin{array}{ccc}{\widehat{b}}_1\hfill & 0\hfill & -{\widehat{b}}_3\hfill \\ 0\hfill & 1\hfill & 0\hfill \\ -{\widehat{b}}_3\hfill & 0\hfill & {\widehat{b}}_1\hfill \end{array}\right)\left(\begin{array}{c}{\widehat{x}}_1\hfill \\ {\widehat{x}}_2\hfill \\ {\widehat{x}}_3\hfill \end{array}\right).$$

(79)

Then, $\widehat{\mathbf{x}}\left(\widehat{w}\right)$ turns into

$$\widehat{\mathbf{x}}\left(\widehat{w}\right)=cosh\widehat{w}{\widehat{\mathbf{r}}}_1+sinh\widehat{w}{\widehat{\mathbf{r}}}_2,$$

(80)

for ${\widehat{b}}_1{\widehat{d}}_3-{\widehat{b}}_3{\widehat{d}}_1=0$. Let $\chi ({\chi }_1,{\chi }_2,{\chi }_3)$ be a point on $\widehat{\mathbf{x}}\left(\widehat{w}\right)$, then

$$\left(\widehat{x}\right):\chi (w,w^{*},\rho )=(0,0,w^{*})+\rho (coshw,sinhw,0),\rho \in \mathbb{R},$$

(81)

which yields that

$${\chi }_1=\rho coshw,{\chi }_2=\rho sinhw,{\chi }_3=w^{*}.$$

(82)

So, if we take $w^{*}=hw$, h signaling the pitch of the locomotion ${\mathbb{L}}_m/\mathbb{L}$. Then,

$${\chi }_3=\frac{1}{h}{coth}^{-1}\frac{{\chi }_1}{{\chi }_2},$$

(83)

which is a one-parameter family of $\mathbb{T}-like$ helicoid of the second kind; where for $h=1$, $-3\le w\le 3$, $-1\le \rho \le 1$, a member is shown in (Figure 7).

Figure 7. A $\mathbb{T}-like$ helicoid of the 2nd kind.

For more kinematic analysis of the inflection $\mathbb{T}-like$ line congruence $\left(\widehat{x}\right)$, from Equation (30) we can write the equation

$$\widehat{c}:{\widehat{x}}_1\widehat{\varrho }(1-{\widehat{x}}_1^2)+{\widehat{x}}_3=0,$$

(84)

which is a curve of third degree. The real part of Equation (84) recognizes a $\mathbb{T}-like$ inflection cone for the real spherical part of ${\mathbb{L}}_m/{\mathbb{L}}_f$ and is pointed out by

$$c:x_1\varrho (1-x_1^2)+x_3=0.$$

(85)

The mutual lines of the $\mathbb{T}-like$ inflection cone with a real hyperbolic unit sphere concentrated at the head of the cone defines a hyperbolic spherical curve. Furthermore, there is a $\mathbb{T}-like$ plane for each $\mathbb{T}-like$ line, united with each ruling of a $\mathbb{T}-like$ inflection cone, given by the dual part of Equation (84):

$$\pi :\varrho \left(x_{1}h+x_1^{*}-2x_1^2{x}_1^{*}\right)+x_3^{*}=0,$$

(86)

where $x_1,x_2,$ and $x_3$ are the hyperbolic direction cosines of the line $\widehat{\mathbf{x}}$ and $x_1^{*},x_2^{*},$ and $x_3^{*}$ are specified by

$$x_1^{*}=-q_2{x}_3+q_3{x}_2,x_2^{*}=q_3{x}_1-q_1{x}_3,x_3^{*}=q_1{x}_2-q_2{x}_1,$$

(87)

where $\mathbf{q}(q_1,$$q_2,q_3)\in \widehat{\mathbf{x}}$. Equation (84) represents a third-degree equation, it follows that the $\mathbb{T}-like$ line congruence can be traced by all common lines of two cubic $\mathbb{T}-like$ line complexes, as described by Equations (85) and (86). Therefore, the Plückerian coordinates that describe the $\mathbb{T}-like$ lines $\widehat{\mathbf{x}}\in \widehat{c}$ may be expressed by the Equations (21), (85) and (86). In general, these coordinates represent a $\mathbb{T}-like$ ruled surface in the fixed space ${\mathbb{L}}_f$. However, from Equations (63), (64), (85) and (86), respectively, we obtain

$$c:\varrho sinh2\vartheta +2sin\phi =0,$$

(88)

and

$$\pi :{\varrho }^{*}sinh2\vartheta +2\varrho {\vartheta }^{*}cosh2\vartheta +2{\phi }^{*}cos\phi =0.$$

(89)

If the Equation (88) is resolved with respect to $\vartheta$, we have

$$sinh2\vartheta =-\left(\frac{2sin\phi }{\varrho }\right),\mathrm{and}cosh2\vartheta =\pm \frac{1}{\varrho }\sqrt{{\varrho }^2+4{sin}^2\phi }.$$

(90)

Hence, from Equations (89) and (90), we attain

$$\pi :hsin\phi \mp \sqrt{{\varrho }^2+4{sin}^2\phi }{\vartheta }^{*}-{\phi }^{*}cos\phi =0.$$

(91)

Equation (91) is linear in ${\phi }^{*}$ and ${\vartheta }^{*}$ of the $\mathbb{T}-like$ line $\widehat{\mathbf{x}}$. Hence, the $\mathbb{T}-like$ lines in a stationary direction within the ${\mathbb{L}}_m$-space can be found on the $\mathbb{T}-like$ plane denoted as $\pi$. As illustrated in Figure 8, the angle $\phi$ serves to differentiate the central normal $\widehat{\mathbf{t}}$. Consequently, Equation (91) yields two $\mathbb{T}-like$ lines $L^{+}$ and $L^{-}$ within the $\mathbb{T}-like$ plane $\pi$: $Sp\{{\widehat{\mathbf{r}}}_1,\widehat{\mathbf{t}}\}$ (where $L^{+}$ and $L^{-}$ align with the inflection circle in planar locomotions). Also, if the distance ${\vartheta }^{*}$ on the central normal $\widehat{\mathbf{t}}$ from the $\mathbb{ISA}$ is taken as the independent parameter, we obtain

$$\pi :{\phi }^{*}=\mp \left(\frac{\sqrt{{\varrho }^2+4{sin}^2\phi }}{cos\phi }\right){\vartheta }^{*}+htan\phi .$$

(92)

We remark that $L^{+}$ (or $L^{-})$ will alternate its place if ${\vartheta }^{*}$ is realized as a various value, but $\phi =$ constant. Further, the $\mathbb{T}-like$ plane $\pi$ is various if $\phi$ of $L^{+}$ (or $L^{-})$ has various value, but ${\vartheta }^{*}=$ consent. Consequently, the collection of all $\mathbb{T}-like$ lines $L^{+}$, and $L^{-}$ pointed out by Equation (92) is an inflection $\mathbb{T}-like$ congruence for all values of $({\phi }^{*},{\vartheta }^{*})$.

Figure 8. $\mathbb{T}-like$ inflection line congruence.

However, the ownerships of this inflection $\mathbb{T}-like$ congruence are clarified as follows: via Figure 8, the two $\mathbb{T}-like$ lines $L^{+}$ and $L^{-}$ are intersected on the $\mathbb{ISA}$ at distance $htan\phi$. For the orientation $\phi =0$, these $\mathbb{T}-like$ lines passing through the origin ($\mathbf{s}=\mathbf{0})$ and attain the minimal slope is $\pm \varrho .$ For $\phi =\pi /2$, the $\mathbb{T}-like$ lines are parallel and located on opposite sides of the $\mathbb{ISA}$ at a specific distance $h/\sqrt{{\varrho }^2+4}$. Furthermore, if the Equation (88) is resolved with respect to $\phi$, we obtain

$$\phi =-{sin}^{-1}\left(\frac{\varrho sinh2\vartheta }{2}\right).$$

(93)

By substituting Equation (93) into Equation (63), we find

$$x\left(\vartheta \right)=\left(\cosh \vartheta ,cos\left[{sin}^{-1}\left(\frac{\varrho sinh2\vartheta }{2}\right)\right]sinh\vartheta ,-\frac{\varrho sinh\left(2\vartheta \right)}{2}sinh\vartheta \right).$$

(94)

Equation (94) appears the inflection $\mathbb{T}-like$ curve of the hyperbolic spherical part of the locomotion ${\mathbb{L}}_m/{\mathbb{L}}_f$. Further, from the Equations (70), (90) and (94), we obtain

$$\left(\widehat{x}\right):\left.\begin{array}{c}{\xi }_1(\vartheta ,\rho )={\phi }^{*}+\rho cosh\vartheta ,\hfill \\ {\xi }_2(\vartheta ,\rho )={\vartheta }^{*}\left(\frac{\varrho sinh2\vartheta }{2}\right)+\rho cos\left[{sin}^{-1}\left(\frac{\varrho sinh2\vartheta }{2}\right)\right]sinh\vartheta ,\hfill \\ {\xi }_3(\vartheta ,\rho )={\vartheta }^{*}cos\left[{sin}^{-1}\left(\frac{\varrho sinh2\vartheta }{2}\right)\right]-\rho \frac{\varrho sinh2\vartheta }{2}sinh\vartheta .\hfill \end{array}\right\}$$

(95)

For epitome, via Equations (94) and (95), we have

(1)

Hyperbolic spherical inflection curve with its inflection timelike ruled surface: for $\omega =0.3$, ${\vartheta }^{*}=1,$${\phi }^{*}=0$, $-1.3\le \vartheta \le 1.3,$$-5\le v\le 5$ (Figure 9 and Figure 10).

Figure 9. Hyperbolic inflection curve with $\omega =0.3$.

Figure 10. $\mathbb{T}-like$ Inflection ruled surface.

(2)

Hyperbolic spherical inflection curve with its inflection $\mathbb{T}-like$ ruled surface: for $\omega =-0.3$, ${\vartheta }^{*}=1,$${\phi }^{*}=0$, $-1.3\le \vartheta \le 1.3,$$-5\le v\le 5$ (Figure 11 and Figure 12).

Figure 11. Hyperbolic inflection curve with $\omega =-0.3$.

Figure 12. $\mathbb{T}-like$ Inflection ruled surface.

5. Conclusions

In this paper, the kinematic-geometry of a $\mathbb{T}-like$ trajectory is defined in terms of the axodes invariants of one-parameter hyperbolic spatial locomotion. Then, a new $\mathbb{DF}$ of a $\mathbb{T}-like$ line-trajectory is gained in distinct forms. In symmetry with the plane and spherical locomotions, a new $\mathbb{T}-like$ congruence is pointed and investigated in detail. The main result in this paper is to generalize the $\mathbb{ES}$ formula in the hyperbolic locomotion. We introduced the dual angle, which is represented in Equation (36), and we restricted it to be steady up to 2nd order. Hence, we obtain Equation (39), which introduces the $\mathbb{DA}$. Through this equation, we gave corollary 2 and corollary 3. Also, we reformulated $\mathbb{ES}$ formula for the axodes in a new form given in Equations (47)–(49). Furthermore, in Section 4 of this work, we defined and studied inflection $\mathbb{T}-like$ line congruence, which is the spatial synonym of the inflection circle of planer kinematics. The findings presented in this study have the potential to make significant contributions to the field of spatial locomotion, as well as offer practical applications in the domains of mechanical mathematics and engineering. In our forthcoming research, we intend to explore various applications of the kinematic-geometry of one-parameter hyperbolic spatial locomotion in conjunction with singularity theory, submanifold theory, etc., in [22,23,24,25] in order to derive additional novel findings and properties.