Optimal Treatment Strategy for Cancer Based on Mathematical Modeling and Impulse Control Theory

Abstract

Adaptive therapy is a new type of cancer treatment in which time and dose are dynamically changed according to different individuals, which is very different from conventional cancer treatment strategies that use the maximum dose to kill the tumor cells. However, how to determine the time and dose of drug treatment is a challenging problem. In this paper, a competition model between drug-sensitive cells and drug-resistant cells was established, in which pulse intervention was introduced. In addition, based on the theory of pulse optimal control, three pulse optimal control strategies are proposed in the process of cancer treatment by controlling the pulse interval and dose, minimizing the number of tumor cells at the end of the day at minimal cost. Finally, three optimization strategies were compared, using numerical simulation, in terms of tumor burden and the effect on drug-resistant cells. The results show that the hybrid control strategy has the best effect. This work would provide some new ideas for the treatment of cancer.

1. Introduction

Cancer is the leading cause of death in most countries and regions in the world, and China ranks first in the number of cancer deaths in the world [1]. How to treat this kind of disease more effectively has become the problem that many scholars study. In reference [2], MTD therapy mainly controls tumor burden by killing sensitive subpopulations with high frequency administration. In references [3,4], adaptive therapy, as a new approach to cancer therapy, exploits the competitive interaction between drug-sensitivity and drug-resistance subpopulations; a stable tumor burden is maintained by allowing a large number of therapy-sensitive cells to survive. However, with the continuation of the treatment cycle, there will be a large number of drug-resistant cells, and this will ultimately lead to treatment failure [5,6] as scholars continue to study and refine. In reference [7], treatment time was shortened by adjusting tumor baseline burden based on a competing model of three different prostate cancer cell populations. In reference [8], a competitive model of drug sensitivity and drug resistance of tumor cells was established. A new dynamic optimization problem with constraints was proposed to dynamically adjust the treatment cycle and adaptive treatment dose for prostate cancer. In reference [9], the benefits of adaptive therapy were enhanced by considering the benefits of intratumoral competition and tumor control, killing sensitive cells, assessing the time to stop the treatment cycle, and switching to high-frequency dosing.

The pulse phenomenon is that, for some reason, the state of the system will change or be destroyed in a short time, thus changing the original trajectory. At present, many achievements have been made in the research of pulse effect in the model [10]. However, pulse therapy is rare in cancer treatment. In the tumor system, sensitive cells are easily regulated by drugs, while resistant cells can only be regulated indirectly by sensitive cells. Therefore, the number of sensitive cells significantly decreased after pulse administration, further regulating the number of drug-resistant cells. Based on this, a competition model with an impulsive effect between sensitive cells and drug-resistant cells was established in this paper. The time and dose of pulse administration were further studied. At present, the analysis of pulse optimal control theory and numerical techniques have been well developed. Taking references [11,12,13,14,15,16] as examples, the theory and method of pulse optimization were introduced in detail, and the time scale transformation method was widely used in pulse time optimization. The aim of this paper is to select the optimal pulse time and dose in finite time according to the pulse optimal control theory, and to minimize the drug cost and the final tumor burden.

The structure of this paper is as follows. In Section 2, a competitive model of drug-sensitive and drug-resistant cells after pulse intervention is established, and the model is analyzed theoretically. In Section 3, by means of time scaling and translation, three optimal control strategies, based on different pulse intervention time and dosage, are proposed in finite time by using a gradient calculation. In Section 4, based on numerical simulation, three control strategies are compared in terms of tumor burden and the number of drug-resistant cells, and the most effective control strategy is proposed. In the fifth part, a simple conclusion is drawn.

2. Mathematical Model and Its Theoretical Analysis

2.1. A Competition Model for Sensitive and Resistant Cells with Impulsive Effects

First, considering the interaction between prostate cancer cell lines, Liu et al. [8] established a competitive model for sensitive and resistant cells, as shown below.

$$\left\{\begin{array}{c}{\displaystyle \frac{d{T}_1\left(t\right)}{dt}={\lambda }_1{T}_1\left[1-\frac{T_1{a}_{11}+T_2{a}_{12}(1+\alpha \beta \left(t\right))}{K_1}\right]-{\mu }_1{T}_1,}\hfill \\ {\displaystyle \frac{d{T}_2\left(t\right)}{dt}={\lambda }_2{T}_2\left[1-\frac{T_1{a}_{21}+T_2{a}_{22}}{K_2}\right]-{\mu }_2{T}_2.}\hfill \end{array}\right.$$

(1)

where $T_1$ represents drug-sensitive cells, $T_2$ represents drug-resistant cells, ${\lambda }_1$ and ${\lambda }_2$ represent the net growth rate of cells, $K_1$ represents the environmental capacity of drug-sensitive cancer cells, $K_2$ represents the environmental capacity of drug-resistant cancer cells, ${\mu }_1$ and ${\mu }_2$ represent the natural mortality of cells, ${\left(a_{ij}\right)}_{2\times 2}$ represents competition between sensitive and resistant cells, $\alpha$ represents the patient’s sensitivity to the targeted drug, and $\beta$ is the drug dose.

Considering the impact of impulsive intervention on the model, the following model is obtained:

$$\left\{\begin{array}{c}\left.\begin{array}{c}{\displaystyle \frac{d{T}_1\left(t\right)}{dt}={\lambda }_1{T}_1\left[1-\frac{T_1{a}_{11}+T_2{a}_{12}}{K_1}\right]-{\mu }_1{T}_1,}\hfill \\ {\displaystyle \frac{d{T}_2\left(t\right)}{dt}={\lambda }_2{T}_2\left[1-\frac{T_1{a}_{21}+T_2{a}_{22}}{K_2}\right]-{\mu }_2{T}_2,}\hfill \end{array}\right\}t\ne t_k,\hfill \\ \left.\begin{array}{c}{\displaystyle T_1\left(t_k^{+}\right)=(1-p_k)T_1\left(t_k\right),}\hfill \\ {\displaystyle T_2\left(t_k^{+}\right)=(1+q_k)T_2\left(t_k\right),}\hfill \end{array}\right\}t=t_k,k=1,2,\dots ,n-1.\hfill \end{array}\right.$$

(2)

Having initial conditions of

$$T_1\left(0\right)=T_{10},T_2\left(0\right)=T_{20}.$$

where $t_k$ is the pulse time, $p_k, k=1,2,\dots ,n-1$ is the dosage, and $q_k, k=1,2,\dots ,n-1$ is an increase in drug-resistant cells; ${\lambda }_1$, ${\lambda }_2$, $K_1$, $K_2$, ${\mu }_1$, ${\mu }_2$ $p_k$, $q_k$, and ${\left(a_{ij}\right)}_{2\times 2}$ are constant.

2.2. Preliminaries

First, we will introduce and prove some theorems of the Lotka–Volterra model with impulsive effects [17,18,19], which are important to our follow-up results.

We consider the subsystem of the model

$$\left\{\begin{array}{c}{\displaystyle \frac{d{T}_1\left(t\right)}{dt}=T_1\left(t\right)\left[({\lambda }_1-{\mu }_1)-{\displaystyle \frac{{\lambda }_1{a}_{11}}{K_1}}{T}_1\left(t\right)\right],t\ne t_k,}\hfill \\ {\displaystyle T_1\left(t_k^{+}\right)=(1-p_k)T_1\left(t_k\right),t=t_k, k=1,2,\dots ,n-1.}\hfill \end{array}\right.$$

(3)

Theorem 1.

If there are constants ${\eta }_i(i=1,2)$ such that

$$({\lambda }_1-{\mu }_1){\eta }_i+\underset{t\to +\infty }{lim\; inf}\sum _{t\le t_k<t+{\eta }_i}ln(1-p_k)>0,$$

(4)

$$h_1(t,\tau )=\sum _{t\le t_k<t+\tau }ln(1-p_k),$$

(5)

$h_1(t,\tau )$ is a bounded function on $t\in R_{+}$, $0\le \tau \le max\left\{{\eta }_1,{\eta }_2\right\}$. Then,

(1) There are constants m and M such that

$$m\le \underset{t\to +\infty }{lim\; inf}{T}_1\left(t\right)\le \underset{t\to +\infty }{lim\; sup}{T}_1\left(t\right)\le M,$$

(6)

where $T_1\left(t\right)$ is any solution of a subsystem (3).

(2)$\underset{t\to +\infty }{lim}(T_{11}\left(t\right)-T_{12}\left(t\right))=0$, where $T_{11}\left(t\right)$ and $T_{12}\left(t\right)$ are two arbitrary solutions of a subsystem (3).

Proof. 

For convenience, let $({\lambda }_1-{\mu }_1)=a$, ${\displaystyle \frac{{\lambda }_1{a}_{11}}{K_1}}=b$. By conditions (4) and (5), there are constants $m_1$ and $m_2$, $\delta$ and $T_0$, such that for all $t\ge T_0$, we can get

$${\int }_t^{t+{\eta }_1}(a-b{m}_1)ds+\sum _{t\le t_k<t+{\eta }_1}ln(1-p_k)<-\delta ,$$

$${\int }_t^{t+{\eta }_2}(a-b{m}_2)ds+\sum _{t\le t_k<t+{\eta }_2}ln(1-p_k)>\delta .$$

Because $h_1(t,\tau )$ is a bounded function on $t\in R_{+}$, $0\le \tau \le max\left\{{\eta }_1,{\eta }_2\right\}$, there is a constant $Y_1$ such that for any $t\in R_{+}$.

$$|h_1(t,\tau )|=|\sum _{t\le t_k<t+\tau }ln(1-p_k)|<Y_1.$$

Let $T_1\left(t\right)$ be any solution of a subsystem (3). If $T_1\left(t\right)\ge m_1$, for $t\ge T^{{}^{\prime }}$, there is $t=T^{{}^{\prime }}+\kappa \eta$, when $\kappa >0$ is an integer, from $T^{{}^{\prime }}$ to t, to solve subsystem (3), we can get

$$\begin{array}{cc}\hfill T_1\left(t\right)& =T_1\left(T^{{}^{\prime }}\right)\prod _{T^{{}^{\prime }}<t_k<t}(1-p_k)exp{\int }_{T^{{}^{\prime }}}^t(a-b{T}_1\left(s\right))ds\hfill \\ \hfill & =T_1\left(T^{{}^{\prime }}\right)exp({\int }_{T^{{}^{\prime }}}^t(a-b{T}_1\left(s\right))ds+\sum _{T^{{}^{\prime }}\le t_k<t}ln(1-p_k))\hfill \\ \hfill & \le T_1\left(T^{{}^{\prime }}\right))exp({\int }_{T_0}^{T^{{}^{\prime }}+{\eta }_1}(a-b{m}_1)ds+\sum _{T^{{}^{\prime }}\le t_k<T^{{}^{\prime }}+{\eta }_1}ln(1-p_k))+\dots \hfill \\ \hfill & +{\int }_{T^{{}^{\prime }}+(\kappa -1){\eta }_1}^{T^{{}^{\prime }}+{\eta }_1}(a-b{m}_1)ds+\sum _{T^{{}^{\prime }}+(\kappa -1){\eta }_1\le t_k<T^{{}^{\prime }}+{\eta }_1}ln(1-p_k))\hfill \\ \hfill & =T_1\left(T^{{}^{\prime }}\right)exp(H_1+\sum _{T^{{}^{\prime }}\le t_k<T^{{}^{\prime }}+{\eta }_1}ln(1-p_k)+\dots \hfill \\ \hfill & +H_1+\sum _{T^{{}^{\prime }}+(\kappa -1){\eta }_1\le t_k<T^{{}^{\prime }}+\kappa \eta }ln(1-p_k\left)\right)\hfill \\ \hfill & \le T_1\left(T^{{}^{\prime }}\right)exp\left(-\kappa \delta \right),\hfill \end{array}$$

where $H_1=((a-b{m}_1){\eta }_1),$ when $\kappa \to \infty$, $T_1\left(t\right)\to 0$, this is a contradictory.

If $T_1\left(t\right)$ oscillates with respect to $m_1$, we can choose two sequences $\left\{{\gamma }_n\right\}$ and $\left\{{\gamma }_n^{*}\right\}$ which satisfy

$$\begin{array}{c}0<{\gamma }_1<{\gamma }_1^{*}<\dots <{\gamma }_n<{\gamma }_n^{*}<\dots ,\\ {\displaystyle \underset{n\to +\infty }{lim}}{\gamma }_n={\displaystyle \underset{n\to +\infty }{lim}}{{\gamma }_n}^{*}=\infty ,\end{array}$$

(7)

$$T_1\left({\gamma }_n\right)\le m_1,T_1\left({\gamma }_n^{+}\right)\ge m_1,T_1\left({\gamma }_n^{*}\right)\ge m_1,T_1\left({\gamma }_n^{{*}^{+}}\right)\le m_1,$$

(8)

$$T_1\left(t\right)\ge m_1,t\in ({\gamma }_n,{\gamma }_n^{*}),T_1\left(t\right)\le m_1,t\in ({\gamma }_n^{*},{\gamma }_{n+1}).$$

(9)

Therefore, when n is large enough, ${\gamma }_n\ge T^{{}^{\prime }}$, then for $t\in ({\gamma }_n,{\gamma }_n^{*})$, there is

$$\dot{T_1\left(t\right)}\le T_1\left(t\right)\left(a-b{m}_1\right), t\ne t_k.$$

(10)

Select an integer $\kappa$, where $t={\gamma }_n+\kappa {\eta }_1+{\mu }_1$ and $0\le {\mu }_1<{\eta }_1$, with

$$\begin{array}{cc}\hfill T_1\left(t\right)& =T_1\left({\gamma }_n\right)exp\left({\int }_{{\gamma }_n}^t(a-b{T}_1\left(s\right))ds+\sum _{{\gamma }_n\le t_k<t}ln(1-p_k)\right)\hfill \\ \hfill & \le m_{1}exp({\int }_{{\gamma }_n}^{{\gamma }_n+{\eta }_1}(a-b{m}_1)ds+\sum _{{\gamma }_n\le t_k<{\gamma }_n+{\eta }_1}ln(1-p_k))+\dots \hfill \\ \hfill & +{\int }_{{\gamma }_n+(\kappa -1){\eta }_1}^{{\gamma }_n+\kappa {\eta }_1}(a-b{m}_1)ds+\sum _{{\gamma }_n+(\kappa -1){\eta }_1\le t_k<\gamma +\kappa {\eta }_1}ln(1-p_k))\hfill \\ \hfill & +{\int }_{{\gamma }_n+\kappa {\eta }_1}^{{\gamma }_n+\kappa {\eta }_1+{\mu }_1}(a-b{m}_1)ds+\sum _{{\gamma }_n+\kappa {\eta }_1\le t_k<\gamma +\kappa {\eta }_1+{\mu }_1}ln(1-p_k))\hfill \\ \hfill & =m_{1}exp(H_1+\sum _{{\gamma }_n\le t_k<{\gamma }_n+{\eta }_1}ln(1-p_k)+\dots \hfill \\ \hfill & +H_1+\sum _{{\gamma }_n+(\kappa -1){\eta }_1\le t_k<{\gamma }_n+\kappa {\eta }_1}ln(1-p_k\left)\right)\hfill \\ \hfill & +{\int }_{{\gamma }_n+\kappa {\eta }_1}^{{\gamma }_n+\kappa {\eta }_1+{\mu }_1}(a-b{m}_1)ds+\sum _{{\gamma }_n+\kappa {\eta }_1\le t_k<\gamma +\kappa {\theta }_1+{\mu }_1}ln(1-p_k))\hfill \\ \hfill & \le m_{1}exp((-\kappa \delta )+{\int }_{{\gamma }_n+\kappa {\eta }_1}^{{\gamma }_n+\kappa {\eta }_1+{\mu }_1}(a-b{m}_1)ds\hfill \\ \hfill & +\sum _{{\gamma }_n+\kappa {\eta }_1\le t_k<\gamma +\kappa {\eta }_1+{\mu }_1}ln(1-p_k))\hfill \\ \hfill & \le m_{1}exp\left((a-b{m}_1){\mu }_1+Y_1\right)\hfill \\ \hfill & =m_{1}exp(H_1+Y_1),\hfill \end{array}$$

where $H_1=((a-b{m}_1){\eta }_1)$. About $t\in ({\gamma }_n^{*},{\gamma }_{n+1})$, there is $T_1\left(t\right)\le m_1\le m_{1}exp(H_1+Y_1)$. Therefore, we have $T_1\left(t\right)<m_1\le m_{1}exp(H_1+Y_1)$, $t\ge T_0$.

Now prove that $m\le \underset{t\to +\infty }{lim\; inf}{T}_1\left(t\right)$. If $T^{{}^{″}}>T^{{}^{\prime }}$, there is $T_1\left(t\right)\le m_2$, then for $t\ge T^{{}^{″}}+\kappa \eta$, where $\kappa \ge 0$ is an integer. We can get

$$\begin{array}{cc}\hfill T_1\left(t\right)& =T_1\left(T^{{}^{″}}\right)\prod _{T^{{}^{\prime }}<t_k<t}(1-p_k)exp{\int }_{T^{{}^{″}}}^t(a-b{T}_1\left(s\right))ds\hfill \\ \hfill & =T_1\left(T^{{}^{″}}\right)exp\left({\int }_{T^{{}^{″}}}^t(a-b{T}_1\left(s\right))ds+\sum _{T^{{}^{″}}\le t_k<t}ln(1-p_k)\right)\hfill \\ \hfill & \ge T_1\left(T^{{}^{″}}\right)exp({\int }_{T^{{}^{″}}}^{T^{{}^{″}}+{\eta }_2}(a-b{m}_2)ds+\sum _{T^{{}^{″}}\le t_k<T^{{}^{″}}+{\eta }_2}ln(1-p_k))+\dots \hfill \\ \hfill & +{\int }_{T^{{}^{″}}+(\kappa -1){\eta }_2}^{T^{{}^{″}}+\kappa {\eta }_2}(a-b{m}_2)ds+\sum _{T^{{}^{″}}+(\kappa -1){\eta }_2\le t_k<T^{{}^{″}}+\kappa {\eta }_2}ln(1-p_k))\hfill \\ \hfill & =T_1\left(T^{{}^{″}}\right)exp(H_2+\sum _{T^{{}^{″}}\le t_k<T^{{}^{″}}+{\eta }_2}ln(1-p_k)+\dots \hfill \\ \hfill & +H_2+\sum _{T^{{}^{″}}+(\kappa -1){\eta }_2\le t_k<T^{{}^{″}}+\kappa {\eta }_2}ln(1-p_k\left)\right)\hfill \\ \hfill & \ge T_1\left(T^{{}^{″}}\right)exp\left(\kappa \delta \right),\hfill \end{array}$$

where $H_2=((a-b{m}_2){\eta }_2),$ when $\kappa \to \infty$, $T_1\left(t\right)\to \infty$, this is contradictory.

If $T_1\left(t\right)$ oscillates with respect to $m_2$, we can choose two sequences $\left\{{\gamma }_n\right\}$ and $\left\{{\gamma }_n^{*}\right\}$ which satisfy

$$\begin{gathered} 0<{\gamma }_1<{\gamma }_1^{*}<\dots <{\gamma }_n<{\gamma }_n^{*}<\dots , \\ \underset{n\to +\infty }{lim}{\gamma }_n=\underset{n\to +\infty }{lim}{{\gamma }_n}^{*}=\infty , \end{gathered}$$

(11)

$$T_1\left({\gamma }_n\right)\ge m_2,T_1\left({\gamma }_n^{+}\right)\le m_2,T_1\left({\gamma }_n^{*}\right)\le m_2,T_1\left({\gamma }_n^{{*}^{+}}\right)\ge m_2,$$

(12)

$$T_1\left(t\right)\le m_2,t\in ({\gamma }_n,{\gamma }_n^{*}),T_1\left(t\right)\ge m_2,t\in ({\gamma }_n^{*},{\gamma }_{n+1}).$$

(13)

Therefore, when n is large enough, ${\gamma }_n\ge T^{{}^{″}}$, then for $t\in ({\gamma }_n,{\gamma }_n^{*})$, there is $\dot{T_1\left(t\right)}\ge T_1\left(t\right)\left(a-b{m}_2\right)$, $t\ne t_k$. Select an integer $\kappa$, where $t={\gamma }_n+\kappa {\eta }_2+{\mu }_2$ and $0\le {\mu }_2<{\eta }_2$, with

$$\begin{array}{cc}\hfill T_1\left(t\right)& =T_1\left({\gamma }_n\right)exp\left({\int }_{{\gamma }_n}^t(a-b{T}_1\left(s\right))ds+\sum _{{\gamma }_n\le t_k<t}ln(1-p_k)\right)\hfill \\ \hfill & \ge m_{2}exp({\int }_{{\gamma }_n}^{{\gamma }_n+{\eta }_2}(a-b{m}_2)ds+\sum _{{\gamma }_n\le t_k<{\gamma }_n+{\eta }_2}ln(1-p_k))+\dots \hfill \\ \hfill & +{\int }_{{\gamma }_n+(\kappa -1){\eta }_2}^{{\gamma }_n+\kappa {\eta }_2}(a-b{m}_2)ds+\sum _{{\gamma }_n+(\kappa -1){\eta }_2\le t_k<{\gamma }_n+\kappa {\eta }_2}ln(1-p_k))\hfill \\ \hfill & +{\int }_{{\gamma }_n+\kappa {\eta }_2}^{{\gamma }_n+\kappa {\eta }_2+{\mu }_2}(a-b{m}_2)ds+\sum _{{\gamma }_n+\kappa {\eta }_2\le t_k<{\gamma }_n+\kappa {\eta }_2+{\mu }_2}ln(1-p_k))\hfill \\ \hfill & =m_{2}exp(H_2+\sum _{{\gamma }_n\le t_k<{\gamma }_n+{\eta }_2}ln(1-p_k)+\dots \hfill \\ \hfill & +H_2+\sum _{{\gamma }_n+(\kappa -1){\eta }_2\le t_k<{\gamma }_n+\kappa {\eta }_2}ln(1-p_k\left)\right)\hfill \\ \hfill & +{\int }_{{\gamma }_n+\kappa {\eta }_2}^{{\gamma }_n+\kappa {\eta }_2+{\mu }_2}(a-b{m}_2)ds+\sum _{{\gamma }_n+\kappa {\eta }_2\le t_k<\gamma +\kappa {\eta }_2+{\mu }_2}ln(1-p_k))\hfill \\ \hfill & \ge m_{2}exp(\left(\kappa \delta \right)+{\int }_{{\gamma }_n+\kappa {\eta }_2}^{{\gamma }_n+\kappa {\eta }_2+{\mu }_2}(a-b{m}_2)ds\hfill \\ \hfill & +\sum _{{\gamma }_n+\kappa {\eta }_2\le t_k<\gamma +\kappa {\eta }_2+{\mu }_2}ln(1-p_k))\hfill \\ \hfill & \ge m_{2}exp\left((a-b{m}_2){\mu }_2+Y_1\right)\hfill \\ \hfill & \ge m_{2}exp(-H_2-Y_1),\hfill \end{array}$$

where $H_2=((a-b{m}_2){\eta }_2).$ About $t\in ({\gamma }_n^{*},{\gamma }_{n+1})$, there is $T_1\left(t\right)\ge m_2\ge m_{2}exp(-H_2-Y_1)$.

Therefore, we have $T_1\left(t\right)\ge m_{2}exp(-H_2-Y_1)$, $t\ge T^{{}^{\prime }}$, then the assertion (1) is completed. Next, we prove any two solutions $T_{11}\left(t\right)$ and $T_{12}\left(t\right)$ of a subsystem to satisfy

$$\underset{t\to +\infty }{lim}(T_{11}\left(t\right)-T_{12}\left(t\right))=0.$$

(14)

Selecting any constants $M_1$ and $M_2$, from assertion (1) we can get

$$M_1\le T_{11}\left(t\right),T_{12}\left(t\right)\le M_2,t\ge 0.$$

(15)

Selecting a Lyapunov function $V\left(t\right)=|ln{T}_{11}\left(t\right)-ln{T}_{12}\left(t\right)\left)\right|$, $V\left(t\right)$ is a bounded function on $R_{+}$. According to the subsystem (3), there is

$V\left(t_k^{+}\right)=|ln(1-p_k)T_{11}\left(t_k\right)-ln(1-p_k)T_{12}\left(t_k\right)\left)\right|=V\left(t_k\right).$

$$\begin{array}{cc}\hfill D^{+}V& =sign(T_{11}\left(t\right)-T_{12}\left(t\right))\left[{\displaystyle \frac{{\dot{T}}_{11}\left(t\right)}{T_{11}\left(t\right)}}-{\displaystyle \frac{{\dot{T}}_{12}\left(t\right)}{T_{12}\left(t\right)}}\right]\hfill \\ \hfill & =sign(T_{11}\left(t\right)-T_{12}\left(t\right)){\displaystyle \frac{T_{11}\left[a-b{T}_{11}\right]}{T_{11}}}-{\displaystyle \frac{T_{12}\left[a-b{T}_{12}\right]}{T_{12}}}\hfill \\ \hfill & =-b|T_{11}-T_{12}|\hfill \\ \hfill & <-b{M}_{1}V\left(t\right).\hfill \end{array}$$

(16)

Therefore, $V\left(t\right)\le V\left(0\right)exp(-b{M}_{1}t)$. Then, when $t\to \infty$, $V\left(t\right)\to 0$. The assertion (2) is completed. □

2.3. Theoretical Analysis

In this section, we prove the permanence and global attractiveness of the model by using the knowledge of preparation. First, the permanence of system (2) is proved.

There are two subsystems:

$$\left\{\begin{array}{c}{\displaystyle \frac{d{T}_1\left(t\right)}{dt}=T_1\left(t\right)\left[({\lambda }_1-{\mu }_1)-{\displaystyle \frac{{\lambda }_1{a}_{11}}{K_1}}{T}_1\left(t\right)\right],t\ne t_k,}\hfill \\ {\displaystyle T_1\left(t_k^{+}\right)=(1-p_k)T_1\left(t_k\right),t=t_k,k=1,2,\dots ,n-1,}\hfill \end{array}\right.$$

(17)

$$\left\{\begin{array}{c}{\displaystyle \frac{d{T}_2\left(t\right)}{dt}=T_2\left(t\right)\left[({\lambda }_2-{\mu }_2)-{\displaystyle \frac{{\lambda }_2{a}_{22}}{K_2}}{T}_2\left(t\right)\right],t\ne t_k,}\hfill \\ {\displaystyle T_2\left(t_k^{+}\right)=(1+q_k)T_2\left(t_k\right),t=t_k,k=1,2,\dots ,n-1.}\hfill \end{array}\right.$$

(18)

For solutions $T_1^{*}\left(t\right)$ and $T_2^{*}\left(t\right)$ of (17) and (18), the permanence of system (2) is obtained as follows:

Theorem 2.

If there are constants ${\theta }_i(i=1,2)$ such that

$$\underset{t\to +\infty }{lim\; inf}\left({\int }_t^{t+{\theta }_1}(({\lambda }_1-{\mu }_1)-{\displaystyle \frac{{\lambda }_1{a}_{12}}{K_1}}{T_2}^{*}\left(s\right))ds+\sum _{t\le t_k<t+{\theta }_1}ln(1-p_k)\right)>0,$$

(19)

$$\underset{t\to +\infty }{lim\; inf}\left({\int }_t^{t+{\theta }_2}(({\lambda }_2-{\mu }_2)-{\displaystyle \frac{{\lambda }_2{a}_{21}}{K_2}}{T_1}^{*}\left(s\right))ds+\sum _{t\le t_k<t+{\theta }_2}ln(1+q_k)\right)>0,$$

(20)

$$\begin{array}{cc}\hfill h_1(t,\tau )& =\sum _{t\le t_k<t+\tau }ln(1-p_k),\hfill \\ \hfill h_2(t,\tau )& =\sum _{t\le t_k<t+\tau }ln(1+q_k).\hfill \end{array}$$

$h_1(t,\tau )$ and $h_2(t,\tau )$ is bounded on $t\in R_{+}$, and $0\le \tau \le max\left\{{\theta }_i,{\eta }_i\right\}$.

Then, the system (2) is permanence. There are normal numbers m and M, so that any positive solution $Z\left(t\right)=(T_1\left(t\right),T_2\left(t\right))$ of system (2), we have

$$\begin{array}{c}\hfill m\le \underset{t\to +\infty }{lim\; inf}{T}_1\left(t\right)\le \underset{t\to +\infty }{lim\; sup}{T}_1\left(t\right)\le M,\\ \hfill m\le \underset{t\to +\infty }{lim\; inf}{T}_2\left(t\right)\le \underset{t\to +\infty }{lim\; sup}{T}_2\left(t\right)\le M.\end{array}$$

Proof. 

For convenience, let $({\lambda }_1-{\mu }_1)=a, {\displaystyle \frac{{\lambda }_1{a}_{11}}{K_1}}=b, {\displaystyle \frac{{\lambda }_1{a}_{12}}{K_1}}=c, ({\lambda }_2-{\mu }_2)=d,$ ${\displaystyle \frac{{\lambda }_2{a}_{21}}{K_2}}=e, {\displaystyle \frac{{\lambda }_2{a}_{22}}{K_2}}=f$. According to the conditions (19) and (20), it can be seen that there are two positive constants ${\psi }_0$ and T, so that for all $t\ge T$. We can get

$$\begin{array}{c}\hfill {\int }_t^{t+{\theta }_1}a-c({T_2}^{*}\left(s\right)+{\psi }_0)ds+\sum _{t\le t_k<t+{\theta }_1}ln(1-p_k)>{\psi }_0,\\ \hfill {\int }_t^{t+{\theta }_2}d-e({T_1}^{*}\left(s\right)+{\psi }_0)ds+\sum _{t\le t_k<t+{\theta }_2}ln(1+q_k)>{\psi }_0.\end{array}$$

Since $h_1$ and $h_2$ is bounded on $t\in R_{+}$, where $0\le \tau \le max\left\{{\theta }_i,{\eta }_i\right\}$, then there are constants $Y_1,Y_2$ such that

$$|h_1(t,\tau )|=|\sum _{t\le t_k<t+\tau }ln(1-p_k)|<Y_1,$$

$$|h_2(t,\tau )|=|\sum _{t\le t_k<t+\tau }ln(1+q_k)|<Y_2.$$

Let $Z\left(t\right)=(T_1\left(t\right),T_2\left(t\right))$ be any positive solution of the system (2). Since

$$\dot{T_1\left(t\right)}\le T_1\left(t\right)\left(a-b{T}_1\left(t\right)\right),t\ne t_k.$$

(21)

According to the comparison theorem, when there is $t\ge 0$, $T_1\left(t\right)\le \varphi \left(t\right)$, where $\varphi \left(t\right)$ is the positive solution of the system (17), the initial condition $\varphi \left(0\right)=T_1\left(0\right)$, according to Theorem 1, there is a positive constant $T^1\ge T$, when $t\ge T^1$

$$T_1\left(t\right)\le {T_1}^{*}\left(t\right)+{\psi }_0.$$

(22)

Choosing the constant $M_1=sup\left\{{T_1}^{*}\left(t\right)+{\psi }_0\right\}$, then $0<M_1<\infty$, obviously for all $t\ge T^1$, there is $T_1\left(t\right)\le M_1$.

Similarly, we can obtain $T_2\left(t\right)\le M_2=sup\left\{{T_2}^{*}\left(t\right)+{\psi }_0,t\in R_{+}\right\}$, choose $M=max\left\{M_1,M_2\right\}$, then

$$\underset{t\to +\infty }{lim\; sup}{T}_1\left(t\right)<M_1,\underset{t\to +\infty }{lim\; sup}{T}_2\left(t\right)<M_2.$$

(23)

Now we prove

$$m_1\le \underset{t\to +\infty }{lim\; inf}{T}_1\left(t\right),m_2\le \underset{t\to +\infty }{lim\; inf}{T}_2\left(t\right).$$

If there is $T_1\left(t\right)\le {\psi }_0$ for all $t\ge T^2\ge T$, then for $t=T^2+\kappa {\theta }_1$, where $\kappa >0$ is an integer. We can get

$$\begin{array}{cc}\hfill T_1\left(t\right)& =T_1\left(T^2\right)exp({\int }_{T^2}^t(a-b{T}_1\left(s\right)-c{T}_2\left(s\right))ds+\sum _{T^2\le t_k<t}ln(1-p_k))\hfill \\ \hfill & \ge T_1\left(T^2\right)exp({\int }_{T^2}^{T^2+{\theta }_1}(a-b{\psi }_0-c({T_2}^{*}\left(s\right)+{\psi }_0))ds\hfill \\ \hfill & +\sum _{T^2\le t_k<T^2+{\theta }_1}ln(1-p_k))+\dots +{\int }_{T^2+(\kappa -1){\theta }_1}^{T^2+\kappa {\theta }_1}(a-b{\psi }_0-c({T_2}^{*}\left(s\right)+{\psi }_0))ds\hfill \\ \hfill & +\sum _{T^2+(\kappa -1){\theta }_1\le t_k<T^2+\kappa {\theta }_1}ln(1-p_k))\hfill \\ \hfill & \ge T_1\left(T^2\right)exp(\kappa {\psi }_0+Y_1).\hfill \end{array}$$

Then, when $\kappa \to \infty$ has $T_1\left(t\right)\to \infty$, this is a contradiction.

If $T_1\left(t\right)$ oscillates with respect to ${\psi }_0$, we can choose two sequences $\left\{{\gamma }_n\right\}$ and $\left\{{\gamma }_n^{*}\right\}$ which satisfy

$$0<{\gamma }_1<{\gamma }_1^{*}<\dots <{\gamma }_n<{\gamma }_n^{*}<\dots ,\underset{n\to +\infty }{lim}{\gamma }_n=\underset{n\to +\infty }{lim}{{\gamma }_n}^{*}=\infty ,$$

$$T_1\left({\gamma }_n\right)\ge {\psi }_0,T_1\left({\gamma }_n^{+}\right)\le {\psi }_0,T_1\left({\gamma }_n^{*}\right)\le {\psi }_0,T_1\left({\gamma }_n^{{*}^{+}}\right)\ge {\psi }_0,$$

$$T_1\left(t\right)\le {\psi }_0,t\in ({\gamma }_n,{\gamma }_n^{*}),T_1\left(t\right)\ge {\psi }_0,t\in ({\gamma }_n^{*},{\gamma }_{n+1}).$$

Therefore, when n is large enough, ${\gamma }_n\ge T$, then for $t\in ({\gamma }_n,{\gamma }_n^{*})$, there is $\dot{T_1\left(t\right)}\ge T_1\left(t\right)\left(a-b{\psi }_0-c({T_2}^{*}\left(s\right)+{\psi }_0)\right),t\ne t_k$. Select an integer $\kappa \ge 0$, where $t={\gamma }_n+\kappa {\theta }_1+{\epsilon }_1$ and $0\le {\epsilon }_1<{\theta }_1$, with

$$\begin{array}{cc}\hfill T_1\left(t\right)& =T_1\left({\gamma }_n\right)exp\left({\int }_{{\gamma }_n}^t\left(a-b{T}_1\left(s\right)-c{T}_2\left(s\right)\right)ds+\sum _{{\gamma }_n\le t_k<t}ln(1-p_k)\right)\hfill \\ \hfill & \ge {\psi }_{0}exp({\int }_{{\gamma }_n}^{{\gamma }_n+{\theta }_1}(a-b{\psi }_0-c({T_2}^{*}\left(s\right)+{\psi }_0)ds\hfill \\ \hfill & +\sum _{{\gamma }_n\le t_k<{\gamma }_n+{\theta }_1}ln(1-p_k))+\dots +{\int }_{{\gamma }_n+(\kappa -1){\theta }_1}^{{\gamma }_n+\kappa {\theta }_1}(a-b{\psi }_0-c({T_2}^{*}\left(s\right)+{\psi }_0)ds\hfill \\ \hfill & +\sum _{{\gamma }_n+(\kappa -1){\theta }_1\le t_k<{\gamma }_n+\kappa {\theta }_1}ln(1-p_k))+{\int }_{{\gamma }_n+\kappa {\theta }_1}^{{\gamma }_n+\kappa {\theta }_1+{\epsilon }_1}(a-b{\psi }_0-c({T_2}^{*}\left(s\right)+{\psi }_0)ds\hfill \\ & +\sum _{{\gamma }_n+\kappa {\theta }_1\le t_k<{\gamma }_n+\kappa {\theta }_1+{\epsilon }_1}ln(1-p_k))\hfill \\ \hfill & \ge {\psi }_{0}exp(-{\beta }_1{\theta }_1-Y_1),\hfill \end{array}$$

where ${\beta }_1={sup}_{t\in R_{+}}(a+b{\psi }_0+c(T_1^{*}+{\psi }_0))$.

About $t\in ({\gamma }_n^{*},{\gamma }_{n+1})$, there is $T_1\left(t\right)\ge {\psi }_0\ge {\psi }_{0}exp(-{\beta }_1{\theta }_1-Y_1)$, we have $T_1\left(t\right)\ge {\psi }_0>{\psi }_{0}exp(-{\beta }_1{\theta }_1-Y_1)$, when $t\ge T^2$. Similarly, we can obtain

$$\underset{t\to +\infty }{lim\; inf}{T}_2\left(t\right)\ge {\psi }_{0}exp(-{\beta }_2{\theta }_2-Y_2),$$

where ${\beta }_2={sup}_{t\in R_{+}}(d+e{\psi }_0+f(T_2^{*}+{\psi }_0))$.

Let $m=min\left\{{\psi }_{0}exp(-{\beta }_1{\theta }_1-Y_1),(-{\beta }_2{\theta }_2-Y_2)\right\}$. Then, m is independent of any positive solution of Equation (2). Therefore

$$m\le \underset{t\to +\infty }{lim\; inf}{T}_1\left(t\right),m\le \underset{t\to +\infty }{lim\; sup}{T}_2\left(t\right).$$

(24)

From (23) and (24), we finally understand that the system (2) is permanent.

□

Next, we prove the global attractiveness of the system (2).

Theorem 3.

Suppose there are two positive constants ${\omega }_1$ and ${\omega }_2$, and a nonnegative integer F, such that

$$-{\omega }_1{\displaystyle \frac{{\lambda }_1{a}_{11}}{K_1}}+{\omega }_2{\displaystyle \frac{{\lambda }_2{a}_{21}}{K_2}}\le -F,-{\omega }_2{\displaystyle \frac{{\lambda }_2{a}_{22}}{K_2}}+{\omega }_1{\displaystyle \frac{{\lambda }_1{a}_{12}}{K_1}}\le -F,t\ge 0.$$

Then, for any positive solution $Z_1\left(t\right)=(T_1^1\left(t\right),T_2^1\left(t\right))$, $Z_2\left(t\right)=(T_1^2\left(t\right),T_2^2\left(t\right))$ of the system of Equations (2), there is

$$\underset{t\to +\infty }{lim}(Z_1\left(t\right)-Z_2\left(t\right))=0.$$

(25)

Proof. 

For convenience, let ${\displaystyle \frac{{\lambda }_1{a}_{11}}{K_1}}=b,{\displaystyle \frac{{\lambda }_2{a}_{21}}{K_2}}=e,{\displaystyle \frac{{\lambda }_2{a}_{22}}{K_2}}=f,{\displaystyle \frac{{\lambda }_1{a}_{12}}{K_1}}=c$. For any solution $Z_1\left(t\right)=(T_1^1\left(t\right),T_2^1\left(t\right))$, $Z_2\left(t\right)=(T_1^2\left(t\right),T_2^2\left(t\right))$, it can be obtained from Theorem 2 that there are two positive constants C and D satisfying the following conditions, so that when $t\ge 0$, there is

$$C<T_1^i\left(t\right),T_2^i\left(t\right)<D.$$

Selecting the Lyapunov function

$$V\left(t\right)={\omega }_1|ln{T_1}^1\left(t\right)-ln{T_2}^1\left(t\right)\left)\right|+{\omega }_2|ln{T_1}^2\left(t\right)-ln{T_2}^2\left(t\right)\left)\right|.$$

such that

$$\begin{array}{cc}\hfill V\left(t_k^{+}\right)& ={\omega }_1|ln(1-p_k){T_1}^1\left(t\right)-ln(1+q_k){T_2}^1\left(t\right)|\hfill \\ \hfill & +{\omega }_2|ln(1-p_k){T_1}^2\left(t\right)-ln(1+q_k){T_2}^2\left(t\right)|\hfill \\ \hfill & =V\left(t_k\right).\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill D^{+}V& ={\omega }_{1}sign({T_1}^1\left(t\right)-{T_2}^1\left(t\right))(-b({T_1}^1\left(t\right)-{T_2}^1\left(t\right))-c({T_2}^1\left(t\right)-{T_2}^2\left(t\right)))\hfill \\ \hfill & ={\omega }_{2}sign({T_2}^1\left(t\right)-{T_2}^2\left(t\right))(-e({T_1}^1\left(t\right)-{T_2}^1\left(t\right))-f({T_2}^1\left(t\right)-{T_2}^2\left(t\right)))\hfill \\ \hfill & \le (-{\omega }_{1}b+{\omega }_{2}e)|{T_1}^1\left(t\right)-{T_2}^1\left(t\right)|+(-{\omega }_{2}f+{\omega }_{1}c)|{T_2}^1\left(t\right)-{T_2}^2\left(t\right)|\hfill \\ \hfill & \le -\delta FV\left(t\right),\hfill \end{array}$$

where $\delta =Cmin{\omega }_i,i=1,2$, $V\left(t\right)\le V\left(0\right)exp(-\delta Ft)$.

Then, when $t\to \infty$, $V\left(t\right)\to 0$. Therefore,

$$\underset{t\to +\infty }{lim}(Z_1\left(t\right)-Z_2\left(t\right))=0,$$

and the proof is completed. □

3. Optimal Control Strategies

In this section, we will consider three pulse optimal control strategies. Considering the effects of drugs on sensitive cells, studies were conducted with pulse interval and dose as control variables, with the goal of minimizing costs and the number of sensitive and resistant cells at the terminal moment, and therefore, we consider the following objective function at a finite time interval $[0, T].$

$$minJ(\mathit{\eta },\mathit{p})=\sum _{k=1}^{n-1}{p}_{k}C+T_1\left(T\right)+T_2\left(T\right).$$

(26)

$\mathit{\eta }=({\eta }_1,{\eta }_2,\dots ,{\eta }_n)$ is time of pulse intervention, $\mathit{p}=(p_1,p_2,\dots ,p_{n-1})$ is the drug dose. C is the cost of the drug.

According to the optimal control theory of impulsive systems, because the existing optimization techniques cannot be directly solved (26) (reference [15]), can be based on the time scale transformation method to be solved. Finally, the gradient of the target function to the pulse interval and the drug dose is obtained. It is very important to seek the best control strategy for tumor therapy. We consider three control strategies to find the optimal pulse interval and dose, as shown below.

3.1. Optimal Pulse Time and Dose

Given the initial model

$$\left\{\begin{array}{c}\left.\begin{array}{c}{\displaystyle \frac{d{T}_1\left(t\right)}{dt}={\lambda }_1{T}_1\left[1-\frac{T_1{a}_{11}+T_2{a}_{12}}{K_1}\right]-{\mu }_1{T}_1,}\hfill \\ {\displaystyle \frac{d{T}_2\left(t\right)}{dt}={\lambda }_2{T}_2\left[1-\frac{T_1{a}_{21}+T_2{a}_{22}}{K_2}\right]-{\mu }_2{T}_2,}\hfill \end{array}\right\}t\ne t_k,\hfill \\ \left.\begin{array}{c}{\displaystyle T_1\left(t_k^{+}\right)=(1-p_k)T_1\left(t_k\right),}\hfill \\ {\displaystyle T_2\left(t_k^{+}\right)=(1+q_k)T_2\left(t_k\right),}\hfill \end{array}\right\}t=t_k, k=1,2,\dots ,n-1.\hfill \end{array}\right.$$

(27)

The control variables $p_k$ and ${\eta }_k$ satisfy the condition

$$p_k^1\le p_k\le p_k^2, k=1,\dots ,n-1,$$

(28)

$$0=t_0\le t_1\le \dots \le t_{n-1}\le t_n=t_f,$$

(29)

$$t_k-t_{k-1}={\eta }_k,$$

(30)

$$x_k\le {\eta }_k\le y_k, k=1,\dots ,n.$$

$p_k^1$, $p_k^2$, $x_k$, and $y_k$ are given non-negative constants.

We first construct a transformation from $t\in [0, T]$ to $s\in [0, n]$, which maps the injection time $0,t_1,t_2,\dots ,t_{n-1},T$ to a definite time point $s=0,1,\dots ,n.$

We introduce time scaling changes

$$\frac{\mathrm{d}t\left(s\right)}{\mathrm{d}s}=\nu \left(s\right).$$

There are initial conditions

$$t\left(0\right)=0.$$

$\nu \left(s\right)$ is called time scaling control and is piecewise constant function that may be discontinuous at Pulse Time $s=1,2,\dots ,n-1$, then

$$\nu \left(s\right)=\sum _{k=1}^n{\eta }_k{\chi }_{(k-1,k)}\left(s\right).$$

${\chi }_I\left(s\right)$ is the indicating function of I, defining

$${\chi }_I\left(t\right)=\left\{\begin{array}{cc}\hfill 1,& t\in I,\hfill \\ \hfill 0,& else.\hfill \end{array}\right.$$

After the time scaling transformation, Equation (27) transformed into

$$\left\{\begin{array}{c}\left.\begin{array}{c}{\displaystyle \frac{d{T}_1\left(s\right)}{ds}=\nu \left(s\right)\left[{\lambda }_1{T}_1\left[1-\frac{T_1{a}_{11}+T_2{a}_{12}}{K_1}\right]-{\mu }_1{T}_1\right],}\hfill \\ {\displaystyle \frac{d{T}_2\left(s\right)}{ds}=\nu \left(s\right)\left[{\lambda }_2{T}_2\left[1-\frac{T_1{a}_{21}+T_2{a}_{22}}{K_2}\right]-{\mu }_2{T}_2\right],}\hfill \end{array}\right\}s\in [0, n],\hfill \\ \left.\begin{array}{c}{\displaystyle T_1\left(k^{+}\right)=(1-p_k)T_1\left(t_k\right),}\hfill \\ {\displaystyle T_2\left(k^{+}\right)=(1+q_k)T_2\left(t_k\right),}\hfill \end{array}\right\}k=1,2,\dots ,n-1.\hfill \end{array}\right.$$

(31)

The objective function becomes

$$\tilde{J}(\mathit{\eta },\mathit{p})=\sum _{k=1}^{n-1}{p}_{k}C+T_1\left(n\right)+T_2\left(n\right).$$

(32)

Since (32) is still difficult to solve, we introduce the time translation transform

For $k=1,\dots ,n-1,n$, define

$$T_{1k}\left(s\right)=T_1(s+k-1),T_{2k}\left(s\right)=T_2(s+k-1),{\pi }_k\left(s\right)=t(s+k-1).$$

(33)

Time translation transform defined by (33), system (31), and (32) transformed into

$$\left\{\begin{array}{c}\left.\begin{array}{c}{\displaystyle \frac{d{T}_{1k}\left(s\right)}{ds}=\nu \left(s\right)\left[{\lambda }_1{T}_{1k}\left(s\right)\left[1-\frac{T_{1k}\left(s\right)a_{11}+T_{2k}\left(s\right)a_{12}}{K_1}\right]-{\mu }_1{T}_{1k}\left(s\right)\right],}\hfill \\ {\displaystyle \frac{d{T}_{2k}\left(s\right)}{ds}=\nu \left(s\right)\left[{\lambda }_2{T}_{2k}\left(s\right)\left[1-\frac{T_{1k}\left(s\right)a_{21}+T_{2k}\left(s\right)a_{22}}{K_2}\right]-{\mu }_2{T}_{2k}\left(s\right)\right],}\hfill \end{array}\right\}s\in [0, 1],\hfill \\ \left.\begin{array}{c}{\displaystyle T_{1k}\left(0\right)=(1-p_{k-1})T_{1k-1}\left(1\right),}\hfill \\ {\displaystyle T_{2k}\left(0\right)=(1+q_{k-1})T_{2k-1}\left(1\right),}\hfill \end{array}\right\}k=2,\dots ,n,\hfill \\ {\displaystyle \frac{d{\pi }_k}{ds}={\eta }_k,k=1,\dots ,n.}\hfill \end{array}\right.$$

(34)

The corresponding objective function is

$$\widehat{J}(\mathit{\eta },\mathit{p})=\sum _{k=1}^{n-1}{p}_{k}C+T_{1n}\left(1\right)+T_{2n}\left(1\right).$$

(35)

According to reference [18], we define the Hamiltonian function

$H_k(s,\nu \left(s\right),T_{1k}\left(s\right),T_{2k}\left(s\right),{\mathit{\lambda }}_k\left(s\right),p_k)={\lambda }_1^k\left(s\right)\dot{T_1^k\left(s\right)}+{\lambda }_2^k\left(s\right)\dot{T_2^k\left(s\right)}$.

Theorem 4.

If the continuous functions ${\mathit{\lambda }}^k\left(s\right)$ satisfy the adjoint equations

$${\dot{\lambda }}_1^k\left(s\right)=-{\displaystyle \frac{\partial H_k}{\partial T_{1k}}}=-{\eta }_k\left({\lambda }_1^k\left(s\right)[{\lambda }_1-{\displaystyle \frac{(2a_{11}{T}_{1k}\left(s\right)+a_{12}{T}_{2k}\left(s\right)){\lambda }_1}{K_1}}-{\mu }_1]-{\lambda }_2^k\left(s\right){\displaystyle \frac{{\lambda }_2{a}_{21}{T}_{2k}}{K_2}}\right).$$

(36)

$${\dot{\lambda }}_2^k\left(s\right)=-{\displaystyle \frac{\partial H_k}{\partial T_{2k}}}=-{\eta }_k\left({\lambda }_2^k\left(s\right)[{\lambda }_2-{\displaystyle \frac{(2a_{22}{T}_{2k}\left(s\right)+a_{21}{T}_{1k}\left(s\right)){\lambda }_2}{K_2}}-{\mu }_2]-{\lambda }_1^k\left(s\right){\displaystyle \frac{{\lambda }_1{a}_{12}{T}_{1k}}{K_1}}\right).$$

(37)

With boundary conditions

$${\lambda }_1^k\left(1\right)=1,{\lambda }_2^k\left(1\right)=1.$$

(38)

$${\lambda }_1^k\left(1\right)=(1-p_k){\lambda }_1^{k+1}\left(0\right),{\lambda }_2^k\left(1\right)=(1+q_k){\lambda }_2^{k+1}\left(0\right).$$

(39)

The gradient of the formula with respect to ${\eta }_j(j=1,2,\dots ,n-1)$ is

$$\begin{array}{cc}\hfill {\nabla }_{{\eta }_j}J({\eta }_j,p_k)& ={\int }_0^1({\lambda }_1^j\left(s\right)\left[{\lambda }_1{T}_{1j}\left(s\right)(1-{\displaystyle \frac{a_{11}{T}_{1j}\left(s\right)+a_{12}{T}_{2j}\left(s\right)}{K_1}})-{\mu }_1{T}_{1k}\right]\hfill \\ \hfill & +{\lambda }_2^j\left(s\right)\left[{\lambda }_2{T}_{2j}\left(s\right)(1-{\displaystyle \frac{a_{21}{T}_{1j}\left(s\right)+a_{22}{T}_{2j}\left(s\right)}{K_2}})-{\mu }_2{T}_{2k}\right])ds.\hfill \end{array}$$

For $j=2,\dots ,n.$

$$\begin{array}{cc}\hfill {\nabla }_{p_k}J({\eta }_j,p_k)& =C-\left({{\lambda }_1}^{k+1}\left(0\right)T_{1k}\left(1\right)\right).\hfill \end{array}$$

For $k=1,2,\dots ,n-1.$

Proof. 

Known using Theorem 4.

$${\dot{\lambda }}_1^k\left(s\right)=-{\displaystyle \frac{\partial H_k}{\partial T_{1k}}},{\dot{\lambda }}_2^k\left(s\right)=-{\displaystyle \frac{\partial H_k}{\partial T_{2k}}}.$$

(40)

With boundary conditions

$${\lambda }_1^k\left(1\right)=1,{\lambda }_2^k\left(1\right)=1,$$

(41)

$${\lambda }_1^k\left(1\right)=(1-p_k){\lambda }_1^{k+1}\left(0\right),{\lambda }_2^k\left(1\right)=(1-q_k){\lambda }_2^{k+1}\left(0\right).$$

(42)

we define

$$\mathit{N}\left(1\right)={\left(\begin{array}{cc}{T}_1\left(1\right)& T_2\left(1\right)\end{array}\right)}^T,$$

$${\mathit{N}}_k\left(0\right)={\psi }^{k-1}({\mathit{N}}_{k-1}\left(1\right),p_k,q_k).$$

From (34), we can obtain

$${\mathit{\psi }}^{k-1}(N_{k-1}\left(0\right),p_k,q_k)=\left(\begin{array}{cc}(1-p_k)T_{1k}\left(1\right)& (1+q_k)T_{2k}\left(1\right)\end{array}\right).$$

Using the gradient Formula [15],

$$\begin{array}{cc}\hfill {\nabla }_{{\eta }_j}J({\eta }_j,p_1)& ={\int }_0^1\sum _{k=1}^n{\displaystyle \frac{\partial H_k(s,\mathit{\tau },T_{1k}\left(s\right),T_{2k}\left(s\right),{\mathit{\lambda }}_k\left(s\right),P)}{\partial {\eta }_j}}ds\hfill \\ \hfill & ={\int }_0^1({\lambda }_1^j\left(s\right)\left[{\lambda }_1{T}_{1j}\left(s\right)(1-{\displaystyle \frac{a_{11}{T}_{1j}\left(s\right)+a_{12}{T}_{2j}\left(s\right)}{K_1}})-{\mu }_1{T}_{1k}\right]\hfill \\ \hfill & +{\lambda }_2^j\left(s\right)\left[{\lambda }_2{T}_{2j}\left(s\right)(1-{\displaystyle \frac{a_{21}{T}_{1j}\left(s\right)+a_{22}{T}_{2j}\left(s\right)}{K_2}})-{\mu }_2{T}_{2k}\right])ds.\hfill \end{array}$$

For $j=2,\dots ,n.$

$$\begin{array}{cc}\hfill {\nabla }_{p_k}J({\eta }_j,p_k)& =C+\sum _{k=1}^{n-1}{\left({\lambda }^{k+1}\left(0\right)\right)}^T{\displaystyle \frac{\partial {\mathit{\psi }}^k(N_k\left(1\right),p_k,q_k)}{\partial p_k}}\hfill \\ \hfill & =C-\left({{\lambda }_1}^{k+1}\left(0\right)T_{1k}\left(1\right)\right).\hfill \end{array}$$

For $k=1,2,\dots ,n-1.$

Based on Theorem 4, we briefly consider the latter two measures. □

3.2. The Optimal Dosage at a Fixed Time

If $p_k=p_1$, ${\eta }_k={\eta }_1$, then

$$\begin{array}{cc}\hfill {\nabla }_{p_1}J\left(p_1\right)& =(n-1)C+\sum _{k=1}^{n-1}{\left({\lambda }^{k+1}\left(0\right)\right)}^T{\displaystyle \frac{\partial {\mathit{\psi }}^k(N_k\left(1\right),p_1,q_1)}{\partial p_1}}\hfill \\ \hfill & =(n-1)C-\sum _{k=1}^{n-1}\left({{\lambda }_1}^{k+1}\left(0\right)T_{1k}\left(1\right)\right).\hfill \end{array}$$

3.3. Optimal Pulse Time and Constant Drug Dose

If $p_k=p_1$, ${\eta }_j=({\eta }_1,{\eta }_1,\dots ,{\eta }_{n-1})$, then

$$\begin{array}{cc}\hfill {\nabla }_{{\eta }_j}J({\eta }_j,p_1)& ={\int }_0^1\sum _{k=1}^n{\displaystyle \frac{\partial H_k(s,\mathit{\tau },T_{1k}\left(s\right),T_{2k}\left(s\right),{\mathit{\lambda }}_k\left(s\right),P)}{\partial {\eta }_j}}ds\hfill \\ \hfill & ={\int }_0^1({\lambda }_1^j\left(s\right)\left[{\lambda }_1{T}_{1j}\left(s\right)(1-{\displaystyle \frac{a_{11}{T}_{1j}\left(s\right)+a_{12}{T}_{2j}\left(s\right)}{K_1}})-{\mu }_1{T}_{1k}\right]\hfill \\ \hfill & +{\lambda }_2^j\left(s\right)\left[{\lambda }_2{T}_{2j}\left(s\right)(1-{\displaystyle \frac{a_{21}{T}_{1j}\left(s\right)+a_{22}{T}_{2j}\left(s\right)}{K_2}})-{\mu }_2{T}_{2k}\right])ds.\hfill \end{array}$$

For $j=2,\dots ,n-1.$

$$\begin{array}{cc}\hfill {\nabla }_{p_1}J({\eta }_j,p_1)& =(n-1)C+\sum _{k=1}^{n-1}{\left({\lambda }^{k+1}\left(0\right)\right)}^T{\displaystyle \frac{\partial {\mathit{\psi }}^k(N_k\left(1\right),p_1,q_1)}{\partial p_1}}\hfill \\ \hfill & =(n-1)C-\sum _{k=1}^{n-1}\left({{\lambda }_1}^{k+1}\left(0\right)T_{1k}\left(1\right)\right).\hfill \end{array}$$

4. Numerical Simulation

In this section, we simulate three control strategies, and then select the most effective strategy through the effect. We assume that drug-resistant cells grow at a rate of 0.01 and obtain the optimal objective function by determining the appropriate control parameters, namely pulse interval and drug dose.

Select the parameters

$${\lambda }_1=0.02, {\lambda }_2=0.5, {\mu }_1=0.001, {\mu }_2=0.0005, a_{11}=0.2,$$

$$a_{12}=0.1, a_{21}=0.170, a_{22}=0.2, K_1=1000, K_2=1500.$$

The initial number of sensitive cells and resistant cells $T_1\left(0\right)=8000$, $T_2\left(0\right)=1.$

4.1. The Optimal Dosage at a Fixed Time

Suppose the period of the pulse $\eta =20$. Drug therapy is performed at Pulse Time Point $t_1=4,t_2=8,t_3=12,t_4=18.$

Suppose that the dosage constraints are as follows:

$$0\le p_1\le 1.$$

The optimal dosage $p_1^{*}=0.5337$, the optimal objective function $J^{*}=1318.4819$, and $T_1^{*}=474.8244$ and $T_2^{*}=736.9175$ at the terminal time are calculated by using MATLAB software 2018a. Figure 1 shows the optimal dose at a fixed time, Figure 2 shows how the number of drug-sensitive and drug-resistant cells evolves at a given time under optimal pulse control, initial pulse control, and no pulse control. The black dotted line represents the trajectory of the cell under the optimal pulse control, and the blue dotted line represents the trajectory of the cell under the optimal pulse control. O (474.8244, 736.9175), M (571.4893, 653.6824), and N (9265.3104, 0) denote the number of sensitive and resistant cells at the terminal moment under the three control strategies.

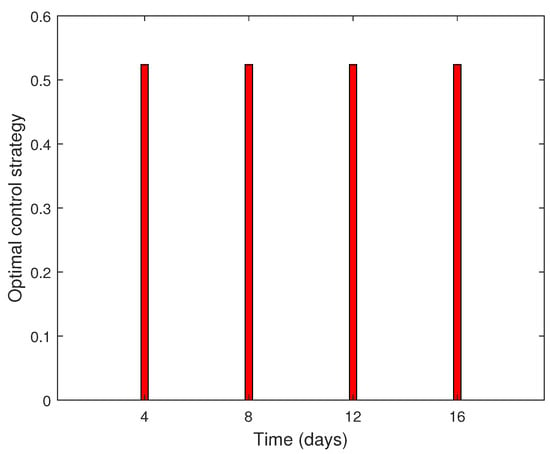
Figure 1. Optimal control strategy.

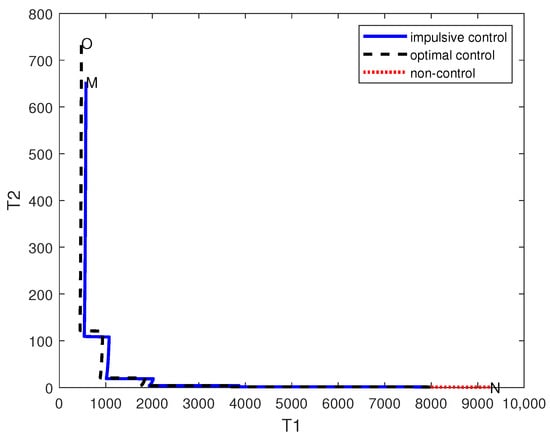
Figure 2. The dynamic behavior of T1 and T2.

From Figure 2, we can see that the application of impulse control significantly reduces the tumor burden.

4.2. Optimal Pulse Time and Constant Drug Dose

The initial values for the pulse dose and time interval are assumed to be

$${\eta }_1={\eta }_2={\eta }_3={\eta }_4=4.$$

$$p_1=0.5.$$

The pulse interval satisfies constraint $1\le {\eta }_i\le 10$. The optimal pulse dosage and time interval are obtained through numerical simulation

$${\eta }_1^{*}=10, {\eta }_2^{*}=7, {\eta }_3^{*}=1, {\eta }_4^{*}=1, {\eta }_5^{*}=1.$$

$$p_1^{*}=0.7307.$$

The number of $T_1^{*}=42.8566$ and $T_2^{*}=133.6778$ cells at the terminal moment and the optimal value of objective function is $J^{*}=322.6744.$ Figure 3 shows the optimal dose at an unfixed time. Figure 4 shows how the number of drug-sensitive and drug-resistant cells evolves over a given time period under optimal pulse control, initial pulse control, and pulse-free control. O (42.8566, 133.6778), M (571.4893, 653.6824), and N (9265.3104, 0) indicate the number of terminal-moment-sensitive and -resistant cells under the three control strategies. Obviously, this control strategy not only reduced the tumor burden, but also further controlled the change in drug-resistant cells.

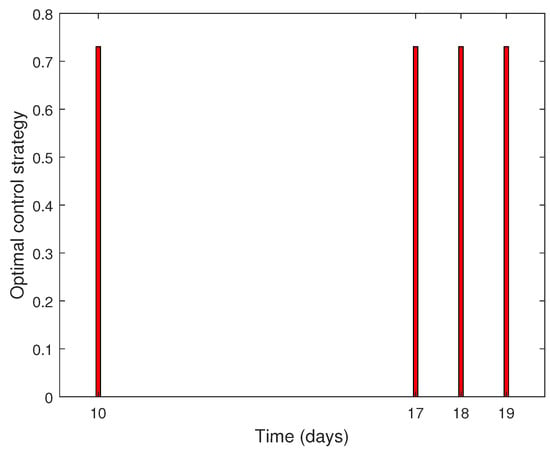
Figure 3. Optimal control strategy.

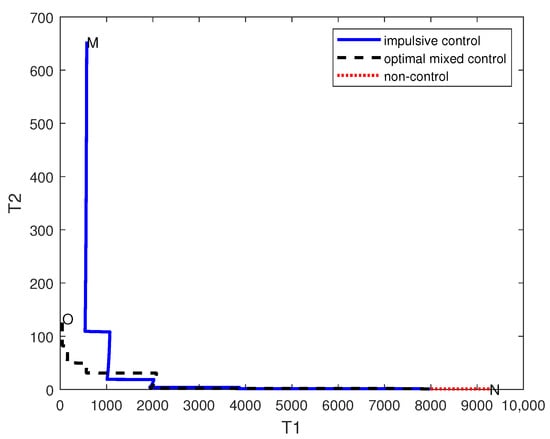
Figure 4. The dynamic behavior of T1 and T2.

From Figure 4, we can see that tumor burden is significantly reduced by applying pulse control, and that optimal pulse control can further inhibit the growth of drug-resistant cells compared to initial pulse control.

4.3. Optimal Pulse Time and Dose

The initial values for the pulse dose and time interval are assumed to be

$${\eta }_1={\eta }_2={\eta }_3={\eta }_4=4.$$

$$p_1=p_2=p_3=p_4=0.5.$$

The pulse interval satisfies constraint $1\le {\eta }_i\le 10$. The optimal pulse dosage and time interval are obtained through numerical simulation

$${\eta }_1^{*}=9.9964, {\eta }_2^{*}=5.7180, {\eta }_3^{*}=1.9823, {\eta }_4^{*}=1.2926, {\eta }_5^{*}=1.0074.$$

$$p_1^{*}=0.7116, p_2^{*}=0.6503, p_3^{*}=0.7621, p_4^{*}=0.8686.$$

The number of $T_1^{*}=25.7732$ and $T_2^{*}=139.8360$ cells at the terminal moment and the optimal value of objective function is $J^{*}=315.4579.$ Figure 5 shows the optimal strategy under the combined control of pulse timing and dose. Figure 6 shows how the number of drug-sensitive and drug-resistant cells evolves over a given time period under optimal pulse control, initial pulse control, and pulse-free control. O (25.7732, 139.8360), M (571.4893, 653.6824), and N (9265.3104, 0) indicate the number of terminal-moment-sensitive and -resistant cells under the three control strategies. Obviously, compared to the previous strategy, the tumor burden is further reduced.

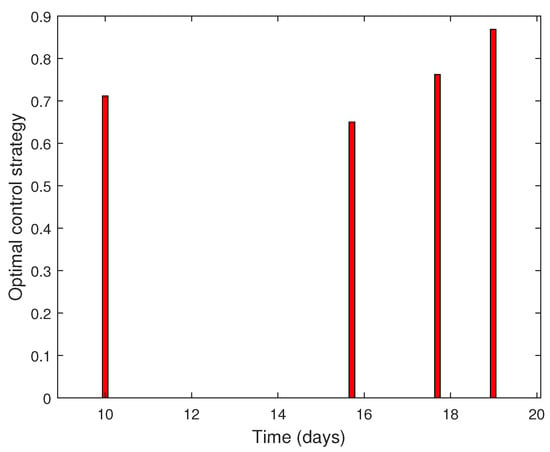
Figure 5. Optimal control strategy.

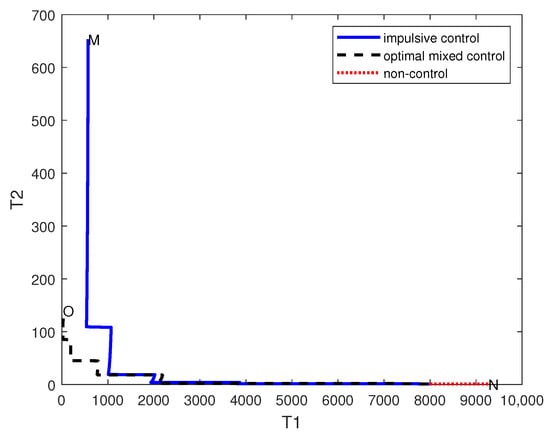
Figure 6. The dynamic behavior of T1 and T2.

From Figure 6, we can see that the optimal control strategy also reduces the number of sensitive cells and suppresses the number of drug-resistant cells.

Based on the pulse optimal control strategy, it is found that the pulse intervention can significantly reduce the tumor load. Compared with the three optimal controls, fixed-time optimal controls can reduce tumor burden, but lead to an increase in the number of drug-resistant cells. Compared with an optimal strategy for a given dose, the mixed strategy cannot only inhibit the growth of drug-resistant cells, but also minimize the terminal tumor burden because, in the process of cancer treatment, along with the continuation of the treatment cycle, the proportion of drug-resistant cells increases, ultimately leading to treatment failure. Thus, for three optimal control strategies, the results of numerical simulations suggest that mixed optimal control can effectively suppress the number of drug-resistant cells while achieving a relatively small tumor burden. Therefore, a mixed control strategy is the most effective way to treat cancer. In the process of cancer treatment, pulse intervention, in order to find the optimal pulse interval and dose, can maintain a small tumor burden and, at the same time, inhibit the rapid increase in drug-resistant cells, delaying human life. Data were selected from reference [8], where ${\lambda }_2,{\mu }_1,{\mu }_2,a_{12},a_{21}$; the remaining data, in order to obtain better results, were random values.

5. Conclusions

As a new approach to cancer treatment, adaptive therapy is a dynamic regulatory process. However, with the continuation of the treatment cycle, there will be a large number of drug-resistant cells, and this will ultimately lead to treatment failure. Using the research methods in references [15,20], this paper proposes a competition model between sensitive cells and drug-resistant cells, in which multiple pulse intervention measures are introduced. Firstly, the permanence and global attractiveness of the model are analyzed, which provide a theoretical basis for the following work. At the same time, pulse intervention can reduce the number of sensitive cells, further affecting the number of drug-resistant cells. Therefore, how should we reasonably select the time and dose of pulse intervention in order to achieve the best results? In this paper, based on different pulse control theories, three kinds of pulse optimal control are studied with the time and dose of pulse intervention as control variables; the three optimal control strategies are compared in terms of the tumor burden and the effect on drug-resistant cells. The results show that the mixed control strategy is the most effective for cancer treatment, because it cannot only suppress the number of drug-resistant cells, but also, at the terminal moment, the tumor burden is relatively minimal. Our study provides new ideas for the treatment of cancer; on the other hand, there are few studies on the application of pulse intervention during cancer treatment. Therefore, there are still more challenges in theoretical research, numerical analysis, etc. More research ideas are worth further exploration.