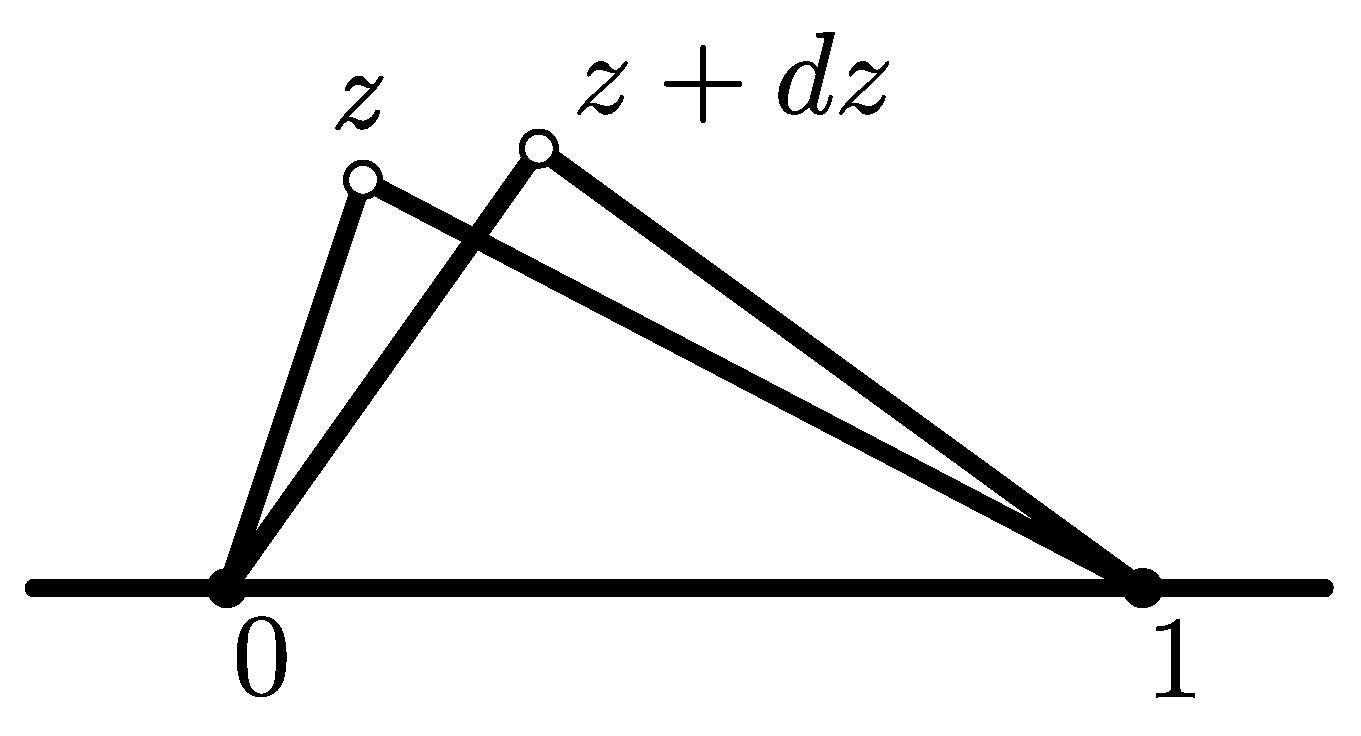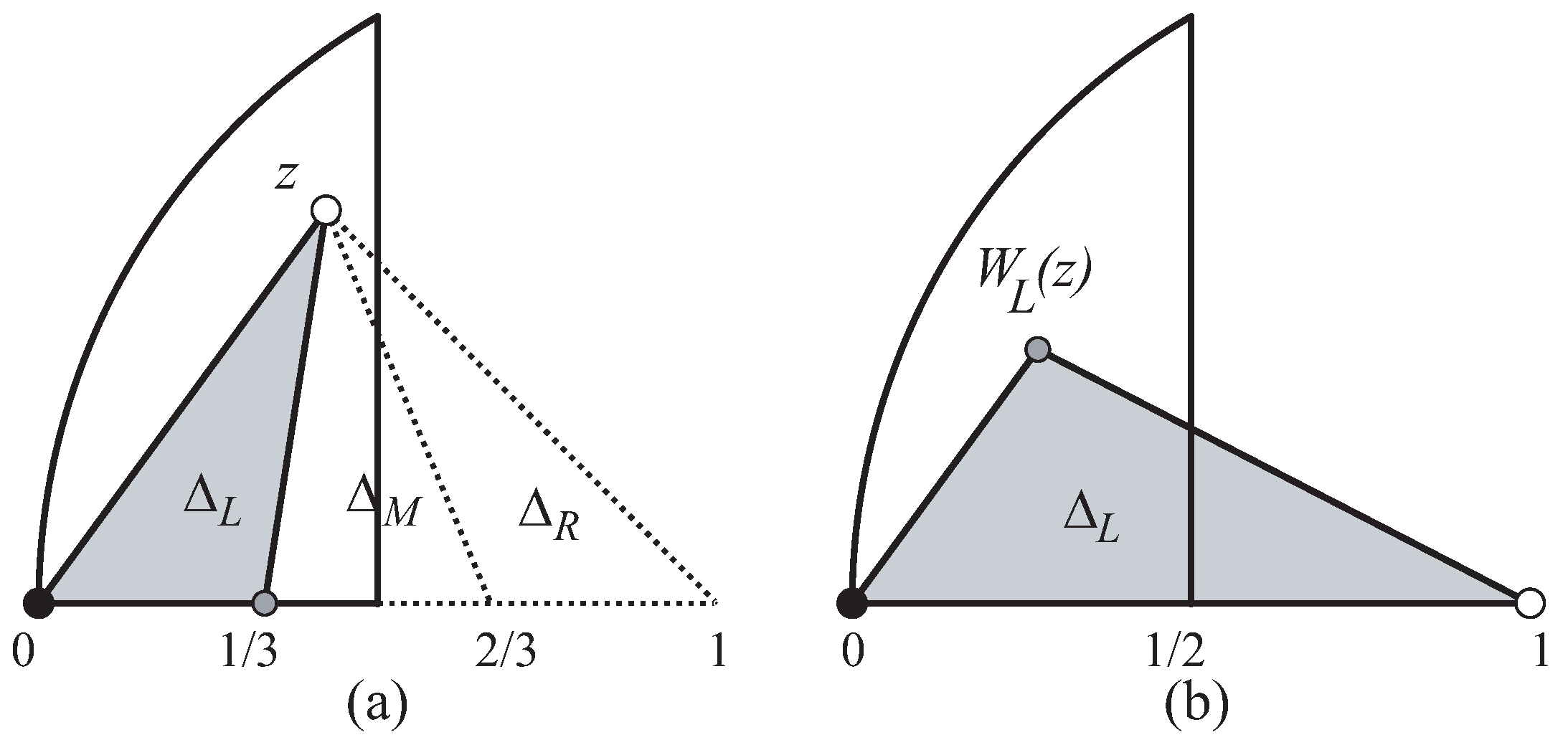1. Introduction
It is well known that numerical mesh generation and adaptive meshing or local refinement of a given mesh are the main steps in many areas such as geometric modelling, computer graphics, or the finite element method (FEM). Also, the geometry of the generated elements is important for the numerical convergence of the method. The grid generation as well as a proper local refinement or coarsening strategies are of the most importance to find the solution strategy in these problems [
1,
2].
One of the possibilities to refine a given simplicial mesh is to employ some type of partition. Partitions of simplices, triangles, or tetrahedra have been studied profusely, and issuessuch as the non-degeneracy or stability condition as well as the conformity and the nestedness of the refined meshes are usually addressed [
3,
4,
5,
6].
For the longest-edge bisection of triangles, the non-degeneracy was proved by Rosenberg and Stenger [
7] and similar results have been presented recently for the longest-edge trisection or in general for the longest
n-section of triangles. See [
8] and references therein.
The longest-edge trisection (3T-LE) of a triangle is obtained by joining the two equally spaced points of the longest-edge with the opposite vertex. The present note studies the triangle similarity classes that appear by the iterative application of the 3T-LE.
The 2T-LE of triangles has finite orbit always (see [
9,
10]). However, the number of similarity classes appearing by the iterative application of the 3T-LE to a single initial triangle is not finite in general. There are only three exceptions to this fact: the right triangle with side lengths proportional to 1:
:
and the other two triangles in its orbit. In this paper, we prove this fact by the discrete dynamics in a space of triangular shapes endowed with hyperbolic distance.
2. Space of Triangular Shapes and the Hyperbolic Metric in the Space of Triangular Shapes
2.1. Normalized Triangle Region or Space of Triangular Shapes
Since only the shape of triangles will be taken into account here, it is very convenient to have a way to represent the shape of a triangle in a univocal and systematic way, in a subset of the complex plane.
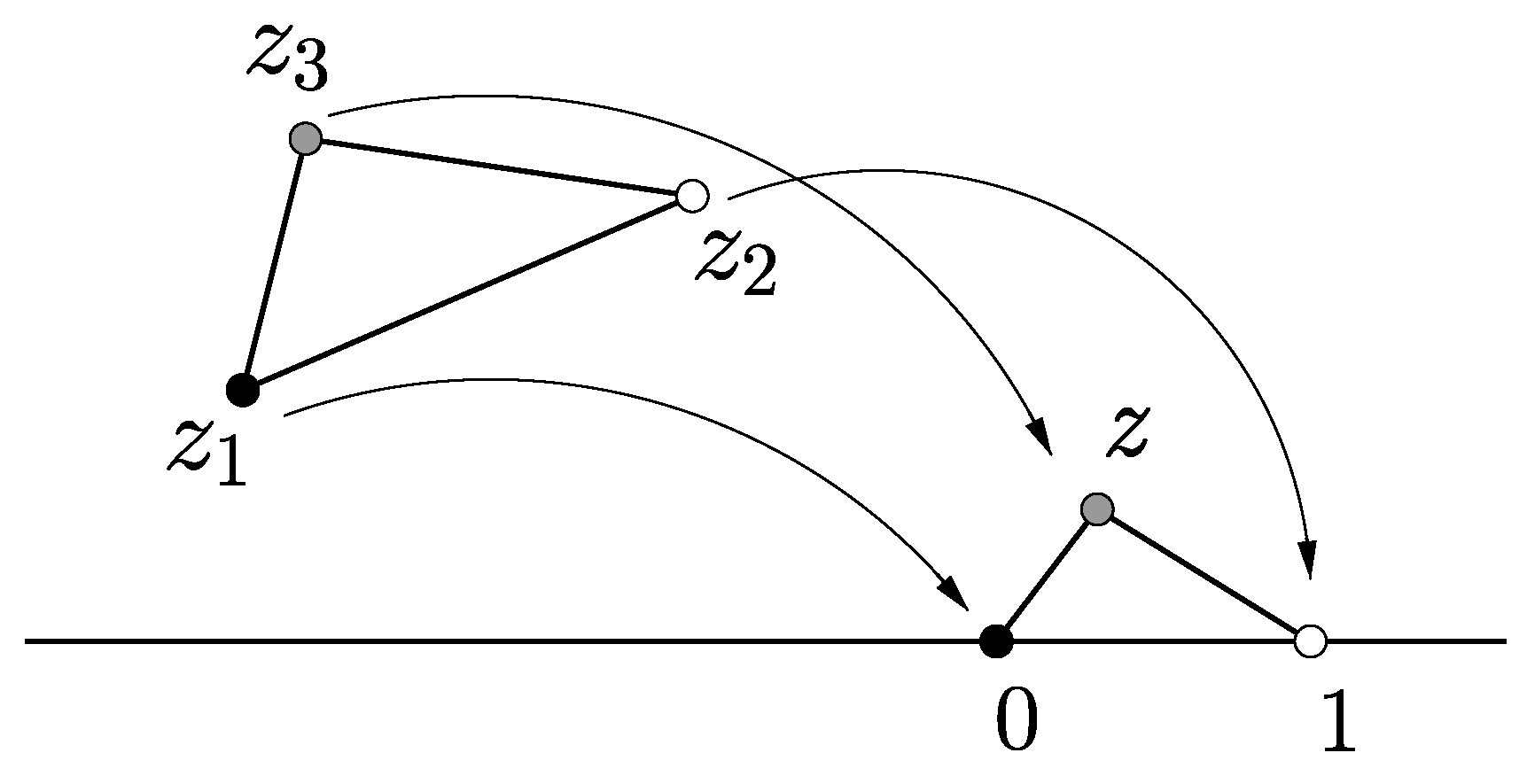
Let
,
, and
be three points in the complex plane such that at least two of them are different. For example, let
. Then, the triangle with vertices
,
, and
has the same shape as the triangle with vertices 0, 1, and
. The real part and imaginary part of complex
z are called Bookstein’s coordinates [
11,
12]. See
Figure 1.
By means of Bookstein’s coordinates, we may use the complex plane as a space of triangular shapes. An idea of this space of triangular shapes is shown in
Figure 2, where each triangle is drawn with its center of the base at the position corresponding to its Bookstein’s coordinates. See
Figure 2, which is similar to the one given in [
13].
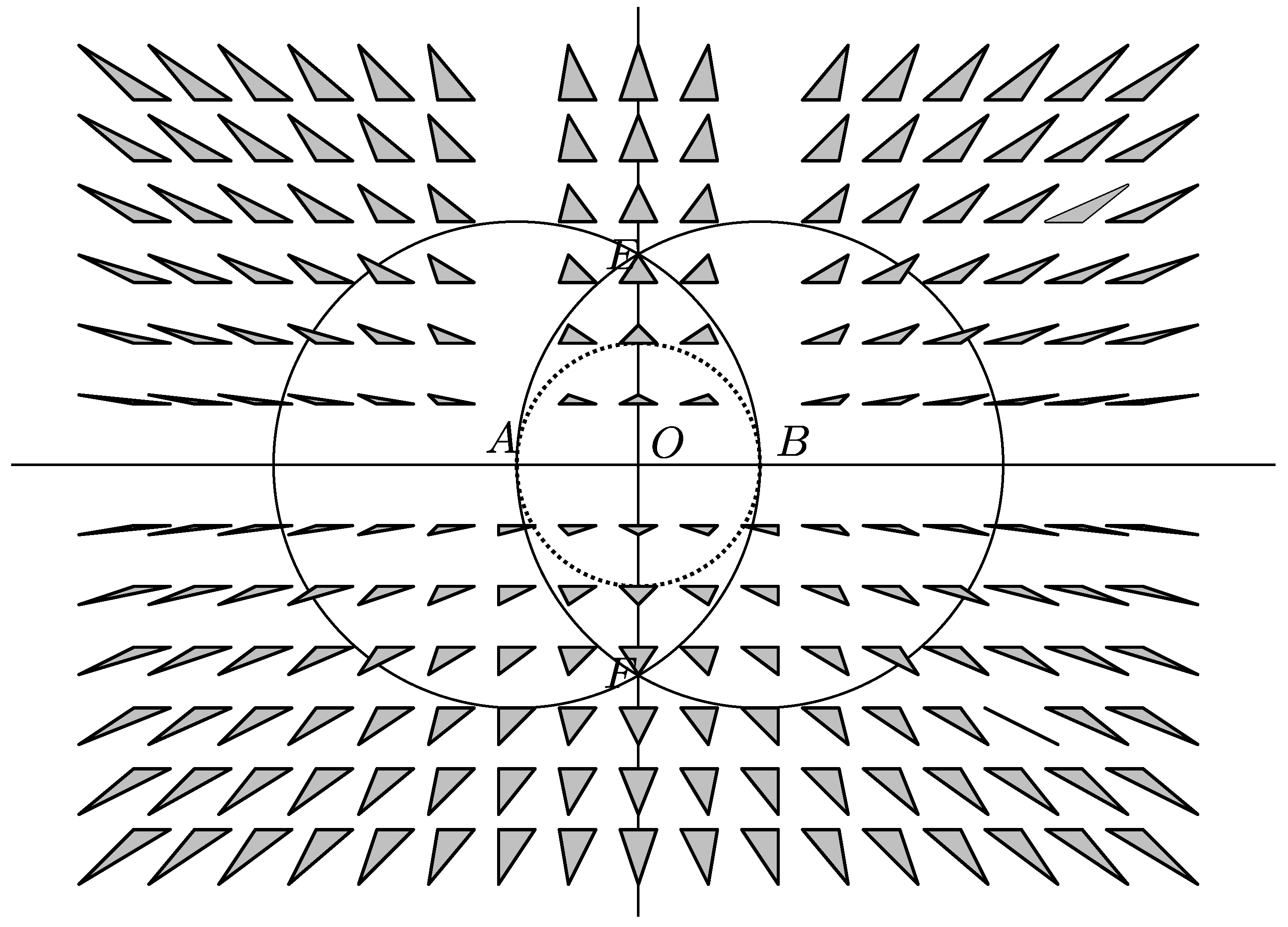
In
Figure 2, equilateral triangles correspond to points
and
, points
E and
F in the Figure. Right triangles are located on the lines with equations
and
and on the circumference
. Isosceles triangles are on the line
and on the circumferences
and
. Degenerate triangles have their vertices on the line
.
The upper semiplane may be subdivided into six regions by the line and the circumferences and . Since the permutation of the vertices of any triangle does not change its shape, we may assign one point in each of these six regions of the upper plane.
In order to achieve a bijective relation between any triangle shape and a point of a subset of the complex plane, we have to chose one of these regions as a normalized region. By using scaling, symmetries, translations, and rotations, we may associate with any given triangle a normalized triangle similar to the former one. This normalized triangle has the two vertices of the longest edge at points 0 and 1 of the real axes, and the opposite vertex to the longest edge on the upper half plane and on the left of the line . That is, the opposite vertex to the longest edge is in the set . Then, there is a bijection between the points in and the classes of similar triangles. .
Region
is called here the normalized region or space of triangular shapes. See
Figure 3.
2.2. Introduction to the Hyperbolic Metric in the Space of Triangular Shapes
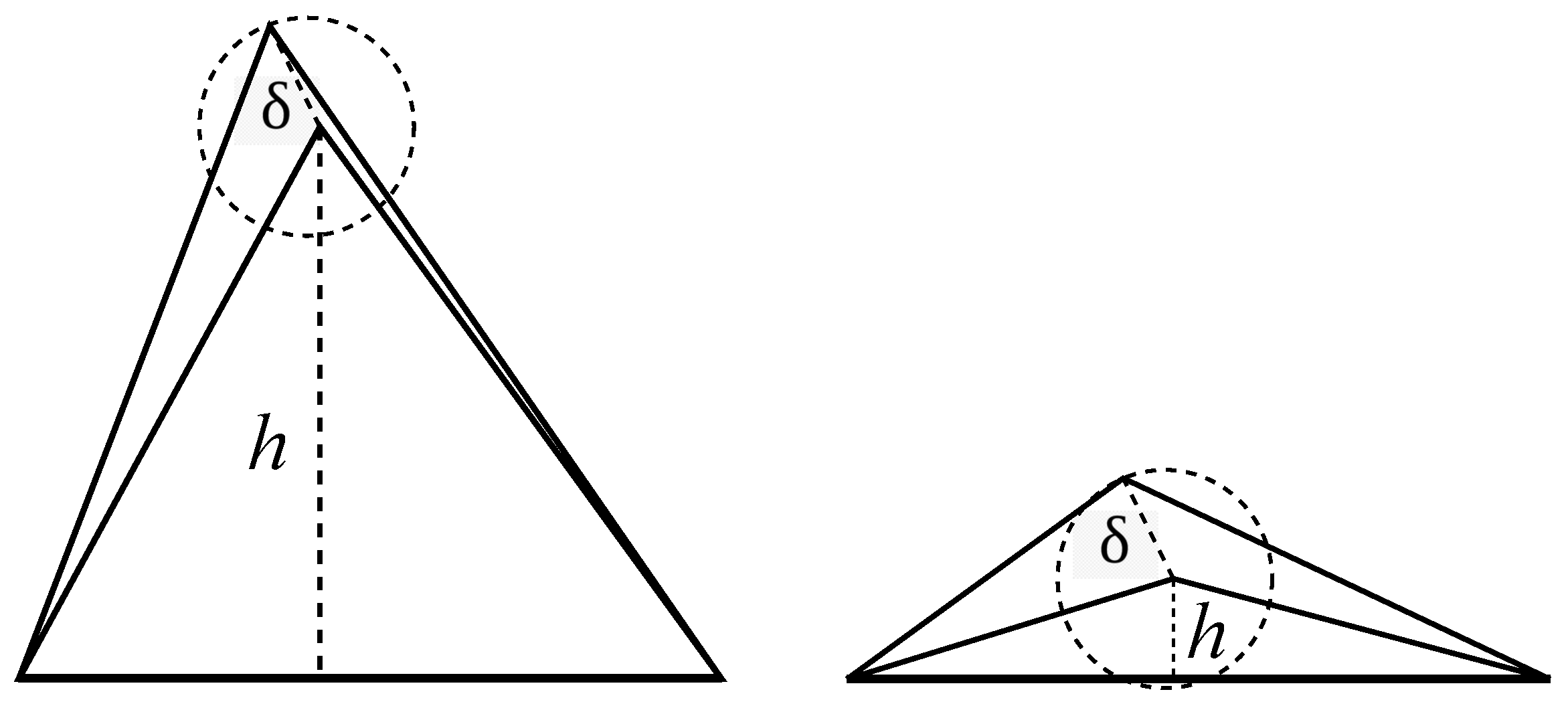
Let us consider on one hand two triangles both with Bookstein’s coordinates close to the real axis and at a Euclidean distance
. On the other hand, let us consider two other triangles with Bookstein’s coordinates at the same Euclidean distance
but far away from the real axis. The same Euclidean distance
is less important when the distance to the real axis grows
h; it is understandable to consider the hyperbolic distance between points representing triangular shapes [
13]. See
Figure 4.
A more formal justification of the election of the hyperbolic distance may be found in [
14] and may be extended to higher dimensions.
Let
and
in the upper semiplane of the respective Bookstein’s coordinates of two triangles. The affine transformation applying 0, 1,
z, respectively, to 0, 1,
w is a linear transformation, which may be written as a product of a column vector by the upper triangular matrix
If
w is a small perturbation of
z, then
, with
, and
. See
Figure 5.
In that case, matrix
may be written as
, where
I is the
identity matrix and
In order to find the eigenvalues of
, we find first the eigenvalues of
. Since
is a perturbation of the identity matrix, it follows that
after canceling less significant terms. Using the last expression, the characteristic equation for the eigenvalues is written as
The last equation is of the second degree in
. The eigenvalues
and
of
are the two roots of this equation and may be found explicitly as
Let
be the largest eigenvalue and
be the smallest one. Since
z is in the upper upper plane, coordinates
. Therefore,
corresponds to the sign + and
to the sign − in expression (
1). Considering
and
infinitesimal variations of the unity, they may be written as
and
.
The eigenvalues of
are the square roots of the eigenvalues of
. They are also perturbations of the unity that may be written as
and therefore,
By using the expression of
and
, it is obtained that the infinitesimal distance between two points with Bookstein’s coordinates
z and
is given by
which may be recognized as the expression for the hyperbolic metric for the Poincare plane.
2.3. Poincare Model the the Hyperbolic Plane
Let
is the upper semi-plane. Here, the distance is defined by
. For a continuous curve
given by
, its length with this metric is given by
The hyperbolic distance between
and
is defined as the minimum of the lengths of all paths joining points
and
:
The last expression has all the properties of a distance in
, and
. Note that the semi-line
for
holds the distance between any two of its points.
A curve that covers the minimum distance between any of its points is called a geodesic curve. A transformation of the semi-plane into itself is said to be an isometry if it preserves the hyperbolic metric.
In the Poincare semi-plane, the geodesic lines or hyperbolic lines are the semi-lines and the semi-circumferences that are the intersection with of lines and circumferences orthogonal to the line .
3. Complex Functions Associated with the 3T-LE in the Space of Triangular Shapes
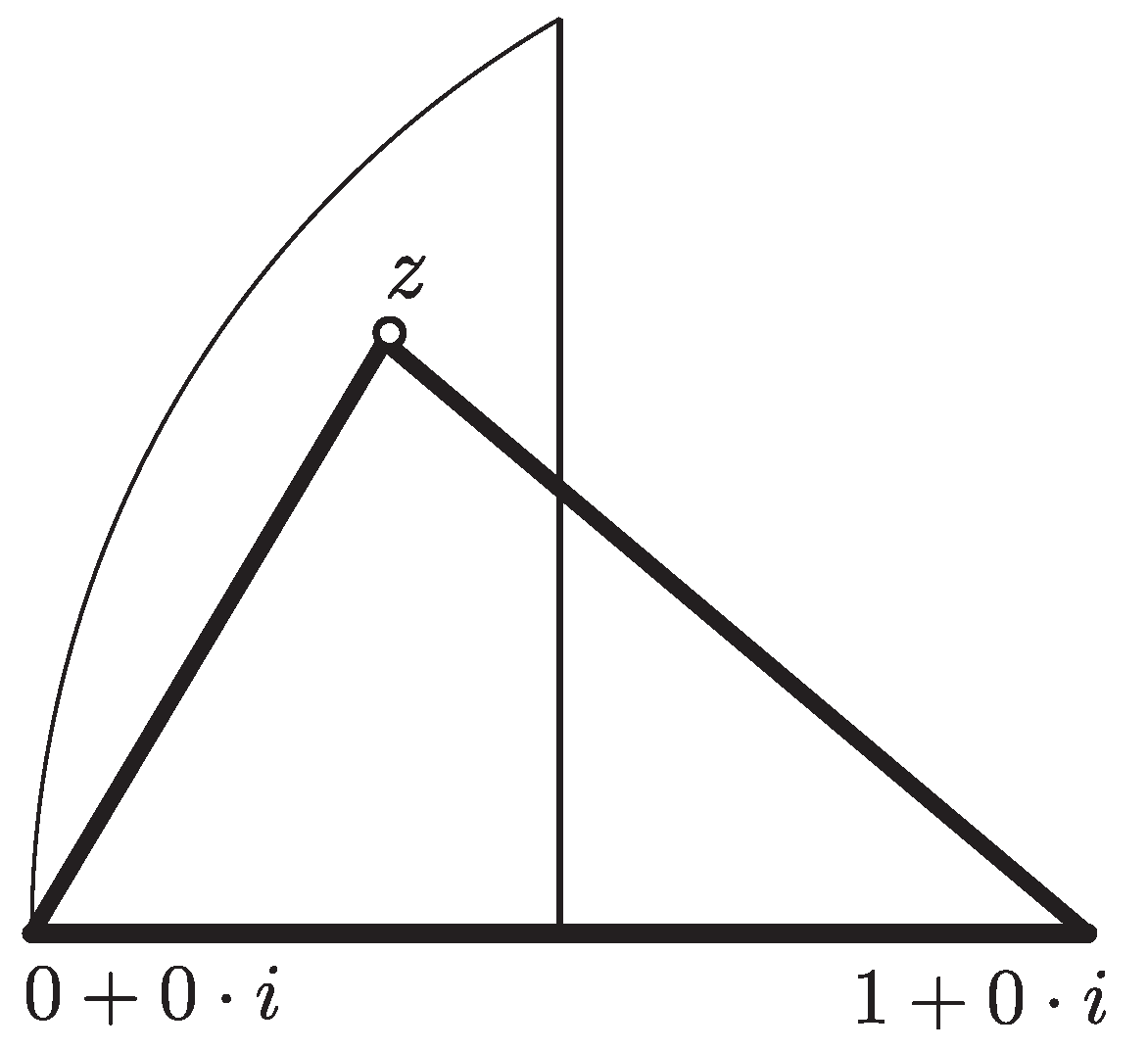
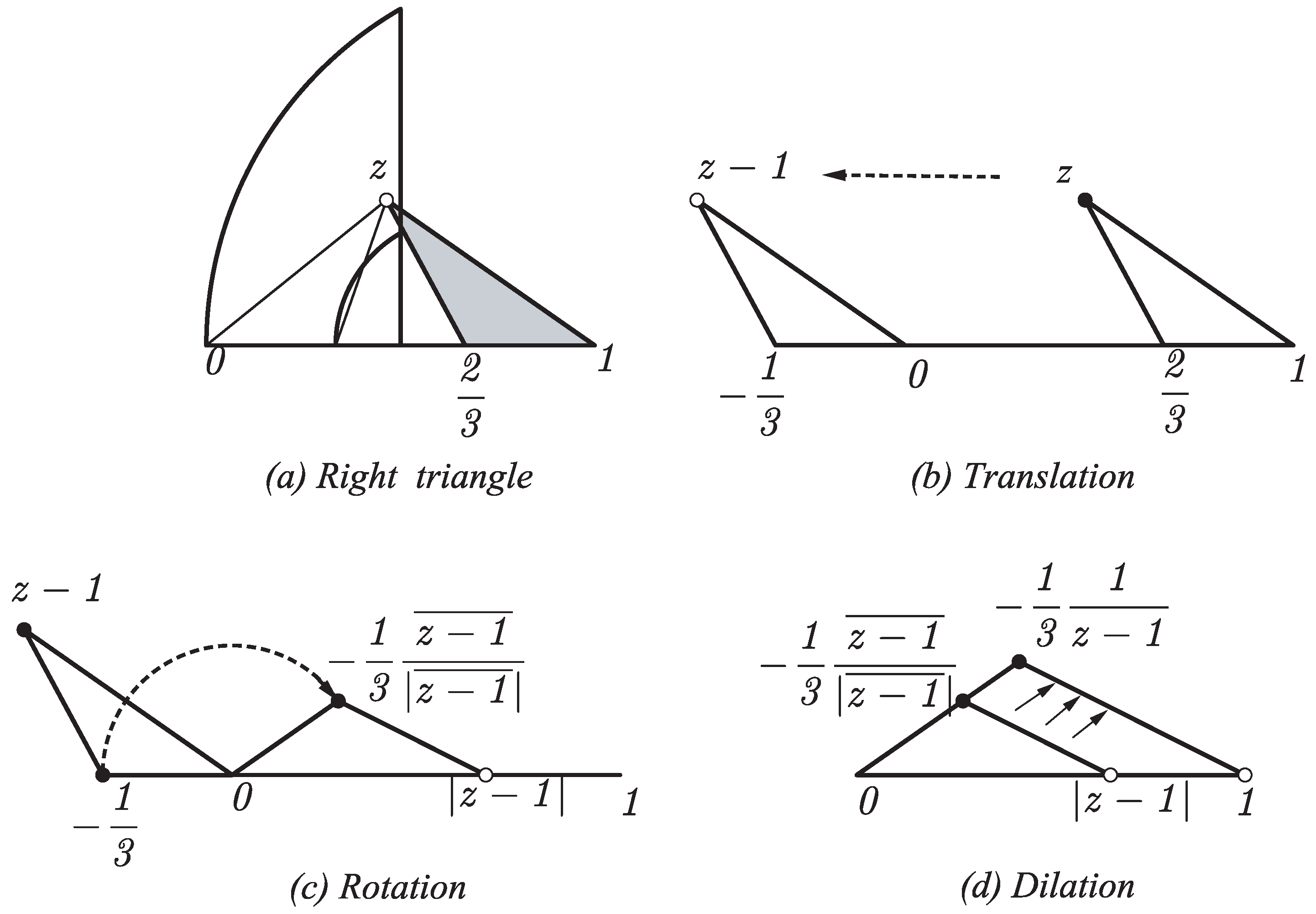
Definition 1. Let Δ be a normalized triangle with associated point . By the 3T-LE partition applied to triangle Δ, three triangles are obtained. These triangles are called the left, middle, and right triangle. The left triangle is the triangle with vertices 0, , and z. The middle triangle is the triangle with vertices , , and z. Finally the right triangle is the triangle with vertices , 1, and z.
Definition 2. The normalization of the triangle gives a complex number . (see Figure 6). A complex function can be defined if this complex number is associated with z. In this way, left function is defined as the function of the region Σ into itself with , where z is the complex number associated with the initial triangle Δ. Functions and are associated, respectively, with and and are defined similarly. Figure 6a shows the 3T-LE of a triangle where the left triangle
is in gray, and
Figure 6b shows triangle
and
.
In this way, the normalization process reduces the LE-trisection method to the discrete dynamic in the space of triangles associated with the three complex functions , , and .
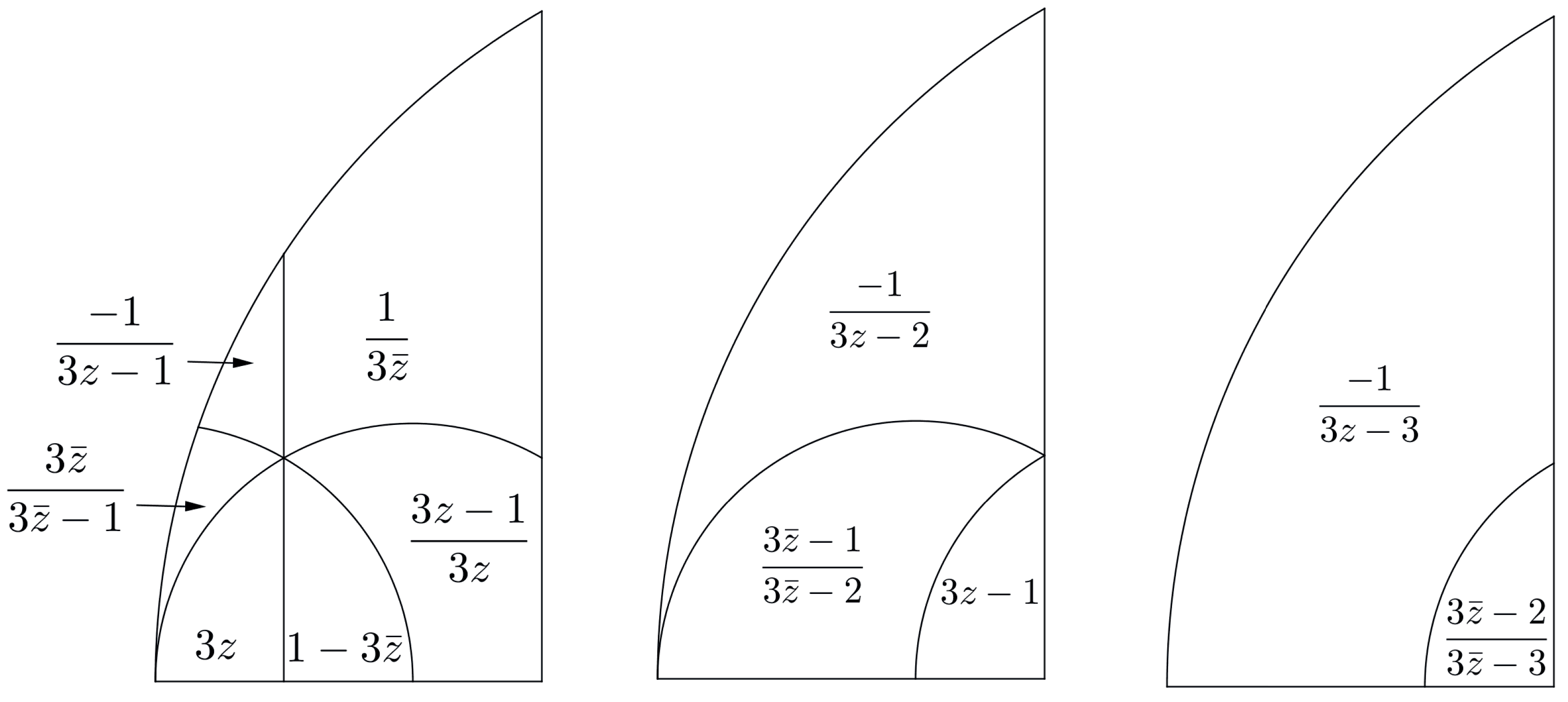
For the sake of completeness, the next Propositions show the boundaries for the subsets where functions , , and are defined as well as their explicit expressions in each subset. The different expressions for the piecewise functions , , and depend on the relative position of the longest edge on each triangle.
Proposition 1. The boundary lines for the subregions of Σ, where functions , , and are defined, are straight line and circular arcs , , and .
Proof. These regions depend on the relative position of the edges of triangles
,
y
according to their length. The different possibilities are shown in
Figure 7 and
Table 1. □
Proposition 2. The different expressions for the piecewise functions , , and are as shown in Figure 8. It should be noted that the expressions in
Figure 8 are isometries in the Poincare semi-plane model for the hyperbolic plane.
Figure 9 shows how to deduce the expression of
for a point
z belonging to the upper subregion given in
Figure 8. In order to normalize the right triangle in gray in
Figure 9a, we apply first a translation in
Figure 9b, then a rotation such that the longest edge of the rotated triangle is on the opposite real axes in
Figure 9c and finally a dilation such that the longest edge is on segment
in
Figure 9d. The last expression is the value
.
Proposition 3. Let W be any of the functions , , and . Then, W is invariant about the reflections with respect to the geodesic lines which appear in its definition.
Proof. These lines are geodesics according to the Poincare half-plane model for the hyperbolic plane. We may talk therefore about reflection with respect to these lines, taking into account that it means inversion in the case of a circumference or symmetry in the case of a right line. □
4. Discrete Dynamic of the 3T-LE Partition in the Space of Triangles
Definition 3. Let . The set of complex numbers obtained by iterative application of functions , , and to z and its successors is named orbit of z by the 3T-LE partition, and it is denoted by . The cardinal of will be denoted by .
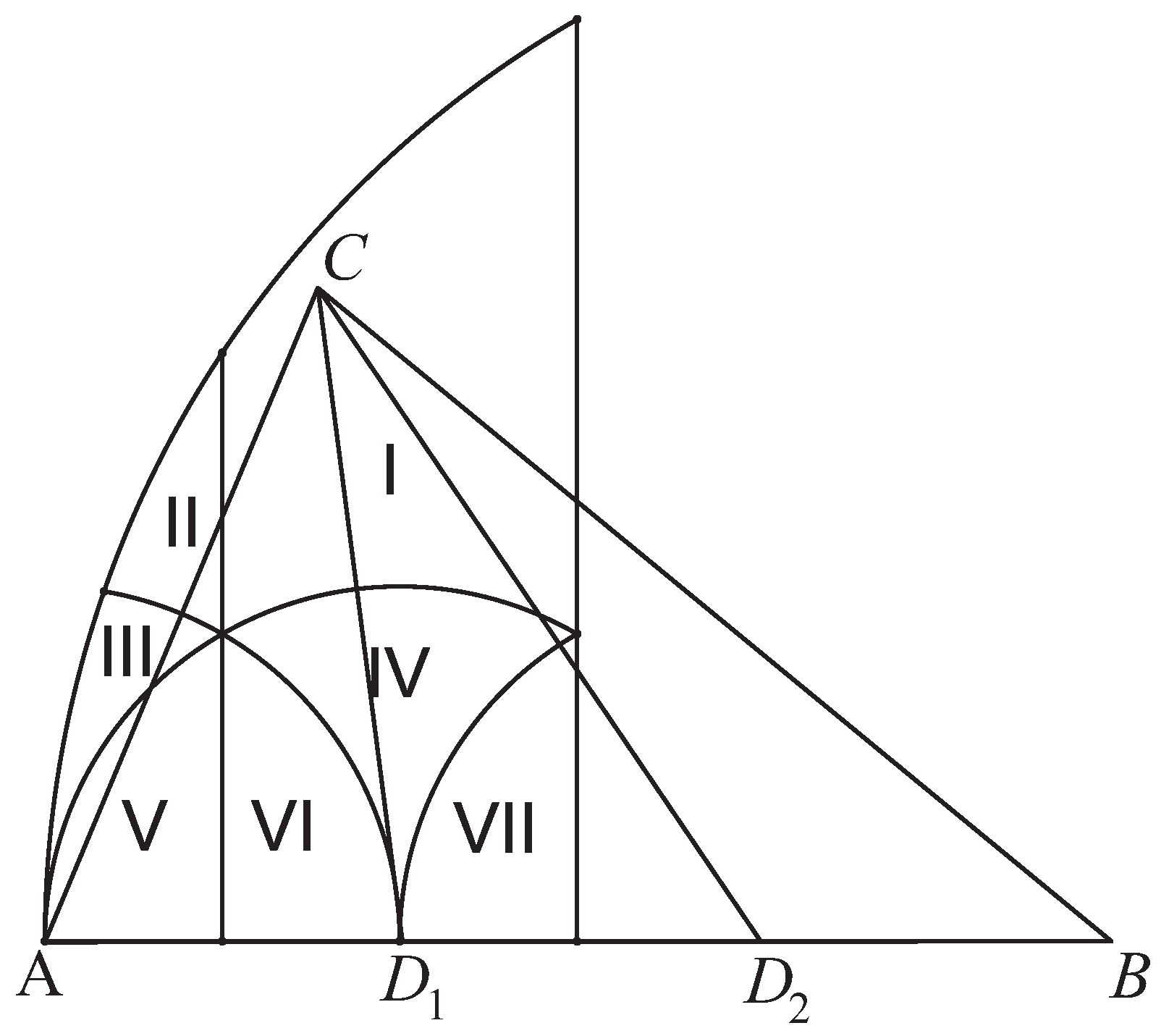
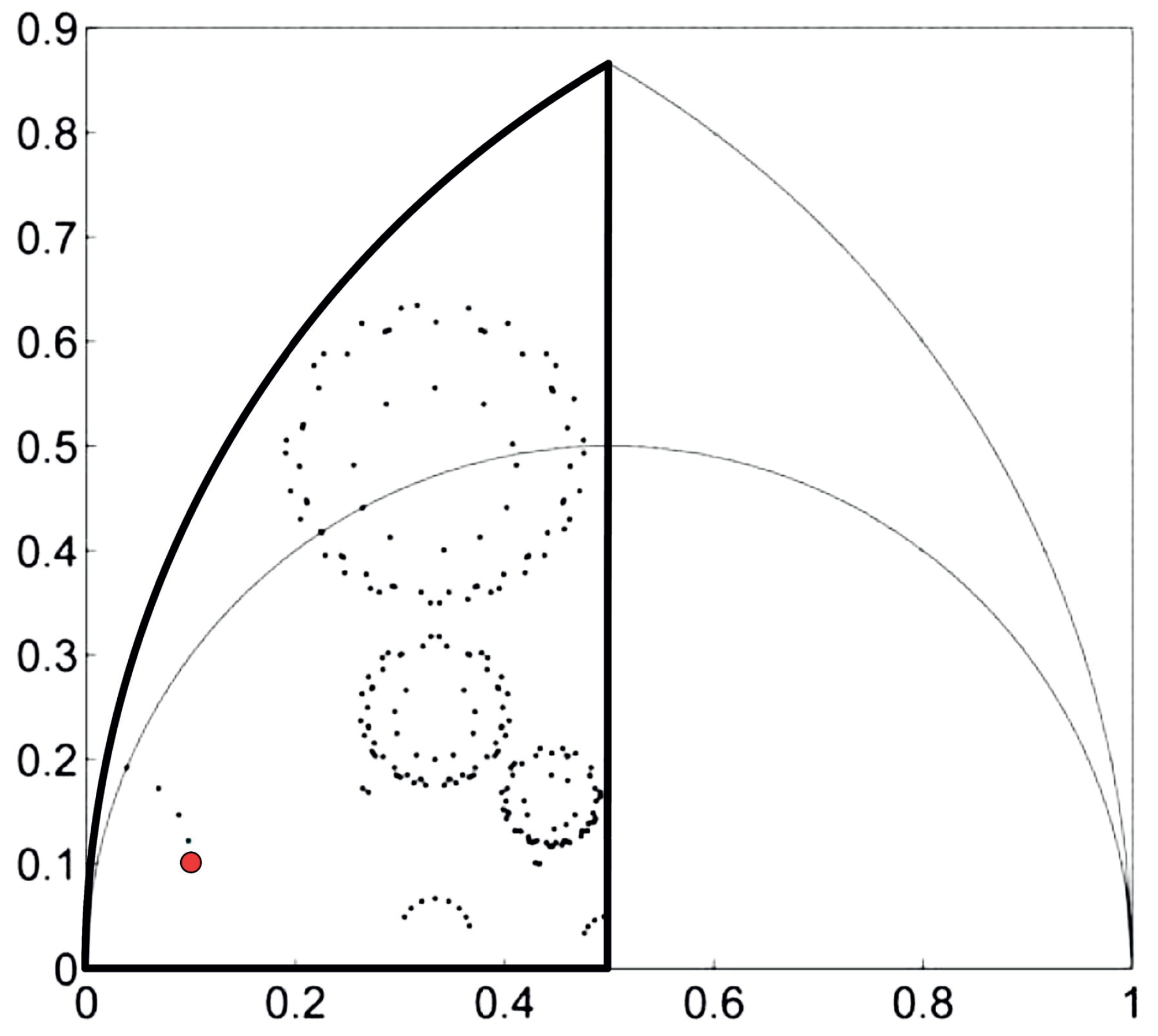
We will show in this section that there are exactly three points in the space of triangular shapes with finite orbits. In addition, any other point will have an infinite orbit with infinite points in three circles with centers at the points with finite orbits.
Proposition 4. If , then its orbit is , where and .
Proof. It follows easily since , , , , , , , , and . □
The orbits of points
, and
are finite. These points correspond to the three shapes of the triangles obtained from the standard paper size by 3T-LE. Any other orbit has typical aspect showed in
Figure 10: every point of the orbit is in circles around
, except perhaps a finite number of points.
Some facts about the Poincare semi-plane model and the hyperbolic geometry are naturally related to the discrete dynamic in the space of triangular shapes. See, for example, [
15,
16,
17]. Here,
d is the Poincare hyperbolic distance in the semi-plane:
Definition 4. Let and be two points in the half-plane. Then, the hyperbolic distance between them, , is defined by the expression Our next goal is to prove that points
, and
are the only ones with finite orbits. One interesting property of functions
,
, and
is the non-increasing property as the following lemma establishes. For a proof of it, see [
18].
Lemma 1. Let and let W be , , or . Then, .
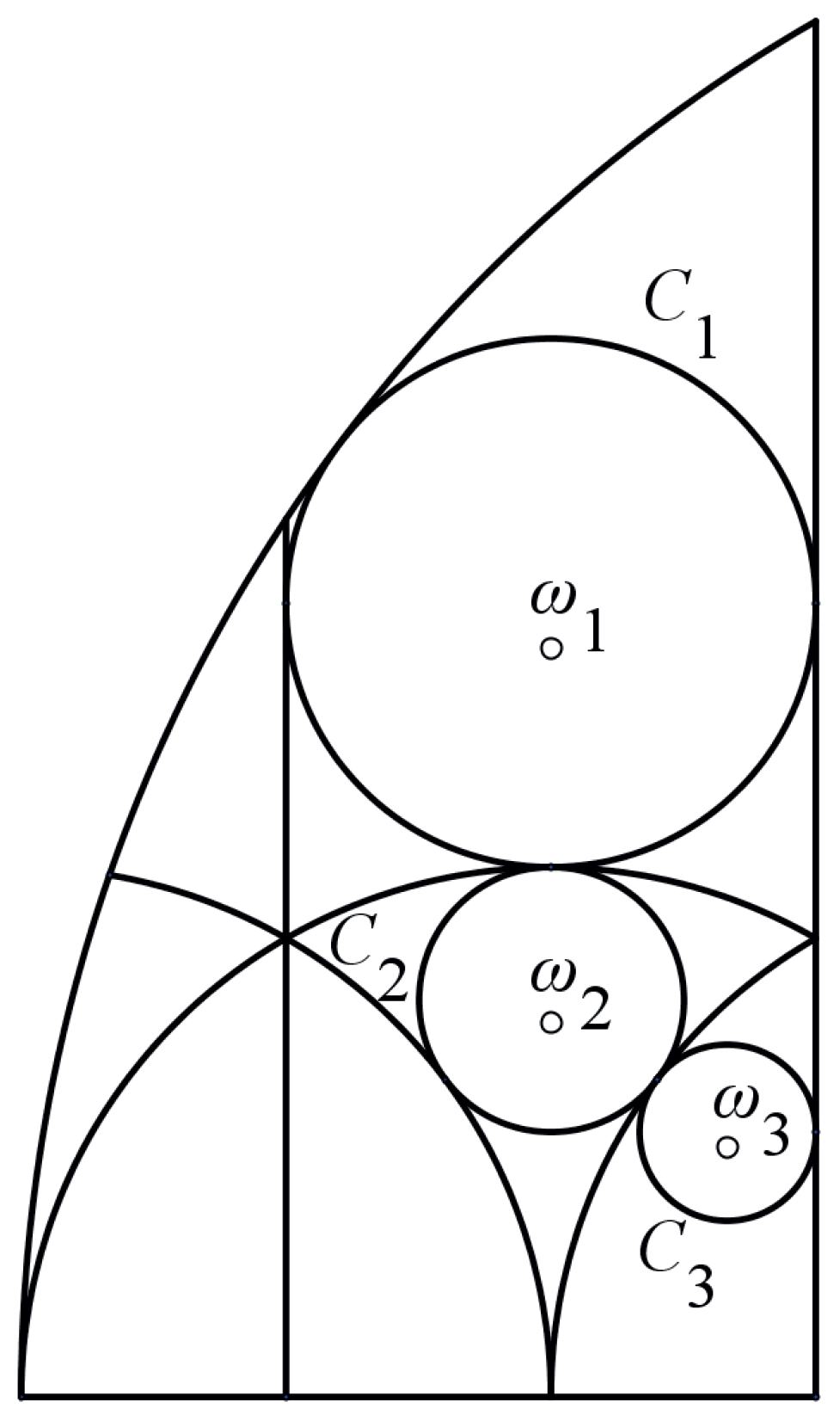
Proposition 5. Circumferences , , and , respectively, of equationshave centers, respectively, as the points , , . These circumferences have radius with the hyperbolic distance, and they are tangent to the boundary lines of the regions defining functions , , and . Proof. The proof follows by the definition of hyperbolic distance. See
Figure 11. For example, in circumference
, the points at maximum and minimum height, respectively, are
, and
. Therefore, according to the formula for the hyperbolic distance (
2), and the diameter of circumference
is
. Let
be the center of circumference
. Then, the radius will be given by
, and hence,
, so effectively
is as in the proposition. Analogously, the radius and center for circumferences
and
may be deduced. Notice that circumferences
,
, and
may be written with the hyperbolic distance as
, respectively, for
. □
Lemma 2 ([
19] (page 40))
. is not a rational multiple of π for any odd number . The following proposition explains the characteristic circular formations of the orbits of the 3T-LE.
Proposition 6. Let with for some . Then, the orbit of ω, , is dense in any circumference for .
Proof. , , and interchange the hyperbolic circles with radius and centers for , or they are hyperbolic rotations in these circles. These rotations are not rational multiples of , and then any point , as in the hypothesis, has an orbit dense in the circumferences for . Notice that function is given by , which corresponds to an hyperbolic rotation with center . Since the derivative of at is , the angle of the hyperbolic rotation is . Because , , is not a rational multiple of , because of Lemma 2 for and also is not a rational multiple of .
Since is not a rational multiple of , if , then . Therefore, the orbit is not finite. However, our goal is to prove that the orbit is dense in the hyperbolic circle with center and radius r. Let L be the hyperbolic length of that circle, and let z be such that . We have to prove that for every there is a point in such that its hyperbolic distance to z is less than . Let such that . Let us consider the points , which are all different. Since they are points, two of them are in a hyperbolic circular arc of length . It follows that there exist such that . Therefore, the points are on a circle to a distance less than each from the following because is an isometry. Hence, there exists such that . □
Proposition 7. Let with . Then, for some .
Proof. Since the orbit
is finite, the sequence
is cyclic, so there exist
N and
p such that
for
. If
, then
is a point belonging to the subset of
invariant by
, so
. Let us suppose that
, and
p is the lower integer with that property. Let
for
different points. By the non-increasing property of the distance
Then,
Therefore,
are in the same region of definition of
where there is
. In that region,
, which is a hyperbolic rotation with center
and angle
as in Proposition 6. But then
is not a rational multiple of
which is a contradiction. Hence, there is an integer
N such that
. Let us consider the lower
N with that property. If
or
, then by using the expression of
it follows that
for some
. Let us assume that
. Then, either
or
.
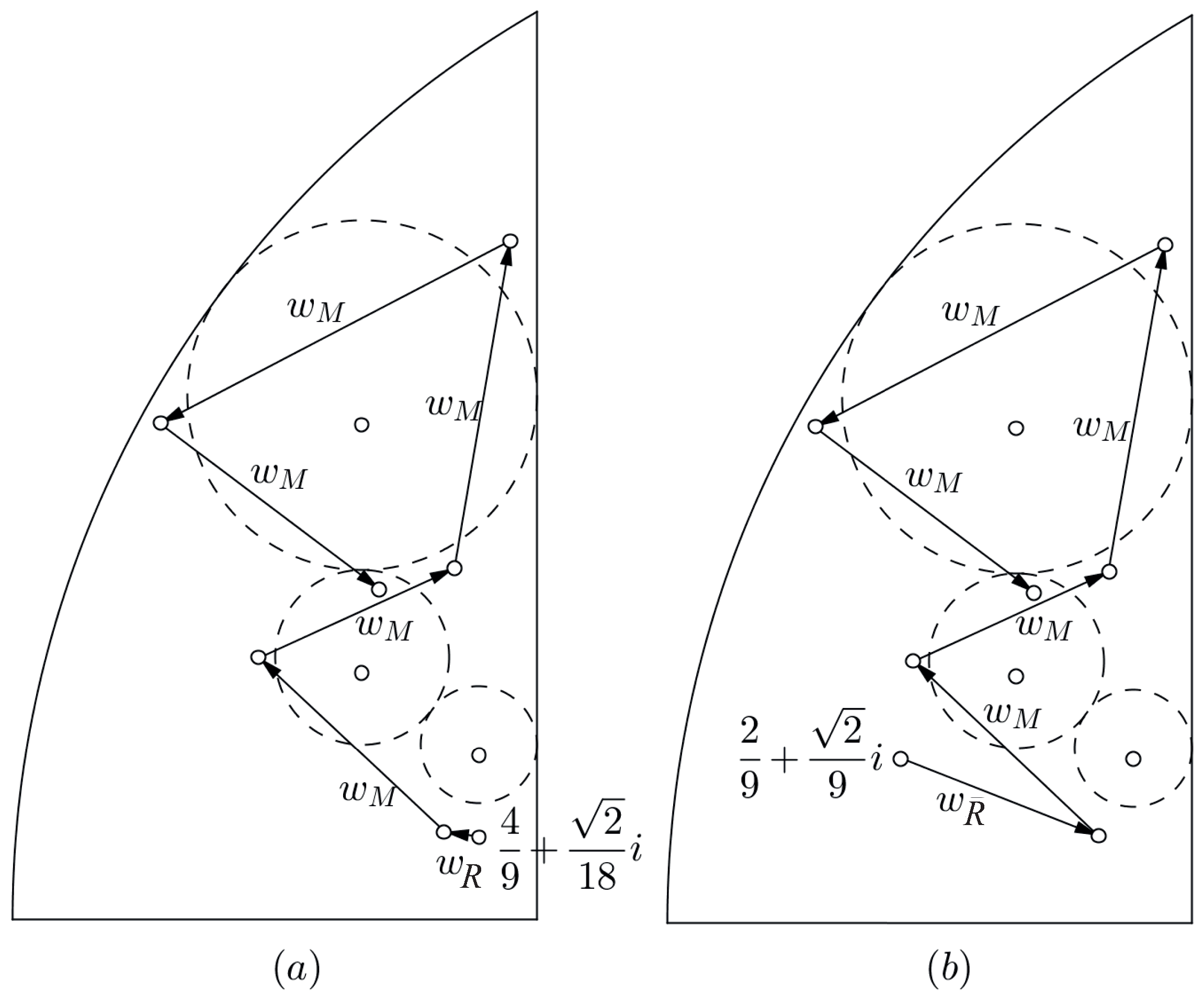
If
, then its pre-image
by
is either
or
. In both cases, it is not possible that the orbit is finite, because applying
a point is obtained to a distance less than
to
. See
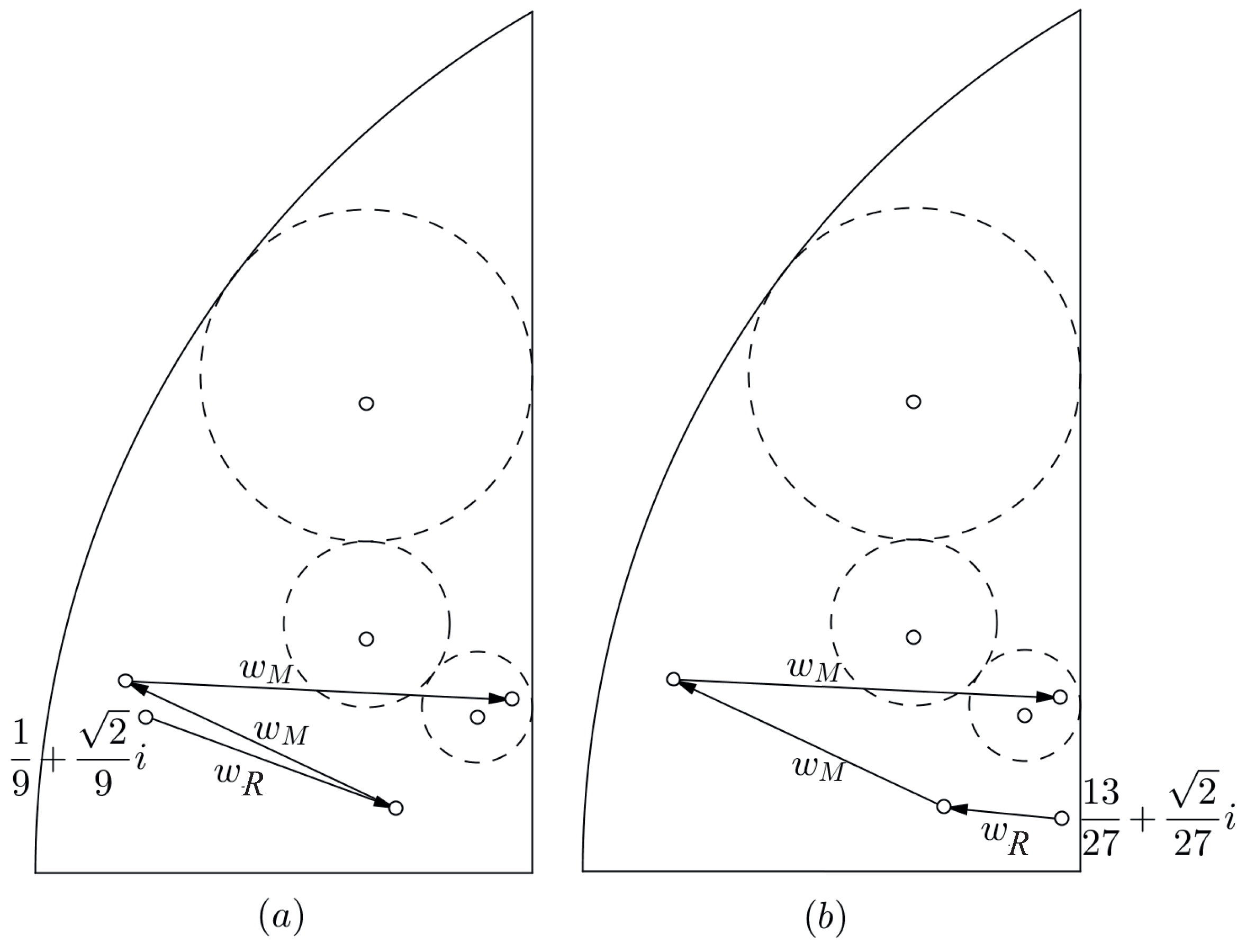
Figure 12a,b, and Proposition 6 applies. As a consequence, the orbit is dense in the circle and so it is not finite.
On the other hand, if
, then its pre-image
by
is either
or
. Again, it is not possible that
is finite, because applying in both cases
a point is obtained to a distance less than
to
, and again, Proposition 6 applies. See
Figure 13a,b. □