Abstract
In all organizations, many decision analysts acquire their skills through the experience of facing challenges to structure complex problems. Therefore, every day, the use of tools to integrate indicators through multi-attribute ordering, component-based separation, and clustering to reduce the criteria required for decision-making and the achievement of goals and objectives is more frequent. Thus, our proposal consists of a new hybrid-hierarchical model for the classification and prediction of country indicators such as inflation, unemployment, population growth, and labor force, among others, in a decision-making environment using unsupervised neural networks and type-3 fuzzy systems. The contribution is achieving a type-3 fuzzy aggregation method in which the hierarchy is first represented by neural networks and later a set of type-1, type-2, and type-3 systems to combine the results, which allows multiple indicators to be separated and then integrated in an appropriate fashion. We can point out as one of the advantages of utilizing the method that the user can evaluate a range of qualities in multiple variables through the classification and prediction of time series attributes and assess a range of qualities for decision-making with uncertainty, according to the results of the simulations carried out.
Keywords:
classification; decision-making; hybrid-hierarchical model; interval type-3 fuzzy system; neural networks; prediction MSC:
03B52; 03E72; 62P30
1. Introduction
Multi-criteria decision analysis (MCDA) is a set of techniques that aim to establish a hierarchy among multiple options, generally seeking to order them from the most suitable to the least suitable. Choosing one or several options is a complex task since, to achieve several goals or objectives, it is common to choose more than one option, and the more beneficial an option is, the higher its cost. Thus, the cost-benefit relationship is frequently in conflict when making the decision.
MCDA consists of a group of techniques used to face complex problems where there are economic and non-economic goals, seeking to serve as a support tool for decision-making by simplifying the problem into several parts, weighing the objectives, and putting all the pieces together again at the end [1,2].
The indicators are used as measurement units that allow for evaluating performance, profitability, productivity, service quality, and time management, among others. To integrate an indicator, generally the first step is to identify the objective whose fulfillment is to be verified and the policy, program, or project to which it is associated.
In the case of primary and secondary indicators, the combination of the compliance assessment produces information to analyze the performance of any area of the organization and verify compliance with the objectives in terms of results. The most important thing is that they can be a key and fundamental piece in detecting and anticipating deviations in the achievement of objectives.
Currently, the recording of historical information using economic and non-economic indicators seeks to know how a variable is performing in different areas and, at the same time, in which it can improve. In the case of a group of countries, it is possible to highlight the similarities and discrepancies between them in order to establish progress, setbacks, or stagnation in the economic events that occurred on a certain date.
Therefore, our motivation arises from the need to have an intelligent computational model that manages to evaluate the fulfillment of each one of the goals and objectives established to solve a complex problem. Then, later, integrate the results of the evaluation and make comparisons through the management of uncertainty in decision-making using neural networks and fuzzy systems for the classification of multiple indicators or variables. It is important to point out that both kinds of methods have previously shown good results in solving complex decision-making problems [3,4,5]. The final goal is to produce information to analyze the performance of any area of the organization and verify compliance with the objectives in terms of results.
Thus, simulating the decision-making process carried out by a person considering the uncertainty and challenges of choosing among different options, which may or may not be fully available, is the key contribution of this article, which is achieved by combining neural networks with hierarchically nested fuzzy systems. These systems consist of type-1, type-2, and interval type-3 fuzzy for integration [6]. This represents the main advantage of our method when compared to existing methods in the literature, which generally use aggregation methods with binary outputs.
In recent years, researchers have proposed multiple hybrid models that combine aspects of the fuzzy set theory proposed in the 1960s by Zadeh with traditional mathematical models and also the intuitive fuzzy set theory by example for treating drug addict patients [7]; risk evaluation on agricultural products [8]; electric vehicle charging dispatch [9]; and mapping (fuzzy ranking) the linguistic judgments [10,11] of the MCDM problems. Unlike our method, which uses various linguistic terms based on the theory of fuzzy sets. In addition, an unsupervised neural network, the self-organizing map (SOM), is used as part of the method to cluster the data, which, in combination with type-3 fuzzy systems, offers a unique hybrid approach.
This article is formed in the following fashion: In Section 2, some theoretical aspects are presented. A succinct description of the problem is shown in Section 3. The method is outlined in Section 4. Experiments and a brief discussion of the results are indicated in Section 5 and Section 6. Lastly, Section 7 outlines the conclusions.
2. Basic Concepts
In this section, we present a general summary of the theoretical aspects considered to carry out the development of our proposal, which mainly contemplate the neural networks and fuzzy systems that have been utilized as intelligent techniques [12,13].
2.1. Self-Organizing Map
SOM is frequently used to perform unsupervised classification (Figure 1). It operates using three vectors: the first is the input x, the second is the weight m, and the third is the output with s elements, where each element represents the negative of the distance between the x and m matrix vectors constructed from the r rows of the input weight matrix. The competitive function returns a 1 to the winning neuron; however, all other neurons assign a 0.
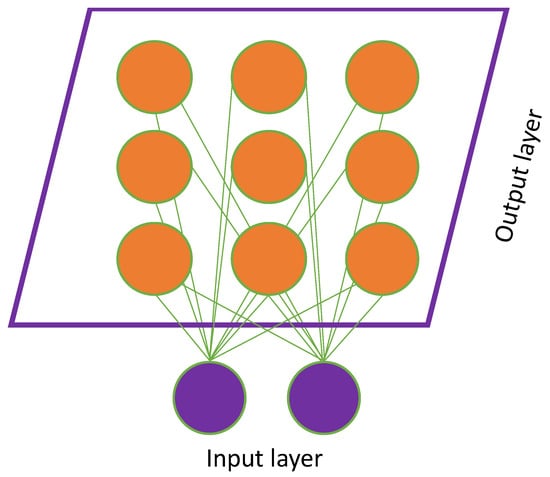
Figure 1.
SOM neural network architecture.
We define the best match to be a unit with index c that can be expressed by Equations (1) and (2), which represent the similarity matching:
Moreover, the neuron learns from an input vector and adjusts its weights, as shown in Equation (3):
where m is the input weight vector, i is an index position, is a vector time index, α is the learning rate, N is a set of units, c is an index to define the best match to be at unit, and x is an input vector [14].
2.2. Type-2 Fuzzy Sets
We can refer to the uncertainty that affects decision-making and try to model it by utilizing interval type-2 fuzzy logic, where the goal is to model uncertainty as an information attribute instead of using type-1, which only represents vagueness.
In both type-1 and type-2 fuzzy sets, the fundamentals of fuzzy logic stay the same; basically, a type-2 system is integrated by fuzzy rules, where each of their components consists of type-2 sets containing type-1 membership functions (MFs). In this kind of system, the uncertainty is modeled in the definition of the membership function (MF).
We can summarize that the main difference is that in type-2, the degree of membership is an interval with two limits (0 and 1) with which uncertainty can be handled, while defuzzification is configured to obtain a crisp output from the type-2 system.
A General type-2 fuzzy set A is formed by a primary variable x with domain X and a secondary variable u with domain Jx. It can be mathematically expressed as (4).
In General Type-2 Fuzzy Logic, the membership functions are tridimensional functions composed of a collection of secondary membership functions [15,16,17].
2.3. Interval Type-3 Fuzzy Systems
In more complicated situations, such as simulating the decision-making process carried out by a person considering the uncertainty and challenges of choosing among different options, which may or may not be fully available, to finally integrate the results of the evaluation and make comparisons through the management of uncertainty, it is possible that a hierarchical approach is needed, where several simpler fuzzy systems are used, and then an aggregator fuzzy system is needed to combine the outputs of the simpler systems [18,19,20].
In this case, type-3 could help us combine the outputs of type-2 fuzzy systems. In this section, we first postulate the basic type-3 terminology.
Definition 1.
A type-3 fuzzy set (T3 FS), called , is expressed by (5)a MF of , in in , where is the primary variable universe of , x. The MF of is postulated by (or ) and labeled a type-3 MF (T3 MF):
Expression (7) is postulated as a T3 FS MF with formulas (8)–(10):
where is the primary MF, is the secondary MF and is the tertiary MF.
If , the T3 FS, , is simplified to an interval type-3 fuzzy set (IT3 FS) called , postulated by Expressions (11)–(14).
where
Assuming that and the lower and upper MFs are general type-2 MFs (T2 MFs) on plane , Formula (5) is simplified to an interval type-3 MF (IT3 MF), , postulated by Formula (15).
In this case, the lower T2 MF is a subset of the upper T2 MF this is, , then . Then, an IT3 FS is expressed by two T2 FSs, one lower with T2 MF and another upper , with T2 MF postulated by Expressions (16) and (17) (see Figure 2).
where, the secondary MFs of and are T1 MFs postulated by Formulas (18) and (19).
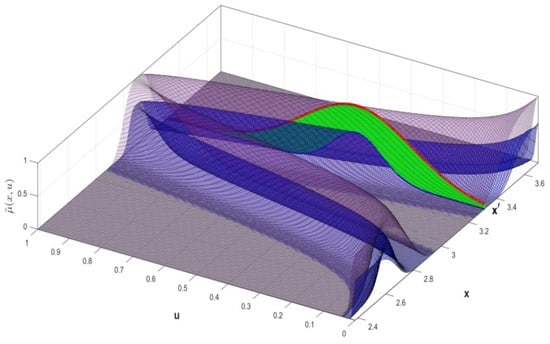
Figure 2.
IT3 FS illustration.
2.4. Multi-Criteria Decision Making
Multi-criteria decision-making is part of the area of knowledge known as operations research (OR), where one of its objectives is to carry out an analysis of the solutions to problems in the national, social, or organizational spheres.
It can be said that an indicator is used as a measurement unit, and it is useful when its predictions are beneficial and improve the results of the benchmark of the element in comparison to the results obtained when the indicator is ignored. In general, the usefulness of an indicator is reflected when it helps to issue early warnings about possible economic changes so that decision-makers can anticipate severe recession scenarios. This highlights one of the main benefits of considering global or international events when evaluating the threats or vulnerabilities of a nation. In an increasingly integrated world economy, vulnerabilities that build up on the global level can potentially be transmitted to countries around the world [21,22].
It is relevant to find a correct method to rank countries based on development indicators, whether economic or non-economic, with which it is possible to make a fair comparison between their strengths and weaknesses [23].
In the field of artificial intelligence, a constant challenge is to simulate a decision in a system using basic connectors that operate from a general perspective. In order to adequately take in the environment, a system requires knowledge provided by reliable sources of information, for which more than one source is needed, whether it is a sensor or an expert. Therefore, the information provided by several sensors (or experts) should be combined to improve data reliability and accuracy [24,25,26]. The system may have multiple criteria, known as a multi-criteria decision problem.
3. Problem Description
The World Development Indicators are the World Bank’s compilation of cross-country indicators. It consists of a set of relevant, high-quality statistics about global development and poverty. Among its characteristics, we can mention that to carry out the compilation, multiple international sources are used that have international recognition. In addition to presenting the most up-to-date and precise global development data available. So, we pretend to integrate the results of the neural network evaluation and make comparisons through the management of uncertainty in decision-making using hierarchical fuzzy systems for the classification of some of these indicators or variables combined with each other [27,28,29].
For this work, we selected nine datasets for each of the 20 countries in Latin America, and it should be noted that no preprocessing was carried out prior to its use (Table 1) [30].

Table 1.
List of countries.
Each dataset consists of six attributes: country name, country code, series name, series code, year, and value. We can observe the period selected in Table 2.

Table 2.
Dataset period for time series.
For the dataset of inflation, GNI, GNI per capita, and GDP per capita, we only used the last value of the time series for Cuba (2020–2021) and Venezuela (2015–2021) because data for these periods were unavailable.
4. Proposed Method
In this work, we propose a computational model that consists of two phases: For the first phase, we carried out clustering and prediction [31,32,33] of the selected time series using neural networks (NNs) [34,35,36]. We then integrated the results by using a hierarchical approach of type-1, interval type-2, and general type-2 fuzzy models (Figure 3).
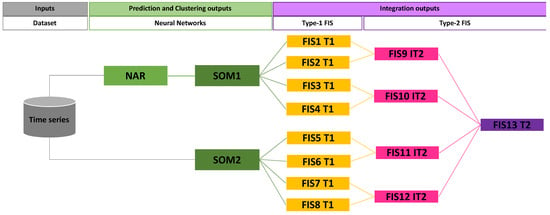
Figure 3.
Graphical description of the method (Phase A).
For the second phase, we perform similar tasks to the first phase [37,38,39], only that instead of the final integration of the hierarchical fuzzy system [40,41,42], this is performed using an interval type-3 instead of the generalized type-2 fuzzy system (Figure 4).
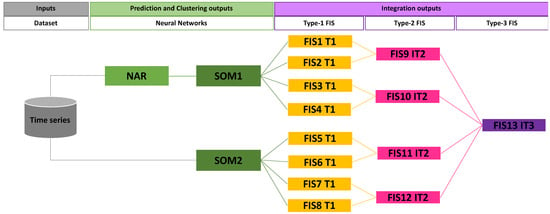
Figure 4.
Description of the method (Phase B).
Finally, with these results of type-2 and type-3 fuzzy inference systems, which operate as integrators of the results, we expect to achieve the best global result for this problem [43,44,45].
Type-1 systems, utilized to aggregate the NN results, are formed by two to three inputs and one output in all cases; they are Mamdani type, with nine to thirteen fuzzy rules and centroid defuzzification (Table 3), where the MF parameters were manually tested until obtaining these parameter values. The MFs (Figure 5) are triangular, and the linguistic variables of each function are Very few (VFW), Few (FW), Many (MN), Too many (TMN).

Table 3.
Type-1 fuzzy system membership function parameters.
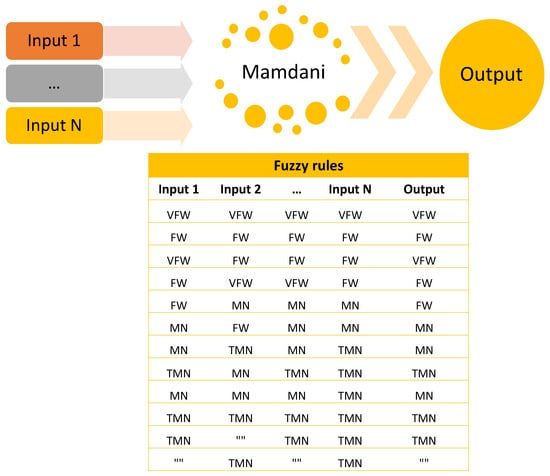
Figure 5.
Type-1 system general design.
Interval type-2 systems utilized to aggregate the results of type-1 consist of two inputs and one output. In all cases, the MFs are triangular, and the linguistic variables of each function are Low (LW), Medium (MD), High (HG). These are of Mamdani type, with twelve fuzzy rules and centroid defuzzification (Table 4), where the MF parameters were manually tested until obtaining these parameter values (Figure 6).

Table 4.
Interval Type-2 MF parameters.
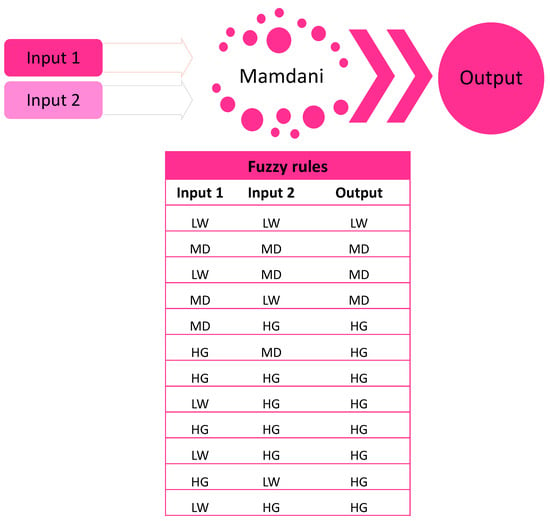
Figure 6.
Illustration of Interval Type-2 system general design.
In Equation (20), we show the average of the weights of the rules after type reduction, by which the final output is calculated.
where yi(t) are the rule outputs, i = 1, …12, are the MF values at the rule outputs, i = 1, …12, and y(t) is the global output.
Generalized type-2 systems utilized to aggregate the results of interval type-2 systems consist of four inputs and one output, which is Mamdani type; the MFs are trapezoidal and Gaussian; and the linguistic variables of each function are Low (LW), Medium (MD), and High (HG); nine fuzzy rules; and the centroid defuzzification method (Table 5).

Table 5.
Generalized Type-2 fuzzy system MF parameters.
The type-3 system utilized to aggregate the results of the interval type-2 systems is the same as for the generalized system; the only difference is that all MFs are Gaussian; therefore, parameter values are presented in Table 6. In this Table, σ represents the standard deviation, m is the center, is the lower scale, and is the lower lag.

Table 6.
Interval Type-3 fuzzy system membership function parameters.
For both generalized type-2 and type-3 systems, the MF parameters and rules were manually tested until obtaining these values (Figure 7).
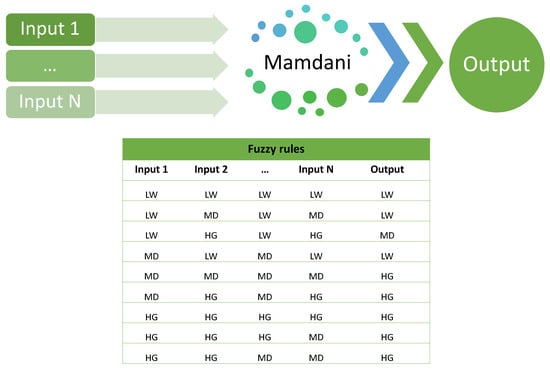
Figure 7.
Illustration of Generalized Type-2 and Type-3 systems general design.
The architecture of the type-3 system is depicted in Figure 8. It consists of four inputs and one output, and the linguistic variables of each function are Low (LW), Medium (MD), High (HG), and nine fuzzy rules.
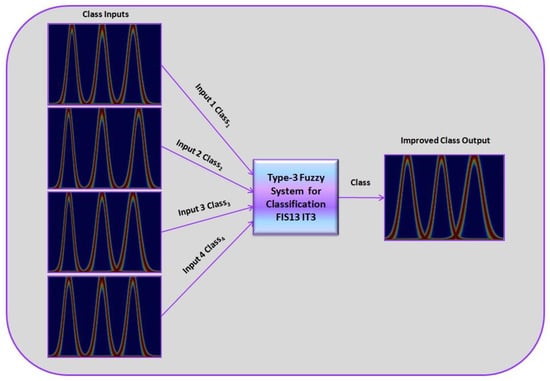
Figure 8.
Illustration of the type-3 fuzzy system general architecture.
The visual description of the MFs for the type-3 system is presented in the following Figure 9 and Figure 10. In particular, Figure 9 illustrates the MFs: (Low (LW), Medium (MD), and High (HG) for the four inputs of the type-3 system.
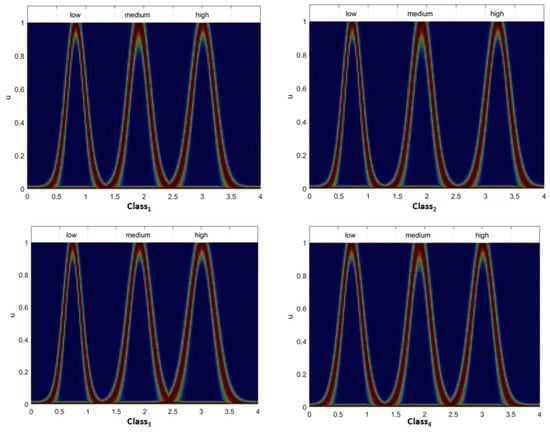
Figure 9.
Illustration of MFs for inputs of Type-3 FIS.
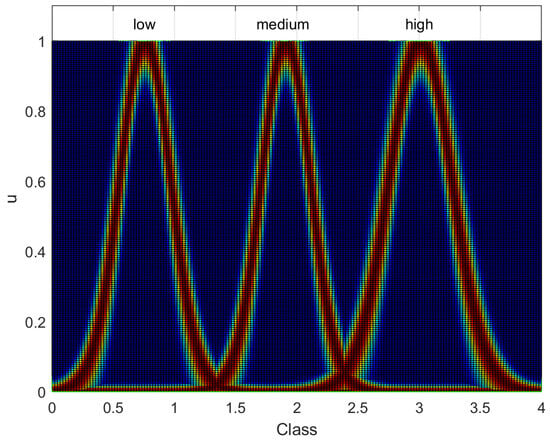
Figure 10.
Illustration of MFs for the output of the fuzzy system.
Figure 10 illustrates the MFs (Low (LW), Medium (MD), and High (HG) of the final output of the Type-3 FIS, through which the results of the multiple type-1 FIS and type-2 FIS used previously are integrated.
Finally, Figure 11 and Figure 12 exhibit two different perspectives of the type-3 fuzzy model by illustrating nonlinear surfaces, highlighting the nonlinearity of the decision process.
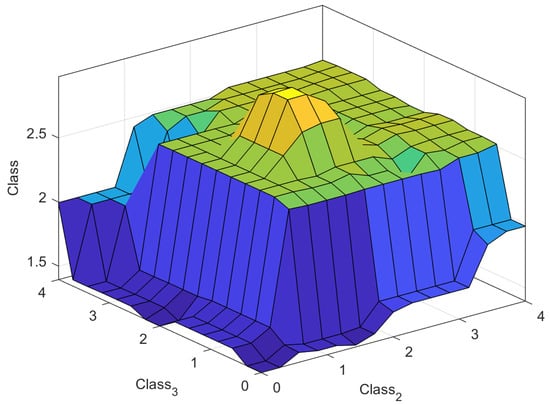
Figure 11.
Surface for the output in relation to inputs 2 and 3.
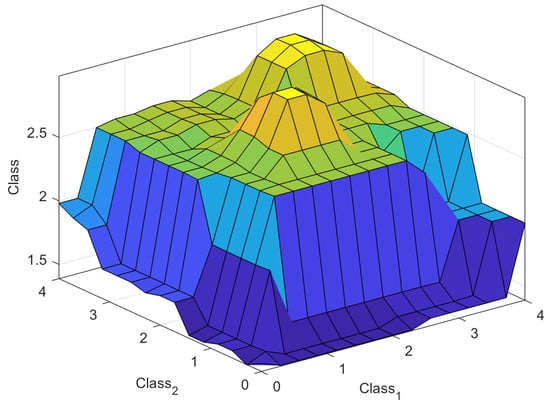
Figure 12.
Surface for the output in relation to inputs 1 and 2.
5. Experimental Results
To make the prediction of the historical data of 20 countries, we use Nonlinear autoregressive (NAR) NN with 12 neurons (hidden layer), using 70% of the data for training and the rest for validation and testing (with a total of 30 executions). To evaluate the prediction made by the NAR NN, we use the relative Root Mean Square Error (%RMSE) for the variables (time series) of the data set, showing the best, average, and worst %RMSE (Table 7).

Table 7.
Results of NAR prediction of historical data.
The clustering of the time series of 20 countries was carried out first based on the historical data in four classes (C1,C2,C3,C4) and second on the prediction (Table 7) of historical data in four classes (C1,C2,C3,C4), both through the use of Self Organizing Maps, with a total of 30 executions (Table 8 and Table 9). For each of the variables, the countries with similar data (time series) were classified into one of the four clusters, represented by columns C1, C2, C3, and C4.

Table 8.
Results of SOM clustering based on historical data.

Table 9.
Results of SOM clustering based on predictions of historical data.
The variable GDP per capita growth is the one that concentrates the most countries in cluster C1 and the fewest countries in clusters C2, C3, and C4. Moreover, the Inflation variable concentrates the most countries in cluster C2, two countries in cluster C4, and clusters C1 and C3 have one country each (Table 8). In both cases, the countries that were part of the clusters with the least number of elements are different.
For the classification of the countries based on the future values predicted with the NAR network, we note that for the variables GDP per capita growth and life expectancy at birth, most of the countries were classified in cluster C1. For most of the rest of the variables, the great majority were classified in the C2 cluster, except for the population growth and GNI per capita variables, which showed balanced groups of countries in the four clusters.
In the first instance, we obtained the classification of the prediction and the historical values of the time series (Inflation, Population growth, Unemployment, Labor force, Population, life expectancy, GNI, GNI PP, and GDP PP for the selected countries) by using unsupervised neural networks. So, the results obtained were integrated using a type-1 fuzzy system: first, the classification was based on the prediction of the future values of each time series (Table 10), and later, the classification was made with the historical values (Table 11).

Table 10.
Results of Type-1 FIS (prediction values).

Table 11.
Results of Type-1 FIS (historical values).
The integration results of the type-1 fuzzy systems using interval type-2 systems are presented in (Table 12). For each of the countries, the classification obtained through the type-2 FIS showed different results because that depends on each of the four inputs (which are the outputs of the set of type-1 fuzzy systems).

Table 12.
Results of Interval type-2 FIS (integration of type-1 FISs).
The integration of the results of the interval type-2 by using generalized type-2 and type-3 fuzzy systems is presented in (Table 13). For each of the countries, the classification obtained through the Generalized Type-2 FIS showed similar results because that depends on each of the four inputs (which are the outputs of the set of Interval Type-2 FIS) in comparison with the Interval Type-3 FIS, which manages to classify nine countries in a different category than the rest of the countries.

Table 13.
Results comparison of type-2 and Interval type-3 (integration of Interval type-2 FISs).
6. Discussion of Results
We have aimed to obtain a model to rank multiple indicators for a determined cluster of countries using NNs and type-1, type-2, and type-3 hierarchical systems. Since most of the countries have been classified by officially recognized international sources, in the fuzzy integration results, most countries presented very similar results. We noted that the results obtained by supervised neural networks for prediction and the type-1 and interval type-2 systems presented good results for a group of two or more variables. However, when integrating the results by the generalized type-2 and by interval type-3, we noted that with the latter, better results were obtained by being able to separate a larger number of countries in comparison with the generalized type-2. We can conclude that the simulation results demonstrate that it is possible to utilize interval type-3 to integrate the indicators of multiple countries in a better way than with generalized type-2 systems.
7. Conclusions
We outlined in this work a classification and prediction model for the Inflation, Population growth, Unemployment, Labor force, Population, life expectancy, GNI, GNI PP, and GDP PP time series for the selected countries, utilizing multiple neural networks, type-1 systems, and type-2 and type-3 fuzzy integrators.
Simulation results show that it is possible to predict future values based on historical data using supervised networks, and later, countries with similar historical and future values of indicators can be clustered using unsupervised neural networks.
The results demonstrate that it is possible to use type-1, type-2, and interval type-3 systems to estimate the final country indicator, with the latter being the one that exhibits the best results during the experiments.
Thus, the key contribution of this paper, which is achieved by combining neural networks with hierarchically nested fuzzy systems, consists of simulating the decision-making process carried out by a person considering the uncertainty and challenges of choosing between different options, which may or may not be fully available.
Based on the experiments, we noticed the advantages of our proposal for classifying the information as a decision-making tool because these systems utilize type-1, type-2, and type-3 fuzzy integration, with which it is possible to integrate individual indicators or the results obtained from the combination of multiple indicators, taking advantage of fuzzy set theory.
With the integration of the classification results through the nested set of fuzzy systems described above, it is possible to consider each of the indicators by country and, in turn, transmit timely and relevant information for the analysis of economic and social reality, which makes our model a powerful support tool for decision-making.
In addition, it is also possible to highlight the similarities and differences between a country or a group of countries in order to establish advances, setbacks, or stagnation in the economic events that occurred on a certain date. The foregoing seeks to know how a country or state is performing in different areas and, at the same time, in which areas it can improve.
One of the limitations of this study is that when dealing with global indicators, there are frequently insufficient comprehensive measures in some time series; therefore, making comparisons in terms of indicators is a complex task, as occurs in most of the statistics of countries.
As activities to carry out in future works, we have the idea of designing a model that consists of a set of type-2 and type-3 systems, aiming at integrating a higher number of financial and demographic variables, among others, to expand the range of economic and non-economic aspects of the problem to be solved.
Author Contributions
Conceptualization, M.R. and P.M.; methodology, P.M. and O.C.; software, M.R.; validation, M.R. and P.M.; formal analysis, P.M. and O.C.; investigation, M.R.; writing—original draft preparation, M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not Applicable.
Acknowledgments
We acknowledge the support given by Tijuana Institute of Technology, Tecnologico Nacional de Mexico and CONAHCYT of Mexico for their support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Azzabi, L.; Azzabi, D.; Kobi, A. The Multi-Criteria Approach Decision. In The Multi-Criteria Approach for Decision Support; International Series in Operations Research & Management Science; Springer: Cham, Switzerland, 2020; Volume 300, pp. 1–23. [Google Scholar] [CrossRef]
- Zhao, S.; Dong, Y.; Martíne, L.; Pedrycz, W. Analysis of Ranking Consistency in Linguistic Multiple Attribute Decision Making: The Roles of Granularity and Decision Rules. IEEE Trans. Fuzzy Syst. 2022, 30, 2266–2278. [Google Scholar] [CrossRef]
- Morente-Molinera, J.; Wang, Y.-W.; Gong, Z.; Morfeq, A.; Al-Hmouz, R.; Herrera-Viedma, E. Reducing Criteria in Multicriteria Group Decision-Making Methods Using Hierarchical Clustering Methods and Fuzzy Ontologies. IEEE Trans. Fuzzy Syst. 2022, 30, 1585–1598. [Google Scholar] [CrossRef]
- Pan, X.; Wang, Y.; He, S.; Chin, K. A Dynamic Programming Algorithm Based Clustering Model and Its Application to Interval Type-2 Fuzzy Large-Scale Group Decision-Making Problem. IEEE Trans. Fuzzy Syst. 2022, 30, 108–120. [Google Scholar] [CrossRef]
- Baskov, O.V.; Noghin, V.D. Type-2 Fuzzy Sets and Their Application in Decision-Making: General Concepts. Sci. Tech. Inf. Proc. 2022, 49, 283–291. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Interval Type-3 Fuzzy Decision-Making in Material Surface Quality Control. In Soft Computing and Optimization; SCOTA 2021; Springer Proceedings in Mathematics & Statistics; Jabeen, S.D., Ali, J., Castillo, O., Eds.; Springer: Singapore, 2022; Volume 404. [Google Scholar] [CrossRef]
- Devi, A.; Jayanthi, D. An approach to interval-valued possibility intuitionistic fuzzy soft sets for treating drug addict patients based on decision making. In Proceedings of the 2023 2nd International Conference on Advancements in Electrical, Electronics, Communication, Computing and Automation (ICAECA), Coimbatore, India, 16–17 June 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, D.; Su, J.; Zhang, F. Specialized Risk Evaluation of Agricultural Products on Live-Streaming e-Commerce Platforms using Interval-Valued Intuitionistic Fuzzy Group Decision-Making. In Proceedings of the 2022 International Conference on Intelligent Computing and Machine Learning (2ICML), Qingdao, China, 14–16 April 2023; pp. 47–50. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Luo, F.; Chen, G.; Dong, Z.; Huang, T. Electric Vehicles Charging Dispatch and Optimal Bidding for Frequency Regulation Based on Intuitionistic Fuzzy Decision Making. IEEE Trans. Fuzzy Syst. 2023, 31, 596–608. [Google Scholar] [CrossRef]
- Chiao, K.P. Interval Type 2 Intuitionistic Fuzzy Sets Ranking Method Based on the General Graded Mean Integration Rep-resentation with Application to Multiple Criteria Decision Making. In Proceedings of the 2021 International Conference on Machine Learning and Cybernetics (ICMLC), Adelaide, Australia, 4–5 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Chiao, K.P. MCDM Prioritization Based on Interval Type 2 Intuitionistic Fuzzy Sets Ranking with Parametric General Graded Mean Integration Representation. In Proceedings of the 2022 International Conference on Fuzzy Theory and Its Applications (iFUZZY), Kaohsiung, Taiwan, 3–5 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Z. Trapezoidal interval type-2 fuzzy aggregation operators and their application to multiple attribute group decision making. Neural Comput. Appl. 2018, 29, 1039–1054. [Google Scholar] [CrossRef]
- Chen, Z.; Wan, S.; Dong, J. An efficiency-based interval type-2 fuzzy multi-criteria group decision making for makeshift hospital selection. Appl. Soft Comput. 2022, 115, 108243. [Google Scholar] [CrossRef]
- Ramírez, M.; Melin, P. A New Interval Type-2 Fuzzy Aggregation Approach for Combining Multiple Neural Networks in Clustering and Prediction of Time Series. Int. J. Fuzzy Syst. 2023, 25, 1077–1104. [Google Scholar] [CrossRef]
- Sayedabbas, S.; Scott, D. An investigation of complex fuzzy sets for large-scale learning. Fuzzy Sets Syst. 2023, 471, 108660. [Google Scholar] [CrossRef]
- Melin, P.; Ontiveros-Robles, E.; Castillo, O. Background and Theory. In New Medical Diagnosis Models Based on Generalized Type-2 Fuzzy Logic; Springer Briefs in Applied Sciences and Technology; Springer: Cham, Switzerland, 2021; pp. 5–28. [Google Scholar] [CrossRef]
- Ontiveros-Robles, E.; Castillo, O.; Melin, P. Comparative study of interval Type-2 and general Type-2 fuzzy systems in medical diagnosis. Inf. Sci. 2020, 37–53. [Google Scholar] [CrossRef]
- Castillo, O.; Castro, J.R.; Melin, P. Interval Type-3 Fuzzy Sets. In Interval Type-3 Fuzzy Systems: Theory and Design; Studies in Fuzziness and Soft Computing; Springer: Cham, Switzerland, 2022; Volume 418. [Google Scholar] [CrossRef]
- Vafaie, R.H.; Mohammadzadeh, A.; Piran, M.J. A new type-3 fuzzy predictive controller for MEMS gyroscopes. Nonlinear Dyn. 2021, 106, 381–403. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Castillo, O.; Band, S.S.; Mosavi, A. A Novel Fractional-Order Multiple-Model Type-3 Fuzzy Control for Nonlinear Systems with Unmodeled Dynamics. Int. J. Fuzzy Syst. 2021, 23, 1633–1651. [Google Scholar] [CrossRef]
- Putra, M.Y.; Arini, F.A.; Malik, I.M. Fuzzy Multi-Criteria Decision Making for Optimization of Housing Construction Financing. In Proceedings of the 2021 Sixth International Conference on Informatics and Computing (ICIC), Jakarta, Indonesia, 3–4 November 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Rostam, M.; FazelZarandi, M.H. A new interval type-2 fuzzy reasoning method for classification systems based on normal forms of a possibility-based fuzzy measure. Inf. Sci. 2021, 581, 567–586. [Google Scholar] [CrossRef]
- Thakkar, J.J. Introduction. In Multi-Criteria Decision Making; Studies in Systems, Decision and Control; Springer: Singapore, 2021; Volume 336, pp. 1–25. [Google Scholar] [CrossRef]
- Melin, P.; Monica, J.C.; Sanchez, D.; Castillo, O. Multiple Ensemble Neural Network Models with Fuzzy Response Aggregation for Predicting COVID-19 Time Series: The Case of Mexico. Healthcare 2020, 8, 181. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.T.; Qin, J.D. A New Representation Method for Type-2 Fuzzy Sets and Its Application to Multiple Criteria Decision Making. Int. J. Fuzzy Syst. 2023, 25, 1171–1190. [Google Scholar] [CrossRef]
- Cheng, C.H.; Chen, M.Y.; Chang, J.R. Linguistic multi-criteria decision-making aggregation model based on situational ME-LOWA and ME-LOWGA operators. Granul. Comput. 2023, 8, 97–110. [Google Scholar] [CrossRef]
- Dombi, J.; Csiszár, O. Introduction—Aggregation and Intelligent Decision. In Explainable Neural Networks Based on Fuzzy Logic and Multi-criteria Decision Tools; Studies in Fuzziness and Soft Computing; Springer: Cham, Switezerland, 2021; Volume 408, pp. ix–xi. [Google Scholar] [CrossRef]
- Gupta, A.; Sharma, K. Ranking of Countries Using World Development Indicators: A Computational Approach. In Proceedings of the 2020 11th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kharagpur, India, 1–3 July 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Sharma, J.; Arora, M.; Sonia, A.A. An illustrative study on Multi Criteria Decision Making Approach: Analytical Hierarchy Process. In Proceedings of the 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Noida, India, 28–29 April 2022; pp. 2000–2005. [Google Scholar] [CrossRef]
- The World Bank Data: World Development Indicators. Available online: https://datatopics.worldbank.org/world-development-indicators/ (accessed on 6 May 2023).
- Ding, X.; Hao, K.; Cai, X.; Tang, S.; Chen, L.; Zhang, H. A Novel Similarity Measurement and Clustering Framework for Time Series Based on Convolution Neural Networks. IEEE Access 2020, 8, 173158–173168. [Google Scholar] [CrossRef]
- Egrioglu, E.; Bas, E. A new hybrid recurrent artificial neural network for time series forecasting. Neural Comput. Appl. 2023, 35, 2855–2865. [Google Scholar] [CrossRef]
- Pirani, M.; Thakkar, P.; Jivrani, P.; Bohara, P.M.; Garg, D. A Comparative Analysis of ARIMA, GRU, LSTM and BiLSTM on Financial Time Series Forecasting. In Proceedings of the 2022 IEEE International Conference on Distributed Computing and Electrical Circuits and Electronics (ICDCECE), Ballari, India, 23–24 April 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Kan, V.; Alsova, O. Forecasting Meteorological Indicators Based on Neural Networks. In Proceedings of the 2022 IEEE International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), Yekaterinburg, Russian Federation, 11–13 November 2022; pp. 1620–1625. [Google Scholar] [CrossRef]
- Wu, J.L.; Lu, M.; Wang, C.Y. Forecasting metro rail transit passenger flow with multiple-attention deep neural networks and surrounding vehicle detection devices. Appl. Intell. 2023, 53, 18531–18546. [Google Scholar] [CrossRef]
- Xu, S.; Li, W.; Zhu, Y.; Xu, A. A novel hybrid model for six main pollutant concentrations forecasting based on improved LSTM neural networks. Sci. Rep. 2022, 12, 14434. [Google Scholar] [CrossRef]
- Ali, M.; Syed, M.A.; Khalid, M. NARX Recurrent Neural Network Based Short Term Residential Load Forecasting Considering the Effects of Multiple Weather Features. In Proceedings of the 2022 IEEE IAS Global Conference on Emerging Technologies (GlobConET), Arad, Romania, 20–22 May 2022; pp. 557–561. [Google Scholar] [CrossRef]
- Sehrawat, P.K.; Vishwakarma, D.K. Comparative Analysis of Time Series Models on COVID-19 Predictions. In Proceedings of the 2022 International Conference on Sustainable Computing and Data Communication Systems (ICSCDS), Erode, India, 7–9 April 2022; pp. 710–715. [Google Scholar] [CrossRef]
- Rahman, M.M.; Shakeri, M.; Khatun, F.; Tiong, S.K.; Alkahtani, A.A.; Samsudin, N.A.; Amin, N.; Pasupuleti, J.; Hasan, M.K. A comprehensive study and performance analysis of deep neural network-based approaches in wind time-series forecasting. J. Reliab. Intell. Environ. 2022, 9, 183–200. [Google Scholar] [CrossRef]
- Sohrabi, F.; Reza, M.; Mirabbasi, R.; Tahroudi, M. Daily solar radiation estimation in Belleville station, Illinois, using ensemble artificial intelligence approaches. Eng. Appl. Artif. Intell. 2023, 120, 105839. [Google Scholar] [CrossRef]
- Siłka, J.; Wieczorek, M.; Woźniak, M. Recurrent neural network model for high-speed train vibration prediction from time series. Neural Comput. Applic. 2022, 34, 13305–13318. [Google Scholar] [CrossRef]
- Xu, H.; Yoo, S. A Deep Neural Network for Multivariate Time Series Clustering with Result Interpretation. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Wang, H.; Huang, X.; Gao, S.; Yang, Z.; Gao, T.; Zhao, Q.; Ding, H. Electric vehicle charging load clustering and load forecasting based on long short term memory neural network. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 3196–3200. [Google Scholar] [CrossRef]
- Yao, J.; Lu, B.; Zhang, J. Multi-Step-Ahead Tool State Monitoring Using Clustering Feature-Based Recurrent Fuzzy Neural Networks. IEEE Access 2021, 9, 113443–113453. [Google Scholar] [CrossRef]
- Bhardwaj, V.; Bhavsar, P.; Patnaik, D. Forecasting GDP per capita of OECD countries using machine learning and deep learning models. In Proceedings of the 2022 Interdisciplinary Research in Technology and Management (IRTM), Kolkata, India, 24–26 February 2022; pp. 1–6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).