On Implicit Time–Fractal–Fractional Differential Equation
Abstract
:1. Introduction
2. Preliminaries
- and
- .
3. Main Results
3.1. Existence and Uniqueness Result
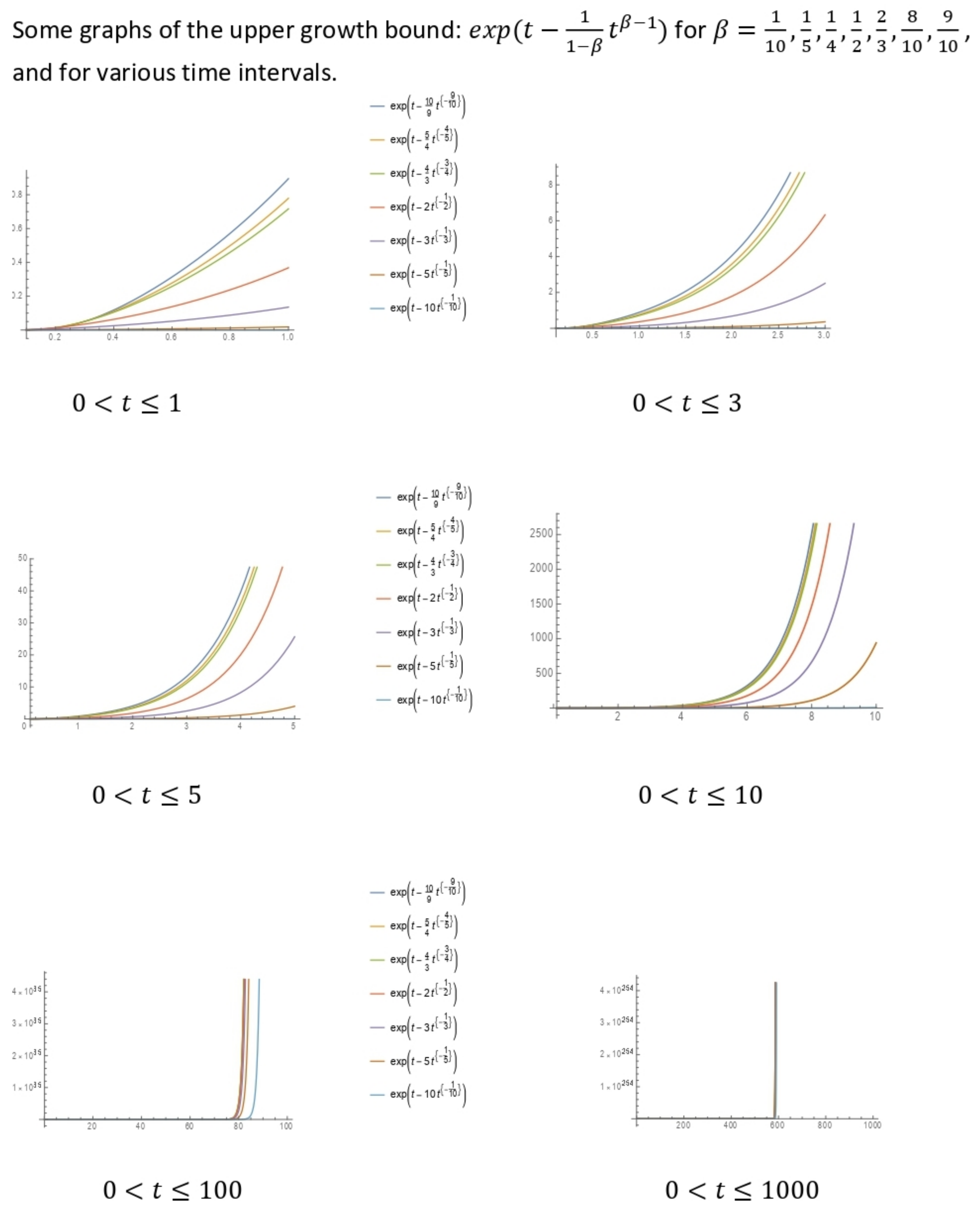
Exponential Growth
- (i)
- Given that . It follows thatwhere and .
- (ii)
- Given that and . Thenwhere , and .
3.2. Asymptotic Property of the Solution
4. Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atangana, A. Fractal–fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solit. Fract. 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Atangana, A.; Akgu¨l, A.; Owolabi, K.M. Analysis of Frac-tal–fractional differential equations. Alex. Eng. J. 2020, 59, 1117–1134. [Google Scholar] [CrossRef]
- Araz, S.I. Numerical analysis of a new Volterra integro-differential equation involving fractal–fractional operators. Chaos Solit. Fract. 2020, 130, 109396. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A.; Akgu¨l, A. Modelling and Analysis of Fractal-fractional partial differential equations: Application to reaction-diffusion model. Alex. Eng. J. 2020, 59, 2477–2490. [Google Scholar] [CrossRef]
- He, J.-H. Fractal calculus and its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- Hosseininia, M.; Heydari, M.H.; Avazzadeh, Z. The Numerical Treatment of Non-linear Fractal–fractional 2D EMDEN-FOWLER equation utilizing 2D Chelyshkov polynomials. Fractals 2020, 28, 2040042. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Atangana, A. New chaotic attractors: Applications of fractal-fractional differentiation and integration. Math. Methods Appl. Sci. 2020, 44, 3036–3065. [Google Scholar] [CrossRef]
- Saad, K.M.; Alqhtani, M.; Gómez-Aguilar, J.F. Fractal-fractional study of the hepatitis C virus infection model. Results Phys. 2020, 19, 103555. [Google Scholar] [CrossRef]
- Zuniga-Aguilar, C.J.; Gómez-Aguilar, J.F.; Romero-Ugalde, H.M.; Ja-hanshahi, H.; Alsaadi, F.E. Fractal-fractional neuro-adaptive method for system identification. Eng. Comput. 2020, 240, 1–24. [Google Scholar] [CrossRef]
- Abro, K.A.; Atangana, A.; Gómez-Aguilar, J.F. Ferromagnetic chaos in thermal convection of fluid through fractal-fractional differentiation. J. Therm. Anal. Calorim. 2022, 147, 8461–84733. [Google Scholar] [CrossRef]
- Nane, E.; Nwaeze, E.R.; Omaba, M.E. Asymptotic behavior and non-existence of global solution to a class of conformable time-fractional stochastic differential equation. Stat. Probab. Lett. 2020, 163, 108792. [Google Scholar] [CrossRef] [Green Version]
- Omaba, M.E. On Space-Fractional Heat Equation with Non-homogeneous Fractional Time Poisson Process. Progr. Fract. Differ. Appl. 2020, 6, 67–79. [Google Scholar]
- Omaba, M.E.; Nwaeze, E.R. Moment Bound of Solution to a Class of Conformable Time-Fractional Stochastic Equation. Fractal Fract. 2019, 3, 18. [Google Scholar] [CrossRef] [Green Version]
- Asma; Gómez-Aguilar, J.F.; ur Rahman, G.; Javed, M. Stability for fractional order implicit ψ-Hilfer differential equations. Math. Methods Appl. Sci. 2021, 45, 2701–2712. [Google Scholar] [CrossRef]
- Benchohra, M.; Lazreg, J.E. Existence results for nonlinear implicit fractional dif-ferential equations. Surv. Math. Its Appl. 2014, 9, 79–92. [Google Scholar]
- Borisut, P.; Bantaojai, T. Implicit fractional differential equations with nonlocal frac-tional integral conditions. Thai J. Math. 2021, 19, 993–1003. [Google Scholar]
- Shabbir, A.S.; Shah, K.; Abdeljawad, T. Stability analysis for a class of implicit frac-tional differential equations involving Atangana–Baleanu fractional derivative. Adv. Differ. Equ. 2021, 2021, 395. [Google Scholar] [CrossRef]
- Benchohra, M.; Souid, M.S. Integrable solutions for implicit fractional order dif-ferential equations. Arch. Math. 2015, 51, 67–76. [Google Scholar]
- Benchohra, M.; Bouriaha, S. Existence and stability results for nonlinear boundary value problem for implicit differential equations of fractional order. Moroc. J. Pure Appl. Anal. 2017, 1, 22–37. [Google Scholar] [CrossRef] [Green Version]
- Kucche, K.D.; Nieto, J.J.; Venktesh, V. Theory of nonlinear implicit fractional differ-ential equations. Diff. Equ. Dyn. Syst. 2016, 38, 1–17. [Google Scholar]
- Nieto, J.J.; Ouahab, A.; Venktesh, V. Implicit fractional differential equations via Liou-ville–Caputo derivative. Mathematics 2015, 3, 398–411. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and nonsingular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, H.M.; Choi, J. Zeta and q-Zeta Functions and Associated Series and Inte-Grals; Elsevier: Amsterdam, The Netherlands, 2012; pp. 1–140. [Google Scholar]
- Helton, J.W.; Klep, I.; Mccullough, S.; Schweighofer, M. Dilations, linear matrix ine-qualities, the matrix cube problem and beta distribution. Memiors Am. Math. Soc. 2019, 257, 1232. [Google Scholar]
- Aono, Y.; Nguyen, P.Q.; Seito, T.; Shiketa, J. Lower Bounds on Lattice Enumeration with Extreme Pruning. In Proceedings of the 38th Annual International Cryptology Conference, IACR, Santa-Barbara, CA, USA, 19–23 August 2018. [Google Scholar] [CrossRef] [Green Version]
- Shao, J.; Meng, F. Gronwall-Bellman Type Inequalities and Their Applications to Frac-tional Differential equations. Abstr. Appl. Anal. 2013, 2013, 217641. [Google Scholar] [CrossRef] [Green Version]
- Di Giuseppe, E.; Moroni, M.; Caputo, M. Flux in porous Media with Memory: Models and Experiment. Transp. Porous. Med. 2010, 83, 479–500. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omaba, M.E.; Mukiawa, S.E.; Nwaeze, E.R. On Implicit Time–Fractal–Fractional Differential Equation. Axioms 2022, 11, 348. https://doi.org/10.3390/axioms11070348
Omaba ME, Mukiawa SE, Nwaeze ER. On Implicit Time–Fractal–Fractional Differential Equation. Axioms. 2022; 11(7):348. https://doi.org/10.3390/axioms11070348
Chicago/Turabian StyleOmaba, McSylvester Ejighikeme, Soh Edwin Mukiawa, and Eze R. Nwaeze. 2022. "On Implicit Time–Fractal–Fractional Differential Equation" Axioms 11, no. 7: 348. https://doi.org/10.3390/axioms11070348
APA StyleOmaba, M. E., Mukiawa, S. E., & Nwaeze, E. R. (2022). On Implicit Time–Fractal–Fractional Differential Equation. Axioms, 11(7), 348. https://doi.org/10.3390/axioms11070348





