TT-M Finite Element Algorithm for the Coupled Schrödinger–Boussinesq Equations
Abstract
1. Introduction
- Detailed proofs of stability and error estimates for TT-M FE system are done;
- Numerical examples are given to verify the correctness of the theory results, to reflect the dynamic behavior of solutions and to illustrate the computational efficiency compared with the standard nonliear finite element method.
2. Weak Formulation and TT-M Finite Element Scheme
2.1. Weak Formulation
2.2. TT-M Finite Element Scheme
3. Stability Analysis
4. Error Analysis
5. Numerical Tests
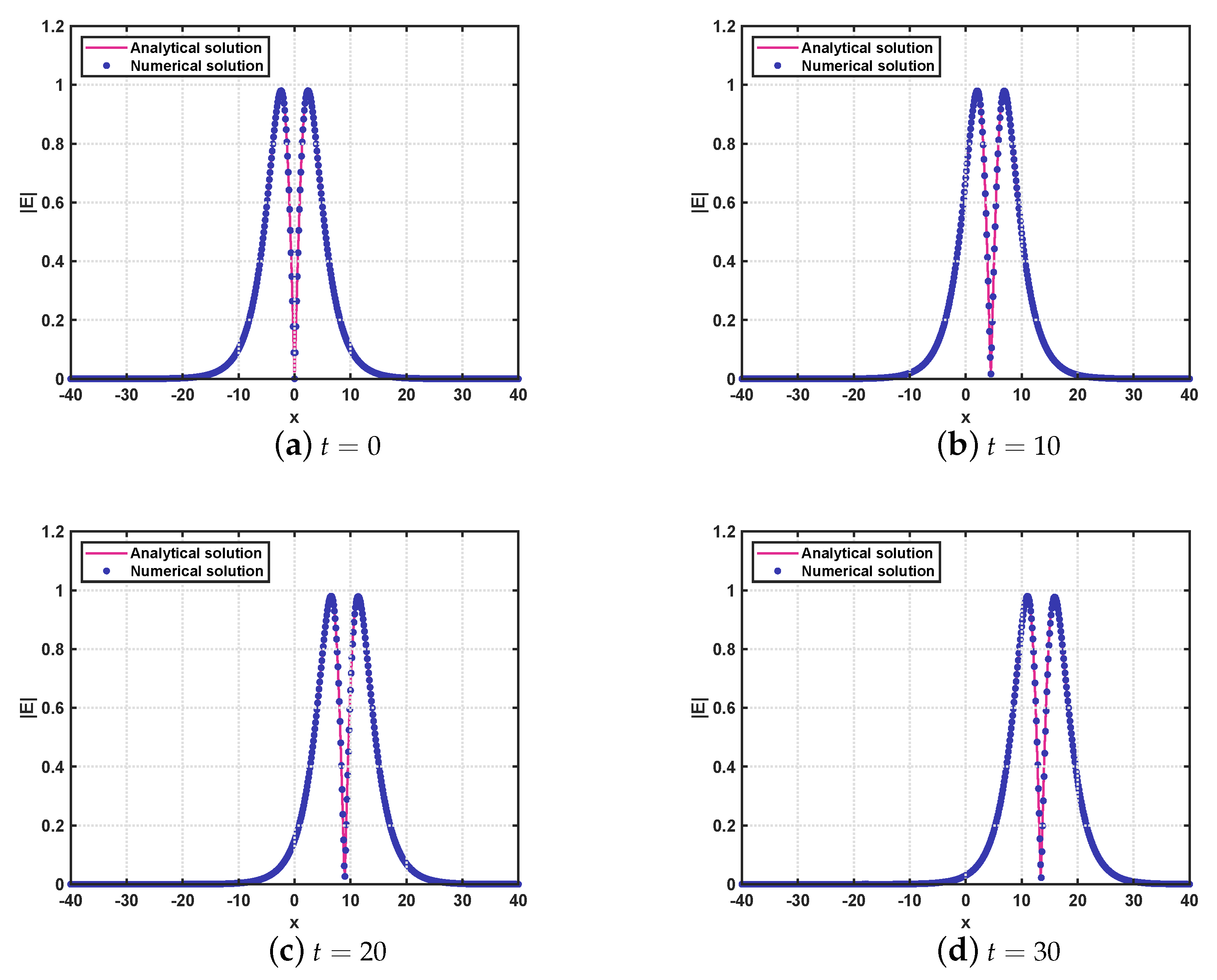
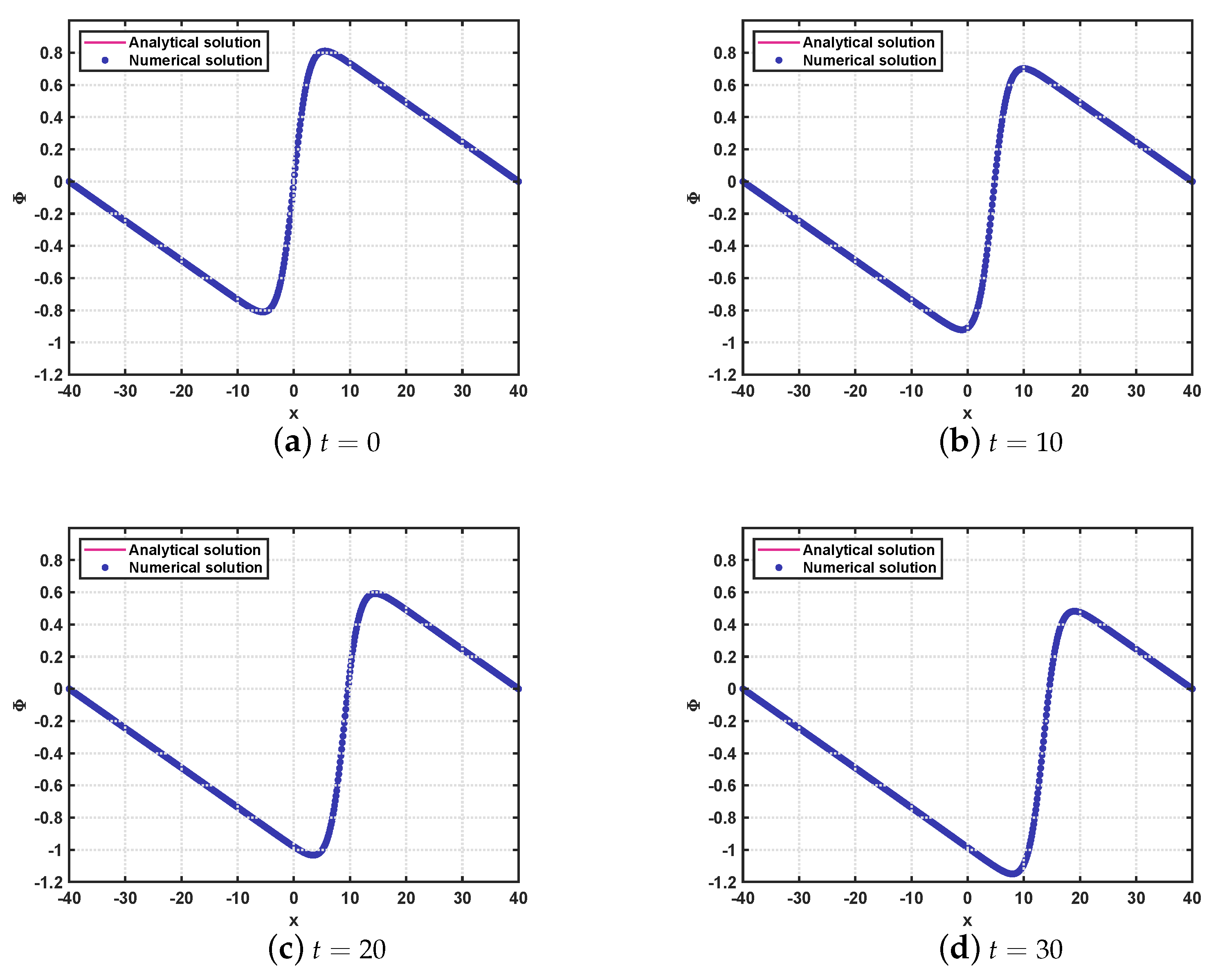
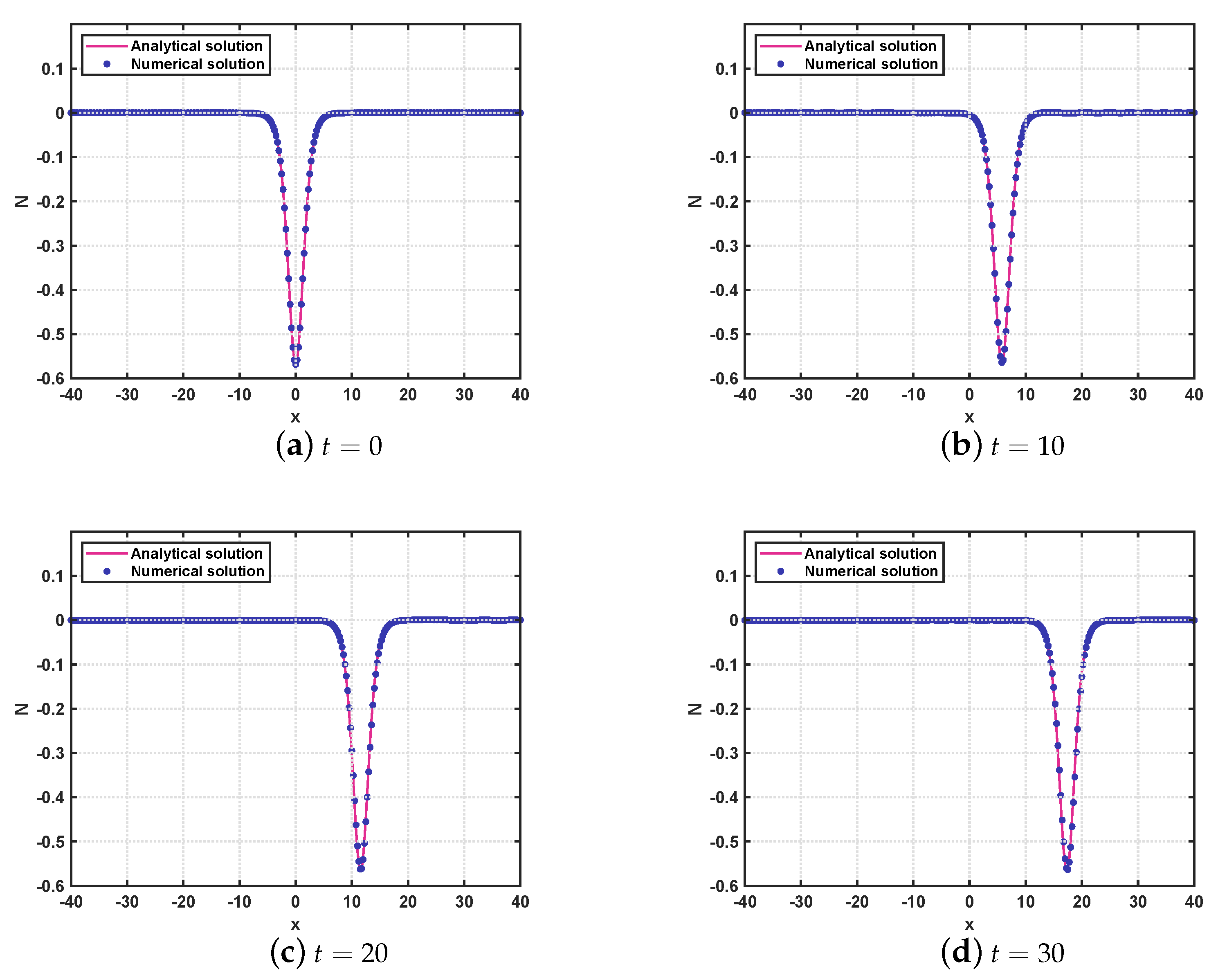
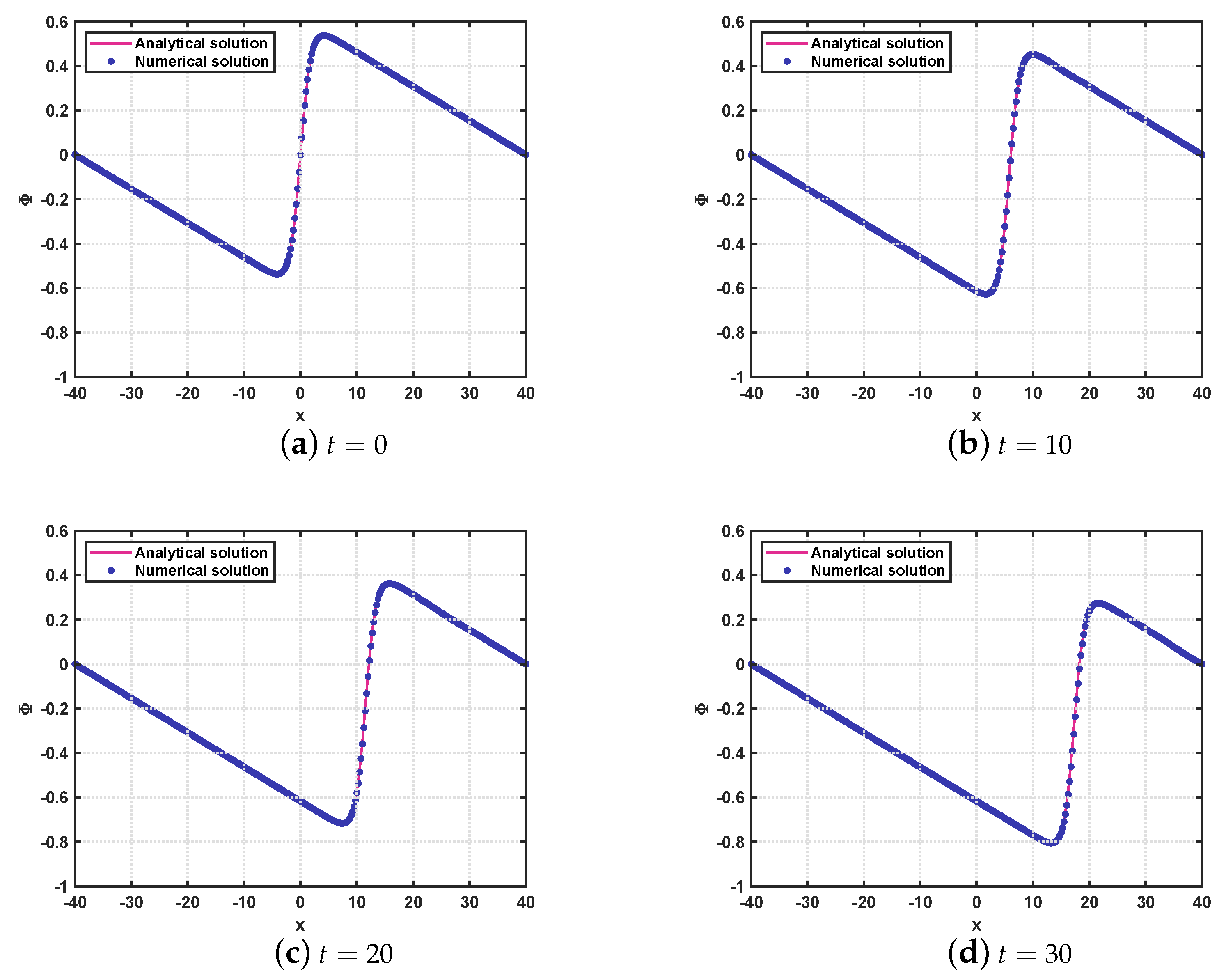
5.1. Example 1
5.2. Example 2
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yajima, N.; Satsuma, J. Soliton solutions in a diatomic lattice system. Prog. Theor. Phys. 1979, 62, 370–378. [Google Scholar] [CrossRef]
- Rao, N.N. Coupled scalar field equations for nonlinear wave modulations in dispersive media. Pramana J. Phys. 1996, 46, 161–202. [Google Scholar] [CrossRef]
- Liao, F.; Zhang, L.M.; Wang, S.S. Numerical analysis of cubic orthogonal spline collocation methods for the coupled Schrödinger-Boussinesq equations. Appl. Numer. Math. 2017, 119, 194–212. [Google Scholar] [CrossRef]
- Guo, B.L.; Du, X.Y. The behavior of attractors for damped Schrödinger-Boussinesq equation. Commun. Nonlinear Sci. Numer. Simul. 2001, 6, 54–60. [Google Scholar] [CrossRef]
- Bilige, S.; Chaolu, T.; Wang, X.M. Application of the extended simplest equation method to the coupled Schrödinger-Boussinesq equation. Appl. Math. Comput. 2013, 224, 517–523. [Google Scholar] [CrossRef]
- Guo, B.L. The global solution of the system of equations for complex Schrödinger field coupled with Boussinesq type self-consistent field. Acta Math. Sin. 1983, 26, 295–306. (In Chinese) [Google Scholar] [CrossRef]
- Li, Y.S.; Chen, Q.Y. Finite dimensional global attractor for dissipative Schrödinger-Boussinesq equations. J. Math. Anal. Appl. 1997, 205, 107–132. [Google Scholar] [CrossRef][Green Version]
- Guo, B.L.; Chen, F.X. Finite dimensional behavior of global attractors for weakly damped nonlinear Schrödinger-Boussinesq equations. Physica D 1996, 93, 101–118. [Google Scholar]
- Farah, L.G.; Pastor, A. On the periodic Schrödinger-Boussinesq system. J. Math. Anal. Appl. 2010, 368, 330–349. [Google Scholar] [CrossRef]
- Guo, B.L.; Du, X.Y. Existence of the periodic solution for the weakly damped Schrödinger-Boussinesq equation. J. Math. Anal. Appl. 2001, 262, 453–472. [Google Scholar] [CrossRef]
- Hon, Y.V.; Fan, E.G. A series of exact solutions for coupled Higgs field equation and coupled Schrödinger-Boussinesq equation. Nonlinear Anal. 2009, 71, 3501–3508. [Google Scholar] [CrossRef]
- Rao, N.N. Exact solutions of coupled scalar field equations. J. Phys. A Math. Gen. 1989, 22, 4813–4825. [Google Scholar] [CrossRef]
- Xia, Y.R.; Li, Z.B. Exact explicit solutions of the nonlinear Schrödinger equation coupled to the Boussinesq equation. Acta Math. Sci. 2003, 23, 453–460. [Google Scholar]
- Liao, F.; Zhang, L.M.; Wang, S.S. Time-splitting combined with exponential wave integrator Fourier pseudospectral method for Schrödinger-Boussinesq system. Commun. Nonlinear Sci. Numer. Simulat. 2018, 55, 93–104. [Google Scholar] [CrossRef]
- Zhang, L.M.; Bai, D.M.; Wang, S.S. Numerical analysis for a conservative difference scheme to solve the Schrödinger-Boussinesq equation. J. Comput. Appl. Math. 2011, 235, 4899–4915. [Google Scholar] [CrossRef]
- Liao, F.; Zhang, L.M. Conservative compact finite difference scheme for the coupled Schrödinger-Boussinesq equation. Numer. Meth. Part. Differ. Equ. 2016, 32, 1667–1688. [Google Scholar] [CrossRef]
- Deng, D.W.; Wu, Q. Analysis of the linearly energy- and mass-preserving finite difference methods for the coupled Schrödinger-Boussinesq equations. Appl. Numer. Math. 2021, 170, 14–38. [Google Scholar] [CrossRef]
- Zheng, J.D.; Xiang, X.M. The finite element analysis for the equation system coupling the complex Schrödinger and real Boussinesq fields. Math. Numer. Sin. 1987, 9, 133–143. [Google Scholar]
- Bai, D.M.; Zhang, L.M. The quadratic B-spline finite element method for the coupled Schrödinger-Boussinesq equations. Int. J. Comput. Math. 2011, 88, 1714–1729. [Google Scholar] [CrossRef]
- Huang, L.Y.; Jiao, Y.D.; Liang, D.M. Multi-symplectic scheme for the coupled Schrödinger-Boussinesq equations. Chin. Phys. B 2013, 7, 070201. [Google Scholar] [CrossRef]
- Cai, J.X.; Chen, J.; Yang, B. Efficient energy-preserving wavelet collocation schemes for the coupled nonlinear Schrödinger-Boussinesq system. Appl. Math. Comput. 2019, 357, 1–11. [Google Scholar] [CrossRef]
- Guo, B.L.; Chen, G.N. The convergence of Galerkin-Fourier method for equation of Schrödinger-Boussinesq field. J. Comput. Math. 1984, 2, 344–355. [Google Scholar]
- Liu, Y.; Yu, Z.D.; Li, H.; Liu, F.W.; Wang, J.F. Time two-mesh algorithm combined with finite element method for time fractional water wave model. Int. J. Heat Mass Transf. 2018, 120, 1132–1145. [Google Scholar] [CrossRef]
- Yin, B.L.; Liu, Y.; Li, H.; He, S. Fast algorithm based on TT-M FE system for space fractional Allen-Cahn equations with smooth and non-smooth solutions. J. Comput. Phys. 2019, 379, 351–372. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, E.Y.; Yin, B.L.; Li, H.; Wang, J.F. TT-M finite element algorithm for a two-dimensional space fractional Gray-Scott model. Comput. Math. Appl. 2020, 80, 1793–1809. [Google Scholar] [CrossRef]
- Wen, C.; Liu, Y.; Yin, B.L.; Li, H.; Wang, J.F. Fast second-order time two-mesh mixed finite element method for a nonlinear distributed-order sub-diffusion model. Numer. Algorithms 2021, 88, 523–553. [Google Scholar] [CrossRef]
- Wang, D.X.; Du, Q.Q.; Zhang, J.W.; Jia, H.E. A fast time two-mesh algorithm for Allen-Cahn equation. Bull. Malays. Math. Sci. Soc. 2020, 43, 2417–2441. [Google Scholar] [CrossRef]
- Qiu, W.L.; Xu, D.; Guo, J.; Zhou, J. A time two-grid algorithm based on finite difference method for the two-dimensional nonlinear time-fractional mobile/immobile transport model. Numer. Algorithms 2020, 85, 39–58. [Google Scholar] [CrossRef]
- Niu, Y.X.; Liu, Y.; Li, H.; Liu, F.W. Fast high-order compact difference scheme for the nonlinear distributed-order fractional Sobolev model appearing in porous media. 2021; submitted. [Google Scholar]
- Tutueva, A.; Karimov, T.; Butusov, D. Semi-implicit and semi-explicit Adams-Bashforth-Moulton methods. Mathematics 2020, 8, 780. [Google Scholar] [CrossRef]
- Tutueva, A.; Butusov, D. Avoiding dynamical degradation in computer simulation of chaotic systems using semi-explicit integration: Rössler oscillator case. Fract. Fract. 2021, 5, 214. [Google Scholar] [CrossRef]
- Thomee, V. Galerkin Finite Element Method for Parabolic Problems; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Wen, C.; Wang, J.F.; Liu, Y.; Li, H.; Fang, Z.C. Unconditionally optimal time two-mesh mixed finite element algorithm for a nonlinear distributed-order fourth-order equation. 2022; submitted. [Google Scholar]
- Li, M.; Huang, C.M.; Wang, P.D. Galerkin finite element method for nonlinear fractional Schrödinger equations. Numer. Algorithms 2017, 74, 499–525. [Google Scholar] [CrossRef]
- Li, D.F.; Wang, J.L.; Zhang, J.W. Unconditionally convergent L1-Galerkin FEMs for nonlinear time-fractional Schrödinger equations. SIAM J. Sci. Comput. 2017, 39, A3067–A3088. [Google Scholar] [CrossRef]
- Yin, B.L.; Wang, J.F.; Liu, Y.; Li, H. A structure preserving difference scheme with fast algorithms for high dimensional nonlinear space-fractional Schrödinger equations. J. Comput. Phys. 2021, 425, 109869. [Google Scholar] [CrossRef]
- Liu, Q.; Zeng, F.H.; Li, C.P. Finite difference method for time-space-fractional Schrödinger equation. Int. J. Comput. Math. 2015, 92, 1439–1451. [Google Scholar] [CrossRef]
- Ran, M.; Zhang, C. Linearized Crank-Nicolson scheme for the nonlinear time-space fractional Schrödinger equations. J. Comput. Appl. Math. 2019, 355, 218–231. [Google Scholar] [CrossRef]
- Zheng, M.; Liu, F.; Jin, Z. The global analysis on the spectral collocation method for time fractional Schrödinger equation. Appl. Math. Comput. 2020, 365, 124689. [Google Scholar] [CrossRef]
- Wang, Y.; Mei, L.; Li, Q.; Bu, L. Split-step spectral Galerkin method for the two-dimensional nonlinear space-fractional Schrödinger equation. Appl. Numer. Math. 2019, 136, 257–278. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, X.; Wang, C.; Chen, S. Crank-Nicolson Fourier spectral methods for the space fractional nonlinear Schrödinger equation and its parameter estimation. Int. J. Comput. Math. 2019, 96, 238–263. [Google Scholar] [CrossRef]
- Wang, D.L.; Xiao, A.G.; Yang, W. A linearly implicit conservative difference scheme for the space fractional coupled nonlinear Schrödinger equations. J. Comput. Phys. 2014, 272, 644–655. [Google Scholar] [CrossRef]
- Iqbal, A.; Hamid, N.N.A.; Ismail, A.I.M.; Abbas, M. Galerkin approximation with quintic B-spline as basis and weight functions for solving second order coupled nonlinear Schrödinger equations. Math. Comput. Simulat. 2021, 187, 1–16. [Google Scholar] [CrossRef]
- Ma, Y.P.; Kong, L.H.; Hong, J.L.; Cao, Y. High-order compact splitting multisymplectic method for the coupled nonlinear Schrödinger equations. Comput. Math. Appl. 2011, 61, 319–333. [Google Scholar] [CrossRef]


| Standard FE Algorithm | |||||||
|---|---|---|---|---|---|---|---|
| Rate | Rate | Rate | CPU(s) | ||||
| 1.5458 × | 2.8961 × | 6.7647 × | 1.77 | ||||
| 3.8651 × | 1.9997 | 7.3072 × | 1.9867 | 1.7086 × | 1.9852 | 3.25 | |
| 9.6635 × | 1.9999 | 1.8335 × | 1.9948 | 4.2815 × | 1.9966 | 8.83 | |
| 2.4162 × | 1.9998 | 4.5865 × | 1.9991 | 1.0709 × | 1.9993 | 53.00 | |
| 6.0442 × | 1.9991 | 1.1459 × | 2.0009 | 2.6761 × | 2.0006 | 317.05 | |
| TT-M FE Algorithm | |||||||
| Rate | Rate | Rate | CPU(s) | ||||
| 1.5458 × | 2.8962 × | 6.7647 × | 1.77 | ||||
| 3.8651 × | 1.9997 | 7.3073 × | 1.9867 | 1.7086 × | 1.9852 | 3.07 | |
| 9.6632 × | 1.9999 | 1.8336 × | 1.9947 | 4.2816 × | 1.9966 | 8.76 | |
| 2.4160 × | 1.9999 | 4.5878 × | 1.9988 | 1.0710 × | 1.9991 | 53.56 | |
| 6.0414 × | 1.9996 | 1.1472 × | 1.9997 | 2.6779 × | 1.9998 | 282.96 | |
| Standard FE Algorithm | |||||||
|---|---|---|---|---|---|---|---|
| Rate | Rate | Rate | CPU(s) | ||||
| 1.5913 × | 2.5619 × | 6.2220 × | 0.02 | ||||
| 3.9807 × | 1.9991 | 6.4235 × | 1.9958 | 1.5737 × | 1.9833 | 0.06 | |
| 9.9505 × | 2.0002 | 1.6056 × | 2.0002 | 3.9462 × | 1.9956 | 0.31 | |
| 2.4882 × | 1.9997 | 4.0175 × | 1.9988 | 9.8720 × | 1.9991 | 3.13 | |
| 6.2204 × | 2.0000 | 1.0039 × | 2.0007 | 2.4666 × | 2.0008 | 36.44 | |
| 1.5551 × | 2.0000 | 2.5105 × | 1.9996 | 6.1688 × | 1.9994 | 443.56 | |
| TT-M FE Algorithm | |||||||
| Rate | Rate | Rate | CPU(s) | ||||
| 1.5984 × | 2.8722 × | 6.7901 × | 0.04 | ||||
| 3.9951 × | 2.0003 | 7.1917 × | 1.9978 | 1.7111 × | 1.9885 | 0.05 | |
| 9.9906 × | 1.9996 | 1.7973 × | 2.0005 | 4.2867 × | 1.9970 | 0.26 | |
| 2.4977 × | 2.0000 | 4.4967 × | 1.9989 | 1.0721 × | 1.9995 | 2.85 | |
| 6.2444 × | 2.0000 | 1.1240 × | 2.0003 | 2.6806 × | 1.9998 | 31.30 | |
| 1.5611 × | 2.0000 | 2.8100 × | 1.9999 | 6.7016 × | 2.0000 | 343.06 | |
| Standard FE Algorithm | |||||||
|---|---|---|---|---|---|---|---|
| Rate | Rate | Rate | CPU(s) | ||||
| 9.7274 × | 5.1130 × | 9.3026 × | 62.39 | ||||
| 2.4921 × | 1.9647 | 1.3201 × | 1.9535 | 2.3933 × | 1.9586 | 385.42 | |
| 6.2693 × | 1.9910 | 3.3276 × | 1.9881 | 6.0274 × | 1.9894 | 3093.74 | |
| TT-M FE Algorithm | |||||||
| Rate | Rate | Rate | CPU(s) | ||||
| 9.7274 × | 5.1130 × | 9.3027 × | 51.98 | ||||
| 2.4921 × | 1.9647 | 1.3201 × | 1.9535 | 2.3934 × | 1.9586 | 297.16 | |
| 6.2698 × | 1.9909 | 3.3279 × | 1.9880 | 6.0284 × | 1.9892 | 2521.57 | |
| Standard FE Algorithm | |||||||
|---|---|---|---|---|---|---|---|
| Rate | Rate | Rate | CPU(s) | ||||
| 9.6515 × | 4.9930 × | 9.0913 × | 1.09 | ||||
| 2.4741 × | 1.9638 | 1.2908 × | 1.9516 | 2.3431 × | 1.9561 | 13.35 | |
| 6.2254 × | 1.9907 | 3.2549 × | 1.9876 | 5.9038 × | 1.9887 | 137.33 | |
| 1.5589 × | 1.9977 | 8.1550 × | 1.9969 | 1.4789 × | 1.9971 | 2000.16 | |
| TT-M FE Algorithm | |||||||
| Rate | Rate | Rate | CPU(s) | ||||
| 9.9179 × | 5.1934 × | 9.7061 × | 1.05 | ||||
| 2.5426 × | 1.9637 | 1.3388 × | 1.9558 | 2.4873 × | 1.9643 | 9.97 | |
| 6.3972 × | 1.9908 | 3.3734 × | 1.9886 | 6.2584 × | 1.9907 | 112.46 | |
| 1.6019 × | 1.9977 | 8.4504 × | 1.9971 | 1.5671 × | 1.9977 | 1246.46 | |
| Standard FE Algorithm | |||||||
|---|---|---|---|---|---|---|---|
| Rate | Rate | Rate | CPU(s) | ||||
| 8.1725 × | 5.0737 × | 6.2883 × | 49.55 | ||||
| 2.1093 × | 1.9540 | 1.3275 × | 1.9343 | 1.6315 × | 1.9465 | 364.28 | |
| 5.3172 × | 1.9880 | 3.3580 × | 1.9830 | 4.1181 × | 1.9861 | 3037.39 | |
| TT-M FE Algorithm | |||||||
| Rate | Rate | Rate | CPU(s) | ||||
| 8.1726 × | 5.0738 × | 6.2884 × | 53.02 | ||||
| 2.1094 × | 1.9540 | 1.3276 × | 1.9343 | 1.6315 × | 1.9465 | 284.42 | |
| 5.3179 × | 1.9879 | 3.3584 × | 1.9829 | 4.1189 × | 1.9859 | 2551.25 | |
| Standard FE Algorithm | |||||||
|---|---|---|---|---|---|---|---|
| Rate | Rate | Rate | CPU(s) | ||||
| 8.2622 × | 4.8094 × | 5.9645 × | 1.14 | ||||
| 2.1377 × | 1.9505 | 1.2609 × | 1.9314 | 1.5536 × | 1.9408 | 12.62 | |
| 5.3921 × | 1.9871 | 3.1915 × | 1.9821 | 3.9261 × | 1.9845 | 125.44 | |
| 1.3509 × | 1.9970 | 8.0053 × | 1.9952 | 9.8422 × | 1.9961 | 1333.25 | |
| TT-M FE Algorithm | |||||||
| Rate | Rate | Rate | CPU(s) | ||||
| 8.9536 × | 5.1280 × | 6.7564 × | 0.99 | ||||
| 2.2549 × | 1.9894 | 1.3252 × | 1.9521 | 1.6945 × | 1.9954 | 9.36 | |
| 5.6463 × | 1.9977 | 3.3410 × | 1.9879 | 4.2393 × | 1.9989 | 100.56 | |
| 1.4121 × | 1.9995 | 8.3702 × | 1.9970 | 1.0600 × | 1.9998 | 1112.97 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Sun, Z.; Liu, Y.; Li, H. TT-M Finite Element Algorithm for the Coupled Schrödinger–Boussinesq Equations. Axioms 2022, 11, 314. https://doi.org/10.3390/axioms11070314
Tian J, Sun Z, Liu Y, Li H. TT-M Finite Element Algorithm for the Coupled Schrödinger–Boussinesq Equations. Axioms. 2022; 11(7):314. https://doi.org/10.3390/axioms11070314
Chicago/Turabian StyleTian, Jiale, Ziyu Sun, Yang Liu, and Hong Li. 2022. "TT-M Finite Element Algorithm for the Coupled Schrödinger–Boussinesq Equations" Axioms 11, no. 7: 314. https://doi.org/10.3390/axioms11070314
APA StyleTian, J., Sun, Z., Liu, Y., & Li, H. (2022). TT-M Finite Element Algorithm for the Coupled Schrödinger–Boussinesq Equations. Axioms, 11(7), 314. https://doi.org/10.3390/axioms11070314







