Pattern Formation Induced by Fuzzy Fractional-Order Model of COVID-19
Abstract
:1. Introduction
2. Preliminaries
- (i)
- ρ is normal.
- (ii)
- ρ is upper semicontinuous on .
- (iii)
- ρ is convex.
- (iv)
- is compact.
- (a)
- is left continuous, bounded, and increasing function over and right continuous at 0.
- (b)
- is left continuous, bounded, and increasing function over and right continuous at 0.
- (c)
- (i)
- for all ;
- (ii)
- for all ;
- (iii)
- for all ;
- (iv)
- is a complete metric space.
3. Main Result
3.1. Existence–Uniqueness
3.2. Procedure for Solution
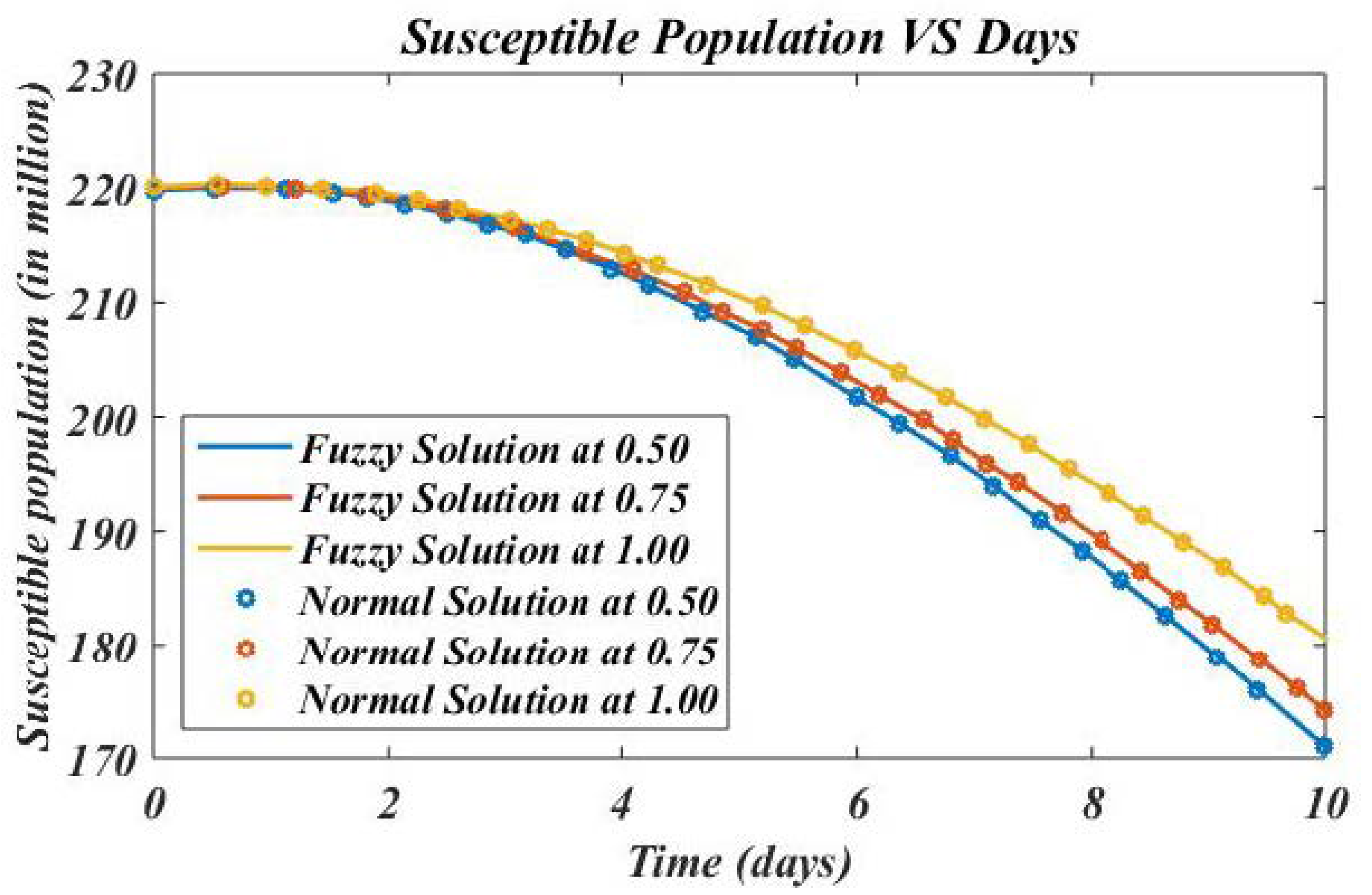
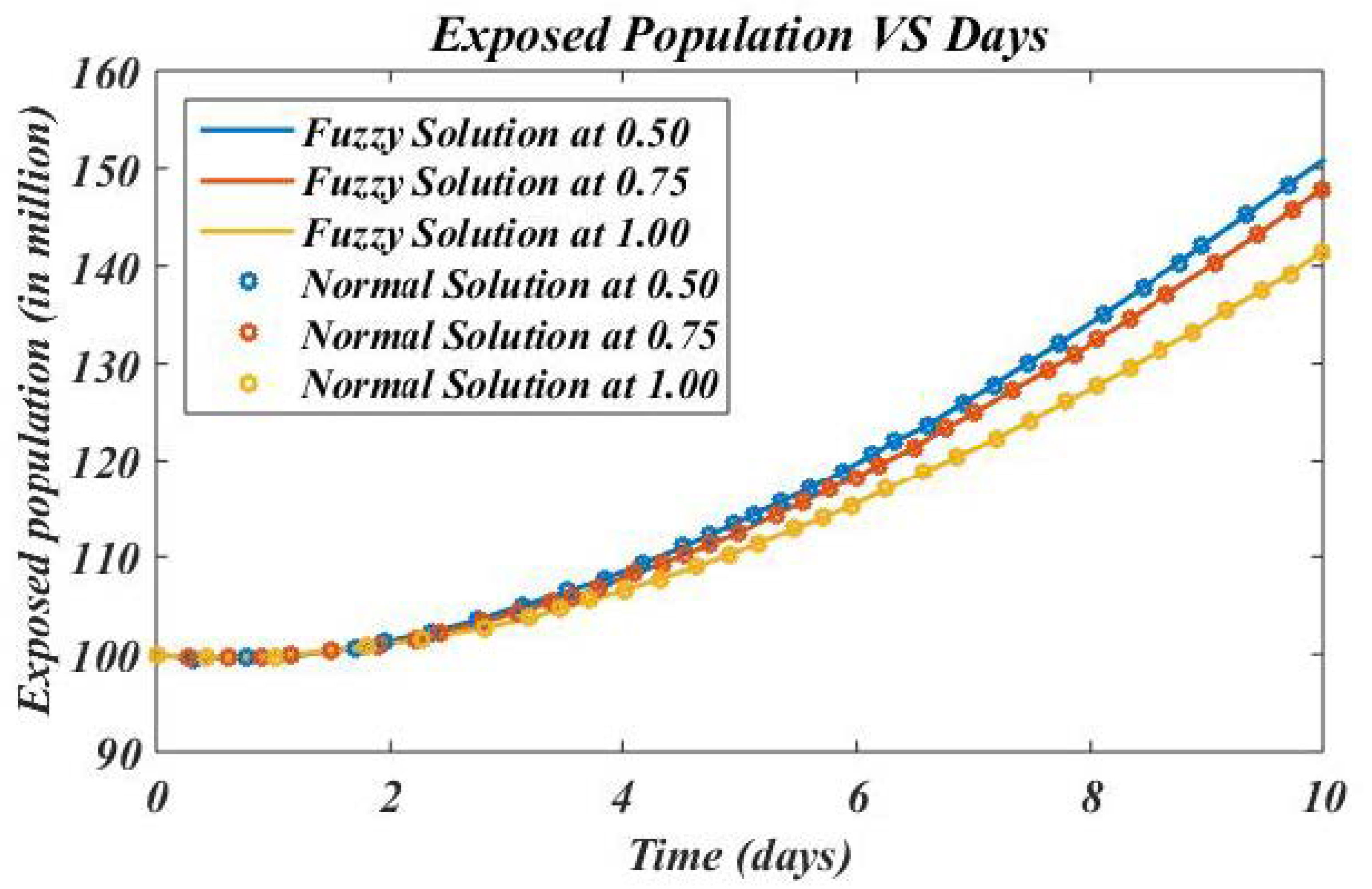
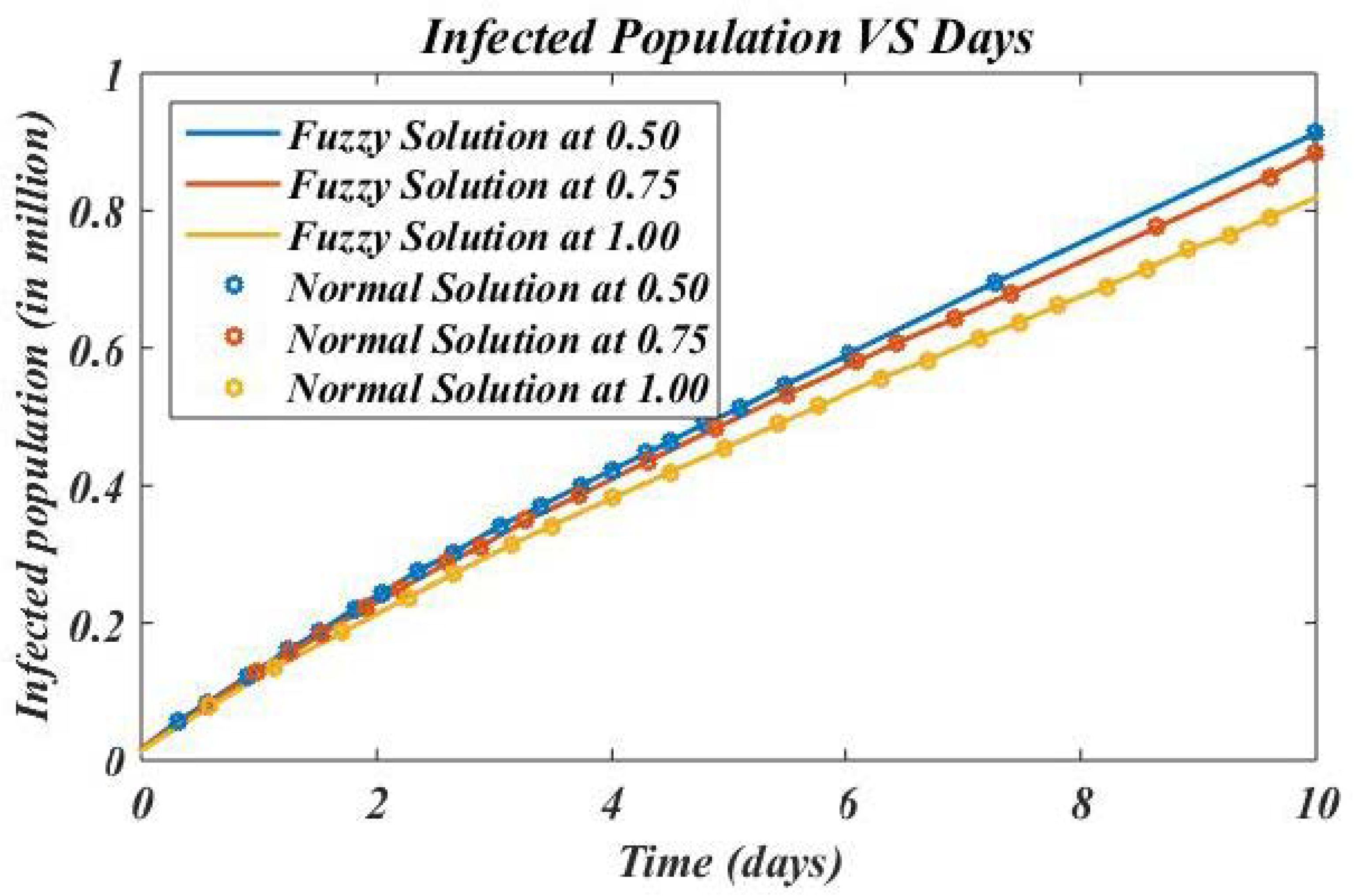
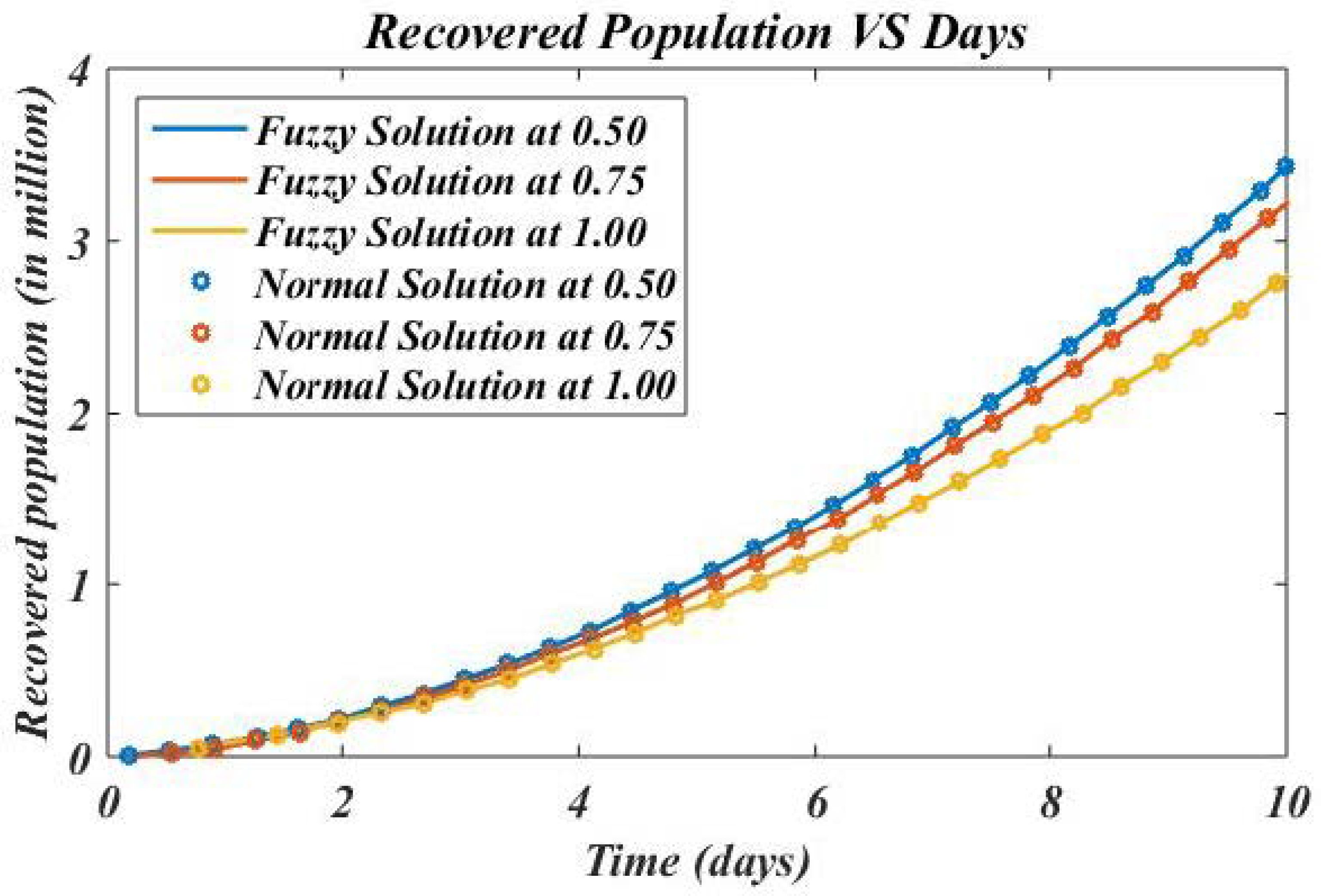
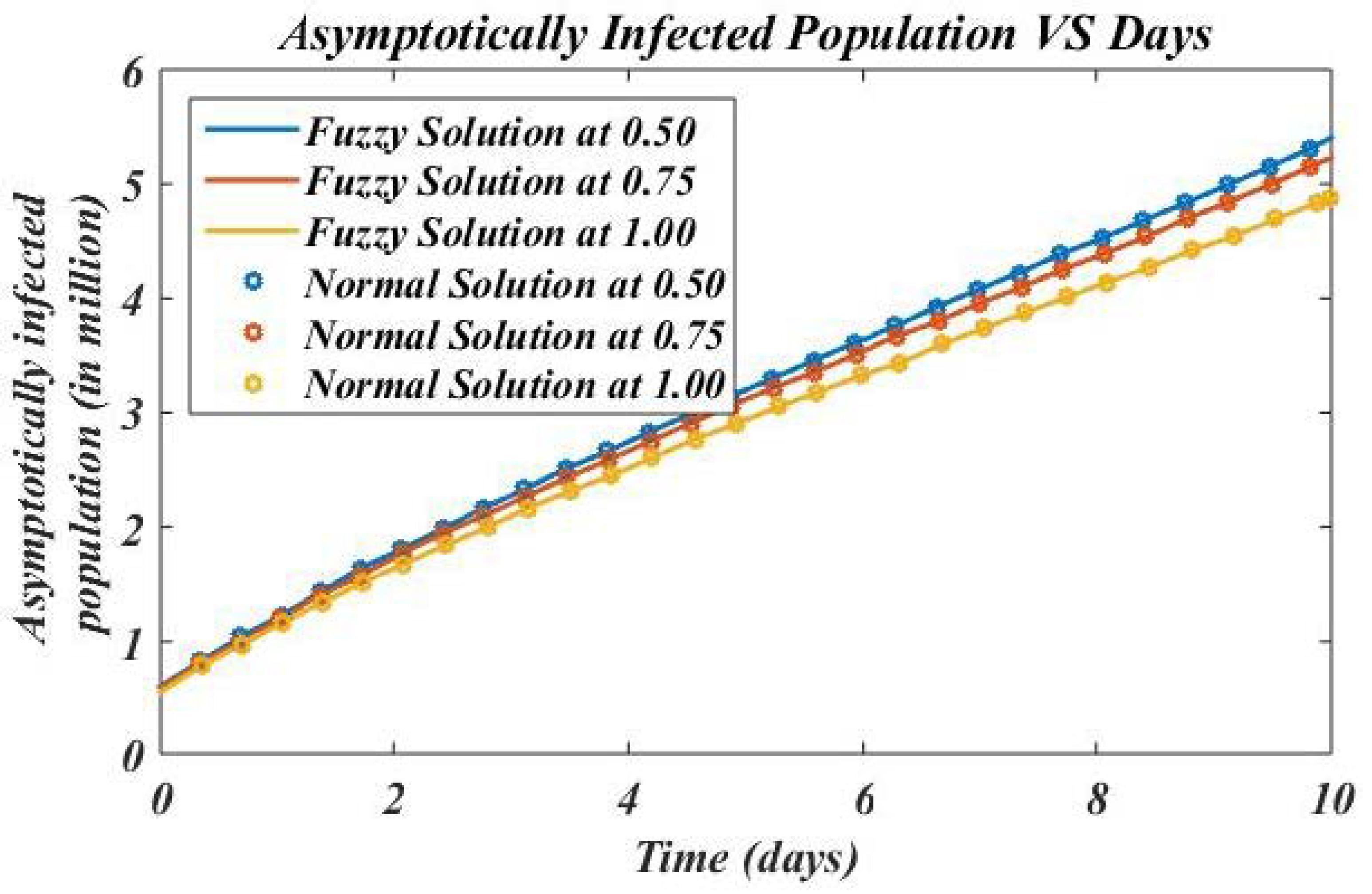
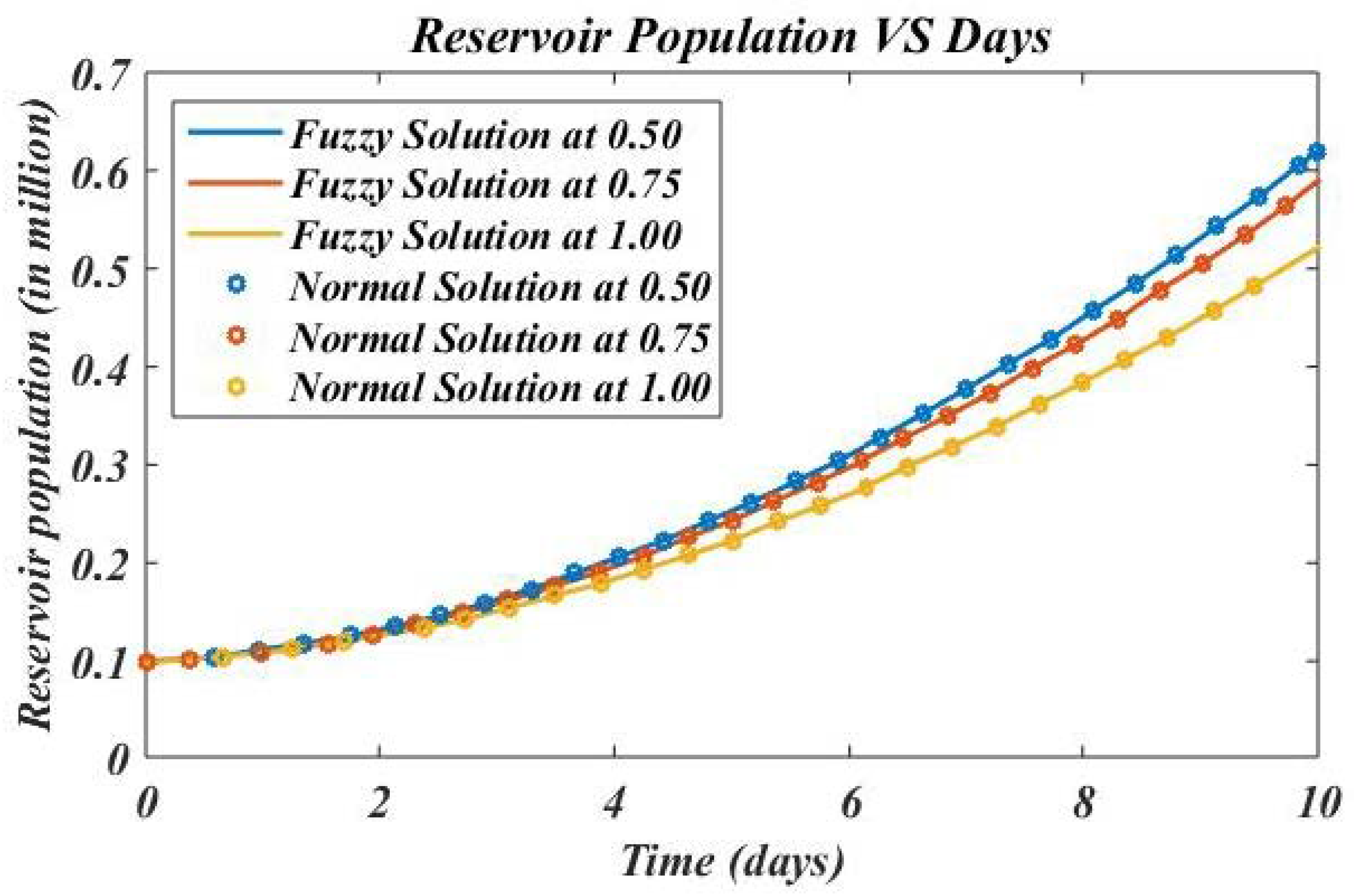
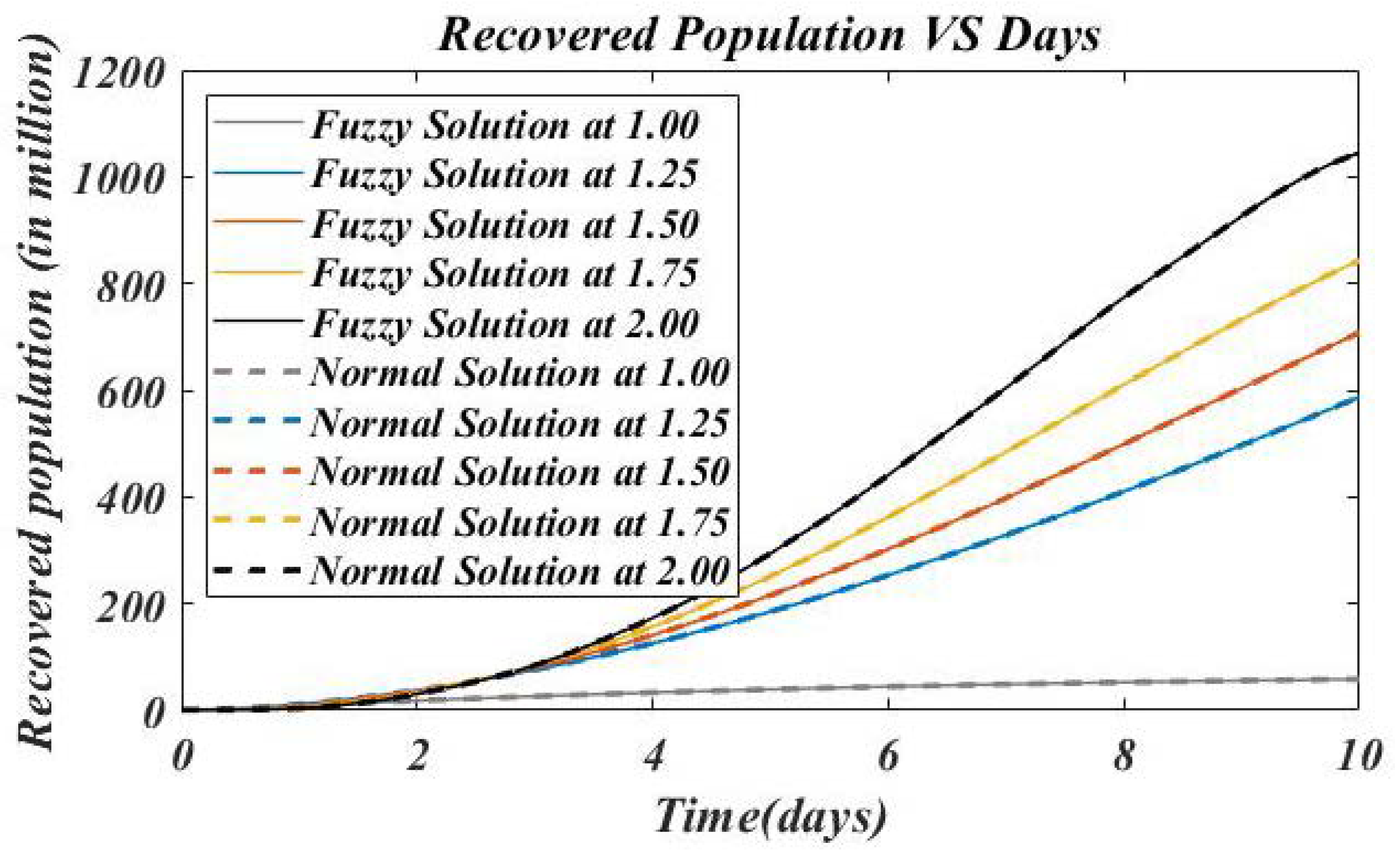
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chan, J.F.W.; Kok, K.H.; Zhu, Z.; Chu, H.; To, K.K.W.; Yuan, S.; Yuen, K.Y. Genomic characterization of the 2019 novel human-pathogenic coronavirus isolated from a patient with atypical pneumonia after visiting Wuhan. Emerg. Microbes Infect. 2020, 9, 221–236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, H.; Stratton, C.W.; Tang, Y.W. Outbreak of pneumonia of unknown etiology in Wuhan, China: The mystery and the miracle. J. Med. Virol. 2020, 92, 401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ji, W.; Wang, W.; Zhao, X.; Zai, J.; Li, X. Homologous recombination within the spike glycoprotein of the newly identified coronavirus may boost cross-species transmission from snake to human. J. Med. Virol. 2020, 92, 433–440. [Google Scholar] [CrossRef]
- Fahmi, I. World Health Organization Coronavirus Disease 2019 (COVID-19) Situation Report; WHO: Geneva, Switzerland, 2019. [Google Scholar]
- Chen, Y.; Guo, D. Molecular mechanisms of coronavirus RNA capping and methylation. Virol. Sin. 2016, 31, 3–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.F.; Shi, Z.; Zhang, S.; Field, H.; Daszak, P.; Eaton, B.T. Review of bats and SARS. Emerg. Infect. Dis. 2006, 12, 1834. [Google Scholar] [CrossRef]
- Ge, X.Y.; Li, J.L.; Yang, X.L.; Chmura, A.A.; Zhu, G.; Epstein, J.H.; Mazet, J.K.; Hu, B.; Zhang, W.; Peng, C.; et al. Isolation and characterization of a bat SARS-like coronavirus that uses the ACE2 receptor. Nature 2013, 503, 535–538. [Google Scholar] [CrossRef]
- Lu, R.; Zhao, X.; Li, J.; Niu, P.; Yang, B.; Wu, H.; Wang, W.; Song, H.; Huang, B.; Zhu, N.; et al. Genomic characterisation and epidemiology of 2019 novel coronavirus: Implications for virus origins and receptor binding. Lancet 2020, 395, 565–574. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.; Yang, X.L.; Wang, X.G.; Hu, B.; Zhang, L.; Zhang, W.; Si, H.-R.; Zhu, Y.; Li, B.; Huang, C.-L.; et al. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature 2020, 579, 270–273. [Google Scholar] [CrossRef] [Green Version]
- Tian, X.; Li, C.; Huang, A.; Xia, S.; Lu, S.; Shi, Z.; Lu, L.; Jiang, S.; Yang, Z.; Wu, Y.; et al. Potent binding of 2019 novel coronavirus spike protein by a SARS coronavirus-specific human monoclonal antibody. Emerg. Microbes Infect. 2020, 9, 382–385. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, S.F.; Quadeer, A.A.; McKay, M.R. Preliminary identification of potential vaccine targets for 2019-nCoV based on SARS-CoV immunological studies. Viruses 2020, 12, 254. [Google Scholar] [CrossRef] [Green Version]
- Chaudhury, S.; Berrondo, M.; Weitzner, B.D.; Muthu, P.; Bergman, H.; Gray, J.J. Benchmarking and analysis of protein docking performance in Rosetta v3. 2. PLoS ONE 2011, 6, e22477. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Lakshmikantham, V.; Nieto, J.J. On the concept of solution for fractional differential equations with uncertainty. Nonlinear Anal. Theory Methods Appl. 2010, 72, 2859–2862. [Google Scholar] [CrossRef]
- Asjad, M.I.; Aleem, M.; Ahmadian, A.; Salahshour, S.; Ferrara, M. New trends of fractional modeling and heat and mass transfer investigation of (SWCNTs and MWCNTs)-CMC based nanofluids flow over inclined plate with generalized boundary conditions. Chin. J. Phys. 2020, 66, 497–516. [Google Scholar] [CrossRef]
- Abbas, A.; Shafqat, R.; Jeelani, M.B.; Alharthi, N.H. Significance of Chemical Reaction and Lorentz Force on Third-Grade Fluid Flow and Heat Transfer with Darcy-Forchheimer Law over an Inclined Exponentially Stretching Sheet Embedded in a Porous Medium. Symmetry 2022, 14, 779. [Google Scholar] [CrossRef]
- Abbas, A.; Shafqat, R.; Jeelani, M.B.; Alharthi, N.H. Convective Heat and Mass Transfer in Third-Grade Fluid with Darcy–Forchheimer Relation in the Presence of Thermal-Diffusion and Diffusion-Thermo Effects over an Exponentially Inclined Stretching Sheet Surrounded by a Porous Medium: A CFD Study. Processes 2022, 10, 776. [Google Scholar] [CrossRef]
- Kaleva, O. Fuzzy differential equations. Fuzzy Sets Syst. 1987, 24, 301–317. [Google Scholar] [CrossRef]
- Lupulescu, V. Fractional calculus for interval-valued functions. Fuzzy Sets Syst. 2015, 265, 63–85. [Google Scholar] [CrossRef]
- Arshad, S.; Lupulescu, V. Fractional differential equation with the fuzzy initial condition. Electron. J. Differ. Equ. 2011, 34, 1–8. [Google Scholar]
- Benchohra, M.; Cabada, A.; Seba, D. An existence result for nonlinear fractional differential equations on Banach spaces. Bound. Value Probl. 2009, 2009, 628916. [Google Scholar] [CrossRef] [Green Version]
- Belmekki, M.; Nieto, J.; Rodriguez-Lopez, R. Existence of periodic solution for a nonlinear fractional differential equation. Bound. Value Probl. 2009, 2009, 324561. [Google Scholar] [CrossRef] [Green Version]
- Park, J.Y.; Han, H.K. Existence and uniqueness theorem for a solution of fuzzy Volterra integral equations. Fuzzy Sets Syst. 1999, 105, 481–488. [Google Scholar] [CrossRef]
- Ali, N.; Khan, R.A. Existence of positive solution to a class of fractional differential equations with three point boundary conditions. Math. Sci. Lett. 2016, 5, 291–296. [Google Scholar] [CrossRef]
- Khan, R.A.; Shah, K. Existence and uniqueness of solutions to fractional order multi-point boundary value problems. Commun. Appl. Anal. 2015, 19, 515–525. [Google Scholar]
- Lakshmikantham, V.; Leela, S. Nagumo-type uniqueness result for fractional differential equations. Nonlinear Anal. 2009, 71, 2886–2889. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Lakshmikantham, V.; Vatsala, A.S. Basic theory of fractional differential equations. Nonlinear Anal. Theory Methods Appl. 2008, 69, 2677–2682. [Google Scholar] [CrossRef]
- Perfilieva, I. Fuzzy transforms: Theory and applications. Fuzzy Sets Syst. 2006, 157, 993–1023. [Google Scholar] [CrossRef]
- Salahshour, S.; Allahviranloo, T. Application of fuzzy differential transform method for solving fuzzy Volterra integral equations. Appl. Math. Model. 2013, 37, 1016–1027. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Salahshour, S.; Abbasbandy, S. Explicit solutions of fractional differential equations with uncertainty. Soft Comput. 2012, 16, 297–302. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Ahmadi, M.B. Fuzzy laplace transforms. Soft Comput. 2010, 14, 235. [Google Scholar] [CrossRef]
- Zhu, Y. Stability analysis of fuzzy linear differential equations. Fuzzy Optim. Decis. Mak. 2010, 9, 169–186. [Google Scholar] [CrossRef]
- Niazi, A.U.K.; He, J.; Shafqat, R.; Ahmed, B. Existence, Uniqueness, and Eq–Ulam-Type Stability of Fuzzy Fractional Differential Equation. Fractal Fract. 2021, 5, 66. [Google Scholar] [CrossRef]
- Iqbal, N.; Niazi, A.U.K.; Shafqat, R.; Zaland, S. Existence and Uniqueness of Mild Solution for Fractional-Order Controlled Fuzzy Evolution Equation. J. Funct. Spaces 2021, 2021, 5795065. [Google Scholar] [CrossRef]
- Shafqat, R.; Niazi, A.U.K.; Jeelani, M.B.; Alharthi, N.H. Existence and Uniqueness of Mild Solution Where α∈(1,2) for Fuzzy Fractional Evolution Equations with Uncertainty. Fractal Fract. 2022, 6, 65. [Google Scholar] [CrossRef]
- Abuasbeh, K.; Shafqat, R.; Niazi, A.U.K.; Awadalla, M. Local and Global Existence and Uniqueness of Solution for Time-Fractional Fuzzy Navier–Stokes Equations. Fractal Fract. 2022, 6, 330. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Shah, K.; Salahshour, S.; Ahmadian, A.; Ciano, T. Fuzzy fractional-order model of the novel coronavirus. Adv. Differ. Equations 2020, 2020, 472. [Google Scholar] [CrossRef]
- Gottwald, S. Fuzzy Set Theory and Its Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991; ISBN 0-7923-9075-X. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems; World Scientific: Singapore, 1996; pp. 394–432. [Google Scholar]

| Notation | Parameters Description | Numerical Value |
|---|---|---|
| Birth rate | 1 | |
| Death rate of infected population | ||
| Transmission coefficient | 0.05 | |
| Disease transmission coefficient | 0.001231 | |
| Signified incubation period | 0.001234, 0.05 | |
| Recovery rate of | 0.1389 | |
| Influence of virus from and to | 0.0398, 0.01 | |
| Amount of asymptotic infection | 0.1243 | |
| Transmissibility multiple | 0.02 | |
| Elimination rate of virus from | 0.01 | |
| Initial value of susceptible | 220 million | |
| Initial value of infected | 0.015 million | |
| Initial value of exposed | 100 million | |
| Initial value of asymptotically infected | 0.60 million | |
| Initial value of recovered | 0 million | |
| Initial value of reservoir | 0.1 million |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alnahdi, A.S.; Shafqat, R.; Niazi, A.U.K.; Jeelani, M.B. Pattern Formation Induced by Fuzzy Fractional-Order Model of COVID-19. Axioms 2022, 11, 313. https://doi.org/10.3390/axioms11070313
Alnahdi AS, Shafqat R, Niazi AUK, Jeelani MB. Pattern Formation Induced by Fuzzy Fractional-Order Model of COVID-19. Axioms. 2022; 11(7):313. https://doi.org/10.3390/axioms11070313
Chicago/Turabian StyleAlnahdi, Abeer S., Ramsha Shafqat, Azmat Ullah Khan Niazi, and Mdi Begum Jeelani. 2022. "Pattern Formation Induced by Fuzzy Fractional-Order Model of COVID-19" Axioms 11, no. 7: 313. https://doi.org/10.3390/axioms11070313
APA StyleAlnahdi, A. S., Shafqat, R., Niazi, A. U. K., & Jeelani, M. B. (2022). Pattern Formation Induced by Fuzzy Fractional-Order Model of COVID-19. Axioms, 11(7), 313. https://doi.org/10.3390/axioms11070313






