Dynamical Analysis of a Modified Epidemic Model with Saturated Incidence Rate and Incomplete Treatment
Abstract
:1. Introduction
2. Model Formulation
3. Mathematical Analysis
3.1. Positivity and Boundedness of Solutions
3.2. Non-Endemic Equilibrium Point
3.3. Basic Reproduction Number
3.4. Endemic Equilibrium Points
3.5. Local Stability of Equilibrium Points
3.6. Global Stability of Equilibrium Points
- For , we get
- For , we get
- For , we get
- For , we get
- For , we get
3.7. Control Optimal Problem
- State equations for this model rewriting with the condition, , , ,
- Co-state equation
- Stationer condition , with , then we getbecause satisfies the minimization problem of the optimal control with as the optimal control of system.
4. Numerical Simulation
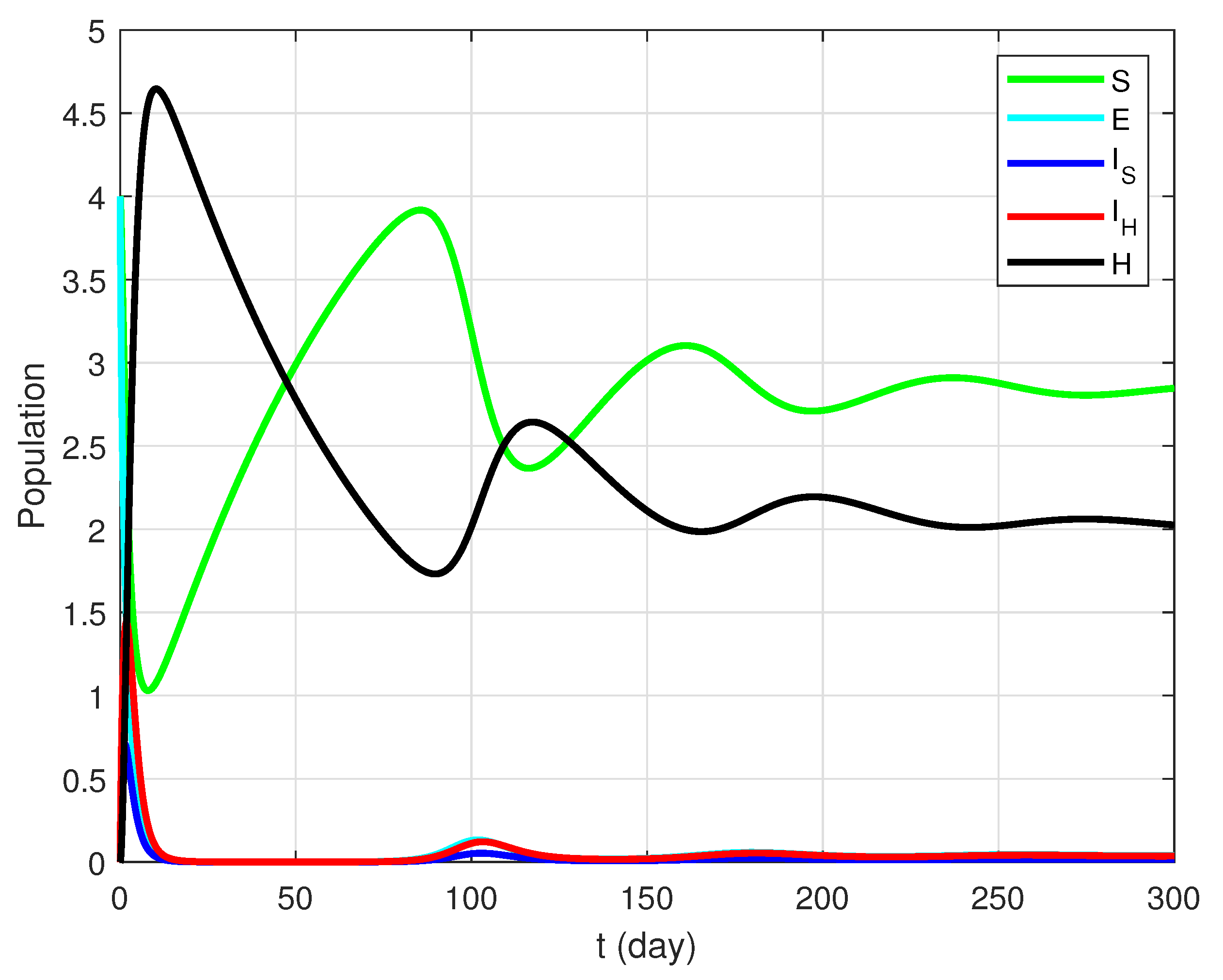
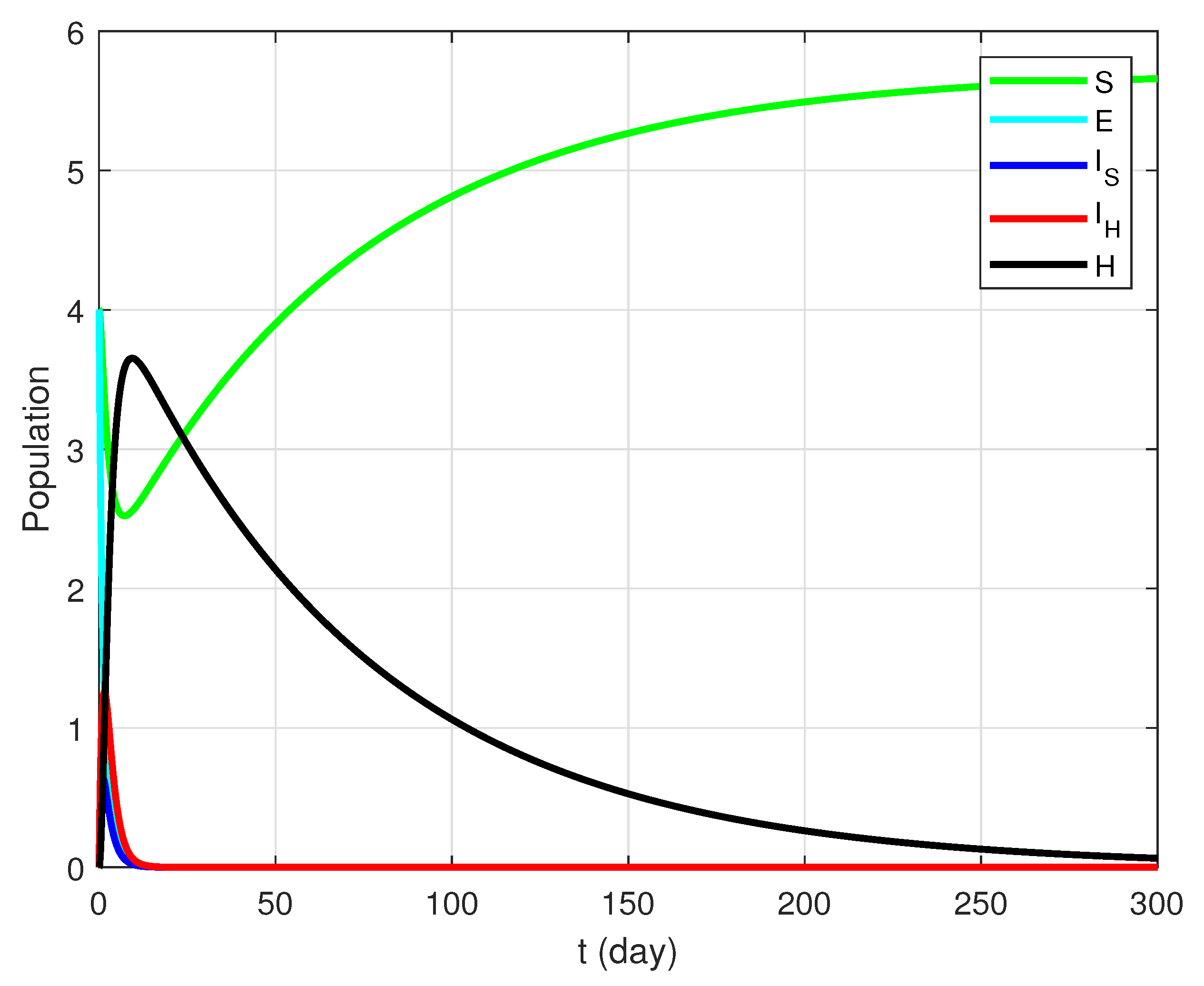
4.1. Case for
4.2. Case
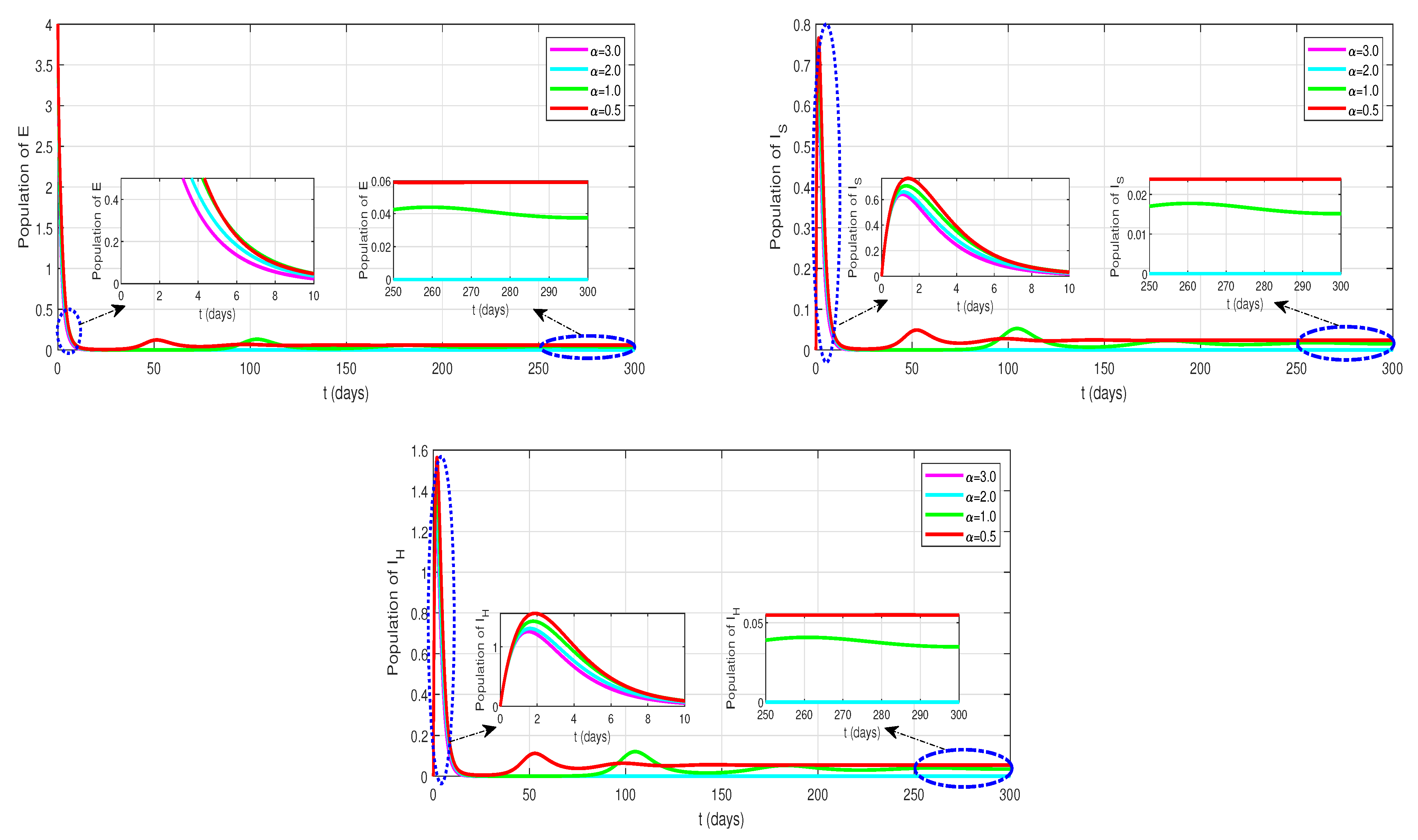
4.3. Effect of Parameters and on
- (1)
- For the study the effect of saturated incidence rate, we choose the various of , where and . The details of each change due to the value-change for the rate of saturated incidence () on the , and classes can be seen in Figure 4. Significantly, the value-changes of have an impact on the humans of E, and . Thus, the changes in the parameter value of the saturated incidence really influented the numbers of exposed (E), infected humans with home treated (), and infected humans with hospital treated ().
- (2)
- Next, to study the effect of the rate of incomplete treatment, we choose the various of , where and . The value-changes of incomplete treatment () affect the population of each class: E, , and H are illustrated in Figure 5. When the value of the incomplete treatment is increased, the impact has reduced the number of exposed (E), and infected humans with home treated (). Meanwhile, the number of humans in the healed class (H) increases. Thus, the humans of , and classes are relatively changed for every .
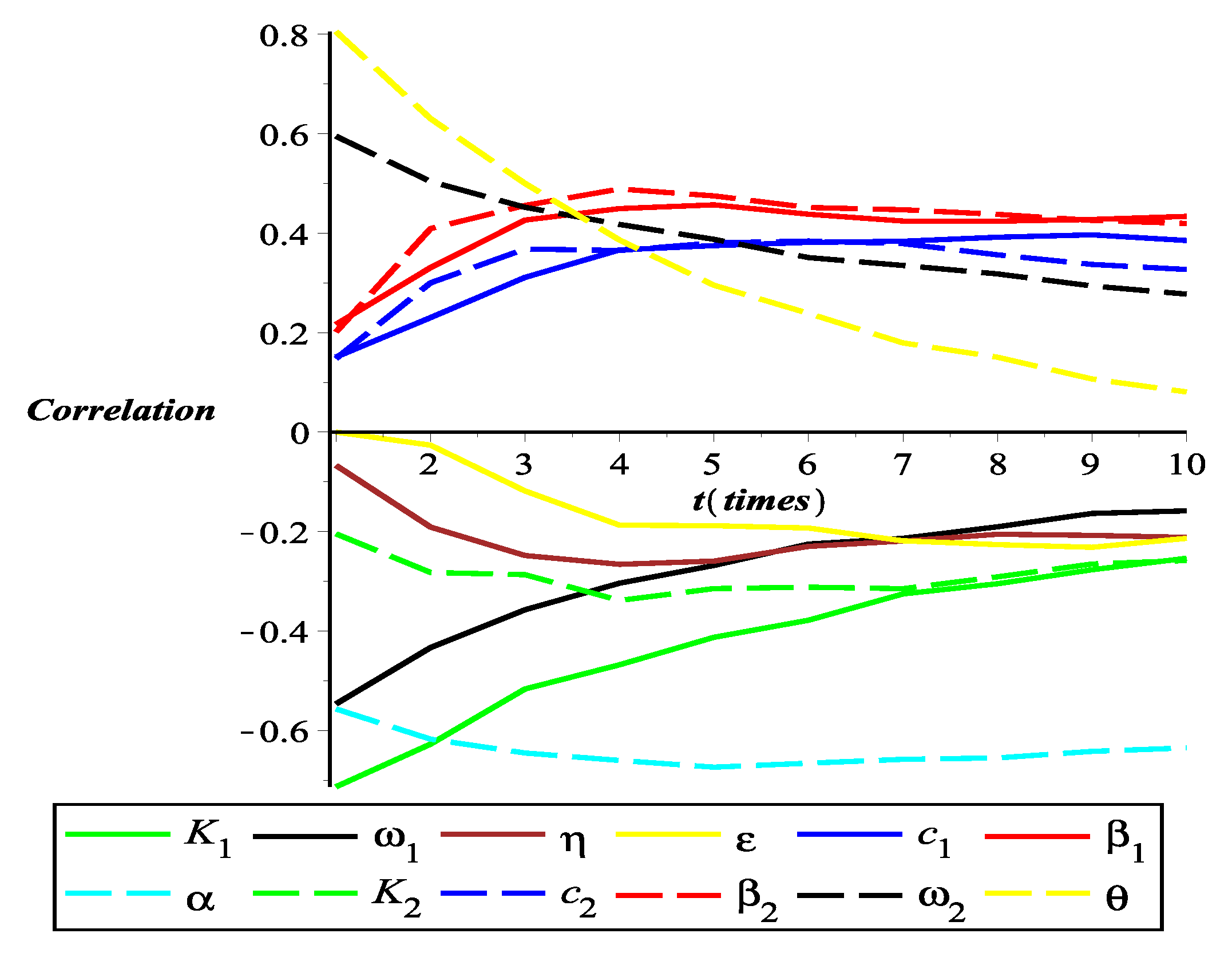
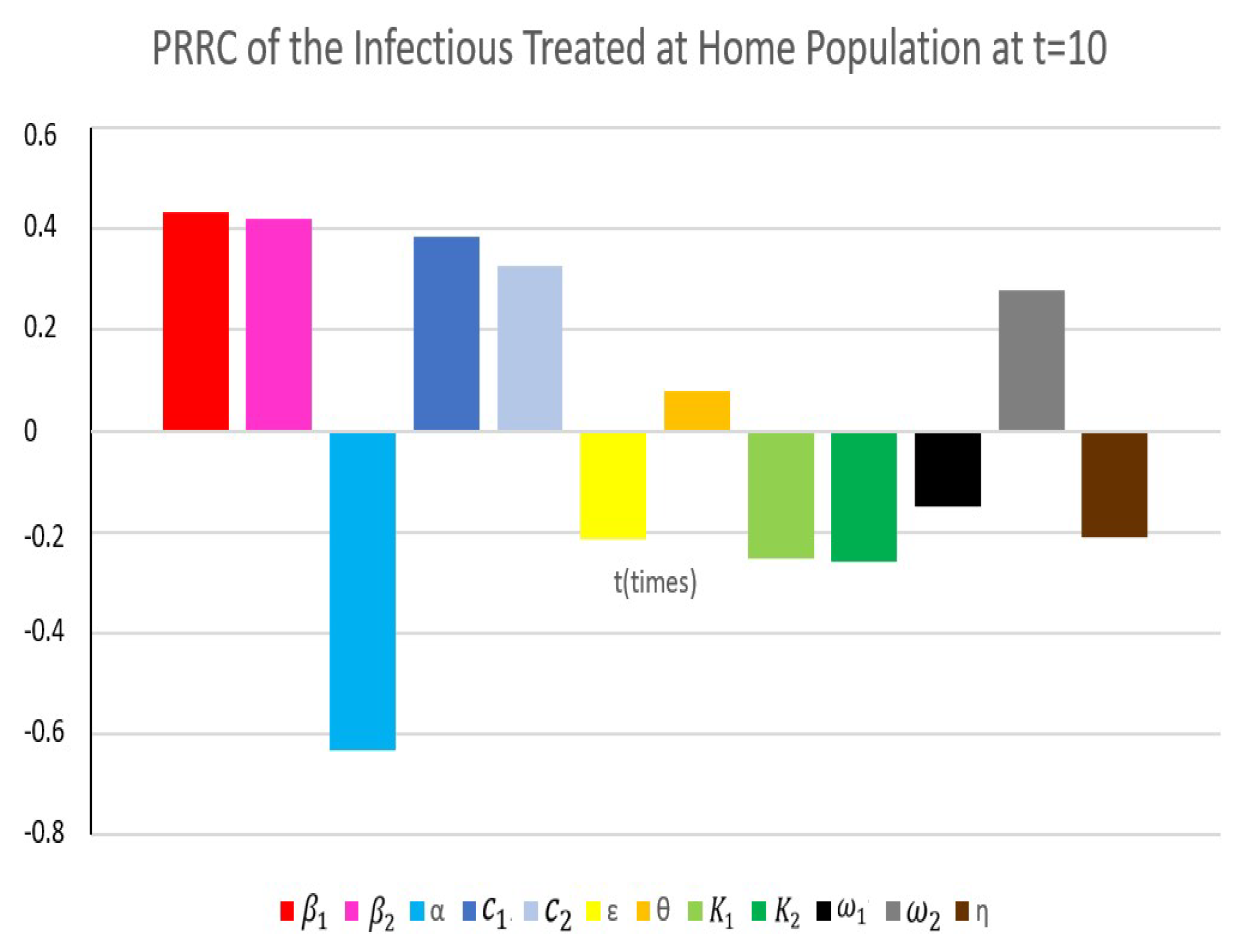
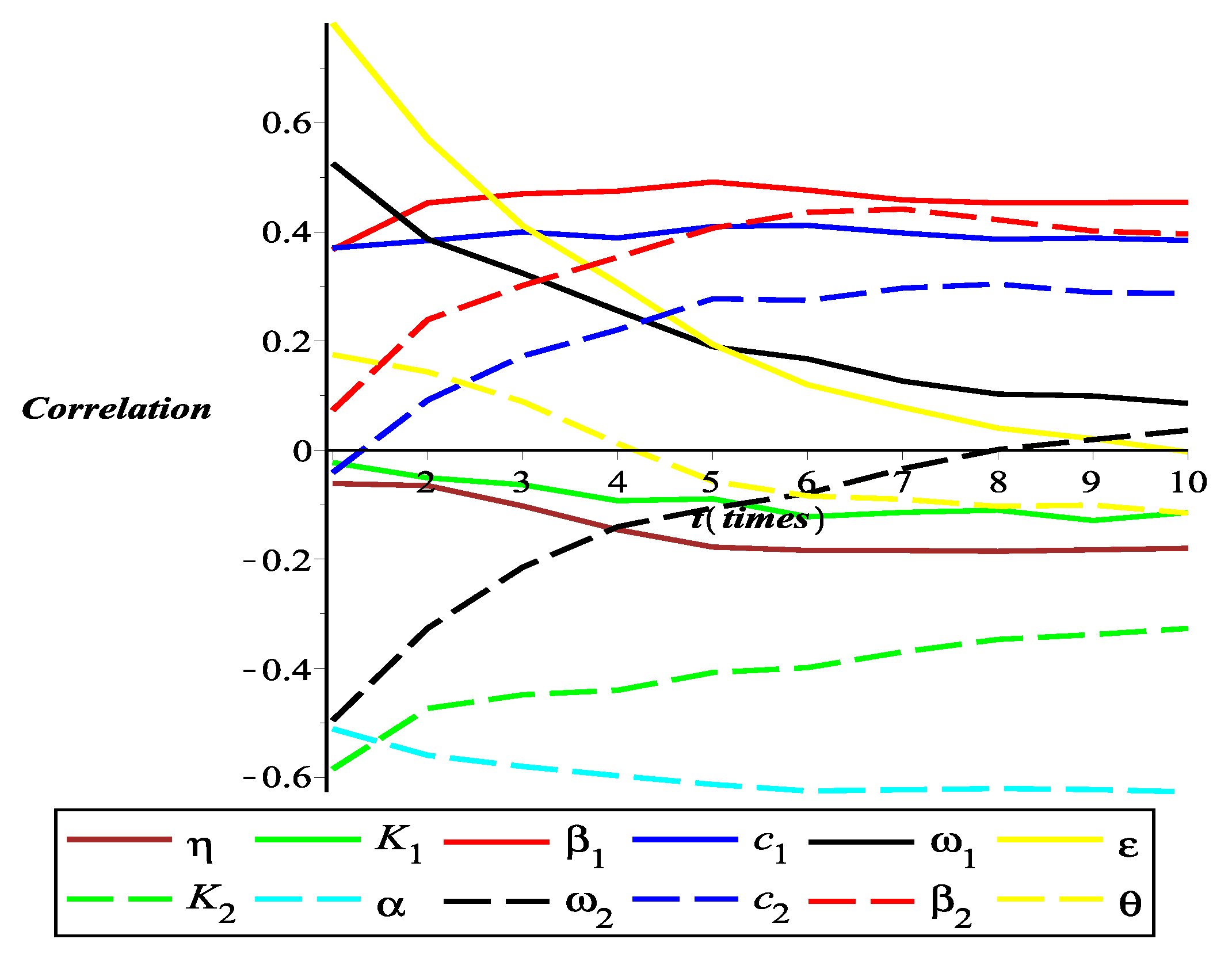
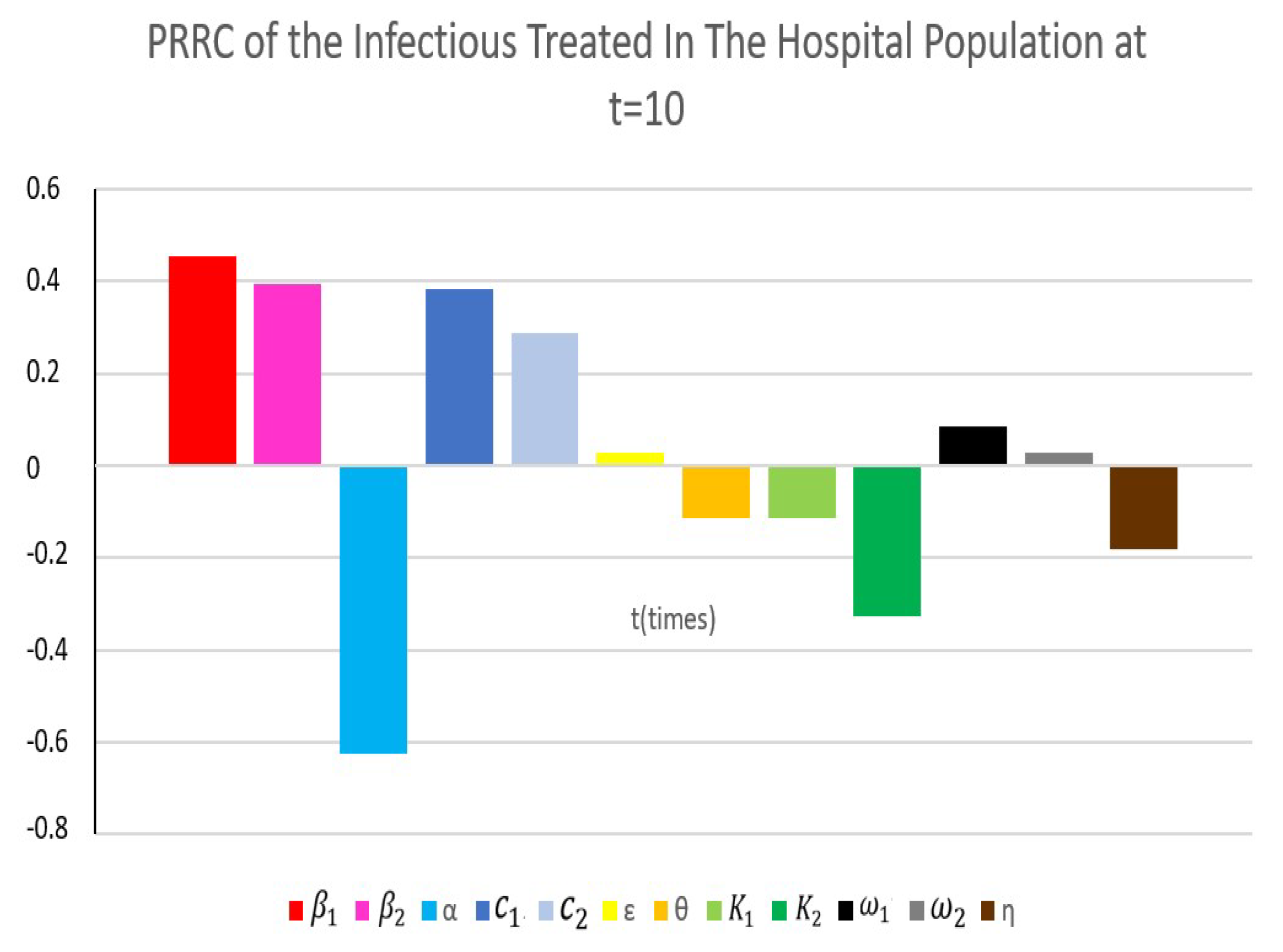
4.4. Partial Rank Correlation Coefficient
4.5. Optimal Control
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Proof of Analysis for Endemic Point Numerically
Appendix B. The Proof of Analysis for Non-Endemic Point Numerically
References
- Caetano, C.; Morgado, M.L.; Patrício, P.; Pereira, J.F.; Nunes, B. Mathematical modelling of the impact of non-pharmacological strategies to control the COVID-19 epidemic in Portugal. Mathematics 2021, 9, 1084. [Google Scholar] [CrossRef]
- Chen, H.; Haus, B.; Mercorelli, P. Extension of SEIR compartmental models for constructive Lyapunov control of COVID-19 and analysis in terms of practical stability. Mathematics 2021, 9, 2076. [Google Scholar] [CrossRef]
- Husniah, H.; Ruhanda, R.; Supriatna, A.K.; Biswas, M.H.A. SEIR mathematical model of convalescent plasma transfusion to reduce COVID-19 disease transmission. Mathematics 2021, 9, 2857. [Google Scholar] [CrossRef]
- Beay, L.K.; Kasbawati; Toaha, S. Effects of human and mosquito migrations on the dynamical behavior of the spread of malaria. AIP Conf. Proc. 2017, 1825, 020006. [Google Scholar] [CrossRef] [Green Version]
- Wongvanich, N.; Tang, I.-M.; Dubois, M.-A.; Pongsumpun, P. Mathematical modeling and optimal control of the Hand Foot Mouth Disease affected by regional residency in Thailand. Mathematics 2021, 9, 2863. [Google Scholar] [CrossRef]
- Islam, M.R.; Peace, A.; Medina, D.; Oraby, T. Integer versus fractional order SEIR deterministic and stochastic models of Measles. Int. J. Environ. Res. Public Health 2020, 17, 2014. [Google Scholar] [CrossRef] [Green Version]
- Saito, M.M.; Imoto, S.; Yamaguchi, R.; Sato, H.; Nakada, H.; Kami, M.; Miyano, S.; Higuchi, T. Extension and verification of the SEIR model on the 2009 Influenza A (H1N1) pandemic in Japan. Math. Biosci. 2013, 246, 47–54. [Google Scholar] [CrossRef]
- Imran, M.; Usman, M.; Dur-e-Ahmad, M.; Khan, A. Transmission dynamics of Zika Fever: A SEIR based model. Differ. Equ. Dyn. Syst. 2021, 29, 463–486. [Google Scholar] [CrossRef]
- Dantas, E.; Tosin, M.; Cunha, A., Jr. Calibration of a SEIR–SEI epidemic model to describe the Zika virus outbreak in Brazil. Appl. Math. Comp. 2018, 338, 249–259. [Google Scholar] [CrossRef] [Green Version]
- Das, K.; Murthy, B.S.N.; Samad, S.A.; Biswas, M.H.A. Mathematical transmission analysis of SEIR Tuberculosis disease model. Sens. Int. 2021, 2, 100120. [Google Scholar] [CrossRef]
- Liu, G.; Chen, J.; Liang, Z.; Peng, Z.; Li, J. Dynamical analysis and optimal control for a SEIR model based on virus mutation in WSNs. Mathematics 2021, 9, 929. [Google Scholar] [CrossRef]
- Coronel, A.; Huancas, F.; Hess, I.; Lozada, E.; Novoa-Muñoz, F. Analysis of a SEIR-KS mathematical model for computer virus propagation in a periodic environment. Mathematics 2020, 8, 761. [Google Scholar] [CrossRef]
- Tuberculosis Chemotherapy Centre. A concurrent comparison of home and sanatorium treatment of Pulmonary Tuberculosis in South India. Bull. World Health Organ. 1959, 21, 51–144. [Google Scholar]
- Suter, F.; Consolaro, E.; Pedroni, S.; Moroni, C.; Pastò, E.; Paganini, M.V.; Pravettoni, G.; Cantarelli, U.; Rubis, N.; Perico, N.; et al. A simple, home-therapy algorithm to prevent hospitalisation for COVID–19 patients: A retrospective observational matched-cohort study. EClinicalMedicine 2021, 37, 100941. [Google Scholar] [CrossRef]
- Consolaro, E.; Suter, F.; Rubis, N.; Pedroni, S.; Moroni, C.; Pastò, E.; Paganini, M.V.; Pravettoni, G.; Cantarelli, U.; Perico, N.; et al. A Home-Treatment Algorithm Based on Anti-inflammatory Drugs to Prevent Hospitalization of Patients With Early COVID-19: A Matched-Cohort Study (COVER 2). Front. Med. 2022, 9, 785785. [Google Scholar] [CrossRef]
- Huo, H.F.; Zou, M.X. Modelling effects of treatment at home on Tuberculosis transmission dynamics. Appl. Math. Model. 2016, 40, 9474–9484. [Google Scholar] [CrossRef]
- Yıldız, T.A.; Karaoğlu, E. Optimal control strategies for Tuberculosis dynamics with exogenous reinfections in case of treatment at home and treatment in hospital. Nonlinear Dyn. 2019, 97, 2643–2659. [Google Scholar] [CrossRef]
- Simorangkir, G.M.; Aldila, D.; Tasman, H. Modelling the effect of hospitalization in Tuberculosis spread. AIP Conf. Proc. 2020, 2264, 020006. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, M.; Hou, Q.; Xie, B. Dynamical analysis of an SEIRS model with incomplete recovery and relapse on networks and its optimal vaccination control. Res. Sq. 2021, 1, 1–30. [Google Scholar] [CrossRef]
- Tudor, D. A deterministic model for herpes infections in human and animal populations. Siam Rev. 1990, 32, 136–139. [Google Scholar] [CrossRef]
- Ullah, I.; Ahmad, S.; Al-Mdallal, Q.; Khan, Z.A.; Khan, H.; Khan, A. Stability analysis of a dynamical model of Tuberculosis with incomplete treatment. Adv. Differ. Equ. 2020, 499, 1–14. [Google Scholar] [CrossRef]
- Neyrolles, O.; Hernández-Pando, R.; Pietri-Rouxel, F.; Fornès, P.; Tailleux, L.; Payán, J.A.B.; Pivert, E.; Bordat, Y.; Aguilar, D.; Prévost, M.-C.; et al. Is adipose tissue a place for Mycobacterium Tuberculosis persistence? PLoS ONE 2006, 1, e43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Li, J.; Ma, Z.; Liu, L. Global stability of two models with incomplete treatment for Tuberculosis. Chaos Solitons Fractals 2010, 43, 79–85. [Google Scholar] [CrossRef]
- Rahman, M.U.; Arfan, M.; Shah, Z.; Kumam, P.; Shutaywi, M. Nonlinear fractional mathematical model of tuberculosis (TB) disease with incomplete treatment under Atangana-Baleanu derivative. Alex. Eng. J. 2021, 60, 2845–2856. [Google Scholar] [CrossRef]
- Jafari, M.; Kheiri, H.; Jabbari, A. Backward bifurcation in a fractional-order and two-patch model of tuberculosis epidemic with incomplete treatment. Int. J. Biomath. 2021, 14, 2150007. [Google Scholar] [CrossRef]
- Suryanto, A.; Darti, I. On the nonstandard numerical discretization of SIR epidemic model with a saturated incidence rate and vaccination. AIMS Math. 2020, 6, 141–155. [Google Scholar] [CrossRef]
- Thirthar, A.A.; Naji, R.K.; Bozkurt, F.; Yousef, A. Modeling and analysis of an SI1I2R epidemic model with nonlinear incidence and general recovery functions of I1. Chaos Solitons Fractals 2021, 145, 110746. [Google Scholar] [CrossRef]
- Li, L.; Sun, C.; Jia, J. Optimal control of a delayed SIRC epidemic model with saturated incidence rate. Optim. Control Appl. Meth. 2018, 40, 367–374. [Google Scholar] [CrossRef]
- Bentaleb, D.; Harroudi, S.; Amine, S.; Allali, K. Analysis and optimal control of a multistrain SEIR epidemic model with saturated incidence rate and treatment. Differ. Equ. Dyn. Syst. 2020, 1, 1–17. [Google Scholar] [CrossRef]
- Khan, M.A.; Khan, Y.; Islam, S. Complex dynamics of an SEIR epidemic model with saturated incidence rate and treatment. Phys. A 2018, 493, 210–227. [Google Scholar] [CrossRef]
- Mushayabasa, S. A simple epidemiological model for typhoid with saturated incidence rate and treatment effect. Int. J. Math. Comput. Sci. 2012, 6, 688–695. [Google Scholar] [CrossRef]
- Alshammari, F.S.; Khan, M.A. Dynamic behaviors of a modified SIR model with nonlinear incidence and recovery rates. Alex. Eng. J. 2021, 60, 2997–3005. [Google Scholar] [CrossRef]
- Hussain, G.; Khan, A.; Zahri, M.; Zaman, G. Stochastic permanence of an epidemic model with a saturated incidence rate. Chaos Solitons Fractals 2020, 139, 110005. [Google Scholar] [CrossRef]
- Okuonghae, D. Backward bifurcation of an epidemiological model with saturated incidence, isolation and treatment functions. Qual. Theory Dyn. Syst. 2020, 18, 413–440. [Google Scholar] [CrossRef]
- Baba, I.A.; Abdulkadir, R.A.; Esmaili, P. Analysis of tuberculosis model with saturated incidence rate and optimal control. Physica A 2020, 540, 123237. [Google Scholar] [CrossRef]
- Mengistu, A.K.; Witbooi, P.J. Mathematical analysis of TB model with vaccination and saturated incidence rate. Abstr. Appl. Anal. 2020, 2020, 6669997. [Google Scholar] [CrossRef]
- Indrayani, S.W.; Kusumawinahyu, W.M.; Trisilowati. Dynamical Analysis on the model of Tuberculosis spread with vaccination and saturated incident rate. IOP Conf. Ser. Mater. Sci. Eng. 2019, 546, 052032. [Google Scholar] [CrossRef]
- Sutimin; Herdiana, R.; Soelistyo U, R.H.; Permatasari, A.H. Stability analysis of Tuberculosis epidemic model with saturated infection force. E3S Web Conf. 2020, 202, 12023. [Google Scholar] [CrossRef]
- Khan, T.; Zaman, G. Classification of different Hepatitis B infected individuals with saturated incidence rate. SpringerPlus 2016, 5, 1082. [Google Scholar] [CrossRef] [Green Version]
- Andayani, P. The effect of social media for a Zika virus transmission with Beddington DeAngelis incidence rate: Modeling and analysis. AIP Conf. Proc. 2019, 2183, 090003. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Din, R. On global dynamics of COVID-19 by using SQIR type model under non-linear saturated incidence rate. Alex. Eng. J. 2021, 60, 393–399. [Google Scholar] [CrossRef]
- Omame, A.; Okuonghae, D. A co-infection model for oncogenic Human Papillomavirus and Tuberculosis with optimal control and Cost-Effectiveness analysis. Optim. Control Appl. Meth. 2021, 42, 1081–1101. [Google Scholar] [CrossRef]
- Samui, P.; Mondal, J.; Khajanchi, S. A mathematical model for COVID-19 transmission dynamics with a case study of India. Chaos Solitons Fractals 2020, 140, 110173. [Google Scholar] [CrossRef] [PubMed]
- Nur, W.; Trisilowati; Suryanto, A.; Kusumawinahyu, W.M. Schistosomiasis model incorporating snail predator as biological control agent. Mathematics 2021, 9, 1858. [Google Scholar] [CrossRef]
- Anggriani, N.; Beay, L.K. Modeling of COVID–19 spread with self–isolation at home and hospitalized classes. Results Phys. 2022, 36, 105378. [Google Scholar] [CrossRef]
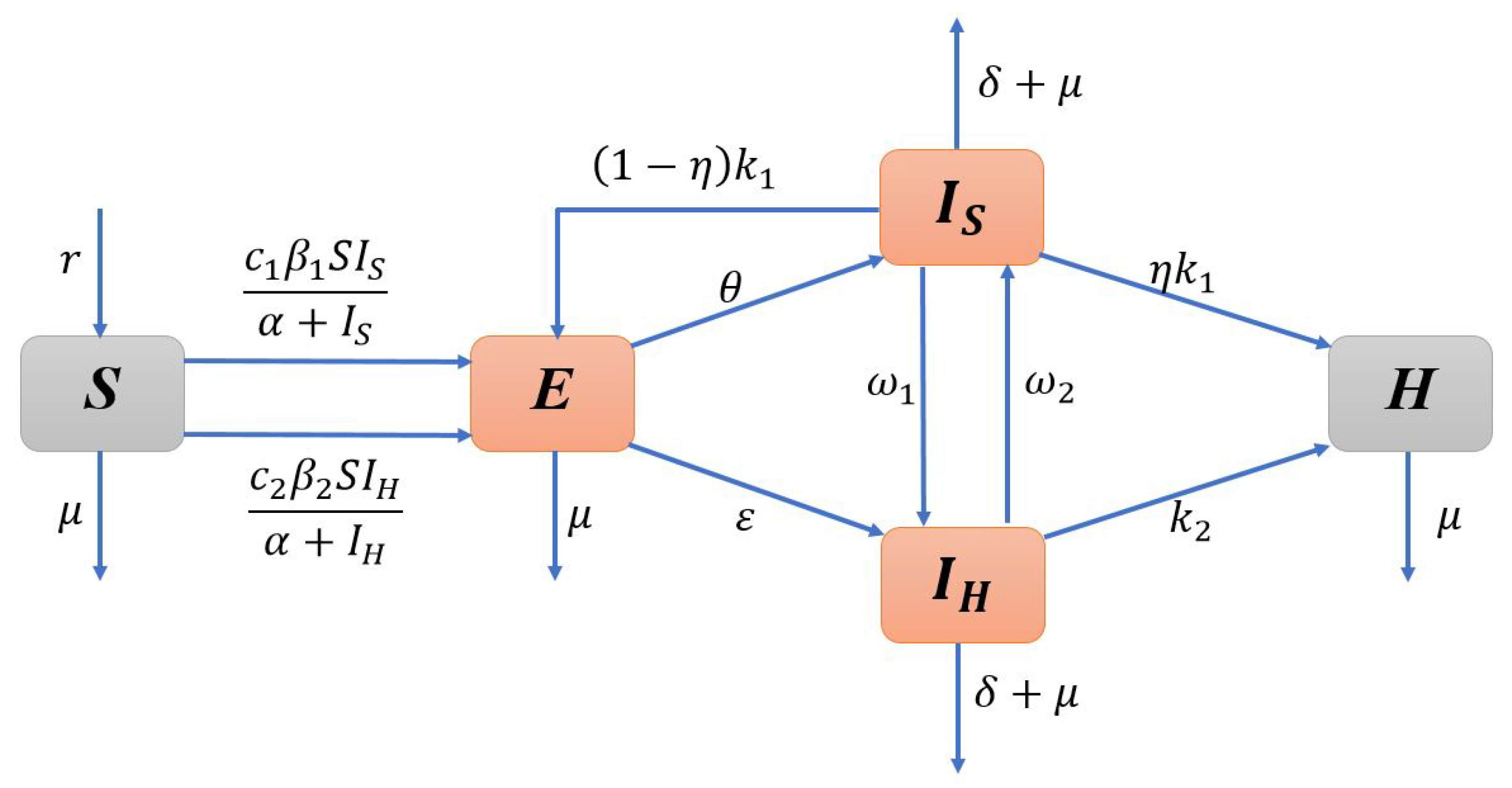




| Notation | Description |
|---|---|
| r | Recruitment rate of susceptible humans |
| Probability of transmission rate due to contact with | |
| Probability of transmission rate due to contact with | |
| Coefficient of maximum contact rate with | |
| Coefficient of maximum contact rate with | |
| A positive constant that represents the intervention levels | |
| Natural mortality rate | |
| Mortality rate induced by disease in the and classes | |
| Progression from E to | |
| Progression from E to | |
| Rate of successful treatment in | |
| Rate of successful treatment in | |
| Progression from to | |
| Progression from to | |
| Coefficient of efficient treatment in |
| Notation | Value | Units |
|---|---|---|
| r | 0.08 | |
| 0.75 | ||
| 0.1 | ||
| 1 | ||
| 0.5 | ||
| 0.5–3.0 | ||
| 0.014 | ||
| 0.2 | ||
| 0.87 | ||
| 0.09 | ||
| 0.09 | ||
| 0.72 | ||
| 0.92 | ||
| 0.069 | ||
| 0.10–1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beay, L.K.; Anggriani, N. Dynamical Analysis of a Modified Epidemic Model with Saturated Incidence Rate and Incomplete Treatment. Axioms 2022, 11, 256. https://doi.org/10.3390/axioms11060256
Beay LK, Anggriani N. Dynamical Analysis of a Modified Epidemic Model with Saturated Incidence Rate and Incomplete Treatment. Axioms. 2022; 11(6):256. https://doi.org/10.3390/axioms11060256
Chicago/Turabian StyleBeay, Lazarus Kalvein, and Nursanti Anggriani. 2022. "Dynamical Analysis of a Modified Epidemic Model with Saturated Incidence Rate and Incomplete Treatment" Axioms 11, no. 6: 256. https://doi.org/10.3390/axioms11060256
APA StyleBeay, L. K., & Anggriani, N. (2022). Dynamical Analysis of a Modified Epidemic Model with Saturated Incidence Rate and Incomplete Treatment. Axioms, 11(6), 256. https://doi.org/10.3390/axioms11060256






