Abstract
This article demonstrates how the new Double Laplace–Sumudu transform (DLST) is successfully implemented in combination with the iterative method to obtain the exact solutions of nonlinear partial differential equations (NLPDEs) by considering specified conditions. The solutions of nonlinear terms of these equations were determined by using the successive iterative procedure. The proposed technique has the advantage of generating exact solutions, and it is easy to apply analytically on the given problems. In addition, the theorems handling the mode properties of the DLST have been proved. To prove the usability and effectiveness of this method, examples have been given. The results show that the presented method holds promise for solving other types of NLPDEs.
Keywords:
double Laplace–Sumudu transform; single Laplace transform; single Sumudu transform; new iterative method; nonlinear partial differential equations MSC:
26A33; 44A30
1. Introduction
Many nonlinear phenomena are an essential part of applied science and engineering. Nonlinear equations are observed in different types of physics-related problems: fluid dynamics, plasma physics, solid mechanics, quantum field theory, wave propagation in shallow water, and many others. The models are controlled in their range of validity by partial differential equations. The widespread use of these equations is the main reason why mathematicians have become aware of them. Nevertheless, it is neither numerically nor theoretically easy to find a solution to these mathematical problems. In the latest studies, much attention has been paid to obtaining exact or approximate solutions to these types of equations.
It is, therefore, becoming familiar with all analytical and numerical methods and the newly developed methods for solving nonlinear partial differential equations is increasingly important: for example, the Adomian decomposition method [1,2,3,4,5,6,7], the variational iteration method [8,9], the homotopy perturbation method [10], and the reduced differential transform method [11,12,13,14,15,16,17,18,19] and others [19,20,21,22].
Recently, a new double integral transform called DLST has been successfully implemented to solve some integral and partial differential equations [23,24,25,26]. Furthermore, in [27,28,29,30,31,32,33] an attractive formula for the DLST of the Caputo fractional derivative was obtained and used to construct a series for some families of linear fractional differential equations. Unfortunately, this transformation does not solve nonlinear problems or many complex mathematical models like other integral transforms. As a result, some researchers have combined these integral transforms with other methods such as the differential transform method, the homotopy perturbation method, the Adomian decomposition method, and the variational iteration method [34,35,36,37,38,39,40] for solving many nonlinear differential equations.
In the present study, we consider the general nonlinear partial differential equation, which covers the majority of the nonlinear partial differential equations solved in [30,32,33,35,36], of the following form:
with the initial conditions (ICs)
and the conditions
where and are the given coefficients and are positive integers. is nonlinear term, and is the source term in the following form .
The main aim of this study is to use the DLST method, including the new iterative method (NIM) planned by Daftardar-Gejji and Jafari in [39], to seek out an exact solution of the nonlinear partial differential equations of type (1) subject to ICs (2) and the conditions (3). The new iterative method (NIM) has been extensively employed by several researchers for the treatment of linear and nonlinear ordinary and partial differential equations of integer and fractional order (see [41,42,43,44,45]). The advantage of the DLST method coupled with the iterative method is that, compared to other known methods (see [45,46]), it provides fast convergence of the exact solution without any restrictive assumptions about the solution. The aim of this study is to present a faster method to find the exact solution of nonlinear PDE via DLST.
The following things will be discussed in the remaining parts of this paper: Section 2 includes basic definitions, properties, and theorems of the DLST. Section 3 of this paper provides the description of the model and the method for obtaining exact analytical solutions of the given nonlinear PDEs using the DLST coupled with an iterative method. Section 4 shows the application of the proposed method to six illustrative examples in order to show its liability, convergence, and efficiency. Finally, Section 5 contains concluding remarks.
2. Basic Definitions and Theorems
This section covers basic definitions of the DLST for some functions of two variables, the existence and the uniqueness conditions for the DLST, and some properties of the DLST for derivatives. For more details about DLST, see [24,25,26].
Definition 1.
Leta piecewise function defined on a region, then the DLST ofis denoted byand is defined as follows:
where , and and are complex variables, provided that the integral exists.
The relationship below clearly demonstrates the linearity of DLST:
where and are nonzero constants.
Definition 2.
The inverse DLSTis defined by the following.
2.1. Fundamental Properties of the DLST
In Table 1, we introduce the DLST for some functions of two variables, which can be found in [24,25].

Table 1.
The DLST for some functions of two variables [24,25].
2.2. Existence and Uniqueness Conditions for the DLST
If function is of exponential order and at and , then there exist a nonnegative constant such that and ; we have the following:
and we write the following:
as tend to infinity or the following is obtained.
Then, is the exponential order as tend to infinity.
Theorem 1.
(Existence). Letbe defined on regionof exponential orderand, then the DLST ofdefined for all and supplied and .
Proof of Theorem 1.
We find, from definition 1, the following.
Thus, from Equation (7), we obtain the following.
□
Theorem 2.
(Uniqueness). Letandbe the DLST of the continuous functionsanddefined for, , respectively. If, then
In the following arguments, we present some properties of the DLST for derivatives.
2.3. Properties of Derivatives
Let , then the following is the case.
Proof.
In order to prove Equation (8), consider the following.
Let ; thus, we have the following.
For Equation (9), we obtain the following.
Let then
It is simple to demonstrate Equations (10) and (11).
In general, the above results can be extended as follows, and the proof can be shown by mathematical induction.
□
The following results are some properties of the DLST and that can be found in [14,15,16].
Property 1.
(Changing of scale property). If, then we have the following.
Proof.
According to definition 1, the following is the case.
Suppose and in Equation (15), we obtain the following.
□
Property 2.
(First shifting property). If, then the following is obtained.
For proof, see [24].
Property 3.
(Second shifting property). If , then the following is obtained.
For the proof, see [24,25].
Property 4.
(Convolution).
If and
, then the following is the case:
where the following is obtained.
For the proof, see [14,15,17].
3. Principle of the DLST-Iterative (DLST-I) Method
In this section, we introduce a new approach for solving PDEs, which is the DLST-I method. The main idea of this technique is to apply DLST on the given PDE to obtain the equation in a new space. Then, we use the iterative method to decompose nonlinear terms and solve the equation.
Finally, we apply the inverse DLAT to obtain the solution of the target equation in the original space.
Applying DLST on Equation (1), we obtain the following.
Using the single (LT) for ICs (2) and the single (ST) for the conditions in Equation (3), we obtain the following.
By substituting Equation (22) in Equation (21), we have the following.
Simplifying Equation (23), we obtain the following.
Taking the inverse LSTD of Equation (24), we obtain the following.
Now, use the iterative approach by assuming the following.
Substituting Equation (26) in Equation (25), we obtain the following.
is a nonlinear term that can be decomposed into the following.
Substituting Equation (28) in Equation (27), we obtain the following.
Following that, we obtain the recurrence relations as follows.
As a result, we have the series solution of Equation (1), which is stated as follows.
4. Elucidative Examples
In this section, six interesting examples of nonlinear partial differential equations are solved to demonstrate the performance and efficiency of the DLST-I method.
Example 1.
Consider the nonlinear Dissipative wave equation [1]:
with ICs
and the following conditions.
Solution.
Applying the DLST on Equation (34) and the single (LT) on Equation (35) and the single (ST) on Equation (36), we obtain the following.
Taking the inverse DLST on Equation (37), we obtain the following.
Now, using the iterative approach, substitute Equation (26) in Equation (38) and use the formulas in Equations (30)–(32); we obtain the following solution components.
As a result, we have the solution of Equation (34) as follows.
Figure 1 below, shows the solution of the initial value problem (34) and (35).
□
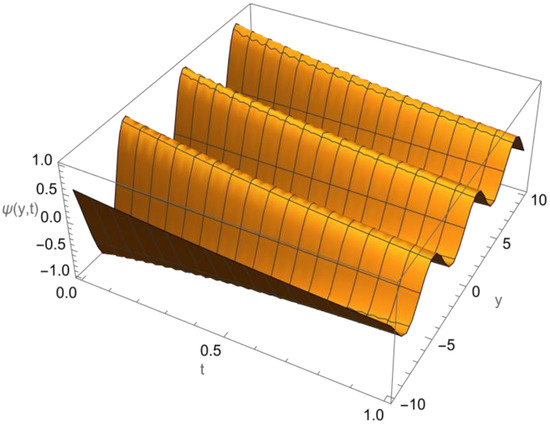
Figure 1.
Exact solution of Example 1.
Example 2.
Consider the following nonhomogeneous KdV equation [5]:
with IC
and the following conditions.
Solution.
Running the DLST on Equation (43) and the single (LT) on Equation (44) and the single (ST) on Equation (45), we obtain the following.
Taking the inverse DLST on Equation (46), we obtain the following.
Using the iterative approach, substitute Equation (26) in Equation (47) and use Formulas (30)–(32); we obtain the following solution components.
As a result, we have the solution of Equation (43) as follows.
Figure 2 below, shows the solution of initial value problem (43) and (44).
□
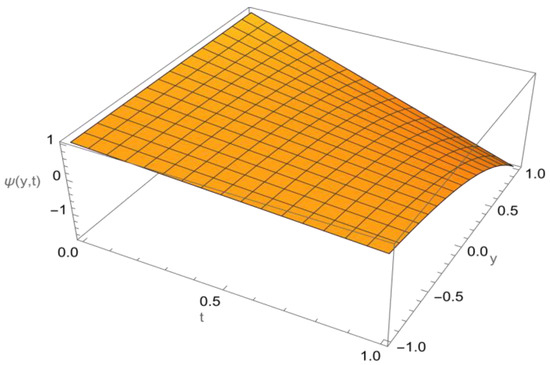
Figure 2.
Exact solution of Example 2.
Example 3.
Consider the non-homogeneous advection problem [35]:
with IC.
Solution.
Taking the DLST on Equation (52) and the single (LT) on Equation (53), we obtain the following.
Taking the inverse DLST on Equation (54), we obtain the following.
Now, using the iterative approach, substitute Equation (26) in Equation (55) and use Formulas (30)–(32); we obtain the following solution components.
As a result, we have the solution of Equation (52) as follows.
Figure 3 below, shows the solution of initial value problem (52) and (53).
□
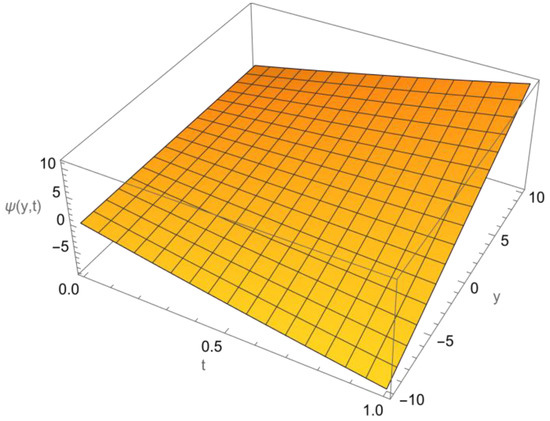
Figure 3.
Exact solution of Example 3.
Example 4.
Consider the nonlinear Klein–Gordon equation [46]:
with the ICs
and the conditions.
Solution.
Running DLST on Equation (60) and the single (LT) on Equation (61) and the single (ST) on Equation (62), we obtain the following.
Taking the inverse DLST on Equation (63), we obtain the following.
Using the iterative approach, substitute Equation (26) in Equation (64) and use Formulas (30)–(32); we obtain the following solution components.
As a result, we have the solution of Equation (60) as follows.
Figure 4 below, shows the solution of initial value problem (60) and (61).
□
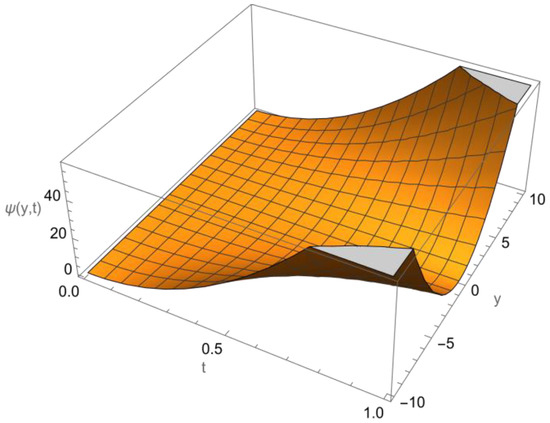
Figure 4.
Exact solution of Example 4.
Example 5.
Consider the nonhomogeneous fifth order KdV equation [6]:
with the IC
and the conditions.
Solution.
Running the DLST on Equation (69) and the single (LT) on Equation (70) and the single (ST) on Equation (71), we obtain the following.
Taking the inverse DLST on Equation (72), we obtain the following.
Using the iterative approach, substitute Equation (26) in Equation (73) and use Formulas (30)–(32), we obtain the following solution components.
As a result, we have the solution of Equation (69) as follows
Figure 5 below, shows the solution of initial value problem (69) and (70).
□
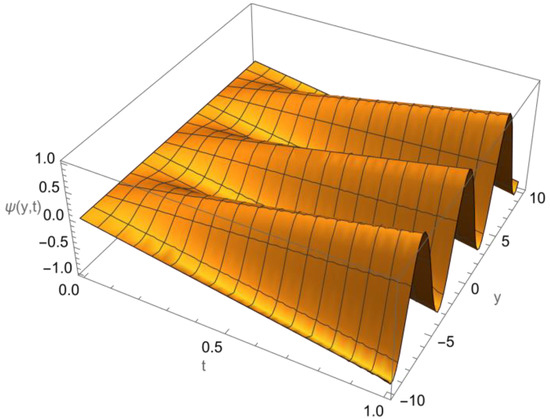
Figure 5.
Exact solution of Example 5.
Example 6.
Consider the following non-linear telegraph equation [45]:
with the ICs
and the conditions.
Solution.
Applying the DLST on Equation (78) and the single (LT) on Equation (79) and the single (ST) on Equation (80), we obtain the following.
Taking the inverse DLST on Equation (81), we obtain the following.
Using the iterative approach substitute Equation (26) in Equation (82) and Formulas (30)–(32), we obtain the following solution components.
As a result, we have the solution of Equation (78) as follows.
Figure 6 below, shows the solution of initial value problem (78) and (79).
□
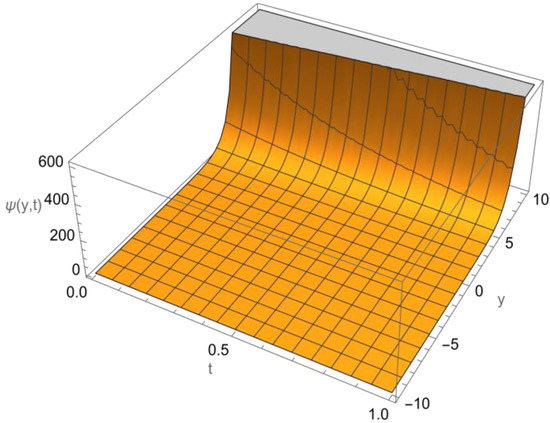
Figure 6.
Exact solution of Example 6.
5. Conclusions
In this paper, we presented a new method—that is, a combination of the double Laplace–Sumudu transform and a numerical method, which is known as an iterative method, to obtain the exact solutions of the nonlinear partial differential equations with initial conditions, which are widely used in mathematical physics. Six examples are given to demonstrate the applicability of the method under consideration. The suggested method’s answers to Examples 1, 2, 3, 4, 5, and 6 are in good agreement with the same problem examined in [40,42,45,46], and nontrivial problems treated using earlier approaches become trivial in the sense that the following decomposition:
consists of a single term, i.e., . We concluded from our research that using the double Laplace–Sumudu transform in combination with the iterative method yields very practical analytical findings with less computational work.
Author Contributions
Data curation, R.S., S.A.A. and A.Q.; formal analysis, S.A.A., R.S. and A.Q.; investigation, S.A.A., R.S. and A.Q.; methodology, S.A.A., R.S. and A.Q.; project administration, A.Q., R.S. and S.A.A.; resources, S.A.A., R.S. and A.Q.; writing—original draft, A.Q., R.S. and S.A.A.; writing—review and editing, S.A.A., R.S. and A.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors express their gratitude to the dear referees, who wish to remain anonymous, and the editor for their helpful suggestions, which improved the final version of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Adomian, G. A review of the decomposition method and some recent results for nonlinear equations. Math. Comput. Model. 1990, 13, 17–43. [Google Scholar] [CrossRef]
- Adomian, G. Nonlinear dissipative wave equations. Appl. Math. Lett. 1998, 11, 125–126. [Google Scholar] [CrossRef][Green Version]
- Kaya, D. A new approach to solve a nonlinear wave equation. Bull. Malays. Math. Soc. 1998, 21, 95–100. [Google Scholar]
- Kaya, D.; Inc, M. On the solution of the nonlinear wave equation by the decomposition method. Bull. Malays. Math. Soc. 1999, 22, 151–155. [Google Scholar]
- Kaya, D.; Aassila, M. An application for a generalized KdV equation by the decomposition method. Phys. Lett. A 2002, 299, 201–206. [Google Scholar] [CrossRef]
- Kaya, D. An explicit and numerical solutions of some fifth-order KdV equation by decomposition method. Appl. Math. Comput. 2003, 144, 353–363. [Google Scholar] [CrossRef]
- Pamuk, S. Solution of the porous media equation by Adomian’s decomposition method. Phys. Lett. A 2005, 344, 184–188. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The variational iteration method: A reliable analytic tool for solving linear and nonlinear wave equations. Comput. Math. Appl. 2007, 54, 926–932. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The variational iteration method: A powerful scheme for handling linear and nonlinear diffusion equations. Comput. Math. Appl. 2007, 54, 933–939. [Google Scholar] [CrossRef]
- Rafei, M.; Ganji, D.D. Explicit solutions of Helmholtz equation and fifth-order KdV equation using homotopy perturbation method. Int. J. Nonlinear Sci. Numer. Simul. 2006, 7, 321–329. [Google Scholar] [CrossRef]
- Keskin, Y.; Oturanc, G. Reduced differential transform method for solving linear and nonlinear wave equations. Iran. J. Sci. Technol. Trans. A 2010, 34, 113–122. [Google Scholar]
- Keskin, Y.; Oturanc, G. Reduced differential transform method for generalized KdV equations. Math. Comput. Appl. 2010, 15, 382–393. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D.; Zarghami Vahid, K.; Mobayen, S. A general fractional formulation and tracking control for immunogenic tumor dynamics. Math. Methods Appl. Sci. 2022, 45, 667–680. [Google Scholar] [CrossRef]
- Khater, M. Diverse bistable dark novel explicit wave solutions of cubic–quintic nonlinear Helmholtz model. Mod. Phys. Lett. B 2021, 35, 2150441. [Google Scholar] [CrossRef]
- Saadeh, R. Numerical algorithm to solve a coupled system of fractional order using a novel reproducing kernel method. Alex. Eng. J. 2021, 60, 4583–4591. [Google Scholar] [CrossRef]
- Saadeh, R.; Ghazal, B. A new approach on transforms: Formable integral transform and its applications. Axioms 2021, 10, 332. [Google Scholar] [CrossRef]
- Khater, M.; Lu, D. Analytical versus numerical solutions of the nonlinear fractional time–space telegraph equation. Mod. Phys. Lett. B 2021, 35, 2150372. [Google Scholar] [CrossRef]
- Erturk, V.S.; Godwe, E.; Baleanu, D.; Kumare, P.; Asadf, J.; Jajarmig, A. Novel fractional-order Lagrangian to describe motion of beam on nanowire. Acta Phys. Pol. A 2021, 140, 265–272. [Google Scholar] [CrossRef]
- Qazza, A.; Burqan, A.; Saadeh, R. A new attractive method in solving families of fractional differential equations by a new transform. Mathematics 2021, 9, 3039. [Google Scholar] [CrossRef]
- Burqan, A.; Saadeh, R.; Qazza, A. A novel numerical approach in solving fractional neutral pantograph equations via the ARA integral transform. Symmetry 2022, 14, 50. [Google Scholar] [CrossRef]
- Baleanu, D.; Ghassabzade, F.; Nieto, J.J.; Jajarmi, A. On a new and generalized fractional model for a real cholera outbreak. Alex. Eng. J. 2022, 61, 9175–9186. [Google Scholar] [CrossRef]
- Khater, M.A. Diverse solitary and Jacobian solutions in a continually laminated fluid with respect to shear flows through the Ostrovsky equation. Mod. Phys. Lett. B 2021, 35, 2150220. [Google Scholar] [CrossRef]
- Sakamoto, K.; Yamamoto, M. Initial value boundary value problems for fractional diffusion wave equations and applications to some inverse problems. J. Math. Anal. Appl. 2011, 382, 426–447. [Google Scholar] [CrossRef]
- Ahmed, S.; Elzaki, T.; Elbadri, M.; Mohamed, M.Z. Solution of partial differential equations by new double integral transform (Laplace-Sumudu transform). Ain Shams Eng. J. 2021, 12, 4045–4049. [Google Scholar] [CrossRef]
- Ahmed, S.; Elzaki, T.; Hassan, A.A. Solution of integral differential equations by new double integral transform (Laplace-Sumudu transform). J. Abstr. Appl. Anal. 2020, 2020, 4725150. [Google Scholar] [CrossRef]
- Ahmed, S. Applications of new double integral transform (Laplace-Sumudu transform) in mathematical physics. J. Abstr. Appl. Anal. 2021, 2021, 6625247. [Google Scholar] [CrossRef]
- Elzaki, T.; Ahmed, S.; Areshi, M.; Chamekh, M. Fractional partial differential equations and novel double integral transform. J. King Saud Univ. Sci. 2022, 34, 101832. [Google Scholar] [CrossRef]
- Baleanu, D.; Hassan Abadi, M.; Jajarmi, A.; Zarghami Vahid, K.; Nieto, J.J. A new comparative study on the general fractional model of COVID-19 with isolation and quarantine effects. Alex. Eng. J. 2022, 61, 4779–4791. [Google Scholar] [CrossRef]
- Khater, M.A. Abundant breather and semi-analytical investigation: On high-frequency waves’ dynamics in the relaxation medium. Mod. Phys. Lett. B 2021, 35, 2150372. [Google Scholar] [CrossRef]
- Mishra, H.K.; Nagar, A.K. He-Laplace method for linear and nonlinear partial differential equations. J. Appl. Math. 2012, 2012, 180315. [Google Scholar]
- Hamza, A.E.; Elzaki, T. Application of homotopy perturbation and Sumudu Transform Method for Solving Burgers Equations. Am. J. Theor. Appl. Stat. 2015, 4, 480–483. [Google Scholar] [CrossRef]
- Hilal, E.; Elzaki, T. Solution of nonlinear partial differential equations by new Laplace variational iteration method. J. Funct. Spaces 2014, 2014, 790714. [Google Scholar] [CrossRef]
- Khater, M.A. Abundant wave solutions of the perturbed Gerdjikov–Ivanov equation in telecommunication industry. Mod. Phys. B 2021, 35, 2150456. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D.; Zarghami Vahid, K.; Mohammadi Pirouz, H.; Asad, J.H. A new and general fractional Lagrangian approach: A capacitor microphone case study. Results Phys. 2021, 31, 104950. [Google Scholar] [CrossRef]
- Khan, Y.; Wu, Q. Homotopy perturbation transform method for nonlinear equations using He’s polynomials. Comput. Math. Appl. 2011, 61, 1963–1967. [Google Scholar] [CrossRef]
- Eltayeb, H.; Kilicman, A. A note on double Laplace transform and telegraphic equations. Abstr. Appl. Anal. 2013, 2013, 932578. [Google Scholar] [CrossRef]
- Dhunde, R.R.; Waghamare, G.L. Double Laplace iterative method for solving nonlinear partial differential equations. New Trends Math. Sci. 2019, 7, 138–149. [Google Scholar] [CrossRef]
- Eltayeb, H. A note on double Laplace decomposition method and nonlinear partial differential equations. New Trends Math. Sci. 2017, 5, 156–164. [Google Scholar] [CrossRef]
- Gejji, V.D.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]
- Ali, L.; Islam, S.; Gul, T.; Amiri, I.S. Solution of nonlinear problems by a new analytical technique using Daftardar-Gejji and Jafari polynomials. Adv. Mech. Eng. 2019, 11, 1687814019896962. [Google Scholar] [CrossRef]
- AL-Jawary, M.A.; Radhi, G.H.; Ravnik, J. Daftardar—Jafari method for solving nonlinear thin film flow problem. Arab. J. Basic Appl. Sci. 2018, 25, 20–27. [Google Scholar] [CrossRef]
- AL-Jawary, M.A. Analytic solutions for solving fourth-order parabolic partial differential equations with variable coefficients. Int. J. Adv. Sci. Tech. Res. 2015, 3, 531–535. [Google Scholar]
- Al-luhaibi, M.S. New iterative method for fractional gas dynamics and coupled Burger’s equations. Sci. World J. 2015, 2015, 153124. [Google Scholar] [CrossRef] [PubMed]
- Dhunde, R.R.; Waghamare, G.L. Double Laplace transform combined with iterative method for solving non-linear telegraph equation. J. Indian Math. Soc. 2016, 83, 221–230. [Google Scholar]
- Dhunde, R.R.; Waghamare, G.L. Analytical solution of the nonlinear Klein-Gordon equation using double Laplace transform and iterative method. Am. J. Comput. Appl. Math. 2016, 6, 195–201. [Google Scholar]
- Wazwaz, A.M. Partial Differential Equations and Solitary Wave’s Theory; Springer: New York, NY, USA; NDordrecht, The Netherlands; Berlin/Heidelberg, Germany, 2009. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).