Retrial Queuing-Inventory Systems with Delayed Feedback and Instantaneous Damaging of Items

Abstract

This paper studies a Markov model of a queuing-inventory system with primary, retrial, and feedback customers. Primary customers form a Poisson flow, and if an inventory level is positive upon their arrival, they instantly receive the items. If the inventory level is equal to zero upon arrival of a primary customer, then this customer, according to the Bernoulli scheme, either leaves the system or goes into an infinite buffer to repeat their request in the future. The rate of retrial customers is constant, and if the inventory level is zero upon arrival of a retrial customer, then this customer, according to the Bernoulli scheme, either leaves orbit or remains in orbit to repeat its request in the future. According to the Bernoulli scheme, each served primary or retrial customer either leaves the system or feedbacks into orbit to repeat their request. Destructive customers that form a Poisson flow cause damage to items. Unlike primary, retrial, and feedback customers, destructive customers do not require items, since, upon arrival of such customers, the inventory level instantly decreases by one. The system adopted one of two replenishment policies: (s, Q) or (s, S). In both policies, the lead time is a random variable that has an exponential distribution. It is shown that the mathematical model of the system under study was a two-dimensional Markov chain with an infinite state space. Algorithms for calculating the elements of the generating matrices of the constructed chains were developed, and the ergodicity conditions for both policies were found. To calculate the steady-state probabilities, a matrix-geometric method was used. Formulas were found for calculating the main performance measures of the system. The results of the numerical experiments, including the minimization of the total cost, are demonstrated.

1. Introduction

Queues in which primary customers find all of the servers busy and/or the waiting room occupied and either go to orbit to try again to obtain a service after a random period of time or leave the system forever are called retrial queues (RQs). RQ models have been studied in detail in a large number of works. For a comprehensive survey and a list of references in this field, see [1,2].

Another frequently caused phenomenon in queuing systems is feedback. Queues in which each a serviced customer joins the system either with a certain probability or leaves forever with complementary probability are called queues with feedback (QFB). If the feedback customers return to the system immediately after the completion of the service, then this system is called a queue with instantaneous feedback (QwIFB); otherwise, if feedback customers return to the system after a certain delay, then this system is called a queue with delayed feedback (QwDFB). Note that in practice, there are queues with both kinds of feedback. In other words, in some queues, some of the feedback customers join the system immediately after completion of the service and some of the other feedback customers join the system after a certain delay, i.e., after completion of the service, some customers go to virtual orbit for “thinking” before coming back to obtain additional service. Some QFBs might impose restrictions on the number of feedbacks, i.e., there are queues with single and multiple feedbacks. A QFB is often caused in computer systems with a round-robin discipline, in communication networks with retransmission of erroneous data (packets), in manufacturing with the rework of defectively produced items, etc. For state-of-the-art theory on QFB, see [3,4,5,6,7,8,9,10,11,12,13] and their references.

Over the last decade, many researchers investigated models of retrial queues with delayed feedback (RQwDFB), i.e., queues in which both retrial and feedback phenomena are combined, see [14,15,16,17,18,19,20]. For a detailed review of works devoted to RQwDFB, see [21] and its reference list.

Note that feedback is also a common issue in queuing-inventory systems (QIS), as customers will return to purchase inventory after consuming items that were previously purchased. In other words, the period of time that the customer uses to consume the items might be considered as the sojourn time of the customer in orbit.

A recent detailed review of works in which models of QIS were investigated can be found in [22]. From the indicated review, we can conclude that even though the application of a QIS with delayed feedback (QISwDFB) is very relevant, these models were considered in only a few papers.

It seems that the first time the feedback phenomenon in QIS was introduced was in [23,24]. In [23], the model QISwDFR M/M/1/N/(s, Q)/∞/M with a finite capacity for orbit by feedback customers was considered. Hereinafter, we used modified Kendall notations for symbolical representation of QIS models, which was proposed in [25]. New components were added to the classical Kendall notations to indicate the replenishment policy (RP) in use, the type of cumulative distribution function (CDF) of the inventory’s lifetime (the symbol ∞ in the corresponding position means that items are non-perishable) and the type of CDF of the inventory delivery time (0 in the corresponding position means that the inventory delivery time is zero). The retrial rate of the feedback customers from orbit is a linear function of the number of customers in orbit. A recursive algorithm for calculating the joint probability distribution of the inventory level, the number of customers in orbit, the number of customers in the waiting room, and the status of the server was developed. The main performance measures in the steady-state were derived, and the long-run total expected cost rate was also calculated. The authors derived the Laplace–Stieljes transforms of the waiting time distribution of both the primary as well as the feedback customers. A more complex model of perishable QISwDFB MAP/M/1/N/(s, Q)+(s, S)/M/PH was considered in [24]; here, the symbol “+” indicates that, depending on the state of the system, either the (s, Q) or (s, S) policy was used. To study this system, the MGM was employed, formulas for calculating the performance measures of the system were obtained, and the total cost (TC) minimization problem was solved. A similar model was considered in [26]. Two main differences from the model in [23] are that the orbit capacity is infinite and retrial rate is constant. Here, Neuts’ matrix-geometric method (MGM) [27] was used to analyze the model and both the busy period distribution and the waiting time distribution of primary and feedback customers. In all of these models, the authors assumed that the retrial customer required only the service, and they joined the server if there were no primary customers in the system or if the inventory level was zero, or both.

An important subclass of QIS are systems with perishable inventories in which the lifetime of the items is a finite random variable. For a detailed review of works devoted to QIS with perishable inventories, see review paper [28] and its reference list. Among recent works along this direction, References [29,30,31,32,33,34,35,36] should be noted. For brevity, we did not consider here the results obtained in the indicated papers (for this purpose, see [25]). In a more relevant paper [37], two models of perishable QISwDFB M/M/1/N/(s, Q)/M/M and M/M/1/∞/(s, Q)/M/M were considered. There are three options after the completion of service to the primary customer: (1) the customer leaves the system without purchasing an inventory item; (2) the customer purchases the item and leaves the system; (3) the customer does not purchase the item and joins the orbit for feedback. Probabilities were introduced to evaluate the three indicated options. To calculate the joint probability distribution of the inventory level, the number of customers in orbit, and the number of customers in the queue, the space merging method was developed. The authors assumed that there were several sources for executing the order with different costs and lead times. The problem of minimizing the total cost by choosing a pair of sources and the reorder level was solved.

It is worthy to note that all papers [28,29,30,31,32,33,34,35,36,37] assumed that inventory deteriorates after some random (positive) time. At the same time, in real life, stocks in systems can be instantly destroyed (for example, due to the negligence of warehouse workers or because of technical accidents). In addition, new customers are repeated if there are no stocks at the time of their arrival, and already serviced customers are returned to the system after spending purchased stocks. In other words, models of retrial QISwDFB (RQISwDFB) with instantly damaged items adequately describe many QIS in real life. However, to the best of our knowledge, these models have not been studied in the available literature. Based on these facts, in this paper, the first attempt was made to develop a method for calculating and optimizing the performance measures of such systems under various replenishment policies.

To be more specific, we note that the main differences between the model studied here and the models considered in the literature are as follows:

• In all the known models of QISwDFB, the authors assumed that orbit for repeated customers can be formed only by feedback customers but not by primary customers. We considered a model in which some of the primary customers in some situations (for instance, when an inventory level is zero) might also be going to orbit to repeat their request in the future;
• We propose a model of RQISwDFB in which items might be damaged (destroyed) instantaneously due to the fact of technical reasons;
• We developed a unify method to calculate the performance measures of the proposed models under various replenishment policies.

The paper is organized as follows. In Section 2, we describe the models and formulate the problem. In Section 3, an analysis of the models is carried out using the matrix-geometric method, and the stability conditions under different replenishment policies are derived. Formulas for calculations of the main performance measures are presented in Section 4. A numerical illustration, including the minimization of the total cost, is provided in Section 5. Section 6 concludes the study.

2. Description of Models and Formulation of the Problem

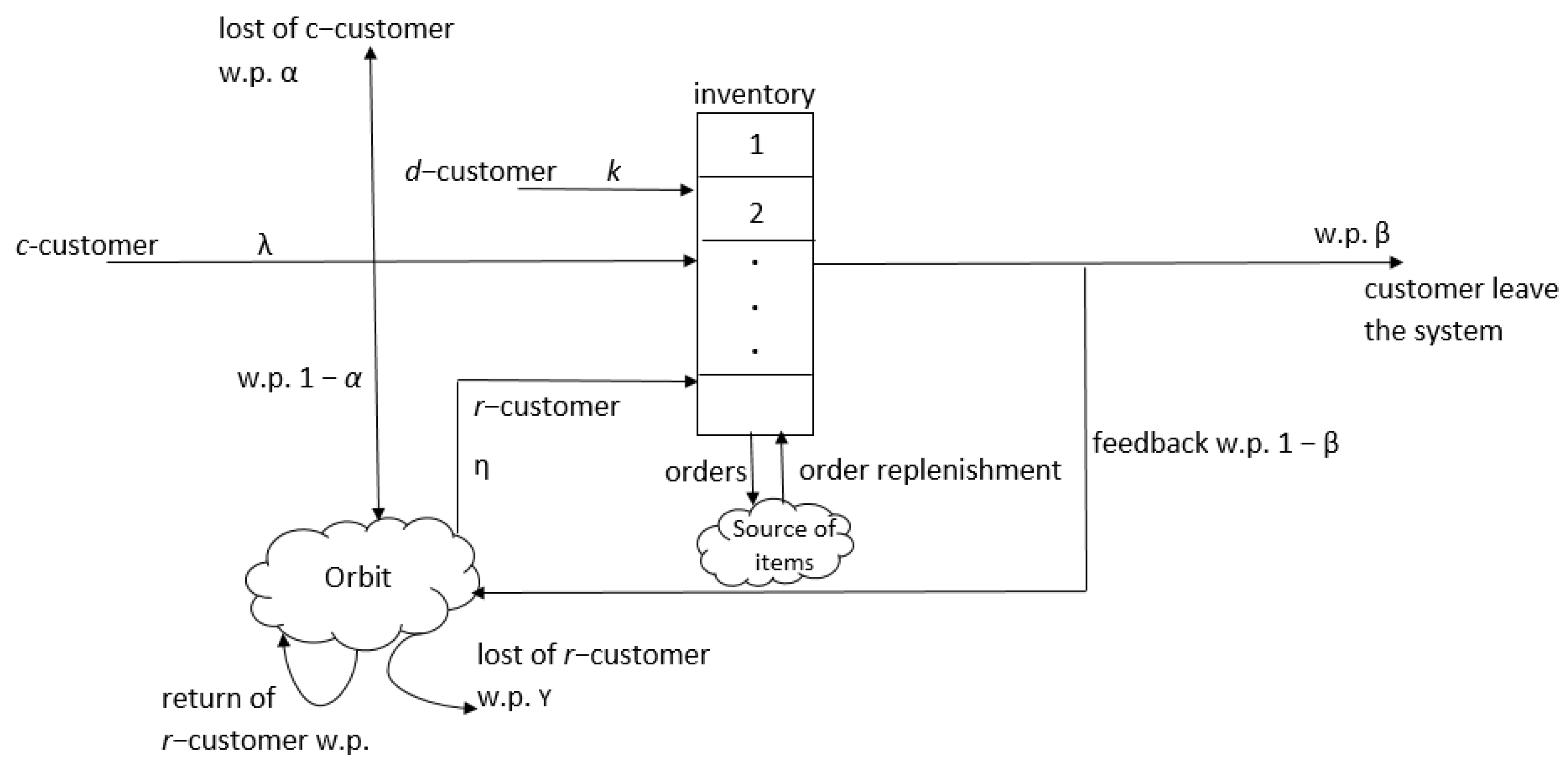
A general block diagram of the studied systems is shown in Figure 1. The proposed model was considered under the following assumptions.

1. We considered QIS with a storage with the maximum capacity S, S < ∞;

2. The flow of primary customers (p-customers) was considered to be Poisson with the parameter λ. For simplicity of presentation, without loss of generality, it was assumed that each p-customer required an item of one size. This means that if at the moment of receipt of the p-customer the inventory level is positive, then they instantly receive the item (i.e., service time is zero) and the inventory level of the system decreases by one. If at the moment of receipt of a p-customer the inventory level is equal to zero, then this customer, according to the Bernoulli scheme, either leaves the system with probability (w.p.) α, or with a complementary probability of 1 – α, it goes to the orbit to repeat its request. The customers in the orbit are called retrial customers (r-customers). The orbit is assumed to be infinite in size;

3. A p-customer that has already received an inventory can demand additional inventory after a positive random time (delayed feedback). More specifically, each served p-customer, according to the Bernoulli scheme, either leaves the system w.p. β permanently, or with a complementary probability of 1 – β, goes to the orbit to repeat its request. Customers that require re-servicing are called feedback customers (f-customers). It is considered that the orbit for r-customers and f-customers is common, and in the orbit, these customers are considered identical. Therefore, further customers in orbit, regardless of their type, are simply called retrial customers. Customers from the orbit arrive with a constant intensity, i.e., the intensity of the arrival of r-customers does not depend on their number in the orbit. This means that only the r-customer at the head of the orbit can repeat the request to obtain the inventory. The time between arrivals of r-customers has an exponential d.f. with parameter η. It is believed that r-customers can repeat their requests many times, i.e., if at the moment of arrival of the r-customers the inventory level is equal to zero, then according to the Bernoulli scheme, they either leave the orbit w.p. γ, or with a complementary probability of 1 – γ, remain in the orbit to repeat their request;

4. A distinctive feature of the studied models is that in addition to p-customers, r-customers, and f-customers, they also contain a flow of destructive customers (d-customers). Unlike p-customers and r-customers, d-customers do not require inventory, but they destroy them, i.e., at the moment d-customers arrive, the inventory level decreases by one. It was assumed that the flow of d-customers is Poisson with the parameter κ. If at the moment of receipt of a d-customer the inventory level is equal to zero, then this customer does not affect the operation of the system;

5. Systems that use one of two replenishment policies (RPs) were studied here: (s, Q) or (s, S) policies. When using the (s, Q) policy, it was assumed that if the inventory level decreases, then an order is made to a higher-level storage to replenish the inventory, while the order volume is constant and equal to Q = S − s; in order to avoid multiple orders, it was considered that s < (S/2). When using the (s, S) policy, it was assumed that if the inventory level drops to s, 0 ≤ s < (S/2), then an order is made to a higher-level storage to replenish the inventory, while at the time of the order’s execution, the stock level of the system reaches the maximal value of S. When both policies are used, the order is completed with a random delay, i.e., the lead time is a random variable having an exponential d.f. with an average value of ν⁻¹.

Our problem has two parts: (1) find the joint distribution of the number of r-customers in the orbit and the inventory level of the system; (2) find the following performance measures of the system: (i) average inventory level; (ii) average order size (if using the (s, S) policy); (iii) average number of r-customers in the orbit; (iv) average reorder rate; (v) average damaging rate of inventory; (vi) loss probability of p-customers; (vii) loss probability of r-customers.

In Section 3 and Section 4, we consider solving problems 1 and 2, respectively.

3. The Proposed Method for Solving the Problem

Let us first consider a case when using the (s, Q) policy. Based on the above assumptions regarding the form of d.f. of random variables participating in the formation of the model, we concluded that the studied QIS is described by a two-dimensional Markov chain (2D MC). At an arbitrary moment in time, the state of this 2D MC is given by the two-dimensional vector $(n,m)$, where the component $n$ indicates the number of r-customers in the orbit, $n=0, 1, \dots$; component $m$ determines the inventory level, $m=0, 1, \dots , S$. This means that the state space of a given 2D MC is defined as follows:

$$E={\displaystyle \underset{n=0}{\overset{\infty }{\cup }}L\left(n\right)},$$

(1)

where $L\left(n\right)=\left\{\left(n, 0\right), \left(n, 1\right), \dots , \left(n, S\right)\right\}$ is called the level $n, n=0, 1, 2, \dots$.

The elements of the generator of the studied 2D MC are indicated by $q\left(\left(n_1,m_1\right), \left(n_2,m_2\right)\right)$, i.e., these values determine the transition rates from state $(n_1,m_1)\in E$ to state $(n_2,m_2)\in E$. These values are determined based on the following arguments. Let the initial state of the system be $(n_1,m_1)\in E$.

• If in the initial state $(n_1,m_1)$ the inventory level is positive (i.e., $m_1>0$), then when a p-customer arrives that does not require repeated servicing and also when a d-customer arrives, the transition to the state $(n_1,m_1-1)$ is made. In other words, there is a transition from the state $(n_1,m_1)$ to state $(n_1,m_1-1)$. In this case, the total rate of such transitions is equal to $\lambda \beta +\kappa$;
• If in the initial state $(n_1,m_1)$ the inventory level is positive (i.e., $m_1>0$), then when a p-customer that requires repeated servicing arrives, a transition is made to the state $(n_1+1,m_1-1)$; the rate of such transitions is equal to $\lambda \left(1-\beta \right)$;
• If in the initial state $(n_1,m_1)$ the inventory level is equal to zero (i.e., $m_1=0$), then when a p-customer w.p. $1-\alpha$ arrives, a transition is made to the state $\left(n_1+1, 0\right)$; the rate of such transitions is equal to $\lambda \left(1-\alpha \right)$;
• If in the initial state $(n_1,m_1)$ the inventory level is positive (i.e., $m_1>0$) and there is at least one r-customer in the orbit (i.e., $n_1>0$), then when an r-customer arrives, a transition is made to the state $(n_1-1,m_1-1)$; the rate of such transitions is equal to $\eta$;
• If in the initial state $(n_1,m_1)$ the inventory level is equal to zero (i.e., $m_1=0$) and there is at least one r-customer in the orbit (i.e., $n_1>0$), then when an r-customer w.p. $\gamma$ arrives, a transition is made to the state $(n_1-1, 0)$; the rate of such transitions is equal to $\eta \gamma$;
• If in the initial state $(n_1,m_1)$ the inventory level is less or equal to $s$ (i.e., $m_1\le s$), then when the order is executed, a transition is made to the state $(n_1,m_1+S-s)$; the rate of such transitions is equal to $\nu$.

Therefore, the positive elements of the generator of the studied 2D MC are calculated from the following relations:

$$q\left(\left(n_1,m_1\right), \left(n_2,m_2\right)\right)=\{\begin{array}{ll}\lambda \beta +\kappa \hfill & \mathrm{if} m_1>0 , \left(n_2,m_2\right)=\left(n_1,m_1-1\right) ,\hfill \\ \eta \hfill & \mathrm{if} n_1{m}_1>0 , \left(n_2,m_2\right)=\left(n_1-1,m_1-1\right) , \hfill \\ \eta \gamma \hfill & \mathrm{if} n_1>0, \left(n_2, 0\right)=\left(n_1-1, 0\right) ,\hfill \\ \lambda \left(1-\alpha \right)\hfill & \mathrm{if} \left(n_2, 0\right)=\left(n_1+1, 0\right) ,\hfill \\ \nu \hfill & \mathrm{if} m_1\le s , \left(n_2,m_2\right)=\left(n_1,m_1+S-s\right) ,\hfill \\ \lambda \left(1-\beta \right)\hfill & \mathrm{if} m_1>0, \left(n_2, m_2\right)=\left(n_1+1, m_1-1\right) . \hfill \end{array}$$

(2)

Next, we renumbered the states from (1) in lexicographic order, i.e., states we renumbered according to the order $\left(0, 0\right), \left(0, 1\right), \dots , \left(0, S\right), \left(1, 0\right), \left(1, 1\right), \dots , \left(1, S\right), \dots$ Then, from relations (2), we concluded that the studied 2D MC is a level-independent quasi-birth–death (LIQBD) process with generator:

$$G=\left(\begin{array}{llllll}B\hfill & A_0\hfill & O\hfill & O\hfill & O\hfill & \dots \hfill \\ A_2\hfill & A_1\hfill & A_0\hfill & O\hfill & O\hfill & \dots \hfill \\ O\hfill & A_2\hfill & A_1\hfill & A_0\hfill & O\hfill & \dots \hfill \\ O\hfill & O\hfill & A_2\hfill & A_1\hfill & A_0\hfill & \dots \hfill \\ O\hfill & O\hfill & O\hfill & A_2\hfill & A_1\hfill & \dots \hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill & \ddots \hfill \end{array}\right)$$

(3)

In (3), by $O$ we denote a null square matrix with a dimension of $S+1$, and $B=\Vert b_{ij}\Vert$ and $A_k =\Vert a_{ij}^{(k)}\Vert , i,j=0, 1, \dots , S,$ are square matrices with the same dimension. From relation (2), we concluded that the elements of the block matrices, $B=\Vert b_{ij}\Vert$ and $A_k =\Vert a_{ij}^{(k)}\Vert , i,j=0, 1, \dots , S,$ are determined by the following relations:

$$b_{ij}=\{\begin{array}{ll}\nu \hfill & \mathrm{if} i\le s, j=i+S-s ,\hfill \\ \lambda \beta +\kappa \hfill & \mathrm{if} i>0, j=i-1 ,\hfill \\ -\left(\nu +\lambda \left(1-\alpha \right)\right)\hfill & \mathrm{if} i=j=0 ,\hfill \\ -\left(\nu +\kappa +\lambda \right)\hfill & \mathrm{if} 0<i\le s, i=j ,\hfill \\ -\left(\kappa +\lambda \right)\hfill & \mathrm{if} s<i\le S , i=j ,\hfill \\ 0\hfill & \mathrm{in} \mathrm{other} \mathrm{cases};\hfill \end{array}$$

(4)

$$a_{ij}^{(0)}=\{\begin{array}{ll}\lambda \left(1-\alpha \right) ,\hfill & i=j=0 ,\hfill \\ \lambda \left(1-\beta \right) ,\hfill & i>0 , j=i-1 ,\hfill \\ 0\hfill & \mathrm{in} \mathrm{other} \mathrm{cases};\hfill \end{array}$$

(5)

$$a_{ij}^{(1)}=\{\begin{array}{ll}\nu \hfill & \mathrm{if} 0\le i\le s, j=i+S-s ,\hfill \\ \lambda \beta +\kappa \hfill & \mathrm{if} i>0, j=i-1 ,\hfill \\ -\left(\nu +\lambda \left(1-\alpha \right)+\eta \gamma \right)\hfill & \mathrm{if} i=j=0 ,\hfill \\ -\left(\nu +\kappa +\lambda +\eta \right)\hfill & \mathrm{if} 0<i\le s, i=j ,\hfill \\ -\left(\kappa +\lambda +\eta \right)\hfill & \mathrm{if} i>s, i=j ,\hfill \\ 0\hfill & \mathrm{in} \mathrm{other} \mathrm{cases} ;\hfill \end{array}$$

(6)

$$a_{ij}^{(2)}=\{\begin{array}{ll}\eta \gamma \hfill & \mathrm{if} i=j=0 ,\hfill \\ \eta \hfill & \mathrm{if} i>1 , j=i-1 ,\hfill \\ 0\hfill & \mathrm{in} \mathrm{other} \mathrm{cases}.\hfill \end{array}$$

(7)

We denote the steady-state probabilities corresponding to the generator $A=A_0+A_1+A_2$ by $\mathbf{\pi }=\left(\pi \left(0\right), \pi \left(1\right), \dots , \pi \left(S\right)\right)$. In other words, the vector $\mathbf{\pi }$ is a solution to the following system of equilibrium equations (SEEs):

$$\mathbf{\pi }A=\mathbf{0}, \mathbf{\pi }\mathit{e}=1$$

(8)

where 0 denotes a null vector row of size S + 1, and e indicates the column vector of size S + 1, all the components of which are equal to 1.

From (5)–(7), we find that the elements of the generator $A =\Vert a_{ij}\Vert , i,j=0, 1, \dots , S,$ are defined as follows:

$$a_{ij}=\{\begin{array}{ll}-\nu \hfill & \mathrm{if} i=j=0 ,\hfill \\ \nu \hfill & \mathrm{if} 0\le i\le s , j=i+S-s ,\hfill \\ \lambda +\kappa +\eta \hfill & \mathrm{if} i>0 , j=i-1 ,\hfill \\ -\left(\lambda +\kappa +\nu +\eta \right)\hfill & \mathrm{if} 0<i\le s , j=i ,\hfill \\ -\left(\lambda +\kappa +\eta \right)\hfill & \mathrm{if} i>s , j=i ,\hfill \\ 0\hfill & \mathrm{in} \mathrm{other} \mathrm{cases}.\hfill \end{array}$$

(9)

Theorem 1.

When using the (s, Q) policy, the system is ergodic if and only if the following condition is satisfied:

$$\lambda \left(\pi \left(0\right)\left(1-\alpha \right)+\left(1-\pi \left(0\right)\right)\left(1-\beta \right)\right)<\eta \left(1-\left(1-\gamma \right)\pi \left(0\right)\right),$$

(10)

$$\begin{array}{l}\pi \left(0\right)={\left({\displaystyle \sum _{i=0}^s{\chi }_i}+\left(S-2s-1\right){\chi }_s+\theta {\displaystyle \sum _{m=S-s}^S{\displaystyle \sum _{i=m-S+s}^s{\chi }_i}}\right)}^{-1};\\ \theta =\frac{\nu }{\lambda +\kappa +\eta } , {\chi }_0=1 , {\chi }_m=\theta {\left(1+\theta \right)}^{m-1}, 1\le m\le s+1 .\end{array}$$

Proof. 

From relation (9), we conclude that SEE (8) has the following form:

For the cases $0\le m\le s:$

$$\left(\nu +\left(\lambda +\kappa +\eta \right)\left(1-{\delta }_{m,0}\right)\right)\pi \left(m\right)=\left(\lambda +\kappa +\eta \right)\pi \left(m+1\right);$$

(11)

For the cases $s+1\le m\le S-s:$

$$\left(\lambda +\kappa +\eta \right)\pi \left(m\right)=\left(\lambda +\kappa +\eta \right)\pi \left(m+1\right);$$

(12)

For the cases $S-s\le m\le S:$

$$\left(\lambda +\kappa +\eta \right)\pi \left(m\right)=\left(\lambda +\kappa +\eta \right)\pi \left(m+1\right)\psi \left(s+1\le m\le S-1\right)+\nu \pi \left(m-S+s\right).$$

(13)

Hereinafter, ${\delta }_{x,y}$ represents the Kronecker symbols, and $\psi \left(A\right)$ is the indicator function of the event A.

The SEEs (11)–(13) can be solved analytically using the recursive method. Thus, taking into account the above notation from Equation (11), we find that $\pi \left(m\right)={\chi }_m\pi \left(0\right) \mathrm{for} 1\le m\le s+1.$ On the other hand, from Equation (12), we find that $\pi \left(m\right)=\pi \left(m+1\right) \mathrm{for} s+1\le m<S-s,$ i.e., $\pi \left(m\right)={\chi }_s\pi \left(0\right) \mathrm{for} s+1\le m<S-s.$ In Equation (13), recurrent procedures are performed starting with the equation for $m=S$, e.g., the equation for the case $m=S$ is taken into account in the equation for the case $m=S-1$. Then, we obtain that $\pi \left(m\right)=\theta {\displaystyle \sum _{i=m-S+s}^s{\chi }_i\pi \left(0\right)} \mathrm{for} S-s\le m\le S.$ In other words, the desired probabilities $\pi \left(m\right), m=1, \dots , S,$ are expressed through $\pi \left(0\right)$as follows:

$$\pi (m)=\{\begin{array}{ll}{\chi }_m\pi \left(0\right) ,\hfill & \mathrm{if} 1\le m\le s ,\hfill \\ {\chi }_s\pi \left(0\right) ,\hfill & \mathrm{if} s+1\le m<S-s ,\hfill \\ \theta {\displaystyle \sum _{i=m-S+s}^s{\chi }_i\pi \left(0\right)} ,\hfill & \mathrm{if} S-s\le m\le S ,\hfill \end{array}$$

(14)

where the unknown probability, $\pi (0)$, is determined from the normalization condition, i.e., $\pi \left(0\right)+\pi \left(1\right)+\dots \pi \left(S\right)=1.$ From (14), we conclude that $\pi (0)$ is determined using relation (10).

Further, according to [27] (pp. 81–83), we conclude that the studied LIQBD is ergodic if and only if the following condition is satisfied:

$$\mathit{\pi }{A}_0\mathit{e}<\mathit{\pi }{A}_2\mathit{e}.$$

(15)

Taking into account (5), (7), and (14), after certain transformations from (15), we obtain that relation (10) is true. The theorem is proved. □

Remark 1.

It is important to note that the found ergodicity condition (10) has an exact probabilistic meaning. Indeed, in inequality (10), the left-hand side is the weighted rate of arrival of p-customers and f-customers into the orbit, and its right-hand side determines the weighted rate of arrival of requests from the orbit. Thus, condition (10) means the following: the weighted total intensity of p-customers and f-customers for the orbit must be less than the weighted intensity of r-customers. Note that condition (10) can be replaced by a rough but, at the same time, easy-to-check condition $\lambda \max \left\{1-\alpha , 1-\beta \right\}<\eta \gamma$. The last condition is obtained by taking into account $\lambda \left(\pi \left(0\right)\left(1-\alpha \right)+\left(1-\pi \left(0\right)\right)\left(1-\beta \right)\right)\le \lambda \max \left\{1-\alpha , 1-\beta \right\}$,$\eta \left(1-\left(1-\gamma \right)\pi \left(0\right)\right)>\eta \gamma .$ In other words, the rough condition also has a probabilistic meaning: the left side is the reachable upper bound of the rate of arrival of p-customers and f-customers into the orbit, and the right side is the unreachable lower bound of the rate of loss of r-customers from the orbit. It is important to note that the resulting rough ergodicity condition does not depend on either the intensity of d-customers or the lead time (we will see later that this condition also does not depend on the accepted RP).

If the ergodicity condition (10) is satisfied, then the steady-state probabilities ${\mathit{p}}_n=\left(p\left(n, 0\right), p\left(n, 1\right), \dots , p\left(n, S\right)\right), n=0, 1, \dots .$, corresponding to the generator, G, are calculated from the following equations:

$${\mathit{p}}_n={\mathit{p}}_0{R}^n, n\ge 1,$$

(16)

where R is the minimal non-negative solution to the following matrix-quadratic equation:

$$R^2{A}_2+R{A}_1+A_0=0.$$

Boundary probabilities, ${\mathit{p}}_0$, are found from the following systems of equations with a normalizing condition:

$$\begin{gathered} {\mathit{p}}_0\left(B+R{A}_2\right)=\mathbf{0} . \\ {\mathit{p}}_0{\left(I-R\right)}^{-1}\mathit{e}=1 , \end{gathered}$$

(17)

where I is the unit matrix of size $S+1$.

Now let us consider the system when using the (s, S) policy. In this model, a 2D MC with a state space (1) also describes the system under study. The generator elements of this 2D MC are defined similarly to (2), with the only difference being the sixth line on the right side of the specified formula, i.e., here the positive values of the indicated quantities are calculated from the following relations:

$$\tilde{q}\left(\left(n_1,m_1\right), \left(n_2,m_2\right)\right)=\{\begin{array}{ll}\lambda \beta +\kappa \hfill & \mathrm{if} m_1>0 , \left(n_2,m_2\right)=\left(n_1,m_1-1\right) ,\hfill \\ \eta \hfill & \mathrm{if} n_1{m}_1>0 , \left(n_2,m_2\right)=\left(n_1-1,m_1-1\right) , \hfill \\ \eta \gamma \hfill & \mathrm{if} n_1>0, \left(n_2, 0\right)=\left(n_1-1, 0\right) ,\hfill \\ \lambda \left(1-\alpha \right)\hfill & \mathrm{if} \left(n_2, 0\right)=\left(n_1+1, 0\right) ,\hfill \\ \nu \hfill & \mathrm{if} m_1\le s , \left(n_2,m_2\right)=\left(n_1,S\right) ,\hfill \\ \lambda \left(1-\beta \right)\hfill & \mathrm{if} m_1>0, \left(n_2, m_2\right)=\left(n_1+1, m_1-1\right) . \hfill \end{array}$$

(18)

From (18), we conclude that this 2D MC is an LIQBD with generator:

$$\tilde{G}=\left(\begin{array}{llllll}\tilde{B}\hfill & A_0\hfill & O\hfill & O\hfill & O\hfill & \dots \hfill \\ A_2\hfill & {\tilde{A}}_1\hfill & A_0\hfill & O\hfill & O\hfill & \dots \hfill \\ O\hfill & A_2\hfill & {\tilde{A}}_1\hfill & A_0\hfill & O\hfill & \dots \hfill \\ O\hfill & O\hfill & A_2\hfill & {\tilde{A}}_1\hfill & A_0\hfill & \dots \hfill \\ O\hfill & O\hfill & O\hfill & A_2\hfill & {\tilde{A}}_1\hfill & \dots \hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill & \ddots \hfill \end{array}\right)$$

(19)

Here, the elements of the matrices $\tilde{B}=\Vert b_{ij}\Vert$ and ${\tilde{A}}_1 =\Vert {\tilde{a}}_{ij}^{(1)}\Vert , i,j=0, 1, \dots , S,$ are determined as follows:

$${\tilde{b}}_{ij}=\{\begin{array}{ll}\nu \hfill & \mathrm{if} i\le s, j=S ,\hfill \\ \lambda \beta +\kappa \hfill & \mathrm{if} i>0, j=i-1 ,\hfill \\ -\left(\nu +\lambda \left(1-\alpha \right)\right)\hfill & \mathrm{if} i=j=0 ,\hfill \\ -\left(\nu +\kappa +\lambda \right)\hfill & \mathrm{if} 0<i\le s, i=j ,\hfill \\ -\left(\kappa +\lambda \right)\hfill & \mathrm{if} s<i\le S , i=j ,\hfill \\ 0\hfill & \mathrm{in} \mathrm{other} \mathrm{cases};\hfill \end{array}$$

(20)

$${\tilde{a}}_{ij}^{(1)}=\{\begin{array}{ll}\nu \hfill & \mathrm{if} 0\le i\le s, j=S ,\hfill \\ \lambda \beta +\kappa \hfill & \mathrm{if} i>0, j=i-1 ,\hfill \\ -\left(\nu +\lambda \left(1-\alpha \right)+\eta \gamma \right)\hfill & \mathrm{if} i=j=0 ,\hfill \\ -\left(\nu +\kappa +\lambda +\eta \right)\hfill & \mathrm{if} 0<i\le s, i=j ,\hfill \\ -\left(\kappa +\lambda +\eta \right)\hfill & \mathrm{if} i>s, i=j ,\hfill \\ 0\hfill & \mathrm{in} \mathrm{other} \mathrm{caes} ;\hfill \end{array}$$

(21)

Let $\tilde{\mathit{\pi }}=\left(\tilde{\pi }\left(0\right), \tilde{\pi }\left(1\right), \dots , \tilde{\pi }\left(S\right)\right)$ be the steady-state probability vector of the generator $\tilde{A}=A_0+{\tilde{A}}_1+A_2$, i.e.,

$$\tilde{\mathit{\pi }}\tilde{A}=\mathbf{0}, \tilde{\mathit{\pi }}\mathit{e}=1$$

(22)

From relations (5), (7), and (21), we conclude that the elements of the generator $\tilde{A}$are determined as follows:

$${\tilde{a}}_{ij}=\{\begin{array}{ll}-\nu \hfill & \mathrm{if} i=j=0 ,\hfill \\ \nu \hfill & \mathrm{if} 0\le i\le s , j=S ,\hfill \\ \lambda +\kappa +\eta \hfill & \mathrm{if} i>0 , j=i-1 ,\hfill \\ -\left(\lambda +\kappa +\nu +\eta \right)\hfill & \mathrm{if} 0<i\le s , j=i ,\hfill \\ -\left(\lambda +\kappa +\eta \right)\hfill & \mathrm{if} i>s , j=i ,\hfill \\ 0\hfill & \mathrm{in} \mathrm{other} \mathrm{cases}.\hfill \end{array}$$

(23)

Theorem 2.

When using the (s, S) policy, the system is ergodic if and only if condition (10) is satisfied, where $\pi \left(0\right)$ is replaced by the following value:

$$\tilde{\pi }(0)={\left({\displaystyle \sum _{m=0}^s{\chi }_m}+\left(S-s\right){\chi }_{s+1}\right)}^{-1} .$$

(24)

Proof. 

From relation (23), we conclude that SEE (22) has the following explicit form:

For the cases $0\le m\le s :$

$$\left(\nu +\left(\lambda +\kappa +\eta \right)\left(1-{\delta }_{m,0}\right)\right)\pi \left(m\right)=\left(\lambda +\kappa +\eta \right)\pi \left(m+1\right) ;$$

(25)

For the cases $s+1\le m\le S :$

$$\left(\lambda +\kappa +\eta \right)\pi \left(m\right)=\left(\lambda +\kappa +\eta \right)\pi \left(m+1\right)\psi \left(s+1\le m\le S-1\right)+\nu {\displaystyle \sum _{m=0}^s\pi \left(m\right)}{\delta }_{m,S}.$$

(26)

As above (see the solution to the SEEs (11)–(13)), the obtained SEEs (25) and (26) can also be solved in a recursive manner. Thus, from Equation (25), we find that $\tilde{\pi }\left(m\right)={\chi }_m\tilde{\pi }\left(0\right) для 1\le m\le s+1.$ On the other hand, from Equation (26) at $m=s+1, \dots , S-1,$ we find that $\tilde{\pi }\left(m\right)=\tilde{\pi }\left(m+1\right)$. In other words, in this case the desired probabilities $\tilde{\pi }\left(m\right), m=1, \dots , S,$ are expressed through $\tilde{\pi }\left(0\right)$ as follows:

$$\tilde{\pi }(m)=\{\begin{array}{ll}{\chi }_m\tilde{\pi }\left(0\right) ,\hfill & \mathrm{if} 1\le m\le s,\hfill \\ {\chi }_{s+1}\tilde{\pi }\left(0\right) ,\hfill & \mathrm{if} s+1\le m\le S,\hfill \end{array}$$

(27)

where the probability $\tilde{\pi }(0)$ is determined from the normalization condition, i.e., $\tilde{\pi }(0)$ is determined from relation (24).

As above, the studied LIQBD is ergodic if and only if condition (15) is satisfied for the vector $\tilde{\mathit{\pi }}$. Then, taking into account (5), (7), and (27), after certain transformations from (15), we obtain that Theorem 2 is true. □

Further, the steady-state probabilities ${\tilde{\mathit{p}}}_n=\left(\tilde{p}\left(n, 0\right), \tilde{p}\left(n, 1\right), \dots , \tilde{p}\left(n, S\right)\right), n=0, 1, \dots .$, corresponding to the generator $\tilde{G}$ are determined similarly to relations (16) and (17).

Calculating the steady-state probabilities of the constructed 2D MCs allows us to determinate the main performance measures of the system when using both replenishment policies. Next, in Section 4, we propose formulas to calculate the indicated measures.

4. Performance Measures

Note that when using the (s, Q) policy, the required quantities are calculated as follows (when using the (s, S) policy, in all formulas the quantities $p\left(n,m\right)$ are substituted by $\tilde{p}\left(n,m\right)$).

• Average inventory level (S_av):

$$S_{av}={\displaystyle \sum _{m=1}^{S}m{\displaystyle \sum _{n=0}^{\infty }p\left(n,m\right)}} ;$$

(28)

• Average number of r-customers in orbit (L_o):

$$L_o={\displaystyle \sum _{n=1}^{\infty }n{\displaystyle \sum _{m=0}^{S}p\left(n,m\right)}} ;$$

(29)

• Average reorder rate (RR):

$$RR=\left(\lambda +\left(s+1\right)\gamma \right){\displaystyle \sum _{n=0}^{\infty }p\left(n,s+1\right)}+\eta {\displaystyle \sum _{n=1}^{\infty }p\left(n,s+1\right)} ;$$

(30)

• Average damaging rate of stocks (DRS):

$$DRS=\kappa \left(1-{\displaystyle \sum _{n=0}^{\infty }p\left(n, 0\right)}\right) ;$$

(31)

• Loss probability of p-customers (P_p):

$$P_p=\alpha {\displaystyle \sum _{n=0}^{\infty }p\left(n, 0\right)} ;$$

(32)

• Loss probability of r-customers (P_r):

$$P_r=\gamma {\displaystyle \sum _{n=1}^{\infty }p\left(n, 0\right)}.$$

(33)

Note that when using the (s, S) policy, the order size is a variable magnitude, and for this policy, we can calculate an average order size (V_av) as follows:

$$V_{av}={\displaystyle \sum _{m=S-s}^{S}m}{\displaystyle \sum _{n=0}^{\infty }\tilde{p}\left(n, S-m\right)}.$$

(34)

5. Numerical Results

Below, we demonstrate the results of numerical experiments that had two goals: one was to study the behavior of performance measures (28)–(34) with respect to changes in the values of the initial parameters, and the other goal was to solve the problem of minimizing the total cost (TC).

Regarding the first goal, we point to the results of the numerical experiments for a hypothetical model, which are shown in

Table 1. Dependence of the performance measures on parameter λ; η = 15, κ = 8, ν = 10, α = 0.4, and β = γ = 0.6.

λ	Sav	Vav	Lo	DRS	Pp	Pr	RR
10	11.7522	2.1573	0.3797	7.8331	0.0083	0.0062	1.021
	10.8955		0.3817	7.8122	0.0094	0.0069	1.1479
11	11.669	2.2882	0.4369	7.8076	0.0096	0.0076	1.0937
	10.7737		0.4398	7.7826	0.0109	0.0086	1.2353
12	11.5862	2.418	0.4997	7.7809	0.0109	0.0091	1.1657
	10.6535		0.5037	7.7513	0.0124	0.0104	1.3219
13	11.5037	2.5469	0.5689	7.7530	0.0123	0.0108	1.2367
	10.5349		0.5744	7.7185	0.0141	0.0124	1.4077
14	11.4218	2.6747	0.6455	7.7240	0.0138	0.0127	1.3068
	10.4180		0.6530	7.6843	0.0158	0.0145	1.4927
15	11.3403	2.8014	0.7308	7.694	0.0152	0.0147	1.3760
	10.3027		0.7409	7.6488	0.0175	0.0169	1.5770
16	11.2595	2.9271	0.8263	7.6630	0.0168	0.0168	1.4444
	10.1890		0.8396	7.6120	0.0193	0.0194	1.6604

,

Table 2. Dependence of the performance measures on parameter η; λ = 20, κ = 8, ν = 10, α = 0.4, and β = γ = 0.6.

η	Sav	Vav	Lo	DRS	Pp	Pr	RR
10	10.9374	3.4280	5.6455	7.5341	0.02329	0.0322	1.7156
	9.7368		4.0258	7.4577	0.02711	0.0376	1.9928
11	10.9381	3.4262	3.4532	7.5335	0.02332	0.0308	1.7143
	9.7397		3.6180	7.4570	0.02714	0.0360	1.9913
12	10.939	3.4244	2.4883	7.533	0.02334	0.0296	1.7130
	9.7424		2.5859	7.4563	0.02718	0.0346	1.9899
13	10.9400	3.4227	1.9454	7.5325	0.02337	0.0285	1.7118
	9.7448		2.0124	7.4557	0.02721	0.0333	1.9885
14	10.9412	3.4211	1.5973	7.532	0.02339	0.0275	1.7106
	9.7471		1.6474	7.4551	0.02724	0.0322	1.9872
15	10.9424	3.4195	1.3550	7.5316	0.02341	0.0266	1.7096
	9.7493		1.3946	7.4546	0.02726	0.0311	1.9859
16	10.9437	3.4180	1.1766	7.5312	0.02343	0.0258	1.7085
	9.7512		1.2091	7.4542	0.02728	0.0302	1.9847

,

Table 3. Dependence of performance measures on parameter κ; λ = 20, η = 15, ν = 10, α = 0.4, β = γ = 0.6.

κ	Sav	Vav	Lo	DRS	Pp	Pr	RR
3	11.2217	2.9860	1.3031	2.8680	0.0176	0.0202	1.7523
	10.1356		1.3315	2.8476	0.0203	0.0234	2.0169
4	11.1650	3.0741	1.3138	3.8127	0.0187	0.0215	1.7435
	10.0564		1.3436	3.7834	0.0216	0.0249	2.0109
5	11.1087	3.1615	1.3238	4.7515	0.01987	0.0227	1.7349
	9.9782		1.3560	4.7121	0.0230	0.0264	2.0048
6	11.0528	3.3482	1.3341	5.6843	0.0210	0.0240	1.7264
	9.9009		1.3686	5.6336	0.0244	0.0279	1.9986
7	10.9974	3.3342	1.3448	6.6111	0.0222	0.0253	1.7179
	9.8246		1.3815	6.5479	0.0258	0.0295	1.9923
8	10.9424	3.4195	1.3550	7.5316	0.0234	0.0266	1.7096
	9.7493		1.3946	7.5446	0.0272	0.0311	1.9859
9	10.8879	3.5041	1.3657	8.4459	0.0247	0.0279	1.7013
	9.6748		1.4079	8.3538	0.0287	0.0327	1.9795

,

Table 4. Dependence of the performance measures on parameter ν; λ = 20, η = 15, κ = 8, α = 0.4, and β = γ = 0.6.

ν	Sav	Vav	Lo	DRS	Pp	Pr	RR
6	9.7263	5.2923	1.7275	6.9079	0.0546	0.0646	1.5301
	8.1746		1.8717	6.6997	0.0650	0.0777	1.8157
7	10.1369	4.6634	1.5793	7.1340	0.0433	0.0506	1.5894
	8.6872		1.6788	6.9738	0.0513	0.0603	1.8779
8	10.4621	4.1631	1.4787	7.3029	0.0348	0.0402	1.6392
	9.1066		1.5500	7.1785	0.0410	0.0477	1.9240
9	10.7254	3.7563	1.4073	7.4317	0.0284	0.0325	1.6765
	9.4553		1.4599	7.3342	0.0332	0.0383	1.9590
10	10.9424	3.4195	1.3550	7.5316	0.0234	0.0266	1.7096
	9.7493		1.3946	7.4546	0.0273	0.0311	1.9859
11	11.124	3.1364	1.3155	7.6103	0.0195	0.0220	1.7377
	10.0001		1.3459	7.5490	0.0225	0.0260	2.0070
12	11.2779	2.8953	1.2852	7.6731	0.0163	0.0184	1.7620
	10.0164		1.3089	7.6239	0.0188	0.0212	2.0236

,

Table 5. Dependence of the performance measures on parameter α; λ = 20, η = 15, κ = 8, ν = 10, and β = γ = 0.6.

α	Sav	Vav	Lo	DRS	Pp	Pr	RR
0	10.9088	3.4590	1.7259	7.5221	0	0.0302	1.7304
	9.7106		1.8545	7.4403	0	0.0356	2.0160
0.2	10.9252	3.4388	1.5183	7.5271	0.0118	0.0286	1.7197
	9.7305		1.5943	7.4478	0.0138	0.0336	2.0005
0.4	10.9424	3.4195	1.3550	7.5316	0.0234	0.0266	1.7096
	9.7493		1.3946	7.4546	0.0273	0.0311	1.9859
0.6	10.9609	3.4013	1.2284	7.5356	0.0348	0.0241	1.7000
	9.7668		1.2433	7.4606	0.0404	0.0280	1.9724
0.8	10.9807	3.3844	1.1321	7.5390	0.0461	0.0207	1.6912
	9.7834		1.1304	7.4657	0.0534	0.0240	1.9601
1	11.0018	3.3692	1.0605	7.5418	0.0573	0.0164	1.6834
	9.7991		1.0478	7.4760	0.0662	0.0188	1.9492

,

Table 6. Dependence of the performance measures on parameter β; λ = 20, η = 15, κ = 8, ν = 10, α = 0.4, and γ = 0.6.

β	Sav	Vav	Lo	DRS	Pp	Pr	RR
0.4	11.6434	2.3403	0.6862	7.7951	0.0102	0.0090	1.1224
	9.4626		4.9466	7.3420	0.0328	0.0445	2.1992
0.6	11.7522	2.1573	0.3797	7.8331	0.0083	0.0061	1.0208
	9.7493		1.3946	7.4546	0.0272	0.0311	1.9859
0.8	11.8572	1.9715	0.1658	7.8701	0.0065	0.0038	0.9172
	10.0492		0.4890	7.5689	0.0216	0.0198	1.7630
1	11.9568	1.7830	0.0081	7.9056	0.0047	0.0019	0.8114
	10.3624		0.0701	7.6833	0.0158	0.0106	1.5302

and

Table 7. Dependence of the performance measures on parameter γ; λ = 20, η = 15, κ = 8, ν = 10, α = 0.4, and β = 0.6.

γ	Sav	Vav	Lo	DRS	Pp	Pr	RR
0	10.908	3.4569	1.6675	7.5230	0.0238	0	1.5353
	9.7125		1.7853	7.4410	0.0279	0	1.7903
0.2	10.9200	3.4431	1.5410	7.5263	0.0237	0.0098	1.5927
	9.7261		1.6247	7.4465	0.0276	0.0116	1.8544
0.4	10.9315	3.4306	1.4382	7.5291	0.0235	0.0187	1.6508
	9.7384		1.4966	7.4508	0.0274	0.0219	1.9196
0.6	10.9424	3.4195	1.3550	7.5316	0.0234	0.0266	1.7096
	9.7493		1.3946	7.4546	0.0272	0.0311	1.9859
0.8	10.9525	3.4097	1.2877	7.5337	0.0233	0.0336	1.7689
	9.7588		1.3134	7.4578	0.0271	0.0391	2.0533
1	10.9618	3.4012	1.2332	7.5355	0.0232	0.0396	1.8288
	9.7671		1.2485	7.4606	0.0269	0.0461	2.1216

. In all experiments, it was assumed that S = 20 and s = 5. In the respective columns of these tables, the top row corresponds to the (s, S) policy and the bottom row to the (s, Q) policy. The values of the initial parameters are indicated after the title of each table.

As a result of the analysis of the data in these tables, it is possible to draw conclusions regarding the behavior of the performance measures (28)–(34). Note that not all of the results of the numerical experiments corresponded to theoretical expectations. Thus, the behavior of function S_av with respect to changing parameter η seems counterintuitive (see Table 2). Indeed, it was theoretically expected that when using both RPs, with an increase in the intensity of r-orders, the average stock level of the system would decrease. However, from Table 2, we conclude that these expectations did not come true; with the growth of parameter η, the function S_av, though at a very low rate, grew. In the same way, it was expected that when using the policy (s, S), the function V_av should increase with an increasing parameter η, but it also decreased at a very low rate. On the other hand, the function V_av decreased because the function S_av increased.

Other theoretically unexpected results were the behavior of function RR with respect to the increase in parameters ν (see Table 4) and γ (see Table 7). Thus, when using both RPs, as these parameters increased, as expected, the function S_av grew, but function RR also grew. However, with the increase in the average inventory level, a decrease in the intensity of reorders was expected. It is important to note that the rates of change of these performance measures were very small values, since changes in their values are often observed in the third decimal place after the decimal point. In other words, these facts can be explained by the accuracy of machine calculations. At the same time, such behavior by these performance measures was observed with a wide range of changes in the initial data of the studied models. The rest of the results confirmed the theoretical expectations.

Let us now consider the second goal of our numerical experiments. Note that in real systems, often only the order point (i.e., parameter s) is the controlled parameter. Based on this fact, the problem of minimizing the TC was solved here by choosing the optimal value of the order point for fixed values of the initial parameters when using both RPs.

The TC is calculated as follows:

$$\mathrm{TC}\left(s\right)=\left(K+c_o{V}_{av}\right)RR\left(s\right)+c_h{S}_{av}\left(s\right)+c_{d}DRS\left(s\right)+c_p\lambda P_p\left(s\right)+c_r\eta P_r\left(s\right)+c_w{L}_o\left(s\right),$$

(35)

where $K$ is the fixed cost of one order; $c_o$ is the cost of one unit of order value; $c_h$ is the storage cost per unit of inventory volume per unit of time; $c_d$ is the cost of damaging one unit of stock; $c_p$ are the penalties for losing one p-customer; $c_r$ are the penalties for losing one r-customer; $c_w$ is the cost per unit of waiting time in the orbit of one r-customer.

The optimization problem is as follows: let all parameters of the model be fixed, except for parameter s, as it is required to find such a value s in order to minimize (35). The minimization problem (35) always has a solution, since the domain of feasible solutions $X=\left\{s:0<s<\left(S/2\right)\right\}$ is a discrete finite set.

The results of solving this problem for the hypothetical model in which S = 16 are shown in

Table 8. Results of the optimization problem; the optimal (minimal) value of the TC is indicated in bold type.

S	TC
	(s, Q) Policy	(s, S) Policy
2	4332	3057
3	4288	2962
4	4277	2918
5	4332	2913
6	4384	2940
7	4470	2994

. Here, the values of the initial parameters of the model and the coefficients in function (35) were chosen as follows:

$$\lambda =10, \kappa =8, \nu =10, \eta =15, \alpha =\beta =\gamma =0.6 ;$$

$$K=100, c_o=100, c_h=100, c_d=150, c_p=120, c_r=1200,c_w=100.$$

It can be seen from Table 8 that the values for TC when using the (s, Q) policy were much larger than when using the (s, S) policy, and the optimal value of parameter s for the (s, Q) policy was equal to four, while for the (s, S) policy it was equal to five.

6. Conclusions

The paper proposed Markovian models of RQISwDFB with a positive lead-time in which two replenishment policies, (s, Q) and (s, S), are used. Three kinds of consumer customers (i.e., primary, retrial, and feedback customers) were considered, and a common and an infinite orbit for retrial and feedback customers were organized. It was assumed that in addition to these customers, there are destructive customers that do not require items, but upon arrival of such a customer, the inventory level instantly decreases by one due to damage to items. Two-dimensional Markov chains that describe the investigated systems were constructed and their ergodicity conditions for both policies were found. The steady-state probabilities and performance measures of the investigated systems were calculated via the matrix-geometric method. Numerical experiments, including the minimization of the total cost, were demonstrated. These models can have application in the mathematical analysis of many physical systems.

As direction of future work, similar models in which the size of damaged items is a random variable with a known CDF could be studied. Another direction is the investigation of these models with MAP (Markov arrival process) flows of primary and retrial customers as well as with PH (phase-type) distribution of service times for customers of different types.