The State of the Art of Data Mining Algorithms for Predicting the COVID-19 Pandemic
Abstract
1. Introduction
2. Related Works
3. Mathematical Epidemiological Models Used in the Prediction of COVID-19
- Equilibrium epidemiological systems. One of the important objectives in the study of a disease is to know if it will persist in a specific population, or if this disease gradually disappears until its eradication [9]. There are two types of equilibrium: Disease-free and Endemic. Disease-free Equilibrium: In this type, the proportion of exposed and infectious individuals is zero so that the disease is eradicated [9,12], that is, this situation occurs when the infectious subpopulations are canceled [13]. Endemic Equilibrium: In this type, the proportion of exposed and infectious individuals is not zero [14]; however, the capacity of the system is stable enough to remain in equilibrium even with small disturbances. These small disturbances cause the epidemiological models to begin to evolve away from a state of infection [9]. In this case, the disease cannot be totally eradicated but remains in the population. The equilibrium in epidemiological systems has been thoroughly analyzed in the research works [12,14,15] where they simulate preventive measures, containment, and the possible impact of a pandemic in the population.
- Basic Reproduction Number. In an epidemic, a very important parameter is the Basic Reproduction Number (R0), it allows us to distinguish between an epidemic state (when the pathological process exceeds the expected contagions and the geographical limits) and an endemic state (when the pathological process remains stationary for an extended period of time). The Basic Reproduction Number is essential to be able to understand the nature of the different diseases and their temporal evolutions [13]. The (R0) is defined as the mean number of secondary infections that occur when an infectious individual is introduced into a susceptible population. It can be represented as R0 [9], that is, the number of individuals to be infected from patient zero. In order to eradicate an infection, it is necessary to reduce the R0 below unity [13]. This is sometimes accomplished through immunization programs, which have the effect of transferring members of the susceptible class (S) to the recovered class (R). The smaller the , the slower the epidemic will evolve. In practice, for a specific real epidemic, observing the epidemic allows us to measure R0 and, them estimate [11].
4. The State of the Art for Predicting the COVID-19 Pandemic Using Data Mining Algorithms
- Prediction with epidemiological models using mathematical algorithms
- Prediction with machine learning and/or data mining algorithms
- COVID-19 Datasets.
4.1. Approach Used for the Papers Selection
4.2. Prediction with Epidemiological Models Using Mathematical Algorithms
4.3. Prediction with Machine Learning and/or Data Mining Algorithms
4.4. Performance Measurement or Evaluation
4.5. COVID-19 Datasets
5. Discussion of the State of the Art
- Explaining and predicting the dynamics of a disease.
- Discovering patterns or extracting relevant information.
- Taking into account that mathematical models (like some data mining tools) has several variations in their complexity.
- Studying the pandemic evolution in the short and medium term
- Predicting values based on historical data.
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, R. Machine Learning and Cognition in Enterprises: Business Intelligence Transformed; Apress: Berkeley, CA, USA, 2017. [Google Scholar] [CrossRef]
- Albahri, A.S.; Hamid, R.A.; Alwan, J.K.; Al-Qays, Z.; Zaidan, A.A.; Zaidan, B.B.; AlAmoodi, A.H.; Khlaf, J.M.; Almahdi, E.M.; Thabet, E.; et al. Role of biological Data Mining and Machine Learning Techniques in Detecting and Diagnosing the Novel Coronavirus (COVID-19): A Systematic Review. J. Med. Syst. 2020, 44, 122. [Google Scholar] [CrossRef] [PubMed]
- Ray, D.; Salvatore, M.; Bhattacharyya, R.; Wang, L.; Du, J.; Mohammed, S.; Purkayastha, S.; Halder, A.; Rix, A.; Barker, D.; et al. Predictions, Role of Interventions and Effects of a Historic National Lockdown in India’s Response to the the COVID-19 Pandemic: Data Science Call to Arms. Harv. Data Sci. Rev. 2020, 1–67. [Google Scholar] [CrossRef]
- Gupta, M.K.; Chandra, P. A comprehensive survey of data mining. Int. J. Inf. Technol. 2020, 12, 1243–1257. [Google Scholar] [CrossRef]
- Smyth, P. Data mining: Data analysis on a grand scale? Stat. Methods Med. Res. 2000, 9, 309–327. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Mehrotra, A.; Agarwal, R. A Review of use of data mining during COVID-19 Pandemic. Turk. J. Comput. Math. Educ. 2021, 12, 4547–4552. [Google Scholar]
- Safdari, R.; Rezayi, S.; Saeedi, S.; Tanhapour, M.; Gholamzadeh, M. Using data mining techniques for fight and control epidemics: A scoping review. Heal. Technol. 2021, 11, 759–771. [Google Scholar] [CrossRef]
- Clement, C.; Ponnusamy, V.; Chandrasekaran, S.; Nandakumar, R. A survery on Mathematical Machine Learning and Deep Learning Models for COVID-19 Transmission and Diagnosis. IEEE Rev. Biomed. Eng. 2022, 15, 325–340. [Google Scholar] [CrossRef]
- Malen, E.E. Modelos Epidemiológicos Y Vacunación: Implementación y Análisis de dos Estrategias de Vacunación en el Modelo SEIR; Grado en Ingeniería Electrónica, Facultad de Ciencia y tecnología/Zientzia eta Teknologia Fakultatea, Universidad del País Vasco: Bizkaia Leioa, Spain, 2020; pp. 1–43. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the Mathematical Theory of epidemics. Proc. R. Soc. London Ser. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Gutiérrez, J.; Varona, J. Análisis de la Posible Evolución de la Epidemia de Coronavirus COVID-19 por Medio de un Modelo SEIR; IMUS: Instituto de Matemáticas de la Universidad de Sevilla: Sevilla, Spain, 2020; pp. 1–14. [Google Scholar]
- Mishra, A.M.; Purohit, S.D.; Owolabi, K.M.; Sharma, Y.D. A nonlinear epidemiological model considering asymptotic and quarantine classes for SARS CoV-2 virus. Chaos Solitons Fractals 2020, 138, 109953. [Google Scholar] [CrossRef]
- Josu, F.P. Puntos de Equilibrio, Estabilidad y Simulación de la Relación Anfitrión-Vector en un Modelo Epidémico; Facultad de Ciencia y tecnología/Zientzia eta Teknologia Fakultatea, Universidad del País Vasco: Bizkaia Leioa, Spain, 2019; pp. 1–43. [Google Scholar]
- Zhang, Z.; Zeb, A.; Alzahrani, E.; Iqbal, S. Crowding effects on the dynamics of COVID-19 mathematical model. Adv. Differ. Equ. A Springer Open J. 2020, 675, 675. [Google Scholar] [CrossRef]
- Kassa, S.M.; Njagarah, J.B.; Terefe, Y.A. Analysis of the mitigation strategies for COVID-19: From mathematical modelling perspective. Chaos Solitons Fractals 2020, 138, 109968. [Google Scholar] [CrossRef] [PubMed]
- Rovira, L.G.; Rodríguez, M.M. Modelos Matemáticos Compartimentales en Epidemiología; de Farmacia, F., Ed.; Universidad de la Laguna (ULL): Santa Cruz de Tenerife, Spain, 2015; pp. 1–28. [Google Scholar]
- Fong, S.J.; Li, G.; Dey, N.; Crespo, R.G.; Herrera-Viedma, E. Composite Monte Carlo decision making under high uncertainty of novel coronavirus epidemic using hybridized deep learning and fuzzy rule induction. Appl. Soft Comput. J. 2020, 93, 106282. [Google Scholar] [CrossRef] [PubMed]
- Soukhovolsky, V.; Kovalev, A.; Pitt, A.; Kessel, B. A new modelling of the COVID 19 pandemic. Chaos Solitons Fractals 2020, 139, 110039. [Google Scholar] [CrossRef] [PubMed]
- Tuli, S.; Tuli, S.; Tuli, R.; Gill, S.S. Predicting the growth and trend of COVID-19 pandemic using machine learning and cloud computing. Internet Things 2020, 11, 100222. [Google Scholar] [CrossRef]
- Noor, S.; Akram, W.; Ahmed, T.; Qurat-Ul-Ain, Q.-U. Predicting COVID-19 Incidence Using Data Mining Techniques: A case study of Pakistan. Brain Broad Res. Artif. Intell. Neurosci. 2020, 11, 168–184. [Google Scholar] [CrossRef]
- Car, Z.; Šegota, S.B.; Anđelić, N.; Lorencin, I.; Mrzljak, V. Modeling the Spread of COVID-19 Infection Using a Multilayer Perceptron. Hindawi. Comput. Math. Methods Med. 2020, 2020, 5714714. [Google Scholar] [CrossRef]
- Ardabili, S.F.; Mosavi, A.; Ghamisi, P.; Ferdinand, F.; Varkonyi-Koczy, A.R.; Reuter, U.; Atkinson, P.M. COVID-19 Outbreak Prediction with Machine Learning. Preprints 2020, 13, 249. [Google Scholar]
- Behnam, A.; Jahanmahin, R. A data analytics approach for COVID-19 spread and end prediction (with a case study in Iran). Modeling Earth Syst. Environ. 2021, 8, 579–589. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Baskonus, H.M.; Prakasha, D.G.; Kumar, P. A new study of unreported cases of 2019-nCOV epidemic outbreaks. Chaos Solitons Fractals 2020, 138, 109929. [Google Scholar] [CrossRef]
- Farooq, J.; Bazaz, M.A. A novel adaptive deep learning model of Covid-19 with focus on mortality reduction strategies. Chaos Solitons Fractals 2020, 138, 110148. [Google Scholar] [CrossRef]
- Arango-Londoño, D.; Ortega-Lenis, D.; Muñoz, E.; Cuartas, D.E.; Caicedo, D.; Mena, J.; Torres, M.; Méndez, F. Predicciones de un modelo SEIR para casos de COVID-19 en Cali, Colombia. Rev. Salud Pública 2020, 22, 1–6. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.-S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Djilali, S.; Ghanbari, B. Coronavirus pandemic: A predictive analysis of the peak outbreak epidemic in South Africa, Turkey, and Brazil. Chaos Solitons Fractals 2020, 138, 109971. [Google Scholar] [CrossRef] [PubMed]
- Russo, L.; Anastassopoulou, C.; Tsakris, A.; Bifulco, G.N.; Campana, E.F.; Toraldo, G.; Siettos, C. Tracing day-zero and forecasting the COVID19 outbreak in Lombardy, Italy: A compartmental modelling and numerical optimization approach. PLoS ONE 2020, 15, e0240649. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, X.; Sun, H.; Tick, G.R.; Wei, W.; Jin, B. Applicability of time fractional derivative models for simulating the dynamics and mitigation scenarios of COVID-19. Chaos Solitons Fractals 2020, 138, 109959. [Google Scholar] [CrossRef]
- Capistrán, M.A.; Capella, A.; Christen, J.A. Forecasting hospital demand during COVID-19 pandemic outbreaks. In CIMAT-CONACYT, UNAM.; Cornell University: Ithaca, NY, USA, 2020; pp. 1–30. Available online: https://arxiv.org/abs/2006.01873 (accessed on 24 February 2021).
- Tan, S.-D.; Chen, L. Real-Time Differential Epidemic Analysis and Prediction for COVID-19 Pandemic; Department of Electrical and Computer Engineering, University of California: San Diego, CA, USA, 2020; pp. 1–9. Available online: https://arxiv.org/abs/2004.06888 (accessed on 1 May 2021).
- Alkahtani, B.S.T.; Alzaid, S.S. A novel mathematics model of COVID-19 with fractional derivative. Stability and numerical analysis. Chaos Solitons Fractals 2020, 138, 110006. [Google Scholar] [CrossRef]
- Hasan, N. A Methodological Approach for Predicting COVID-19 Epidemic Using EEMD-ANN Hybrid Model. Internet Things 2020, 11, 100228. [Google Scholar] [CrossRef]
- Torrealba-Rodriguez, O.; Conde-Gutiérrez, R.; Hernández-Javier, A. Modeling and prediction of COVID-19 in Mexico applying mathematical and computational models. Chaos Solitons Fractals 2020, 138, 109946. [Google Scholar] [CrossRef]
- Saba, A.; Elsheikh, A. Forecasting the prevalence of COVID-19 outbreak in Egypt using on linear autoregressive artificial neural networks. Process Saf. Environ. Prot. 2020, 141, 1–8. [Google Scholar] [CrossRef]
- Kırbaş, I.; Sözen, A.; Tuncer, A.D.; Kazancıoğlu, F. Comparative analysis and forecasting of COVID-19 cases in various European countries with ARIMA, NARNN and LSTM approaches. Chaos Solitons Fractals 2020, 138, 110015. [Google Scholar] [CrossRef]
- Basu, S.; Campbell, R. Going by the numbers: Learning and modeling COVID19 disease dynamics. Chaos, Solitons and Fractals. Nonlinear Sci. Nonequilibrium Complex Phenom. 2020, 138, 110140. [Google Scholar] [CrossRef]
- Chaurasia, V.; Pal, S. Application of machine learning time series analysis for prediction COVID-19 pandemic. Res. Biomed. Eng. Soc. Bras. Eng. Biomed. 2020 2020, 38, 35–47. [Google Scholar] [CrossRef]
- Datilo, P.M.; Ismail, Z.; Dare, J. A Review of Epidemic Forecasting Using Artificial Neural Networks. Int. J. Epidemiol. Res. 2019, 6, 132–143. [Google Scholar] [CrossRef]
- Pal, R.; Sekh, A.A.; Kar, S.; Prasad, D.K. Neural Network Based Country Wise Risk Prediction of COVID-19. Appl. Sci. 2020, 10, 6448. [Google Scholar] [CrossRef]
- Muhammad, L.J.; Islam, M.; Usman, S.S.; Ayon, S.I. Predictive Data Mining Models for Novel Coronavirus (COVID-19) Infected Patients’ Recovery. SN Comput. Sci. A Springer Nat. J. 2020, 1, 1–7. [Google Scholar] [CrossRef]
- Iwendi, C.; Bashir, A.K.; Peshkar, A.; Sujatha, R.; Chatterjee, J.M.; Pasupuleti, S.; Mishra, R.; Pillai, S.; Jo, O. COVID-19 Patient Health Prediction Using Boosted Random Forest Algorithm. Front. Public Health 2020, 8, 357. [Google Scholar] [CrossRef]
- Pasamontes, J.C. 2.7 Evaluación de los Sistemas. In Estrategias de Incorporación de Conocimiento Sintáctico y Semántico en Sistemas de Comprensión de Habla Continua en Español; Colás, J.P., Español, E.D., Eds.; Escuela Técnica Superior de Ingenieros de Telecomunicación: Madrid, Spain, 2001; Volume 12, Available online: http://elies.rediris.es/elies12/cap27.htm (accessed on 8 March 2021).
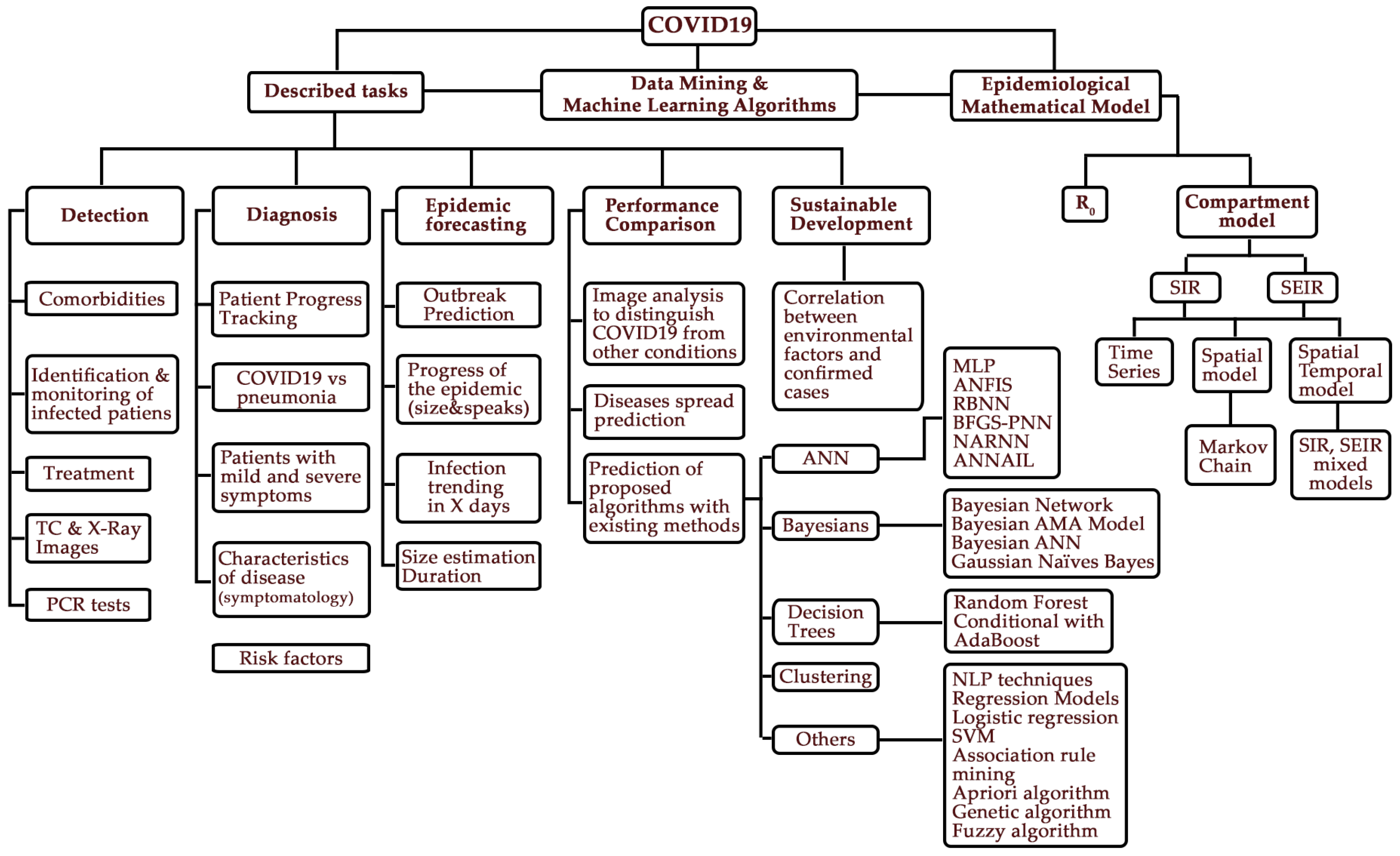
| Model | Estates | Definition | Mathematical Equations | Scheme |
|---|---|---|---|---|
| SIS | S (Susceptible) I (Infected) | A susceptible S (t), when passing to the infected I (t) group, can die as a result of the disease or naturally, but births are considered over time, thus there is a renewal of individuals susceptible to the disease, that is, the number of infected people never reaches the total population N, a balance is maintained between infected individuals with those who are susceptible. | 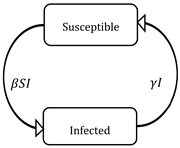 | |
| SIR | S (Susceptible) I (Infected) R (Recovered) | Individuals start out as susceptible S (t) to a given pathogen and, if they become infected I (t) R (t), they progress to the other two states. (1) | 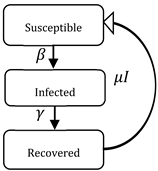 | |
| SEIR | S (Susceptible) E (Exposed) I (Infected) R(Recovered) | The exposed E (t) state is added, in which the disease has a long latency or incubation period, during which it may or may not infect I (t) other, die or recover R (t). | 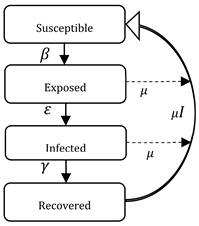 | |
| : Susceptible individuals. : Exposed and in latency individuals. : Infected individuals. : Recovered individuals with immunity. : Total population. | : Time : Average time of infections (for a single individual). : Average incubation time. : Infection rate (probability that a person becomes ill when in contact with an infected person). : Average death rate (probability that an infected individual will die from disease). | |||
| Reference | Country | Task Performed | Epidemiological Mathematical Model | Mathematical Prediction Algorithms |
|---|---|---|---|---|
| [3] | India | Evaluate the effectiveness of protocols | eSIR |
|
| [14] | Pakistan | Predict Growth and Transmission | SIR |
|
| [15] | Botswana South Africa | Predict Growth and Transmission | SSCIRE |
|
| [18] | Russia Israel | Predict Growth and Transmission | SIR |
|
| [19] | India | Predict Growth and Transmission | SIR |
|
| [20] | Pakistan | Spread | SIR |
|
| [21] | Croatia | Spread | SIR |
|
| [22] | Germany | Spread | SIR |
|
| [23] | Iran | Prevalence or Decrease in Spread with respect to other factors | SIRD |
|
| [24] | China India Turkey | Prevalence or Decrease in Spread with respect to other factors | SIRU |
|
| [25] | India | Prevalence or Decrease in Spread with respect to other factors | SIRVD |
|
| Reference | Country | Task Performed | Epidemiological Mathematical Model | Mathematical Prediction Algorithms |
|---|---|---|---|---|
| [12] | India Vietnam Nigeria | Mitigation scenario modeling | SEIR(AQ-I) |
|
| [26] | Colombia | Predictive analysis of the epidemic outbreak | SEIR |
|
| [27] | China | Predictive analysis of the epidemic outbreak | S(in-out) EIR |
|
| [28] | Algeria | Predictive analysis of the epidemic outbreak | SEIR |
|
| [29] | Egypt | Predictive analysis of the epidemic outbreak | SEIIRD |
|
| [30] | USA China | Mitigation scenario modeling | SEIR with a FDE model |
|
| [31] | México | Mitigation scenario modeling | SEIRD |
|
| [32] | USA | Trending of change in disease dynamics | SEIRDP |
|
| [33] | Saudi Arabia | Spread modeling | SIDARTHE |
|
| Reference | Prediction Task Performed | Techniques of Machine Learning or Data Mining |
|---|---|---|
| [3] | Impact of 21-day lockdown on the number of infections |
|
| [11] | Initial Period of an Outbreak |
|
| [19] | Forecast in the growth and transmission of the COVID-19 disease exploring its incidence in 10-day intervals |
|
| [20] | Possible incidence |
|
| [21] | Mining data to predict the spread of a pandemic |
|
| [22,34] | Epidemic forecast |
|
| [23] | Predict the peaks of an outbreak |
|
| [25] | Transmission dynamics and the prevention mechanism of COVID-19 |
|
| [27] | Predict the peaks and amplitude of the epidemic |
|
| [32] | Predict specific risk |
|
| [35] |
| |
| [36] | Evaluate the accumulated data of confirmed cases of COVID-19 in Egypt |
|
| [37] | Modeling of cumulative data of confirmed cases from 8 European countries |
|
| [38] | Assess the effectiveness of mitigation measures |
|
| [39] |
| |
| [40] | Predict the evolution of the COVID-19 pandemic |
|
| [41] |
| |
| [42] | Predict recovery of infected patients |
|
| [43] | Use of geographic and demographic data to predict case severity and possible recovery or death |
|
| References | Performance Measurement or Evaluation. |
|---|---|
| [17,20,36,37,38,39] | Root Mean Square Error (RMSE) |
| [18,19,21,34,35,36] | Coefficient of Determination (R2) |
| [19,22,27,34,37] | Mean Square Error (MSE) |
| [19,37] | Mean Absolute Percentage Error (MAPE) |
| [20,36] | Mean Absolute Error (MAE) |
| [21] | Cross-validation using K-fold algorithm with 5-folds |
| [22] | Correlation Coefficient |
| [31] | Runge-Kutta method |
| [34] | MinMaxScaler |
| [36] | Deviation Ratio (DR) Coefficient of Residual Mass (CRM) |
| [37] | Peak Signal-to-Noise Ratio (PSNR) Normalized Root-Mean-Square Error (NRMSE) Symmetric Mean Absolute Percentage Error (SMAPE) |
| [40] | Sum of Squared Error (SSE) |
| [41] | Bayesian optimization |
| [42,43] | Accuracy |
| [43] | Precision Recall F1 Score |
| Reference | Description | Data Sources |
|---|---|---|
| [3] | Official Data of India | covid19india.org (accessed on 1 May 2021) |
| [3,18,21,34] | Johns Hopkins University Center for Systems Science and Engineering (JHU CSSE) ESRI Living Atlas and the Johns Hopkins University Applied Physics Laboratory (JHU APL) | https://coronavirus.jhu.edu/map.html https://seandavi.github.io/sars2pack/reference/jhu_data.html (accessed on 1 May 2021) |
| [17] | Data from the Chinese Center for Disease Control and Prevention (CDCP) | http://www.chinacdc.cn/en/ (accessed on 1 May 2021) |
| [18,23,39] | OMS Global Data Set. | https://data.humdata.org/dataset/coronavirus-covid-19-cases-and-deaths, 2020 (accessed on 1 May 2021) |
| [19] | Global dataset, with some interactive charts. | Our World in Data de Hannah Ritchie2 https://ourworldindata.org/coronavirus-source-data https://collaboration.coraltele.com/covid/ (accessed on 1 May 2021) |
| [20] | Global data set of time series, confirmed cases, recovered and deaths. | Humandata.org. (accessed on 1 May 2021) |
| [22] | Global data for Italy, Germany, Iran, USA, and China | https://www.worldometers.info/coronavirus/country (accessed on 1 May 2021) |
| [26] | Secretaría de Salud Municipal de Cali. Departamento Administrativo Nacional de Estadística. | https://www.cali.gov.co/salud/publicaciones/152840/boletines-epidemiologicos/ https://www.dane.gov.co/index.php/estadisticas-por-tema/demografia-y-poblacion/proyecciones-de-poblacion (accessed on 1 May 2021) |
| [27] | China National Health Commission. | http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml (accessed on 1 May 2021) |
| [29] | Emphasis was placed on the basic reproduction number R0. | COVID-19 Community Mobility Reports released by Google |
| [31,35] | Secretaría de Salud de México | https://www.gob.mx/salud/documentos/coronavirus-covid-19-comunicado-tecnico-diario-238449 (accessed on 1 May 2021) https://coronavirus.conacyt.mx/proyectos/ama.html (accessed on 1 May 2021) |
| [36] | Official data from the Egyptian Ministry of Health and Population. | https://www.gavi.org/covid19?gclid=CjwKCAjw7J6EBhBDEiwA5UUM2j8GID2GCD588LbiMzU2L1ragN06l1Ct7kSNuxbKX0AuiLUsexiKDhoCxI4QAvD_BwE (accessed on 1 May 2021) |
| [37] | European Center for Disease Prevention and Control. | https://www.ecdc.europa.eu/en/publications-data/download-todays-data-geographic-distribution-covid-19-cases-worldwide (accessed on 1 May 2021) |
| [42] | Korea Centers for Disease and Prevention (KCDC). | http://www.kdca.go.kr/index.es?sid=a3 (accessed on 1 May 2021) |
| [43] | Official Data of South Africa. | https://www.kaggle.com/sudalairajkumar/novel-corona-virus-2019-dataset/ https://github.com/Atharva-Peshkar/Covid-19-Patient-Health-Analytics (accessed on 1 May 2021) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortés-Martínez, K.V.; Estrada-Esquivel, H.; Martínez-Rebollar, A.; Hernández-Pérez, Y.; Ortiz-Hernández, J. The State of the Art of Data Mining Algorithms for Predicting the COVID-19 Pandemic. Axioms 2022, 11, 242. https://doi.org/10.3390/axioms11050242
Cortés-Martínez KV, Estrada-Esquivel H, Martínez-Rebollar A, Hernández-Pérez Y, Ortiz-Hernández J. The State of the Art of Data Mining Algorithms for Predicting the COVID-19 Pandemic. Axioms. 2022; 11(5):242. https://doi.org/10.3390/axioms11050242
Chicago/Turabian StyleCortés-Martínez, Keila Vasthi, Hugo Estrada-Esquivel, Alicia Martínez-Rebollar, Yasmín Hernández-Pérez, and Javier Ortiz-Hernández. 2022. "The State of the Art of Data Mining Algorithms for Predicting the COVID-19 Pandemic" Axioms 11, no. 5: 242. https://doi.org/10.3390/axioms11050242
APA StyleCortés-Martínez, K. V., Estrada-Esquivel, H., Martínez-Rebollar, A., Hernández-Pérez, Y., & Ortiz-Hernández, J. (2022). The State of the Art of Data Mining Algorithms for Predicting the COVID-19 Pandemic. Axioms, 11(5), 242. https://doi.org/10.3390/axioms11050242







