Exponential Multistep Methods for Stiff Delay Differential Equations
Abstract
:1. Introduction
2. Exponential Multistep Methods
2.1. Construction of Exponential Multistep Methods
2.2. Stiff Convergence of Exponential Multistep Methods
3. Exponential Rosenbrock Multistep Methods
3.1. Construction of Exponential Rosenbrock Multistep Methods
3.2. Stiff Convergence of Exponential Rosenbrock Multistep Methods
4. Numerical Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- MacDonals, N. Biological Delay Systems: Linear Stability Theory; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Hu, H. Dynamics of Controlled Mechanical Systems with Delayed Feedback; Springer: New York, NY, USA, 2002. [Google Scholar]
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic: Boston, MA, USA, 1993. [Google Scholar]
- Stépán, G. Retarded Dynamical Systems: Stability and Characteristic Functions; Longman Scientific and Technical: Marlow, NY, USA, 1989. [Google Scholar]
- Hale, J. History of delay equations. In Delay Differential Equations and Applications; Arino, O., Hbid, M., Dads, E.A., Eds.; Springer: Amsterdam, The Netherlands, 2006; pp. 1–28. [Google Scholar]
- Abd-Rabo, M.A.; Zakarya, M.; Cesarano, C.; Aly, S. Bifurcation analysis of time-delay model of consumer with the advertising effect. Symmetry 2021, 13, 417. [Google Scholar] [CrossRef]
- Duary, A.; Das, S.; Arif, M.G.; Abualnaja, K.M.; Khan, M.A.A.; Zakarya, M.; Shaikh, A.A. Advance and delay in payments with the price-discount inventory model for deteriorating items under capacity constraint and partially backlogged shortages. Alex. Eng. J. 2022, 61, 1735–1745. [Google Scholar] [CrossRef]
- Bellen, A.; Zennaro, M. Numerical Methods for Delay Differential Equations; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Certaine, J. The solution of ordinary differential equations with large time constants. In Mathematical Methods for Digital Computers; Ralston, A., Wilf, H., Eds.; Wiley: New York, NY, USA, 1960; pp. 128–132. [Google Scholar]
- Hochbruck, M.; Ostermann, A. Explicit exponential Runge–Kutta methods for semilinear parabolic problems. SIAM J. Numer. Anal. 2005, 43, 1069–1090. [Google Scholar] [CrossRef] [Green Version]
- Hochbruck, M.; Ostermann, A. Exponential Runge–Kutta methods for parabolic problems. Appl. Numer. Math. 2005, 53, 323–339. [Google Scholar] [CrossRef] [Green Version]
- Calvo, M.P.; Palencia, C. A Class of Explicit Multistep Exponential Integrators for Semilinear Problems. Numer. Math. 2006, 102, 367–381. [Google Scholar] [CrossRef]
- Hochbruck, M.; Ostermann, A. Exponential multistep methods of Adams-type. BIT 2011, 51, 889–908. [Google Scholar] [CrossRef] [Green Version]
- Hochbruck, M.; Ostermann, A.; Schweitzer, J. Exponential Rosenbrock-type methods. SIAM J. Numer. Anal. 2009, 47, 786–803. [Google Scholar] [CrossRef]
- Luan, V.T.; Ostermann, A. Exponential Rosenbrock methods of order five—Construction, analysis and numerical comparisons. J. Comput. Appl. Math. 2014, 255, 417–431. [Google Scholar] [CrossRef]
- Luan, V.T.; Ostermann, A. Parallel exponential Rosenbrock methods. Comput. Math. Appl. 2016, 71, 1137–1150. [Google Scholar] [CrossRef]
- Koskela, A.; Ostermann, A. Exponential Taylor methods: Analysis and implementation. Comput. Math. Appl. 2013, 65, 487–499. [Google Scholar] [CrossRef]
- Ostermann, A.; Thalhammer, M.; Wright, W. A class of explicit exponential general linear methods. BIT 2006, 46, 409–431. [Google Scholar] [CrossRef]
- Minchev, B.; Wright, W. A Review of Exponential Integrators for First Order Semi-Linear Problems; Technical Report; Norwegian University of Science and Technology: Trondheim, Norway, 2005. [Google Scholar]
- Zhao, J.; Zhan, R.; Xu, Y. D-convergence and conditional GDN-stability of exponential Runge–Kutta methods for semilinear delay differential equations. Appl. Math. Comput. 2018, 339, 45–58. [Google Scholar] [CrossRef]
- Zhao, J.; Zhan, R.; Xu, Y. Explicit exponential Runge–Kutta methods for semilinear parabolic delay differential equations. Math. Comput. Simul. 2020, 178, 366–381. [Google Scholar] [CrossRef]
- Fang, J.; Zhan, R. High order explicit exponential Runge–Kutta methods for semilinear delay differential equations. J. Comput. Appl. Math. 2021, 388. [Google Scholar] [CrossRef]
- Moler, C.; Loan, C.V. Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later. SIAM Rev. 2003, 45, 3–49. [Google Scholar] [CrossRef]
- Al-Mohy, A.; Higham, N. Computing the action of the matrix exponential, with an application to the exponential integrators. SIAM J. Sci. Comput. 2011, 33, 488–511. [Google Scholar] [CrossRef]
- Jawecki, T. A study of defect-based error estimates for the Krylov approximation of ϕ-functions. Numer. Algorithms 2022, 90, 323–361. [Google Scholar] [CrossRef]
- Li, D.; Yang, S.; Lan, J. Efficient and accurate computation for the ϕ-functions arising from exponential integrators. Calcolo 2022, 59, 1–24. [Google Scholar] [CrossRef]
- Pazy, A. Semigroups of Linear Operators and Applications to Partial Differential Equations; Springer: New York, NY, USA, 1983. [Google Scholar]
- Hairer, E.; Norsett, S.; Wanner, G. Solving Ordinary Differential Equations. I. Nonstiff Problems; Springer Series in Computational Mathematics; Springer: Heidelberg, Germany; New York, NY, USA, 1993. [Google Scholar]
- Ali, K.K.; Mohamed, E.M.; Abd El salam, M.A.; Nisar, K.S.; Khashan, M.M.; Zakarya, M. A collocation approach for multiterm variable-order fractional delay-differential equations using shifted Chebyshev polynomials. Alex. Eng. J. 2022, 61, 3511–3526. [Google Scholar] [CrossRef]
- Ghany, H.A.; Ibrahim, M.Z.N. Generalized solutions of wick-type stochastic KdV-Burgers equations using exp-function method. Int. Rev. Phys. 2014, 8. [Google Scholar]
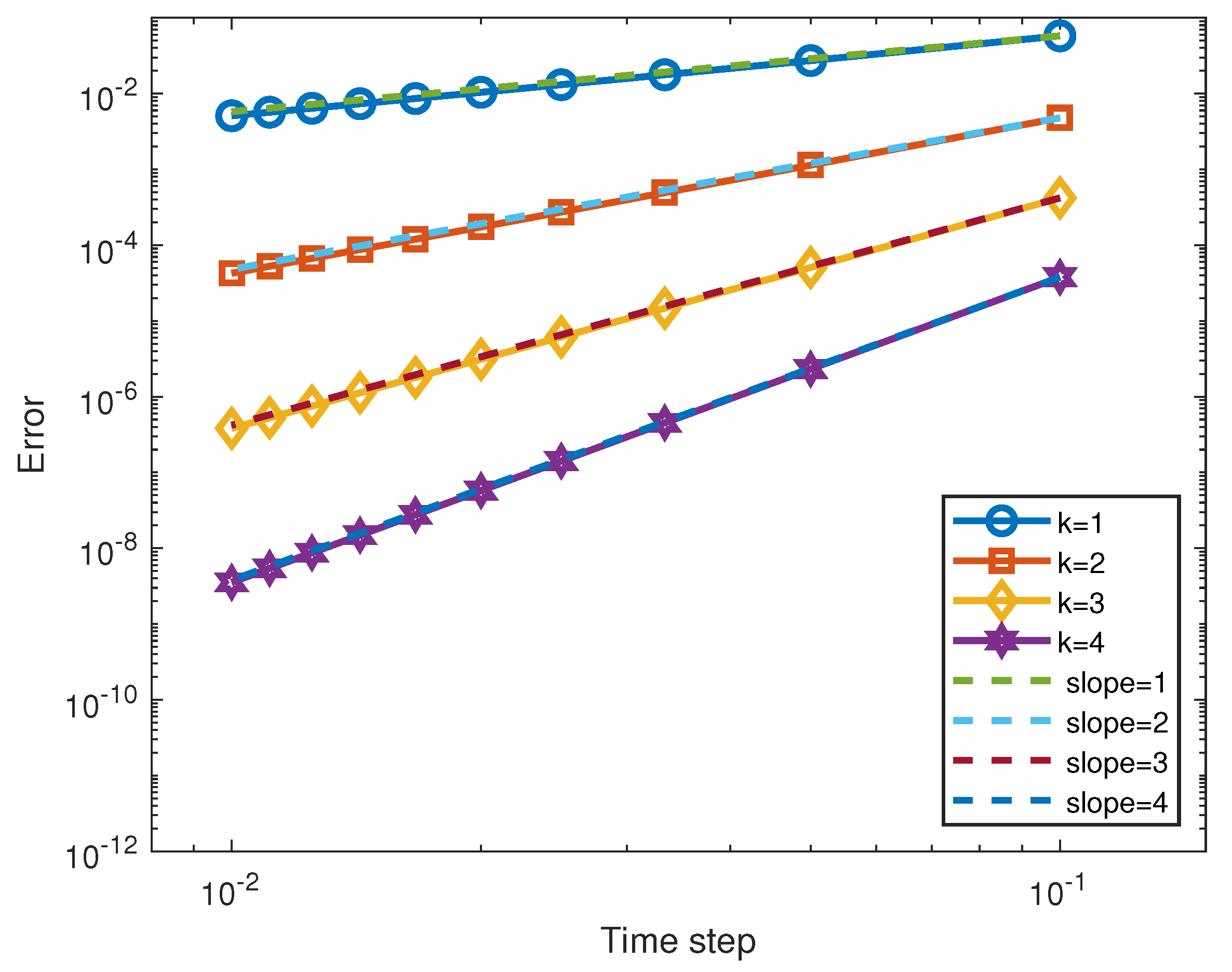


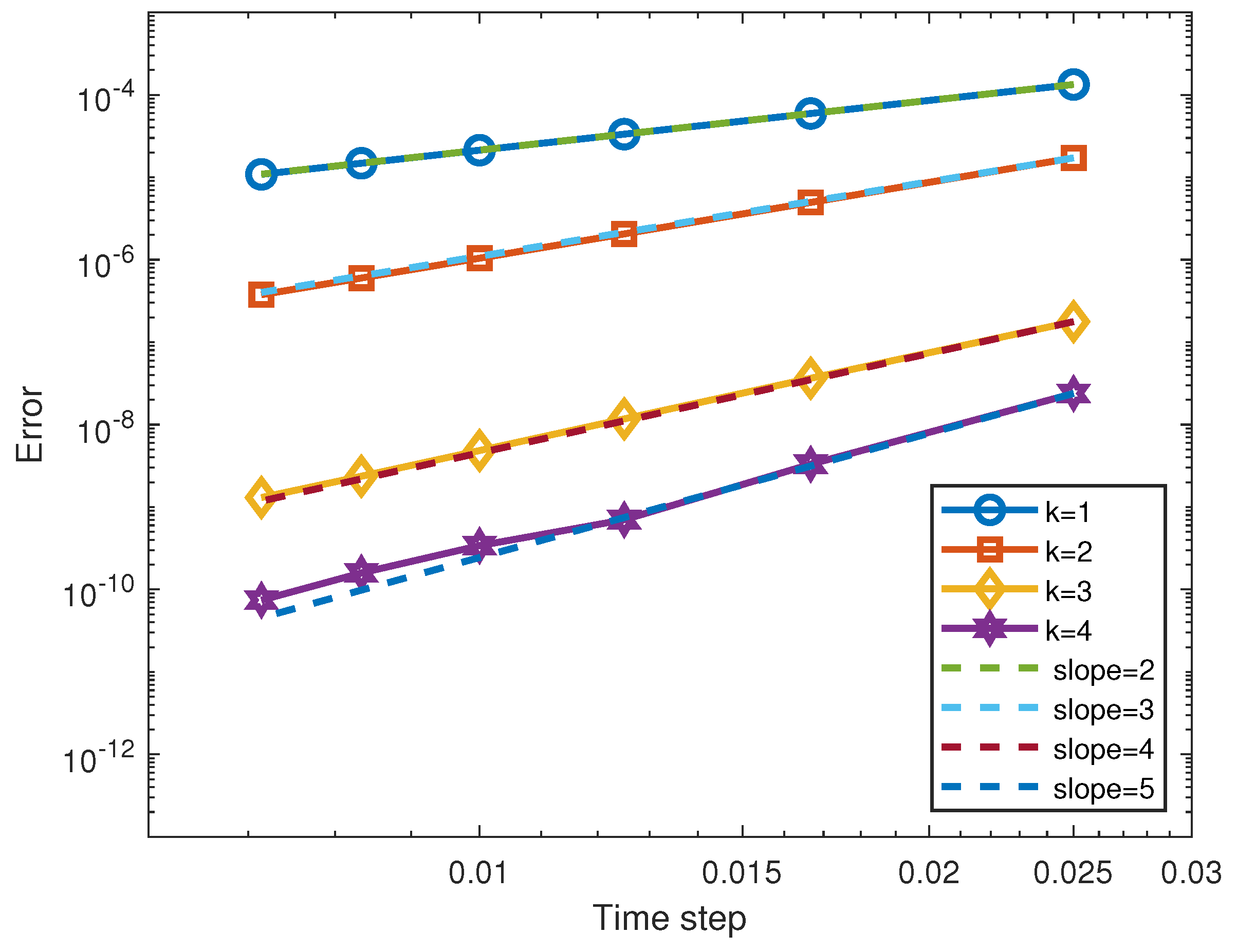
| Adams linear multistep methods | |||
| exponential multistep method | |||
| exponential Rosenbrock multistep method |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, R.; Chen, W.; Chen, X.; Zhang, R. Exponential Multistep Methods for Stiff Delay Differential Equations. Axioms 2022, 11, 185. https://doi.org/10.3390/axioms11050185
Zhan R, Chen W, Chen X, Zhang R. Exponential Multistep Methods for Stiff Delay Differential Equations. Axioms. 2022; 11(5):185. https://doi.org/10.3390/axioms11050185
Chicago/Turabian StyleZhan, Rui, Weihong Chen, Xinji Chen, and Runjie Zhang. 2022. "Exponential Multistep Methods for Stiff Delay Differential Equations" Axioms 11, no. 5: 185. https://doi.org/10.3390/axioms11050185
APA StyleZhan, R., Chen, W., Chen, X., & Zhang, R. (2022). Exponential Multistep Methods for Stiff Delay Differential Equations. Axioms, 11(5), 185. https://doi.org/10.3390/axioms11050185






