Almost Optimality of the Orthogonal Super Greedy Algorithm for μ-Coherent Dictionaries ^†

Abstract

We study the approximation capability of the orthogonal super greedy algorithm (OSGA) with respect to $\mu$-coherent dictionaries in Hilbert spaces. We establish the Lebesgue-type inequalities for OSGA, which show that the OSGA provides an almost optimal approximation on the first $[1/(18\mathsf{\mu }\mathrm{s}\left)\right]$ steps. Moreover, we improve the asymptotic constant in the Lebesgue-type inequality of OGA obtained by Livshitz E D.

1. Introduction

Approximation by the sparse linear combination of elements from a fixed redundant system continues to develop actively, which is driven not only by theoretical interest but also by frequent applications from areas such as signal processing and machine learning, cf. [1,2,3,4,5,6,7]. This type of approximation is called highly nonlinear approximation. Greedy-type algorithms have been used as a tool for generating such approximations. Among others, the orthogonal greedy algorithm (OGA) has been widely used in practice. In fact, the OGA is regarded as the most powerful algorithm to solve the problem of approximation with respect to redundant systems, cf. [8,9,10].

We recall some notations and definitions from the theory of greedy algorithms. Let $\mathcal{H}$ be a Hilbert space with an inner product $⟨·,·⟩$ and the norm $\parallel x\parallel :={⟨x,x⟩}^{\frac{1}{2}}.$ We say that a set $\mathcal{D}$ of elements from $\mathcal{H}$ is a dictionary if

$$g\in \mathcal{D}\Rightarrow \parallel g\parallel =1,\mathrm{and}\overline{\mathrm{span}}\mathcal{D}=\mathcal{H}.$$

We consider redundant dictionaries, which have been utilized frequently in the field of signal processing. Here, a redundant dictionary means that the elements of the dictionary may be linearly dependent.

We now recall the definition of the OGA from [1].

ORTHOGONAL GREEDY ALGORITHM (OGA)

Set $f_0:=f\in \mathcal{H},G_0^{OGA}(f,\mathcal{D}):=0.$ For each $m\ge 0$, we inductively find $g_{m+1}\in \mathcal{D}$ such that

$$|⟨f_m,g_{m+1}⟩|=\underset{g\in \mathcal{D}}{sup}|⟨f_m,g⟩|$$

and define

$$G_m^{OGA}(f,\mathcal{D}):=P_{\mathrm{span}\{g_1,g_2,\cdots ,g_m\}}(f),$$

$$f_{m+1}:=f-G_{m+1}^{OGA}(f,\mathcal{D}),$$

where $P_{\mathrm{span}\{g_1,g_2,\cdots ,g_m\}}$ is the operator of the orthogonal projection onto $\mathrm{span}\{g_1,g_2,···,g_m\}$.

In [11], Liu and Temlyakov proposed the orthogonal super greedy algorithm (OSGA). The OSGA selects more than one element from a dictionary in each iteration step and hence reduces the computational burden of the conventional OGA. Therefore, the OSGA is more efficient than the OGA from the viewpoint of the computational complexity.

ORTHOGONAL SUPER GREEDY ALGORITHM (OSGA(s))

Set $f_0:=f\in \mathcal{H},G_0^{OSGA}(f,\mathcal{D}):=0.$ For a natural number $s\ge 1$ and each $m\ge 0$, we inductively define:

(1)

$g_{(m-1)s+1},g_{(m-1)s+2},\cdots ,g_{ms}\in \mathcal{D}$ are elements of the dictionary $\mathcal{D},$ satisfying the following inequality. Denote $I_m=[(m-1)s+1,ms]$ and assume that

$$\underset{i\in I_m}{min}|⟨f_{m-1},g_i⟩|\ge \underset{g\in \mathcal{D},g\ne g_i,i\in I_m}{sup}|⟨f_{m-1},g⟩|.$$

(2)

Let $H_m:=H_m(f):=\mathrm{span}\{g_1,g_1,\cdots ,g_{ms}\}$ and $P_{H_m}$ denote the operator of the orthogonal projection onto $H_m.$ Define

$$G_m(f):=G_m(f,\mathcal{D}):=G_m^s(f,\mathcal{D}):=P_{H_m}(f).$$

(3)

Define the residual after the m-th iteration of the algorithm

$$f_m:=f_m^s:=f-G_m(f,\mathcal{D}).$$

Note that, in the case $s=1,$ OSGA(s) coincides with OGA.

In this paper, we study the approximation capability of the OSGA with respect to $\mu$-coherent dictionaries in Hilbert spaces. We denote by

$$\mu =\mu (\mathcal{D})=\underset{g\ne h,g,h\in \mathcal{D}}{sup}|⟨g,h⟩|$$

the coherence of a dictionary. The coherence $\mu$ is a blunt instrument to measure the redundancy of dictionaries. It is clear that if $\mathcal{D}$ is an orthonormal basis, then $\mu (\mathcal{D})=0$. The smaller the $\mu (\mathcal{D}),$ the more the $\mathcal{D}$ resembles an orthonormal basis. We study dictionaries with small values of coherence $\mu (\mathcal{D})>0,$ and call them $\mu$-coherent dictionaries.

In [11], the authors found that such computational burden reduction of OSGA does not degrade the approximation capability if f belongs to the closure of the convex hull of the symmetrized dictionary ${\mathcal{D}}^{\pm }:=\{\pm g,g\in \mathcal{D}\}$, which is denoted by $A_1(\mathcal{D})$.

Theorem 1.

Let $\mathcal{D}$ be a dictionary with coherence parameter $\mu :=\mu (\mathcal{D}).$ Then, for $s\le {(2\mu )}^{-1},$ the algorithm OSGA(s) provides an approximation of $f\in A_1(\mathcal{D})$ with the following error bound:

$$\parallel f_m^s{\parallel }^2\le 40.5{(sm)}^{-1},m=1,2,\dots .$$

It seems that a dimensional independent convergence rate was deduced, but the condition that the target element belongs to $A_1(\mathcal{D})$ becomes more and more stringent as the number of the elements in $\mathcal{D}$ grows, cf. [2].

Fang, Lin, and Xu [12] studied the behavior of OSGA for $f\in \mathcal{H}.$ They defined ${\mathcal{L}}_1=\{f:f={\sum }_{g\in \mathcal{D}}{a}_{g}g\}$ and ${\parallel f\parallel }_{{\mathcal{L}}_1}:=inf\{{\sum }_{g\in \mathcal{D}}|a_g|:f={\sum }_{g\in \mathcal{D}}{a}_{g}g\}$ for $f\in {\mathcal{L}}_1$, and obtained the following theorem.

Theorem 2.

Let $\mathcal{D}$ be a dictionary with coherence $\mu .$ Then, for all $f\in \mathcal{H},$$h\in {\mathcal{L}}_1$ and arbitrary $s\le {(2\mu )}^{-1}+1,$ the OSGA(s) provides an approximation of f with the error bound:

$$\parallel f_m^s{\parallel }^2\le {\parallel f-h\parallel }^2+\frac{27}{2}{\parallel h\parallel }_{{\mathcal{L}}_1}^2{(sm)}^{-1},k=1,2,\dots .$$

The $\mu$-coherence of a dictionary is used in OSGA, which implies that computational burden reduction does not degenerate the approximation capability. Moreover, if $\mu >\frac{1}{2},$ then OSGA coincides with OGA.

Let ${\Sigma }_m$ denote the collection of elements in $\mathcal{H}$, which can be expressed as a linear combination of, at most, m elements of the dictionary $\mathcal{D}$, namely

$${\Sigma }_m:={\Sigma }_m(\mathcal{D})=\{g:g=\sum _{i\in \mathrm{\Lambda }}{c}_i{g}_i,g_i\in \mathcal{D},\mathrm{\Lambda }\subset \mathbb{N},\#(\mathrm{\Lambda })\le m\}.$$

For an element $f\in \mathcal{H}$, we define its best m-term approximation error by

$${\sigma }_m(f):={\sigma }_m(f,\mathcal{D}):=\underset{g\in {\Sigma }_m}{inf}\parallel f-g\parallel .$$

The inequality connecting the error of greedy approximation and the error of best m-term approximation is called the Lebesgue-type inequality, cf. [13,14,15]. In this paper, we will establish the Lebesgue-type inequalities for OSGA with respect to $\mu$-coherent dictionaries.

We first recall some results on the efficiency of OGA with respect to $\mu$-coherent dictionaries. These results relate the error of OGA’s $A(m)$-th approximation to the error of the best m-term approximation with an extra multiplier:

$$\parallel f_{A(m)}(f,\mathcal{D})\parallel \le B(m){\sigma }_m(f,\mathcal{D})\mathrm{for}m\le C(\mu ),$$

(1)

where $A(m)\in \mathbb{N},B(m),C(\mu )\in \mathbb{R}.$ Gillbert, Muthukrishnan, and Strauss [16] gave the first Lebesgue-type inequality for OGA. They proved

$$\parallel f_m\parallel \le 8m^{\frac{1}{2}}{\sigma }_m(f,\mathcal{D})\mathrm{for}1\le m\le \frac{1}{8\sqrt{2}\mu }-1.$$

The constant in the above inequality was improved by Tropp in [17]:

$$\parallel f_m{\parallel \le (1+6m)}^{\frac{1}{2}}{\sigma }_m(f)\mathrm{for}1\le m\le \frac{1}{3\mu }.$$

Donoho, Elad, and Temlyakov [18] dramatically improved the factor in front of ${\sigma }_m$ and obtained that

$$\parallel f_{[mlogm]}\parallel \le 24{\sigma }_m(f)\mathrm{for}1\le m\le \frac{1}{20{\mu }^{\frac{2}{3}}},$$

where the constant 24 is not the best. Many researchers have sought to improve the factor $B(m).$ Temlyakov and Zheltov improved the above inequality in [4]. They obtained

$$\parallel f_{m\lfloor 2^{\sqrt{logm}}\rfloor }(f,\mathcal{D})\parallel \le 3{\sigma }_m(f,\mathcal{D})\mathrm{for}m\lfloor 2^{\sqrt{logm}}\rfloor \le \frac{1}{26\mu }.$$

Livshitz [19] took the parameters $A(m):=2m,B(m):=2.7,C(\mu ):=\frac{1}{20}$ in (1) and obtained the following profound result.

Theorem 3.

For every μ-coherent dictionary $\mathcal{D}$ and any $f\in \mathcal{H},$ the OGA applied to f provides

$$\parallel f_{2m}\parallel \le 2.7{\sigma }_m(f,\mathcal{D})\mathrm{for}1\le m\le \frac{1}{20\mu }.$$

By using the same method as in [19], Ye and Wei [20] improved slightly the constant 2.7.

Based on the above works, we give the error bound of the form (1) for OSGA with respect to dictionaries with small but non-vanishing coherence.

Theorem 4.

Let $\mathcal{D}$ be a dictionary with coherence $\mu .$ Then, for any $f\in \mathcal{H}$ and any $ϵ>0,$ the OSGA(s) applied to f provides

$$\parallel f_{Am}\parallel \le 2.24(1+ϵ){\sigma }_m(f)$$

(2)

for all $1\le m\le \frac{1}{18\mu s},\frac{3}{100}\le \mu \le \frac{1}{18}$ and an absolute constant $A\ge 2.$

Remark 1.

1. 

We remark that the values of μ and A for which (2) holds are coupled. For example, it is possible to obtain a smaller value of μ at the price of a larger value of A. Moreover, for sufficiently large A, μ can be arbitrarily close to zero.

2. 

Our results improve Theorem 3 only in the asymptotic constant and not in the rate. Under the condition of Theorem 4, for $s=1,$ taking $(A,ϵ,\mu )$ as $(2,0.1,0.03),$ we can obtain $\parallel f_{2m}\parallel \le 2.5{\sigma }_m(f,\mathcal{D}).$ Comparing it with Theorem 3, the constant that we obtain is better.

3. 

The specific constant 2.24 in (2) is not the best. By adjusting parameters A and $\mu ,$ we can obtain a more general estimation:

$$\parallel f_{Am}\parallel \le C(A)(1+ϵ){\sigma }_m(f)$$

for ${\alpha }_A\le \mu \le \frac{1}{18},$ where $C(A)$ and ${\alpha }_A$ are interdependent. Thus, Theorem 4 shows that OSGA(s) can achieve an almost optimal approximation on the first $[1/(18\mathsf{\mu }\mathrm{s})]$ steps for dictionaries with small but non-vanishing coherence.

The paper is organized as follows. In Section 2, we establish several preliminary lemmas. In Section 3, for some closed subspace L of $\mathcal{H},$ as defined below, we first give the estimations of $P_L^{\perp }(f_n)$ in different situations based on the lemmas in Section 2. Then, we estimate the $P_L(f_n).$ Finally, combining the above two estimations, we provide the detailed proof of Theorem 4. In Section 4, we test the performance of the OSGA in the case of finite dimensional Euclidean space. In Section 5, we make some concluding remarks on our work.

2. Preliminary Lemmas

In this section, we will introduce several quantities and discuss their properties, which are important to the proof of our main result. By the condition of Theorem 4, we have

$$\mu \le m\mu s\le Am\mu s\le \frac{1}{18}.$$

We establish three preliminary lemmas.

Lemma 1.

Let $n\le Ams,h\in \mathcal{H},g_i\in \mathcal{D},1\le i\le n.$ Assume that

$$P_{\mathrm{span}\{g_1,g_2,\cdots ,g_n\}}h=\sum _{i=1}^n{c}_i{g}_i,$$

then, we have

$$\underset{1\le i\le n}{max}|c_i|\le k_1\underset{1\le i\le n}{max}|⟨h,g_i⟩|,$$

where $k_1=\frac{1}{1-\mu Ams}\le \frac{18}{17}.$

Proof. 

For any $g_l\in \mathcal{D},1\le l\le n,$ we have

$$\begin{array}{cc}\hfill |⟨h,g_l⟩|& =|⟨P_{\mathrm{span}\{g_1,g_2,\cdots ,g_n\}}h,g_l⟩|\hfill \\ & =|⟨\sum _{i=1}^n{c}_i{g}_i,g_l⟩|\hfill \\ & \ge |c_l|-\sum _{i\ne l}|c_i||⟨g_i,g_l⟩|\hfill \\ & \ge |c_l|-\mu (\underset{1\le i\le n}{max}|c_i|)(n-1).\hfill \end{array}$$

This implies

$$\underset{1\le l\le n}{max}|c_l|\le \frac{1}{1-\mu (n-1)}\underset{1\le l\le n}{max}|⟨h,g_l⟩|\le \frac{1}{1-\mu Ams}\underset{1\le l\le n}{max}|⟨h,g_l⟩|,$$

where $k_1=\frac{1}{1-\mu Ams}\le \frac{18}{17}.$

□

For $ϵ>0,$ by the definition of ${\sigma }_m(f),$ there exist $b_j\in \mathbb{R},{\psi }_j\in \mathcal{D},1\le j\le m$ such that

$$\parallel f-\sum _{j=1}^m{b}_j{\psi }_j\parallel \le (1+ϵ){\sigma }_m(f).$$

(3)

For $1\le n\le Am,$ we set

$$d_n:=\sum _{j\in I_n}|⟨f_{n-1},g_j⟩|.$$

(4)

Assume that $x_{i,n},n\ge 1,1\le i\le ns,$ satisfying the equation

$$f_n=f_{n-1}-P_{H_n}(f_{n-1})=f_{n-1}-\sum _{i=1}^{ns}{x}_{i,n}{g}_i.$$

(5)

Next, we give the estimates of ${\{x_{i,n}\}}_{i=1}^{ns}$ and $\{d_n\}$ for $n\ge 1$ in turn. Applying Lemma 1, we have the following estimates for $x_{i,n}$.

Lemma 2.

For $n\le Am,$ we have

$$|x_{i,n}|\le k_1\mu d_n\mathrm{for}1\le i\le (n-1)s;$$

$$|x_{i,n}-⟨f_{n-1},g_i⟩|\le k_1\mu d_n\mathrm{for}(n-1)s+1\le i\le ns.$$

Proof. 

Define

$$h=f_{n-1}-\sum _{i\in I_n}⟨f_{n-1},g_i⟩g_i.$$

Since

$$\begin{array}{cc}\hfill f_n& =f_{n-1}-P_{H_n}(f_{n-1})\hfill \\ & =f_{n-1}-\sum _{i\in I_n}⟨f_{n-1},g_i⟩g_i-P_{H_n}(f_{n-1}-\sum _{i\in I_n}⟨f_{n-1},g_i⟩g_i)\hfill \\ & =h-P_{H_n}(h)\hfill \end{array}$$

(6)

and, for any $1\le j\le (n-1)s,$ $⟨f_{n-1},g_j⟩=0,$ we have

$$|⟨h,g_j⟩|=|⟨f_{n-1}-\sum _{i\in I_n}⟨f_{n-1},g_i⟩g_i,g_j⟩|\le \sum _{i\in I_n}|⟨f_{n-1},g_i⟩|\mu =\mu d_n.$$

(7)

For $(n-1)s+1\le j\le ns,$ we have

$$\begin{array}{cc}\hfill |⟨h,g_j⟩|& =|⟨f_{n-1}-\sum _{i\in I_n}<f_{n-1},g_i>g_i,g_j⟩|\hfill \\ & =|⟨f_{n-1},g_j⟩-\sum _{i\in I_n}⟨f_{n-1},g_i⟩⟨g_i,g_j⟩|\hfill \\ & =|⟨f_{n-1},g_j⟩-⟨f_{n-1},g_j⟩-\sum _{i,j\in I_n,i\ne j}⟨f_{n-1},g_i⟩⟨g_i,g_j⟩|\hfill \\ & \le \sum _{i,j\in I_n,i\ne j}|⟨f_{n-1},g_i⟩⟨g_i,g_j⟩|\hfill \\ & \le \mu d_n.\hfill \end{array}$$

(8)

Let $P_{H_n}(h)={\sum }_{i=1}^{ns}{x}_{i,n}^{{}^{\prime }}{g}_i.$ Combining (5) with (6), we have

$$f_{n-1}-\sum _{i\in I_n}⟨f_{n-1},g_i⟩g_i-\sum _{i=1}^{ns}{x}_{i,n}^{{}^{\prime }}{g}_i=f_n=f_{n-1}-\sum _{i=1}^{ns}{x}_{i,n}{g}_i.$$

Thus, for $1\le i\le (n-1)s,x_{i,n}^{{}^{\prime }}=x_{i,n};$ for $(n-1)s+1\le i\le ns,⟨f_{n-1},g_i⟩+x_{i,n}^{{}^{\prime }}=x_{i,n}.$ By Lemma 1 and inequalities (7) and (8), we obtain

$$\underset{1\le i\le ns}{max}|x_{i,n}^{{}^{\prime }}|\le k_1\underset{1\le i\le ns}{max}|⟨h,g_i⟩|\le k_1\mu d_n.$$

Thus, for $1\le i\le (n-1)s,$

$$|x_{i,n}|=|x_{i,n}^{{}^{\prime }}|\le \underset{1\le i\le ns}{max}|x_{i,n}^{{}^{\prime }}|\le k_1\mu d_n;$$

for $(n-1)s+1\le i\le ns,$

$$|x_{i,n}-⟨f_{n-1},g_i⟩|=|x_{i,n}^{{}^{\prime }}|\le \underset{1\le i\le ns}{max}|x_{i,n}^{{}^{\prime }}|\le k_1\mu d_n.$$

□

We proceed to the estimate of $\{d_n\}.$

Lemma 3.

For any $1\le l\le n\le Am+1,$ we have

$$d_n\le k_2{d}_l,$$

where $k_2=exp\left(Ams\mu \left(1+\frac{Ams\mu }{1-Ams\mu }\right)\right)\le exp\left(\frac{1}{17}\right).$

Proof. 

For $1\le n\le Am,$ according to the definition of $d_n$, we have

$$\begin{array}{cc}\hfill d_{n+1}& =\sum _{i\in I_{n+1}}|⟨f_n,g_i⟩|\le s|⟨f_n,g_{ns+1}⟩|\hfill \\ & =s|⟨f_{n-1}-P_{H_n}(f_{n-1}),g_{ns+1}⟩|\hfill \\ & =s|⟨f_{n-1}-\sum _{i=1}^{ns}{x}_{i,n}{g}_i,g_{ns+1}⟩|\hfill \\ & \le s(|⟨f_{n-1},g_{ns+1}⟩|+\sum _{i=1}^{ns}|x_{i,n}||⟨g_i,g_{ns+1}⟩|).\hfill \end{array}$$

(9)

We continue to estimate the two summands of the right-hand side of the above inequality. For the first summand, the greedy step implies

$$s|⟨f_{n-1},g_{ns+1}⟩|\le s|⟨f_{n-1},g_{ns}⟩|\le \sum _{I_n}|⟨f_{n-1},g_i⟩|=d_n.$$

(10)

For the second summand, by Lemma 1, we have

$$\begin{array}{cc}\hfill s\sum _{i=1}^{ns}|x_{i,n}||⟨g_i,g_{ns+1}⟩|& \le s\mu \sum _{i=1}^{ns}|x_{i,n}|\le s\mu (\sum _{i=1}^{(n-1)s}|x_{i,n}|+\sum _{i=(n-1)s+1}^{ns}|x_{i,n}|)\hfill \\ & \le s\mu ((n-1)s{k}_1\mu d_n+\sum _{i\in I_n}(k_1\mu d_n+|⟨f_{n-1},g_i⟩|))\hfill \\ & =s\mu ((n-1)s{k}_1\mu d_n+s{k}_1\mu d_n+d_n)\hfill \\ & =d_n\mu s(1+ns{k}_1\mu )\hfill \\ & \le d_n\mu s(1+Ams\mu k_1).\hfill \end{array}$$

(11)

Combining inequalities (9)–(11) with Lemma 2, we conclude that

$$d_{n+1}\le d_n+\left(1+\frac{Ams\mu }{1-Ams\mu }\right)d_n\mu s=\left[1+\left(1+\frac{Ams\mu }{1-Ams\mu }\right)\mu s\right]d_n.$$

Thus, for any n and $1\le l\le n\le Am+1,$ we have

$$\begin{array}{cc}\hfill d_n& \le \left[1+\left(1+\frac{Ams\mu }{1-Ams\mu }\right)\mu s\right]d_{n-1}\le \cdots \le {\left[1+\left(1+\frac{Ams\mu }{1-Ams\mu }\right)\mu s\right]}^{n-l}{d}_l\hfill \\ & \le {\left[1+\left(1+\frac{Ams\mu }{1-Ams\mu }\right)\mu s\right]}^{Am}{d}_l\hfill \\ & ={\left[1+\frac{Am\left(1+\frac{Ams\mu }{1-Ams\mu }\right)\mu s}{Am}\right]}^{Am}{d}_l\le exp\left(Am\left(1+\frac{Ams\mu }{1-Ams\mu }\right)\mu s\right)d_l=k_2{d}_l,\hfill \end{array}$$

where $k_2:=exp\left(Ams\mu \left(1+\frac{Ams\mu }{1-Ams\mu }\right)\right)\le exp\left(\frac{1}{17}\right).$ □

3. Proof of Theorem 4

Based on the above preliminary lemmas, we will prove Theorem 4 step by step. We first introduce some notations. Define

$$L:=\mathrm{span}({\psi }_1,\cdots ,{\psi }_m),f_0=f,{\xi }_n:=P_L^{\perp }(f_n),0\le n\le Am.$$

$$T_1:=\{i\in \{1,\cdots ,Ams\}:g_i\in {\{{\psi }_j\}}_{j=1}^m\},T_2:=\{1,\cdots ,Ams\}\backslash T_1.$$

For $d_n,$ we define

$$D:=\sum _{i:1\le i\le Am,T_2\cap I_i\ne \varnothing }{d}_i^2.$$

Let $a_{j,n}\in \mathbb{R},1\le j\le m,0\le n\le Am$ satisfy the following equations

$$P_L(f_n)=\sum _{j=1}^m{a}_{j,n}{\psi }_j.$$

(12)

Thus, for $f_n$, $0\le n\le Am,$ we have

$$f_n:=P_L(f_n)+P_L^{\perp }(f_n)=\sum _{j=1}^m{a}_{j,n}{\psi }_j+{\xi }_n.$$

To obtain the upper bound of $\parallel f_n\parallel ,$ it suffices to estimate $\parallel {\xi }_n\parallel$ and $\parallel P_L(f_n)\parallel .$ By the definitions of sets $T_1,T_2$ and $I_n$ in OSGA, we first give the estimate of $\parallel {\xi }_n\parallel$ according to whether the intersection of $T_2$ and $I_n$ is an empty set.

Theorem 5.

Let n satisfy $1\le n\le Am$ and $I_n\cap T_2=\varnothing .$ Then,

$$\parallel {\xi }_n\parallel \le \parallel {\xi }_{n-1}\parallel +0.22D\mu .$$

Proof. 

Let

$${\mathrm{\Lambda }}_n:={\cup }_{i=1}^n{I}_n,T_2^n:=T_2\cap {\mathrm{\Lambda }}_n,t_n:=|T_2^n|.$$

By Lemma 3, for $1\le l\le n\le Am,$

$$d_n\le k_2\underset{l:I_l\cap T_2^n\ne \varnothing }{min}{d}_l.$$

Then, we have

$$s^{-1}{t}_n{(\underset{I_l\cap T_2^n\ne \varnothing }{min}{d}_l)}^2\le \sum _{I_l\cap T_2^n\ne \varnothing }(\sum _{i\in I_l}|⟨f_{l-1},g_i⟩{|)}^2=\sum _{I_l\cap T_2^n\ne \varnothing }{d}_i^2=D,$$

so, we can obtain that

$$s^{-1}{t}_n{d}_n^2\le k_2^{2}D.$$

(13)

Since $I_n\cap T_2=\varnothing ,$ we obtain $t_n=t_{n-1}.$ We define

$$h:=\sum _{i\in T_2^n}{x}_{i,n}{g}_i=\sum _{i\in T_2^{n-1}}{x}_{i,n}{g}_i.$$

(14)

Note that

$$f_n=f-P_{H_n}(f)=f_{n-1}+P_{H_{n-1}}(f)-P_{H_n}(f_{n-1}+P_{H_{n-1}}(f))=f_{n-1}+P_{H_n}(f_{n-1}).$$

By the definitions of $L,T_1,T_2,{\mathrm{\Lambda }}_n$ and the expression of (14), we have $P_L^{\perp }(P_{H_n}(f_{n-1}))=P_L^{\perp }(h)$. Then, we obtain

$$\begin{array}{cc}\hfill \parallel {\xi }_n{\parallel }^2& =\parallel P_L^{\perp }(f_n){\parallel }^2=\parallel P_L^{\perp }(f_{n-1}-P_{H_n}(f_{n-1})){\parallel }^2={\parallel {\xi }_{n-1}-P_L^{\perp }(h)\parallel }^2\hfill \\ & \le \parallel {\xi }_{n-1}{\parallel }^2+2|⟨{\xi }_{n-1},P_L^{\perp }(h)⟩|+\parallel P_L^{\perp }{(h)\parallel }^2.\hfill \end{array}$$

(15)

To obtain the final result, it suffices to estimate the upper bounds of $|⟨{\xi }_{n-1},P_L^{\perp }(h)⟩|$ and $\parallel P_L^{\perp }{(h)\parallel }^2.$

For $|⟨{\xi }_{n-1},P_L^{\perp }(h)⟩|$, by (12) and (14), we have

$$\begin{array}{cc}\hfill |⟨{\xi }_{n-1},P_L^{\perp }(h)⟩|& =|⟨{\xi }_{n-1},h⟩|=|⟨f_{n-1}-P_L(f_{n-1}),h⟩|=|⟨P_L(f_{n-1}),h⟩|\hfill \\ & =|⟨\sum _{j=1}^m{a}_{j,n-1}{\psi }_j,\sum _{{T_2}^{n-1}}{x}_{i,n}{g}_i⟩|\hfill \\ & \le \sum _{j=1}^m|a_{j,n-1}|·\sum _{{T_2}^{n-1}}|x_{i,n}⟨{\psi }_j,g_i⟩|,\hfill \end{array}$$

(16)

where we have used the fact $<f_{n-1},h>=0.$

On the one hand, for any $1\le l\le m$ and n satisfying $T_2\cap I_n=\varnothing ,$ we obtain

$$\begin{array}{cc}\hfill |⟨\sum _{j=1}^m{a}_{j,n-1}{\psi }_j,{\psi }_l⟩|& =|⟨\sum _{j=1}^m{a}_{j,n-1}{\psi }_j+{\xi }_{n-1},{\psi }_l⟩|=|⟨f_{n-1},{\psi }_l⟩|\hfill \\ & \le \underset{I_n}{max}|⟨f_{n-1},g_i⟩|\le \sum _{I_n}|⟨f_{n-1},g_i⟩|=d_n.\hfill \end{array}$$

(17)

Thus, by Lemma 1 and inequality (17), we obtain

$$\begin{array}{cc}\hfill \sum _{j=1}^m|a_{j,n-1}|& \le m·\underset{1\le j\le m}{max}|a_{j,n-1}|\le m{k}_1\underset{1\le j\le m}{max}|⟨f_{n-1},{\psi }_j⟩|\hfill \\ & \le m{k}_1\underset{1\le j\le m}{max}|⟨P_L(f_{n-1})+{\xi }_{n-1},{\psi }_j⟩|\hfill \\ & =m{k}_1\underset{1\le j\le m}{max}|⟨\sum _{i=1}^m{a}_{i,n-1}{\psi }_i,{\psi }_j⟩|\le m{k}_1{d}_n.\hfill \end{array}$$

(18)

On the other hand, by Lemma 2, we have, for $1\le j\le m,$

$$\begin{array}{c}\hfill \sum _{{T_2}^{n-1}}|x_{i,n}⟨{\psi }_j,g_i⟩|\le \mu t_{n-1}\underset{i\in T_2^{n-1}}{max}|x_{i,n}|\le \mu t_{n-1}{k}_1\mu d_n.\end{array}$$

(19)

Thus, substituting (18) and (19) into (16), and then combining it with (13), we get the estimate

$$\begin{array}{cc}\hfill |⟨{\xi }_{n-1},P_L^{\perp }(h)⟩|& \le \sum _{j=1}^m|a_{j,n-1}|·\sum _{{T_2}^{n-1}}|x_{i,n}⟨{\psi }_j,g_i⟩|\hfill \\ & \le m{\mu }^2{k}_1^2{d}_n^2{t}_{n-1}\hfill \\ & \le m{\mu }^2{k}_1^{2}s{s}^{-1}{d}_n^2{t}_{n-1}\hfill \\ & \le m\mu s{k}_1^2{k}_2^{2}D\mu .\hfill \end{array}$$

(20)

Finally, we estimate $\parallel P_L^{\perp }{(h)\parallel }^2.$

Note that

$$\begin{array}{cc}\hfill \parallel P_L^{\perp }{(h)\parallel }^2& ={\parallel h\parallel }^2={\parallel \sum _{i\in T_2^{n-1}}{x}_{i,n}{g}_i\parallel }^2\hfill \\ & =\sum _{i\in T_2^{n-1}}{x}_{i,n}^2+\sum _{i,j\in T_2^{n-1},i\ne j}|x_{i,n}||x_{j,n}||⟨g_i,g_j⟩|\hfill \\ & \le (\underset{i\in T_2^{n-1}}{max}{x}_{i,n}^2)[t_{n-1}+t_{n-1}^2\mu ]\hfill \\ & \le k_1^2{\mu }^2{d}_n^2[t_n+t_n^2\mu ].\hfill \end{array}$$

By using (13), we have

$$\parallel P_L^{\perp }{(h)\parallel }^2\le k_1^2{\mu }^{2}s{k}_2^{2}D(1+Ams\mu )=k_1^2\mu s(1+Ams\mu )k_2^{2}D\mu .$$

(21)

Combining (15) and (20) with (21), we give

$$\begin{array}{cc}\hfill \parallel {\xi }_n{\parallel }^2& \le \parallel {\xi }_{n-1}{\parallel }^2+2|⟨{\xi }_{n-1},P_L^{\perp }(h)⟩|+\parallel P_L^{\perp }{(h)\parallel }^2\hfill \\ & \le \parallel {\xi }_{n-1}{\parallel }^2+[2m\mu s+\mu s(1+Ams\mu )]k_1^2{k}_2^{2}D\mu \hfill \\ & \le \parallel {\xi }_{n-1}{\parallel }^2+0.22D\mu .\hfill \end{array}$$

□

Theorem 5 gives the estimation of $\parallel {\xi }_n\parallel$ in the situation $I_n\cap T_2=\varnothing .$ The following theorem deals with the situation $I_n\cap T_2\ne \varnothing$.

Theorem 6.

Let n satisfy $1\le n\le Am$ and $I_n\cap T_2=\varnothing .$ Then,

$$\parallel {\xi }_n\parallel \le \parallel {\xi }_{n-1}{\parallel }^2-0.8937d_n^2.$$

Proof. 

Since

$$\begin{array}{cc}\hfill {\xi }_n=P_L^{\perp }(f_n)& =P_L^{\perp }(f_{n-1}-\sum _{i=1}^{ns}{x}_{i,n}{g}_i)\hfill \\ & =P_L^{\perp }(f_{n-1}-\sum _{i\in I_n}{x}_{i,n}{g}_i-\sum _{i\in {\mathrm{\Lambda }}_{n-1}}{x}_{i,n}{g}_i)\hfill \\ & =P_L^{\perp }(f_{n-1}-\sum _{i\in I_n}{x}_{i,n}{g}_i)-P_L^{\perp }(\sum _{i\in {\mathrm{\Lambda }}_{n-1}}{x}_{i,n}{g}_i),\hfill \end{array}$$

we set ${\xi }_n^{{}^{\prime }}=P_L^{\perp }(f_{n-1}-{\sum }_{i\in I_n}{x}_{i,n}{g}_i),h={\sum }_{i\in T_2^{n-1}}{x}_{i,n}{g}_i$ and write ${\xi }_n$ as

$${\xi }_n={\xi }_n^{{}^{\prime }}-P_L^{\perp }(h).$$

According to the following inequality,

$$\parallel {\xi }_n{\parallel }^2=\parallel {\xi }_n^{{}^{\prime }}{\parallel }^2-2⟨{\xi }_n^{{}^{\prime }},P_L^{\perp }(h)⟩+\parallel P_L^{\perp }{(h)\parallel }^2\le \parallel {\xi }_n^{{}^{\prime }}{\parallel }^2-2⟨{\xi }_n^{{}^{\prime }},h⟩+{\parallel h\parallel }^2,$$

(22)

we need to estimate $\parallel {\xi }_n^{{}^{\prime }}{\parallel }^2,⟨{\xi }_n^{{}^{\prime }},h⟩$ and ${\parallel h\parallel }^2.$ We first estimate ${\parallel h\parallel }^2$ by

$$\begin{array}{cc}\hfill {\parallel h\parallel }^2& =\parallel \sum _{i\in T_2^{n-1}}{x}_{i,n}{g}_i{\parallel }^2\hfill \\ & \le k_1^2{\mu }^2{d}_n^2(t_n+t_n^2\mu )\hfill \\ & \le k_1^2{\mu }^2{d}_n^2(Ams+{(Ams)}^2\mu )\hfill \\ & =k_1^2\mu Am\mu s(1+Am\mu s)d_n^2\hfill \\ & \le {\left(\frac{18}{17}\right)}^2\frac{1}{18}\frac{1}{18}\frac{19}{18}{d}_n^2=\frac{19}{5202}{d}_n^2\le 0.0037d_n^2.\hfill \end{array}$$

(23)

Next, we continue to estimate $\parallel {\xi }_n^{{}^{\prime }}{\parallel }^2.$ It is not difficult to see that

$$\begin{array}{cc}\hfill \parallel {\xi }_n^{{}^{\prime }}{\parallel }^2& =\parallel P_L^{\perp }(f_{n-1}-\sum _{i\in I_n}{x}_{i,n}{g}_i){\parallel }^2\hfill \\ & =\parallel {\xi }_{n-1}-P_L^{\perp }(\sum _{i\in I_n}{x}_{i,n}{g}_i){\parallel }^2\hfill \\ & =\parallel {\xi }_{n-1}{\parallel }^2-2⟨{\xi }_{n-1},\sum _{i\in I_n}{x}_{i,n}{g}_i⟩+{\parallel P_L^{\perp }(\sum _{i\in I_n}{x}_{i,n}{g}_i)\parallel }^2\hfill \\ & \le \parallel {\xi }_{n-1}{\parallel }^2-2\sum _{i\in I_n}{x}_{i,n}⟨{\xi }_{n-1},g_i⟩+{\parallel \sum _{i\in I_n}{x}_{i,n}{g}_i\parallel }^2.\hfill \end{array}$$

(24)

Note that

$$\begin{array}{cc}& \sum _{i\in I_n}{x}_{i,n}⟨{\xi }_{n-1},g_i⟩\hfill \\ \hfill =& \sum _{i\in I_n}[(x_{i,n}-⟨f_{n-1},g_i⟩)+⟨f_{n-1},g_i⟩][(⟨{\xi }_{n-1},g_i⟩-⟨f_{n-1},g_i⟩)+⟨f_{n-1},g_i⟩].\hfill \end{array}$$

(25)

By (18), for any $i\in T_2\cap I_n,$ we have

$$\begin{array}{cc}& |⟨{\xi }_{n-1},g_i⟩-⟨f_{n-1},g_i⟩|\hfill \\ \hfill =& |⟨f_{n-1}-\sum _{j=1}^m{a}_{j,n-1}{\psi }_j,g_i⟩-⟨f_{n-1},g_i⟩|\hfill \\ \hfill =& |⟨\sum _{j=1}^m{a}_{j,n-1}{\psi }_j,g_i⟩|\le \sum _{j=1}^m|a_{j,n-1}||⟨{\psi }_j,g_i⟩|\hfill \\ \hfill \le & k_{1}m\mu d_n.\hfill \end{array}$$

(26)

Combining Lemma 2 with inequality (26), we obtain

$$\begin{array}{cc}& \sum _{i\in I_n}{x}_{i,n}⟨{\xi }_{n-1},g_i⟩\hfill \\ \hfill \ge & \sum _{i\in I_n}(⟨f_{n-1},g_i⟩-k_1\mu d_n)(⟨f_{n-1},g_i⟩-m{k}_1\mu d_n)\hfill \\ \hfill =& \sum _{i\in I_n}({⟨f_{n-1},g_i⟩}^2-(k_1\mu d_n+m{k}_1\mu d_n)⟨f_{n-1},g_i⟩+m{k}_1^2{\mu }^2{d}_n^2)\hfill \\ \hfill =& \sum _{i\in I_n}{⟨f_{n-1},g_i⟩}^2-\sum _{i\in I_n}(k_1\mu d_n+m{k}_1\mu d_n)⟨f_{n-1},g_i⟩+\sum _{i\in I_n}m{k}_1^2{\mu }^2{d}_n^2\hfill \\ \hfill \ge & \sum _{i\in I_n}{⟨f_{n-1},g_i⟩}^2-\sum _{i\in I_n}(k_1\mu d_n+m{k}_1\mu d_n)⟨f_{n-1},g_i⟩+ms{k}_1^2{\mu }^2{d}_n^2\hfill \\ \hfill \ge & \sum _{i\in I_n}{⟨f_{n-1},g_i⟩}^2-(k_1\mu +m{k}_1\mu )d_n^2+ms{k}_1^2{\mu }^2{d}_n^2\hfill \\ \hfill \ge & s^{-1}{d}_n^2-(1+m)k_1\mu d_n^2\hfill \\ \hfill \ge & (9A-k_1)(1+m)\mu d_n^2\ge 2\mu (9A-k_1)d_n^2\ge \frac{576}{17}\mu d_n^2\hfill \end{array}$$

(27)

for $0\le s\le \frac{1}{18Am\mu }\le \frac{1}{9(1+m)A\mu }.$ and $m\ge 1,A\ge 2.$

For the last summand of the right-hand side of the inequality in (24), we have

$$\begin{array}{cc}\hfill (\sum _{i\in I_n}|x_{i,n}{|)}^2& \le (\sum _{i\in I_n}(|⟨f_{n-1},g_i⟩|+k_1\mu d_n{))}^2\hfill \\ & \le {(1+k_1\mu s)}^2{d}_n^2\hfill \\ & \le {\left(\frac{18}{17}\right)}^2{d}_n^2.\hfill \end{array}$$

(28)

Thus, combining (27) with (28), for $\frac{3}{100}\le \mu \le \frac{1}{18},$ we have

$$\begin{array}{cc}\hfill \parallel {\xi }_n^{{}^{\prime }}{\parallel }^2& \le \parallel {\xi }_{n-1}{\parallel }^2-2\sum _{i\in I_n}{x}_{i,n}⟨{\xi }_{n-1},g_i⟩+(\sum _{i\in I_n}|x_{i,n}{|)}^2\hfill \\ & \le \parallel {\xi }_{n-1}{\parallel }^2+\left({\left(\frac{18}{17}\right)}^2-2\frac{576}{17}\mu \right)d_n^2\hfill \\ & \le \parallel {\xi }_{n-1}{\parallel }^2-0.9118d_n^2.\hfill \end{array}$$

(29)

We next estimate $|⟨{\xi }_n^{{}^{\prime }},h⟩|.$ Since

$$\begin{array}{cc}\hfill |⟨{\xi }_n^{{}^{\prime }},h⟩|& =|⟨P_L^{\perp }(f_{n-1}-\sum _{i\in I_n}{x}_{i,n}{g}_i),h⟩|=|⟨{\xi }_{n-1}-\sum _{i\in I_n}{x}_{i,n}{P}_L^{\perp }(g_i),h⟩|\hfill \\ & =|⟨f_{n-1}-\sum _{j=1}^m{a}_{j,n-1}{\psi }_j-\sum _{i\in I_n}{x}_{i,n}{P}_L^{\perp }(g_i),h⟩|\hfill \\ & \le |⟨\sum _{j=1}^m{a}_{j,n-1}{\psi }_j,h⟩|+|⟨\sum _{i\in I_n}{x}_{i,n}{P}_L^{\perp }(g_i),h⟩|\hfill \\ & \le \sum _{j=1}^m|a_{j,n-1}||⟨{\psi }_j,h⟩|+\sum _{i\in I_n}|x_{i,n}||⟨P_L^{\perp }(g_i),h⟩|=:A+B,\hfill \end{array}$$

(30)

we need to give the upper bounds of A and $B.$ By (18) and (19), we have

$$\begin{array}{cc}\hfill A& =\sum _{j=1}^m|a_{j,n-1}||⟨{\psi }_j,h⟩|\le \sum _{j=1}^m|a_{j,n-1}|\sum _{i\in T_2^{n-1}}|x_{i,n}||⟨{\psi }_j,g_i⟩|\hfill \\ & \le m{k}_1{d}_n\mu t_{n-1}{k}_1\mu d_n\le m{k}_1{d}_n\mu Ams{k}_1\mu d_n\le k_1^2(Am\mu s)(m\mu )d_n^2\hfill \\ & \le 0.0035d_n^2.\hfill \end{array}$$

(31)

As for $B,$ since for $1\le j\le (n-1)s<i\le ns\le Ams,i,j\in T_2,$ $P_L(g_i)={\sum }_{l=1}^m{c}_l^i{\psi }_l,$ by Lemma 1, we know that

$$\underset{1\le l\le m}{max}|c_l^i|\le k_1\underset{1\le l\le m}{max}|⟨g_i,{\psi }_l⟩|\le k_1\mu ,$$

(32)

and

$$\begin{array}{cc}\hfill |⟨P_L^{\perp }(g_i),g_j⟩|& =|⟨g_i-P_L(g_i),g_j⟩|=|⟨g_i-\sum _{l=1}^m{c}_l^i{\psi }_l,g_j⟩|\hfill \\ & \le |⟨g_i,g_j⟩|+\sum _{l=1}^m|c_l^i||⟨{\psi }_l,g_j⟩|.\hfill \end{array}$$

(33)

Combining (32) with (33), we have

$$\begin{array}{c}\hfill |⟨P_L^{\perp }(g_i),g_j⟩|\le \mu +m\underset{1\le l\le m}{max}|c_l^i|\mu \le \mu +m\mu k_1\mu \le \frac{18}{17}\mu .\end{array}$$

(34)

Using Lemma 1 again, we obtain from (34) that

$$\begin{array}{cc}\hfill B& =\sum _{i\in I_n}|x_{i,n}||⟨P_L^{\perp }(g_i),h⟩|=\sum _{i\in I_n}|x_{i,n}|\sum _{j\in T_2^{n-1}}|x_{j,n}||⟨P_L^{\perp }(g_i),g_j⟩|\hfill \\ & \le \sum _{i\in I_n}(k_1\mu d_n+|⟨f_{n-1},g_j⟩|)\sum _{j\in T_2^{n-1}}|x_{j,n}|\frac{18}{17}\mu \hfill \\ & \le (k_1\mu d_{n}s+d_n)k_1\mu d_n(n-1)s\frac{18}{17}\mu \hfill \\ & \le (k_1\mu s+1)(k_1\mu )(Ams\mu )\frac{18}{17}{d}_n^2\hfill \\ & \le \left(1+\frac{18}{17}\frac{1}{18}\right)\frac{18}{17}\frac{1}{18}\frac{1}{18}\frac{18}{17}{d}_n^2\le 0.0037d_n^2.\hfill \end{array}$$

(35)

Thus, we get the upper bound of $|⟨{\xi }_n^{{}^{\prime }},h⟩|$ by (30), (31) and (35), i.e.,

$$|⟨{\xi }_n^{{}^{\prime }},h⟩|\le A+B\le 0.0072d_n^2.$$

(36)

Combining (22), (23) and (29) with (36), we have

$$\begin{array}{cc}\hfill \parallel {\xi }_n{\parallel }^2& =\parallel {\xi }_n^{{}^{\prime }}{\parallel }^2-2⟨{\xi }_n^{{}^{\prime }},h⟩+{\parallel h\parallel }^2\hfill \\ \hfill & \le \parallel {\xi }_n^{{}^{\prime }}{\parallel }^2+2|⟨{\xi }_n^{{}^{\prime }},h⟩{|+\parallel h\parallel }^2\hfill \\ \hfill & \le \parallel {\xi }_{n-1}{\parallel }^2-0.9118d_n^2+2(0.0072d_n^2)+0.0037d_n^2\hfill \\ \hfill & =\parallel {\xi }_{n-1}{\parallel }^2-0.8937d_n^2.\hfill \end{array}$$

□

It remains to estimate $\parallel P_L(f_n)\parallel$. We first recall a lemma proven by Fang, Lin and Xu in [12].

Lemma 4.

Assume that a dictionary $\mathcal{D}$ has coherence $\mu .$ Then, we have, for any distinct $g_i\in \mathcal{D},a_i\in \mathbb{R},i=1,2,\cdots ,s,$ the inequalities

$$(1-\mu (s-1))\sum _{i=1}^s{a}_i^2\le {\parallel \sum _{i=1}^s{a}_i{g}_i\parallel }^2\le (1+\mu (s-1))\sum _{i=1}^s{a}_i^2.$$

Theorem 7.

For any $1\le n\le Am,$ we have

$$\parallel P_L(f_n){\parallel }^2={\parallel \sum _{j=1}^m{a}_{j,n}{\psi }_j\parallel }^2\le 1.34D.$$

Proof. 

From Lemma 4, we know that

$$\begin{array}{cc}\hfill \parallel P_L(f_n){\parallel }^2& =\parallel \sum _{j=1}^m{a}_{j,n}{\psi }_j{\parallel }^2\le \sum _{j=1}^m{|a_{j,n}|}^2(1+m\mu ).\hfill \end{array}$$

(37)

From Lemmas 1 and 2, we have, for any $1\le l\le n+1,$

$$\begin{array}{cc}\hfill \underset{1\le j\le m}{max}|a_{j,n}|& \le k_1\underset{1\le j\le m}{max}|⟨f_n,{\psi }_j⟩|\le k_1\sum _{i\in I_{n+1}}|⟨f_n,g_i⟩|=k_1{d}_{n+1}\le k_1{k}_2{d}_l.\hfill \end{array}$$

Thus,

$$\begin{array}{c}\hfill \sum _{j=1}^m|a_{j,n}{|}^2\le m\underset{1\le j\le m}{max}{|a_{j,n}|}^2\le {(k_1{k}_2)}^2\sum _{i\in I_l\cap T_2\ne \varnothing }{d}_l^2\le {(k_1{k}_2)}^{2}D.\end{array}$$

(38)

Combining (37) with (38), we have

$$\begin{array}{cc}\hfill \parallel P_L(f_n){\parallel }^2& \le \sum _{j=1}^m{|a_{j,m}|}^2(1+m\mu )\le {(k_1{k}_2)}^{2}D\frac{19}{18}={(k_1{k}_2)}^2\frac{19}{18}D\le 1.34D.\hfill \end{array}$$

(39)

□

Next, using Theorems 5 and 6, we give the estimation of $D.$

Theorem 8.

For $A\ge 1$ and any positive integer $m,$ the following inequalities hold.

$$D^{\frac{1}{2}}\le 1.07(1+ϵ){\sigma }_m(f),\forall ϵ>0,$$

$$\parallel {\xi }_{Am}\parallel \le \parallel {\xi }_0\parallel .$$

Proof. 

From (3), we have

$$\parallel {\xi }_0{\parallel }^2=\parallel P_L^{\perp }{(f)\parallel }^2=\parallel f-P_L{(f)\parallel }^2\le {\parallel f-\sum _{j=1}^m{b}_j{\psi }_j\parallel }^2\le {(1+ϵ)}^2{\sigma }_m^2(f).$$

By using Theorems 5 and 6, we derive

$$\begin{array}{cc}\hfill {(1+ϵ)}^2{\sigma }_m^2(f)& \ge \parallel {\xi }_0{\parallel }^2\ge \parallel {\xi }_0{\parallel }^2-\parallel {\xi }_{Am}{\parallel }^2=\sum _{n=1}^{Am}(\parallel {\xi }_{n-1}{\parallel }^2-\parallel {\xi }_n{\parallel }^2)\hfill \\ & =\sum _{I_n\cap T_2=\varnothing }(\parallel {\xi }_{n-1}{\parallel }^2-\parallel {\xi }_n{\parallel }^2)+\sum _{I_n\cap T_2\ne \varnothing }(\parallel {\xi }_{n-1}{\parallel }^2-\parallel {\xi }_n{\parallel }^2)\hfill \\ & \ge \sum _{I_n\cap T_2=\varnothing }(-0.22D\mu )+\sum _{I_n\cap T_2\ne \varnothing }0.8937d_n^2\hfill \\ & \ge -0.22DAm\mu +0.8937D\hfill \\ & \ge -0.0123D+0.8937D\hfill \\ & =0.8814D>0,\hfill \end{array}$$

which is equivalent to

$$D^{\frac{1}{2}}\le {(0.8814)}^{-\frac{1}{2}}(1+ϵ){\sigma }_m(f)\le 1.07(1+ϵ){\sigma }_m(f).$$

Furthermore, we also have

$$\begin{array}{c}\hfill \parallel {\xi }_{Am}\parallel \le \parallel {\xi }_0\parallel .\end{array}$$

□

Now, we can give the proof of our main result.

Proof of Theorem 4.

Note that

$$\parallel f_{Am}\parallel =\parallel P_L(f_{Am})+{\xi }_{Am}\parallel \le \parallel P_L(f_{Am})\parallel +\parallel {\xi }_{Am}\parallel .$$

From Theorem 7 and Theorem 8, we obtain that

$$\begin{array}{cc}\hfill \parallel f_{Am}\parallel & \le \sqrt{1.34}{D}^{\frac{1}{2}}+\parallel {\xi }_0\parallel \hfill \\ & \le \sqrt{1.34}{D}^{\frac{1}{2}}+(1+ϵ){\sigma }_m(f)\hfill \\ & \le \sqrt{1.34}1.07(1+ϵ){\sigma }_m(f)+(1+ϵ){\sigma }_m(f)\hfill \\ & \le 2.24(1+ϵ){\sigma }_m(f).\hfill \end{array}$$

Thus, we complete the proof of Theorem 4. □

4. Simulation Results

It is known from Theorem 4 that if $f\in {\Sigma }_m$, then ${\sigma }_m(f)=0$, and hence $f=G_m(f)$. In this spirit, the OSGA can be used to recover sparse signals in compressed sensing, which is a new field of signal processing. We remark that in the field of signal processing, the orthogonal super greedy algorithm (OSGA) is also known as orthogonal multi-matching pursuit (OMMP). For the reader’s convenience, we will use the term OMMP instead of OSGA in what follows.

In this section, we test the performance of the orthogonal multi-matching pursuit with parameter s (OMMP(s)). We consider the following model. Suppose that $x\in {\mathbb{R}}^N$ is an unknown N-dimensional signal and we wish to recover it by the given data

$$y=\mathrm{\Phi }x,$$

(40)

where $\mathrm{\Phi }\in {\mathbb{R}}^{M\times N}$ is a known measurement matrix with $M\ll N$. Furthermore, since $M\ll N$, the column vectors of $\mathrm{\Phi }$ are linearly dependent and the collection of these columns can be viewed as a redundant dictionary.

For arbitrary $x,y\in {\mathbb{R}}^N$, define

$$\begin{array}{c}\hfill ⟨x,y⟩=\sum _{j=1}^N{x}_j{y}_j,\end{array}$$

and

$$\begin{array}{c}\hfill {\parallel x\parallel }_2={\left(\sum _{j=1}^N{|x_j|}^2\right)}^{1/2},\end{array}$$

where $x={(x_j)}_{j=1}^N$ and $y={(y_j)}_{j=1}^N.$ Obviously, ${\mathbb{R}}^N$ is a Hilbert space with the inner product $⟨·,·⟩$.

A signal $x\in {\mathbb{R}}^N$ is said to be K-sparse if ${\parallel x\parallel }_0:=\#\mathrm{supp}(x)=\#\{i:x_i\ne 0\}\le K<N$. We will recover the support of a K-sparse signal via OMMP(s) under the model (40). It is well known that OMMP takes the following form; see, for instance, [3].

ORTHOGONAL MULTI MATCHING PURSUIT (OMMP(s))

Input: Measurement matrix $\mathrm{\Phi }$, vector y, and s, the stopping criterion.

Step 1: Set the residual $r^0=y$, an initial approximation $x^0:=0$, the index set ${\mathrm{\Lambda }}^0:=\varnothing$, and the iteration counter $l=0$.

Step 2: Define ${\mathrm{\Lambda }}^{l+1}:={\mathrm{\Lambda }}^l\cup \{i_1,\cdots ,i_s\}$ such that

$$|⟨r^l,{\phi }_{i_1}⟩|\ge \cdots \ge |⟨r^l,{\phi }_{i_s}⟩|\ge \underset{\phi \in \mathrm{\Phi },\phi \ne {\phi }_{i_k},k=1,\cdots ,s}{sup}|⟨r^l,\phi ⟩|.$$

Then,

$$x^l:=\underset{z:\mathrm{supp}(z)\in {\mathrm{\Lambda }}^{l+1}}{argmin}{\parallel y-\mathrm{\Phi }z\parallel }_2$$

and update the residual

$$r^{l+1}:=y-\mathrm{\Phi }{x}^{l+1}.$$

End if the stopping condition is achieved. Otherwise, we set $l:=l+1$ and turn to step 2.

Output: If the algorithm stops at the kth iteration, then output ${\mathrm{\Lambda }}^k$ and ${\widehat{x}}_{{\mathrm{\Lambda }}^k}=x^k$.

In the experiment, we set the measurement matrix $\mathrm{\Phi }$ to be a Gaussian matrix where each entry is selected from the $\mathcal{N}(0,M^{-1})$ distribution and the density function of this distribution is $p(x):=\frac{1}{\sqrt{2\pi M}}{e}^{-x^{2}M/2}$. We execute OMMP(s) with the data vector $y=\mathrm{\Phi }x$ and stop the algorithm when $\#{\mathrm{\Lambda }}^l\ge K$. The mean square error(MSE) of x is defined as follows:

$$\begin{array}{c}\hfill \mathrm{MSE}=\frac{1}{N}\sum _{j=1}^N{(x_j-{\widehat{x}}_{{\mathrm{\Lambda }}_k,j})}^2.\end{array}$$

Figure 1 shows the performance of OMMP(s) with $s=5$ for an input signal in dimension $N=512$ with sparsity level $K=50$ and number of measurements $M=200$, where the red line represents the original signal and the black squares represent the approximation. By repeating the test 1000 times, we calculate the mean square error: MSE = $1.1894\times {10}^{-8}$.

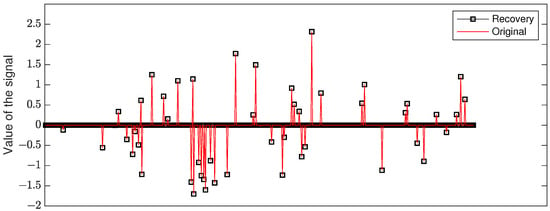
Figure 1. The recovery of an input signal in dimension $N=512$ with sparsity level $K=50$, number of measurements $M=200$ and $s=5$.

Figure 2 describes the case of the dimension $N=256$. It displays which percentage (the average of 100 input signals) of the elements in support can be found correctly as a function of M with $s=3$. If the percentage equals $100\%$, it means that all the elements in support can be found, which implies that the input signal can be exactly recovered. As expected, Figure 2 shows that when the sparsity level K increases, more measurements are necessary to guarantee signal recovery.

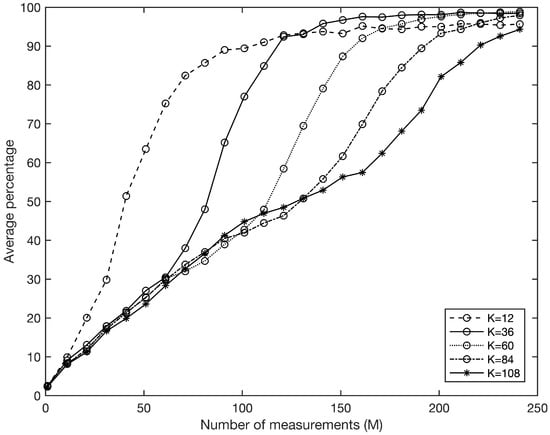
Figure 2. The average percentage of elements in support found correctly (100 input signals) as a function of the number of measurements M for different sparsity levels K in dimension $N=256$ with $s=3$.

5. Concluding Remarks

This paper investigates the error behavior of the orthogonal super greedy algorithm OSGA with respect to $\mu$-coherent dictionaries. The OSGA is simpler than the OGA from the viewpoint of the computational complexity. Under the assumption that the coherence parameter $\mu$ has a lower bound, we establish the ideal Lebesgue-type inequality for the OSGA, which shows that the OSGA provides an almost optimal approximation on the first $[1/(18\mathsf{\mu }\mathrm{s})]$ steps. Moreover, we improve the asymptotic constant in the Lebesgue-type inequality of the OGA obtained in [19]. We develop some new techniques to obtain our results. We found that there exists a strong dependency between the constant A and the coherence parameter $\mu$ in (2). The specific constant 2.24 is not the best; we can change it by adjusting the values of A and $\mu ,$ but the best one is still unknown. In fact, we do not even know if such a constant exists. We will continue to study the improvement of the Lebesgue constant in our future work. As for the applications of the OSGA, our simulation results show that OSGA is very efficient for recovering sparse signals.